Cross-Scale Simulation Study of Porous Medium Heat Exchangers Based on Reliable Cell Selection
Abstract
1. Introduction
2. Experimentation and Simulation
2.1. Model
2.1.1. The Cell Unit Model
2.1.2. Heat Exchangers
2.2. Numerical Simulation
2.2.1. Physical Modeling and Boundary Conditions
2.2.2. Governing Equations
2.2.3. FloEFD Porous Media Replacement Model
2.3. Data Reduction
3. Results and Discussions
3.1. Simulation Validation of the Cell Unit Model
3.2. Heat Transfer and Pressure Drop of the Cell Unit Model
3.2.1. Flow Resistance Characteristics
3.2.2. Heat Transfer Characteristics
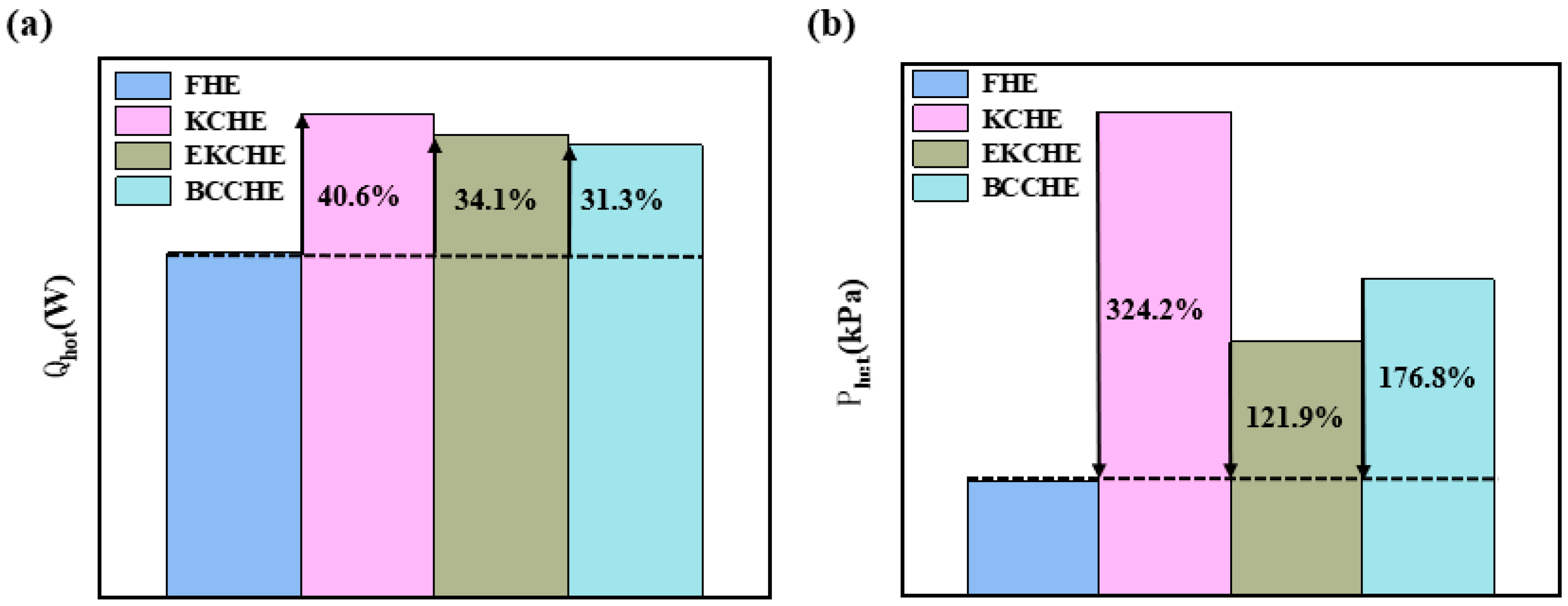
3.3. Heat Transfer and Pressure Drop of the Heat Exchanger
3.4. Comprehensive Performance Comparison and Verification
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Dixit, T.; Ghosh, I. An experimental study on open cell metal foam as extended heat transfer surface. Exp. Therm. Fluid Sci. 2016, 77, 28–37. [Google Scholar] [CrossRef]
- Liu, H.; Yu, Q.N.; Qu, Z.G.; Yang, R. Simulation and analytical validation of forced convection inside open cell metal foams. Int. J. Therm. Sci. 2017, 111, 234–245. [Google Scholar] [CrossRef]
- Fiedler, T.; Movahedi, N. Compact Aluminium Foam Heat Exchangers. Metals 2023, 13, 1440. [Google Scholar] [CrossRef]
- Sulong, M.A.; Ahmad, N.H.; Öchsner, A. Numerical Simulation of the Mechanical Properties of Syntactic Perforated Hollow Sphere Structures. In Proceedings of the 7th International Conference on Porous Metals and Metal Foams 2011, Busan, Republic of Korea, 18–21 September 2011. [Google Scholar]
- Li, Y.T.; Gong, L.; Xu, M.H.; Joshi, Y. Thermal Performance of Metal Foam Heat Sink with Pin Fins for Non-Uniform Heat Flux Electronics Cooling. In Proceedings of the 2019 35th Annual Semiconductor Thermal Measurement, Modeling and Management Symposium (SEMI-THERM), San Jose, CA, USA, 18–22 March 2019; pp. 30–37. [Google Scholar]
- Mahalle, A.M.; Jajoo, B.N. An approach for modeling and simulation of sintered Bronze foam sink for high heat dissipation. Appl. Therm. Eng. 2013, 51, 899–907. [Google Scholar] [CrossRef]
- Chen, A.; Gu, S.; Bennacer, R.; Liu, B. Study on Characteristics of Heat Transfer and Flow Resistance in Random Porous Foam Metal. In Proceedings of the XII International Conference on Computational Heat, Mass and Momentum Transfer (ICCHMT 2019), Rome, Italy, 3–6 September 2019; Mohamad, A., Taler, J., Benim, A.C., Bennacer, R., Suh, S.-H., de Lieto Vollaro, R., Vallati, A., Battista, G., Eds.; EDP Sciences: Les Ulis, France, 2019; p. 128. [Google Scholar]
- Ranut, P. On the effective thermal conductivity of aluminum metal foams: Review and improvement of the available empirical and analytical models. Appl. Therm. Eng. 2016, 101, 496–524. [Google Scholar] [CrossRef]
- Vishkaei, M.Y.; Javaherdeh, K. Experimental investigation of the effects of metal foam porous rings on non-Newtonian fluid flow in a double pipe heat exchanger. Int. Commun. Heat MASS Transf. 2024, 158, 107950. [Google Scholar] [CrossRef]
- T’joen, C.; De Jaeger, P.; Huisseune, H.; De Paepe, M. Thermo-Hydraulic Performance of a Heat Exchanger Consisting of Metal Foam Covered Tubes. In Proceedings of the ASME International Heat Transfer Conference—2010, Vol 4: Heat Transfer Measurement Techniques, Heat Transfer Equipment, Thermoelectrics, Washington, DC, USA, 8–13 August 2010; pp. 361–370. [Google Scholar]
- Zaib, F.; Ganesan, P.; Zaharinie, T.; Chen, Z.; Naganthran, K. Heat transfer performance of a compact heat exchanger based on metal foam and Thermal Interface Material (TIM). Int. J. Heat Mass Transf. 2024, 231, 125861. [Google Scholar] [CrossRef]
- Wang, W.; Guo, J.; Zhang, S.; Yang, J.; Ding, X.; Zhan, X. Numerical study on hydrodynamic characteristics of plate-fin heat exchanger using porous media approach. Comput. Chem. Eng. 2014, 61, 30–37. [Google Scholar] [CrossRef]
- Haider, P.; Freko, P.; Acher, T.; Rehfeldt, S.; Klein, H. Influence of inlet configuration and distributor geometry on the performance of cryogenic plate-fin heat exchangers. Appl. Therm. Eng. 2021, 195, 117197. [Google Scholar] [CrossRef]
- Chung, S.S.; Kim, N.; Jo, H. Effect of flow distribution on heat transfer in Printed Circuit Heat Exchangers using conjugate heat transfer model with a modified porous media approach. Appl. Therm. Eng. 2025, 266, 125540. [Google Scholar] [CrossRef]
- Schaedler, T.A.; Carter, W.B. Architected Cellular Materials. Annu. Rev. Mater. Res. 2016, 46, 187–210. [Google Scholar] [CrossRef]
- Xu, J.J.; Gao, Y.; Huang, H.; Yang, Q.; Guo, L.; Jiang, L. Diamond-structured hollow-tube lattice Ni materials via 3D printing. Sci. China-Chem. 2016, 59, 1632–1637. [Google Scholar] [CrossRef]
- Ho, J.Y.; Leong, K.C. Cylindrical porous inserts for enhancing the thermal and hydraulic performance of water-cooled cold plates. Appl. Therm. Eng. 2017, 121, 863–878. [Google Scholar] [CrossRef]
- Baishya, M.J.; Muthu, N.; Khanikar, P. In pursuit of a high-performance mechanical metamaterial: Simple-cubic-octahedral plate lattice. Int. J. Mech. Sci. 2024, 272, 109189. [Google Scholar] [CrossRef]
- Dhavale, A.A.; Lele, M.M. Numerical investigations on the impact of metallic foam configurations on heat transfer in double tube heat exchanger: A parametric approach. Numer. Heat Transf. Part A-Appl. 2024, 1–53. [Google Scholar] [CrossRef]
- Mishra, A.; Korba, D.; Kaur, I.; Singh, P.; Li, L. Prediction and Validation of Flow Properties in Porous Lattice Structures. J. Fluids Eng.-Trans. ASME 2023, 145, 0414024. [Google Scholar] [CrossRef]
- Buonomo, B.; di Pasqua, A.; Manca, O.; Sekrani, G.; Poncet, S. Numerical Analysis on Pressure Drop and Heat Transfer in Nanofluids at Pore Length Scale in Open Metal Porous Structures with Kelvin Cells. Heat Transf. Eng. 2021, 42, 1614–1624. [Google Scholar] [CrossRef]
- Calati, M.; De Monte, E.; Mancin, S. Numerical analysis of the effects of the structure shape and orientation of kelvin cell porous structures during air forced convection. Appl. Sci. 2021, 11, 6189. [Google Scholar] [CrossRef]
- Iasiello, M.; Bianco, N.; Chiu, W.; Naso, V. Anisotropy effects on convective heat transfer and pressure drop in Kelvin’s open-cell foams. In Proceedings of the 35th Italian-Union-of-Thermp-Fluid Dynamics (UIT) Heat Transfer Conference (UIT2017), Ancona, Italy, 26–28 June 2017; Ricci, R., DAlessandro, V., Eds.; IOP Science: Bristol, UK, 2017; p. 923. [Google Scholar]
- Sun, M.; Zhang, L.; Hu, C.; Zhao, J.; Tang, D.; Song, Y. Forced convective heat transfer in optimized kelvin cells to enhance overall performance. Energy 2022, 242, 122995. [Google Scholar] [CrossRef]
- Sun, M.R.; Yang, L.; Hu, C.Z.; Zhao, J.; Tang, D.; Song, Y. Simulation of forced convective heat transfer in Kelvin cells with optimized skeletons. Int. J. Heat Mass Transf. 2021, 165, 120637. [Google Scholar] [CrossRef]
- Shi, X.H.; Wang, L.X.; Chen, W.; Li, Z.; Chai, X.; Chyu, M.K. Effect of induced vortex and configuration layout on heat transfer enhancement of helium-xenon mixture. Appl. Therm. Eng. 2023, 225, 120168. [Google Scholar] [CrossRef]
- Corbett, T.M.; Thole, K.A. Large eddy simulations of kagome and body centered cubic lattice cells. Int. J. Heat Mass Transf. 2024, 218, 124808. [Google Scholar] [CrossRef]
- Najafi, H.; Najafi, B.; Hoseinpoori, P. Energy and cost optimization of a plate and fin heat exchanger using genetic algorithm. Appl. Therm. Eng. 2011, 31, 1839–1847. [Google Scholar] [CrossRef]
- Collins, I.L.; Weibel, J.A.; Pan, L.; Garimella, S.V. Evaluation of additively manufactured microchannel heat sinks. IEEE Trans. Compon. Packag. Manuf. Technol. 2018, 9, 446–457. [Google Scholar] [CrossRef]
- Schlegel, A.; Benz, P.; Buser, S. Wärmeübertragung und Druckabfall in keramischen Schaumstrukturen bei erzwungener Strömung. Heat Mass Transf. 1993, 28, 259–266. [Google Scholar] [CrossRef]
- Yang, Y.J.; Li, Y.Z.; Si, B.; Zheng, J.; Kang, R. Analysis of the Fin Performance of Offset Strip Fins Used in Plate-Fin Heat Exchangers. J. Heat Transf.-Trans. ASME 2016, 138, 101801. [Google Scholar] [CrossRef]
- Zhang, Z.D.; Yan, G.H.; Sun, M.R.; Li, S.; Zhang, X.; Song, Y.; Liu, Y. Forced convective heat transfer performance of foam-like structures-comparison of the Weaire-Phelan and the Kelvin structures with real metal foam. Int. J. Heat Mass Transf. 2024, 227, 125558. [Google Scholar] [CrossRef]
- Sheng, L.; Su, L.; Zhang, H.; Li, K.; Fang, Y.; Ye, W.; Fang, Y. Numerical investigation on a lithium ion battery thermal management utilizing a serpentine-channel liquid cooling plate exchanger. Int. J. Heat Mass Transf. 2019, 141, 658–668. [Google Scholar] [CrossRef]
- He, Y.L.; Jiang, T.; Du, S.; Xu, G. Research progress on performance boundary of air heat exchanger within flight envelope. Chin. J. Aeronaut. 2025, 46, 61–72. [Google Scholar]
- Dukhan, N.; Bagci, Ö.; Özdemir, M. Metal foam hydrodynamics: Flow regimes from pre-Darcy to turbulent. Int. J. Heat Mass Transf. 2014, 77, 114–123. [Google Scholar] [CrossRef]
- Zhang, Z.D.; Yan, G.H.; Sun, M.R.; Yan, H.; Zhao, J.; Song, Y.; Liu, Y. Pore-scale simulation of forced convection heat transfer in metal foams with uniform and gradient structures. Appl. Therm. Eng. 2023, 225, 120074. [Google Scholar] [CrossRef]
- Zhang, J.H.; Kundu, J.; Manglik, R.M. Effect of fin waviness and spacing on the lateral vortex structure and laminar heat transfer in wavy-plate-fin cores. Int. J. Heat Mass Transf. 2004, 47, 1719–1730. [Google Scholar] [CrossRef]
- Sun, M.R.; Yan, G.H.; Hu, C.Z.; Zhao, J.; Duan, F.; Song, Y. Thermal and hydraulic behaviours of Kelvin cells from metallic three-dimensional printing. Appl. Therm. Eng. 2023, 219, 119433. [Google Scholar] [CrossRef]













| Model | ds (mm) | a (mm) | b (mm) | SV (m2/m3) | |
|---|---|---|---|---|---|
| KCs | 0.8498 | 0.417 | 2.5 | 2.5 | 1867.14 |
| EKCs | 0.8499 | 0.497 | 2.5 | 5 | 1568.18 |
| BCCs | 0.8493 | 0.455 | 2.5 | 2.5 | 1339.25 |
| n (106) | ΔT (°C) | Difference | ΔP (kPa) | Difference | |
|---|---|---|---|---|---|
| Case1 | 3.2 | 20.16 | 15.20% | 8.99 | 3.54% |
| Case2 | 4.3 | 19.10 | 9.13% | 9.01 | 3.33% |
| Case3 | 5.8 | 17.77 | 1.54% | 9.28 | 0.43% |
| Case4 | 8.1 | 17.50 | - | 9.32 | - |
| Parameter | Value | |
|---|---|---|
| Hot side | (kg/s) | 0.12 |
| (K) | 460 | |
| (kPa) | 460 | |
| Cold side | (kg/s) | 0.24 |
| (K) | 330 | |
| (kPa) | 190 | |
| Material | ρ (kg/m3) | Cp (kJ/kg·K) | λs (W/m·K) |
|---|---|---|---|
| GH3625 | 8440 | 430 | 12.1 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liang, Y.; Zhang, J.; Liu, Y.; Sun, M.; Song, Y. Cross-Scale Simulation Study of Porous Medium Heat Exchangers Based on Reliable Cell Selection. Energies 2025, 18, 3510. https://doi.org/10.3390/en18133510
Liang Y, Zhang J, Liu Y, Sun M, Song Y. Cross-Scale Simulation Study of Porous Medium Heat Exchangers Based on Reliable Cell Selection. Energies. 2025; 18(13):3510. https://doi.org/10.3390/en18133510
Chicago/Turabian StyleLiang, Yiqiang, Jun Zhang, Yu Liu, Mingrui Sun, and Yongchen Song. 2025. "Cross-Scale Simulation Study of Porous Medium Heat Exchangers Based on Reliable Cell Selection" Energies 18, no. 13: 3510. https://doi.org/10.3390/en18133510
APA StyleLiang, Y., Zhang, J., Liu, Y., Sun, M., & Song, Y. (2025). Cross-Scale Simulation Study of Porous Medium Heat Exchangers Based on Reliable Cell Selection. Energies, 18(13), 3510. https://doi.org/10.3390/en18133510






