Transient Stability Enhancement of Virtual Synchronous Generator Through Analogical Phase Portrait Analysis
Abstract
1. Introduction
2. Modeling of Grid-Connected VSG and Pendulum
2.1. Modeling of a Grid-Connected VSG
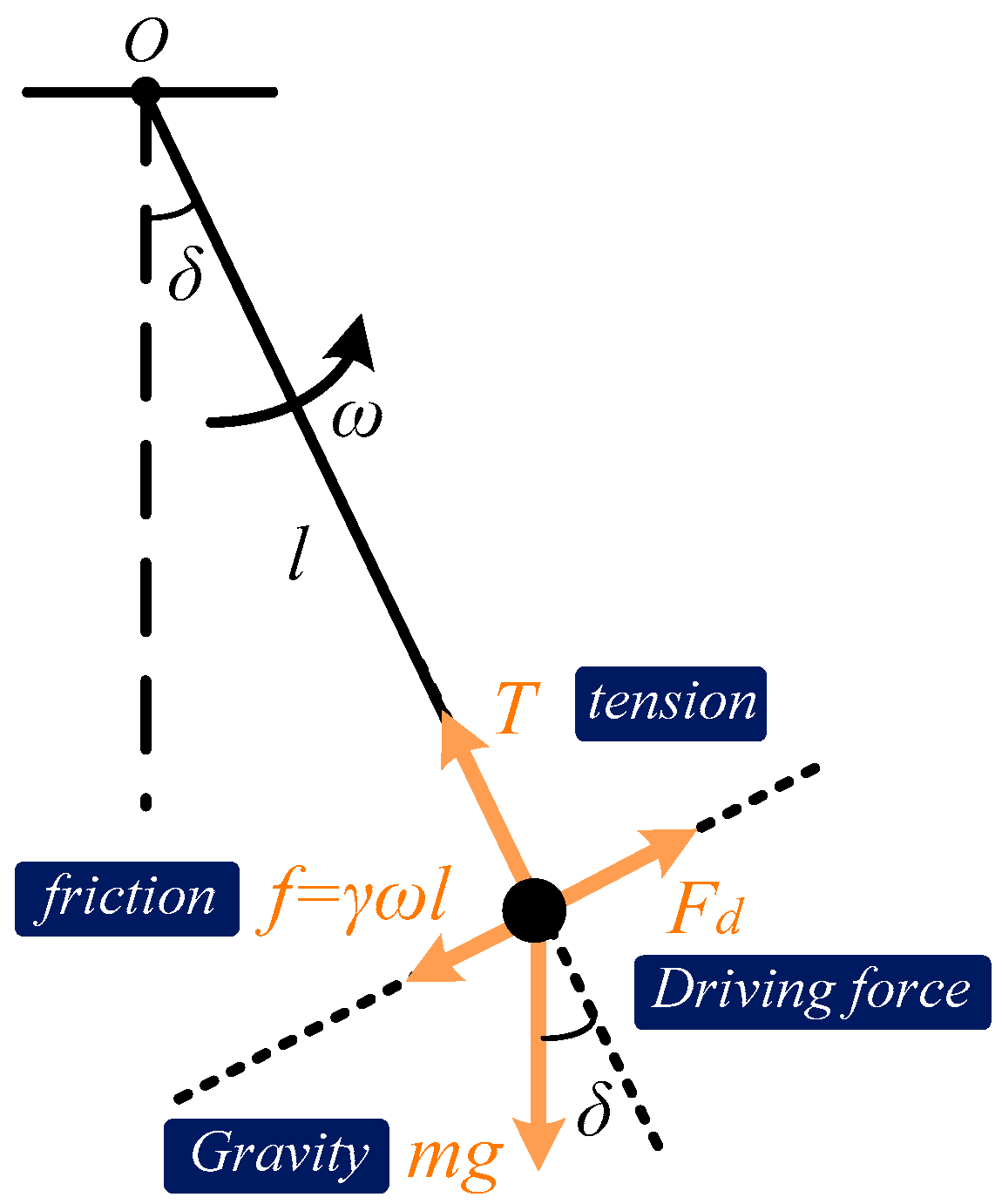
2.2. Modeling of a Simple Pendulum
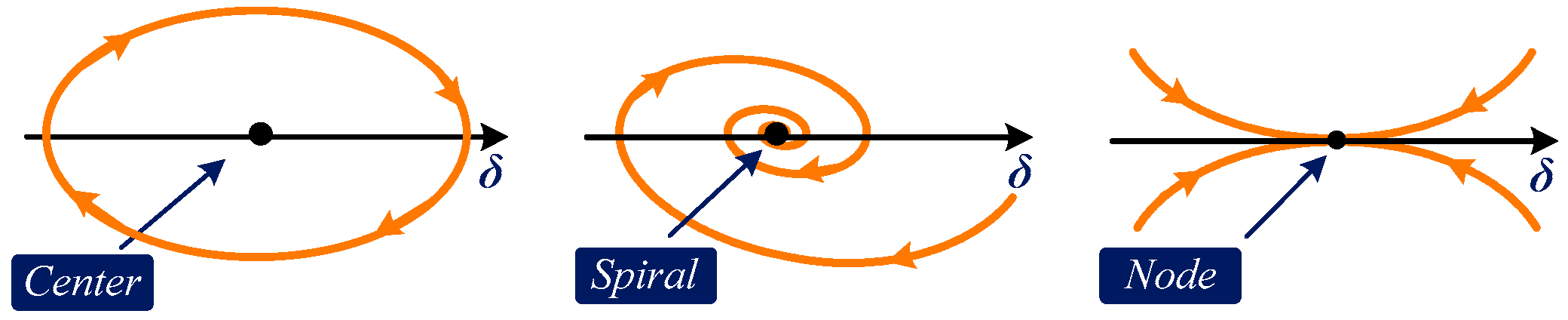
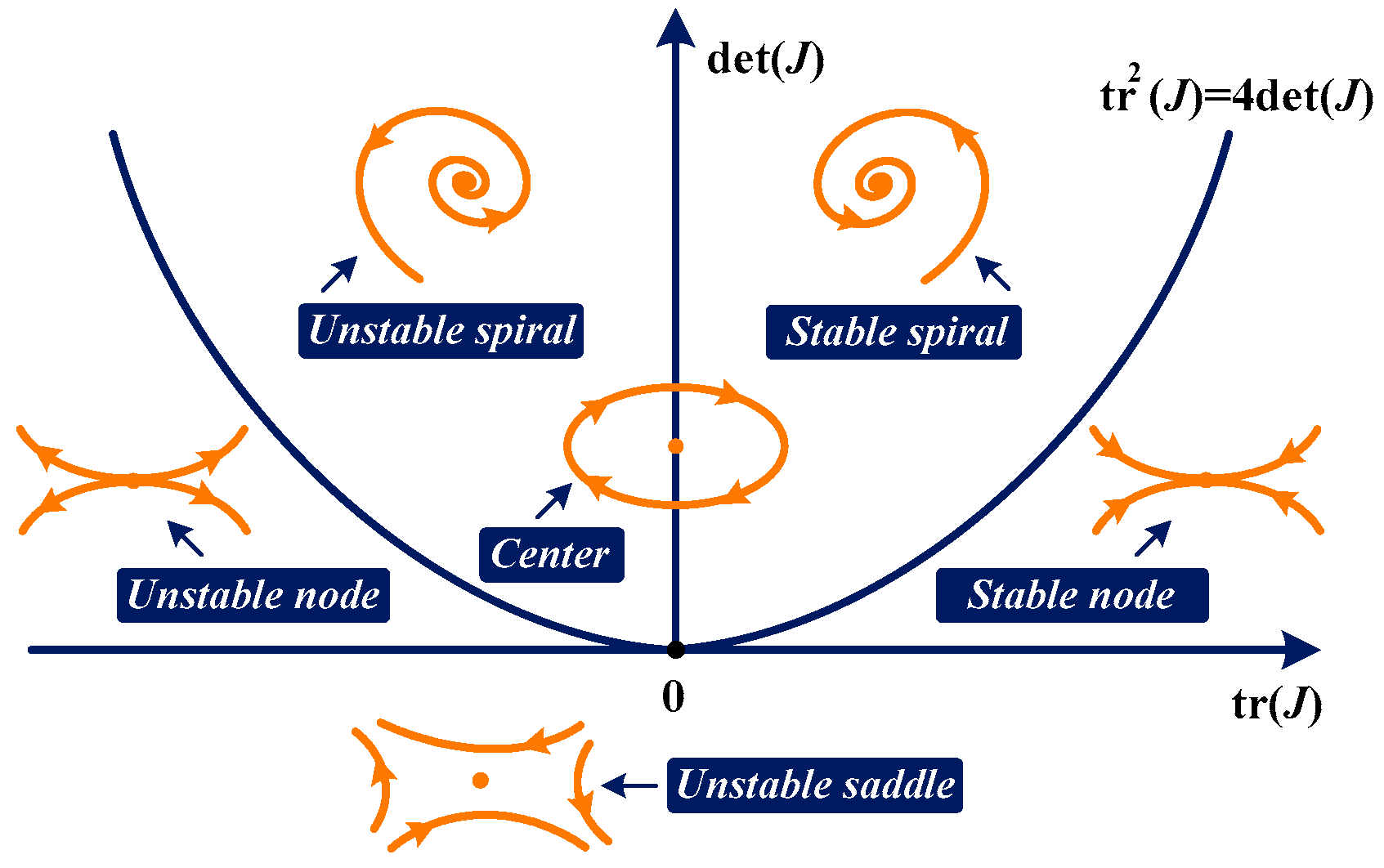
3. Preliminaries on Pendulum Phase Portrait
4. Transient Stability of a Grid-Connected VSG
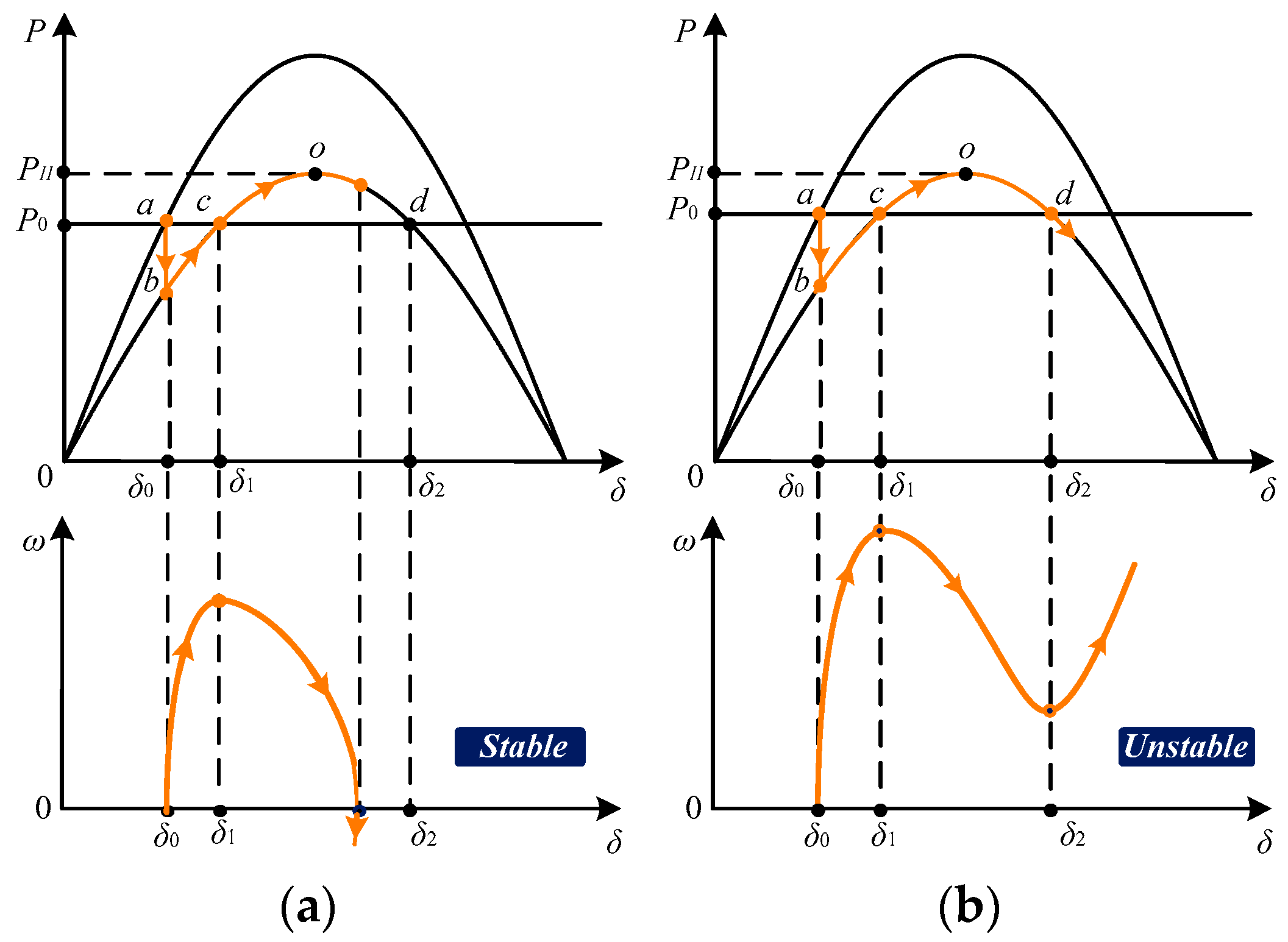
4.1. Transient Stability Without the Damping Effect
4.2. Transient Stability with the Damping Effect
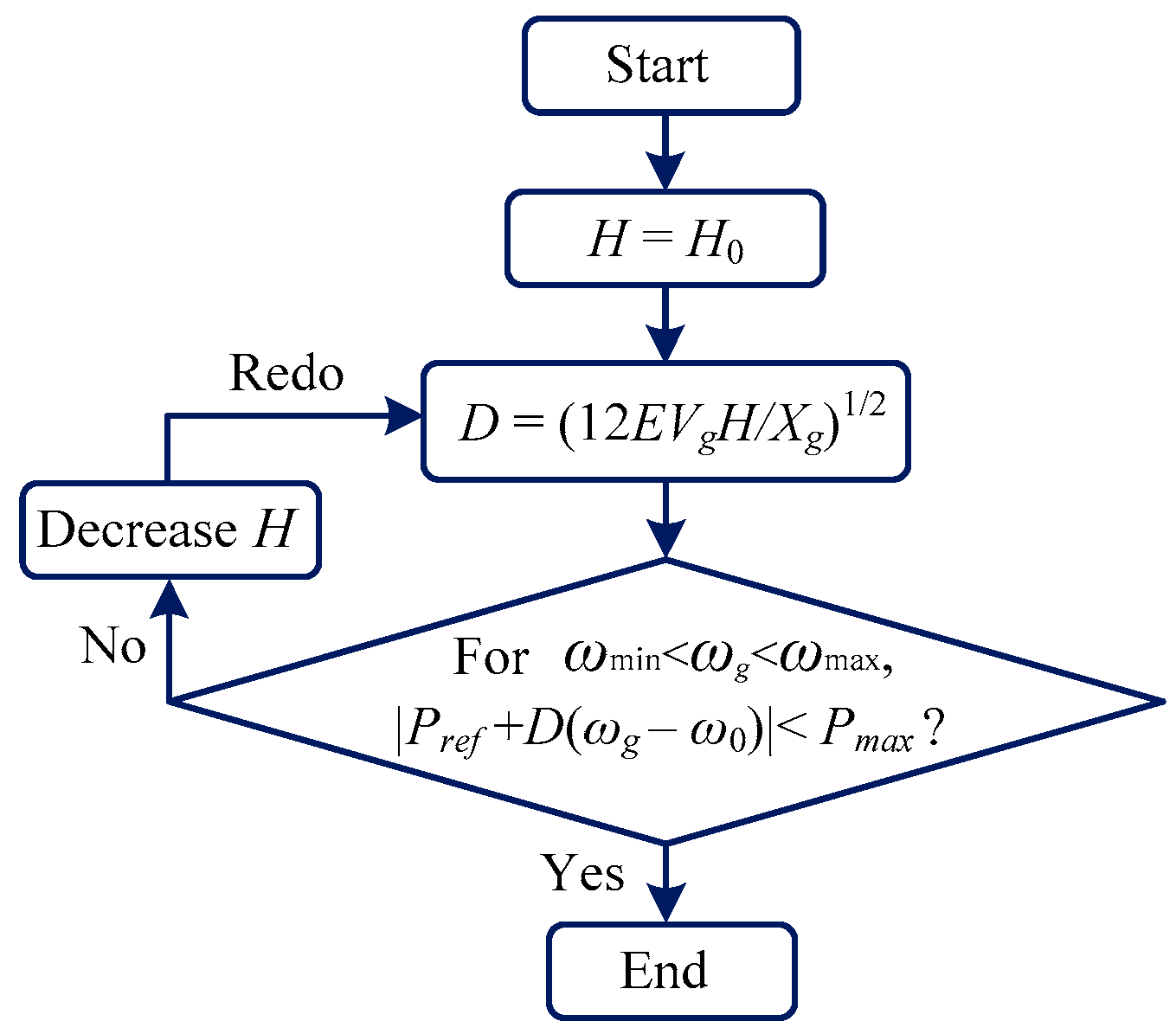
4.3. Parameter Design Procedure
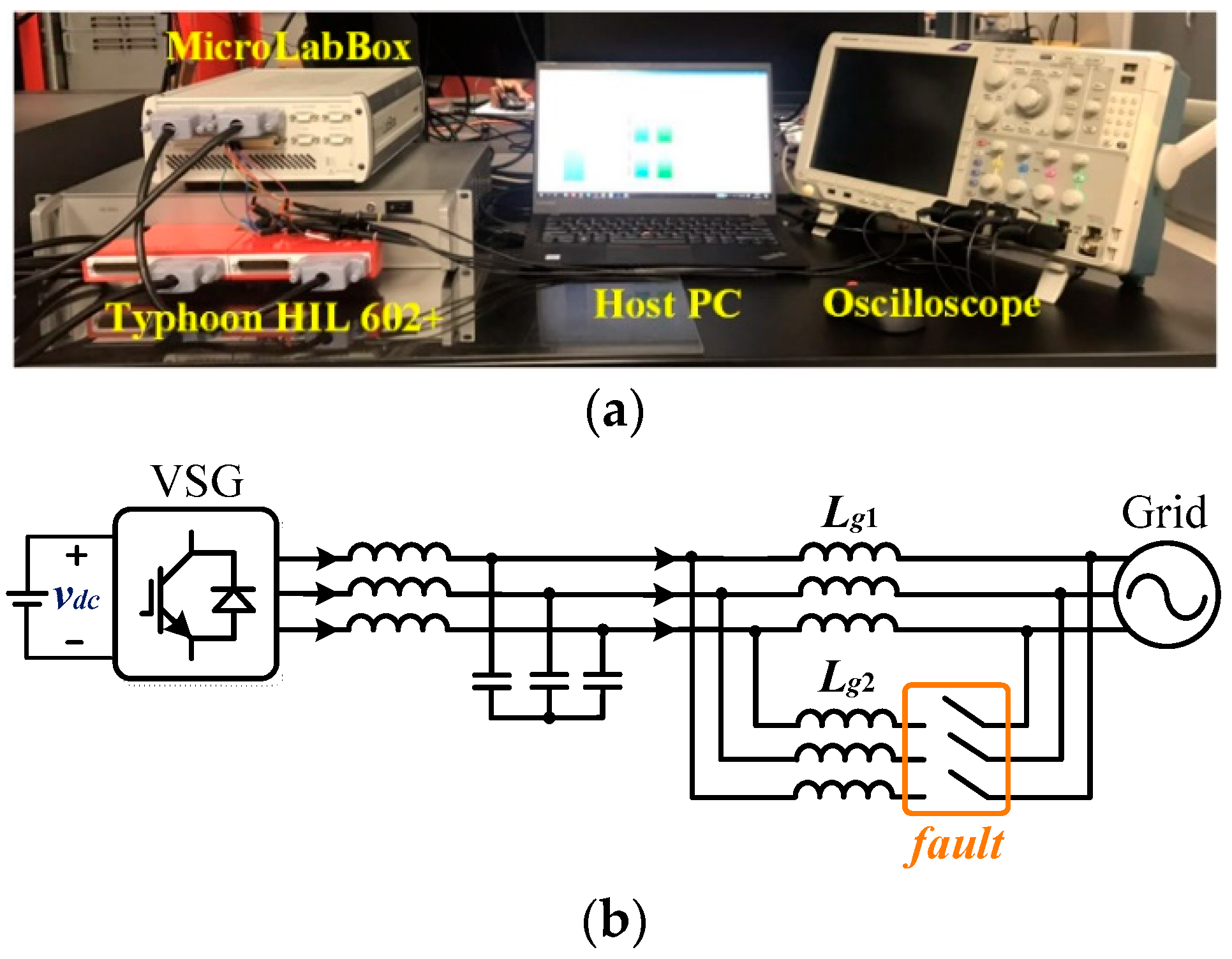
5. Hardware-in-Loop Simulation Results
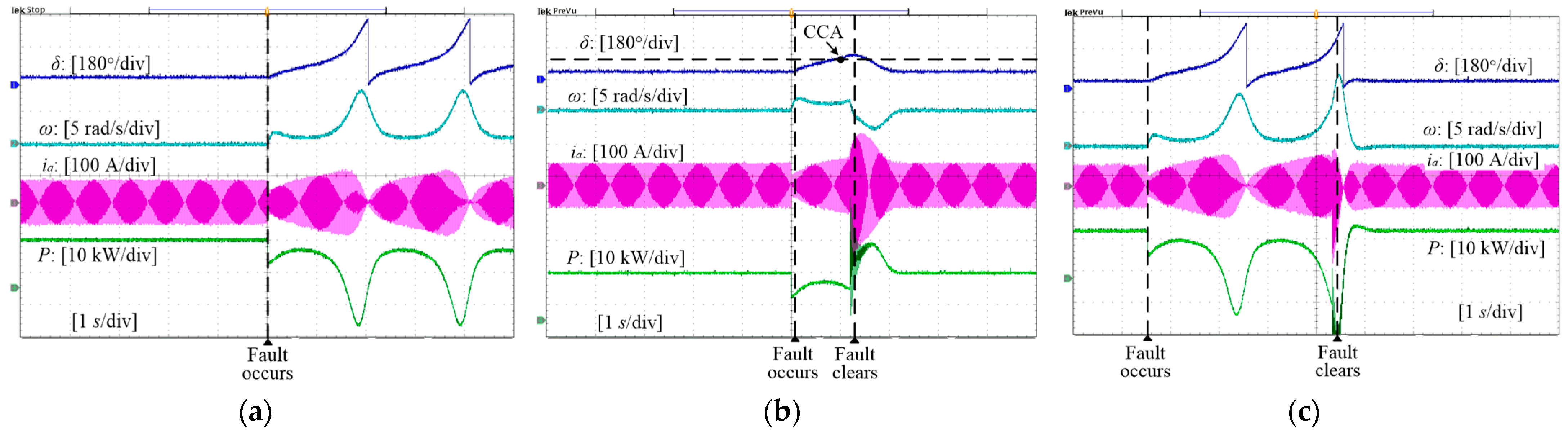
5.1. VSG Responses with Post-Fault Equilibrium
5.2. VSG Responses Without Post-Fault Equilibrium
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Fang, J.; Li, H.; Tang, Y.; Blaabjerg, F. On the Inertia of Future More-Electronics Power Systems. IEEE J. Emerg. Sel. Top. Power Electron. 2019, 7, 2130–2146. [Google Scholar] [CrossRef]
- Huang, Y.; Wang, Y.; Li, C.; Zhao, H.; Wu, Q. Physics Insight of the Inertia of Power Systems and Methods to Provide Inertial Response. CSEE J. Power Energy Syst. 2022, 8, 559–568. [Google Scholar]
- Hatziargyriou, N.; Milanovic, J.; Rahmann, C.; Ajjarapu, V.; Canizares, C.; Erlich, I.; Hill, D.; Hiskens, I.; Kamwa, I.; Pal, B.; et al. Definition and classification of power system stability—Revisited & extended. IEEE Trans. Power Syst. 2021, 36, 3271–3281. [Google Scholar] [CrossRef]
- Rathnayake, D.B.; Razzaghi, R.; Bahrani, B. Generalized Virtual Synchronous Generator Control Design for Renewable Power Systems. IEEE Trans. Sustain. Energy 2022, 13, 1021–1036. [Google Scholar] [CrossRef]
- Driesen, J.; Visscher, K. Virtual Synchronous Generators. In Proceedings of the IEEE PES General Meeting, Pittsburgh, PA, USA, 20–24 July 2008; pp. 1–3. [Google Scholar]
- Liu, J.; Hou, Y.; Guo, J.; Liu, X.; Liu, J. A Cost-Efficient Virtual Synchronous Generator System Based on Coordinated Photovoltaic and Supercapacitor. IEEE Trans. Power Electron. 2023, 38, 16219–16229. [Google Scholar] [CrossRef]
- Li, C.; Yang, Y.; Cao, Y.; Wang, L.; Dragicevic, T.; Blaabjerg, F. Frequency and Voltage Stability Analysis of Grid-Forming Virtual Synchronous Generator Attached to Weak Grid. IEEE J. Emerg. Sel. Top. Power Electron. 2022, 10, 2662–2671. [Google Scholar] [CrossRef]
- Meng, X.; Liu, J.; Liu, Z. A Generalized Droop Control for Grid-Supporting Inverter Based on Comparison Between Traditional Droop Control and Virtual Synchronous Generator Control. IEEE Trans. Power Electron. 2019, 34, 5416–5438. [Google Scholar] [CrossRef]
- Wu, H.; Ruan, X.; Yang, D.; Chen, X.; Zhao, W.; Lv, Z.; Zhong, Q.-C. Small-Signal Modeling and Parameters Design for Virtual Synchronous Generators. IEEE Trans. Ind. Electron. 2016, 63, 4292–4303. [Google Scholar] [CrossRef]
- Roldan-Perez, J.; Rodriguez-Cabero, A.; Prodanovic, M. Design and Analysis of Virtual Synchronous Machines in Inductive and Resistive Weak Grids. IEEE Trans. Energy Convers. 2019, 34, 1818–1828. [Google Scholar] [CrossRef]
- Chen, J.; Donnell, T. Parameter Constraints for Virtual Synchronous Generator Considering Stability. IEEE Trans. Power Syst. 2019, 34, 2479–2481. [Google Scholar] [CrossRef]
- Huang, L.; Xin, H.; Wang, Z. Damping Low-Frequency Oscillations Through VSC-HVdc Stations Operated as Virtual Synchronous Machines. IEEE Trans. Power Electron. 2019, 34, 5803–5818. [Google Scholar] [CrossRef]
- Hirase, Y.; Sugimoto, K.; Sakimoto, K.; Ise, T. Analysis of Resonance in Microgrids and Effects of System Frequency Stabilization Using a Virtual Synchronous Generator. IEEE J. Emerg. Sel. Top. Power Electron. 2016, 4, 1287–1298. [Google Scholar] [CrossRef]
- Ambia, M.N.; Meng, K.; Xiao, W.; Al-Durra, A.; Dong, Z.Y. Interactive Grid Synchronization-Based Virtual Synchronous Generator Control Scheme on Weak Grid Integration. IEEE Trans. Smart Grid 2022, 13, 4057–4071. [Google Scholar] [CrossRef]
- Huang, L.; Xin, H.; Yang, H.; Wang, Z.; Xie, H. Interconnecting Very Weak AC Systems by Multiterminal VSC-HVDC Links with a Unified Virtual Synchronous Control. IEEE J. Emerg. Sel. Top. Power Electron. 2018, 6, 1041–1053. [Google Scholar] [CrossRef]
- Khajehoddin, S.A.; Karimi-Ghartemani, M.; Ebrahimi, M. Grid-Supporting Inverters with Improved Dynamics. IEEE Trans. Ind. Electron. 2019, 66, 3655–3667. [Google Scholar] [CrossRef]
- Tang, C.K.; Graham, C.E.; El-Kady, M.; Alden, R.T.H. Transient stability index from conventional time domain simulation. IEEE Trans. Power Syst. 1994, 9, 1524–1530. [Google Scholar] [CrossRef]
- Kundur, P. Power System Stability and Control; McGraw-Hill: New York, NY, USA, 1994. [Google Scholar]
- Yorino, N.; Priyadi, A.; Kakui, H.; Takeshita, M. A New Method for Obtaining Critical Clearing Time for Transient Stability. IEEE Trans. Power Syst. 2010, 25, 1620–1626. [Google Scholar] [CrossRef]
- Hou, X.; Sun, Y.; Zhang, X.; Lu, J.; Wang, P.; Guerrero, J.M. Improvement of Frequency Regulation in VSG-Based AC Microgrid Via Adaptive Virtual Inertia. IEEE Trans. Power Electron. 2020, 35, 1589–1602. [Google Scholar] [CrossRef]
- Li, D.; Zhu, Q.; Lin, S.; Bian, X.Y. A Self-Adaptive Inertia and Damping Combination Control of VSG to Support Frequency Stability. IEEE Trans. Energy Convers. 2017, 32, 397–398. [Google Scholar] [CrossRef]
- Chang, G.W.; Nguyen, K.T. A New Adaptive Inertia-Based Virtual Synchronous Generator with Even Inverter Output Power Sharing in Islanded Microgrid. IEEE Trans. Ind. Electron. 2024, 71, 10693–10703. [Google Scholar] [CrossRef]
- Xue, Y.; Van Custem, T.; Ribbens-Pavella, M. Extended equal area criterion justifications, generalizations, applications. IEEE Trans. Power Syst. 1989, 4, 44–52. [Google Scholar] [CrossRef]
- Li, R.; Yan, X.; Wang, Y.; Zhang, Q.; Chen, Z. Improved Transient Modeling and Stability Analysis for Grid-Following Wind Turbine: Third-Order Sequence Mapping EAC. IEEE Trans. Power Deliv. 2024, 39, 2015–2027. [Google Scholar] [CrossRef]
- Tang, Y.; Tian, Z.; Zha, X.; Li, X.; Huang, M.; Sun, J. An Improved Equal Area Criterion for Transient Stability Analysis of Converter-Based Microgrid Considering Nonlinear Damping Effect. IEEE Trans. Power Electron. 2022, 37, 11272–11284. [Google Scholar] [CrossRef]
- Paudyal, S.; Ramakrishna, G.; Sachdev, M.S. Application of Equal Area Criterion Conditions in the Time Domain for Out-of-Step Protection. IEEE Trans. Power Deliv. 2010, 25, 600–609. [Google Scholar] [CrossRef]
- Tedrake, R. Underactuated Robotics: Learning, Planning, and Control for Efficient and Agile Machines; Massachusetts Institute of Technology: Cambridge, MA, USA, 2019. [Google Scholar]
- Wu, H.; Wang, X. Design-Oriented Transient Stability Analysis of Grid-Connected Converters with Power Synchronization Control. IEEE Trans. Ind. Electron. 2019, 66, 6473–6482. [Google Scholar] [CrossRef]
- Wu, J.; Ren, S.; Zhu, M.; Wang, Z.; Wang, R.; Qi, Y. Transient Stability Analysis of Virtual Synchronous Machine Considering the Damping Effect. In Proceedings of the 2024 IEEE 7th International Electrical and Energy Conference (CIEEC), Harbin, China, 10–12 May 2024; pp. 2653–2658. [Google Scholar]
- Li, Y.; Liu, J.; Liu, Y.; Yang, S.; Du, Z. Transient stability analysis of virtual synchronous generator with current saturation by multiple Lyapunov functions method. IET Gener. Transm. Distrib. 2024, 18, 1014–1025. [Google Scholar] [CrossRef]
- Shuai, Z.; Shen, C.; Liu, X.; Li, Z.; Shen, Z.J. Transient Angle Stability of Virtual Synchronous Generators Using Lyapunov’s Direct Method. IEEE Trans. Smart Grid 2019, 10, 4648–4661. [Google Scholar] [CrossRef]
- Qi, Y.; Deng, H.; Fang, J.; Tang, Y. Synchronization Stability Analysis of Grid-Forming Inverter: A Black Box Methodology. IEEE Trans. Ind. Electron. 2022, 69, 13069–13078. [Google Scholar] [CrossRef]



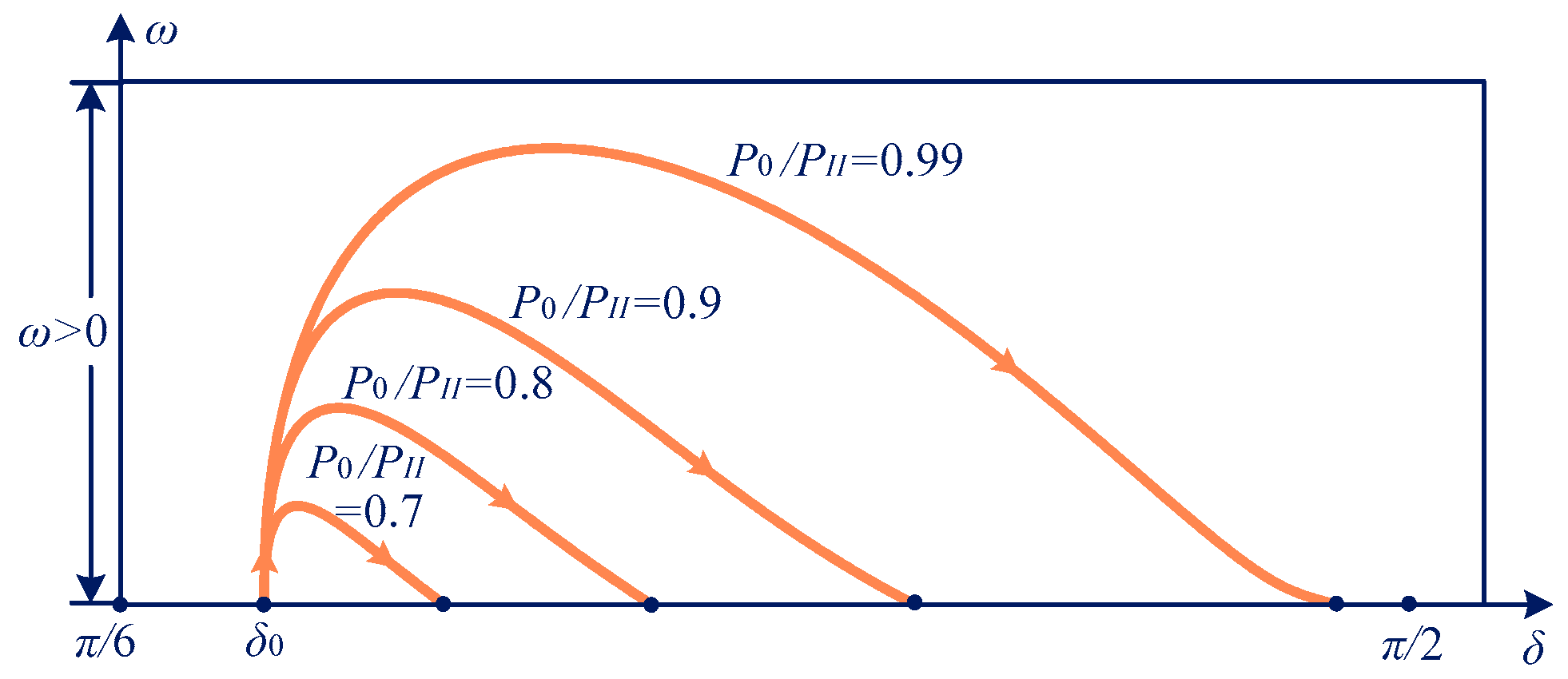


| Parameters | Descriptions | Values |
|---|---|---|
| Vg, E0 | Nominal voltage magnitude | 155 V |
| ω0 | Nominal grid frequency | 50 Hz |
| H | VSG inertia coefficient | 100 |
| D | VSG damping coefficient | 3050 s·W |
| Pref | VSG nominal power at ω0 | 2 kW |
| Lg1, Lg2 | Line impedances | 20 mH |
| PII | Post-fault active power limit | 11.56 kW |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, S.; Wu, J.; Zhong, H.; Qi, Y. Transient Stability Enhancement of Virtual Synchronous Generator Through Analogical Phase Portrait Analysis. Energies 2025, 18, 3495. https://doi.org/10.3390/en18133495
Wu S, Wu J, Zhong H, Qi Y. Transient Stability Enhancement of Virtual Synchronous Generator Through Analogical Phase Portrait Analysis. Energies. 2025; 18(13):3495. https://doi.org/10.3390/en18133495
Chicago/Turabian StyleWu, Si, Jun Wu, Hongyou Zhong, and Yang Qi. 2025. "Transient Stability Enhancement of Virtual Synchronous Generator Through Analogical Phase Portrait Analysis" Energies 18, no. 13: 3495. https://doi.org/10.3390/en18133495
APA StyleWu, S., Wu, J., Zhong, H., & Qi, Y. (2025). Transient Stability Enhancement of Virtual Synchronous Generator Through Analogical Phase Portrait Analysis. Energies, 18(13), 3495. https://doi.org/10.3390/en18133495







