Selective Lithium Plating on Graphite–Silicon Composite Anodes During Fast Charging in Rechargeable Lithium Batteries

Abstract

In this study, we systematically analyzed selective lithium plating on graphite (Gr)–silicon (Si) composite anodes for lithium-ion batteries during fast charging, using electrochemical techniques. To achieve this, half-cells were first constructed with single Gr and Si electrodes, and lithium plating on each electrode was examined at different charging rates. It was observed that lithium plating on both electrodes began at a lower state of charge (SoC) as the charge rate increased. Furthermore, at a given charge rate, lithium plating occurred on the Si electrode at a lower SoC than on the Gr electrode. Based on the experimental findings, the lithium plating behavior of Gr and Si as a function of the charge rate was formulated to investigate the plating behavior of hypothetical composite electrodes with varying Gr–Si ratios. The lithium plating behavior observed on the actual composite electrode was consistent with that predicted from the hypothetical composite electrode, which was simulated using the same Gr–Si ratio based on the behaviors of the individual electrodes. By comparing the results from the single and composite electrodes, it is proposed that lithium plating occurs first on Si and then on Gr at low charge rates, whereas, at high charge rates, it proceeds first on Gr and then on Si. We discuss how to extrapolate the preferential plating signals—namely, plating onto Si at low charge rates and onto Gr at high charge rates—that are not directly evident in the signal from the actual composite electrode.

1. Introduction

Due to climate change and environmental pollution, the demand for eco-friendly transportation solutions (e.g., electric vehicles) and energy storage systems (ESSs) linked to renewable energy sources has significantly increased [1,2,3]. Lithium-ion batteries (LIBs) are currently the most widely used energy storage systems, thanks to their high energy and power densities. With the onset of the fourth industrial revolution, which emphasizes hyper-intelligence, hyper-connectivity, and hyper-convergence, there is an ongoing effort to continuously enhance the performance of energy devices, including LIBs [4,5,6,7]. In particular, the cathode and anode active materials, which have the greatest impact on LIB performance, remain the primary focus of ongoing research and development [8,9]. From an anode perspective, silicon (Si), with a theoretical capacity nearly ten times higher than that of graphite (Gr), has emerged as a promising candidate [10,11,12]. However, previous studies have shown that Si electrodes suffer from significant capacity fading due to the detachment of the active material (Si) caused by large volume changes (>300%) during alloying and dealloying, as well as poor high-rate performance resulting from their low electronic conductivity and sluggish solid-state lithium diffusion [13,14,15].

To address the limitations of Si anodes, several strategies have been explored. These include nanostructuring approaches—such as Si nanowires [16,17,18], nanotubes [19], and porous [20,21] and hollow nanostructures [22,23]—to mitigate volume expansion; surface coatings with carbon [24,25], silver [26], or copper [27] to enhance the electronic conductivity; and techniques to improve solid-state lithium diffusion, such as thin-film electrodes [28], aligned Si architectures [29], and oxygen doping [30]. However, despite these efforts, pure Si has not yet been successfully implemented as a practical anode material for LIBs. From a practical standpoint, efforts to enhance the capacity of pure Gr electrodes by incorporating small amounts of Si into Gr–Si composite electrodes have already been implemented by several battery manufacturers. This approach has been recognized as an effective strategy for achieving high-capacity anodes [31,32,33,34]. In addition to the capacity improvement, the porous composite based on Gr helps to buffer the expansion and contraction of Si, maintaining the integrity of the electrode even during significant volume changes of Si [35,36,37,38].

Despite the advantages of Gr–Si composites, the intrinsic drawbacks of Si—namely, its low electrical conductivity and sluggish solid-state lithium diffusion—result in reduced rate performance compared to pure Gr electrodes [39,40]. To overcome these limitations, various strategies have been proposed, including coating Si thin films onto carbon nanotubes to shorten the electron and ion transport paths [41,42]; enhancing the surface conductivity of Si through different modifications [24,25,26,27,43]; minimizing the lithium diffusion distances using thin-film Gr–Si composite electrodes [28,44]; and promoting lithium diffusion by uniformly dispersing or structurally aligning Si within the composite matrix [29,30,45]. These approaches have significantly improved the high-rate discharge performance. However, in contrast to the substantial progress made in the discharge characteristics, studies on the high-rate charging behavior remain limited—despite its critical importance. While reducing the cell resistance and overpotential is essential during high-rate charging, and many discharge-optimized designs also contribute positively to charging, a unique challenge persists: lithium plating at the anode. This phenomenon demands special attention, as it poses a major obstacle to the practical implementation of fast-charging LIBs.

Under typical charging conditions at room temperature, the anode potential is generally maintained above 0 V vs. Li⁺/Li, which favors lithium insertion into Gr and minimizes the likelihood of lithium plating. However, under low-temperature conditions and/or high charging rates, increased overpotentials can drive the anode potential below 0 V vs. Li⁺/Li, leading to concurrent lithium insertion into Gr and lithium plating on its surface [46,47]. In contrast to the lithium insertion mechanism that governs the lithiation of Gr during charging, Si undergoes lithiation through an alloying reaction with lithium. As a result, when the anode potential drops below 0 V vs. Li⁺/Li during charging, lithium plating on the Si surface and lithium–Si alloying may occur simultaneously [48,49,50]. Beyond this fundamental difference in the lithiation mechanism, Gr and Si also exhibit a significant disparity in their lithium solid-state diffusion coefficients—ranging from 6.5 × 10⁻¹¹ to 1.12 × 10⁻¹⁰ cm²·s⁻¹ for Gr [51] and from 1 × 10⁻¹³ to 1 × 10⁻¹² cm²·s⁻¹ for Si [52]. Given these differences in both the lithiation mechanisms and lithium diffusion kinetics, the overpotentials experienced by Gr and Si during charging are expected to differ, leading to distinct lithium plating behaviors on their respective surfaces.

The most commonly employed approach in lithium plating studies is destructive analysis, which typically involves the post-mortem microscopic examination of lithium deposits [53,54,55] or the spectroscopic quantification of their thickness and amount [56,57,58]. While these methods provide direct evidence of metallic lithium, they are susceptible to surface contamination following battery disassembly and are inherently incapable of capturing the time-dependent dynamics of lithium plating. Non-destructive techniques can overcome many of these limitations. Representative non-destructive approaches include electrochemical methods [59,60,61,62], neutron diffraction [63,64,65], and spectroscopic analyses [66,67,68]. Neutron diffraction offers the reliable detection of light elements such as lithium and provides a high depth resolution within active materials. However, it requires expensive instrumentation, prolonged data acquisition due to the limited beam size, and specially designed cells. Spectroscopic techniques enable time-resolved surface analysis, but their practical use is limited by the need for complex cell configurations and costly equipment. In contrast, electrochemical methods analyze the intrinsic redox signals of the electrode and require no specialized equipment beyond a potentiostat, making them highly versatile and suitable for practical applications.

Electrochemical studies on lithium plating in Gr–Si composite electrodes have employed several approaches: (1) the analysis of the open-circuit voltage (OCV) immediately after charging [69]; (2) voltage and differential capacity (dQ/dV) curve analysis during charging [70,71]; and (3) distribution of relaxation times (DRT) analysis [72,73]. Study (1) investigated the effects of the Si content and temperature on the high-rate performance and the extent of lithium plating, showing increased lithium deposition with higher Si ratios. Study (2) examined capacity fade trends during cycling following lithium plating on the composite electrode. Study (3) analyzed how significant interfacial polarization in Si affects the lithium plating locations and the growth of the solid electrolyte interphase (SEI) layer. In recent studies, methods for detecting lithium plating have been developed using a combination of modeling and impedance spectroscopy [74,75,76,77]. Despite these contributions, prior studies have largely focused on the overall electrochemical response of the composite electrode, without differentiating the behaviors of Gr and Si individually [59], or have exclusively analyzed one of the two components [70]. As a result, they present inherent limitations in elucidating the distinct lithium plating characteristics of Gr and Si, thereby hindering a comprehensive understanding of the lithium plating mechanisms in Gr–Si composite systems.

In this work, we aimed to gain a deeper understanding of the lithium plating behavior in Gr–Si composite electrodes using electrochemical techniques. Previous studies have typically interpreted the electrochemical signals of Gr–Si composite anodes without differentiating the individual contributions of Gr and Si. To address this, the lithium plating behavior was first investigated separately in individual Gr and Si electrodes to compare their distinct electrochemical responses. Additionally, a simple equivalent circuit model, based on the interfacial resistances of both electrodes, was employed to conceptually analyze the current distribution between Gr and Si. This analysis enabled a direct comparison of the lithium plating signals from Gr and Si, offering insights into their respective deposition characteristics and allowing for informed inferences about the behavior in the Gr–Si composite systems. Finally, the same experimental framework was applied to composite electrodes with varying Gr-to-Si ratios to evaluate the influence of the Si content on the lithium plating behavior within the composite structure.

2. Experimental Procedures

2.1. Electrode Fabrication and Cell Preparation

The Gr electrode was composed of artificial graphite (Sigma-Aldrich, >99.95%, D₅₀ ≈ 15 μm, St. Louis, MO, USA) as the active material, Super P (Timcal (Bodio, Switzerland), Carbon Black Super-P Li) as the conductive agent, and polyvinylidene fluoride (PVdF, Sigma-Aldrich, Mw~534,000) as the binder. These components were mixed in a weight ratio of 5:4:1. For the Si electrode, crystalline Si powder (APS ≈ 100 nm, 99%, plasma-synthesized) was used as the active material, with acetylene carbon black (100%, compressed, Thermo Fisher Scientific, Oxford, UK) as the conductive agent and with the same PVdF binder. The Si electrode composition was also mixed in a 5:4:1 weight ratio. The Gr and Si active materials contained within the Gr and Si electrodes, respectively, were ensured to have the same mass. Gr–Si composite electrodes were prepared by mixing Gr and Si in weight ratios of 1:1, 2:1, and 1:2, along with carbon black as the conductive agent and PVdF as the binder, maintaining an overall composition ratio of 5:4:1. These electrodes are hereafter referred to as 1Gr–1Si, 2Gr–1Si, and 1Gr–2Si, respectively. N-methyl-2-pyrrolidinone (NMP, Sigma-Aldrich, ≥99.0%) was used as the solvent to prepare a slurry by dispersing the Gr, Si, carbon black, and binder. The slurry was cast onto copper foil (18 μm, >99.96%, Honjo Metal Co., Osaka, Japan), dried in an oven at 70 °C for 12 h, pressed, and then punched into circular electrodes with a diameter of 16 mm.

The fabricated electrodes were used as working electrodes in a two-electrode half-cell configuration, with lithium metal serving as the counter-electrode. The electrolyte solution, supplied in a pre-mixed form by Dongwha Electrolyte (Nonsan-si, Republic of Korea), contained 1 M lithium hexafluorophosphate (LiPF₆) dissolved in a 3:7 volume ratio mixture of ethylene carbonate (EC) and ethyl methyl carbonate (EMC). A Celgard 2400 membrane was employed as the separator. All cell assembly was conducted in an argon-filled glove box (MBraun, München, Germany) with oxygen and moisture levels maintained below 1 ppm.

2.2. Electrochemical Experiments

2.2.1. Cell Activation

The five fabricated electrodes were assembled into two-electrode half-cells and subjected to initial charge–discharge cycles at a rate of 0.1 C (corresponding to current densities of 37.2, 357.9, 197.0, 143.3, and 250.6 mA·g⁻¹ for Gr, Si, 1Gr–1Si, 2Gr–1Si, and 1Gr–2Si, respectively) within a voltage window of 0.01–1.5 V vs. Li⁺/Li at room temperature (25 °C). The applied current (C-rate) was calculated based on the full lithiation states of Gr and Si—Li₆C and Li_3.75Si, respectively—corresponding to their theoretical capacities of 372 and 3579 mAh·g⁻¹. Although the thermodynamically stable phase of fully lithiated Si is Li_4.4Si, it is known to be kinetically difficult to form [78,79,80]. In practice, lithiation often terminates around the Li_3.75Si composition, as discussed in prior studies [80,81,82]. Therefore, Li_3.75Si, which is more readily formed under practical conditions, was considered as the 100% state of charge (SoC) for Si. Based on these assumptions, the theoretical capacities of the composite electrodes were calculated as 1970, 1433, and 2506 mAh·g⁻¹ for 1Gr–1Si, 2Gr–1Si, and 1Gr–2Si, respectively. Figure 1 presents the initial charge–discharge profiles of the half-cells using the five electrode compositions. The initial discharge capacities were measured to be 320, 1120, 718, 586, and 882 mAh·g⁻¹ for Gr, Si, 1Gr–1Si, 2Gr–1Si, and 1Gr–2Si, respectively. Subsequent constant-current tests were conducted by adjusting the applied current (C-rate) based on the actual specific capacities of each electrode.

2.2.2. Lithium Plating Test

To standardize the SoC across all half-cells described in Section 2.2.1, fully discharged cells were charged to 30% SoC at room temperature at a rate of 0.1 C. This corresponded to current densities of 32, 112, 71.8, 58.6, and 88.2 mA·g⁻¹ for the Gr, Si, 1Gr–1Si, 2Gr–1Si, and 1Gr–2Si electrodes, respectively. After reaching 30% SoC, the cells were rested under open-circuit conditions for 15 min to allow voltage stabilization. Electrochemical impedance spectroscopy (EIS) was then performed over a frequency range of 1 MHz to 100 mHz with a sinusoidal voltage amplitude of 10 mV_rms to investigate the interfacial characteristics of the individual Gr and Si electrodes. To analyze the lithium plating behavior under varying charge rates, SoC 30% cells were charged at constant currents corresponding to C-rates ranging from 2 C to 14 C, in 2 C increments—equivalent to 0.64 to 4.48 A·g⁻¹ for Gr and 2.24 to 15.68 A·g⁻¹ for Si. Charging was continued until each cell reached 100% SoC. Following the charging step, all cells were held under open-circuit conditions for 4 h to monitor the potential relaxation behavior. All charge–discharge and open-circuit relaxation experiments were performed using a multi-channel potentiostat/galvanostat system (VMP3, Bio-Logic, Seyssinet-Pariset, France). Impedance measurements were carried out using a Solartron 1470E multichannel potentiostat coupled with a Solartron 1455A frequency response analyzer (AMETEK Scientific Instruments, Wrexham, UK).

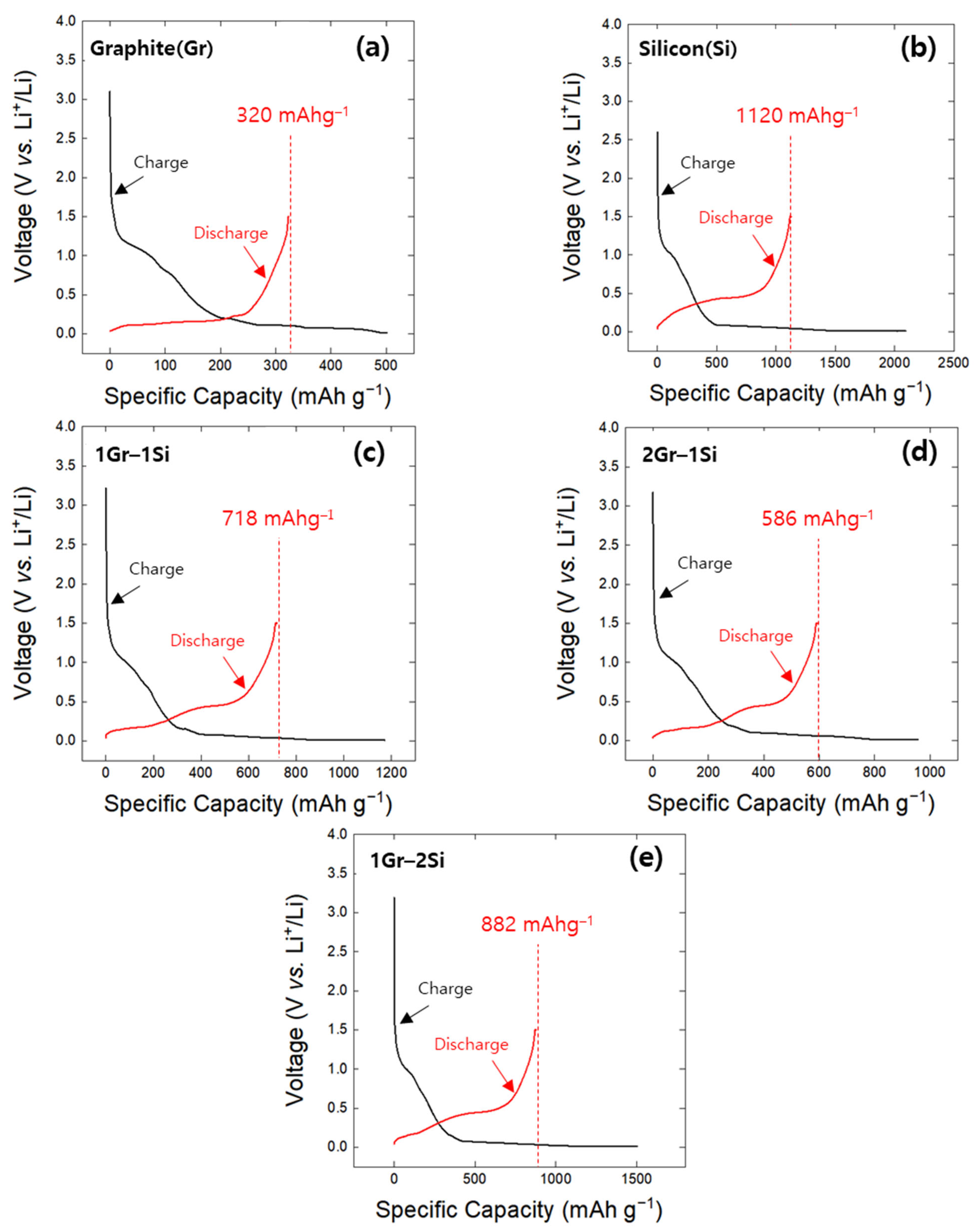
3. Results and Discussion

Figure 2a shows the potential profile of the Gr half-cell charged at a 4 C-rate, plotted as a function of the SoC, along with its corresponding differential curve (dV/dSoC). The overall potential profile closely mirrors the typical shape observed for Gr electrodes. However, a distinct minimum in the potential curve (i.e., dV/dSoC = 0) appears near an SoC of 95% (see inset figure). This feature is associated with the nucleation and growth of lithium on the Gr surface—specifically, lithium plating [70]. That is, the potential curve is divided into two distinct regions—pre-SoC and post-SoC (denoted as regions A and B, respectively, in the figure)—based on the minimum value, which depends on the presence of lithium plating: region A corresponds to the portion before the point where dV/dSoC = 0, while region B refers to the region that follows this point.

In region A, lithium insertion into the Gr structure dominates, resulting in the formation of various compounds (LiC₂₄, LiC₁₈, LiC₁₂, LiC₆) depending on the amount of lithium inserted. In this region, the dV/dSoC remains negative, with the maximum and minimum values on the dV/dSoC curve corresponding to the inflection points in the potential curve. These inflection points are closely associated with phase transitions, often referred to as ‘staging’, within the Gr structure [83]. Compared to previously reported Gr potential profiles, the peak at SoC ≈ 45% is attributed to the LiC₁₈ → LiC₁₂ (stage 2) transition, while the dip at SoC ≈ 65% corresponds to the LiC₁₂ → LiC₆ (stage 1) transition [84]. However, due to the relatively high charge rate used in this study (4 C), the phase transition occurs at lower SoC values than those typically reported in the literature, as a result of the increased overpotential.

In region B, both lithium insertion into the Gr and lithium plating on the Gr occur simultaneously due to the high overpotential. However, the fact that the potential curve stops decreasing and begins to rise after reaching the minimum point suggests that lithium plating becomes the dominant process, surpassing further lithium insertion into the Gr [70]. Therefore, the starting point of region B (where dV/dSoC = 0) can be interpreted as a significant signal for the onset of lithium plating. In this study, the corresponding SoC value is denoted as S_min,Gr and is used as a key indicator for lithium plating analysis. To indirectly confirm the occurrence of lithium plating upon observing a potential minimum during charging, the relaxation behavior of the open-circuit potential was analyzed immediately after a 4 C charge (Figure 2b). Overall, it shows the typical relaxation of the potential, with the potential rising over time. Of particular note is the potential inflection point (the peak in the dV/dt curve) identified near 0.3 h s, which is known to occur when lithium electroplated on the Gr surface is inserted into the Gr [69]. In fact, these two features—namely dV/dSoC = 0 and an inflection point in the open-circuit potential—have been directly and spectroscopically confirmed in the literature as reliable indicators of lithium plating [59,74,77] and are widely recognized as definitive electrochemical signatures that provide clear evidence of its occurrence [69,70,84].

Figure 2c,d present the potential profiles of the Gr half-cell charged at different C-rates and their corresponding differential curves, respectively. As the C-rate increases, the SoC at which the potential minimum occurs (i.e., S_min,Gr) decreases consistently (see red arrow in the inset of Figure 2d). This trend indicates that higher charging rates promote an earlier onset of lithium plating on Gr surfaces [84]. Although not the focus of this study, it is worth noting that, at ultra-high charging rates above 10 C, a first potential minimum appears at even lower SoC values than S_min,Gr. This minimum is not associated with lithium plating but is more likely attributed to kinetic effects—specifically, the rapid rise and subsequent recovery of the lithium concentration on the Gr surface at the onset of charging under ultra-high rates.

Figure 3a presents the potential profiles as a function of the SoC, along with its derivative, for the Si half-cell charged at a 4 C-rate. As in the previous case of Gr (Figure 2a), regions A and B are identified based on the potential minima, with the corresponding SoC values denoted as S_min,Si. Region A, characterized by a continuous decrease in potential with an increasing SoC, corresponds to the alloying of Si with lithium [72]. In contrast, Region B, where the potential rises, is believed to be dominated by lithium plating on the Si rather than alloying. The relaxation behavior of the open-circuit potential immediately after charging is very interesting (Figure 3b). The inflection point observed when lithium on Gr is inserted into the Gr structure under open-circuit conditions (Figure 2b) is similarly seen in the case of lithium-plated Si. Notably, this inflection point is absent in Si samples without lithium plating (see the inset figures), strongly suggesting that it originates from the interaction between surface-plated lithium and Si. Thus, as with Gr, the inflection point in the open-circuit potential curve appears to serve as an indicator of surface lithium deposits on Si. Figure 3c,d demonstrate the potential profiles and their corresponding differential curves, respectively, for the Si half-cell charged at different C-rates. As in the case of Gr, S_min,Si decreases continuously with an increasing C-rate in Si (see red arrow in the inset of Figure 3d). The first potential minimum that appears ahead of S_min,Si at very high-C-rate charging (e.g., 14 C-rate) is neglected here, as in the case of Gr.

Based on Figure 2c,d and Figure 3c,d, the variations in S_min,Gr and S_min,Si with respect to the C-rate are summarized in Figure 4. Interestingly, both S_min,Gr and S_min,Si exhibit a roughly linear relationship with the C-rate. Accordingly, an empirical formula for the C-rate dependence of S_min is derived as follows:

$$S_{min,M}={\alpha }_M·\left(C-rate\right)+c_M,\hspace{1em}where M=Gr or Si$$

(1)

From Figure 4, the empirical parameters are determined as follows: ${\mathsf{\alpha }}_{Gr}=-2.1$, ${\mathrm{c}}_{Gr}=103.6$, ${\mathsf{\alpha }}_{Si}=-0.93$, and ${\mathrm{c}}_{Si}=74.0$. We would like to note that, while a linear trend is observed, this linearity serves as a convenient phenomenological tool for interpretation rather than as the foundation of our conclusions. The key finding is the substantial difference in both the slope and value between Gr and Si.

Given that the kinetics of the reaction at the Gr and Si interfaces are expected to significantly influence lithium plating on each material, we analyze the interfacial resistance of the Gr and Si electrodes. Figure 5 shows the Nyquist plots of the impedance spectra measured from the Gr and Si half-cells at SoC 30%. In both spectra, a positive imaginary impedance at high frequencies is observed, followed by approximately two depressed semicircles and a linear tail in the low-frequency region. The positive imaginary impedance in the high-frequency region is attributed to stray inductance (L) [83]. The subsequent two arcs correspond to the combined signals of surface SEI resistance (R_SEI) and capacitance (C_SEI), followed by the charge transfer resistance (R_ct) and double-layer capacitance (C_dl), respectively [84,85]. The final linear segment in the low-frequency region is known as the Warburg impedance, which reflects lithium-ion diffusion behavior [86]. An equivalent circuit (shown in the inset of Figure 5) is employed to analyze the interfacial resistance components and fit the impedance data, excluding the diffusion tail. Constant phase elements (CPE) are used instead of ideal capacitors to account for the non-ideal interfacial behavior. The impedance data are fitted to the proposed equivalent circuit using the complex nonlinear least squares (CNLS) method via ZView (version 3.5g), within the frequency range of 100 kHz to 1 Hz. The values of the resistance components obtained from the fitting, along with the fitting reliability (chi-squared values), are summarized in

Table 1. Resistance component values obtained from fitting, along with corresponding fitting reliability (chi-squared values).

	${\mathit{R}}_{\mathit{o}\mathit{h}\mathit{m}}$ (Ω)	${\mathit{R}}_{\mathit{S}\mathit{E}\mathit{I}}$ (Ω)	${\mathit{R}}_{\mathit{c}\mathit{t}}$ (Ω)	${\mathit{R}}_{\mathit{i}\mathit{n}\mathit{t}\mathit{f}}$  = ${\mathit{R}}_{\mathit{S}\mathit{E}\mathit{I}}$ + ${\mathit{R}}_{\mathit{c}\mathit{t}}$ (Ω)	Chi-Squared (χ2)
Gr	1.7	2.17	3.96	6.13	5.87 $\times$ 10−5
Si	2.6	3.2	21.6	24.8	2.27 $\times$ 10−4

.

Figure 6a is the equivalent circuit introduced to separately analyze the currents applied to the Gr and Si components during the charging of the Gr–Si composite electrode. Although the equivalent circuit model is a simplification and does not capture the full complexity of electrochemical processes in composite anodes, it is used to conceptually illustrate the current distribution between Gr and Si based on their relative resistances. Under the charging current i, the currents i_Gr and i_Si experienced by Gr and Si, respectively, are determined by the interfacial resistances of the two components in the Gr–Si composite electrode, r_intf,Gr and r_intf,Si, as shown below.

$$i_{Gr}={\displaystyle \frac{r_{intf,si}}{r_{intf,Gr} +r_{intf,si} }}\times i$$

(2a)

$$i_{Si}={\displaystyle \frac{r_{intf,Gr} }{r_{intf,Gr} +r_{intf,si} }}\times i$$

(2b)

In this study, the interfacial resistance of a single Gr electrode was determined to be R_intf,Gr = 6.13 Ω, and that of a single Si electrode was R_intf,Si = 24.8 Ω (Table 1; note—the amounts of Si and Gr active materials in the Si and Gr electrodes were matched (refer to Section 2.1)). Therefore, by using these interfacial resistances and assuming that the weight ratio of Gr to Si in the composite electrode is m_Gr–m_Si, the currents applied to Gr (i_Gr) and Si (i_Si) can be expressed through Equations (3a) and (3b).

$$i_{Gr}={\displaystyle \frac{\frac{R_{intf,Si}}{m_{Si}}}{\frac{R_{intf,Gr}}{m_{Gr}}+\frac{R_{intf,si}}{m_{si}}}}\times i$$

(3a)

$$i_{Si}={\displaystyle \frac{\frac{R_{intf,Gr}}{m_{Gr}}}{\frac{R_{intf,Gr}}{m_{Gr}}+\frac{R_{intf,si}}{m_{si}}}}\times i$$

(3b)

In other words, the interfacial resistance will vary depending on the Gr-to-Si ratio, which will, in turn, affect the currents applied to these materials. When the respective capacities of Gr and Si in the composite electrode are denoted as Q_Gr and Q_Si, the C-rate for each material will be related to the applied current as follows:

$${\left(C-rate\right)}_{Gr}=i_{Gr}/{\mathrm{Q}}_{Gr}$$

(4a)

$${\left(C-rate\right)}_{Si}=i_{Si}/{\mathrm{Q}}_{Si}$$

(4b)

Substituting Equation (3) into Equation (4), we obtain the following relationship:

$${\left(C-rate\right)}_{Gr}={\displaystyle \frac{\frac{R_{intf,si}}{m_{si}}}{\frac{R_{intf,Gr}}{m_{Gr}}+\frac{R_{intf,si}}{m_{si}}}}\times {\displaystyle \frac{i}{Q_{Gr}}}$$

(5a)

$${\left(C-rate\right)}_{Si}={\displaystyle \frac{\frac{R_{intf,Gr}}{m_{Gr}}}{\frac{R_{intf,Gr}}{m_{Gr}}+\frac{R_{intf,si}}{m_{si}}}}\times {\displaystyle \frac{i}{Q_{Si}}}$$

(5b)

Therefore, if the total capacity of the composite electrode is Q, the C-rate (=i/Q) experienced by the entire composite electrode can be expressed in the following two forms:

$$C-rate={\displaystyle \frac{\frac{R_{intf,Gr}}{m_{Gr}}+\frac{R_{intf,si}}{m_{si}}}{\frac{R_{intf,si}}{m_{si}}}}{\displaystyle \frac{Q_{Gr}}{\mathrm{Q}}}\times {\left(C-rate\right)}_{Gr}={\gamma }_{Gr}\times {\left(C-rate\right)}_{Gr}, where {\gamma }_{Gr}={\displaystyle \frac{\frac{R_{intf,Gr}}{m_{Gr}}+\frac{R_{intf,si}}{m_{si}}}{\frac{R_{intf,si}}{m_{si}}}}{\displaystyle \frac{Q_{Gr}}{\mathrm{Q}}}$$

(6a)

$$C-rate={\displaystyle \frac{\frac{R_{intf,Gr}}{m_{Gr}}+\frac{R_{intf,si}}{m_{si}}}{\frac{R_{intf,Gr}}{m_{Gr}}}}{\displaystyle \frac{Q_{Si}}{\mathrm{Q}}}\times {\left(C-rate\right)}_{Si}={\gamma }_{Si}\times {\left(C-rate\right)}_{Si}, where {\gamma }_{Si}={\displaystyle \frac{\frac{R_{intf,Gr}}{m_{Gr}}+\frac{R_{intf,si}}{m_{si}}}{\frac{R_{intf,Gr}}{m_{Gr}}}}{\displaystyle \frac{Q_{Si}}{\mathrm{Q}}}$$

(6b)

Here, ${\mathsf{\gamma }}_{Gr}$ and ${\mathsf{\gamma }}_{Si}$ are constants determined by the compound composition and do not depend on the C-rate, making Equation (6) a linear expression. Substituting Equation (6) into Equation (1) finally gives us Equation (7):

$$S_{min,Gr}={\mathsf{\alpha }}_{Gr}\times {\mathsf{\gamma }}_{Gr}\times {\left(C-rate\right)}_{Gr}+{\mathrm{c}}_{Gr}$$

(7a)

$$S_{min,Si}={\mathsf{\alpha }}_{Si}\times {\mathsf{\gamma }}_{Si}\times {\left(C-rate\right)}_{Si}+{\mathrm{c}}_{Si}$$

(7b)

Using Equation (7), the relationship between the C-rate and S_min was estimated for three hypothetical composite electrodes with different Gr-to-Si ratios: m_Gr–m_Si = 1:1 (1Gr–1Si sample), 2:1 (2Gr–1Si sample), and 1:2 (1Gr–2Si sample), as illustrated in Figure 6b–d. In all three cases, the S_min,Gr value at a low C-rate is higher than S_min,Si; however, due to the higher C-rate dependency of Gr (i.e., slope ${\mathsf{\alpha }}_{Gr}·{\gamma }_{Gr}$ > ${\mathsf{\alpha }}_{Si}·{\gamma }_{Si}$), the two plots intersect at a specific C-rate. To examine how the trend predicted by the hypothetical composite electrodes manifests in real systems, three actual electrodes (1Gr–1Si, 2Gr–1Si, and 1Gr–2Si samples) were fabricated. The variation in the potential curves with the C-rate for these actual samples is shown in Figure 7, and the corresponding minimum points, S_min, for each composite electrode are presented in Figure 8. Notably, in all three actual composite samples, based on the intersection of S_min,Gr (red dashed line) and S_min,Si (blue dashed line) estimated for the individual Gr and Si electrodes, it is confirmed that, at low rates, the experimental results align with the Gr signal (S_min,Gr), while, at high rates, they align with the Si signal (S_min,Si). That is, although S_min,Si < S_min,Gr at low rates and S_min,Gr < S_min,Si at high rates from single-electrode predictions—suggesting that S_min,Si should be reached first at low rates and S_min,Gr at high rates during the charging process—the experimental results show the opposite trend: S_min,Gr appears at low rates and S_min,Si at high rates.

This unusual behavior can be explained as follows: since S_min,Si < S_min,Gr at low rates, based on the intersection point, lithium plating is expected to occur preferentially on the Si surface. However, even during lithium plating on Si, lithium insertion into Gr continues. Although the signal (S_min,Si) from lithium plating on Si may be expected, the overall potential curve of the composite electrode continues to decrease due to the ongoing lithium insertion into Gr, which prevents the S_min,Si signal from appearing. This decline continues until lithium insertion into Gr is complete, at which point lithium plating begins on Gr, resulting in the appearance of the S_min,Gr signal at low rates. Conversely, since S_min,Gr < S_min,Si at high rates, lithium plating occurs first on the Gr surface. However, similar to the low-rate case, the S_min,Gr signal is masked by the potential drop caused by Si alloying, and only the lithium plating signal on Si (S_min,Si) appears once Si alloying is complete. Nevertheless, it should be noted that this interpretation has not yet been experimentally validated and requires further investigation through independent approaches, such as tailored experimental conditions that could uncover masked phenomena [87,88], or complementary spectroscopic analyses.

In summary, at low rates, the signal follows Gr, while lithium plating preferentially occurs on Si, whereas, at high rates, the signal follows Si and lithium plating occurs preferentially on Gr. This indicates that, when the minimum points (S_min) of the potential curve for a Gr–Si composite electrode are plotted as a function of the C-rate (closed symbols in Figure 8), extrapolating the two linear regions on either side of the turning point enables the determination of the SoC at which lithium plating begins on Si and Gr at low and high rates, respectively. In conclusion, by analyzing the variation in the minimum points of the potential curve of a Gr–Si composite electrode with respect to the charging C-rate, the onset points of lithium plating on Si and Gr can be estimated. These results offer valuable insights into the design of fast-charging anodes. Lithium plating typically occurs when the rate of lithium-ion insertion into the electrode material is slower than the supply of lithium ions at the surface, resulting in the formation of metallic lithium instead of intercalated lithium. Therefore, understanding the rate-dependent lithiation and plating characteristics of Gr–Si composites is critical in minimizing the risk of lithium plating. Based on these findings, tailoring electrode formulations can help to optimize their safety and cycle life, particularly under high-rate charging conditions.

4. Conclusions

This study systematically analyzed the selective lithium plating behavior of Gr–Si composite electrodes under high-rate charging. The key findings are summarized as follows:

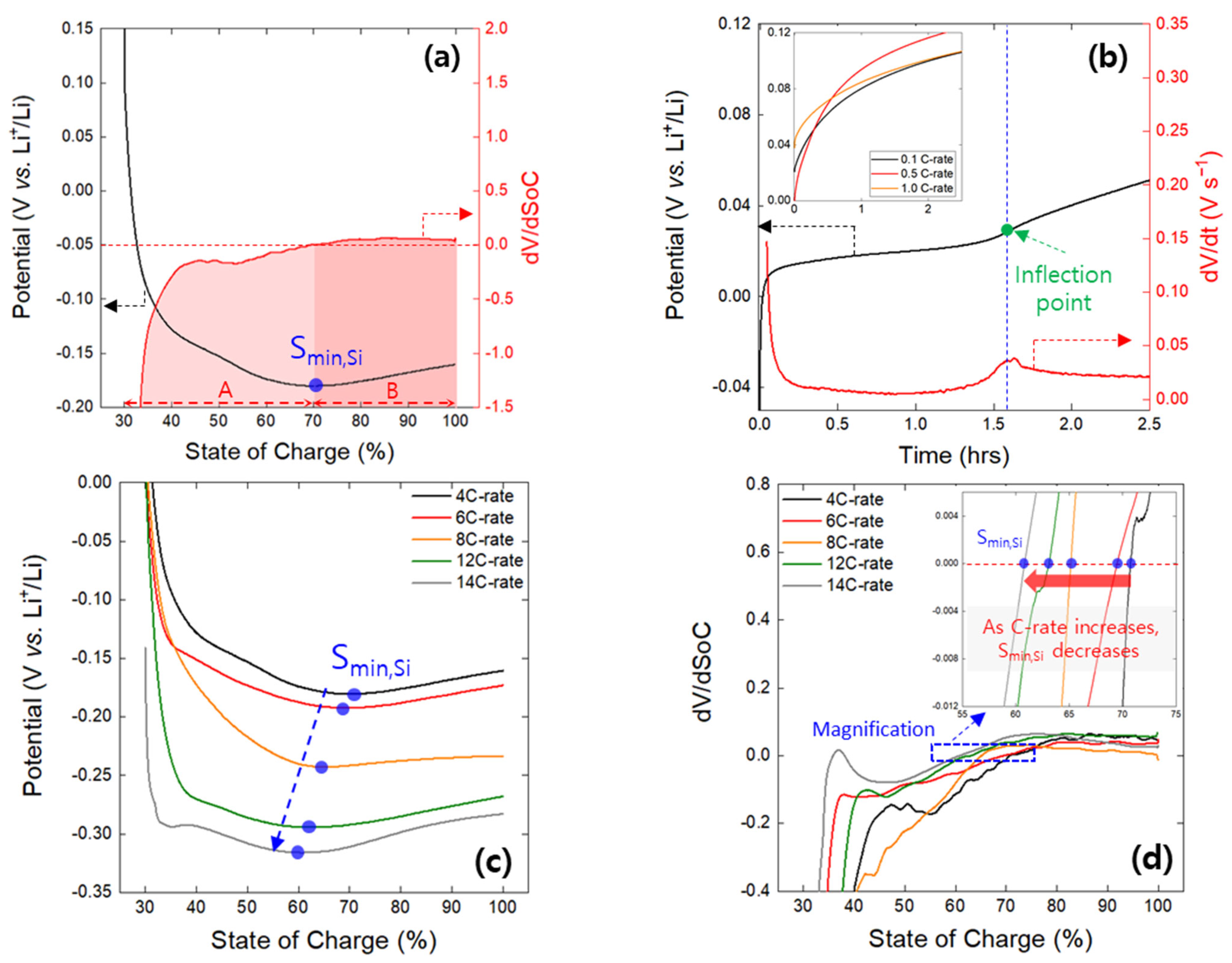
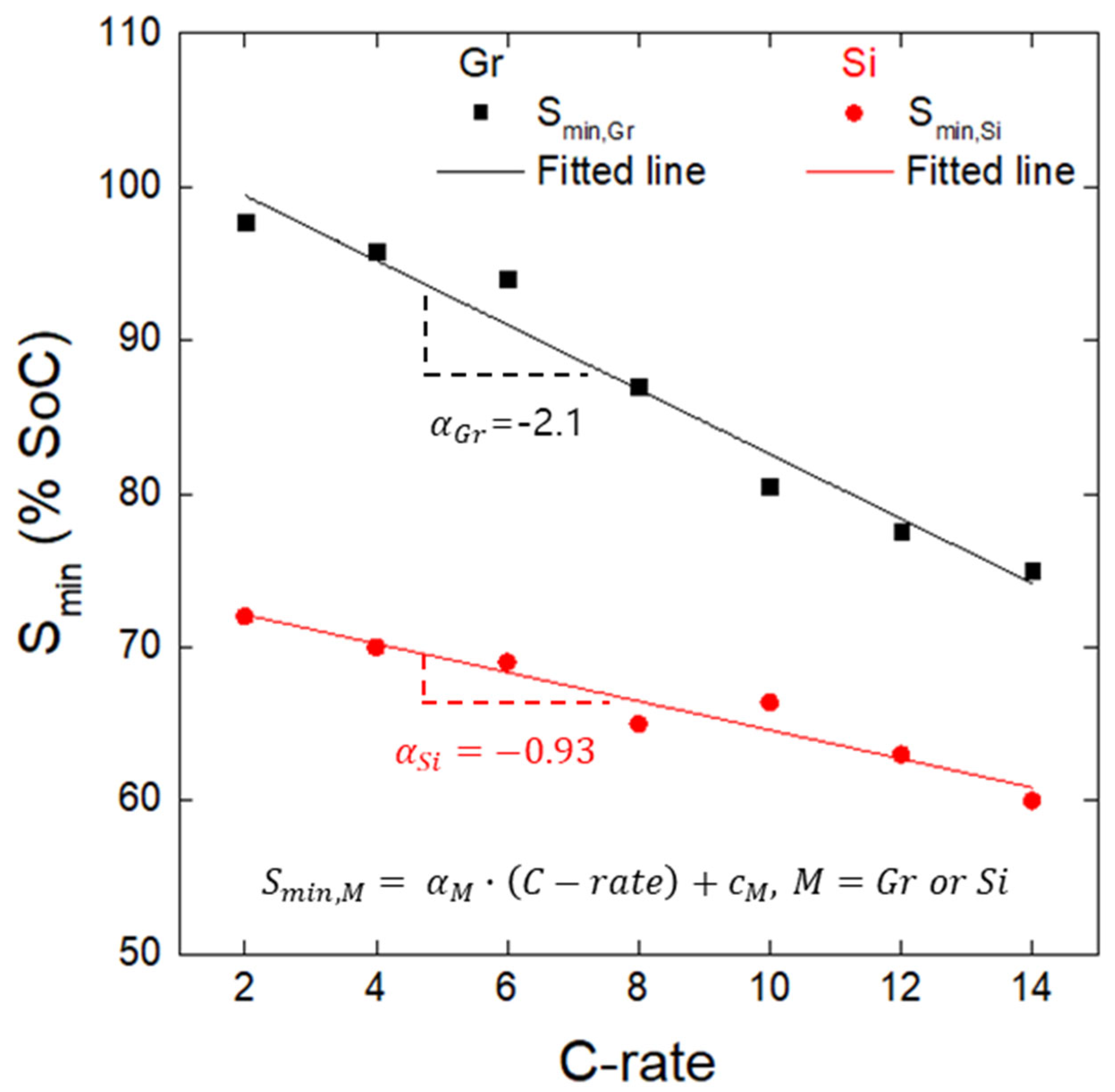
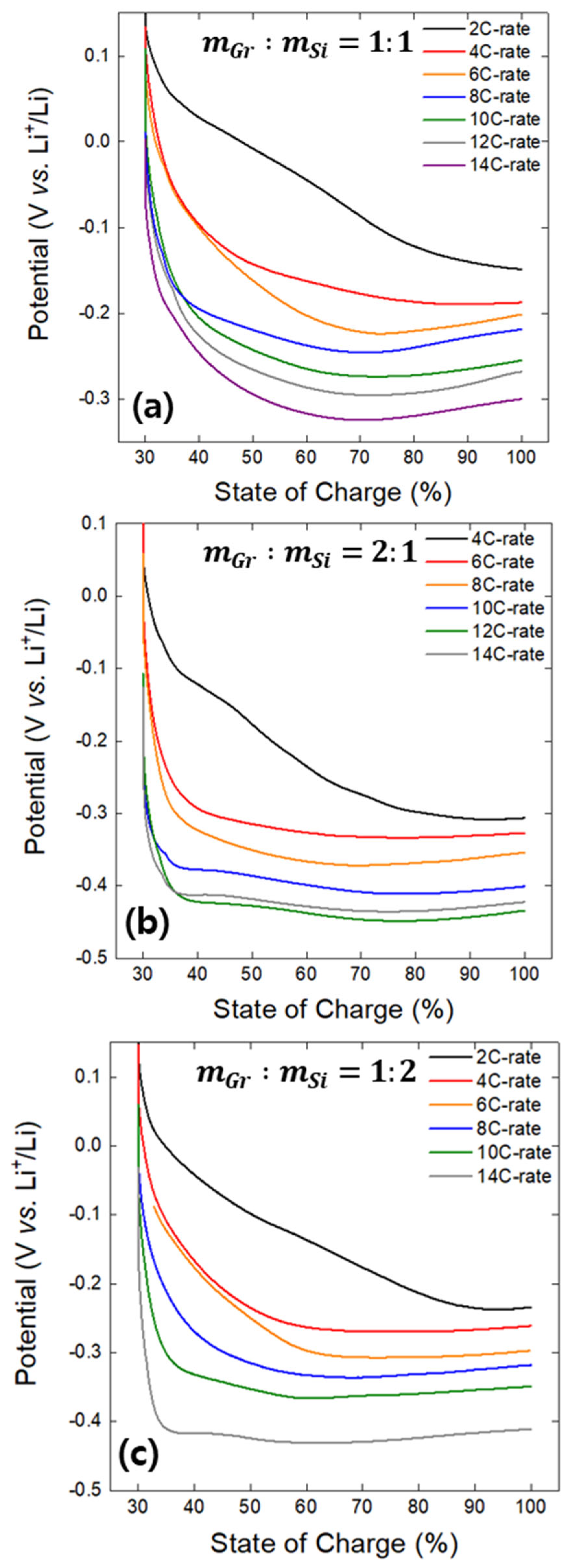
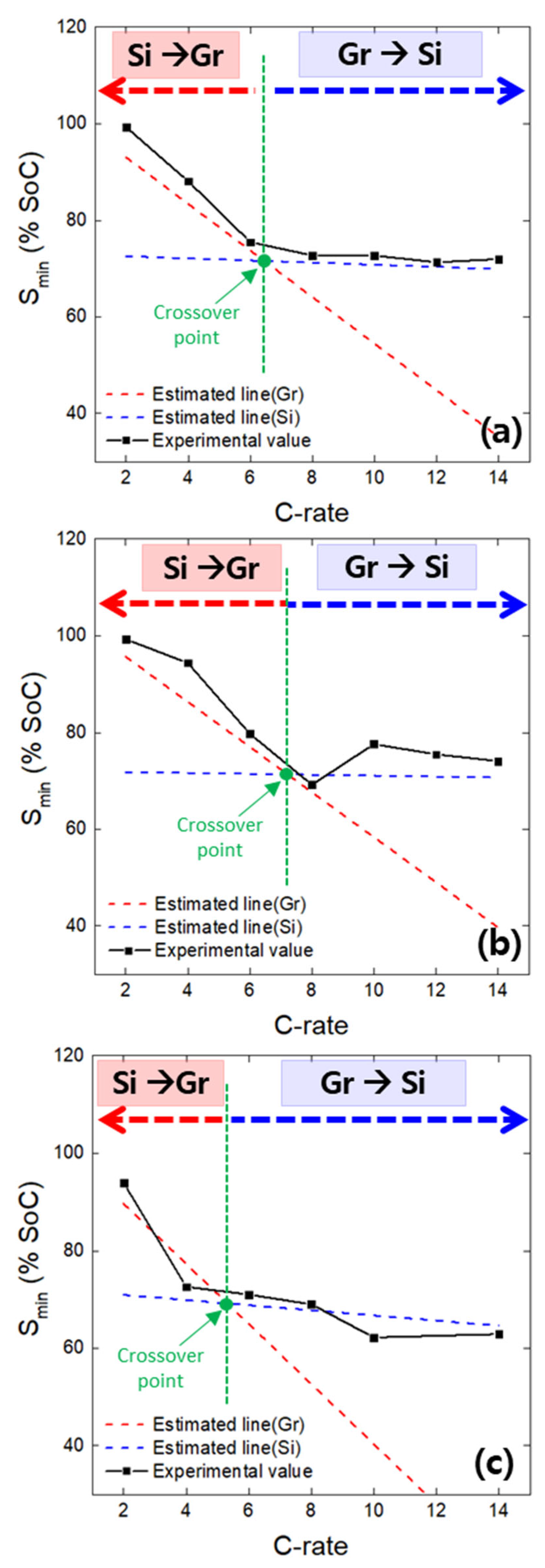
• The minima observed in the charge potential curves of the Gr and Si single electrodes were designated as the onset SoC for lithium plating (S_min). The appearance of inflection points on the open-circuit potential curves of both the Gr and Si electrodes, charged beyond the S_min value, indirectly confirmed the presence of lithium plating on the electrode surfaces. It was confirmed that S_min has a linear relationship with the charging rate (C-rate), and, based on this, a linear empirical equation between S_min and the C-rate was derived.
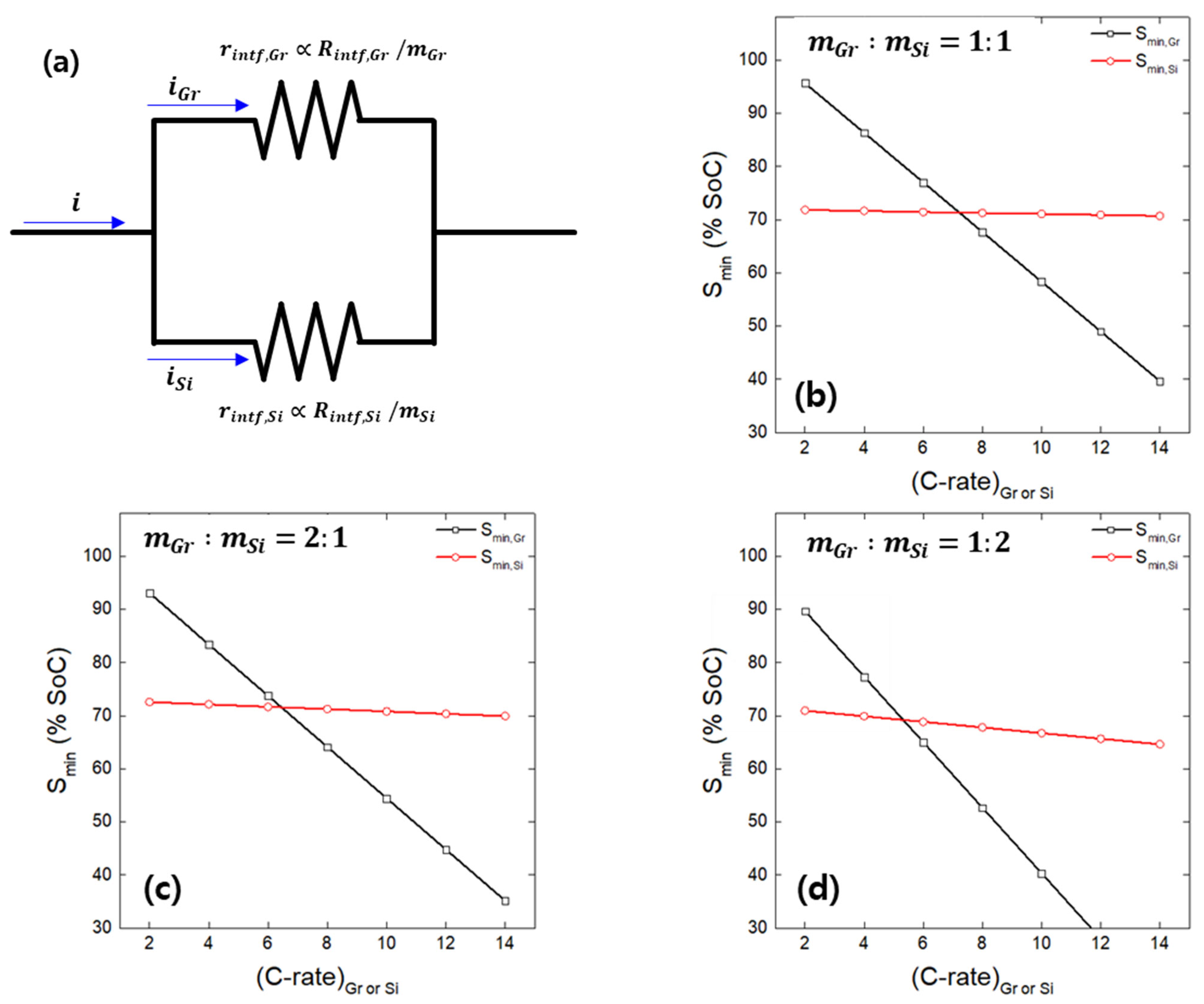
• Based on the interfacial resistances of Gr and Si, the Gr–Si ratio in the composite electrode, and the linear relationship between S_min and the C-rate, the lithium plating behavior on Gr and Si in the hypothetical Gr–Si composite electrode was estimated. Within the charging rate range used in the study (2 to 14 C-rate), it was observed that the S_min values for Gr and Si intersected as the C-rate increased. This suggests that, at a specific C-rate (the crossover point), the active material undergoing preferential lithium plating changes.
• An analysis of the variation in S_min with the C-rate using actual Gr–Si composite electrodes with varying Gr–Si ratios revealed a transition in the lithium plating behavior: S_min followed that of Gr at low rates and Si at high rates, with the crossover point indicating the shift in plating behavior. This unusual behavior observed in the composite electrode is attributed to rate-dependent lithium reaction pathways: at low rates, there is simultaneous lithium plating on Si and lithium insertion into Gr; at high rates, there is simultaneous lithium plating on Gr and lithium alloying with Si. Furthermore, an analysis of the potential curve minima of composite electrodes as a function of the charge C-rate revealed that the onset of lithium plating on Si and Gr can be estimated.
• The observed differences in the lithium plating behavior between Gr and Si are likely influenced by their intrinsic properties. At low C-rates, Gr may tend to favor earlier lithium plating, which could be related to its high electrical conductivity facilitating efficient electron transport during slower lithiation. In contrast, at higher C-rates, Si might become more prone to lithium plating, possibly due to its lower lithium diffusivity, which limits the rate at which lithium ions can diffuse into the material, leading to lithium accumulation and plating on the surface.
• This study provides valuable insights into the C-rate-dependent lithium plating of Gr–Si composite anodes by interpreting it through validated electrochemical signals. However, surface characterization and elemental analysis were not conducted in this work. Incorporating these techniques in future studies could offer a more comprehensive understanding of the electrode’s physicochemical state under fast-charging conditions.