A Method for Predicting the Remaining Life of Lithium-Ion Batteries Based on an Improved Dempster–Shafer Evidence Theory Framework

Abstract

Lithium-ion batteries (LIBs) are widely used in consumer electronics, electric vehicles, and renewable energy systems, but their performance decays with their lifespan, which poses safety risks. Therefore, it is crucial to develop remaining useful life (RUL) prediction technology. This paper proposes a RUL prediction method for lithium-ion batteries based on an improved Dempster–Shafer (D-S) evidence theory framework, which aims to improve the accuracy and robustness of prediction by integrating the advantages of a wavelet packet decomposition convolutional neural network (WPD-CNN) and an extended Kalman filter (EKF). The results show that the improved D-S theory overcomes the limitations of the classical D-S theory, improves the accuracy and robustness of diagnosis and prediction, and can effectively integrate multi-source information. Experimental verification shows that the fused model is significantly better than a single model in terms of prediction accuracy and robustness, providing an efficient and reliable solution for fault diagnosis and health management of lithium-ion batteries.

1. Introduction

As a core energy storage technology, lithium-ion batteries (LIBs) have been widely used in modern society, covering consumer electronics, electric vehicles (EVs), and renewable energy systems, mainly due to their advantages such as high energy density, long cycle life, and low self-discharge rate. However, as the operating life of lithium-ion batteries increases, their performance will inevitably decline gradually, including capacity decay, increased internal resistance, and thermal management problems [1]. This not only reduces the reliability of the battery but also may cause potential safety risks such as overheating, electrolyte leakage, and even explosion. Therefore, the development of accurate and efficient fault diagnosis and remaining useful life (RUL) prediction technology is extremely important to ensure the safe operation of lithium-ion batteries and extend their service life [2].

Currently, research on the fault diagnosis and health status prediction of lithium-ion batteries mainly focuses on two categories of methods: model-based methods and data-driven methods. Model-based methods rely on physical or chemical models of batteries. For example, Chen et al. [3] used equivalent circuit models combined with data-driven methods to improve the accuracy of battery health status (SOH) prediction. Li et al. [4] improved the average estimation error by electrochemical impedance spectroscopy. Meng et al. [5] proposed a hybrid framework of empirical models of degradation. These methods have advantages in describing the intrinsic mechanisms of batteries and capturing their complex dynamics. Compared with traditional methods, these methods have advantages in describing the intrinsic mechanism of the battery and capturing its complex dynamics. For example, the equivalent circuit model represents the dynamic behavior of the battery by fitting the charge and discharge characteristics, while the electrochemical model provides a more accurate description of the degradation mechanism by simulating lithium-ion migration and electrode reactions. Zhang et al. [6] proposed a novel remaining life prediction method based on a double exponential empirical degradation model to fit the degradation of battery capacity and used an extended Kalman filter to improve the standard Kalman filter, effectively improving the prediction accuracy. Fahmy et al. [7] proposed an estimation method that combines the Newton–Raphson algorithm with the extended Kalman filter. This method can well match the actual cycle life with the predicted cycle life and has better accuracy than the linear regression method. However, model-based methods usually require a lot of prior knowledge and are challenging to calibrate due to the complexity of the modeling process. In practical applications, the diversity of battery behavior under different working conditions may cause deviations in the model, thereby increasing the prediction error.

In contrast, data-driven methods have received increasing attention and application in recent years. These methods use machine learning and deep learning algorithms to extract patterns and features from large-scale historical data without the need to accurately model the internal processes of the battery. For example, Li et al. [8] used an end-to-end neural network framework for SOH/RUL prediction. Wang et al. [9] proposed a multi-battery long short-term memory network to improve the accuracy of RUL prediction while reducing the computational burden. Guo et al. [10] used an optimal relevance vector machine with an improved degradation model to achieve stable and accurate prediction.

Li et al. [11] selected the charging data of the battery during the constant-current–constant-voltage process, selected a convolutional neural network to complete the capacity estimation, and verified it on the public security dataset. Pan et al. [12] proposed an adaptive battery remaining life prediction model based on wavelet packet decomposition and a two-dimensional convolutional neural network. The model is efficient in learning the long-term dependence of battery capacity degradation, and the superiority and prediction stability of the model was demonstrated using the NASA Ames Prediction Center of Excellence dataset. In addition, other machine learning and deep learning algorithms have also been widely used in battery state monitoring and RUL prediction. These methods are particularly effective in processing high-dimensional and nonlinear data and have demonstrated excellent performance in capturing complex patterns of battery degradation. However, data-driven methods are highly dependent on the quality and quantity of training data. When data is scarce or noisy, the accuracy and stability of these methods may drop significantly. In addition, the “black box” nature of deep learning models limits their interpretability, which is a key issue in areas with extremely high safety requirements (such as battery systems).

In order to overcome the limitations of the above methods, research in recent years has gradually turned to hybrid methods, combining model-based and data-driven methods to predict battery capacity decay and improve prediction accuracy [13]. On the one hand, model-based methods can provide physical constraints and prior knowledge, thereby enhancing the stability and credibility of data-driven models; on the other hand, data-driven methods can improve the adaptability and generalization ability of model-based methods by analyzing a large amount of operating data. In this context, multi-source information fusion technology has emerged as a promising research direction [14]. Its purpose is to integrate information from different data sources or prediction models to improve the accuracy and robustness of diagnosis and prediction.

As an effective multi-source information fusion method, Dempster–Shafer (D-S) evidence theory has attracted extensive attention in the field of LIBs fault diagnosis [15]. Compared with the traditional Bayesian probability method, D-S theory can simultaneously handle uncertainty and conflicting evidence by introducing trust functions and likelihood measures to represent the uncertainty of evidence. The main advantage of D-S theory is that it can synthesize multiple independent information sources without the need for precise prior probability distribution, thereby providing more reliable diagnosis and prediction results. However, under high-conflict conditions, the classical D-S theory has limitations. For example, when there is a strong conflict between the evidence sources, the fusion results may lose their effectiveness. This highlights the need to improve D-S theory to cope with the challenges of complex battery degradation scenarios.

Wang et al. [16] analyzed multiple factors affecting battery characteristics, constructed an evaluation index system for automotive battery life, and selected the Dempster–Shafer (D-S) evidence theory to integrate and quantify the factors to evaluate the battery life. Wang et al. [17] proposed a prediction method for the remaining useful life (RUL) of lithium-ion batteries based on DS data fusion and a support vector regression particle filter (SVR-PF). The results show that this prediction method can integrate the prediction results of lithium-ion battery RUL from different data sources and improve the prediction accuracy of RUL when less data is available.

In this paper, an improved D-S evidence theory framework is proposed for the fault diagnosis and RUL prediction of lithium-ion batteries. The framework combines the advantages of a wavelet packet decomposition convolutional neural network (WPD-CNN) and EKF and uses the improved D-S theory to fuse their outputs, thereby improving the accuracy and robustness of diagnosis and prediction. Specifically, this study is as follows:

1. WPD-CNN: WPD is used to perform multi-scale decomposition of lithium-ion battery time series data to extract frequency-domain features. These features are then input into the CNN for training and prediction of the RUL of the battery.

2. EKF: The extended Kalman filter is used to estimate the health state of the battery (such as SOH) in real time and dynamically update the model parameters to adapt to different working conditions.

The proposed research framework has important theoretical and practical significance. From a theoretical perspective, it combines the advantages of data-driven methods and model-based methods to provide a scalable solution for lithium-ion battery fault diagnosis. From a practical perspective, the improved D-S theory fusion method overcomes the limitations of the classical D-S theory under high-conflict conditions and provides new ideas for multi-source information fusion in various application scenarios.

The second part is an introduction to the research method, which gives a detailed introduction to the principles of the research method used, explains the experimental data of this paper, and supplements how to select features in the data. The third part verifies the selected method based on the experimental data and explains the accuracy of the method based on the comparison of several methods. The fourth part is the conclusion, which summarizes this paper.

2. Research Methods

This section elaborates on a lithium-ion battery fault diagnosis and RUL prediction method that combines WPD-CNN with EKF. The proposed method combines the advantages of data-driven and model-based techniques to build a robust and accurate diagnostic framework. Specifically, WPD-CNN is used to extract multi-scale features from battery operation data (such as voltage, current, and temperature) to achieve accurate identification of degradation patterns. At the same time, EKF provides a reliable dynamic state-estimation method for dynamic battery systems by modeling the battery health state under nonlinear and uncertain conditions. In order to address the conflicts and uncertainties inherent in the outputs of these two independent models, an improved D-S theory is adopted for information fusion.

The improved D-S theoretical framework introduces adaptive weighting of evidence sources based on the classic Dempster–Shafer combination rule, thereby addressing the challenges posed by high-conflict evidence. The basic belief assignment (BBA) from each information source (i.e., WPD-CNN and EKF) is defined as follows:

$$mi(A)={\displaystyle \frac{wi\cdot Pi(A)}{{\displaystyle {\sum }_j{w}_j\cdot P_j(A)}}}$$

(1)

In the above formula, ${\omega }_i$ represents the adaptive weight assigned to the evidence source, which is determined according to the confidence or reliability of the evidence source (e.g., prediction accuracy or uncertainty level). The fusion of evidence $m_1$ and $m_2$ from WPD-CNN and EKF is performed by the improved Dempster rule:

$$m_{12}(C)={\displaystyle \frac{{\displaystyle {\sum }_{A\cap B=C}{m}_1(A)\cdot m_2(B)}}{1-K}}$$

(2)

$$K={\displaystyle \sum _{A\cap B=\varnothing }{m}_1(A)\cdot m_2(B)}$$

(3)

The conflict coefficient is used to measure the consistency between evidence sources and adaptively adjust the weight distribution during the fusion process, ensuring that highly conflicting evidence is down-weighted, thereby improving the robustness of the fusion result.

The proposed method dynamically combines the complementary strengths of the two prediction models by integrating the outputs of WPD-CNN and EKF using a modified D-S theory (DST) framework. WPD-CNN excels in capturing nonlinear and high-dimensional degradation patterns from data, while EKF provides a model-driven approach to state estimation under uncertainty. The fusion process enables a comprehensive assessment of the battery state of health and RUL, ensuring the achievement of prediction accuracy and robustness.

The hybrid framework is designed to cope with the complex degradation problem of lithium-ion batteries under diverse operating conditions, enabling it to be extended to practical applications. In addition, the use of adaptive weighting in DST fusion introduces a certain flexibility, allowing the framework to dynamically adjust according to the reliability of each prediction source, thereby enhancing its performance in highly uncertain or noisy environments.

2.1. Wavelet Packet Decomposition

WPD is a powerful signal processing technique for analyzing non-stationary signals. WPD extends the traditional wavelet transform by decomposing the approximate coefficients and detail coefficients at each level, enabling a more detailed and multi-scale analysis of signal features. In this study, WPD is used to extract meaningful frequency domain features from battery operation data, which are essential for identifying degradation trends and predicting RUL.

The process of WPD involves iteratively decomposing the input signal $x(t)$ using a set of basis functions derived from the mother wavelet to generate sub-signals. At each level of decomposition, the signal is divided into multiple sub-bands to capture different frequency components. From a mathematical point of view, the decomposition process can be expressed as follows:

$$x(t)={\displaystyle \sum _k{\displaystyle \sum _j{c}_{j,k}{\psi }_{j,k}(t)}}$$

(4)

$c_{j,k}$ are the wavelet packet coefficients at scale $j$ and position $k$, and ${\psi }_{j,k}(t)$ represent the wavelet packet basis functions. These coefficients encapsulate the characteristics of the signal at different frequency bands, making them ideal for identifying features related to battery degradation.

After applying WPD, the extracted coefficients are organized into feature vectors and fed into a CNN for training and prediction. Convolutional neural networks excel in capturing spatial patterns and hierarchical features in data, making them well suited for processing multi-scale features obtained from wavelet packet decomposition. In this study, the structure of the convolutional neural network model consists of multiple convolutional layers, each followed by a rectified linear unit (ReLU) for nonlinear activation and a pooling layer for dimensionality reduction. The final fully connected layer maps high-level features to predict the remaining useful life.

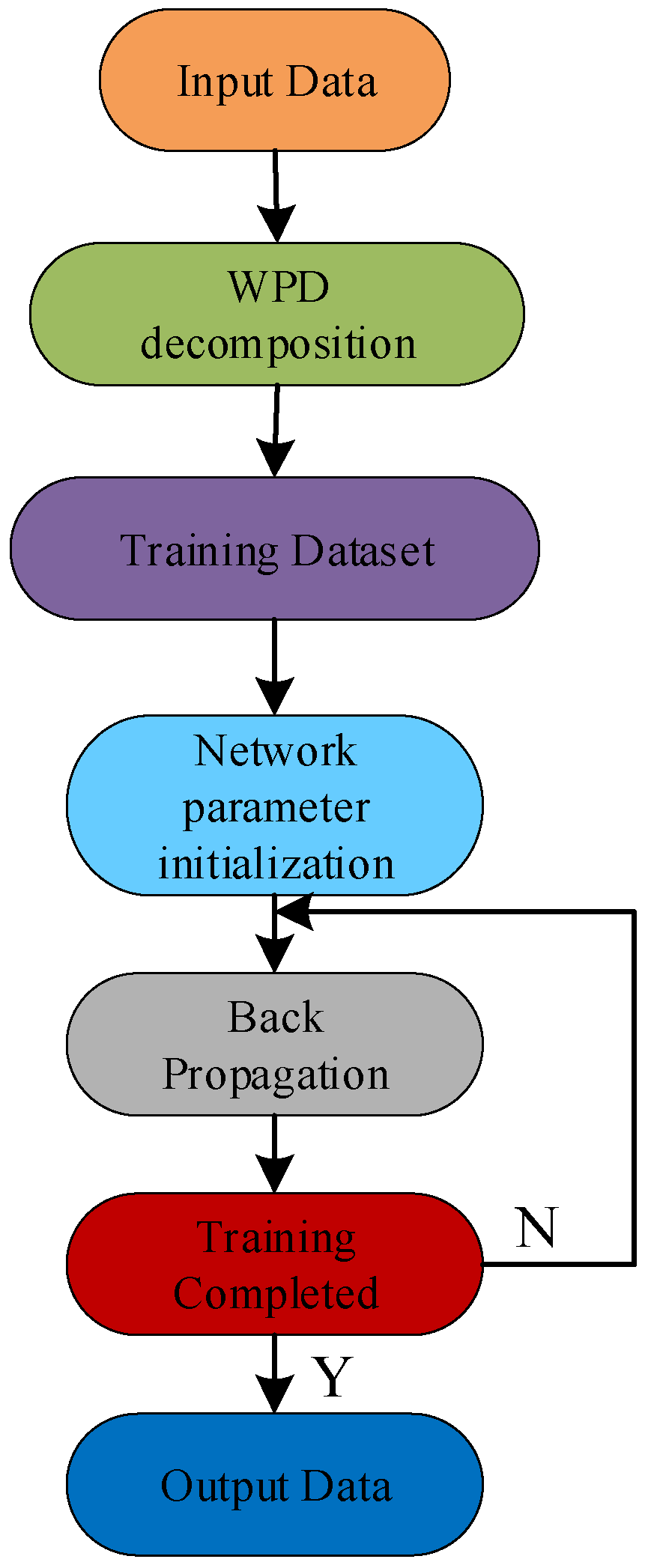
The WPD-CNN model works in two stages: offline training and online prediction. In the offline training stage, the CNN parameters are optimized using historical battery data, allowing the model to learn the complex relationship between multi-scale features and battery degradation patterns. In the online prediction stage, real-time battery data is decomposed through WPD, and the resulting coefficients are input into the trained CNN to predict the RUL. The structural process is shown in Figure 1.

The WPD-CNN framework is highly adaptable and can cope with different operating conditions and battery types because it can capture global and local degradation characteristics. However, the model’s predictions may be affected by uncertainties caused by data noise and model limitations. To address these issues, the output of the WPD-CNN is fused with the output of the EKF using a modified D-S theory. This fusion framework ensures that the final prediction results are both accurate and robust, effectively integrating the advantages of data-driven and model-based approaches.

2.2. Extended Kalman Filter

The EKF is a recursive state-estimation method for nonlinear dynamic systems and an extension of the classic linear Kalman filter (KF). Unlike the KF, which is limited to linear systems, the EKF locally linearizes the nonlinear system equations, enabling state estimation in complex scenarios. This makes the EKF particularly suitable for applications such as lithium-ion battery health state estimation and remaining service life prediction, because the battery degradation process is highly nonlinear and is affected by many factors, such as operating conditions, current load, and ambient temperature. Traditional linear methods have difficulty capturing the complex nonlinear degradation characteristics of lithium-ion batteries, while the EKF can reliably estimate the dynamically changing system state without a detailed understanding of the internal physical mechanism of the battery.

The degradation process of lithium-ion batteries can be modeled as a hidden Markov model (HMM), which is characterized by a state transfer equation and an observation equation. The state transfer equation models the dynamic change in battery capacity as a function of time and operating conditions and is defined as follows:

$$x_k=SO{H}_k$$

(5)

$$x_k=f(x_{k-1},u_{k-1})+w_{k-1}$$

(6)

$x_k$ represents the battery state of health in the $k$ cycle, and $k-1$ is the capacity state in the previous cycle. $f(\cdot )$ is a nonlinear state transfer function used to describe the degradation trend of the battery capacity under the operating condition $u_{k-1}$. $w_{k-1}$ represents the process noise, which is used to capture modeling errors and external disturbances and is assumed to obey a Gaussian distribution with a mean of zero and a covariance of $Q_{k-1}$.

The observation equation establishes the relationship between the system state and the observed data, so that the internal state of the battery can be inferred from the measurable external variables. It is defined as follows:

$$z_k=h(x_k)+v_k$$

(7)

where $z_k$ represents the observation vector, usually obtained by coulomb counting or battery voltage and current measurement; $h(\cdot )$ is a nonlinear observation function that maps the internal state $x_k$ to the observation data. And $v_k$ is the measurement noise, which is assumed to follow a Gaussian distribution $R_k$ with zero mean and covariance.

The EKF dynamically estimates the system state through an iterative prediction and update (correction) process. The core idea is to use the system model to predict the state of the next time step and then correct this prediction based on real-time measurement data to obtain a posterior state estimate.

In the prediction step, the state transition equation is used to predict the system state at the next time step and its associated uncertainty. This can be expressed as follows:

$${\widehat{x}}_{k|k-1}=f({\widehat{x}}_{k-1|k-1},u_{k-1})$$

(8)

$$P_{k|k-1}=F_{k-1}{P}_{k-1|k-1}{F}_{k-1}^{\mathrm{T}}+Q_{k-1}$$

(9)

${\widehat{x}}_{k|k-1}$ is the prior state estimate at $k$ time, derived from the a priori state estimate ${\widehat{x}}_{k-1|k-1}$ at the previous time step using the nonlinear state transfer function $f(\cdot )$ and the operating condition $u_{k-1}$. $P_{k|k-1}$ is the prior error covariance matrix, which quantifies the uncertainty of the predicted state. The linearization of the nonlinear state $f(\cdot )$ transfer function is achieved through the Jacobian matrix $F_{k-1}$, which is defined as follows:

$$F_{k-1}={\left.{\displaystyle \frac{\partial f}{\partial x}}\right|}_{{\widehat{x}}_{k-1|k-1,}{u}_{k-1}}$$

(10)

It captures a local linear approximation of the nonlinear relationship between states. The process noise covariance $Q_{k-1}$ is used to describe the uncertainty introduced in the state prediction process.

In the update step, the predicted state estimate is corrected using real-time measurement data $z_k$.

First, the calculation formula of Kalman gain $K_k$ is as follows:

$$K_k=P_{k|k-1}{H}_k^T{(H_k{P}_{k|k-1}{H}_k^T+R_k)}^{-1}$$

(11)

$H_k$ is the Jacobian matrix of the nonlinear observation function $h(\cdot )$, defined as follows:

$$H_k={\left.{\displaystyle \frac{\partial h}{\partial x}}\right|}_{{\widehat{x}}_{k|k-1}}$$

(12)

It captures the local linear relationship between the state variables $x_k$ and the observed variables $z_k$. The measurement noise covariance matrix $R_k$ reflects the uncertainty in the observed data.

The posterior state estimate ${\widehat{x}}_{k|k}$ is then updated by incorporating the measurement residuals (the difference between the observed and predicted values):

$${\widehat{x}}_{k|k}={\widehat{x}}_{k|k-1}+K_k(z_k-h({\widehat{x}}_{k|k-1}))$$

(13)

$z_k-h({\widehat{x}}_{k|k-1})$ is the residual, representing the difference between the observed measurement and the predicted measurement based on the prior state estimate. Finally, the posterior error covariance matrix is updated as follows:

$$P_{k|k}=(I-K_k{H}_k)P_{k|k-1}$$

(14)

$I$ is the identity matrix, and $P_{k|k}$ represents the updated uncertainty of the state estimate after incorporating the measurement data.

In lithium-ion battery RUL prediction, the prediction step of the EKF is recursively applied to generate future capacity estimates over multiple cycles. These estimates are then compared to a predefined failure threshold to calculate the time to failure (TTF). However, in long-term prediction scenarios, the correction step cannot be performed due to the lack of real-time measurement data, which will lead to the accumulation of uncertainty in the prediction error covariance matrix $P_{k|k-1}$. This uncertainty must be carefully managed to ensure the reliability of the prediction results.

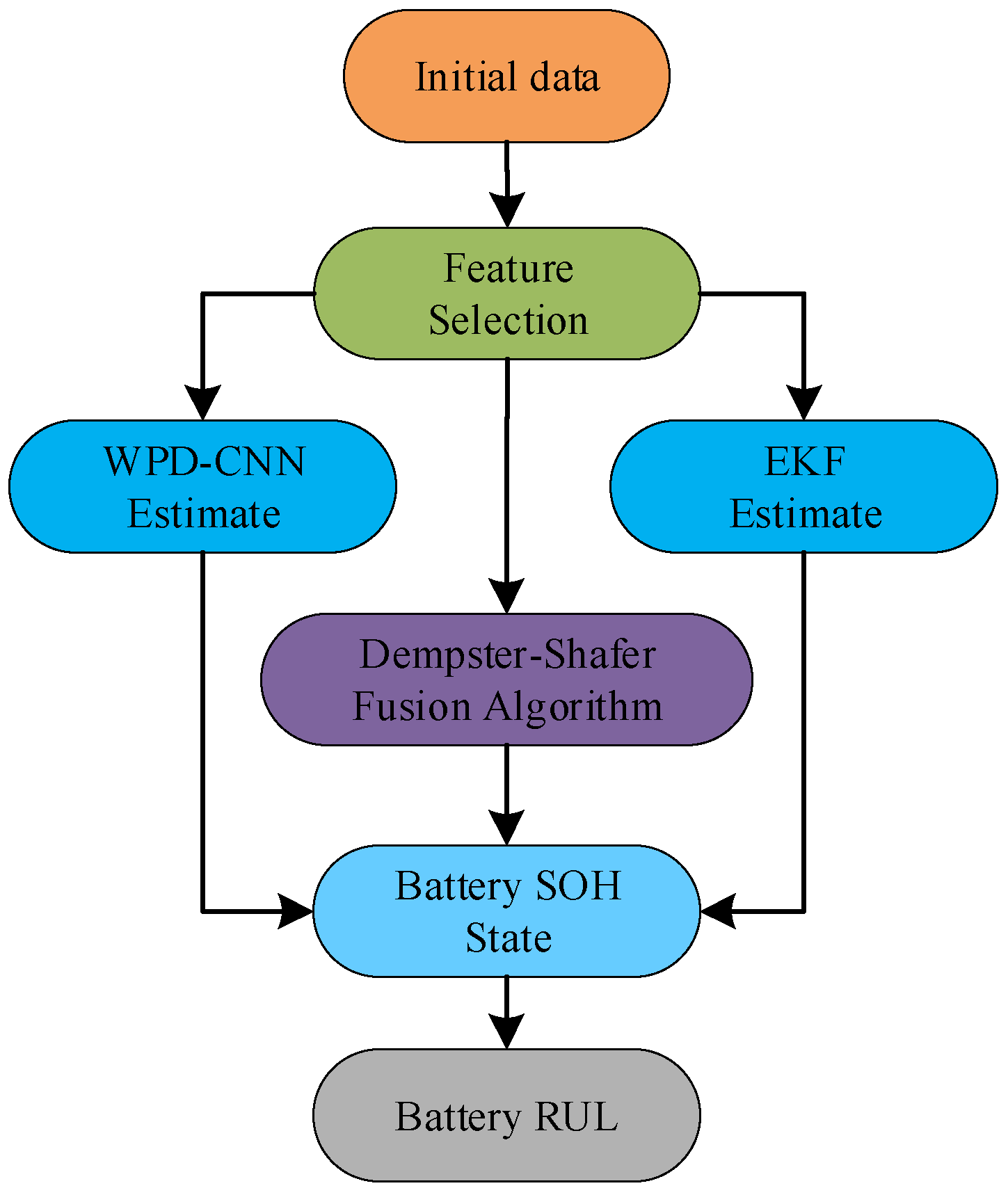
In order to address the limitations of single-model prediction, this study adopts an improved D-S evidence theory framework to fuse the output of the EKF with the results of the WPD-CNN. The overall process of the model is shown in Figure 2. The improved D-S theory dynamically adjusts its weight according to the reliability of the information source, effectively alleviating the uncertainty associated with each method. As a model-driven component in the framework, EKF provides robust physical insights into the degradation process, while its combination with data-driven methods enhances the overall accuracy and robustness of RUL prediction. This hybrid approach ensures a comprehensive and reliable diagnostic framework for lithium-ion battery systems.

2.3. Experimental Data

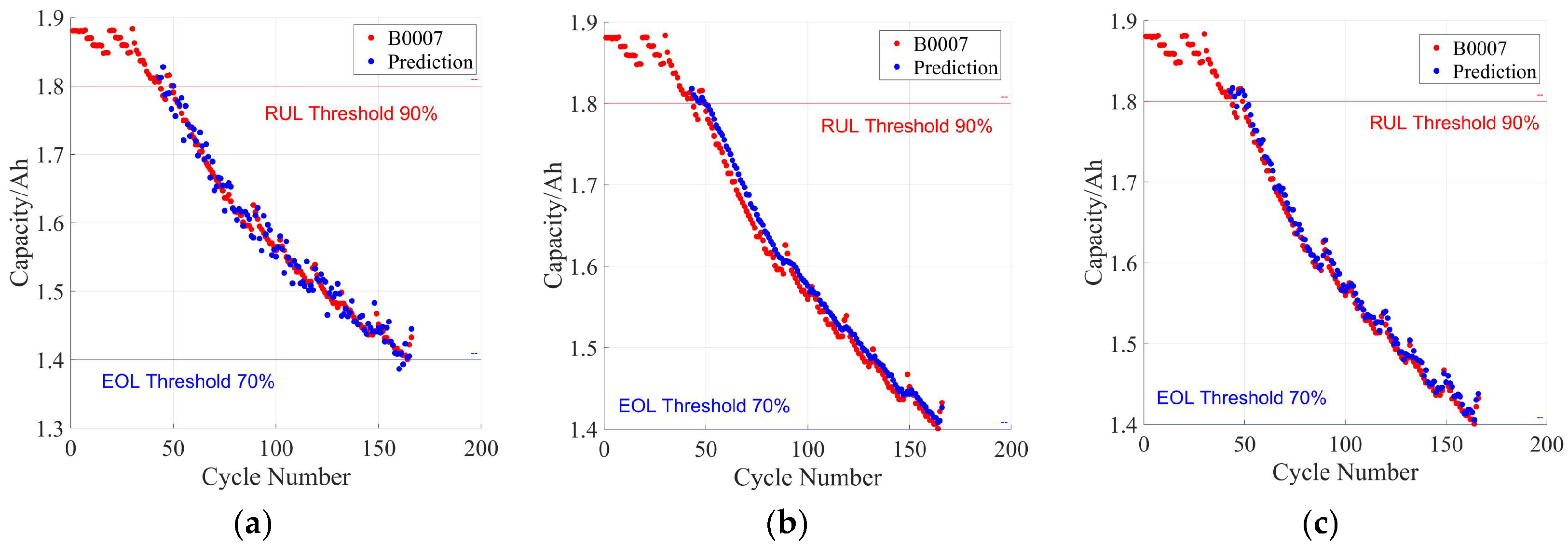
The original dataset of the lithium-ion battery aging cycle comes from the battery charge and discharge aging test data provided by the National Aeronautics and Space Administration (NASA) Center of Excellence. The dataset uses a lithium-ion battery with a nominal capacity of 2 Ah. NASA’s specific experimental settings are as follows: at a room temperature of 24 °C, constant current charging is performed at a current of 1.5 A until the battery voltage reaches 4.2 V, followed by switching to a constant voltage model to continue charging until the charging current drops below 20 mA. Constant current discharge is performed at a current of 2 A until the end of life is reached, and the test is stopped.

2.4. Feature Selection

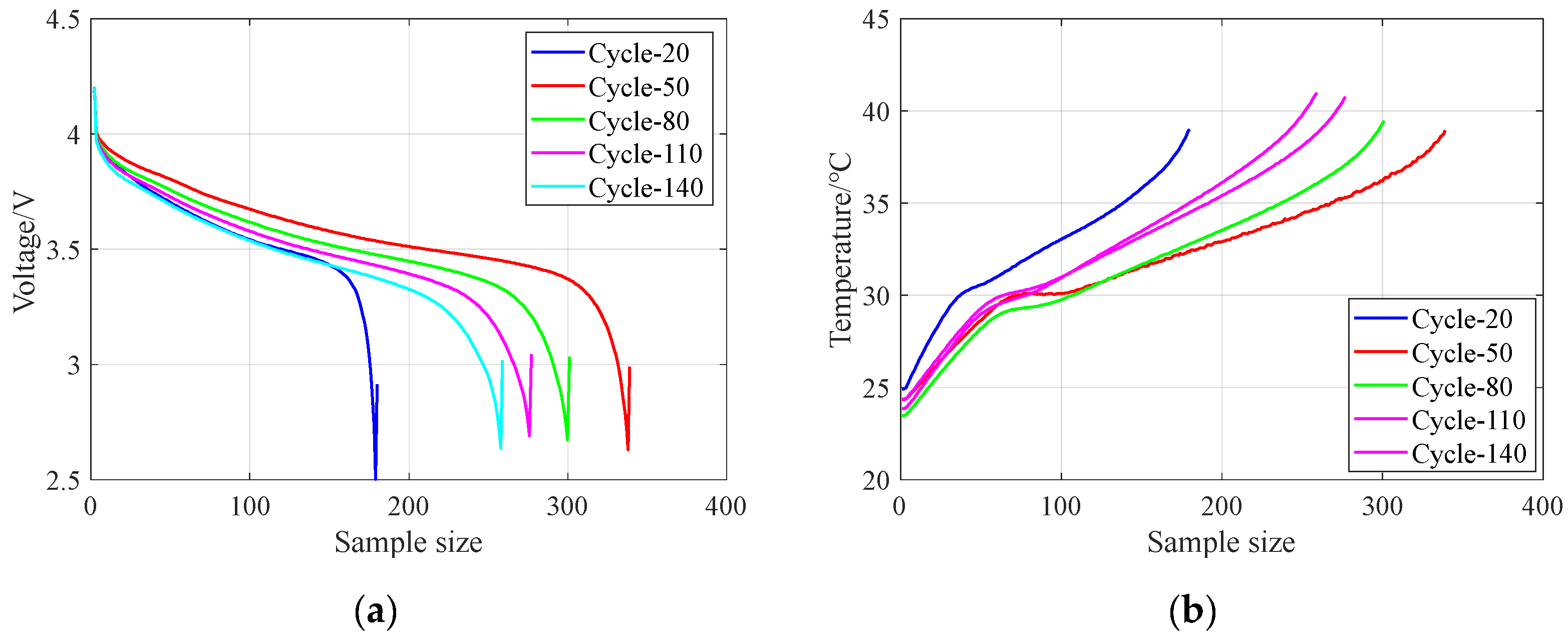
This paper selects battery aging data for analysis, selects aging characteristic quantities in 168 cycles as the input of the model, and selects the voltage and temperature variables of the 20th, 50th, 80th, 110th, and 140th times for illustration. Figure 3a is a schematic diagram of the discharge temperature of the B0005 battery. Figure 3b is a schematic diagram of the discharge voltage of the B0005 battery.

As can be seen from Figure 3, as the number of cycles increases, the temperature of the battery gradually increases, indicating that the internal impedance of the battery is gradually increasing. Therefore, it can also be used as a characteristic of the battery. Under the actual working conditions of the battery, it is not convenient to measure the internal resistance of the battery, which limits the amount of aging. Therefore, we can judge the degree of battery aging by analyzing the internal temperature of the battery.

As the number of cycles increases, the slope of the battery discharge voltage curve gradually changes from flat to steep, indicating that the voltage may serve as a key indicator for battery aging. The characteristics of battery aging are reflected in changes in discharge voltage and temperature. Therefore, the remaining service life of the battery can be estimated by analyzing these two parameters.

3. Results

3.1. Evaluation Indicators

This paper uses the root mean square error (RMSE) and the coefficient of determination (R² score), two indicators used to describe the prediction error, to evaluate the accuracy of the ML model. Their expressions are as follows:

$$R^2=1-{\displaystyle \frac{\frac{1}{n}{\displaystyle {\sum }_{i=1}^n{(y_i-{\stackrel{\cdot }{y}}_i)}^2}}{\frac{1}{n}{\displaystyle {\sum }_{i=1}^n{(y_i-y_i)}^2}}}$$

(15)

$$RMSE=\sqrt{{\displaystyle \frac{1}{n}}{{\displaystyle \sum _{i=1}^n(y-{\stackrel{\cdot }{y}}_i)}}^2}$$

(16)

The closer the R² value is to 1, the better the model performance is, and the closer the RMSE value is to 0, the better the model performance is.

3.2. Comparison of Results

To compare the RUL prediction performance of the three methods, we used data from batteries B0005, B0006, and B0007. The RUL prediction threshold was set to 90% of nominal capacity, and end-of-life (EOL) was defined as 70% of nominal capacity. A high prediction threshold reduces the data available for health status analysis, thereby imposing more stringent conditions on the algorithms. The specific parameters of B0005, B0006, and B0007 batteries are shown in

Table 1. Battery-related parameters.

	Charge Cut-Off Voltage/V	Discharge Cut-Off Voltage/V	Charging Current/A	Discharge Current/A	Rated Capacity/Ah
B0005	4.2	2.7	1.5	2	2
B0006	4.2	2.5	1.5	2	2
B0007	4.2	2.2	1.5	2	2

.

The prediction results are presented as scatter plots in Figure 4, Figure 5 and Figure 6. In these plots, blue markers denote model predictions, and red markers denote observed battery data. Figure 4 depicts the results for battery B0005. For B0005, the WPD-CNN model’s predictions closely match the observed data distribution, achieving R² = 0.93 and RMSE = 0.035. This demonstrates WPD-CNN’s capacity to handle nonlinear, high-dimensional inputs and to extract informative features for accurate RUL estimation. However, EKF predictions exhibit a slight downward bias (R² = 0.89; RMSE = 0.076). This likely reflects the EKF’s reliance on model propagation without real-time corrections, leading to error accumulation over extended horizons. By contrast, the fusion model—via the improved D-S theory and adaptive weighting—yields R² = 0.98 and RMSE = 0.015, demonstrating superior accuracy and stability by effectively combining WPD-CNN’s nonlinear feature extraction with the EKF’s state-estimation robustness.

Figure 5 illustrates the results for battery B0006. For battery B0006, WPD-CNN and EKF individually achieve R² = 0.91 (RMSE = 0.058) and R² = 0.92 (RMSE = 0.032), respectively. Although EKF slightly outperforms WPD-CNN alone, the fusion model achieves R² = 0.998 and RMSE = 0.009, representing an even more robust prediction. This further confirms that the fusion approach leverages WPD-CNN’s ability to capture complex degradation patterns and EKF’s dynamic state-estimation robustness to yield highly accurate RUL forecasts. These results demonstrate that the improved D-S theory effectively integrates complementary model strengths, maintaining excellent performance across diverse battery chemistries and degradation profiles.

Figure 6 presents the results for battery B0007. For B0007, WPD-CNN predictions exhibit substantial fluctuations. This instability may reflect sensitivity to data noise or inherent limitations when modeling specific battery behaviors. EKF predictions display a gradual upward bias, possibly due to insufficient sensitivity to key features in this battery’s data. However, the fusion model effectively suppresses these instabilities, achieving R² = 0.94 and RMSE = 0.007—substantially outperforming either model alone. This demonstrates that the improved D-S theory dynamically adjusts source weights based on reliability, thereby mitigating single-model biases and enhancing prediction stability and confidence. The root mean square errors of various methods are shown in

Table 2. RMSE evaluation indicators of different methods.

	WPD-CNN	EKF	D-S
B0005	0.93	0.89	0.98
B0006	0.91	0.92	0.998
B0007	0.89	0.92	0.94

, and the R² scores are shown in

Table 3. R² score evaluation indicators of different methods.

	WPD-CNN	EKF	D-S
B0005	0.035	0.076	0.015
B0006	0.058	0.032	0.009
B0007	0.085	0.056	0.007

.

Overall, the improved D-S framework addresses high-conflict uncertainty via adaptive weighting, enabling excellent prediction performance across diverse battery datasets. Experimental results confirm that the method not only achieves high-precision RUL forecasts but also demonstrates enhanced robustness and adaptability.

4. Conclusions

This study proposes a method for predicting the remaining useful life (RUL) of lithium-ion batteries based on the improved Dempster–Shafer evidence theory, which effectively solves the problem of high-conflict evidence fusion through an adaptive weighting mechanism. Specifically, the wavelet packet decomposition convolutional neural network (WPD-CNN) is first used to automatically extract battery operation characteristics, and then the extended Kalman filter (EKF) is combined to estimate the battery state in real time, and the outputs of both are regarded as evidence sources and fused. Experimental results show that on multiple standard battery datasets, the determination coefficient R² of the fusion model is increased to 0.94–0.998, and the root mean square error (RMSE) is reduced to 0.007–0.015, which is significantly better than a single data-driven or model-driven method. This article also emphasizes the key influence of reasonable assumptions and uncertainty function design on the fusion effect and points out that the prediction accuracy can be improved by further optimizing the network structure or adjusting the uncertainty allocation strategy. This method has the advantages of both data-driven and model-driven and provides an efficient and reliable RUL prediction solution for battery health management and safe operation in electric vehicles and energy storage systems, which has broad application prospects and promotion value.