The Molecular Dynamics of Signature Gas Diffusions in Synthetic-Ester-Based Oil Under a Range of Thermal Conditions
Abstract
1. Introduction
2. Simulation Methodology
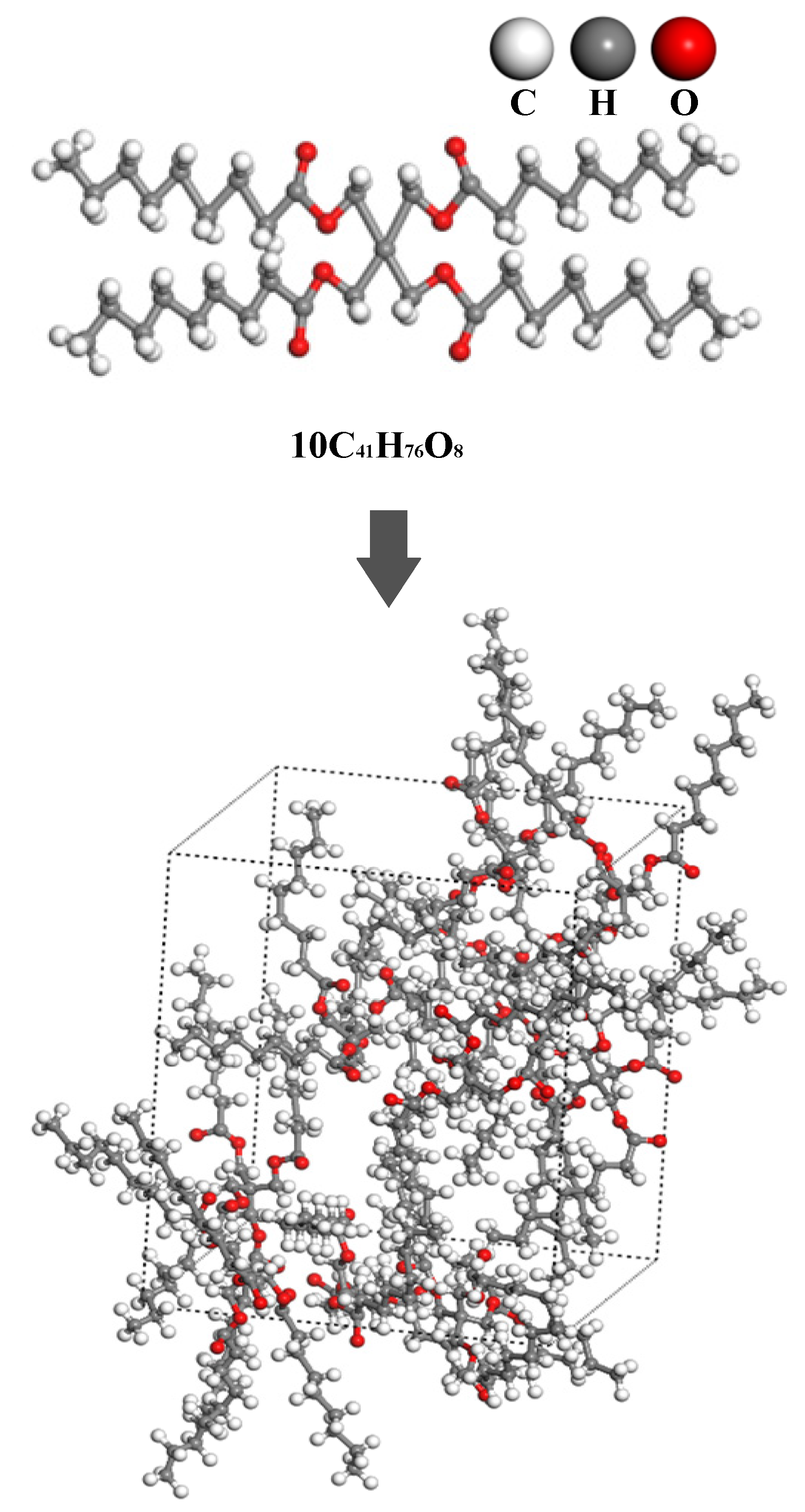
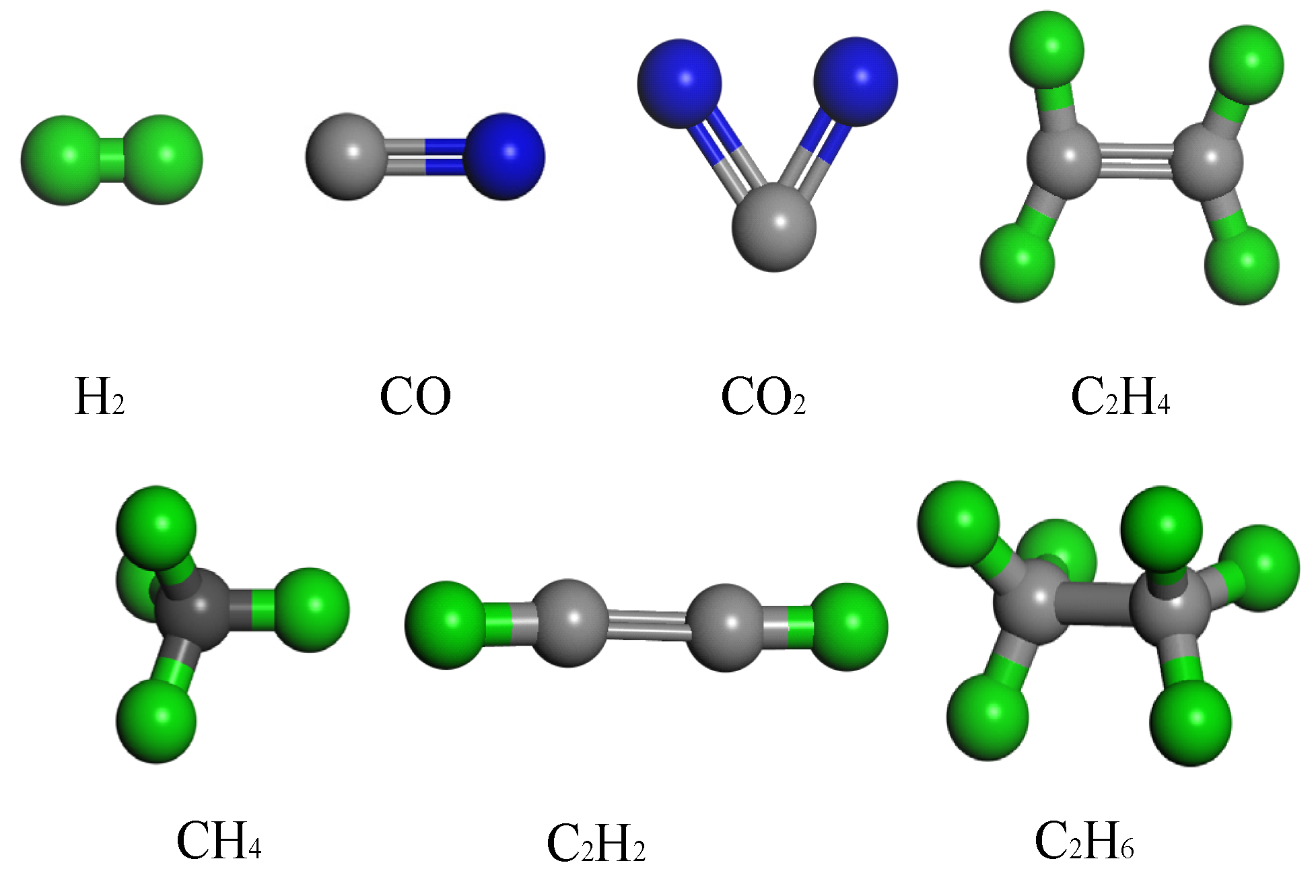
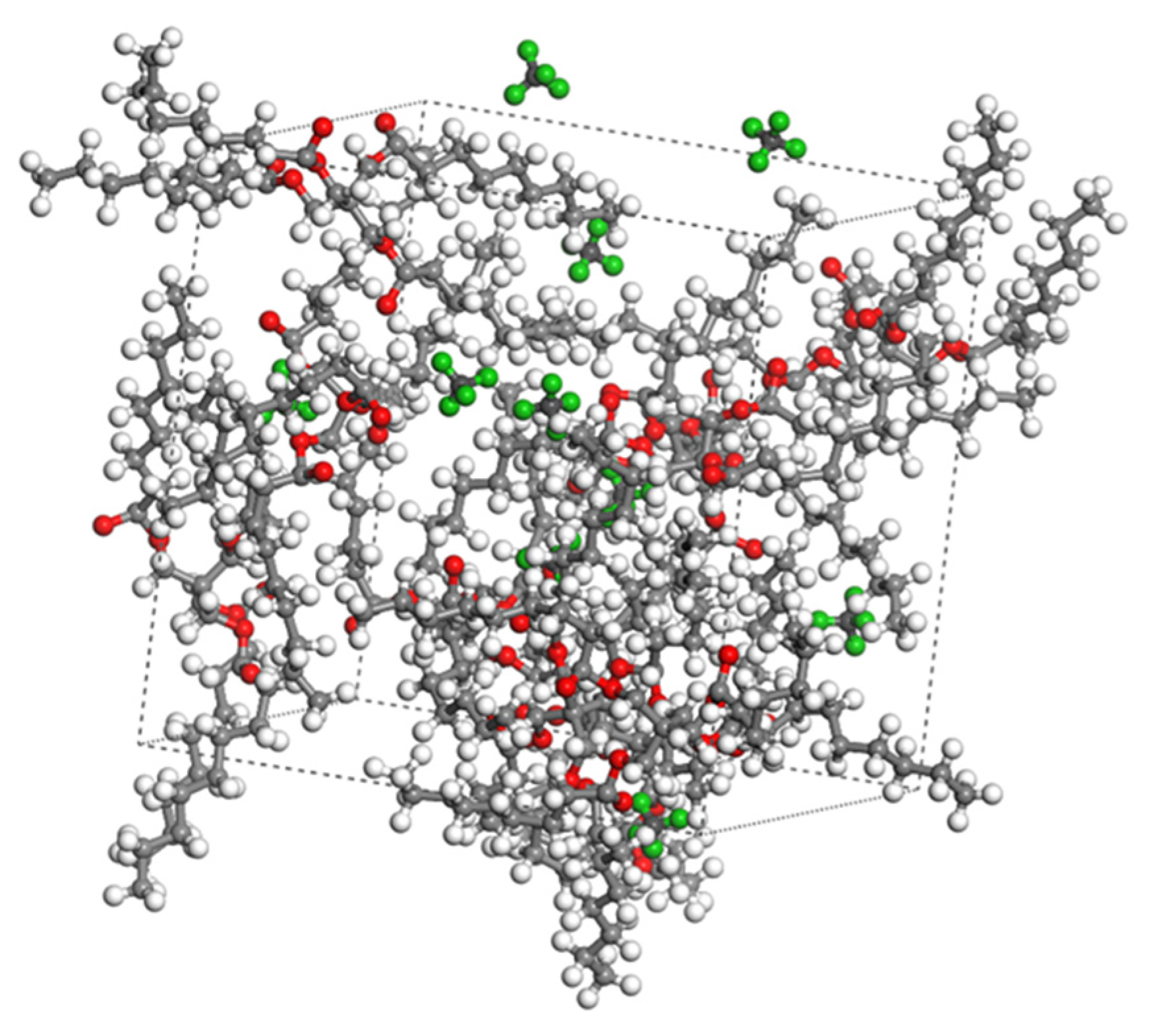
2.1. Molecular Diffusion Modeling of Synthetic Esters
2.2. Simulation Parameter Settings
- (1)
- A preliminary composite model of synthetic ester oil molecules and gas molecules is constructed and undergoes 10,000 steps of geometric structure optimization to eliminate potential atomic overlaps and non-physical contact.
- (2)
- Pressure relaxation is performed under the NPT ensemble for 100 ps to allow the system’s density to converge to 0.95 g/cm3, ensuring the accuracy of subsequent simulations.
3. Results and Discussion
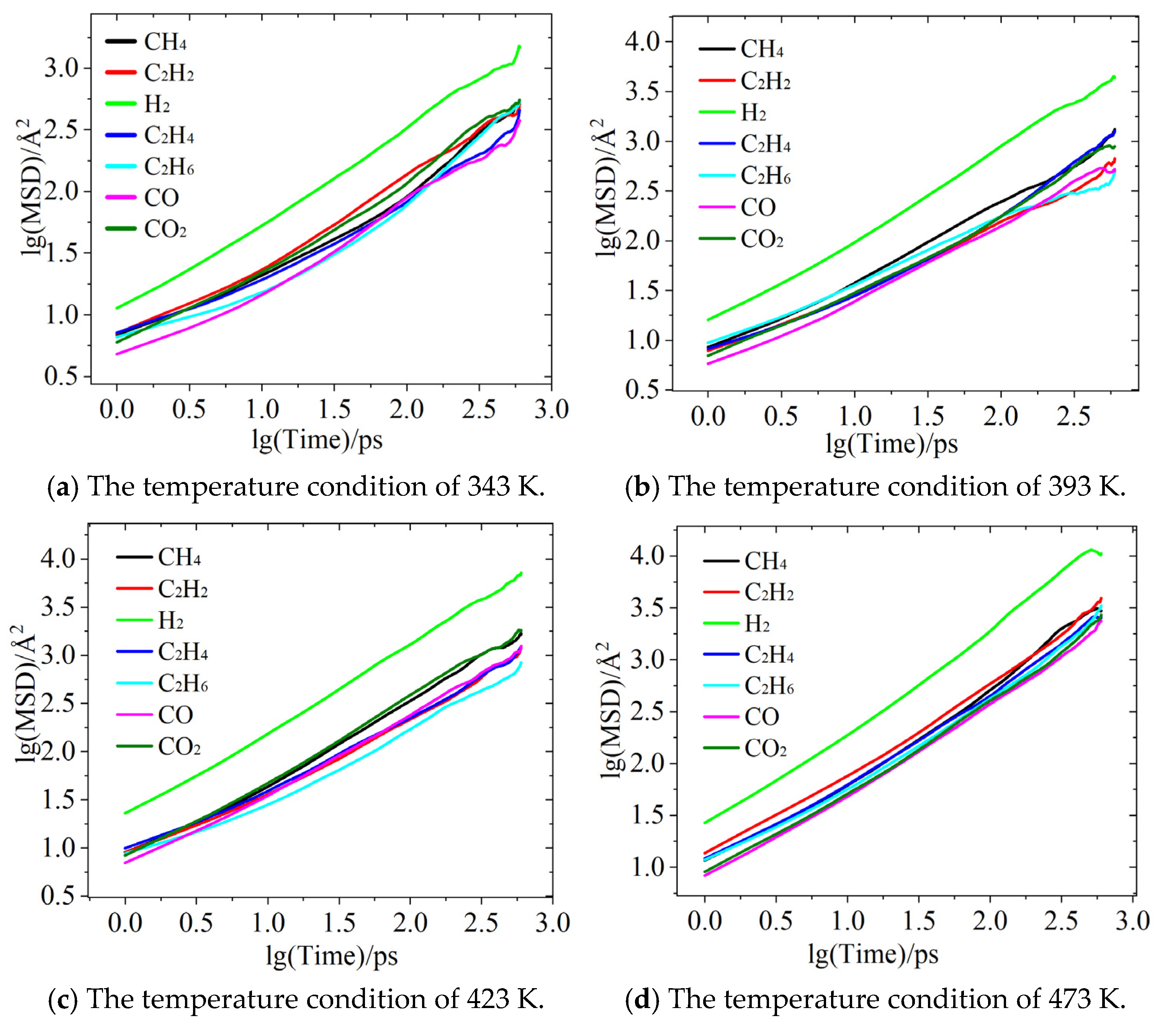
3.1. Characteristic Gas Diffusion Properties
3.2. Characteristic Gas Diffusion Coefficient
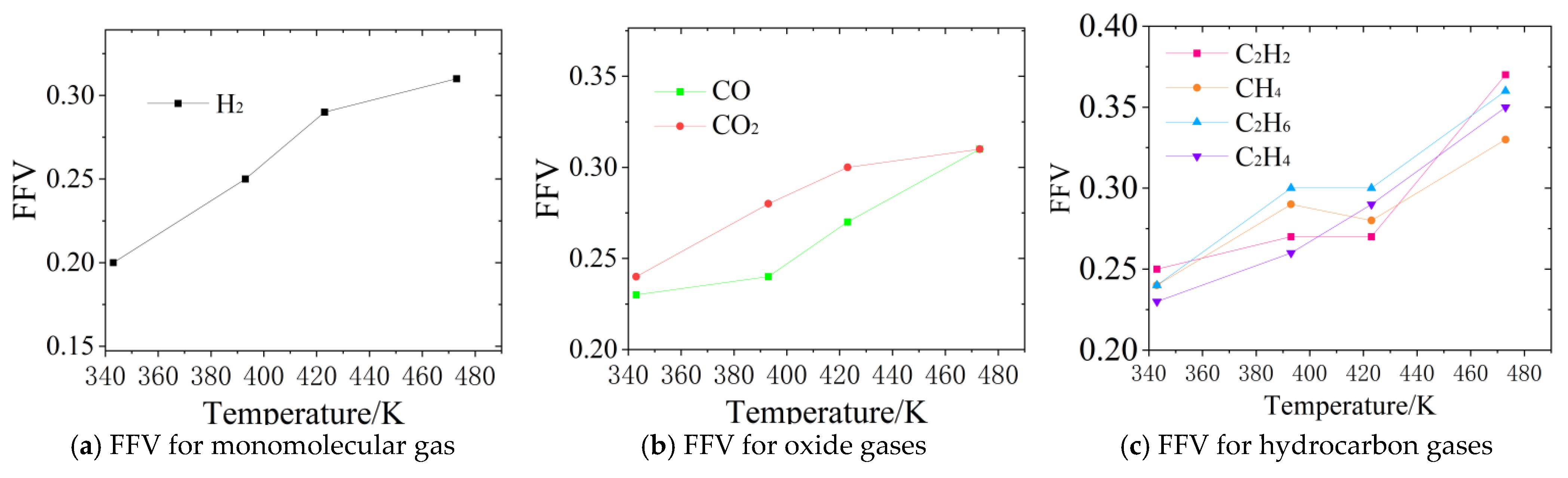
3.3. Analysis of the Free Volume
4. Conclusions
- (1)
- Under varying temperature conditions, the diffusion coefficients of all the gases studied exhibit a nonlinear increase with an increase in temperature. Hydrogen gas (H2), due to its extremely low molecular weight and weak intermolecular forces, shows a dramatic increase in the diffusion coefficient, from 33.430 × 10−6 cm2/s at 343 K to 402.763 × 10−6 cm2/s at 473 K, reflecting a 12-fold increase. This rate of increase is significantly higher than that observed for the other gases. Among the hydrocarbons, C2H2, with its linear molecular structure, demonstrates a notable advantage in diffusion at elevated temperatures, reaching 99.719 × 10−6 cm2/s at 473 K.
- (2)
- As the temperature increases, the free-volume fraction (FFV) of each molecular system rises substantially, ranging from 0.20 to 0.37. This increase is primarily due to thermal effects, which expand the intermolecular gaps and diffusion channels, thereby reducing resistance to gas migration. Furthermore, by correlating changes in diffusion coefficients with variations in FFV, it was observed that the 12-fold increase in the diffusion coefficient of H2 corresponds to a 55% increase in its FFV. This correlation further substantiates the applicability of Free-Volume Theory (FVT) in explaining the diffusion behavior of gases in synthetic esters.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Jovalekic, M.; Vukovic, D.; Tenbohlen, S. Gassing behavior of various alternative insulating liquids under thermal and electrical stress. In Proceedings of the IEEE International Symposium on Electrical Insulation, San Juan, Puerto Rico, 10–13 June 2012. [Google Scholar]
- Li, D.; Rao, X.; Zhang, L.; Zhang, Y.; Ma, S.; Chen, L.; Yu, Z. First-Principle Insight into the Ru-Doped PtSe2 Monolayer for Detection of H2 and C2H2 in Transformer Oil. ACS Omega 2020, 5, 31872–31879. [Google Scholar] [CrossRef] [PubMed]
- Liao, Y.; Zhou, Q.; Hou, W.; Li, J.; Zeng, W. Theoretical study of dissolved gas molecules in transformer oil adsorbed on intrinsic and Cr-doped InP3 monolayer. Appl. Surf. Sci. 2021, 561, 149816. [Google Scholar] [CrossRef]
- Wang, J.; Zhang, X.; Liu, L.; Wang, Z. Dissolved gas analysis in transformer oil using Ni-Doped GaN monolayer: A DFT study. Superlattices Microstruct. 2021, 159, 107055. [Google Scholar] [CrossRef]
- Fan, X.; Luo, H.; Liang, F.; Hu, J.; Liu, W.; Li, C.; He, J. Photon Count Technique as a Potential Tool for Insulation Micro-Defect Detection: Principles and Primary Results. iEnergy 2023, 2, 258–263. [Google Scholar] [CrossRef]
- Fan, X.; Niu, S.; Luo, H.; Liang, J.; Liu, F.; Li, W.; Liu, W.; Gao, W.; Huang, Y.; Li, C.; et al. Photon counting technique as a potential tool in micro-defect detection of epoxy insulation pull rod in gas-insulated switchgears. High Volt. 2024, 9, 267–274. [Google Scholar] [CrossRef]
- Jayyid, U.L.; Fadillah, A.; Kurniawan, M.; Suwarno; Rachmawati; Lesmana, A.; Mutia, S.; Anwar, A. Comparative Study of Mineral Oil, Synthetic Ester, and Natural Ester as Liquid Insulation in Transformers. In Proceedings of the 2024 6th International Conference on Power Engineering and Renewable Energy (ICPERE), Bandung, Indonesia, 5–6 November 2024. [Google Scholar]
- Lee, S.; Jeong, H.; Park, J.; Seok, B.Y.; Ryu, J.; Bae, C. Research on Dielectric Strength Properties of Synthetic Ester Oil. In Proceedings of the 2024 10th International Conference on Condition Monitoring and Diagnosis (CMD), Gangneung, Republic of Korea, 20–24 October 2024. [Google Scholar]
- Guerbas, F.; Adjaout, L.; Abada, A.; Rahal, D. New and Reclamation Transformer Oil Behavior under Accelerated Thermal Aging. In Proceedings of the IEEE International Conference on High Voltage Engineering and Application (ICHVE), Chongqing, China, 10–13 September 2018. [Google Scholar]
- Cheng, C.; Fu, M.; Wu, K.; Ma, Y.; Hao, Y.; Chen, C. Aging Effect on Interface Charges between Oil and Oil Immersed Paper. IEEE Trans. Dielectr. Electr. Insul. 2021, 28, 1579–1587. [Google Scholar] [CrossRef]
- Martins, M.A.G.; Gomes, A.R. Comparative study of the thermal degradation of synthetic and natural esters and mineral oil: Effect of oil type in the thermal degradation of insulating kraft paper. Electr. Insul. Mag. IEEE 2012, 28, 22–28. [Google Scholar] [CrossRef]
- Song, H.; Meng, H.; Yuanxin, Y.; Weiguang, Y.; Yupeng, Y.; Yuzhen, L. Influence of Electric Field Distribution on Breakdown Characteristics of Oil-paper Composite Insulation Under DC Voltage. High Volt. Eng. 2023, 49, 4938–4947. [Google Scholar]
- Zhang, Y.; Wang, F.; Li, S.; Zhang, Y.; Li, J.; Huang, Z. Evaluation of Basic Properties and Thermal Oxidation Aging Performance for Synthetic Ester Insulating Oils. In Proceedings of the 2024 IEEE 7th International Electrical and Energy Conference (CIEEC), Harbin, China, 10–12 May 2024. [Google Scholar]
- Wu, Y.; Lin, Y.; Wu, P.; Xu, J.; Xie, T.; Gao, C.; Hao, J. Pressure Influence Analysis of Dissolved Gas in Insulation Oil Based on Molecular Simulation and Experimental Comparsion. In Proceedings of the 2021 6th Asia Conference on Power and Electrical Engineering (ACPEE), Chongqing, China, 8–11 April 2021; pp. 756–760. [Google Scholar]
- Perrier, C.; Marugan, M.; Beroual, A. DGA comparison between ester and mineral oils. IEEE Trans. Dielectr. Electr. Insul. 2012, 19, 1609–1614. [Google Scholar] [CrossRef]
- Rumpelt, P.; Fritsche, R.; Bakija, B.; Jenau, F. Long-term investigations of partial discharge and gassing behavior of ester-based insulating oils for a heated oil gap. In Proceedings of the International Universities Power Engineering Conference, Heraklion, Greece, 28–31 August 2017. [Google Scholar]
- Lashbrook, M.; Al-Amin, H.; Martin, R. Natural Ester and Synthetic Ester Fluids, Applications and Maintenance. In Proceedings of the 2017 10th Jordanian International Electrical and Electronics Engineering Conference (JIEEEC), Amman, Jordan, 16–17 May 2017. [Google Scholar]
- Suksagoolpanya, S.; Jongvilaikasem, K.; Jariyanurat, K.; Banthoengjai, T.; Jeenmuang, S.; Pattanadech, N. Dissolved Gas Analysis of Palm Oil Compared with Mineral Oil from Different Types of Breakdown Voltage. In Proceedings of the International Conference on Condition Monitoring and Diagnosis, Bangkok, Thailand, 26–28 October 2020. [Google Scholar]
- Suhaimi, N.S.; Ishak, M.T.; Din, M.F.M.; Ariffin, M.M.; Amin, N.A.M.; Hamid, M.H.A. Dissolved Gases Analysis of Rice Bran Oil Under Thermal Fault for Transformer Application. In Proceedings of the 2022 IEEE International Conference on Power and Energy (PECon), Langkawi, Kedah, Malaysia, 5–6 December 2022; pp. 1–6. [Google Scholar]
- Hamid, M.H.A.; Ishak, M.T.; Ariffin, M.M.; Katim, N.I.A.; Amin, N.A.M.; Azis, N. Dissolved gas analysis (DGA) of vegetable oils under electrical stress. In Proceedings of the International Conference on High Voltage Engineering and Power Systems, Denpasar, Indonesia, 2–5 October 2017. [Google Scholar]
- Williamson, C.; Timoshkin, I.V.; MacGregor, S.J.; Wilson, M.P.; Given, M.J.; Sinclair, M.; Jones, A. Impulsive Breakdown of Mineral Oil and Natural and Synthetic Ester Liquids When Containing Varying Levels of Moisture. IEEE Trans. Plasma Sci. 2021, 49, 466–475. [Google Scholar] [CrossRef]
- Przybylek, P.; Gielniak, J. Analysis of Gas Generated in Mineral Oil, Synthetic Ester, and Natural Ester as a Consequence of Thermal Faults. IEEE Access 2019, 7, 65040–65051. [Google Scholar] [CrossRef]
- Przybylek, P. Drying transformer cellulose insulation by means of synthetic ester. IEEE Trans. Dielectr. Electr. Insul. 2017, 24, 2643–2648. [Google Scholar] [CrossRef]
- Gao, B. Molecular dynamics study on thermal decomposition characteristics of synthetic ester oil. Chem. Phys. Lett. 2023, 813, 140302. [Google Scholar] [CrossRef]
- Tao, J.; Zhan, H.; Luo, C.; Hu, S.; Duan, X.; Liao, M. Diffusion Properties of Gas Molecules in Oil–Paper Insulation System Based on Molecular Dynamics Simulation. Energies 2024, 17, 3811. [Google Scholar] [CrossRef]
- Ye, W.; Hao, J.; Chen, Y.; Zhu, M.; Pan, Z.; Hou, F. Difference Analysis of Gas Molecules Diffusion Behavior in Natural Ester and Mineral Oil Based on Molecular Dynamic Simulation. Molecules 2019, 24, 4463. [Google Scholar] [CrossRef] [PubMed]
- Liu, X.H.; Men, R.J.; Jianng, W.; Li, L.; Wang, W.; Lei, Z. Molecular Dynamics Simulation of the Effects of Nano-SiO2 Modified by Different Silane Coupling Agents on the Thermal, Mechanical and Electrical Properties of Polypropylene Nanocomposites. High Volt. Eng. 2025. [Google Scholar] [CrossRef]

| H2 | CO | C2H2 | CH4 | CO2 | C2H6 | C2H4 | ||
|---|---|---|---|---|---|---|---|---|
| 343 K | Slope, k | 2.006 | 0.434 | 0.799 | 0.862 | 0.943 | 0.918 | 0.539 |
| Fitted correlation coefficient, R2 | 0.976 | 0.980 | 0.987 | 0.991 | 0.973 | 0.998 | 0.990 | |
| Diffusion coefficient D/×10−6 cm2/s | 33.430 | 7.225 | 8.992 | 14.365 | 15.722 | 15.295 | 8.992 | |
| 393 K | Slope, k | 6.936 | 1.087 | 2.010 | 1.627 | 1.786 | 0.511 | 2.010 |
| Fitted correlation coefficient, R2 | 0.990 | 0.994 | 0.994 | 0.990 | 0.997 | 0.926 | 0.999 | |
| Diffusion coefficient D/×10−6 cm2/s | 115.607 | 18.113 | 13.915 | 27.112 | 29.770 | 8.510 | 33.494 | |
| 423 K | Slope, k | 10.911 | 1.804 | 1.809 | 2.665 | 2.656 | 1.114 | 1.685 |
| Fitted correlation coefficient, R2 | 0.994 | 0.994 | 0.993 | 0.972 | 0.981 | 0.988 | 0.992 | |
| Diffusion coefficient D/×10−6 cm2/s | 181.85 | 30.074 | 30.154 | 44.410 | 44.263 | 18.559 | 28.088 | |
| 473 K | Slope, k | 24.166 | 3.377 | 5.983 | 6.187 | 3.998 | 4.411 | 4.741 |
| Fitted correlation coefficient, R2 | 0.999 | 0.998 | 0.992 | 0.995 | 0.990 | 0.997 | 0.997 | |
| Diffusion coefficient D/×10−6 cm2/s | 402.763 | 56.278 | 99.719 | 103.119 | 66.631 | 73.524 | 79.014 | |
| H2 | CO | C2H2 | CH4 | CO2 | C2H6 | C2H4 | ||
|---|---|---|---|---|---|---|---|---|
| 343 K | VO/Å3 | 10,350.02 | 10,485.33 | 10,533.40 | 10,529.35 | 10,505.37 | 10,666.58 | 10,625.38 |
| VF/Å3 | 2646.90 | 3142.39 | 3464.01 | 3269.71 | 3281.19 | 3356.80 | 3195.41 | |
| FFV | 0.20 | 0.23 | 0.25 | 0.24 | 0.24 | 0.24 | 0.23 | |
| 393 K | VO/Å3 | 10,160.35 | 10,393.38 | 10,427.70 | 10,257.76 | 10,396.42 | 10,531.99 | 10,533.93 |
| VF/Å3 | 3372.90 | 3366.26 | 3770.76 | 4197.00 | 3944.10 | 4437.33 | 3675.62 | |
| FFV | 0.25 | 0.24 | 0.27 | 0.29 | 0.28 | 0.30 | 0.26 | |
| 423 K | VO/Å3 | 10,104.14 | 10,371.54 | 10,459.69 | 10,437.51 | 10,300.77 | 10,447.81 | 10,475.45 |
| VF/Å3 | 4037.57 | 3794.67 | 3797.13 | 3965.30 | 4510.79 | 4450.45 | 4269.83 | |
| FFV | 0.29 | 0.27 | 0.27 | 0.28 | 0.30 | 0.30 | 0.29 | |
| 473 K | VO/Å3 | 10,004.15 | 10,161.04 | 10,069.42 | 10,126.33 | 10,319.65 | 10,322.82 | 10,165.65 |
| VF/Å3 | 4418.79 | 4601.97 | 5883.93 | 4889.77 | 4559.66 | 5706.45 | 5360.52 | |
| FFV | 0.31 | 0.31 | 0.37 | 0.33 | 0.31 | 0.36 | 0.35 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guo, L.; Wang, H.; Qi, W.; Zhang, J.; Lu, W. The Molecular Dynamics of Signature Gas Diffusions in Synthetic-Ester-Based Oil Under a Range of Thermal Conditions. Energies 2025, 18, 3276. https://doi.org/10.3390/en18133276
Guo L, Wang H, Qi W, Zhang J, Lu W. The Molecular Dynamics of Signature Gas Diffusions in Synthetic-Ester-Based Oil Under a Range of Thermal Conditions. Energies. 2025; 18(13):3276. https://doi.org/10.3390/en18133276
Chicago/Turabian StyleGuo, Liping, Hongliang Wang, Weiwei Qi, Jun Zhang, and Wu Lu. 2025. "The Molecular Dynamics of Signature Gas Diffusions in Synthetic-Ester-Based Oil Under a Range of Thermal Conditions" Energies 18, no. 13: 3276. https://doi.org/10.3390/en18133276
APA StyleGuo, L., Wang, H., Qi, W., Zhang, J., & Lu, W. (2025). The Molecular Dynamics of Signature Gas Diffusions in Synthetic-Ester-Based Oil Under a Range of Thermal Conditions. Energies, 18(13), 3276. https://doi.org/10.3390/en18133276






