Review on Research and Development of Magnetic Bearings

Abstract

This paper reviews the research advancements and development in magnetic bearings. Firstly, from the technical principle, the design differences and application areas of active magnetic bearings, permanent magnetic bearings and hybrid structures are clarified. At the key technology level, focusing on electromagnetic design optimization, control strategy innovation and power-driven energy management, the breakthrough points of multi-physics coupling modeling, vibration suppression and energy efficiency improvement are revealed. Through the analysis of its engineering cases in the fields of high-speed motors, flywheel energy storage, aerospace and so on, the feasibility and economy of the technical scheme are verified. Further, the technical bottlenecks that need to be broken through are pointed out. For the future trend, this paper suggests that integration of interdisciplinary high-precision modeling, intelligent control algorithm and miniaturized integrated design should be deeply integrated to promote the large-scale application of magnetic bearing in frontier fields. This paper provides theoretical reference and engineering practice guidance for the technology iteration and cross-field integration of magnetic bearings.

1. Introduction

The traditional bearings mainly include rolling bearings, sliding bearings and oil film bearings. With the development of industrial technology towards high speed, high precision and high reliability, the limitations of traditional bearings under special working conditions have become increasingly prominent: friction and wear, speed limit, lubrication, vibration and noise, and maintenance costs. These limitations have prompted people to seek new non-contact support technologies, and magnetic bearing is a breakthrough solution that emerged in this context [1,2,3,4,5,6].

Traditional bearings continue to have cost advantages under conventional operating conditions, but their technical limitations are becoming more apparent in specialized environments such as high-speed, vacuum, and ultra-clean conditions. This highlights the clear need for the development of magnetic bearings in such applications. Magnetic bearings represent an advanced support technology that utilizes magnetic forces to achieve non-contact suspension of the rotor. The basic principle involves balancing the rotor’s weight and other loads through the magnetic force generated by electromagnets or permanent magnets (PM), thereby enabling frictionless suspension between the rotor and stator [7,8,9]. Compared with traditional bearings, magnetic bearings have the following advantages: no contact and no wear, high speed, energy saving and efficiency, clean and environmental protection, as well as strong controllability [10,11].

Since its inception in the 19th century, maglev technology has evolved from theoretical exploration to practical engineering applications. Its development can be broadly categorized into three key stages:

1.

Concept Exploration Period (1842–1960):

In 1842, Earnshaw introduced the concept of magnetic levitation and demonstrated that stable levitation of ferromagnetic materials in all degrees of freedom cannot be achieved using only permanent magnets, thereby establishing the mathematical foundation of magnetic levitation theory [12]. In 1937, Kemper filed the first patent related to magnetic levitation technology and proposed the use of actively controlled electromagnets for achieving stable levitation—a milestone in the development of magnetic bearings and maglev transportation systems [13,14].

2.

Technology Development Period (1960–1990):

Between the 1950s and 1960s, Beams successfully applied magnetic levitation to ultra-high-speed centrifuges, marking the first implementation of magnetic support for rotating bodies [15]. In 1972, the LRBA Laboratory pioneered the application of magnetic bearings in satellite reaction wheels, setting a precedent for engineering applications of the technology [16].

3.

Engineering Application Period (1990–Present):

In 1983, the United States employed a magnetic bearing vacuum pump aboard the Space Shuttle, demonstrating its reliability under extreme conditions [17]. By 1997, Draper Laboratory reported a series of advancements in high-temperature magnetic bearings capable of operating at 510 °C for aerospace engine applications [18]. As of 2021, magnetic levitation technology has been widely adopted in molecular pumps, blowers, compressors, and other industrial systems [19,20,21]. According to industry reports [22,23,24,25], the global magnetic bearing market size was about $2 billion in 2023 and is expected to grow to about $3.34 billion by 2032, with a compound annual growth rate (CAGR) of about 5.96% from 2024 to 2032. The top five manufacturers include SKF, Schaeffler, Siemens, GE and NSK, which together occupy more than 60% of the market share.

Table 1. Magnetic bearing application and index [28].

Applications	Power (kW)	Speed (r/min)	Characteristic
Power Generation	2~150	35,000~220,000	Wide power range, super high speed
Flywheel Energy Storage System	120	40,000	High power, high speed
High-Speed Spindles	1~24	9000~180,000	Low power, wide speed range
Turbo Molecular Pumps	Few hundred Watt	100,000	Micropower, ultra-high speed
Gas Compressors	10,000	20,000	Industrial high power, medium speed
Air Compressors	100~150	80~15,000	High power, wide speed range
Micro Turbines	50	80,000	Compact high power
Turbo Generators	30	60,000	High efficiency, high speed

summarizes representative applications and key performance parameters of magnetic bearings [26,27,28]. Despite remarkable progress, magnetic bearing technology still faces several challenges, including high cost (approximately 3–5 times that of conventional bearings), complex control requirements, and limited reliability. In particular, applications involving heavy loads (e.g., large-scale generator sets) and extreme environments (e.g., ultra-high temperatures) continue to demand critical technological breakthroughs. Current research is shifting from single-objective performance optimization toward integrated design approaches that emphasize high speed, high load capacity, and enhanced reliability.

This review aims to provide a systematic overview of the development of magnetic bearing technology, outlining major technical challenges and future research directions. It is intended as a comprehensive reference for both academic researchers and industrial practitioners. The structure of the review is as follows:

• Section 2 discusses the classification and operating principles of magnetic bearings, including the technical characteristics and comparisons of active, passive, and hybrid types.
• Section 3 focuses on core technologies, including structural design, control algorithms, and drive systems.
• Section 4 presents typical application scenarios in energy, transportation, industrial systems, and other domains.
• Section 5 addresses current technical challenges and explores future development trends.
• Section 6 concludes the review with final remarks.

2. Classification and Comparison of Magnetic Bearing

Magnetic bearings can be classified in various ways depending on different criteria:

• Type of Magnetic Force: Attractive or repulsive forces.
• Suspension Mode: Active, passive, or hybrid systems.
• Magnet Type: Superconducting, permanent magnet, or electromagnetic.
• Structural Configuration: Horizontal or vertical orientation; internal or external rotor.
• Degree of Contact: Fully non-contact or partially contact-based systems.
• Control Current Type: Alternating current (AC) or direct current (DC).
• Magnetic Pole Arrangement: Heteropolar or homopolar configurations.
• Degrees of Freedom (DOF): Axial (1 DOF), radial (2 DOF), combined radial-axial (3 DOF), or extended to 4 and 5 DOF systems.

Given the diversity of magnetic bearing types, it is challenging to encompass all variants from a single classification perspective. Therefore, it is reasonable to select a broad classification method that includes most of the styles according to the suspension mode and then subdivides them. At present, the most widely used is classified by suspension mode, that is, active, passive and hybrid magnetic bearings [29,30].

2.1. Classification of Magnetic Bearing

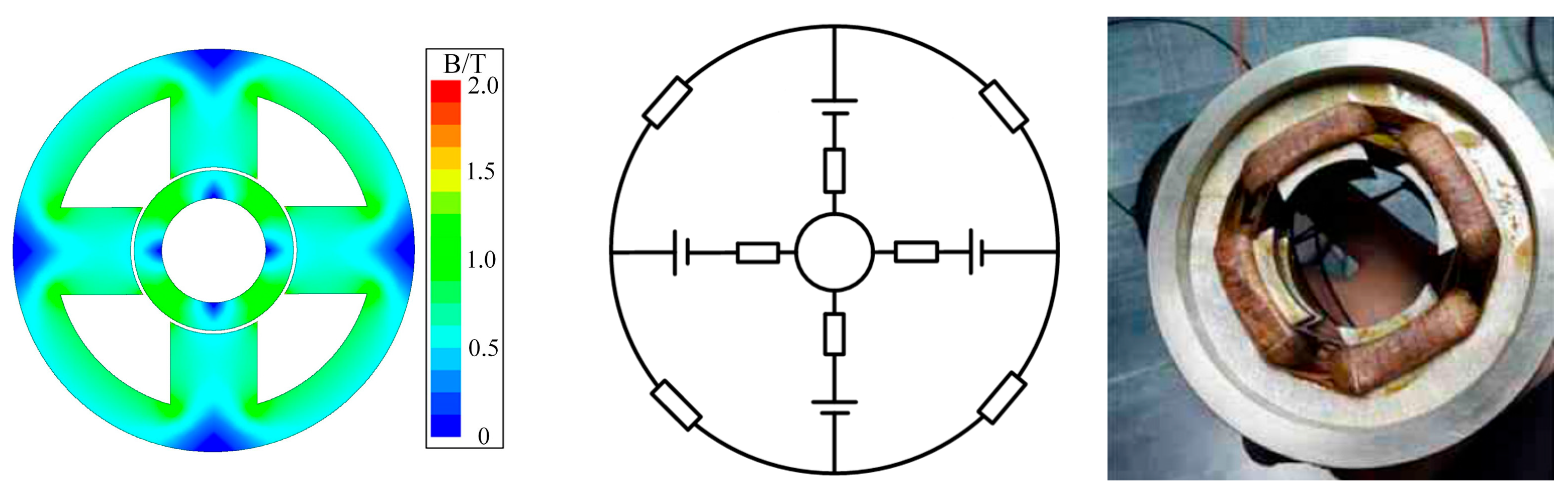
2.1.1. Active Magnetic Bearings

Active Magnetic Bearings (AMB) achieve stable rotor suspension through controllable electromagnetic forces [31,32]. The materials of its stator and rotor are mostly silicon steel sheets or electric pure iron, and the coils are wound with copper wires. The stiffness and damping characteristics of the electromagnetic force can be dynamically adjusted via control algorithms, enabling precise regulation of bearing performance. Due to this controllability, AMBs offer a broader range of applications compared to other types of magnetic bearings. A typical configuration of AMBs is the radial magnetic bearing (RMB). Common structural designs include the 4-pole and 8-pole radial AMB configurations, as illustrated in Figure 1 and Figure 2 [28,33,34].

The 4-pole RMB represents the simplest structural form of radial magnetic bearings. However, in many industrial applications, the 8-pole RMB is more widely adopted due to its superior performance. In an 8-pole configuration, adjacent magnetic poles pair to form four independent magnetic circuits, effectively decoupling the magnetic forces along four radial directions. This structural advantage simplifies control and improves dynamic stability. To regulate the currents in the four coil pairs, either two bipolar power amplifiers or four unipolar power amplifiers can be employed. Position sensors continuously monitor rotor displacement and provide feedback to the control system, which adjusts the coil currents in real time to maintain the rotor at the center position [35], as shown in Figure 3.

2.1.2. Passive Magnetic Bearings

Passive Magnetic Bearings (PMBs) achieve rotor suspension through magnetic fields generated by their own permanent or induced magnetism. A key advantage of PMBs is their simple structure, which requires no active control systems or external power, resulting in zero power consumption. However, this simplicity also means that the stiffness and damping of the system cannot be actively adjusted, which limits their versatility compared to active systems.

PMBs can be classified into three categories based on their suspension mechanisms:

• Superconducting Magnetic Bearings,
• Diamagnetic Magnetic Bearings and
• Permanent Magnetic Bearings.

Among these, superconducting and diamagnetic bearings have limited practical use due to the need for cryogenic environments and inherently low stiffness, respectively. In contrast, permanent magnetic bearings are more commonly employed in practical applications [36,37]. The material of magnetic rings mostly adopts NdFeB with better performance. An example of a permanent magnetic bearing is illustrated in Figure 4.

Compared with AMB, the support force and stiffness provided by PMBs are relatively lower [38,39]. Therefore, PMBs generally adopt a stacked structure of multiple pairs of magnetic rings to achieve higher support stiffness. The basic design consists of two PM rings. Based on polarity and the layout direction, there are four basic configurations [40], namely radially attractive and repulsive types and axially attractive and repulsive types, as shown in Figure 5 and Figure 6. In Figure 5a, when the two rings are offset in the radial direction, the attractive force will pull them back to the middle position, while the repulsive force will push them back to the middle position in Figure 5c.

The attractive-type PMB is an unstable system when compared to the repulsive-type. For instance, in radial PMB (a), if the control failure occurs in the axial direction, the suspended rotor may drop or collide upward, which will damage the brittle magnetic ring. In contrast, the repulsive-type PMB overcomes the shortcomings of the attractive-type PMB. In the case of axial control failure, it can prevent the impact force caused by attraction and avoid damage to the bearing. However, repulsive PMB requires higher PM coercivity to resist demagnetization.

To address the low bearing capacity and stiffness associated with a single pair of magnetic rings, stacking is often used to improve their performance in engineering applications. Eight different topologies can be obtained from two stacking ways and four magnetization combinations [41,42,43]. The various combinations of stacking and magnetization are presented in

Table 2. Stacking structure under different magnetization.

	Axial Magnetized	Radial Magnetized	Vertical Magnetized	Halbach Magnetized
Axial stacking
Radial stacking

.

2.1.3. Hybrid Magnetic Bearings

Hybrid Magnetic Bearings (HMB) are an extension of the AMB design, incorporating permanent magnets (PMs) embedded within the tooth or yoke to generate a static bias magnetic field. This integration allows for the omission of the coil that typically generates the bias field, resulting in a more compact structure, reduced power consumption, and improved power density [44,45]. However, this configuration introduces greater complexity compared to traditional AMBs. For instance, in Figure 7, PMs are embedded in three alternating magnetic poles [46,47]. These permanent magnets create a permanent bias magnetic circuit in conjunction with the adjacent magnetic poles. The control current is then introduced into the coils to adjust the magnetic force. Compared to AMBs, which rely on coils to generate both bias and control magnetic fields, the current required in the coils of HMBs is inherently lower.

2.2. Comparison of Magnetic Bearing

The previous section provides a summary of the classification and fundamental principles of magnetic bearings. This classification framework serves as the foundation for understanding the diversity of magnetic bearing technologies and for selecting the most appropriate technical approaches.

Table 3. Comparison of basic characteristics of three types of magnetic bearings.

Characteristic	AMB	PMB	HMB
Source of force	Electromagnet [33,34]	PM [40,41,42,43]	PM + Electromagnet [46,47]
Control system	sensor and active control	Non-active control	Partial active control
Power consumption	High (continuous power supply)	0	Medium (adjustment only)
Stability	Full degree of freedom and stability	Required auxiliary stabilization	Full degree of freedom and stability
Typical application	High-precision machine tools [48], aircraft engines	Instrument, simple suspension device [43]	Compressor, flywheel energy storage [49]
Nonlinearity	Strong	Medium	Linearization around the operating point
Force density	Medium	Low	High
Speed range (r/min)	104~106	103~104	104~105
Reliability	High (electronic devices limit)	Extremely high (no active parts)	Very high

presents a comparative analysis of the basic characteristics of the three main types of magnetic bearings.

The diverse technical options available for magnetic bearings offer a wide range of choices for various industrial applications.

Table 4. Comparison of the main application fields of three types of magnetic bearings.

Applications	AMB	PMB	HMB	Technical Selection Basis
High-speed precision machining	CNC machine tool spindle [48]	-	Mid-end machine tool [47]	Accuracy and response speed
Fluid machinery	Special operating compressor [50]	Micro-flow pump [42]	Centrifugal compressor, blower [51]	Balance of power and efficiency
Energy equipment	Flywheel energy storage [52]	-	Wind turbine, fuel cell compressor [45]	Reliability and maintenance
Transportation	Maglev train [53]	-	-	Large-scale accurate control
Aerospace	Satellite flywheel [54], APU	Simple suspension device [40]	Space actuators [55]	Environmental adaptability
Medical device	-	Artificial heart pump [56]	-	Zero power consumption and biological compatibility

outlines the current application status and typical use cases of active, permanent magnet, and hybrid magnetic bearings across different industries, highlighting the relationship between their technical characteristics and application requirements.

Magnetic bearings offer numerous advantages; however, each type presents distinct technical challenges and application limitations that directly influence their adoption across various industries.

Table 5. Comparison of the main technical limitations of three types of magnetic bearings.

Technical Limitation	AMB	PMB	HMB	Solutions
Cost	Very high (electronic system)	Low-medium	Medium-high	Scale and integration
Temperature limit	Medium (electronic devices)	High (PM limit)	Medium	high-temperature materials
Stability risk	Control failure	Earnshaw theorem	Medium	Improved protection bearing
Force density	Medium	Low	High	Optimize magnetic circuit
Standardization	High	Low	Low	Promoting industry standards
Typical failure mode	Electronic system failure	PM demagnetization	Electromagnetic under-regulation	Redundancy design

summarizes and compares the primary technical limitations associated with each type of magnetic bearing. These limitations not only act as barriers to the widespread use and implementation of magnetic bearings but also highlight potential avenues for future technological advancements.

3. Research Progress on Key Technologies of Magnetic Bearing

Although magnetic bearings have been successfully applied across various fields, evolving demands require further enhancements in their performance. To fully harness their potential in high-speed and non-contact applications, the development and integration of several key technologies are crucial.

3.1. Topology and Modeling

3.1.1. Bearing Topologies

Various new configurations have been developed based on the conventional 4-pole and 8-pole active RMBs to enhance performance and reduce losses. The 4-pole RMB offers a simple coil layout and structural symmetry, making it ideal for small to medium-sized rotors. However, the magnetic circuits along the x and y axes are coupled. In contrast, the 8-pole RMB provides higher magnetic flux concentration and better control. However, with all eight poles arranged in a single plane and alternating north-south polarity, the magnetic field completes two full cycles per rotor revolution, leading to significant hysteresis and eddy current losses. To overcome these challenges, the 3-pole RMB presents a promising, compact alternative, particularly suited for rotors with small shaft diameters [48,57,58,59,60]. Additionally, using a three-phase inverter for control significantly reduces both system cost and complexity [61,62,63,64,65], as shown in Figure 8.

In the 4-pole and 8-pole RMBs, the displacement in one axis is decoupled from the current and position in the orthogonal axis. However, the structural asymmetry of the 3-pole RMB introduces cross-coupling between electromagnetic forces along the x and y axes, thus increasing control complexity and susceptibility to instability. As a result, decoupling strategies must be integrated into the control algorithm to ensure system stability and precision [48,57,58,59,60,61,62,63,64,65,66,67]. To address this coupling issue, a 6-pole RMB topology has been proposed, as illustrated in Figure 9 [68]. Decoupling among the three pairs of electromagnets can be realized either by connecting coils on diametrically opposed poles or by linking coils on adjacent poles. These configurations enable a reduction in the number of drivers and power amplifiers, thereby lowering system cost and power consumption [47,69,70,71,72]. However, a notable limitation of this design is its relatively low resultant force coefficient due to the 120° spatial separation between electromagnets.

As the rotor diameter increases, the number of poles in magnetic bearings must also be increased to ensure adequate load capacity [73,74]. For instance, 12-pole and 16-pole RMBs, as shown in Figure 10a,b, provide comparable load-bearing capabilities to conventional 8-pole designs for medium- and large-sized rotors while offering reduced magnetic coupling effects and improved magnetic field uniformity. High-pole-count magnetic bearings are well-suited for applications such as industrial compressor blowers and heavy-duty centrifuges. However, these configurations require more power amplifiers and higher driving voltages, posing additional challenges in system design and integration. For magnetic bearings with a high number of poles used in very large rotors (as shown in Figure 10c, the marginal improvement in load capacity diminishes with increasing pole count, though the magnetic field becomes more uniformly distributed [75]. A modular pole design can enhance overall stiffness and mechanical robustness; however, it introduces greater assembly complexity, necessitates precise current control in each coil, and leads to elevated eddy current losses.

Table 6. Comparison of magnetic bearings with different poles.

Poles	Bearing Capacity	Stiffness	Power	Control Complexity	Typical Application
3 poles [57]	Low (micro-rotor)	Low	Medium-high	High	Microsensors, laboratory equipment
4 poles [33]	Medium (medium-small rotor)	Medium	Medium	Medium	Medical equipment, small compressor
6 poles [68]	High (medium rotor)	High	Medium-low	Higher	High-speed centrifuge, CNC machine tool
8 poles [34]	High (medium rotor)	Medium-low	Low	Low	High-speed motor, small flywheel energy storage
12 poles [73]	Medium (medium rotor)	Higher	Medium	Medium	Industrial compressors, medium blowers
16 poles [74]	High (large rotor)	High	High	High	Wind turbine, heavy centrifuge
24/32 poles	Stabilizing (oversized rotor)	Very high	Very high	Very high	Maglev train, nuclear main pump

provides a comparative analysis of magnetic bearing technologies across different pole configurations.

In AMB, the magnetic field is generated entirely by electric coils, which results in significant heat generation. To reduce power consumption, HMB replaces the bias magnetic field coils with permanent magnets (PMs). HMBs are generally classified into homopolar and heteropolar types based on the polarity arrangement of the magnetic poles [47,76,77,78]. In homopolar HMBs, the bias and control magnetic fields are located in different planes, resulting in weak magnetic coupling. These systems typically use a split stator design, with PMs configured as axial rings or multiple rectangular blocks, leading to a relatively longer axial length. In contrast, heteropolar HMBs feature alternating pole polarities, with the bias and control magnetic fields in the same plane, resulting in stronger magnetic coupling but also a higher risk of PM demagnetization. In this configuration, PMs are usually embedded within the stator, resulting in a more compact structure and shorter axial length.

As a result, homopolar HMBs generally exhibit lower rotor eddy current losses, while heteropolar HMBs offer a higher critical speed [79,80]. Figure 11 and Figure 12 illustrate typical configurations of both designs.

3.1.2. Modeling of Electromagnetic Force

The electromagnetic force modeling of magnetic bearing is the core foundation of system design and control, and its accuracy directly affects the bearing characteristics, dynamic response and stability. The current mainstream modeling methods can be divided into two major categories: analytical methods and numerical methods. In the following, the way of electromagnetic force modeling of magnetic suspension bearing is classified and elaborated.

1.

Equivalent Magnetic Circuit Method

The equivalent magnetic circuit method (EMC) is the most classical modeling method for the electromagnetic force of magnetic bearings, which is widely used in AMB and HMB [44,77,81,82,83,84,85,86,87,88]. EMC simplifies the topological relationship of the magnetic circuit and decomposes the magnetic circuit into series or parallel reluctances for calculation. It is suitable for magnetic bearing structures with relatively regular magnetic field distribution. For ease of calculation, only the working air-gap reluctance is generally considered, while the leakage reluctance and the core reluctance are ignored. The advantage of this method is its high calculation efficiency (more than 10 times faster than FEM), but the leakage effect needs to be corrected through the leakage coefficient compensation, with an error of approximately 5% to 10%.

2.

Maxwell Tensor Method

Based on Maxwell’s equations, the electromagnetic force is calculated by integrating the air-gap magnetic field tensor, which is especially suitable for modeling the radial force of AC magnetic bearing [49,89,90,91,92,93,94,95,96]. In [91], an accurate radial force model is established for bearingless motors and quantifies the suspension force through the air-gap flux density component. The stiffness of the magnetic bearing is analyzed and quantified by the Maxwell tensor method in [49], and the error can be within 3%.

3.

Equivalent Magnetic Charge Method

The general magnetic circuit model proposed by Yonnet assumes that the PM is infinite in length, and the magnetic force analytical formula of PMB is derived by combining the equivalent magnetic charge method [97]. This method equivalents the permanent magnet as a virtual magnetic charge distribution and calculates the magnetic force in combination with Coulomb’s law. According to the force relationship between the magnetic charges at two points, the numerical integration model of axial, radial, and Halback magnetized PMB can be established [98,99,100,101]. However, the numerical calculation methods of the model are generally complicated.

4.

Magnetic Network Method

Based on EMC, the magnetic network (MN) method constructs nonlinear equations by further discretizing the magnetic circuit nodes, which takes into account both computational efficiency and accuracy. For spherical magnetic bearings, the magnetic field is segmented accurately based on the flux-tube principle, and the edge flux and flux leakage are calculated accurately [11]. A network model in a spherical coordinate system is established to quantify the multi-degree freedom coupling effect, and more accurate calculation results are obtained.

5.

Subdomain Method

The subdomain method divides the magnetic field region into linear subdomains (such as air gaps, cores, and PMs) and solves them by the magnetic field boundary conditions. The magnetic field problem in sub-regions can be solved by using the vector magnetic potential within each sub-region. In [102,103,104], the radial AMB is divided into air-gap domain and slot domain. The zero-order equation and first-order equation of the magnetic field are calculated in polar coordinates, and the distribution of the magnetic field is obtained by using the method of variable separation.

6.

Finite element method

The finite element method (FEM) is the preferred tool for complex geometry and nonlinear material modeling, which has the highest accuracy and can construct multi-physics coupled models. However, the preprocessing and calculation time of the model are long, which limits the efficiency of design optimization and the speed of system-level simulation.

Table 7. Comparison of electromagnetic force modeling methods.

Modeling Methods	Advantage	Disadvantages	Applicable Scene
Equivalent Magnetic Circuit Method [44,77,81,82,83,84,85,86,87]	Computationally efficient, suitable for fast iterative	Ignore flux leakage and nonlinear effects, which require empirical correction	Magnetic bearing with regular magnetic field distribution, preliminary design stage.
Maxwell Tensor Method [49,89,90,91,92,93,94,95,96]	High precision, quantifiable current stiffness and eddy current loss.	High computational complexity	AC magnetic bearing, solid rotor
Equivalent Magnetic Charge Method [97,98,99,100,101]	Suitable for different magnetization directions, High theoretical accuracy	complex numerical integration model	Analysis of static characteristics of PMB
Magnetic Network Method [11]	Balance Efficiency and precision, Support 3D modeling	The error increases when the network is partitioned coarsely	Complex geometric structure, multi-DOF coupling analysis
Subdomain Method [102,103,104]	High analytical accuracy	Ignore core saturation	5-DOF magnetic bearing, multi-pole structure
FEM	Highest precision support for multi-physics field coupling	time-consuming, the hardware requirement	Analysis of complex physical field distribution

compares and summarizes the electromagnetic force modeling methods mentioned above. For magnetic bearings with different structures, appropriate modeling methods should be selected according to requirements.

3.2. Control Strategy

3.2.1. Classical PID Control

The fundamental distinction between AMB systems and conventional control systems lies in the inherent open-loop instability and negative stiffness characteristics of both AMB and HMB systems [105,106]. These characteristics necessitate the use of closed-loop control to ensure stable rotor suspension and operation [35,107]. In modern industrial applications, the most widely adopted control strategy remains the Proportional-Integral-Derivative (PID) controller due to its simple structure, intuitive parameter tuning, and independence from the physical model of the controlled system [108,109,110]. For AMB systems with multiple DOFs and rigid rotors, each DOF can be considered independently and regulated using decentralized PID control. This approach simplifies the control architecture while maintaining effective dynamic performance [111,112]. Most existing magnetic bearing systems employ decentralized PID controllers or their variants [113,114,115,116,117,118], such as fractional order PID [116,119], segmented PID, Neural network PID [52,120,121], fast optimal PID, expert PID, and fuzzy PID [122,123,124] control, among others.

It should be emphasized that the AMB is a nonlinear and strongly coupled dynamic system. The widely used decentralized PID control strategy, while simple and effective in many cases, does not account for inter-axis coupling, which can significantly affect performance in high-speed and high-precision applications. As industrial demands for higher rotational speed, greater stability, and improved dynamic response continue to rise, traditional decentralized PID control increasingly falls short of meeting modern engineering requirements. To address the multi-input multi-output (MIMO) coupling present in AMB-rigid rotor systems, considerable research has been devoted to decoupling strategies. These aim to transform the coupled system into a set of independent single-input, single-output (SISO) subsystems under specific conditions. This approach preserves the simplicity and tuning advantages of PID controllers while incorporating anti-gyroscopic coupling characteristics from modern control theory, thus enhancing both system stability and control precision. Currently, several decoupling techniques have been applied to AMB systems, including linear state feedback decoupling [125], cross-feedback decoupling control [126,127], and modal decoupling control [128], among others.

3.2.2. Advanced Control Algorithm

Considering the significant nonlinearity and coupling phenomena of the rotor during high-speed rotation, researchers are extending intelligent control methods beyond traditional PID. With the rise of intelligent algorithms and high-performance processors, several more advanced control algorithms have been applied to magnetic bearing control, such as robust control [129,130,131], predictive control [132,133,134], sliding-mode control [135,136,137,138], neural network control [139,140], and adaptive control [54,141,142], fuzzy control [143,144,145], active disturbance rejection control [50,146,147]. These methods and their variants bring solutions to strong nonlinearity, parameter uncertainty, and external disturbances, greatly enhancing stability and accuracy and improving overall static and transient performance.

1.

Robust control

Robust control ensures the system stability under parameter variations or external disturbances by designing controllers that are insensitive to uncertainties, parameters in the model and disturbances. In the magnetic bearings, the robust controller based on μ analysis effectively deals with the high-frequency vibration and modal coupling problems in the rotor dynamics through frequency domain analysis and pole configuration and improves the stability margin of the system. Plus, H∞ control is applied to solve the mode control problem of the magnetic bearing rotor system. The system identification model is established by the orthogonal polynomial fitting method, and the stable suspension and mode suppression of the rotor are realized.

2.

Model Predictive Control (MPC)

MPC predicts future system states and optimizes control inputs based on a system model, making it well-suited for multivariable coupled control in magnetic bearing systems. MPC based on the radial 4-DOF global control model can achieve high-precision tracking of the rotor position and transient response optimization using the state-space model and optimal controller design. This approach demonstrates excellent performance in high-speed rotating machinery. However, it also entails high computational complexity and depends heavily on high-performance processors for real-time implementation.

3.

Sliding-mode control (SMC)

SMC is extensively applied in the nonlinear control of magnetic bearings due to its strong robustness against parameter variations and external disturbances. By appropriately designing the sliding surface and control law, SMC ensures fast convergence and effectively suppresses rotor displacement fluctuations. In applications such as magnetic bearings for wind turbines, the integration of SMC with PID control has been shown to reduce overshoot and enhance response speed. However, the well-known chattering phenomenon associated with SMC remains a challenge and necessitates further improvement through techniques such as adaptive boundary layer design and higher-order sliding mode methods.

4.

Neural network control

Neural networks can effectively model the complex behaviors of magnetic bearings by learning and approximating their nonlinear dynamics. A hybrid control architecture, integrating deep learning with PID feedback, is employed to design a compensation controller, significantly enhancing the suppression of unbalanced vibrations. Additionally, convolutional neural networks (CNN) and gated recurrent units (GRU) are utilized for fault prediction through the analysis of current waveforms and vibration spectra. However, neural networks face challenges, including a reliance on large volumes of training data and the need for optimization to meet real-time performance requirements.

5.

Adaptive control

Adaptive control adjusts system parameters online to accommodate changes, with methods like Model Reference Adaptive Control (MRAC) and Active Disturbance Rejection Control (ADRC). In magnetic bearing control systems, the ADRC algorithm, utilizing an extended state observer, estimates and compensates in real time, thereby minimizing manual parameter adjustments. Intelligent optimization techniques, such as Beetle Antennae Search (BAS), are employed to fine-tune PID parameters, achieving rapid convergence and low energy consumption in multi-DOF magnetic bearings.

6.

Fuzzy control

Fuzzy control does not require the precise mathematical model of the plant or the detailed system dynamics. It is particularly suitable for dealing with the nonlinearity and uncertainty of the magnetic bearing system. It relies on the relationship between error, error rate and output and uses fuzzy reasoning based on control rules to adjust control decisions according to specific system conditions to meet requirements. It overcomes the limitation of traditional PID control that cannot be adjusted in real-time. It also saves the time required for manual control parameter debugging.

7.

Active disturbance rejection control

As an advanced Control method that does not rely on accurate models, Active Disturbance rejection control (ADRC) has been widely used in magnetic bearings in recent years. The core idea is based on real-time estimation and compensation of disturbance. The multi-DOF coupling effect of the magnetic bearing is estimated in real-time through the Extended State Observer (ESO), and the nonlinear feedback control law is combined to realize decoupling and disturbance rejection. ADRC only needs to design the controller based on the input and output data. This property is especially suitable for scenarios where the nonlinear dynamics of magnetic bearings are difficult to model accurately.

A single control algorithm often cannot simultaneously optimize both transient performance and system robustness. Therefore, combining multiple control strategies can yield superior results. For instance, the integration of fuzzy control with PID combines the rule-based flexibility of fuzzy control with the steady-state accuracy of PID, striking a balance between transient response and disturbance rejection in HMB systems [143,145]. Another example is the fusion of adaptive control with robust control to address the strong coupling issues in magnetic bearings. Simulation results demonstrate that this approach reduces errors by over 70% compared to traditional methods [53,54].

Table 8. Comparative analysis of different control strategies.

Control Algorithm	Advantages	Limitations	Typical Application
PID control [111]	Simple structure, clear parameters, easy to implement	Difficult to adapt to nonlinearity/time variation, Limited anti-interference	Low-complexity systems (e.g., laboratory demonstration)
Variable parameter PID [112]	Adjust parameters dynamically, balancing dynamic response with accuracy.	Complex adjustment rules real-time performance is limited	Startup phase or set point changes frequently
Robust control [129]	Parameters and perturbations insensitive, multivariate coupling.	Relying on accurate models, high computational complexity, dynamic performance is limited	High-precision machine tools, aerospace flywheels, and strong interference environments.
Predictive control [132]	Predict the future state based on the model and adapt to nonlinear/time-varying systems.	Large computation, error sensitive, update frequently	Dynamic, high-speed response, multi-target coordination
Sliding-mode control [135]	Strong robustness, quick response, parameter insensitive	Chattering requiring higher-order precise sliding mode design or adaptive control	High anti-interference (e.g., flywheel energy storage)
Neural network control [139]	No need for an accurate mathematical model; online learning	Amount of training data, computationally intensive, poor interpretability	Adaptive adjustment of complex operating (e.g., variable load)
Adaptive control [54]	Automatically adjust parameters to improve robustness.	Slow convergence speed adaptability to fast time-varying systems is limited.	System with parameters changing slowly (e.g., compressor)
Fuzzy control [53]	Dynamically adjust parameters, no need for accurate models, anti-interference.	Rule design relies on experience; parameter tuning is complex, and high-frequency accuracy is insufficient.	Strong nonlinearity and unclear model (e.g., medical devices)

compares the aforementioned control methods.

3.3. Power Drive System and Controller of Bearings

3.3.1. Driver Topology Design

An efficient and stable power amplification system is essential for achieving a magnetic bearing system with high sensitivity, rapid response, and low cost. Traditional linear power amplifiers have been replaced by power electronic converters due to their high loss and large size. One of the earliest solutions is the full-bridge topology shown in Figure 13a [148], which controls the coil current through four switches, offering a three-level output and good transient performance. However, multi-DOF magnetic bearing systems require a large number of devices, leading to high cost and volume. Improved topologies, such as the unipolar half-bridge structure in Figure 13b, reduce the number of devices by half and are ideal for active magnetic bearings (AMBs) that require only unidirectional current [149,150].

However, using an H-bridge topology for each coil requires a large number of electronic devices. Hence, a three-phase full-bridge topology is proposed to control a single degree of freedom (DOF), as shown in Figure 14a [151]. This three-phase topology allows the two coils to share the middle bridge, simplifying the design and reducing the number of switching devices by approximately one-quarter compared to the full-bridge topology.

Despite this improvement, the switching devices in the three-phase full-bridge topology are still underutilized, and redundancy remains in the system. To optimize this, a three-phase half-bridge topology is introduced, where each three-phase half-bridge controls two coils on a single DOF [152]. Depending on the configuration of the switching devices, this topology is divided into the b-t-b structure and the t-b-t structure. The b-t-b structure, shown in Figure 14b,c, offers the advantage of reducing the number of common grounds and gate drive power supplies compared to the t-b-t structure. However, since the output voltage on the shared bridge is fixed at Vdc/2, the DC voltage utilization is halved in comparison to the H-bridge structure.

Building on the shared bridge concept in Figure 15, the number of devices can be further reduced by sharing multiple bridges [153]. As illustrated in Figure 16, the switching devices for the shared bridge are positioned in the upper bridge, which connects to the DC bus, while the switching devices of non-shared bridges are located in the lower bridge connected to the negative pole. These bridges share a drive isolation power supply. In the case of an N-axis magnetic bearing system, only 2N + 1 switching devices and diodes are required. This approach reduces the total number of devices; however, the current on the shared bridge is the sum of the currents from the other bridges, resulting in higher current stress. Consequently, the shared bridge needs to be designed with greater consideration, increasing the risk of failure. To address this, the reverse shared bridge structure is introduced, which modifies the system to reverse half of the coil currents. This configuration causes the currents on the shared bridge to cancel each other out, significantly reducing the current stress. For an N-axis system, this topology requires 2N + 2 switches and diodes.

In the previously discussed shared bridge topology, a single bridge serves as the common node for all coils. To maintain system stability, the average voltage at the midpoint of this common bridge must remain constant, which inherently limits the DC voltage utilization across all H-bridge topologies. This constraint can reduce the control system’s bandwidth. To overcome this limitation, a series coil topology with multiple shared bridges is proposed, allowing the midpoint voltages at both ends of each coil to vary dynamically [154,155]. This approach preserves high DC voltage utilization without increasing the number of switching devices. As shown in Figure 17a, a four-phase, four-bridge topology eliminates the need for a common arm, further reducing the controller’s physical footprint while maintaining performance.

The above-mentioned three-phase topology, shared bridge topology and series coil topology belong to the unipolar switching power amplifier topology, which is generally applied to the AMB system of current superposition type. For HMB of magnetic field superposition type, it is necessary to use the bipolar switching power amplifier to realize the control of the rotor through the bidirectional flow of current. Therefore, to realize the suspension control of the 5-DOF HMB, the topology of the five-phase six-bridge is proposed in Figure 17b [156].

Table 9. Comparison of the topologies of the N-axis system.

Topology	Switches	Diodes	Drive Power	Voltage Utilization
Full bridge [148]	8N	8N	4N + 1	1
Half bridge [149]	4N	4N	2N + 1	1
Three-phase full bridge [151]	6N	6N	3N + 1	0.5
Three-phase half bridge [152]	3N	3N	N + 1	0.5
Shared bridge [153]	2N + 1	2N + 1	2	0.5
Reverse shared bridge [154]	2N + 2	2N + 2	3	0.5
Series coils [155]	2N + 1	2N + 1	N + 1	1

compares the number of devices and DC voltage utilization across various topologies for an N-axis system. Compared to the H-bridge structure, all improved topologies demonstrate a reduction of switching devices. Notably, the series coil topology achieves optimal device efficiency without compromising DC voltage utilization, offering a balanced solution in terms of performance and hardware cost.

3.3.2. Fault-Tolerant Control and Fault Detection

Magnetic bearing systems are primarily used in applications requiring high-speed and high-precision control, where a rotor drop caused by system failure can lead to severe damage. During a suspension failure, the rotor instability manifests as a mechanical process, whereas the associated current failure in the coils is an electrical process. Since electrical dynamics are significantly faster than mechanical responses, the rotor position undergoes minimal change in the immediate aftermath of a fault. Additionally, given that the coil resistance is typically much lower than its inductive reactance, the power amplifier introduces a natural delay. This delay, combined with the response characteristics of power electronic converters, creates an opportunity for implementing fault-tolerant control strategies within the system.

The electromagnetic force in magnetic bearings is a reluctance force, which depends on the magnitude of the current rather than its direction. Therefore, topologies such as the full-bridge and three-phase full-bridge, despite incorporating redundant switching devices, offer a natural advantage for fault-tolerant operation. These redundant components can be repurposed to serve as a backup for an entire drive channel. In the event of a failure, the current path can be rapidly redirected in the opposite direction without affecting the generated electromagnetic force, enabling continuous system operation. For example, in a three-phase full-bridge topology, if a fault occurs in one switch or current path, the system can quickly switch to the redundant half of the bridge. By reversing the current direction through the alternate path while maintaining the same current magnitude, the magnetic force remains unaffected, thereby achieving fault-tolerant control without compromising suspension performance [153]. Figure 18 shows the fault-tolerant operation for three-phase full-bridge topology.

The three-phase full-bridge converter shown in Figure 14a can be conceptualized as comprising two sets of three-phase half-bridge modules: (S2, S3, S4) and (S1, S5, S6). During normal operation, as illustrated in Figure 18a, the first set of switches (highlighted in red) is active, while the remaining switches remain in standby mode without receiving control signals. In this configuration, current flows outward from the shared bridge to the coils. In the event of a failure, the system can switch to the redundant drive mode, as shown in Figure 18b. Here, the second set of switches becomes active (highlighted in red), and the previously used switches are turned off. In this mode, current flows into the shared bridge. Since the electromagnetic force in magnetic bearings is a reluctance force and is independent of the current direction, both drive configurations can generate equivalent suspension forces. This inherent bidirectionality enables fault-tolerant operation, ensuring continuous rotor suspension even under drive system failure.

Common faults in switching devices primarily include open-circuit and short-circuit failures, both of which can cause sudden and abnormal variations in coil currents. As a result, fault detection in magnetic bearing drive systems can be effectively achieved by monitoring and analyzing the total coil current. Significant deviations from expected current profiles may indicate the presence of a switching fault, enabling timely fault diagnosis and the activation of fault-tolerant control mechanisms. To enable rapid fault diagnosis and response, two threshold currents are defined: I_open and I_short. If the total measured coil current falls below I_open, it indicates an open-circuit fault in the switching device. In this case, control of the magnetic bearing rotor can be restored by promptly switching from the faulty drive module to a redundant backup module. Conversely, if the total current exceeds I_short, it signifies a short-circuit fault within the module. Under such conditions, all control signals and drive modules should be immediately shut down to prevent further damage to the system and ensure operational safety. This threshold-based strategy enables fast and reliable protection for high-speed magnetic bearing systems.

3.3.3. Controller Hardware Platform

The hardware platform of the magnetic bearing controller is the key carrier to realize high precision and high real-time control. With the complexity of the control algorithm and the increase of the demand for multi-DOF cooperation, the controller hardware has gradually developed from the early analog circuit to a digital architecture with an embedded microcontroller (such as STM32), digital Signal processor (DSP) and Field Programmable Gate Array (FPGA) as the core. The following elaborates on hardware types, performance characteristics, and typical applications

1.

Embedded Microcontroller

The STM32 series core microcontrollers are widely used in medium and low-complexity maglev systems due to their advantages of low power consumption, high integration and cost. For example, the STM32F4 series (main frequency of 180 MHz) captures the Hall sensor signal through a timer and combines the PID algorithm to achieve single-DOF suspension control with a displacement resolution of ±10 μm [157]. The CAN and Ethernet interfaces of STM32 can realize multi-axis cooperative control, but limited by the computing power, STM32 makes it difficult to meet the real-time requirements of high-speed multi-DOF systems.

2.

Digital Signal Processor

Digital Signal Processor (DSP) has become the mainstream scheme of dynamic control of magnetic bearing because of its high-performance floating-point operation ability and special peripheral equipment. The built-in redundant ADC module supports sensor fault detection and switching, which improves the fault tolerance of the magnetic bearing system. TMS320F28335 (main frequency 150 MHz) is adopted in [158,159] combined with a fault diagnosis algorithm, which can control the fault switching time of magnetic bearing in 5 ms and significantly improve the stability of the system.

3.

Field Programmable Gate Array

With the characteristics of parallel processing and nanosecond delay, a Field Programmable Gate Array (FPGA) plays a key role in high-speed and multi-variable maglev systems. In the speed-holding mode of a high-speed maglev motor, the observation accuracy of steady-speed frequency is better than 5 Hz, and the response time is less than 50 μs [160,161].

The different types of controller hardware of magnetic bearings are summarized in

Table 10. Comparison of controller hardware platform.

Hardware Types	Advantage	Disadvantages	Applicable Scene
STM32 series [157]	Low power consumption, low cost, short development cycle, easy to control	Limited computing power and limited real-time performance	Low complexity scenarios such as medium and low speed, single/two DOF.
DSP [158,159]	High real-time performance, support for complex algorithms	Relying on special development tools, high power consumption	High-speed, multiple DOF and other high-precision scenes
FPGA [160,161]	Strong real-time performance	Long development cycle, high cost	Ultra-high-speed and complex algorithm scenarios.

. It is necessary to take into account both the performance and cost to select the appropriate controller platform.

4. Application Fields and Typical Cases

Building on the aforementioned key technologies, magnetic bearings have found applications across a wide range of fields. Based on application domains and functional requirements, their use can be classified as follows.

4.1. Industrial Field

4.1.1. High-Speed Motor and Compressor

Fully sealed compressors equipped with shielded magnetic bearings and shielded induction motors can be used for various challenging applications, including acid gas handling, subsea compression, wet gas compression, and CO₂ reinjection. The operating conditions for such sealed compressors are examined. Ref. [51] gives an application where the use of canned magnetic bearings for enhanced recovery in a CO₂ environment can eliminate the shaft end seal and thus improve the reliability of the machine.

Table 11. The parameters of the hermetically sealed compressor.

Machine Type	5.8 MW Centrifugal Compressor with Canned Electric Motor
Speed range	2850~9975 r/min continuously variable
Rotor mass	1622 kg
Rotor length	3.3 m
Rotor orientation	Vertical
AMB configuration	Single shaft, 2 radial and 1 axial.

shows its parameters. At the same time, safety is improved due to the reduced risk of gas leakage into the environment, which is also important to underwater applications.

4.1.2. Precision Machine Tool Spindle

By tracking the position of the spindle tool, an AMB controller based on μ-synthesis is designed to minimize the difference between the reference position and the estimated position of the tool [48]. The experimental verification is carried out on the spindle AMB boring machine. At 15,000 r/min, the step-shaped, conical, and convex contours are successfully tracked with steady-state errors of about 8.7% and static and position fluctuation of 0.851 μm and 1.887 μm, respectively. The system shows strong robustness under static loads of 3.2 kg and dynamic loads with a 10 mm eccentricity, which verifies the effectiveness of the proposed method for balancing tracking accuracy and anti-interference ability in high-speed machining. Parameters are listed in

Table 12. The parameters of the high-speed spindle.

Machine Type	10 kW Industrial Grade AMB High-Speed Spindle
Speed range	0~50,000 r/min continuously variable
Static load	3.2 kg
Tracking range	90 μm
Rotor orientation	Horizontal
AMB configuration	Single shaft, 2 radial and 1 axial.

.

4.2. Energy and Transportation Field

4.2.1. Flywheel Energy Storage System

A 5-DOF AMB system, designed for a high-strength steel energy storage flywheel without a shaft and hub, is presented in

Table 13. The parameters of flywheel energy storage system.

Machine Type	100 kW Energy Storage Flywheels
Speed range	3225 r/min
Rotor mass	5440 kg
Outer diameter	2.13 m
Rotor orientation	Vertical
AMB configuration	Single shaft, combination 5-DOF AMB.

[162]. By integrating radial, axial, and tilt suspension functions into a single unit, this design replaces the traditional multi-unit magnetic bearing system, significantly simplifying the structure and reducing costs. Experimental tests demonstrate the system’s capability to support a flywheel weighing 5440 kg and measuring 2 m in diameter, with an air gap of 1.14 mm. These results confirm the bearing’s reliability under high load conditions and validate the design approach. This technology enhances the energy density of the flywheel storage system, achieving twice the capacity of conventional steel flywheels while also reducing material costs, offering strong potential for practical engineering applications.

4.2.2. Wind Turbine Spindle

A design for a small vertical wind turbine based on a magnetic suspension axial flux PM generator is proposed [163]. By integrating PMBs, the turbine achieves frictionless suspension, which minimizes mechanical losses and enhances efficiency. The performance details are provided in

Table 14. The parameters of the prototype.

Machine Type	Small Scale Vertical Axis Wind Turbine
Speed range	200 r/min
Maximum repelling force	124 N
Outer diameter	500 mm
Rotor orientation	Vertical
AMB configuration	Single shaft, PMB.

. Experimental results show that the application of PMBs significantly improves the turbine’s speed and efficiency, particularly under variable wind conditions, outperforming traditional bearing systems. This design simplifies the system by eliminating the need for gear transmission, reducing complexity and costs, and utilizing low-cost materials, making it ideal for home and small-scale applications.

4.3. Extreme Environments

4.3.1. Satellite Momentum Wheel

In the aerospace field, spacecraft orientation is stabilized in the desired direction through attitude control. The control moment gyroscope (CMG) serves as a critical actuator for achieving agile and reliable attitude control. The integration of magnetic bearings significantly reduces the external forces transmitted to both the bearing stator and the spacecraft. By utilizing robust control and adaptive feedforward compensation, both internal multi-parameter disturbances and external continuous disturbances are effectively suppressed. This greatly enhances system stability during high-speed and dynamic operations, making it well-suited for spacecraft attitude control, where stringent micro-vibration requirements must be met [54]. The prototype and relevant parameters are provided in

Table 15. The parameters of moment gyros.

Machine Type	Magnetically Suspended Control Moment Gyros
Stable operating frequency	100 Hz
Rotor mass	16.7 kg
Outer diameter	250 mm
Rotor orientation	Vertical
AMB configuration	Single shaft, 2 radial and 1 axial.

.

4.3.2. Nuclear Reactor Cooling

In nuclear reactors, where temperatures and radiation levels are high, gas-cooled high-temperature reactors (HTRs) rely on high-purity helium as both a coolant and heat carrier. The lubricants or wear debris from traditional bearings may fail or contaminate the helium medium, limiting the reliability of these HTRs. Magnetic bearings present a viable solution to address this challenge [164]. Due to the extremely high operating temperatures of gas-cooled HTRs, traditional bearing materials are prone to failure from thermal expansion or fatigue. In contrast, magnetic bearings, with no mechanical contact and no need for lubrication, offer excellent high-temperature resistance. This eliminates the risk of material thermal deformation, ensuring clean, stable, and efficient operation of the HTR under extreme conditions. A practical application is presented in

Table 16. The parameters of centrifugal helium circulator.

Machine Type	Centrifugal Helium Circulator
Speed range	800~4800 r/min continuously variable
Rotor mass	4000 kg
Rotor length	3.5 m
Rotor orientation	Vertical
AMB configuration	Single shaft, 2 radial and 1 axial.

.

5. Technical Challenges and Future Trends

5.1. Technical Challenges

5.1.1. Multi-Field Coupled Modeling and Calculation

The modeling and calculation of magnetic bearings are critical for linking theoretical design, performance optimization, and practical application [165,166]. However, challenges related to three-dimensional (3-D) electromagnetic field calculations [167,168,169], electromechanical coupling dynamics [170,171,172] and eddy current [173,174] continue to be major bottlenecks in the current development of this technology.

Currently, the equivalent magnetic circuit method remains the most traditional approach for analyzing the magnetic flux of active magnetic bearings (AMB) and hybrid magnetic bearings (HMB) [44,77,82,83]. In this method, the mathematical model of the suspension force is derived by constructing an equivalent magnetic circuit diagram, with parameters determined using typical reluctance formulas and engineering experience [84,85,86,87,88]. However, this approach assumes ideal conditions, neglecting the effects of local material saturation [175,176,177,178,179], eddy current loss, edge magnetic leakage and other factors [180]. Some studies have explored variations of the equivalent magnetic circuit method that account for material nonlinearity and eddy current effects. These advancements significantly reduce the model’s calculation error by incorporating the edge effect, thus improving the accuracy of the 3-D electromagnetic field calculation for magnetic bearings. To further enhance the modeling’s accuracy and generality, the Maxwell tensor method [49,89,90,91,92,93,94,95,96] can also be employed. Nonetheless, factors such as magnetic circuit saturation and edge effects must still be carefully considered.

The stiffness and damping characteristics [181,182,183,184] of magnetic bearings are influenced by electromagnetic forces, control parameters, and rotor dynamics. Transient modeling of magnetic bearing-rotor systems is crucial for optimizing control and mitigating unbalanced vibrations. While the transient model of the rotor on a rigid foundation has been studied, an accurate multi-DOF transient model that accounts for the modal coupling phenomenon of a flexible rotor crossing the critical speed is still required for further refinement.

The modeling and calculation of magnetic bearings have evolved from static analysis of single physical fields to dynamic coupling of multiple fields. Moving forward, overcoming existing bottlenecks will require the integration of high-performance computing, artificial intelligence, and advanced material technologies. By developing high-precision mathematical models, creating intelligent agent models, and fostering interdisciplinary collaboration, the modeling of magnetic bearings will become more efficient and accurate. This will lay the groundwork for their widespread application in fields such as flywheel energy storage, high-speed motors, and aerospace.

5.1.2. Balance Between System Cost and Reliability

The performance of magnetic bearings relies on the precise detection and timely adjustment of rotor displacement through the closed-loop control system. However, the trade-off between cost and reliability of existing sensors has become a major bottleneck, limiting their widespread application. Eddy current sensors, as the predominant displacement detection solution, offer advantages in accuracy and transient response [185,186]. However, their high cost and reliability concerns have driven the industry to explore alternative solutions, such as inductive sensors and self-sensing technologies.

Eddy current sensors operate at high-frequency excitation ranges (typically 500 kHz to 20 MHz) and impose stringent requirements on material uniformity, surface finish, and temperature stability. The manufacturing costs of key components, such as probe coils and signal processing chips, account for approximately 30% to 40% of the total cost of a magnetic bearing system. Traditional magnetic bearing systems closed-loop control needs to obtain real-time displacement signals in 5-DOF, and any failure of the sensors can directly lead to system instability [187]. Additionally, sensor installation can introduce geometric errors, eventually reducing control accuracy.

Inductive sensors measure displacement by detecting variations in inductance and offer a cost advantage—approximately 1/5 that of eddy current sensors [188]. However, they still face challenges, including nonlinear measurement errors, sensitivity to electromagnetic interference, and limited transient response. Sensorless magnetic bearing technologies estimate rotor position indirectly through high-frequency signal injection or state observers, reducing reliance on physical displacement sensors. Despite this advantage, these approaches involve high algorithmic complexity, posing challenges for real-time implementation and system robustness [66].

Achieving a balance between cost and reliability in magnetic bearing systems requires coordinated advancements in both sensor technologies and control algorithms. In the short term, hybrid sensor configurations combined with control correction algorithms offer practical solutions for cost reduction without compromising performance. In the long term, the development of more intelligent sensorless technologies is expected to transform the industry. With these advancements, magnetic bearings are poised for widespread adoption at manageable costs across high-end manufacturing, renewable energy, and other emerging application areas.

5.2. Frontier Development Direction

5.2.1. Intelligent Control System

Although magnetic bearing rotors can be made to rotate around the inertial axis, interference factors such as mass eccentricity and sudden load changes remain unavoidable due to limitations in machining accuracy and material imbalance [189,190]. Overcoming these challenges requires intelligent control systems, which are key to breaking current performance bottlenecks and enabling large-scale industrial applications. Traditional control strategies, such as PID control, often fall short of maintaining robust vibration suppression across the full speed range. For example, while zero-displacement control can effectively eliminate synchronous vibrations, it may lead to instability under varying speed conditions due to phase lag. Disturbances can be estimated using extended state observers (ESO) [191,192], but their effectiveness is constrained by observation bandwidth, which limits their ability to handle high-frequency disturbances. Moreover, the accuracy of control relies heavily on precise system modeling and parameter tuning.

To address these challenges, the second-order generalized integral frequency-locked loop (SOGI-FLL) is employed for real-time speed estimation. By utilizing a variable gain coefficient to adaptively adjust the control loop bandwidth, SOGI-FLL enables effective vibration suppression over a broader frequency range [193]. The model-aided extended state observer (MESO) further enhances system performance by introducing a feedforward compensation link, which mitigates high-frequency disturbances while reducing control voltage and phase delay [194]. Additionally, integrating inductive sensors with self-sensing technology enables the deployment of nonlinear controllers based on deep learning. These controllers can improve system stability by dynamically tuning PID parameters through multi-sensor data fusion. However, the application of reinforcement learning requires extensive simulation data for training, and the synchronization of multi-sensor data—particularly time alignment—remains an active area of research.

The intelligence of magnetic bearing control systems must overcome the challenges of multidisciplinary coupling within the closed-loop framework of perception, decision-making, and execution. This advancement is essential for shifting from passive response to active prediction, enabling more adaptive, robust, and efficient system behavior.

5.2.2. Miniaturized and Integrated Solutions

The miniaturization and integration of magnetic bearings represent critical breakthroughs for their application in emerging fields such as microrobotics, precision medical devices, and aerospace micro-power systems. However, these advancements are still constrained by challenges in electromagnetic topology optimization, thermal management, and multi-physics coupling modeling.

Traditional magnetic bearing systems often rely on the combination of multiple single-degree-of-freedom electromagnets, resulting in a bulky overall structure. For example, a typical five-degree-of-freedom (5-DOF) suspension configuration requires at least two radial bearings and one axial bearing shown in Figure 19, and load structures such as fans, impeller and pump are installed at the end of the rotating shaft, significantly reducing the effective axial length of the motor relative to the total assembled system length. To enhance integration, multi-DOF hybrid magnetic bearing (HMB) topologies are essential. However, in such compact designs, strong coupling among electromagnetic, mechanical vibration, and thermal fields presents significant complexity. Conventional liquid cooling methods are impractical due to strict volume constraints, while passive thermal management depends on high-conductivity materials, increasing overall cost. Additionally, most current control systems rely on discrete power modules such as H-bridges. In a 5-DOF system, this translates to five independent power circuit sets, further complicating integration and increasing spatial and thermal design burdens.

Currently, various multi-DOF integrated magnetic bearing topologies with shared magnetic circuits have been developed, including axial-radial 3-DOF configurations [55,195,196,197,198,199], 4-DOF [200,201,202,203,204,205] and full 5-DOF [56,61,206,207,208] magnetic bearing topologies. In addition, bearingless 5-DOF motor architectures have emerged, integrating magnetic bearing functionality directly into the motor to significantly reduce the system’s axial length [209,210,211]. On the control side, system-level packaging techniques offer substantial reductions in the size of power amplifiers, controllers, and sensors, further promoting miniaturization and integration.

Advancing the miniaturization and integration of magnetic bearings necessitates overcoming the electromagnetic-mechanical-thermal limitations inherent in multidisciplinary coupling. Looking forward, permanent magnet–electromagnetic hybrid topologies and system-level packaging are expected to become focal points of innovation in this field. These advancements will drive the evolution of high-end equipment toward non-contact operation, full intelligence, and ultra-compact form factors, enabling broader applications across next-generation technologies.

6. Conclusions and Perspectives

6.1. Technical Summary

With its advantages of non-contact support, zero friction loss, and maintenance-free operation without lubrication, magnetic bearing technology has become a cornerstone for high-speed precision equipment. This paper provides a comprehensive review of its development, covering the comparative analysis of active, passive, and hybrid magnetic bearing topologies, as well as key technological breakthroughs in electromagnetic structure design, advanced intelligent control algorithms, and integrated power drive systems. Together, these aspects highlight the multi-dimensional value and transformative potential of magnetic bearing technology.

In terms of technical principles, the bearing capacity and stability of magnetic bearings have been significantly enhanced through multi-physical field coupling modeling, active-passive hybrid magnetic circuit design, and the use of high-performance permanent magnet (PM) materials. The evolution of intelligent control strategies is particularly noteworthy, progressing from traditional PID control to adaptive sliding mode control and further advancing to parameter self-tuning systems based on deep learning algorithms. These developments have progressively addressed issues related to strong nonlinear vibrations and rotor interference. In power driver technology, the integration of wide bandgap semiconductor devices and high-frequency switching power amplifiers has led to substantial improvements in energy efficiency and volume reduction compared to previous controllers. On the application front, the successful deployment of magnetic bearings in satellite momentum wheels, high-speed motors, and integrated medical devices demonstrates their potential to replace traditional bearings in a variety of critical systems.

However, current technology still faces several key challenges. The accuracy of multi-field coupling modeling remains insufficient, with significant simulation errors in the interactions between magnetic, thermal, and mechanical fields under complex operating conditions. Additionally, the overall system cost remains high, and the reliance on key materials, such as rare-earth permanent magnets (PM), is constrained by supply chain limitations. Furthermore, the adaptability of magnetic bearings to extreme environments is limited, particularly in terms of PM demagnetization at high temperatures, as well as issues related to sealing and corrosion resistance in deep-sea or high-pressure environments.

6.2. Outlook

The future development of magnetic bearing technology may follow several key pathways:

• Multi-Field Coupled modeling and Accurate Analysis: Magnetic bearings inherently involve the coupling of multiple fields, including electromagnetic, thermodynamic, and mechanical vibration. Future advancements will require the development of more precise multi-field coupling mathematical models to address complex challenges, such as nonlinear vibration and thermal deformation under high-speed and high-load conditions. For example, research could focus on the interaction between magnetic field distribution, thermal effects, and mechanical stress. Additionally, integrating these models with the flexural vibration characteristics of high-speed, flexible rotors will enable the development of response models capable of predicting instability thresholds at critical speeds.
• Innovation of Intelligent Control Algorithm and Strategy: To overcome the limitations of traditional PID control, such as insufficient disturbance rejection, it is essential to integrate modern control theory with artificial intelligence technologies to enhance the system’s robustness against sudden load changes and parameter variations. Employing deep reinforcement learning for control parameter optimization, along with multi-sensor data fusion (including displacement, current, and temperature data), will enable more precise suspension control and improve overall system stability. This approach promises to significantly enhance the adaptability and performance of magnetic bearing systems in dynamic environments.
• Efficient Optimization of Power Drive System: As the core execution unit of magnetic bearings, the power electronic converter must achieve breakthroughs in both topology structure and control efficiency. Advancing shared bridge topologies will reduce the number of power devices, thereby minimizing both the volume and cost of the system. The integration of wide-bandgap SiC/GaN devices will enable higher switching frequencies, while advanced PWM modulation strategies will further reduce losses and optimize operational efficiency. These innovations will significantly enhance the performance and cost-effectiveness of magnetic bearing systems.
• Miniaturization and Integration Design Trend: To meet the demands of medical, aerospace, and precision instrumentation applications, magnetic bearings must be miniaturized and modularized. Integrating the sensor, controller, and power amplifier into a single chip will streamline the system architecture, reduce power consumption, and enhance efficiency. Additionally, optimizing the topology structure is crucial to minimizing weight, which will further support the deployment of magnetic bearings in compact, high-performance systems. These advancements will enable magnetic bearings to be more adaptable and efficient for emerging technologies.

The future development of magnetic bearings will undoubtedly require a multidisciplinary approach. This includes high-precision modeling to guide design, coupled with advanced intelligent control algorithms to enhance transient performance. Additionally, innovation in power electronics will be essential to optimize energy efficiency. Ultimately, the goal is to achieve miniaturization and integration, enabling magnetic bearings to meet the demands of next-generation applications across various industries.