An Improved Maximum Power Point Tracking Control Scheme for Photovoltaic Systems: Integrating Sparrow Search Algorithm-Optimized Support Vector Regression and Optimal Regulation for Enhancing Precision and Robustness
Abstract
1. Introduction
2. PV Power Generation System and Its Modeling
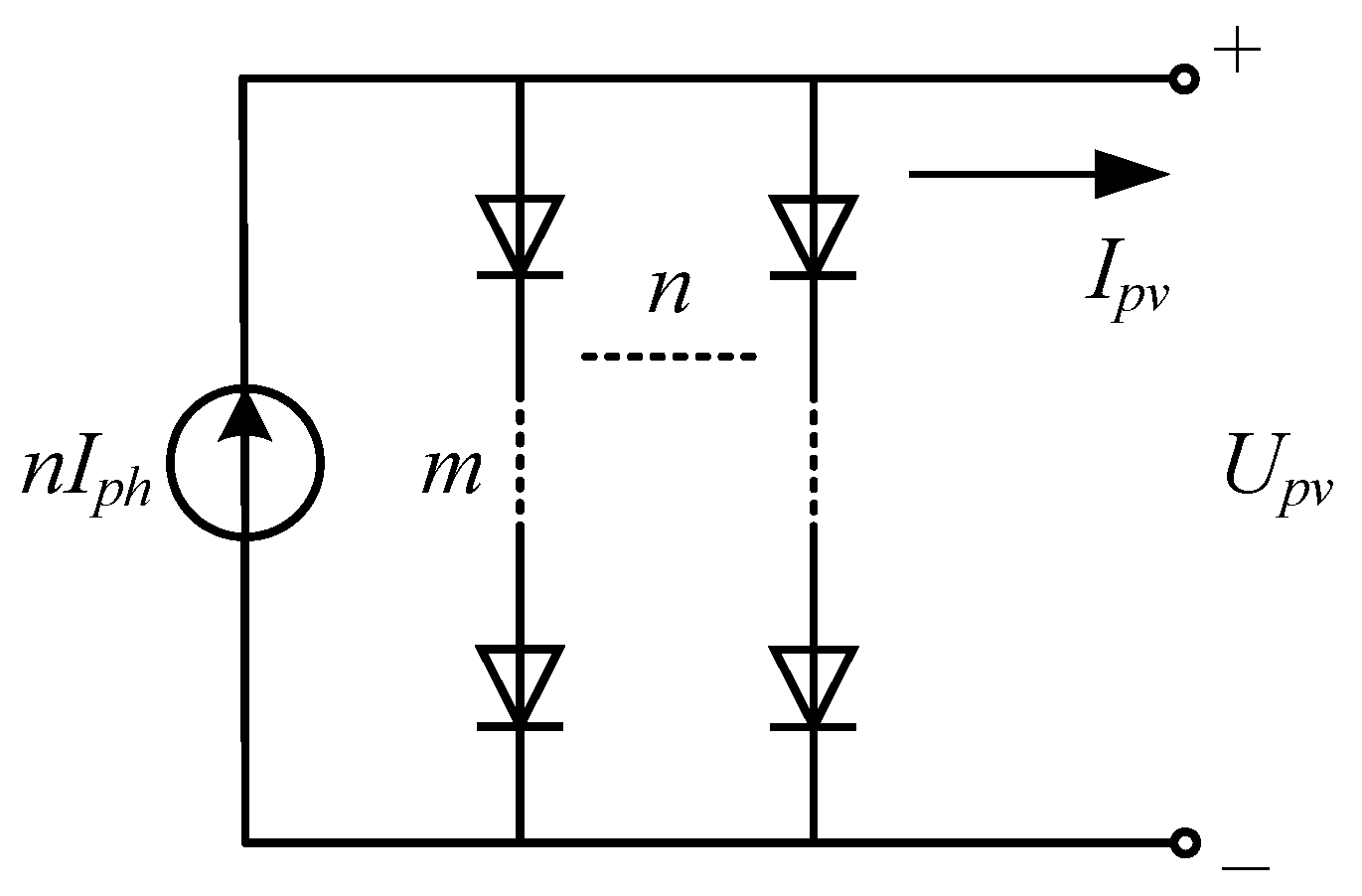
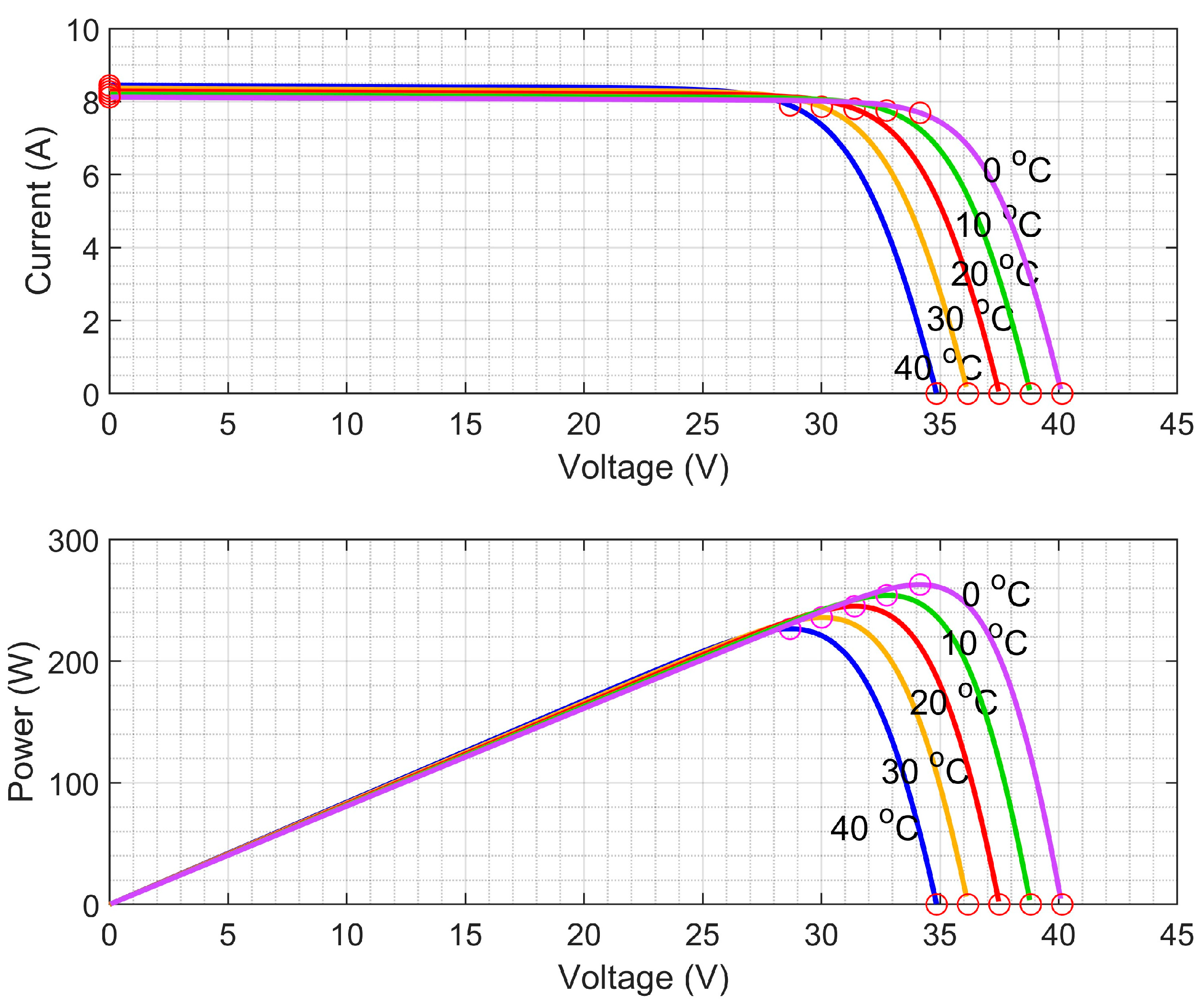
2.1. Characteristics of PV Panel
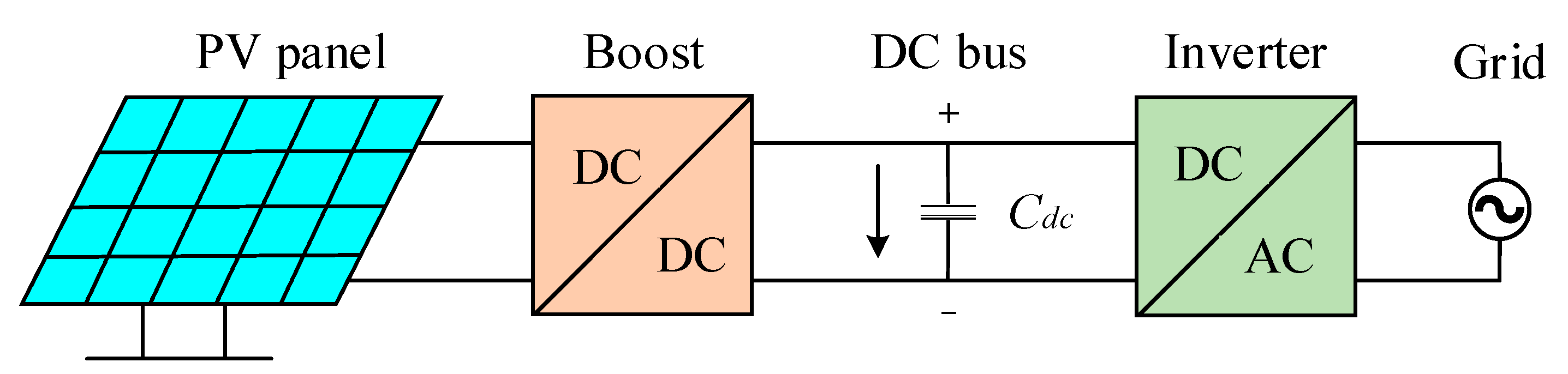
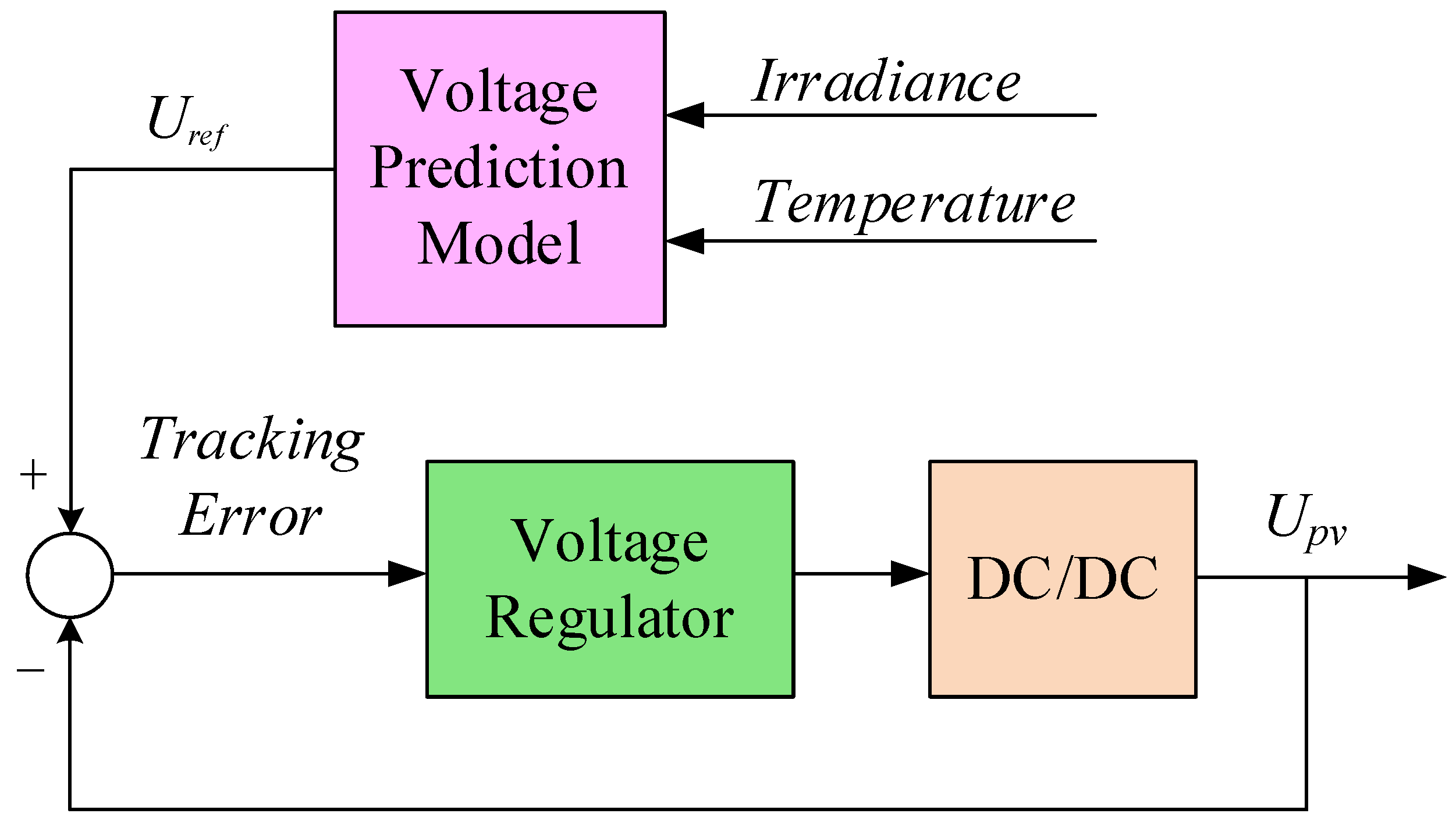
2.2. Structure of PV Power Generation System
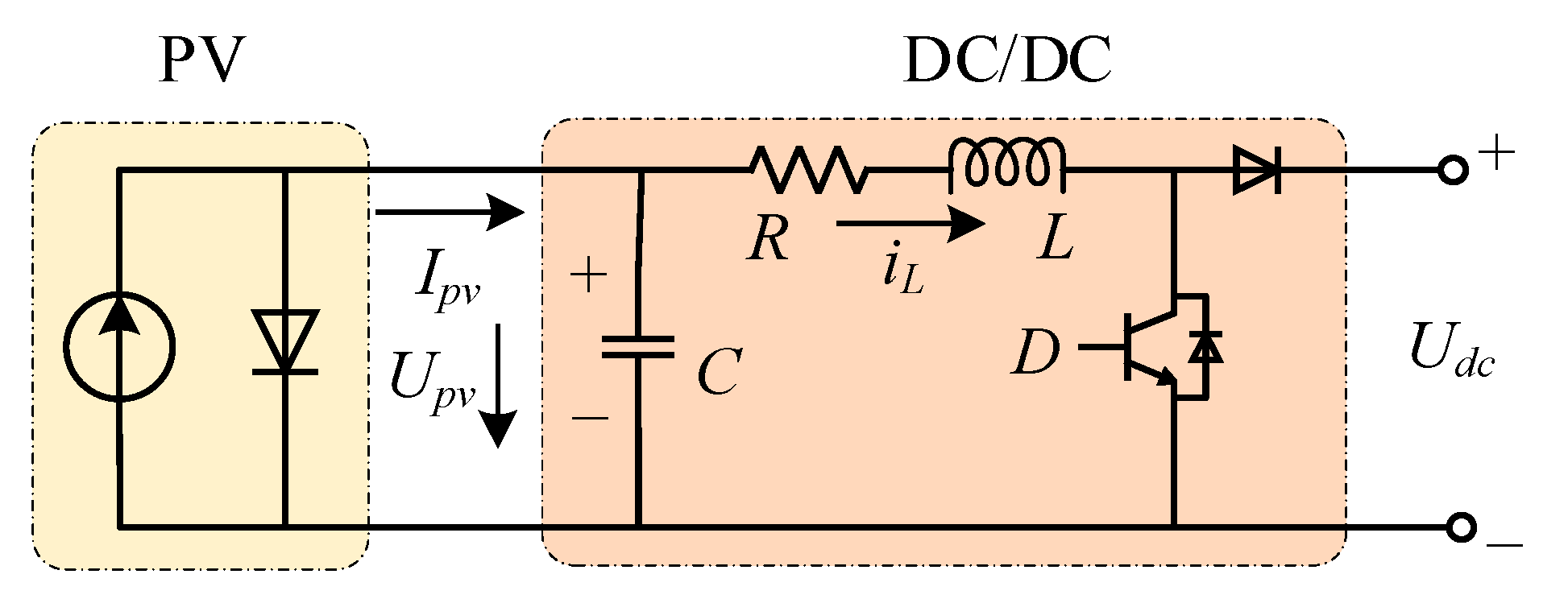
2.3. Modeling of PV Generation System
3. Constructing the Current Prediction Model
3.1. Support Vector Regression
- (1)
- Data preprocessing
- (2)
- Hyperparameter optimization
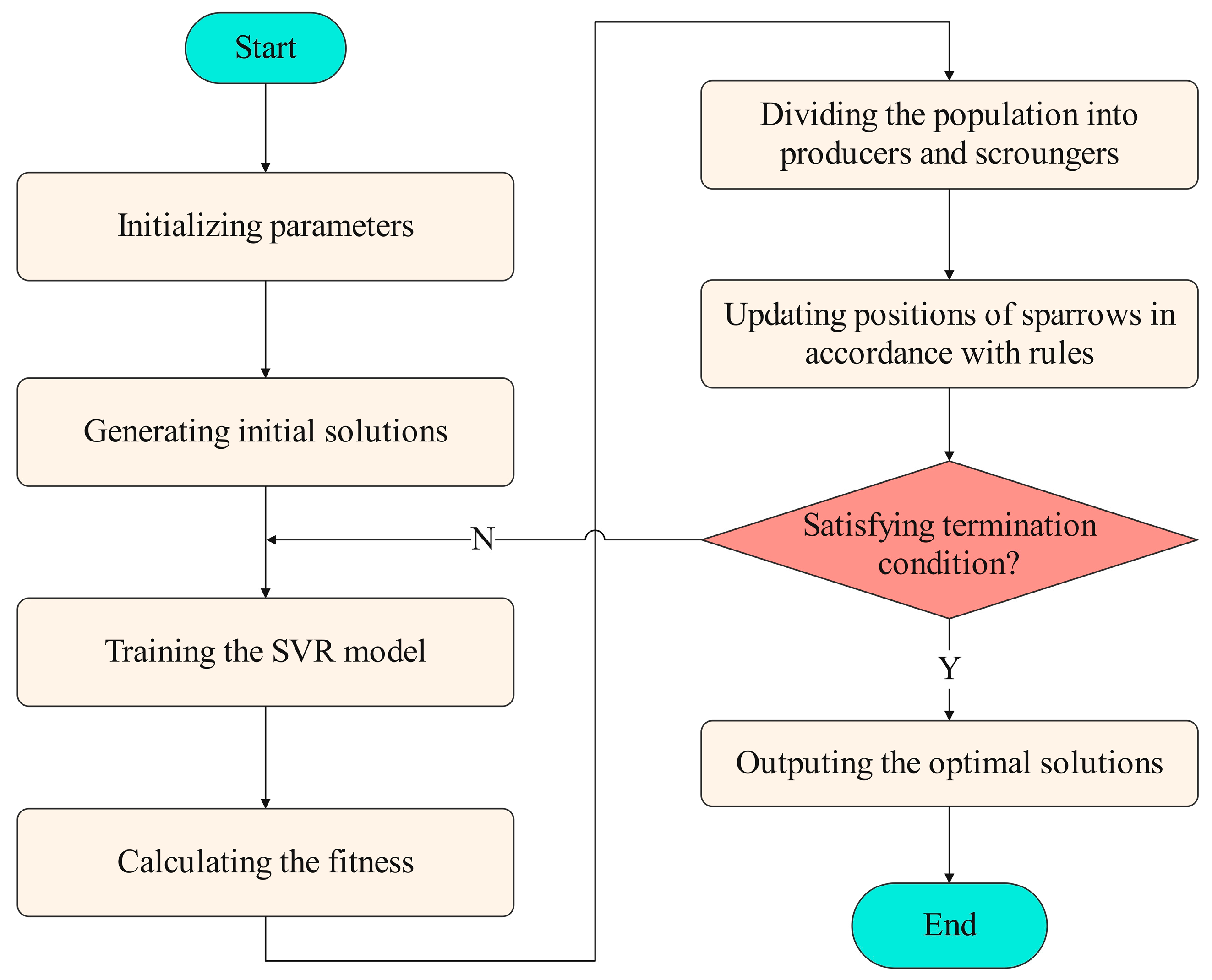
3.2. Sparrow Search Algorithm
- (1)
- The producers responsible for locating areas with abundant food have higher fitness than the scroungers. The fitness is determined by an optimized objective function.
- (2)
- If a predator is perceived and the corresponding alarm value exceeds the threshold, the producers will direct the scroungers to the safe place.
- (3)
- A scrounger can become a producer if its fitness is better. However, the total number of each group remains unchanged; i.e., a producer will turn into a scrounger accordingly.
- (4)
- Scroungers follow the producer with best fitness. During the food-searching process, hungry scroungers with low fitness tend to change their positions to improve their fitness.
- (5)
- The sparrows at the edge of the group will promptly fly to a safe area in case of danger, while the sparrows in the center of the group randomly move to the rest of the group.
4. Robust Current-Tracking Controller Design
4.1. Problem Formulation
4.2. Linear Quadratic Optimal Control
5. Results and Discussion
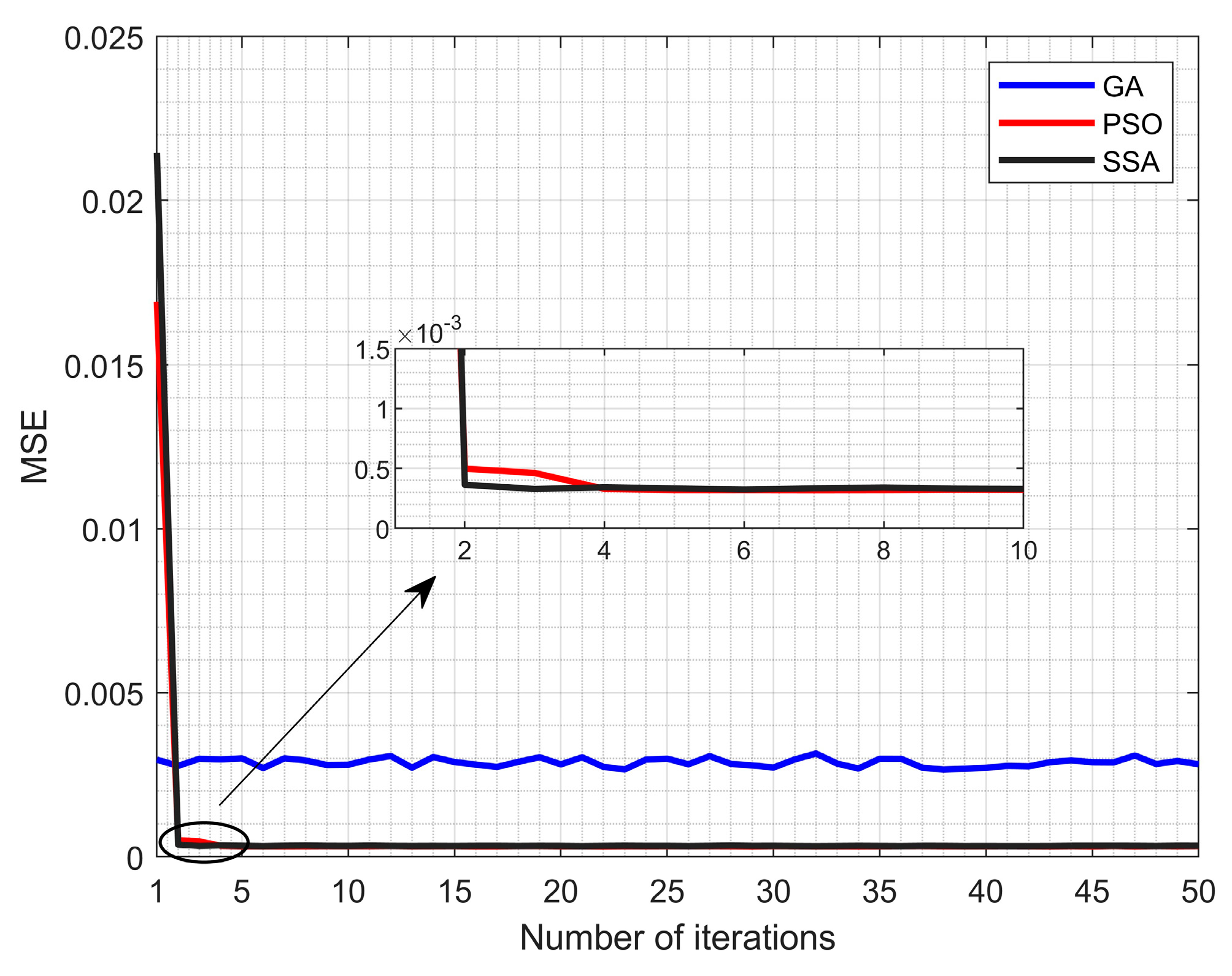
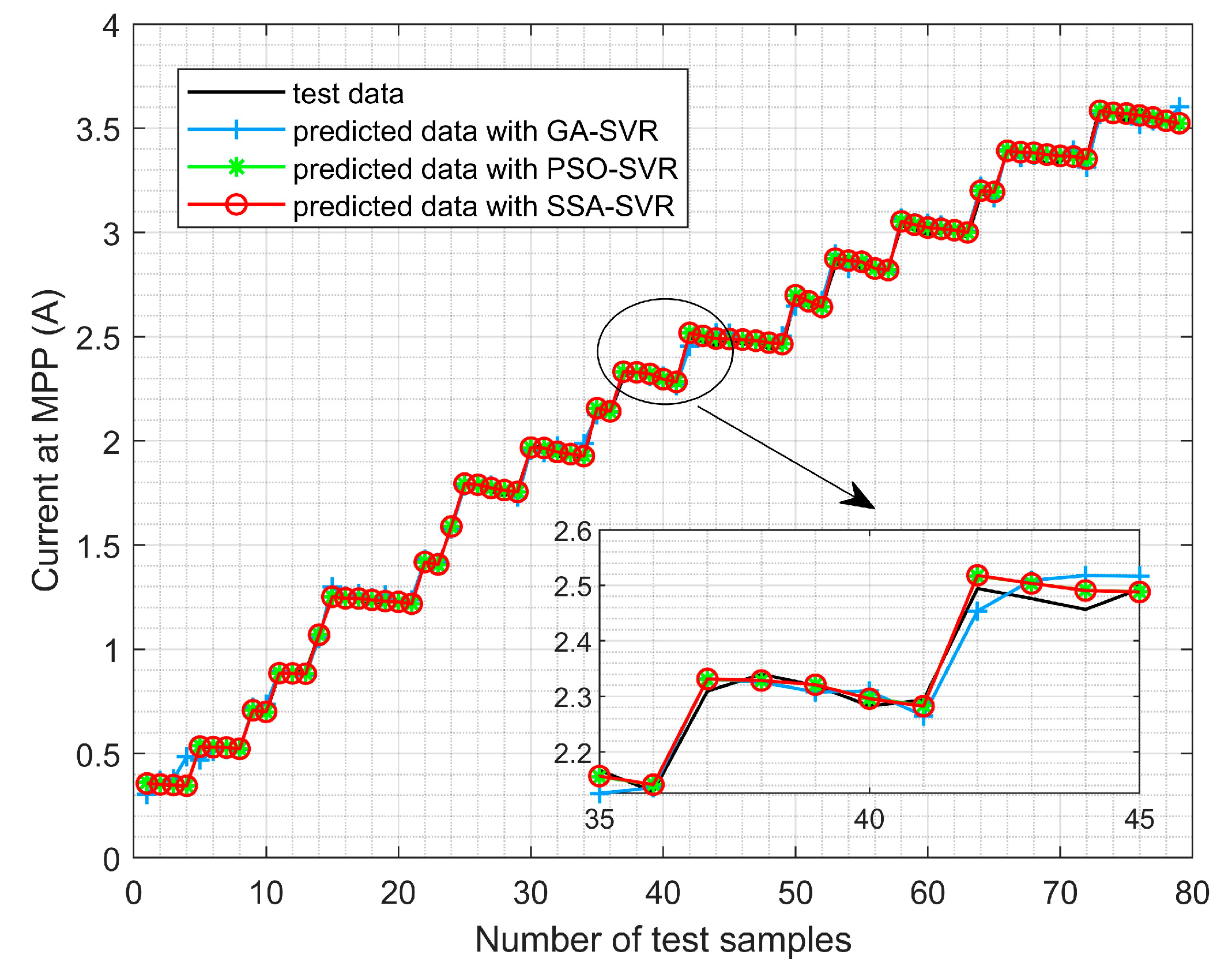
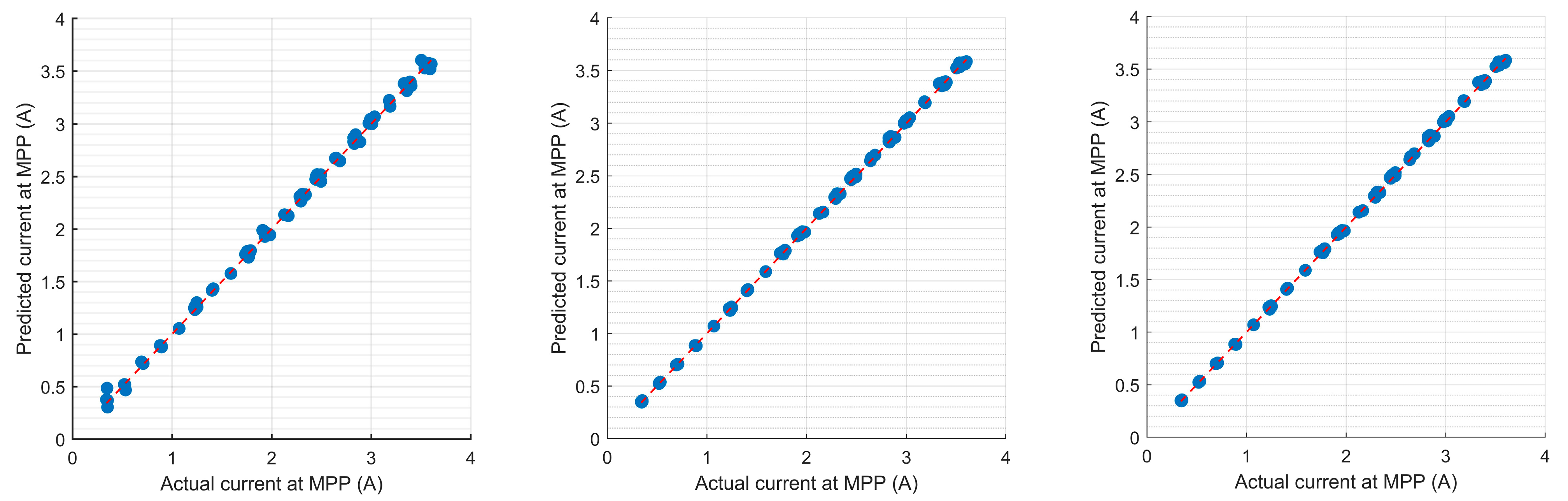
5.1. Predicting the Reference Current at the MPP Based on SSA-SVR
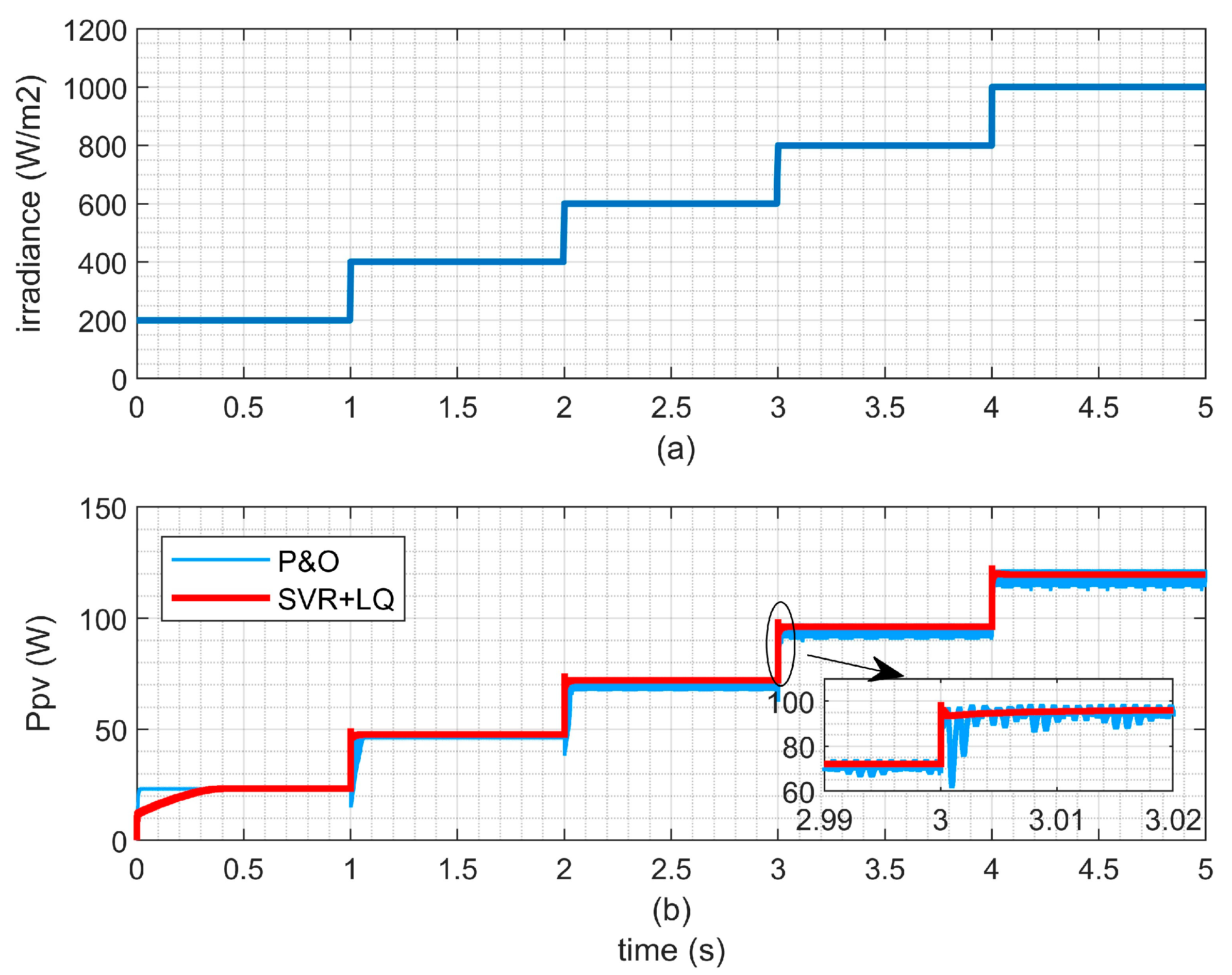
5.2. Performance Analysis of Current Regulation
- (1)
- Performance Comparison between the Current Regulator and P&O
- (2)
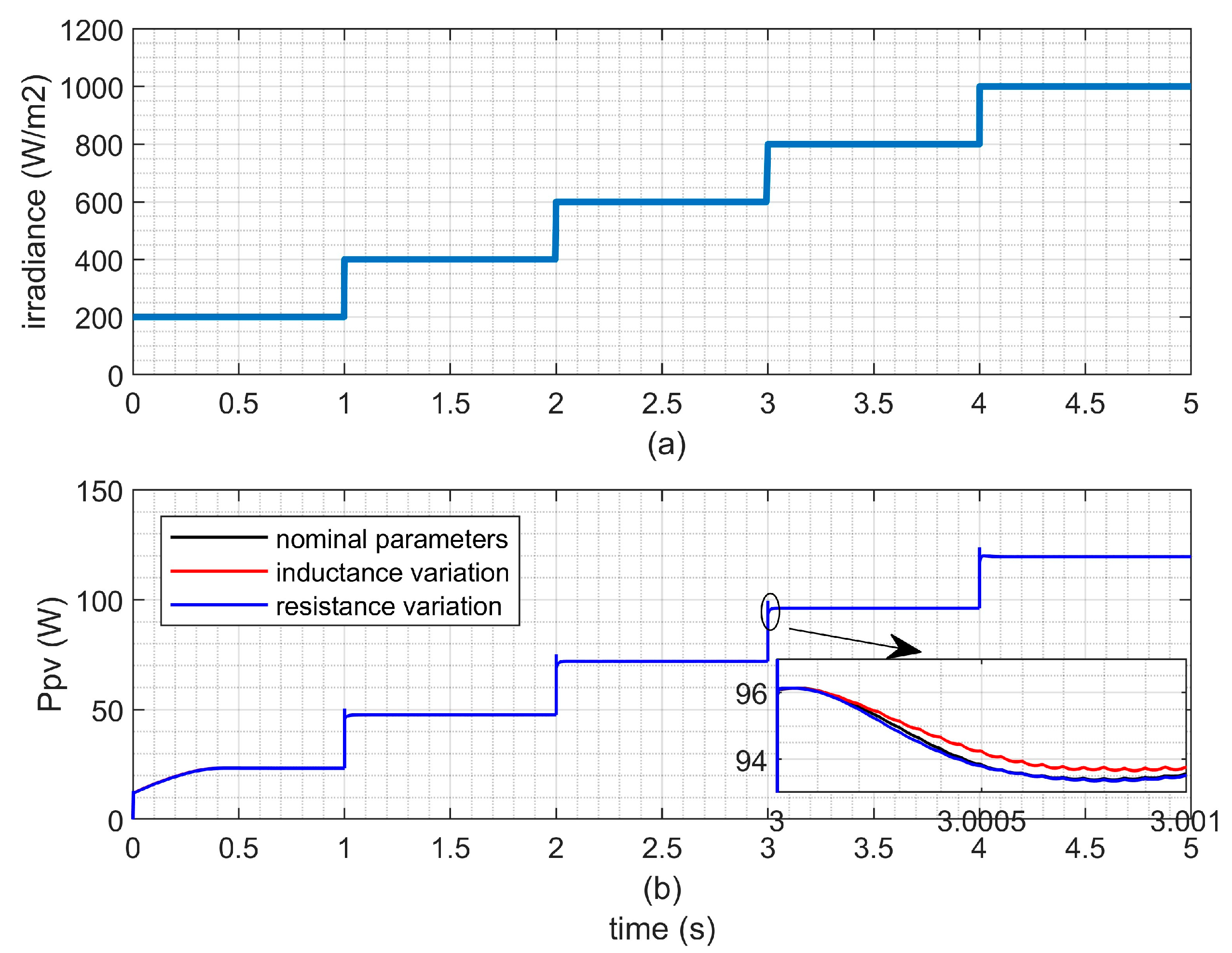
- Robustness Analysis of the Current Regulator
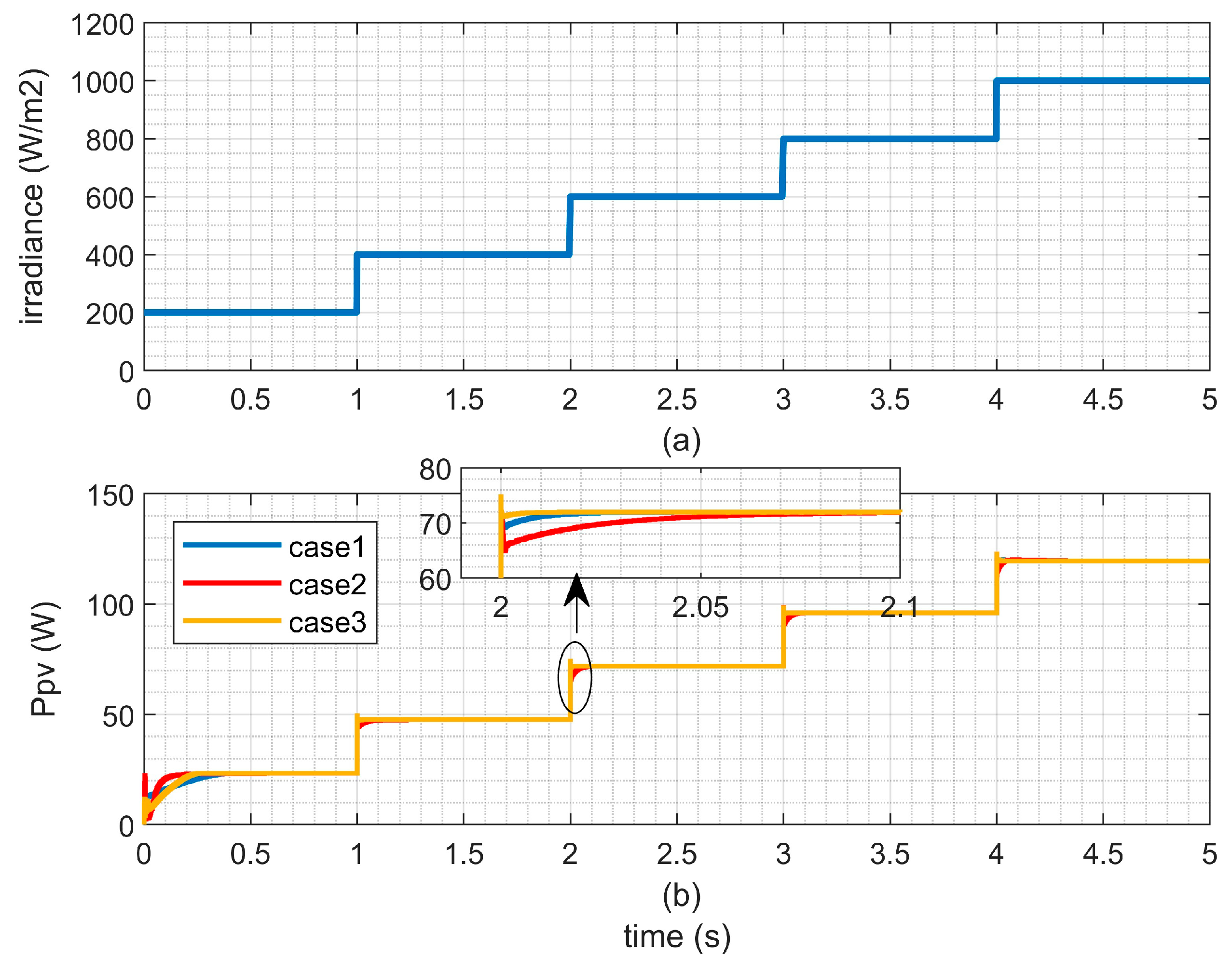
- (3)
- Performance Analysis of LQ Strategy with Different Weighing Matrices
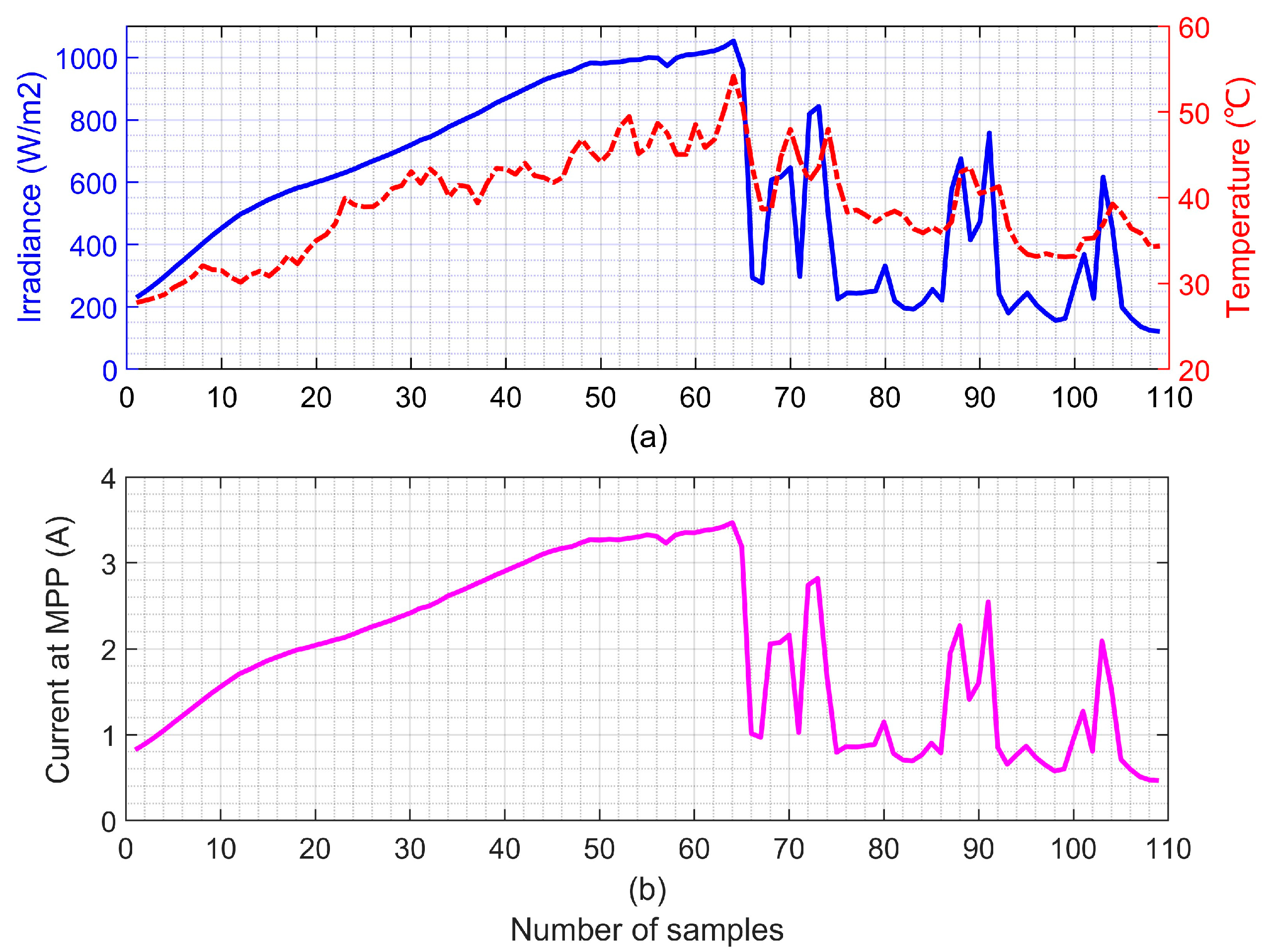
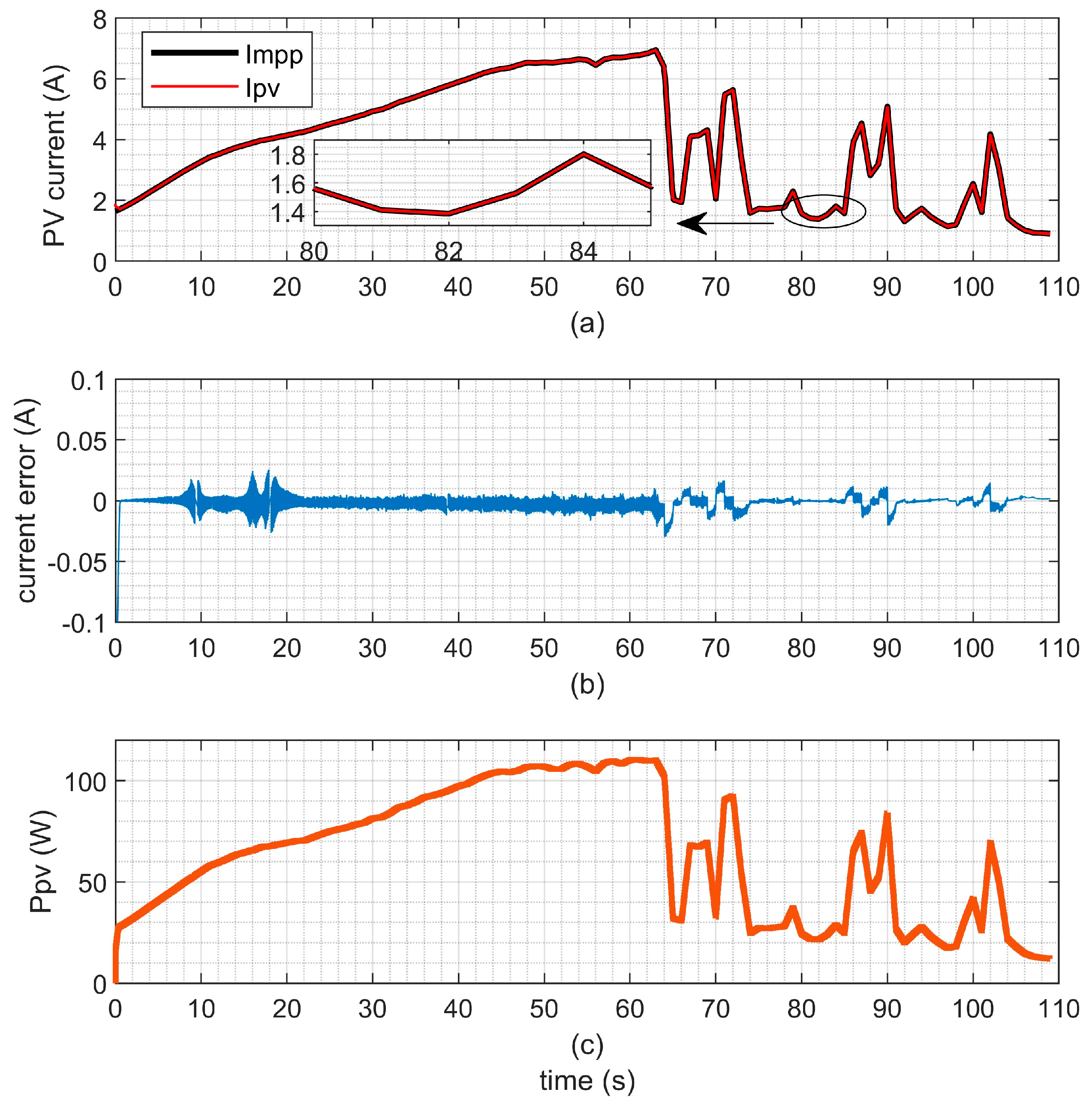
5.3. Effect Verification of MPPT with the Measured Irradiance and Temperature of a Day
6. Conclusions
- (1)
- SSA-SVR is an effective tool to model the nonlinear relationship among irradiation, temperature, and the PV output currents at the MPP. In comparison with other modeling methods in the same test conditions, SSA-SVR can give better prediction results.
- (2)
- The adopted LQ optimal control can both ensure the controlled system’s stability, steady-state performance, and strong robustness under uncertainties of parameter perturbation and disturbances and also achieve a satisfactory dynamic response during the regulating process.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Vodapally, S.N.; Ali, M.H. A Comprehensive Review of Solar Photovoltaic (PV) Technologies, Architecture, and Its Applications to Improved Efficiency. Energies 2023, 16, 319. [Google Scholar] [CrossRef]
- Shakeel, S.R.; Yousaf, H.; Irfan, M.; Rajala, A. Solar PV adoption at household level: Insights based on a systematic literature review. Energy Strateg. Rev. 2023, 50, 101178. [Google Scholar] [CrossRef]
- Huang, C.; Yan, Y.; Madonski, R.; Zhang, Q.; Deng, H. Improving operation strategies for solar-based distributed energy systems: Matching system design with operation. Energy 2023, 276, 127610. [Google Scholar] [CrossRef]
- Zidane, T.E.K.; Aziz, A.S.; Zahraoui, Y.; Kotb, H.; Aboras, K.M.; Kitmo; Jember, Y.B. Grid-connected Solar PV power plants optimization: A review. IEEE Access 2023, 11, 79588–79608. [Google Scholar] [CrossRef]
- Katche, M.L.; Makokha, A.B.; Zachary, S.O.; Adaramola, M.S. A Comprehensive Review of Maximum Power Point Tracking (MPPT) Techniques Used in Solar PV Systems. Energies 2023, 16, 2206. [Google Scholar] [CrossRef]
- Sharma, S.; Jately, V.; Kuchhal, P.; Kala, P.; Azzopardi, B. A Comprehensive Review of Flexible Power-Point-Tracking Algorithms for Grid-Connected Photovoltaic Systems. Energies 2023, 16, 5679. [Google Scholar] [CrossRef]
- Ramírez Torres, J.A.; Lastres Danguillecourt, O.; González Domínguez, R.A.; Ibáñez Duharte, G.R.; Verea Valladares, L.E.; Pantoja Enríquez, J.; Enríquez Santiago, J.A.; López López, A.; Verde Añorve, A. Development and Implementation of the MPPT Based on Incremental Conductance for Voltage and Frequency Control in Single-Stage DC-AC Converters. Energies 2025, 18, 184. [Google Scholar] [CrossRef]
- Khan, M.A.; Usama, M.; Kim, J. Deep Symbolic Regression-Based MPPT Control for a Standalone DC Microgrid System. Energies 2024, 17, 6377. [Google Scholar] [CrossRef]
- Mahdi, A.S.; Mahamad, A.K.; Saon, S.; Tuwoso, T.; Elmunsyah, H.; Mudjanarko, S.W. Maximum power point tracking using perturb and observe, fuzzy logic and ANFIS. Sn Appl. Sci. 2020, 2, 89. [Google Scholar] [CrossRef]
- Podder, A.K.; Roy, N.K.; Pota, H.R. MPPT methods for solar PV systems: A critical review based on tracking nature. IET Renew. Power Gen. 2019, 13, 1615–1632. [Google Scholar] [CrossRef]
- Zhang, Y.; Wang, H.; Zhu, X. Hybrid maximum power point tracking control method for photovoltaic power generation systems. J. Power Electron. 2023, 23, 1542–1550. [Google Scholar] [CrossRef]
- Manna, S.; Akella, A.K.; Singh, D.K. Novel Lyapunov-based rapid and ripple-free MPPT using a robust model reference adaptive controller for solar PV system. Prot. Contr Mod. Pow. 2023, 8, 13–25. [Google Scholar] [CrossRef]
- Feroz Mirza, A.; Mansoor, M.; Ling, Q.; Khan, M.I.; Aldossary, O.M. Advanced Variable Step Size Incremental Conductance MPPT for a Standalone PV System Utilizing a GA-Tuned PID Controller. Energies 2020, 13, 4153. [Google Scholar] [CrossRef]
- Harrag, A.; Messalti, S. Variable step size modified P&O MPPT algorithm using GA-based hybrid offline/online PID controller. Renew. Sustain. Energy Rev. 2015, 49, 1247–1260. [Google Scholar]
- Elobaid, L.M.; Abdelsalam, A.K.; Zakzouk, E.E. Artificial neural network-based photovoltaic maximum power point tracking techniques: A survey. IET Renew. Power Gen. 2015, 9, 1043–1063. [Google Scholar] [CrossRef]
- Venkata Mahesh, P.; Meyyappan, S.; Alla, R. Support Vector Regression Machine Learning based Maximum Power Point Tracking for Solar Photovoltaic systems. Int. J. Electr. Comput. 2023, 14, 100–108. [Google Scholar] [CrossRef]
- Roy, B.; Adhikari, S.; Datta, S.; Devi, K.J.; Devi, A.D.; Ustun, T.S. Harnessing Deep Learning for Enhanced MPPT in Solar PV Systems: An LSTM Approach Using Real-World Data. Electricity 2024, 5, 843–860. [Google Scholar] [CrossRef]
- Jiang, C.; Chen, X.; Jiang, B.; Liang, G. Hybrid genetic algorithm and support vector regression for predicting the shear capacity of recycled aggregate concrete beam. Soft Comput. 2024, 28, 1023–1039. [Google Scholar] [CrossRef]
- Açıkkar, M.; Altunkol, Y. A novel hybrid PSO- and GS-based hyperparameter optimization algorithm for support vector regression. Neural Comput. Appl. 2023, 35, 19961–19977. [Google Scholar] [CrossRef]
- Sakib, M.; Ahmad, S.; Anwar, K.; Saqib, M. Optimizing support vector regression using grey wolf optimizer for enhancing energy efficiency and building prototype architecture. Cluster Comput. 2025, 28, 60. [Google Scholar] [CrossRef]
- Águila-León, J.; Vargas-Salgado, C.; Díaz-Bello, D.; Montagud-Montalvá, C. Optimizing photovoltaic systems: A meta-optimization approach with GWO-Enhanced PSO algorithm for improving MPPT controllers. Renew. Energ. 2024, 230, 120892. [Google Scholar] [CrossRef]
- Eltamaly, A.M. A novel musical chairs algorithm applied for MPPT of PV systems. Renew. Sustain. Energy Rev. 2021, 146, 111135. [Google Scholar] [CrossRef]
- Eltamaly, A.M. A novel particle swarm optimization optimal control parameter determination strategy for maximum power point trackers of partially shaded photovoltaic systems. Eng. Optimiz 2022, 54, 634–650. [Google Scholar] [CrossRef]
- Zhao, Z.; Zhang, M.; Zhang, Z.; Wang, Y.; Cheng, R.; Guo, J.; Yang, P.; Lai, C.S.; Li, P.; Lai, L.L. Hierarchical Pigeon-Inspired Optimization-Based MPPT Method for Photovoltaic Systems Under Complex Partial Shading Conditions. IEEE Trans. Ind. Electron. 2022, 69, 10129–10143. [Google Scholar] [CrossRef]
- Takruri, M.; Farhat, M.; Barambones, O.; Ramos-Hernanz, J.A.; Turkieh, M.J.; Badawi, M.; AlZoubi, H.; Abdus Sakur, M. Maximum Power Point Tracking of PV System Based on Machine Learning. Energies 2020, 13, 692. [Google Scholar] [CrossRef]
- Mohammed, F.A.; Bahgat, M.E.; Elmasry, S.S.; Sharaf, S.M. Design of a maximum power point tracking-based PID controller for DC converter of stand-alone PV system. J. Electr. Syst. Inf. Technol. 2022, 9, 9. [Google Scholar] [CrossRef]
- Ahmad, G.A.K. Maximum power point tracking for a pv system using tuned support vector regression by particle swarm optimization. J. Eng. Res. 2020, 8, 139–152. [Google Scholar]
- Girgis, M.E.; Elkhateeb, N.A. Enhancing photovoltaic MPPT with P&O algorithm performance based on adaptive PID control using exponential forgetting recursive least squares method. Renew. Energy 2024, 237, 121801. [Google Scholar]
- Al-Muthanna, G.; Fang, S.; AL-Wesabi, I.; Ameur, K.; Kotb, H.; AboRas, K.M.; Garni, H.Z.A.; Mas Ud, A.A. A High Speed MPPT Control Utilizing a Hybrid PSO-PID Controller under Partially Shaded Photovoltaic Battery Chargers. Sustainability 2023, 15, 3578. [Google Scholar] [CrossRef]
- Chacko, S.J.; Neeraj, P.C.; Abraham, R.J. Optimizing LQR controllers: A comparative study. Results Control. Optim. 2024, 14, 100387. [Google Scholar] [CrossRef]
- Contreras Carmona, I.; Saldivar, B.; Portillo-Rodríguez, O.; Ramírez Rivera, V.M.; Gil Antonio, L.; Jacinto-Villegas, J.M. A novel strategy for the MPPT in a photovoltaic system via sliding modes control. PLoS ONE 2024, 19, e0311831. [Google Scholar] [CrossRef] [PubMed]
- Yılmaz, M.; Kaleli, A.; Çorapsız, M.F. Machine learning based dynamic super twisting sliding mode controller for increase speed and accuracy of MPPT using real-time data under PSCs. Renew. Energy 2023, 219, 119470. [Google Scholar] [CrossRef]
- Jamshidi, F.; Salehizadeh, M.R.; Yazdani, R.; Azzopardi, B.; Jately, V. An Improved Sliding Mode Controller for MPP Tracking of Photovoltaics. Energies 2023, 16, 2473. [Google Scholar] [CrossRef]
- Wu, Y.; Cong, P.; Wang, Y. Charging Load Forecasting of Electric Vehicles Based on VMD–SSA–SVR. IEEE T Transp. Electr. 2024, 10, 3349–3362. [Google Scholar] [CrossRef]
- Tao, H.; Zhao, S.; Jia, C. Dynamics characteristics of boost converter in maximum power point tracking for photovoltaic power generation. Proc. CSU-EPSA 2022, 34, 26–34. [Google Scholar]
- Smola, A.J.; Schölkopf, B. A tutorial on support vector regression. Stat. Comput. 2004, 14, 199–222. [Google Scholar] [CrossRef]
- Tan, B.; Ke, X.; Tang, D.; Yin, S. Improved Perturb and Observation Method Based on Support Vector Regression. Energies 2019, 12, 1151. [Google Scholar] [CrossRef]
- Xue, J.; Shen, B. A novel swarm intelligence optimization approach: Sparrow search algorithm. Syst. Sci. Control Eng. 2020, 8, 22–34. [Google Scholar] [CrossRef]
- Gharehchopogh, F.S.; Namazi, M.; Ebrahimi, L.; Abdollahzadeh, B. Advances in Sparrow Search Algorithm: A Comprehensive Survey. Arch. Comput. Method. E 2023, 30, 427–455. [Google Scholar] [CrossRef]
- Awadallah, M.A.; Al-Betar, M.A.; Doush, I.A.; Makhadmeh, S.N.; Al-Naymat, G. Recent Versions and Applications of Sparrow Search Algorithm. Arch. Comput. Method. E 2023, 30, 2831–2858. [Google Scholar] [CrossRef]
- Yue, Y.; Cao, L.; Lu, D.; Hu, Z.; Xu, M.; Wang, S.; Li, B.; Ding, H. Review and empirical analysis of sparrow search algorithm. Artif. Intell. Rev. 2023, 56, 10867–10919. [Google Scholar] [CrossRef]
- Yan, S.; Liu, W.; Li, X.; Yang, P.; Wu, F.; Yan, Z. Comparative Study and Improvement Analysis of Sparrow Search Algorithm. Wirel. Commun. Mob. Com. 2022, 2022, 1–15. [Google Scholar] [CrossRef]
- Liu, C.; Qiu, X.; Xu, T.; Wei, W.; Sun, H.; Hou, Y. A Linear Quadratic Regulation Controller Based on Radial Basis Function Network Approximation. Electronics 2024, 13, 4279. [Google Scholar] [CrossRef]
- Li, Q.; Baran, M.E. A Novel Frequency Support Control Method for PV Plants Using Tracking LQR. IEEE T Sustain. Energ. 2020, 11, 2263–2273. [Google Scholar] [CrossRef]
- Harrison, A.; Henry, A.N. Solar PV Data: (a-m) Piecewise Segmentation of the I-V Curve. Figshare. Dataset 2022. Available online: https://figshare.com/articles/dataset/Solar_PV_Data_a-m_Piecewise_segmentation_of_the_I-V_curve/21677555/1?file=38433818 (accessed on 26 April 2025).
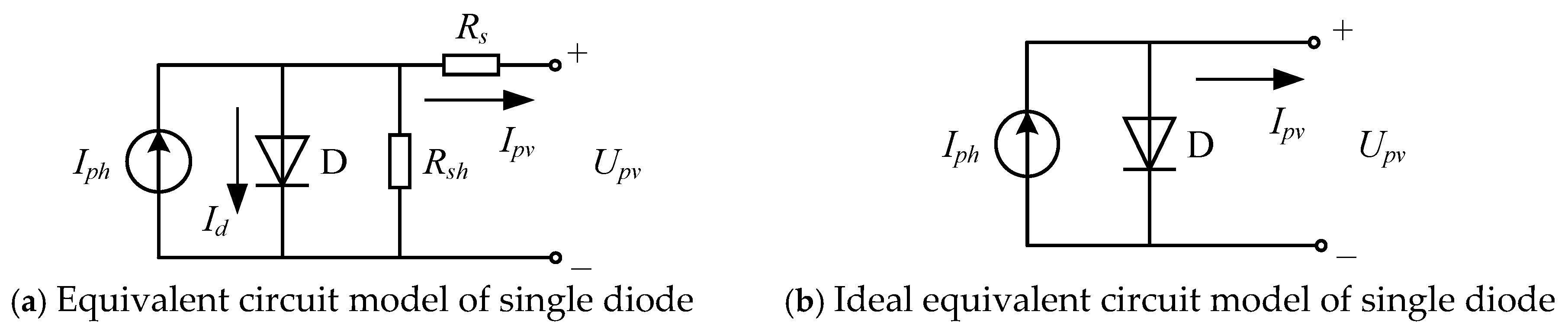
| Technical Scheme | Pros | Cons |
|---|---|---|
| PSO-SVR + PI (Refs. [25,27]) | Give a precise prediction of VMPP; the SVR’s hyperparameters are optimized with PSO | Voltage–current double-closed-loop PI control increases the tuning time, and it is difficult to achieve optimal dynamic performance |
| GPR + SMC (Ref. [32]) | The GPR can also achieve accurate VMPP predictions; high robustness | The GPR is of high computational complexity; the SMC brings in chattering during the tracking process; the controller design of the SMC is complicated |
| SSA-SVR-LQR (this work) | Possesses extremely high prediction accuracy of IMPP; the dynamic performance of the tracking process and steady-state behavior are satisfactory | It is difficult to obtain an original dataset under complex scenarios; the dynamic model of DC/DC must be linearized |
| Algorithm | Parameters |
| GA | crossover rate is 0.8; mutation rate is 0.01 |
| PSO | inertia weight is 0.5; learning factors are 1.5 |
| SSA | ST = 0.8; the proportion of producers is 70% |
| Algorithm | C | g | ε |
|---|---|---|---|
| GA | 343.9078 | 5.8824 | 0.0185 |
| PSO | 717.5694 | 0.01 | 0.01 |
| SSA | 1000 | 0.01 | 0.01 |
| Algorithm | MAE | MSE | RMSE | R2 |
|---|---|---|---|---|
| GA | 0.0262 | 0.0011 | 0.0334 | 0.9988 |
| PSO | 0.0116 | 0.00024 | 0.0151 | 0.9997 |
| SSA | 0.0102 | 0.00019 | 0.0139 | 0.9998 |
| Parameters | Description | Value | Unit |
|---|---|---|---|
| R | Input resistance of DC/DC | 0.0005 | Ω |
| L | Input inductance of DC/DC | 0.002 | H |
| C | Input capacitance of DC/DC | 0.00047 | F |
| Udc | DC bus voltage | 100 | V |
| Uoc | Open-circuit voltage of PV panel | 20.6697 | V |
| Isc | Short-circuit current of PV panel | 3.8756 | A |
| P | Maximum output power of PV panel | 60 | W |
| Rpv | Equivalent resistance of PV panel | 5.3333 | Ω |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
He, M.; Zhou, K.; Xu, Y.; Yu, J.; Qu, Y.; Wen, X. An Improved Maximum Power Point Tracking Control Scheme for Photovoltaic Systems: Integrating Sparrow Search Algorithm-Optimized Support Vector Regression and Optimal Regulation for Enhancing Precision and Robustness. Energies 2025, 18, 3182. https://doi.org/10.3390/en18123182
He M, Zhou K, Xu Y, Yu J, Qu Y, Wen X. An Improved Maximum Power Point Tracking Control Scheme for Photovoltaic Systems: Integrating Sparrow Search Algorithm-Optimized Support Vector Regression and Optimal Regulation for Enhancing Precision and Robustness. Energies. 2025; 18(12):3182. https://doi.org/10.3390/en18123182
Chicago/Turabian StyleHe, Mingjun, Ke Zhou, Yutao Xu, Jinsong Yu, Yangquan Qu, and Xiankui Wen. 2025. "An Improved Maximum Power Point Tracking Control Scheme for Photovoltaic Systems: Integrating Sparrow Search Algorithm-Optimized Support Vector Regression and Optimal Regulation for Enhancing Precision and Robustness" Energies 18, no. 12: 3182. https://doi.org/10.3390/en18123182
APA StyleHe, M., Zhou, K., Xu, Y., Yu, J., Qu, Y., & Wen, X. (2025). An Improved Maximum Power Point Tracking Control Scheme for Photovoltaic Systems: Integrating Sparrow Search Algorithm-Optimized Support Vector Regression and Optimal Regulation for Enhancing Precision and Robustness. Energies, 18(12), 3182. https://doi.org/10.3390/en18123182





