Estimation of Remaining Insulation Lifetime of Aged XLPE Cables with Step-Stress Method Based on Physical-Driven Model
Abstract
1. Introduction
2. Experimental Setup
2.1. Sample Preparation
2.2. Accelerated-Ageing Test Platform
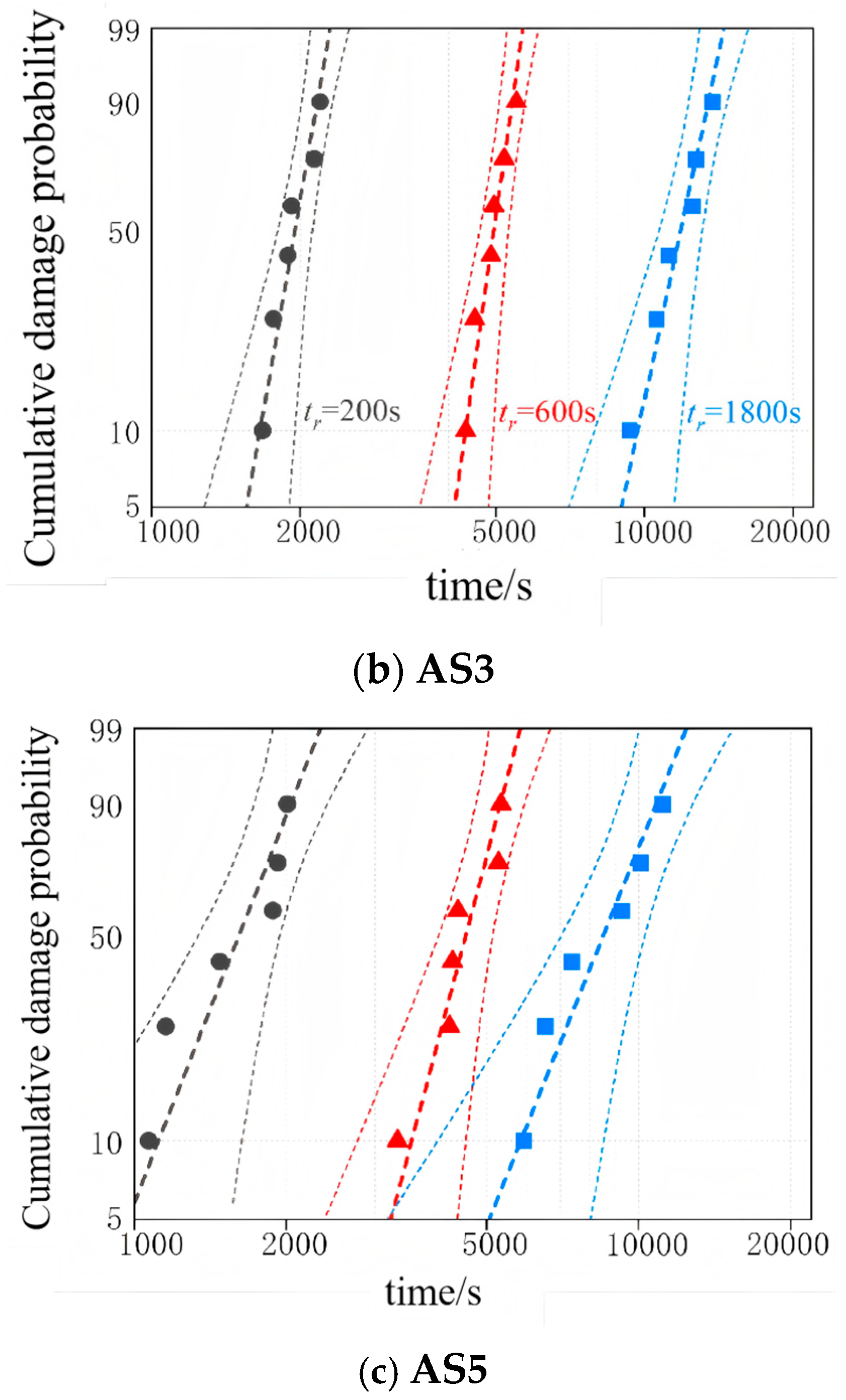
3. Measurement Results
4. Analysis
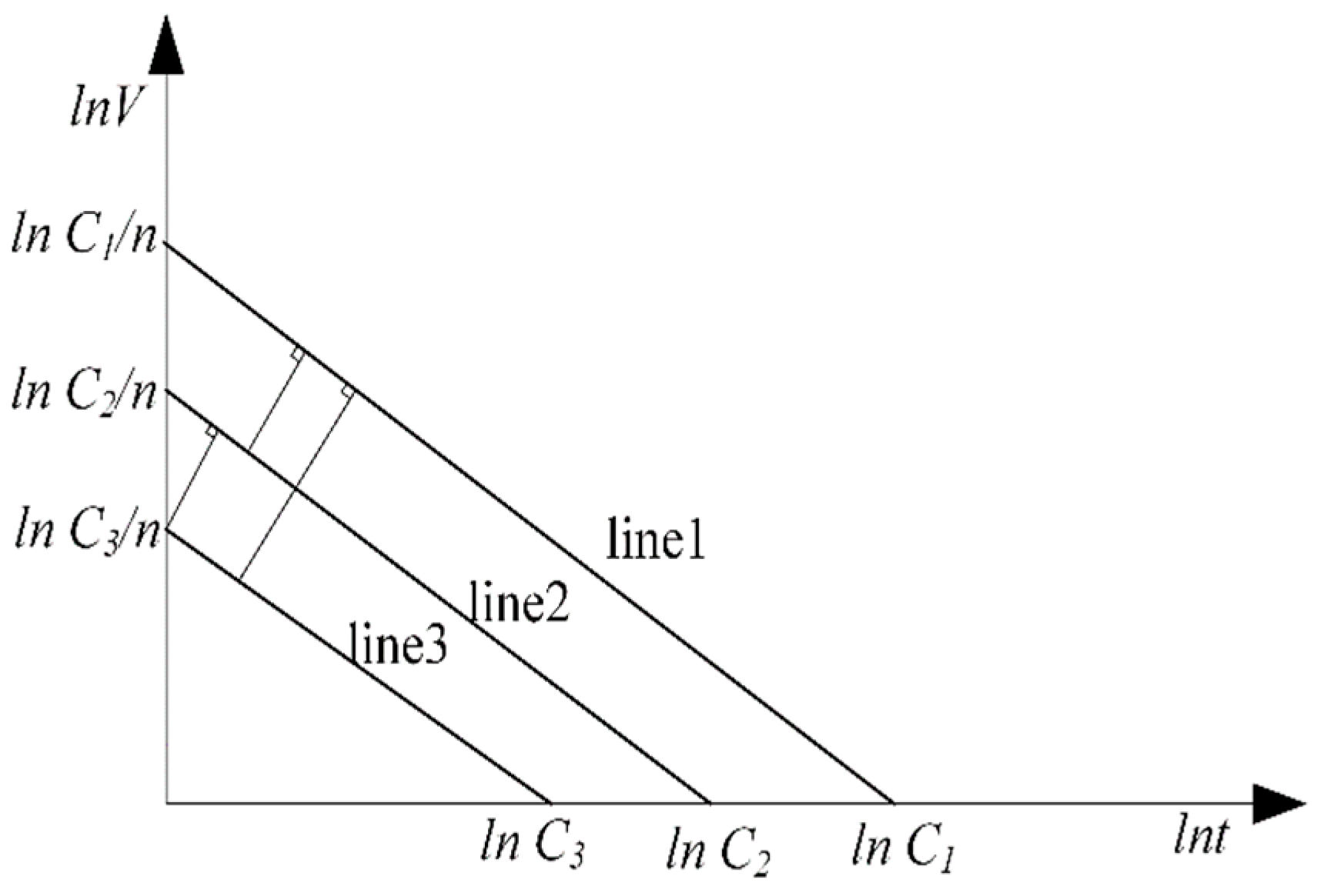
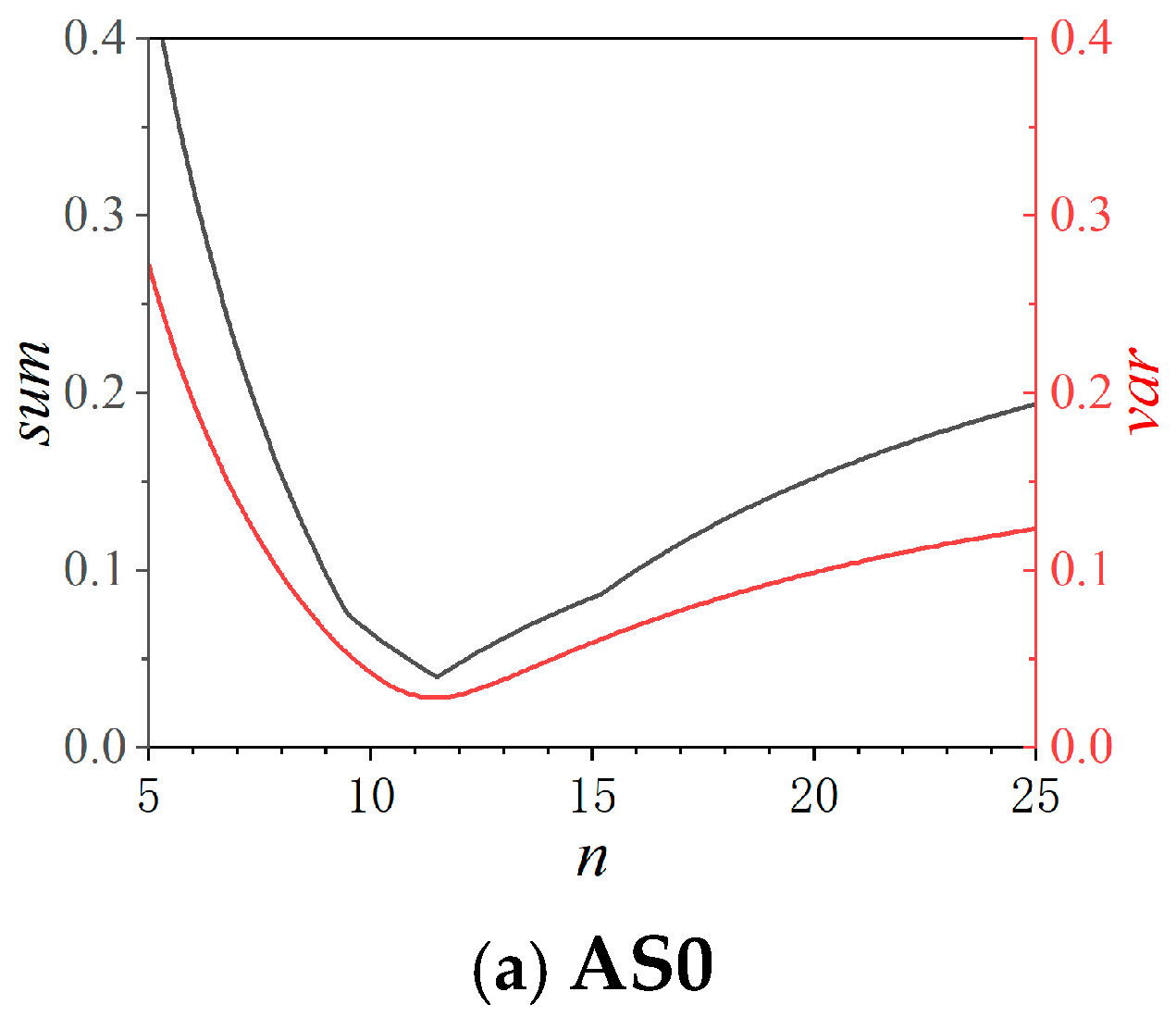
4.1. Insulation Ageing Lifetime Evaluation Based on Inverse Power Model
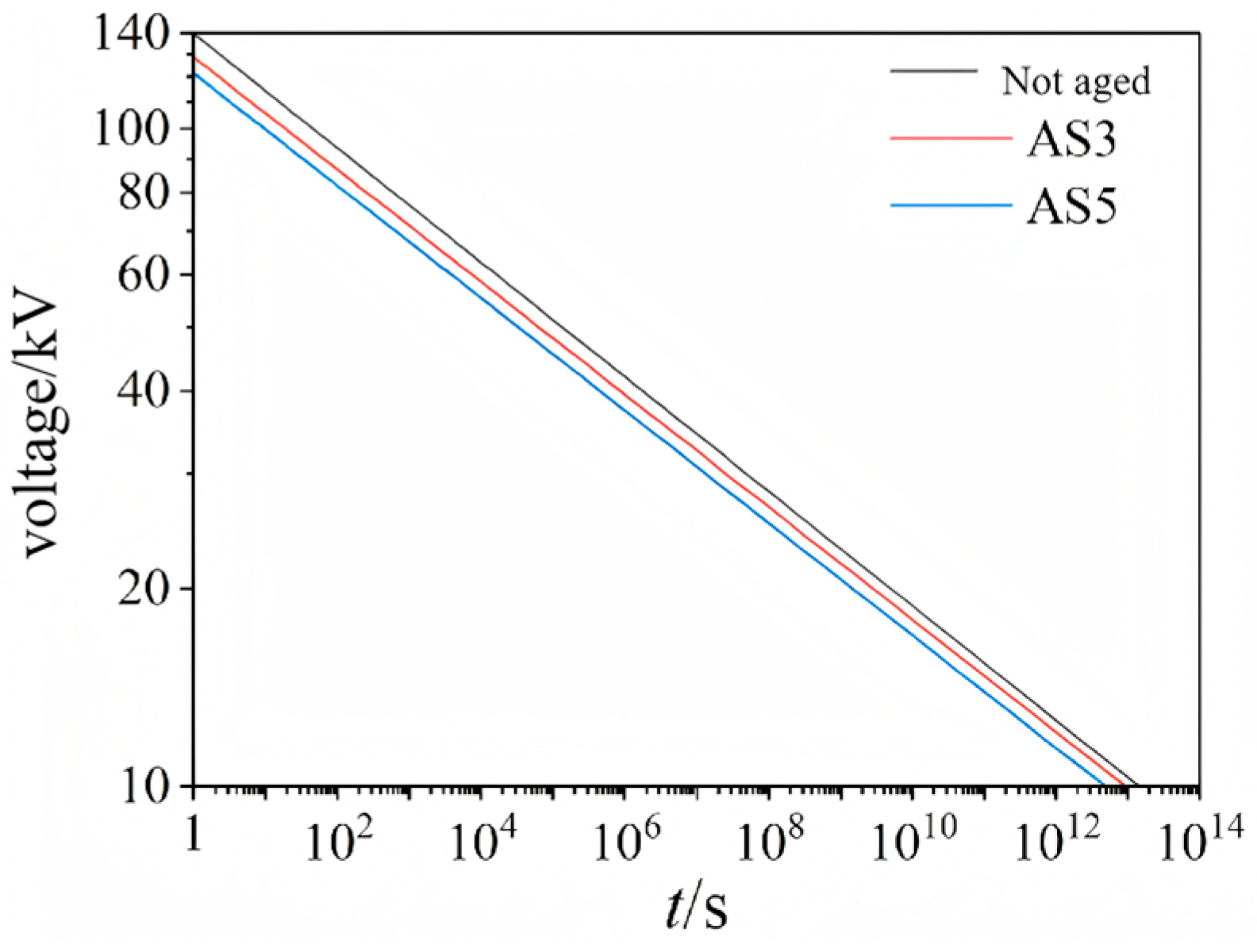
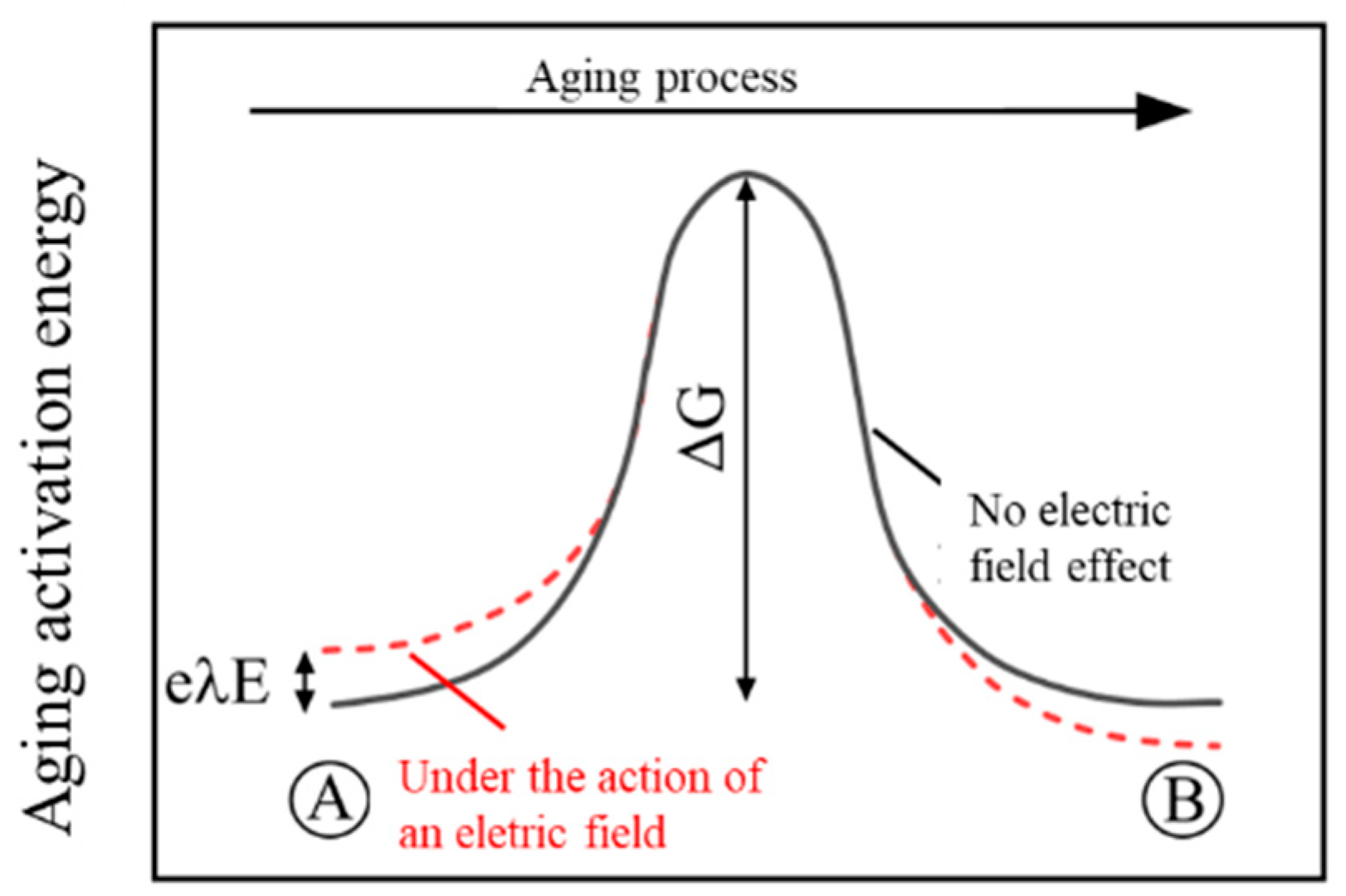
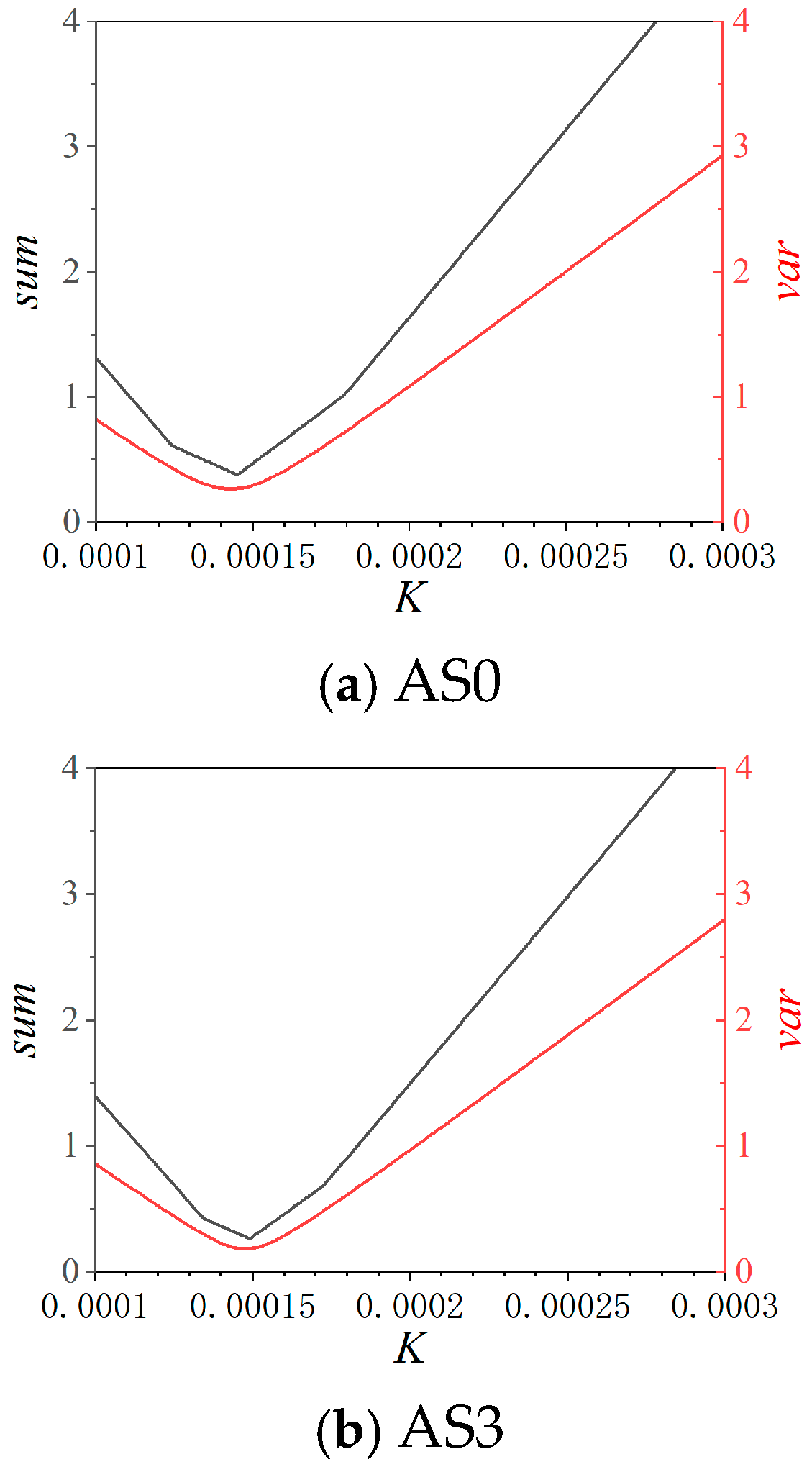
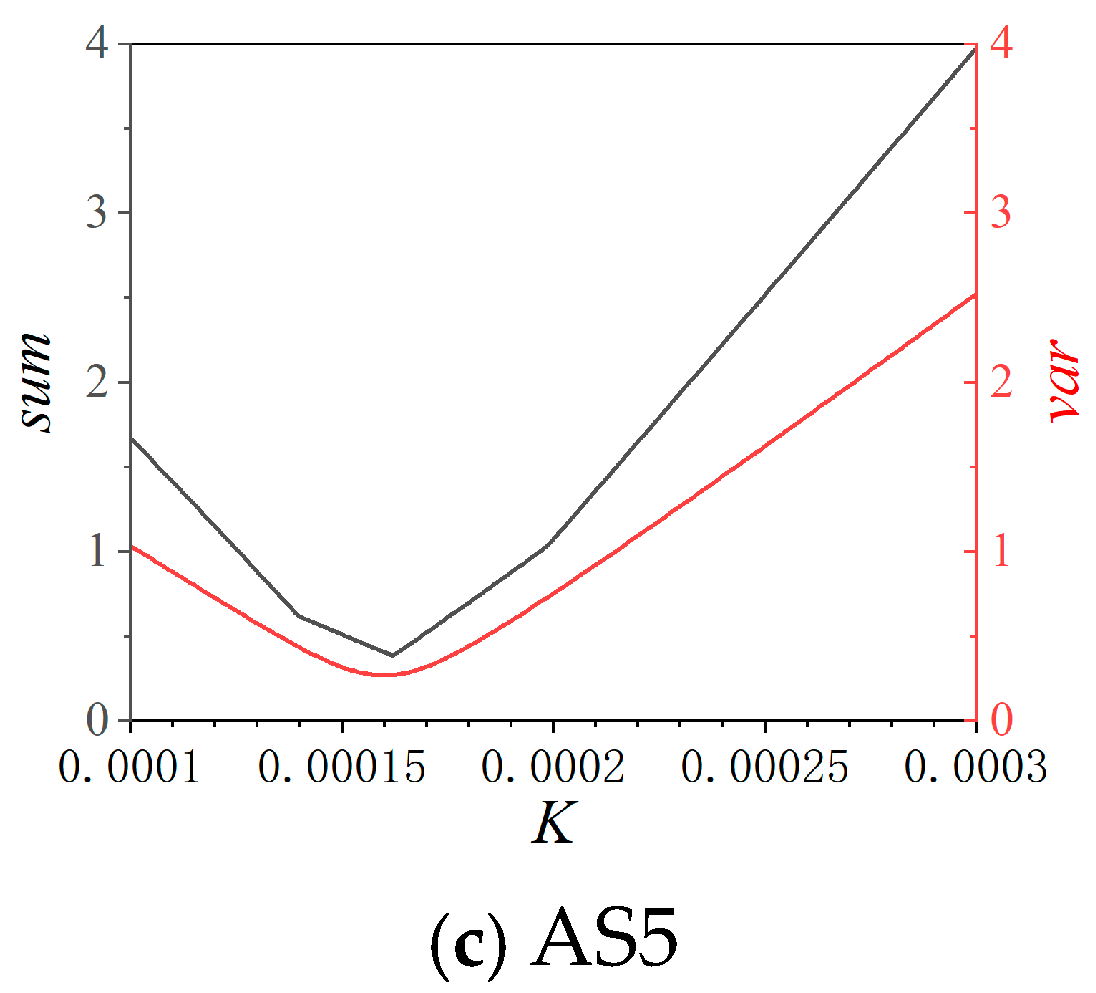
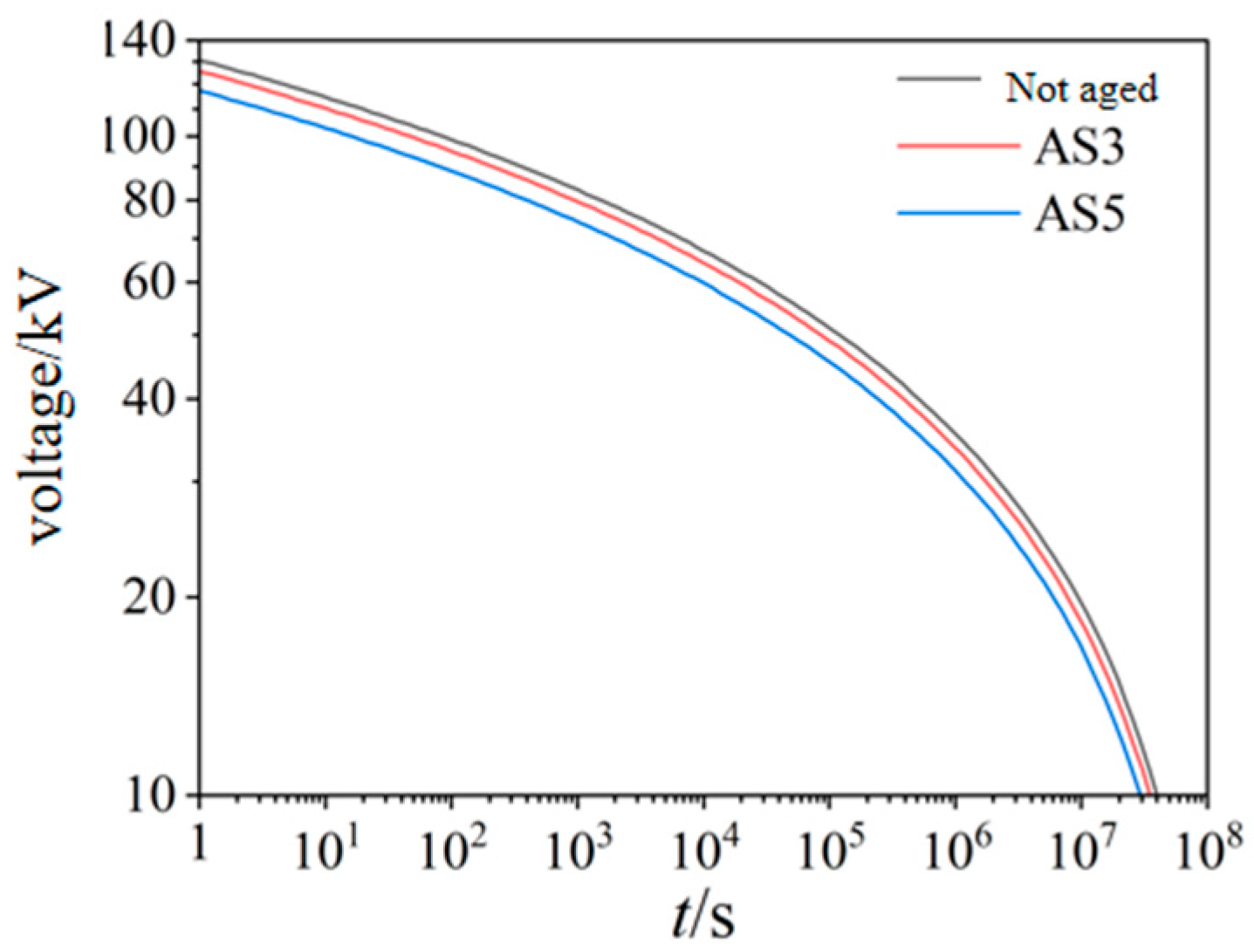
4.2. Insulation Ageing Lifetime Evaluation Based on Crine’s Model
5. Conclusions
- The step-stress method can efficiently obtain the lifetime data of the insulation samples. It is found that the longer the ageing time, the shorter the remaining lifetime of the XLPE sample.
- The ageing parameters n and C of the IPM increase with the ageing time, but they can hardly link to the physics of the ageing process, and they cannot be used as an indicator of the ageing state.
- The activation energy barrier of the Crine model does not change with the ageing process, and so it can be considered as a material intrinsic parameter determined by the material nature. The acceleration distance of the Crine model increases with the ageing time, and it can be regarded as an indicator of the ageing state.
- The Crine model describes a more reasonable ageing lifetime pattern than IPM, especially when the voltage is high and low. The Crine model has a greater potential to be used in the remaining lifetime estimation of the cable insulation or other materials.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Du, B.X.; Li, Z.L.; Yang, Z.R.; Li, J. Application and Research Progress of HVDC Cross-Linked Polyethylene Cables. High Volt. Eng. 2017, 43, 344–354. [Google Scholar]
- Zhou, T.X.; Wang, L.Y.; Ji, X.P.; Han, X.Y. Power Grid Scale Prediction and Optimization Needs Based on Policy Requirements of Modern Infrastructure System. Electr. Power 2024, 57, 1–8. [Google Scholar]
- China Electricity Council. Annual Development Report of China’s Electric Power Industry 2019; China Building Materials Industry Press: Beijing, China, 2019. [Google Scholar]
- Dakin, T.W.; Studniarz, S.A. The voltage endurance of cast and molded resins. In Proceedings of the 1977 EIC 13th Electrical/Electronics Insulation Conference, Chicago, LI, USA, 25–29 September 1977. [Google Scholar]
- Endicott, H.S.; Hatch, B.D.; Sohmer, R.G. Application of the eyring model to capacitor ageing data. IEEE Trans. Compon. Parts 1965, 12, 34–41. [Google Scholar] [CrossRef]
- Lewis, T.J.; Liewellyn, J.P.; Freestone, J.; Hampton, R.N. A newmodel for electrical ageing and breakdown in dielectrics. In Proceedings of the Seventh International Conference on Dielectric Materials, Measurements and Applications, IET, Bath, UK, 23–26 September 1996. [Google Scholar]
- Dissado, L.; Mazzanti, G.; Montanari, G.C. The incorporation of space charge degradation in the life model for electrical insulating materials. IEEE Trans. Dielectr. Electr. Insul. 1995, 2, 1147–1158. [Google Scholar] [CrossRef]
- Crine, J.P.; Parpal, J.L.; Lessard, G. A model of ageing of di-electric extruded cables. In Proceeding of the 3rd International Conference on Conduction and Breakdown in Solid Dielectrics, Trondheim, Norway, 3–6 July 1989. [Google Scholar]
- GB/T 11026.1-2012; National Standard of the People’s Republic of China. Electrical Insulating Materials—Thermal Endurance—Part 1: Ageing Procedures and Evaluation of Test Results. General Administration of Quality Supervision, Inspection and Quarantine of the People’s Republic of China and the Standardization Administration of the People’s Republic of China: Beijing, China, 2012.
- Zhang, Z.; Li, Y.; Zheng, Y.; Li, H.; Zhao, X.; Li, B.; Pei, X.; Cheng, Y. Insulation Aging Assessment Method for HVDC Cable Based on Space Charge Characteristics. Guangdong Electr. Power 2019, 32, 98–105. [Google Scholar]
- Wang, Y.; Lv, Z.; Wang, X.; Wu, K.; Zhang, C.; Li, W.; Dissado, L.A. Estimating the inverse power law aging exponent for the DC aging of XLPE and its nanocomposites at different temperatures. IEEE Trans. Dielectr. Electr. Insul. 2016, 23, 3504–3513. [Google Scholar]
- Xia, W.; Xiaotong, S.; Quanyu, L.; Wu, K.; Tu, D. Research progress on insulation ageing life model based on space charge effect. High Volt. Eng. 2016, 42, 861–867. [Google Scholar]





| Sample | Step Duration (s) | No. | Breakdown Voltage (kV) | Total Time (s) | Last Step Time (s) |
|---|---|---|---|---|---|
| AS0 | 200 | 1 | 95 | 2135 | 90 |
| 2 | 85 | 1678 | 33 | ||
| 3 | 90 | 1920 | 75 | ||
| 4 | 95 | 2194 | 149 | ||
| 5 | 90 | 1887 | 42 | ||
| 6 | 85 | 1762 | 117 | ||
| 600 | 1 | 80 | 4519 | 274 | |
| 2 | 85 | 4884 | 39 | ||
| 3 | 85 | 4954 | 109 | ||
| 4 | 80 | 4337 | 92 | ||
| 5 | 90 | 5494 | 49 | ||
| 6 | 85 | 5191 | 346 | ||
| 1800 | 1 | 80 | 12,696 | 51 | |
| 2 | 80 | 13,725 | 1080 | ||
| 3 | 75 | 11,186 | 341 | ||
| 4 | 90 | 12,509 | 1664 | ||
| 5 | 65 | 10,546 | 1501 | ||
| 6 | 70 | 9327 | 282 | ||
| AS3 | 200 | 1 | 75 | 1374 | 129 |
| 2 | 90 | 2017 | 172 | ||
| 3 | 95 | 2187 | 142 | ||
| 4 | 85 | 1783 | 138 | ||
| 5 | 80 | 1461 | 16 | ||
| 6 | 85 | 1679 | 34 | ||
| 600 | 1 | 90 | 5459 | 14 | |
| 2 | 80 | 4399 | 154 | ||
| 3 | 80 | 4505 | 260 | ||
| 4 | 80 | 4336 | 91 | ||
| 5 | 70 | 3446 | 401 | ||
| 6 | 80 | 4519 | 274 | ||
| 1800 | 1 | 70 | 10,832 | 1787 | |
| 2 | 65 | 8100 | 855 | ||
| 3 | 65 | 8933 | 1688 | ||
| 4 | 80 | 12,723 | 78 | ||
| 5 | 75 | 11,645 | 800 | ||
| 6 | 75 | 11,420 | 575 | ||
| AS5 | 200 | 1 | 80 | 1474 | 29 |
| 2 | 80 | 1550 | 105 | ||
| 3 | 70 | 1106 | 61 | ||
| 4 | 85 | 1768 | 123 | ||
| 5 | 80 | 1528 | 83 | ||
| 6 | 90 | 1935 | 90 | ||
| 600 | 1 | 70 | 3167 | 122 | |
| 2 | 80 | 4273 | 28 | ||
| 3 | 65 | 2522 | 77 | ||
| 4 | 60 | 1993 | 148 | ||
| 5 | 90 | 5801 | 356 | ||
| 6 | 85 | 5165 | 320 | ||
| 1800 | 1 | 70 | 9117 | 72 | |
| 2 | 75 | 10,873 | 28 | ||
| 3 | 75 | 11,768 | 728 | ||
| 4 | 65 | 7381 | 136 | ||
| 5 | 70 | 9195 | 150 | ||
| 6 | 65 | 7956 | 711 |
| Sample | Step Duration (s) | Characteristic Breakdown Voltage (kV) | Characteristic Ageing Time (s) | Last Step Time (s) |
|---|---|---|---|---|
| Un-aged | 200 | 90 | 2015 | 170 |
| 600 | 85 | 5077 | 232 | |
| 1800 | 75 | 12,308 | 1463 | |
| AS3 | 200 | 90 | 1874 | 29 |
| 600 | 80 | 4701 | 456 | |
| 1800 | 75 | 11,284 | 439 | |
| AS5 | 200 | 85 | 1697 | 52 |
| 600 | 80 | 4290 | 45 | |
| 1800 | 70 | 10,539 | 1194 |
| AS0 | AS3 | AS5 | |
|---|---|---|---|
| C1 | 1.6 × 1059 | 2.67 × 1059 | 9.74 × 1060 |
| C2 | 1.13 × 1059 | 1.06 × 1060 | 9.56 × 1060 |
| C3 | 1.69 × 1059 | 4.79 × 1059 | 1.04 × 1061 |
| C | 1.47 × 1059 | 6.2 × 1059 | 9.90 × 1060 |
| n | 11.5 | 11.7 | 12.1 |
| AS0 | AS3 | AS5 | |
|---|---|---|---|
| K | 0.000145 | 0.000149 | 0.00016 |
| L1 | 1.66 × 108 | 1.40 × 108 | 1.49 × 108 |
| L2 | 1.79 × 108 | 1.50 × 108 | 1.93 × 108 |
| L3 | 1.65 × 108 | 1.46 × 108 | 1.93 × 108 |
| L | 1.7 × 108 | 1.45 × 108 | 1.78 × 108 |
| ΔG0 (eV) | 1.269 | 1.265 | 1.27 |
| λ (m) | 0.739 × 10−9 | 0.753 × 10−9 | 0.809 × 10−9 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Shang, Y.; Qu, J.; Wang, J.; Chen, J.; Ma, J.; Xiong, J.; Li, Y.; Lv, Z. Estimation of Remaining Insulation Lifetime of Aged XLPE Cables with Step-Stress Method Based on Physical-Driven Model. Energies 2025, 18, 3179. https://doi.org/10.3390/en18123179
Shang Y, Qu J, Wang J, Chen J, Ma J, Xiong J, Li Y, Lv Z. Estimation of Remaining Insulation Lifetime of Aged XLPE Cables with Step-Stress Method Based on Physical-Driven Model. Energies. 2025; 18(12):3179. https://doi.org/10.3390/en18123179
Chicago/Turabian StyleShang, Yingqiang, Jingjiang Qu, Jingshuang Wang, Jiren Chen, Jingyue Ma, Jun Xiong, Yue Li, and Zepeng Lv. 2025. "Estimation of Remaining Insulation Lifetime of Aged XLPE Cables with Step-Stress Method Based on Physical-Driven Model" Energies 18, no. 12: 3179. https://doi.org/10.3390/en18123179
APA StyleShang, Y., Qu, J., Wang, J., Chen, J., Ma, J., Xiong, J., Li, Y., & Lv, Z. (2025). Estimation of Remaining Insulation Lifetime of Aged XLPE Cables with Step-Stress Method Based on Physical-Driven Model. Energies, 18(12), 3179. https://doi.org/10.3390/en18123179






