FEM Simulation of FDS Response in Oil-Impregnated Paper Insulation of Current Transformers with Axial Aging Variation

Abstract

The aging of oil-impregnated paper (OIP) insulation is one of the key factors influencing the service life of oil-immersed current transformers. Frequency domain spectroscopy (FDS), supported by mathematical models or simulation methods, is commonly used to evaluate insulation conditions. However, traditional aging models typically ignored significant aging differences between the transformer OIP head and straight sections caused by the axial temperature gradient. To address this limitation, an accelerated thermal aging experiment was performed on a full-scale oil-immersed inverted current transformer prototype. Based on the analysis of its internal temperature field, the axial temperature gradient boundary of the main insulation was identified. By applying region-specific aging control strategies to different axial segments, a FEM model incorporating axial aging variation was developed to analyze its influence on FDS. The simulation results closely matched experimental data, with a maximum deviation below 9.22%. The model’s applicability was further confirmed through the aging prediction of an in-service transformer. The proposed model is expected to provide a more accurate basis for predicting the FDS characteristics of OIP insulation in current transformers.

1. Introduction

Oil-immersed CTs are widely deployed in power systems operating at 110 kV and above, serving as critical components for current measurement and protection functions. Their safe and reliable operation is essential for ensuring the long-term stability of the power grid. The main insulation system of these transformers typically adopts an oil-impregnated paper structure, and the gradual aging of the OIP insulation is a key factor influencing their residual service life [1,2]. Over prolonged operation, the insulation experiences irreversible deterioration under thermal, electrical, and mechanical stresses, leading to declines in dielectric strength and mechanical properties. Failure to accurately and promptly assess the aging condition may lead to insulation breakdown and, in extreme cases, catastrophic incidents such as equipment explosions. Therefore, investigating the aging mechanisms of OIP insulation in current transformers and accurately assessing its condition have become crucial research topics.

During long-term service, oil-immersed CTs experience frequent temperature rise phenomena because of elevated operational temperatures and load fluctuations, which significantly accelerate the aging of their OIP insulation. The insulation system relies mainly on a capacitive core formed by alternately wound layers of insulation paper and aluminum foil. Due to the complex structure of the head region, where key components such as the primary conductor, secondary windings, and shielding elements are concentrated, the thermal distribution along the axial direction becomes highly uneven [3,4]. In addition, heat within the insulation is primarily dissipated through convection and thermal conduction by the insulating oil. However, due to the poor thermal conductivity of the insulation materials, heat tends to accumulate in the head region, thereby exacerbating the axial aging differences within the insulation partitions of the current transformer [5,6,7]. These structural and thermal limitations result in noticeable axial insulation aging variations, making it difficult for traditional evaluation methods based on uniform aging assumptions to reflect the true insulation condition of current transformers accurately. Therefore, it is imperative to develop an aging evaluation model that explicitly incorporates axial partition characteristics.

Compared with traditional insulation diagnostic techniques such as power-frequency dielectric loss measurements, capacitance tests, and DC resistance measurements, frequency domain spectroscopy has gained attention as a promising method for OIP insulation assessment because of its strong anti-interference capability and rich diagnostic information. Recent studies have often employed simplified mathematical models or FEM models to correlate the dielectric properties of insulation materials with the structural characteristics of oil-immersed equipment, enabling effective condition assessment in the field. Among them, the XY model has been widely applied for diagnosing the insulation condition of coaxial cylindrical structures such as transformers and bushings. Several researchers have proposed modifications to the XY or X models to incorporate the effects of non-uniform aging [8,9,10,11]. For instance, Xianhao Fan et al. introduced a transformer XY model considering radial non-uniform thermal aging, while Zhicheng Su et al. further improved the X model to evaluate both axial and radial aging differences in bushings [12,13,14]. Krzysztof Walczak et al. proposed a 2XY model based on the axial temperature gradient distribution in bushings, significantly enhancing the reliability of dielectric response analysis [15]. Although these mathematical models have improved reliability under non-uniform aging conditions in transformers and bushings, their direct application to current transformers remains challenging. This is primarily due to the presence of special transitional regions, such as the triangular area in the main insulation of current transformers, as well as the fundamentally different axial thermal gradients in inverted-type current transformers compared with transformers and bushings.

Furthermore, FEM has been extensively applied to various simulations of electrical equipment, including studies on the temperature and electric field distributions in current transformers, providing a solid foundation for insulation aging research. It has been found that FEM models offer higher accuracy than traditional XY models by considering factors such as electric field distortion [13,14]. The combination of FEM and non-uniform insulation aging studies has provided new approaches for predicting FDS characteristics. However, existing research on dielectric response under non-uniform aging conditions has mainly focused on transformers and bushings, while studies on current transformers remain limited because of their structural complexity [12,16,17]. Building upon previous FEM studies of non-uniform insulation aging, this paper analyzes the temperature field distribution in oil-immersed CT, identifies axial temperature gradient boundaries in the main insulation, and applies different aging parameter control strategies to the head region and the straight section within the FEM model. Accordingly, a new FEM model that accounts for axial aging differences in the OIP insulation of current transformers is proposed for FDS simulation and analysis.

To overcome the limitations of conventional aging assessment methods that rely on simplified analytical models or laboratory-prepared paper samples, this study conducted a full-lifetime accelerated thermal aging experiment on a full-scale 500 kV oil-immersed inverted current transformer prototype. Based on the simulated axial temperature gradient, a finite element model was developed to incorporate spatial variations in aging and establish an FDS simulation method for OIP insulation considering axial degradation. This approach overcomes the constraints of traditional XY models and sample-based tests and enables the investigation of aging patterns that are more representative of real operational conditions. The model was validated by comparing the simulated FDS curves with experimental measurements at multiple aging stages and was further applied to an in-service CT that had been operating for several years, demonstrating its practical potential for field insulation condition assessment. The overall technical workflow of this study is illustrated in Figure 1.

2. Theory of the FDS

Frequency domain spectroscopy extends conventional power-frequency capacitance and dielectric loss measurements over a much wider frequency range, typically from 0.1 mHz to 1 kHz. For a linear and homogeneous dielectric material with weak conductivity, the phase difference between current and voltage across the dielectric is not exactly 90° because of the presence of a conductive component G that shares the same phase as the applied voltage when an AC voltage $U^{*}\left(\mathsf{\omega }\right)$ with an angular frequency ω is applied to the electrodes, the resulting current $I^{*}\left(\mathsf{\omega }\right)$ flowing through the dielectric can be described in (1):

$$I^{*}\left(\mathsf{\omega }\right)=\mathrm{j}\mathsf{\omega }C{U}^{*}\left(\mathsf{\omega }\right)+G{U}^{*}\left(\mathsf{\omega }\right)$$

(1)

where G and C can be defined as $G=\mathsf{\omega }{C}_0{\mathsf{\epsilon }}_r^{″}\left(\mathsf{\omega }\right)$ and $C=\mathsf{\omega }{C}_0{\mathsf{\epsilon }}_r^{\prime }\left(\mathsf{\omega }\right)$, with $C_0$ being the vacuum capacitance. Substituting these relations, the current $I^{*}\left(\mathsf{\omega }\right)$ can be further described in (2) [18,19,20]:

$$\begin{array}{l}{I}^{*}\left(\mathsf{\omega }\right)=\mathrm{j}\mathsf{\omega }{C}_0{U}^{*}\left(\mathsf{\omega }\right)({\mathsf{\epsilon }}_r^{\prime }\left(\mathsf{\omega }\right)-{\mathrm{j}\mathsf{\epsilon }}_r^{″}\left(\mathsf{\omega }\right))\\ =\mathrm{j}\mathsf{\omega }{C}_0{U}^{*}\left(\mathsf{\omega }\right){\mathsf{\epsilon }}_r^{*}\left(\mathsf{\omega }\right)\end{array}$$

(2)

Here, ${\mathsf{\epsilon }}_r^{*}\left(\mathsf{\omega }\right)$ is the complex relative permittivity, ${\mathsf{\epsilon }}_r^{\prime }\left(\mathsf{\omega }\right)$ represents the real part of ${\mathsf{\epsilon }}_r^{*}\left(\mathsf{\omega }\right)$ corresponding to the capacitive behavior, ${\mathsf{\epsilon }}_r^{″}\left(\mathsf{\omega }\right)$ represents the imaginary part corresponding to the dielectric loss, capacitance C can be defined as $C={\mathsf{\epsilon }}_0{\mathsf{\epsilon }}_{r}S/d$, S is the electrode area, d is the dielectric thickness, and${\mathsf{\epsilon }}_0$is the vacuum permittivity. Then, the complex capacitance can be expressed as Equation (3):

$$C^{*}\left(\mathsf{\omega }\right)=C^{\prime }\left(\mathsf{\omega }\right)-\mathrm{j}{C}^{″}\left(\mathsf{\omega }\right)={\displaystyle \frac{{\mathsf{\epsilon }}_0\left({\mathsf{\epsilon }}_r^{\prime }\left(\mathsf{\omega }\right)-{\mathrm{j}\mathsf{\epsilon }}_r^{″}\left(\mathsf{\omega }\right)\right)S}{d}}$$

(3)

where $C^{*}\left(\mathsf{\omega }\right)$ is the complex capacitance, $C^{\prime }\left(\mathsf{\omega }\right)$ and $C^{″}\left(\mathsf{\omega }\right)$ are its real part and imaginary part, respectively.

3. Thermal Simulation and Prototype Aging Experiment

3.1. Thermal Simulation

The thermal aging of OIP insulation has a significant impact on the operational lifetime of oil-immersed current transformers. Temperature, as a core variable governing the aging process, directly determines the aging differences across various regions of the insulation. For oil-immersed inverted CTs, due to structural complexity and uneven internal heat source distribution, noticeable temperature variations often occur along the axial direction of the main insulation. Such non-uniform temperature distributions not only intensify localized insulation degradation but also impose stricter requirements on FDS-based aging models, which must avoid assuming uniform aging parameters across the entire structure. To quantify the temperature gradient and identify the axial partition boundaries of the main insulation, a steady-state temperature field simulation of the current transformer under normal operating conditions was conducted in this section, providing a foundation for subsequent aging modeling based on axial partitioning.

A typical 500 kV oil-immersed inverted CT was selected as the study object. A 3D finite element model was established, including the main insulation and a simplified external casing. This current transformer adopts a capacitive insulation structure, with both the primary and secondary windings concentrated within the oil conservator at the head region. The primary winding passes through the center of the secondary winding, and the secondary winding is enclosed within a magnetic shield. The main insulation is divided into two sections: the head insulation and the straight section insulation. The high-voltage screen is located at the outer surface of the main insulation, while the shield acts as the low-voltage screen. Since the oil conservator is a thin-walled structure and the secondary terminal box is far from the head region, their influence on the overall simulation is negligible. Therefore, the model was simplified to include the windings, core, secondary coil, magnetic shield, oil-impregnated paper, oil conservator casing, and insulating oil. A cross-sectional view of the established FEM model is shown in Figure 2. The geometric dimensions of the simulation model are consistent with the full-scale prototype described in Section 3.2, including a total height of 4100 mm, an oil conservator height of 563 mm, a main insulation thickness of 80–100 mm, a primary conductor diameter of 50 mm, and a secondary winding/core region height of 400 mm.

Under normal operating conditions, the heat generation of the oil-immersed inverted CT primarily originates from resistive losses and dielectric losses. The resistive losses mainly come from the secondary windings and the primary conductor. Based on the number of windings, estimated winding resistance, rated secondary current, and the current and resistance of the primary conductor for a typical 500 kV inverted current transformer, the total resistive loss active power $P_r$ can be calculated using Equation (4) [21,22]. These calculated losses are then spatially assigned as volumetric heat sources to the primary conductor and secondary winding regions within the thermal finite element model. The overall dielectric loss active power $P_d$ is typically obtained through high-voltage testing. For simplicity, it is assumed that it is mainly generated by the insulating paper and is calculated as (5), according to which the dielectric loss is assigned to the oil-immersed paper insulation region in the finite element model.

$$P_r=I^{2}R$$

(4)

$$P_d=U^2\mathsf{\omega }C\tan \mathsf{\delta }$$

(5)

When calculating the secondary winding resistance loss, I is the secondary current, and R is the total winding resistance. When calculating the primary conductor loss, I is the primary conductor current, and R is the total resistance of the primary conductor. U is the voltage amplitude on the insulating medium, C is the main insulation equivalent capacitance, and tanδ is the dielectric loss factor. The material parameters were set according to the basic thermal properties of each component. Due to the structural characteristics of the inverted-type design, the flow velocity of the insulating oil is relatively low, and turbulence generally does not occur. Therefore, a laminar flow model was adopted to simulate the internal oil movement. In addition, as a fluid, the insulating oil’s thermal expansion coefficient and dynamic viscosity must also be considered. The thermal expansion coefficient of the insulating oil was approximately set to 0.0007 K⁻¹. Based on the previous literature on the temperature-dependent behavior of transformer oil, the thermal properties of the insulating oil, including density, specific heat capacity, thermal conductivity, and dynamic viscosity, were defined as functions of temperature using empirical formulas, as shown in Equations (6)–(9) [6]. The material properties of the other components are listed in

Table 1. Material properties of model components.

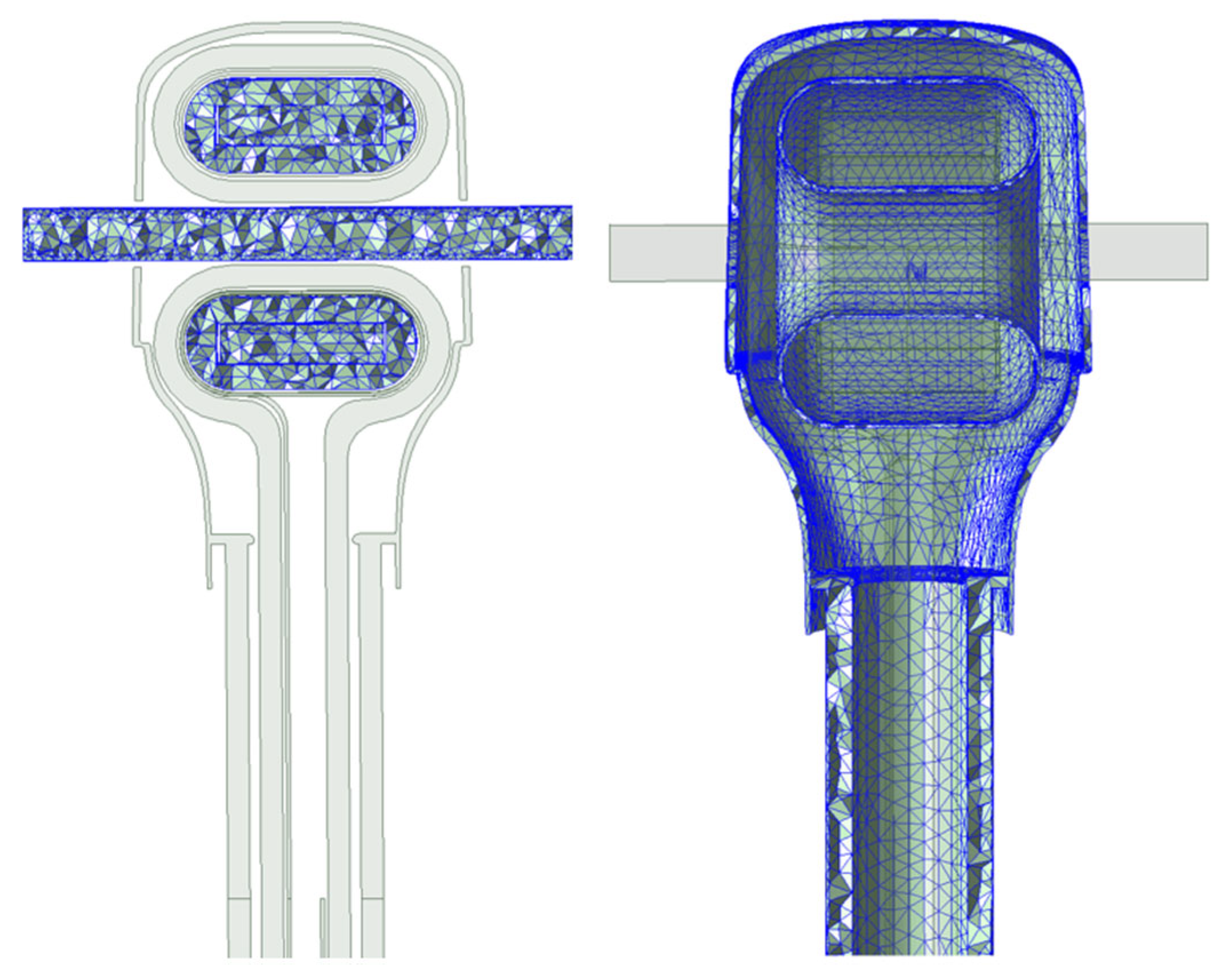
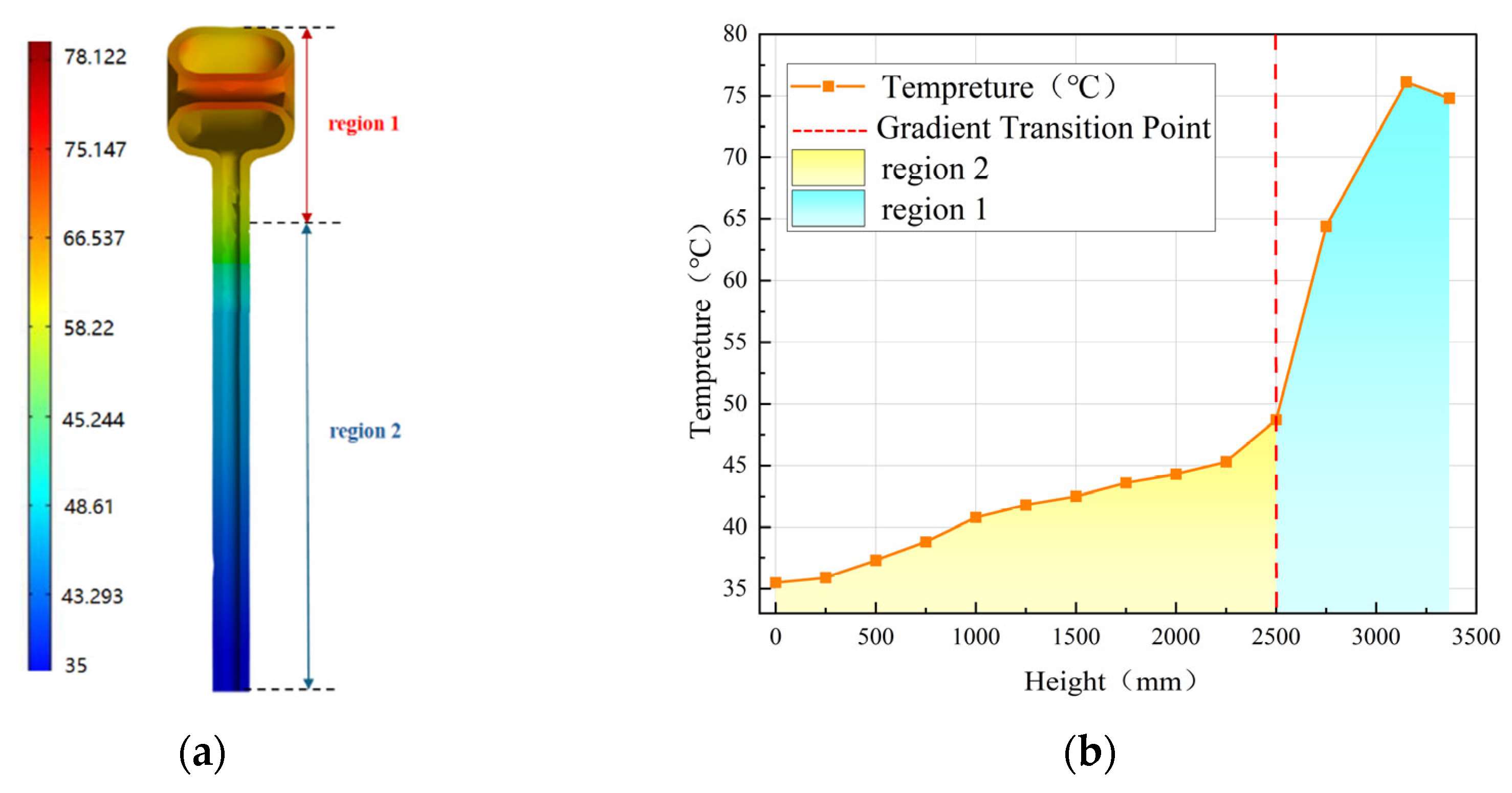
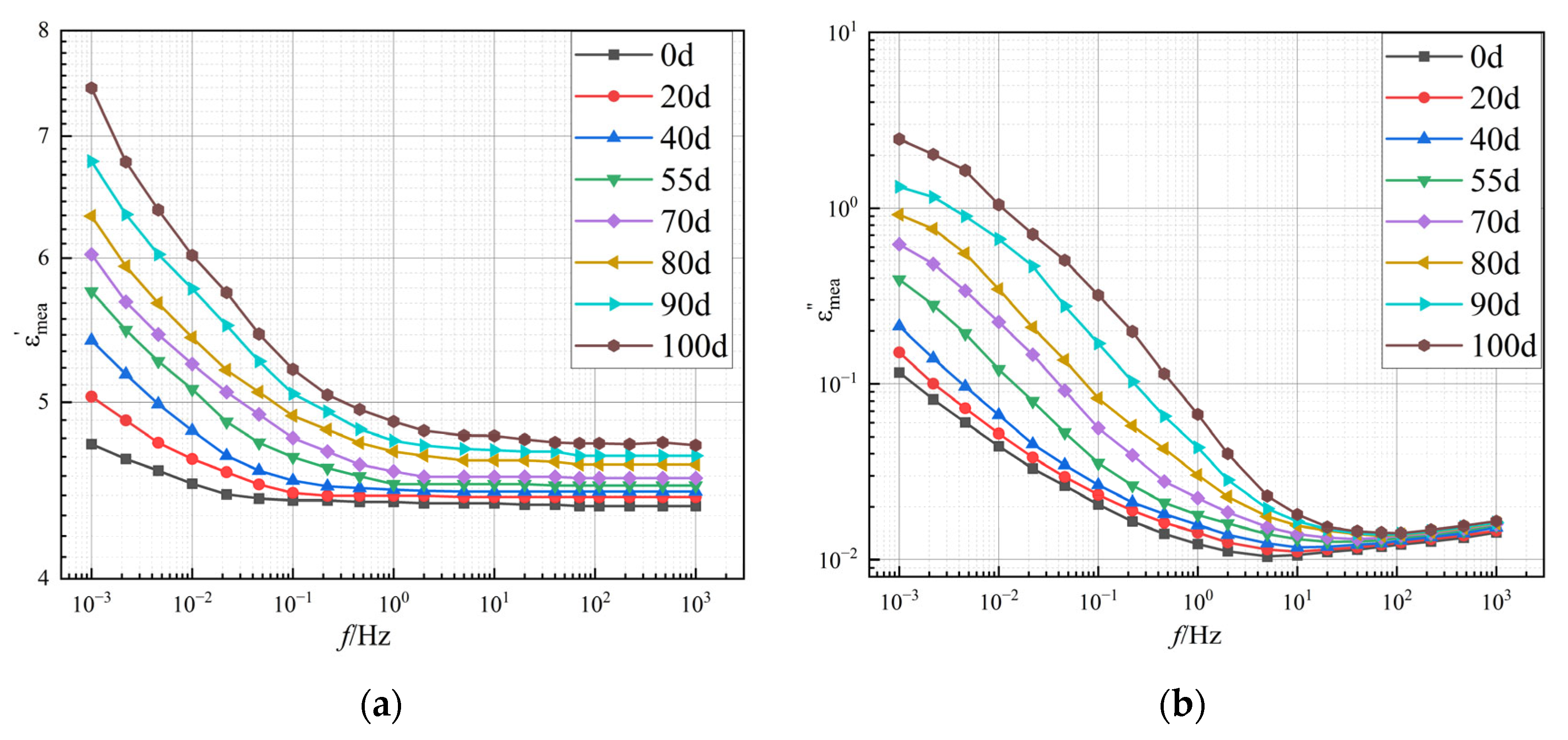
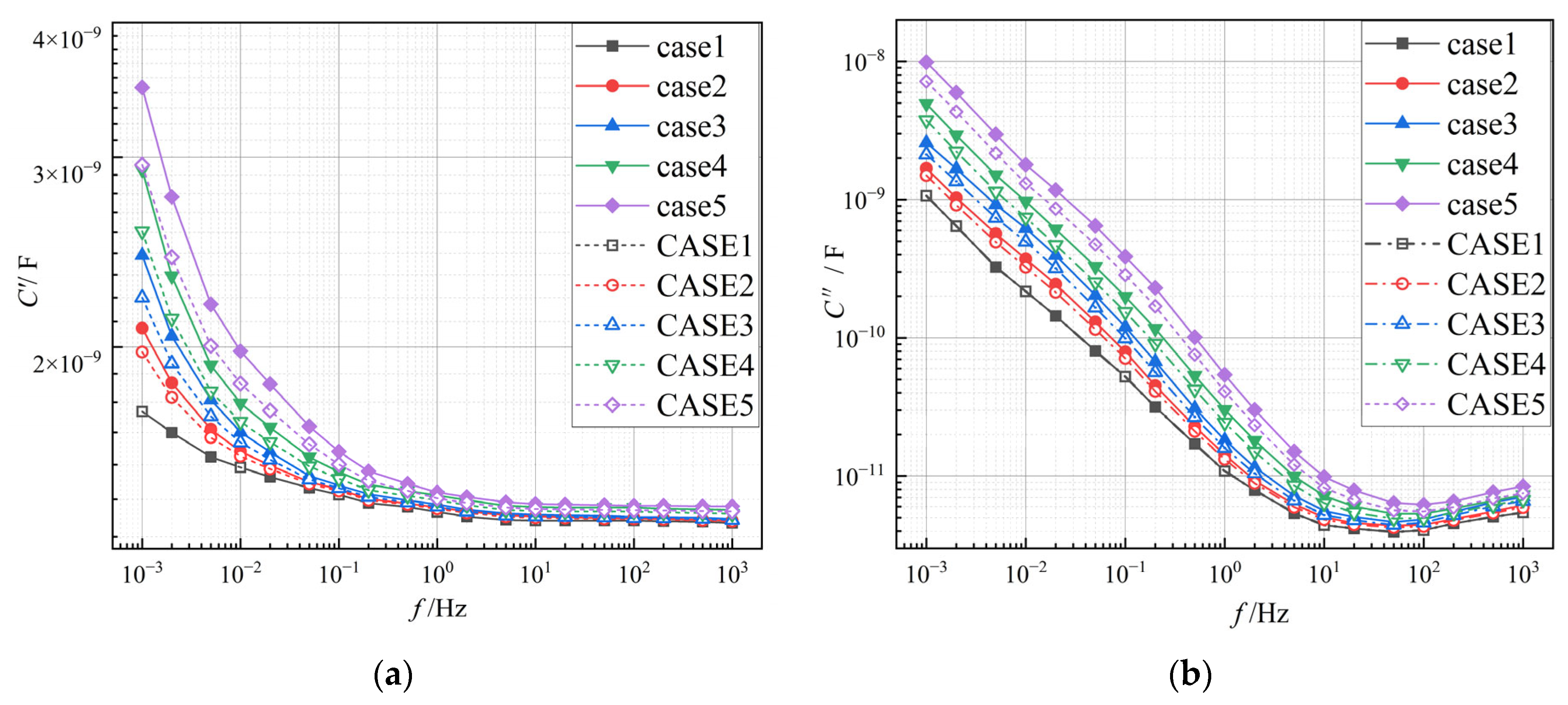
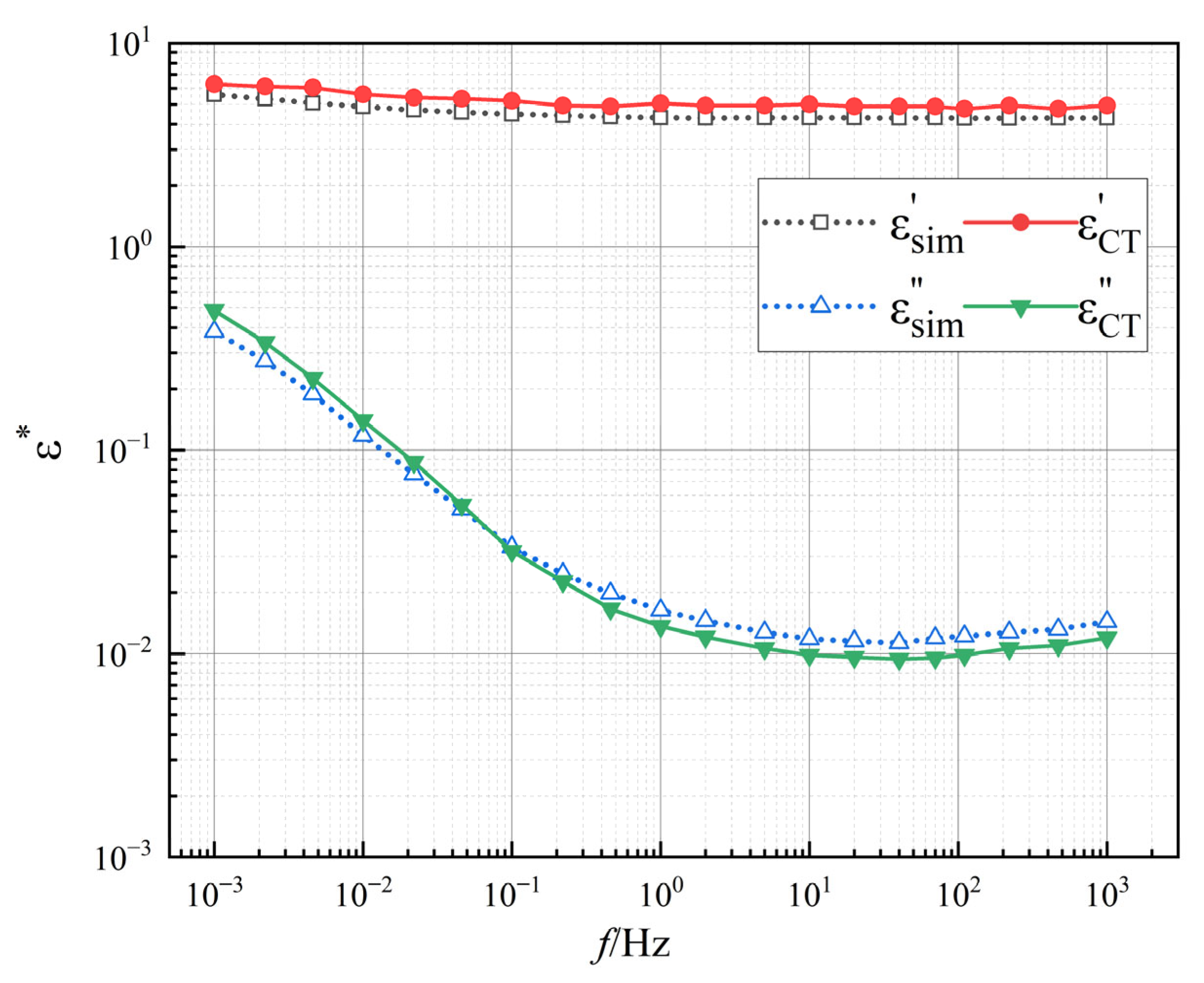
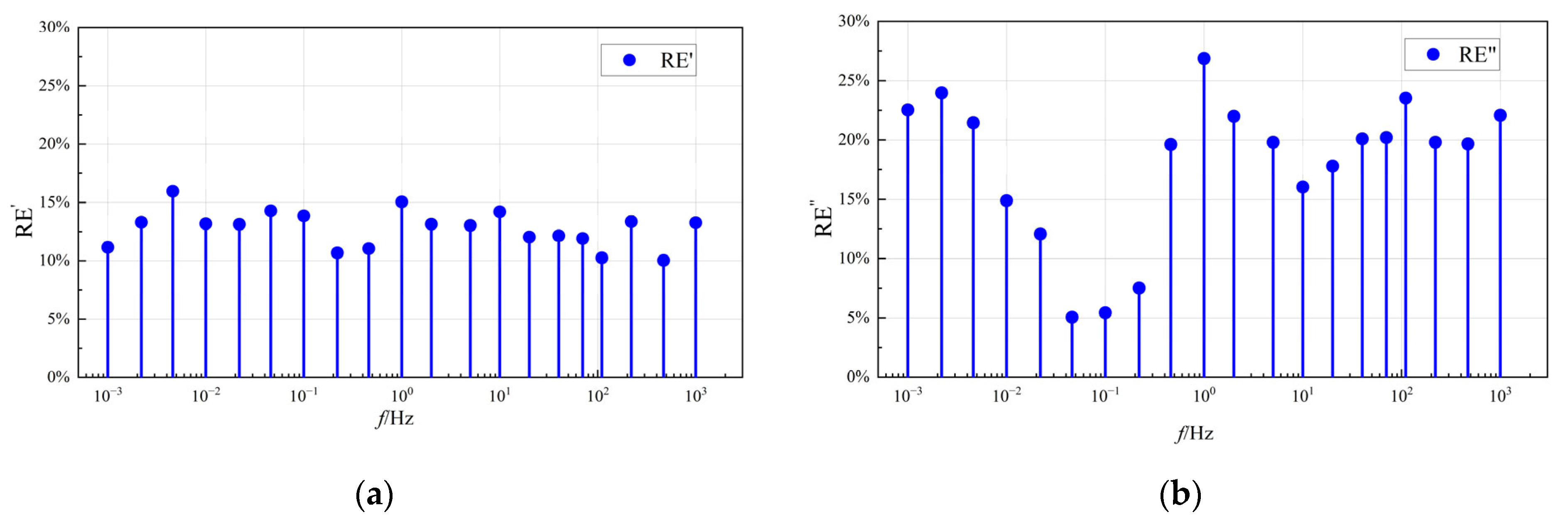
Component	Material	Density/kg·m−3	Specific Heat Capacity/J·(kg·K)−1	Thermal Conductivity/W·(m·K)−1
Primary conductor	Aluminum	2719	871	202.4
Iron core	Silicon steel	7650	502	42.5
insulation	OIP/Aluminum	1200	1800	0.17

.

$$\rho =-0.5809T+839.14$$

(6)

$$C=4.2736T+1761.5$$

(7)

$$K=-0.00008T+0.133$$

(8)

$$\mu =0.0696{\mathrm{e}}^{-0.08T}$$

(9)

where ρ denotes the density (kg/m³), C denotes the specific heat $\mathrm{J}/\left(\mathrm{k}\mathrm{g}·\mathrm{K}\right)$, K denotes the thermal conductivity $\mathrm{W}/\left(\mathrm{m}·\mathrm{K}\right)$, $\mu$ denotes the viscosity $\mathrm{k}\mathrm{g}/\left(\mathrm{m}·\mathrm{s}\right)$, and T denotes the temperature (K).

The temperature field within the computational domain is governed by the energy equation. For the heat transfer process in the oil-immersed current transformer, the heat conduction equation is adopted as the energy governing equation, expressed as:

$$\rho c\left(u\cdot \nabla \right)T=\nabla \cdot \left(K\nabla T\right)+q$$

(10)

where ρ is the density of the insulating oil, c is the specific heat capacity of the insulating oil, u is the fluid velocity field, T is the temperature field, K is the thermal conductivity, and q is the heat flux.

In addition to heat conduction, convective heat transfer also occurs within the oil chamber and on the outer surface of the sheds. Due to the narrow oil gaps inside the current transformer, natural convection within the oil is neglected. Natural convection on the external surface of the transformer is modeled using a heat flux boundary condition, as described by Equations (11) and (12):

$${\left.-K{\displaystyle \frac{\partial T\left(r\right)}{\partial r}}\right|}_{r=r_0}=\mathsf{\alpha }\left(T-T_f\right)$$

(11)

$$T\left(r\right){|}_{r=r_{\infty }}=T_f$$

(12)

where $T_f$ is the ambient temperature in kelvin (K), r is the radial coordinate in the spherical coordinate system, r₀ is the radial position of the boundary, and $\mathsf{\alpha }$ is the convective heat transfer coefficient in units of W·(m²·K).

Due to the flexibility of tetrahedral meshes in handling complex geometries, a tetrahedral mesh was employed for the thermal simulation. A physics-controlled meshing strategy was adopted with a relative tolerance of 1 × 10⁻³ to ensure convergence and solution stability during mesh refinement. The mesh configuration of the thermal simulation model is illustrated in Figure 3. A steady-state simulation was performed under these boundary conditions, and the main insulation’s temperature field distribution was obtained, as shown in Figure 4a. To quantitatively identify the mutation point of the axial temperature gradient, temperature data along the axial centerline of the model were extracted, and a temperature–height profile was plotted, as shown in Figure 4b.

The simulation results reveal significant axial non-uniformity in the internal temperature distribution of the main insulation. Due to the proximity to heat sources and poor heat dissipation conditions, significant temperature accumulation occurs in the head region and near the transition to the straight section. The straight section refers to the vertically extended cylindrical part of the main insulation structure located below the head region, characterized by a relatively uniform geometry and absence of concentrated heat sources. The maximum temperature of the insulation paper in the head region reaches 76.1 °C, representing a 46.1 °C increase over the ambient temperature, while the average temperature in the straight section remains around 42.7 °C, resulting in an overall axial temperature difference of nearly 30 °C. Such temperature differences can lead to localized increases in dielectric losses. If the FDS model were to assume a uniform aging state based on an average condition, the aging severity at hotspot regions would be underestimated, leading to errors in the model.

From the plotted temperature–altitude curve along the axial path, a significant change in temperature gradient slope was observed at approximately 2500 mm from the base (with the base of the straight section taken as the zero height point). The slope increased from about 0.5 °C/100 mm to approximately 6 °C/100 mm, indicating a sharp axial thermal gradient. Combined with structural analysis, this point corresponds to the lower boundary of the oil conservator at the head region, where the density of heat sources transitions from dense to sparse. This point was thus identified as the axial temperature boundary of the main insulation system, forming the basis for applying distinct aging parameter control strategies in subsequent FDS-FEM simulations that account for axial aging variations.

3.2. Accelerated Thermal Aging Test

To simulate the actual aging behavior of the main insulation system in a 500 kV oil-immersed inverted CT, this study deviates from conventional OIP sample testing methods by constructing an accelerated thermal aging platform based on a full-scale CT prototype. The prototype has an overall height of approximately 4100 mm, with a main insulation column diameter of about 290 mm and an insulation thickness ranging from 80 to 100 mm. The height of the oil conservator is approximately 563 mm. These structural dimensions are consistent with those adopted in the finite element model described in Section 4, ensuring a high degree of correspondence between the experimental setup and the numerical simulations. This approach aims to obtain experimental data with greater engineering relevance. According to the results of the temperature field simulation, the temperature rise in the head insulation and its adjacent areas is significantly higher than in the straight section. Based on this observation, the test platform adopts an “inside-out” heat transfer path. A customized magnetic core and matching secondary winding were designed, with the secondary winding energized while the primary conductor was short-circuited. Through electromagnetic induction, current and heat generation were simultaneously realized in both windings. Two primary heat transfer paths were designed: (1) primary conductor→oil gap→insulation paper, and (2) magnetic core and secondary winding→insulating oil→shield→insulation paper. These paths allowed selective heating of specific insulation regions to the desired aging temperature.

To enable precise temperature control and uniform thermal distribution, the secondary winding adopted a double-wire parallel winding structure: each of the five magnetic cores was wound with 750 turns of 1.3 mm diameter copper wire, followed by another 750 turns of 1.6 mm copper wire after an insulation layer was applied. During the heating stage, only the inner 1.3 mm wire was energized. Thermal insulation was wrapped around the oil conservator and expander to reduce heat loss and improve efficiency. Thermocouples were embedded inside the oil conservator to monitor the temperature increases in key areas in real-time.

To obtain dielectric parameters at different stages without disturbing the main insulation, insulation paper samples made of the same material were embedded on the inner wall of the oil conservator. These samples aged synchronously with the head insulation. The simulation results confirmed that the temperature rise was concentrated in the head region, while the straight section experienced only minor changes. Thus, the aging state of the paper samples in the conservator was considered representative of the high-temperature region of the main insulation.

Prior to installation, the insulation paper samples were dried at 90 °C and 50 Pa for 48 h, ensuring an initial moisture content below 0.5% [23,24]. The dried samples were wrapped with a fine copper wire fixed to the inner wall of the conservator using epoxy adhesive, and the wire was extended and secured to the upper part of the expander. This facilitated sample retrieval during the aging process. The paper sample placement process is illustrated in Figure 5.

Referring to the standard GB/T 1094.2-2013 Power transformers―Part 2: Temperature rise for liquid-immersed transformers [25], the test platform was designed based on transformer thermal aging test methods. As shown in Figure 6, component T is the regulator used to regulate voltage during heating; component C is the compensation capacitor for current compensation and phase angle adjustment. A1 and A2 are ammeters for monitoring the current through the secondary winding and the measuring section. The regulator used was model TDGC2J, a single-phase regulator rated at 20 kVA with a maximum output current of 80 A. The compensation capacitor, model BZMJ0.5-50-637 μF, was connected in parallel with the secondary terminals during the heating process to ensure uniform current distribution across all windings, thereby promoting even heating and reducing thermal imbalance in the head region of the main insulation.

The target aging temperature of 120 °C was determined based on DL/T 984-2018 Guidelines for Insulation Aging Evaluation of Oil-Immersed Transformers [26] and the “Rule of Six” commonly used in transformer thermal aging studies. According to this rule, the insulation lifetime is halved for every 6 °C increase above the reference temperature [18,19,23]. Thus, the relationship between aging time at 120 °C and its equivalent normal operation lifespan is shown in

Table 2. Aging time and equivalent normal operating life of CTs at 120 °C.

Aging Time (days)	20	40	55	70	80	90	100
Equivalent Service Life (years)	5.57	11.13	15.31	19.48	22.27	25.05	27.83

.

The accelerated aging was conducted in stages, according to Table 2. After each aging stage, FDS tests were conducted on the prototype. At the same time, dielectric properties of the OIP were measured using a three-electrode system to monitor insulation aging progression.

3.3. FDS Testing of the Prototype and OIP Samples

To obtain the dielectric response characteristics of the current transformer’s main insulation system at different aging stages and to validate the proposed FDS modeling method considering axial aging differences, periodic FDS tests were performed on both the full-scale prototype and the insulation paper samples placed synchronously inside the oil conservator. The testing was conducted using the IDAX-300 manufactured by Megger (Dallas, TX, USA). Based on DFR technology, the instrument is capable of accurately measuring the equivalent inter-winding capacitance and dielectric loss factor across a frequency range of 0.1 mHz to 10 kHz, enabling the precise evaluation of insulation aging. Its non-invasive measurement method allows for online insulation monitoring without disrupting the structure of the current transformer, offering strong adaptability for engineering applications.

During the FDS testing of the prototype, a high-voltage lead was connected to the primary terminal, a test lead was connected to the final screen electrode, and the secondary terminals were short-circuited and grounded. The ground wire of the final screen was left open to avoid the influence of parasitic capacitance [8,9]. To ensure accuracy and repeatability, the test circuit was constructed strictly in accordance with relevant standards, maintaining signal integrity under high-impedance measurement conditions. The on-site FDS testing process of the prototype is shown in Figure 7. Complete FDS measurements were performed at the end of each aging stage during the accelerated thermal aging process, and the corresponding results are presented in Figure 8.

To obtain aging data representative of the head region of the main insulation, the insulation samples embedded in the oil conservator were periodically extracted. These samples were tested in a laboratory environment using a three-electrode test platform, as illustrated in Figure 9. The test platform was based on a standard three-electrode configuration consisting of two parallel circular electrodes and a grounded guard ring to minimize fringe effects and surface leakage currents. Uniform mechanical pressure was applied between the electrodes to ensure reliable and repeatable contact with the paper samples [11,12]. A 200 V peak sinusoidal AC voltage was used as the excitation signal, and the frequency range was kept consistent with the prototype tests, spanning from 0.1 mHz to 10 kHz. The object of measurement was the OIP samples removed at regular intervals during the aging test. The complex permittivity was measured over the full frequency range, allowing for the evaluation of both real and imaginary components. The FDS curves of OIP samples at different aging levels are shown in Figure 10. The extracted dielectric parameters were subsequently used as input data for the FEM dielectric simulation model to account for aging-induced changes in material behavior.

4. Construction of FEM Model for Main Insulation of CT

To accurately simulate the dielectric response behavior of the main insulation in oil-immersed inverted CTs while incorporating axial aging disparities, a 3D finite element simulation model was developed using COMSOL Multiphysics 6.0, as illustrated in Figure 11. The main insulation employs a capacitive structure composed of alternating layers of OIP and aluminum foil capacitive screens. This structure can be equivalently modeled as a multi-stage series capacitor network, incorporating three primary capacitive screens: the high-voltage screen, the intermediate screen, and the final screen. To further homogenize the electric field distribution, end screens are introduced between the main screens, and the local insulation thickness is adjusted accordingly. Based on structural parameters provided by the transformer manufacturer, key geometric dimensions of the main insulation were extracted, as summarized in

Table 3. Key geometric dimensions of the main insulation.

Capacitive Screen	Straight Section Diameter/mm	Inter-Screen Step Difference/mm	Screen Length/mm	Annular Inner Diameter/mm	Annular Outer Diameter/mm
high-voltage screen	289.98	10	1065.58	144.49	890.91
intermediate screen	182.78	14	2262.96	227.34	806.90
final screen	77.52	-	3191.41	309.76	722.40

.

In the finite element simulation of dielectric response, considering that the excitation voltage frequency in actual FDS testing generally does not exceed 5 kHz, the electric field inside the device can be treated as quasi-static. The governing equation for the quasi-static field in the frequency domain is expressed as Equation (13) [17,19]:

$$-\nabla \left(\mathrm{j}\mathsf{\omega }{\mathsf{\epsilon }}_0{\mathsf{\epsilon }}_r^{*}\left(\mathsf{\omega }\right)\cdot \nabla V\right)=0$$

(13)

where V is the electric potential; $\mathsf{\omega }$ is the angular frequency of the excitation source; ${\mathsf{\epsilon }}_0$ is the vacuum permittivity; ${\mathsf{\epsilon }}_r^{*}\left(\mathsf{\omega }\right)$ is the complex relative permittivity, representing the polarization behavior of the material at different frequencies. The complex permittivity was derived based on dielectric data of insulation materials at different aging stages. The real and imaginary parts of the complex permittivity were extracted as shown in Equation (14):

$$\begin{array}{l}{\mathsf{\epsilon }}_r^{*}\left(\mathsf{\omega }\right)={\mathsf{\epsilon }}_r^{\prime }\left(\mathsf{\omega }\right)-{\mathrm{j}\mathsf{\epsilon }}_r^{″}\left(\mathsf{\omega }\right)\\ ={\mathsf{\epsilon }}_r^{\prime }\left(\mathsf{\omega }\right)-\mathrm{j}{\displaystyle \frac{\mathrm{\sigma }\left(\mathsf{\omega }\right)}{{\mathsf{\epsilon }}_0\mathsf{\omega }}}\end{array}$$

(14)

Here, ${\mathsf{\epsilon }}_r^{\prime }\left(\mathsf{\omega }\right)$ and ${\mathsf{\epsilon }}_r^{″}\left(\mathsf{\omega }\right)$ represent the real and imaginary parts of the complex relative permittivity, respectively, and σ is the conductivity of the oil-impregnated paper. Therefore, based on Equations (15) and (16), the relative permittivity ${\mathsf{\epsilon }}_r\left(\mathsf{\omega }\right)$ and conductivity $\mathrm{\sigma }\left(\mathsf{\omega }\right)$ used to define the material properties of the OIP insulation can be derived accordingly [24,27]. To reflect the aging characteristics across different axial regions, a material parameter control strategy was applied, assigning differentiated aging parameters to segmented zones. The conductor components were modeled using aluminum foil, with the electrical conductivity set to 3.030 × 10⁷ S/m.

$$\mathrm{\sigma }\left(\mathsf{\omega }\right)={\mathsf{\epsilon }}_r^{″}\left(\mathsf{\omega }\right){\mathsf{\epsilon }}_0\mathsf{\omega }$$

(15)

$${\mathsf{\epsilon }}_r\left(\mathsf{\omega }\right)={\mathsf{\epsilon }}_r^{\prime }\left(\mathsf{\omega }\right)$$

(16)

In the simulation, a 200 V peak sinusoidal AC voltage was applied to the high-voltage screen, while the final screen was set to zero potential. The intermediate screen was defined as a floating potential to replicate the typical boundary conditions used in FDS tests. The finite element model simulates the global dielectric response by dividing the main insulation into two axial aging zones and assigning different material parameters to each zone. The final output is the total complex capacitance of the structure as a function of frequency, which can be directly compared with the experimental FDS curves. In the FEM-based FDS simulation, temperature is not treated as a variable in the dielectric calculation. The temperature field is only used to divide the insulation into aging regions, and temperature effects are indirectly reflected through the assigned material parameters without explicit thermal-electrical coupling in the model. The mesh was generated using a physics-controlled tetrahedral discretization in COMSOL Multiphysics. The final mesh contains approximately 4,441,317 elements, with a minimum element quality of 0.213 and an average element quality of 0.8746, indicating a high mesh quality. The mesh configuration is shown in Figure 12.

Through global computation, the frequency-dependent complex admittance $Y^{*}\left(\mathsf{\omega }\right)$ of the insulation model was obtained. The corresponding complex capacitance $C^{*}\left(\mathsf{\omega }\right)$ and complex relative permittivity ${\mathsf{\epsilon }}^{*}\left(\mathsf{\omega }\right)$ were then calculated using Equations (17) and (18), where C₀ denotes the geometric capacitance of the insulation structure without losses [28,29]:

$$C^{*}\left(\mathsf{\omega }\right)=C^{\prime }\left(\mathsf{\omega }\right)-\mathrm{j}{C}^{″}\left(\mathsf{\omega }\right)={\displaystyle \frac{Y^{*}\left(\mathsf{\omega }\right)}{\mathrm{j}\mathsf{\omega }}}$$

(17)

$${\mathsf{\epsilon }}^{*}\left(\mathsf{\omega }\right)={\displaystyle \frac{C^{*}\left(\mathsf{\omega }\right)}{C_0}}$$

(18)

where $C^{\prime }\left(\mathsf{\omega }\right)$ is the real part, associated with capacitive energy storage, and $C^{″}\left(\mathsf{\omega }\right)$ is the imaginary part, associated with dielectric losses.

5. Results and Discussion

5.1. Validation of Simulation and Experimental Results

To evaluate the performance improvement of the axial partition aging model over the conventional uniform aging modeling approach and to verify the accuracy of the proposed model, two different simulation aging schemes were constructed: a uniform aging model and an axial partition aging model.

The uniform aging model assumes axial isotropy of the OIP insulation, treating aging as spatially uniform. However, it neglects the influence of the axial aging gradient induced by the internal thermal field. To reduce the complexity of data analysis, dielectric parameters of insulation materials representing five distinct aging levels from FDS experiments were uniformly assigned to the entire main insulation. These simulation cases are denoted as cases 1–5, as listed in

Table 4. Dual input modes of complex permittivity.

Aging Time	Aging Strategy
	Uniform Aging	Localized Aging
0 day aging	case 1	CASE 1
20 day aging	case 2	CASE 2
55 day aging	case 3	CASE 3
80 day aging	case 4	CASE 4
100 day aging	case 5	CASE 5

. In contrast, the axial partition aging model incorporates the temperature field simulation and accelerated aging test results. Material parameters were assigned to different axial regions of the main insulation based on a spatial distribution pattern of “older at the top, newer at the bottom”, corresponding to five aging stages, denoted as CASES 1–5. As shown in Figure 4, the temperature distribution of the main insulation exhibits a distinct transition near a height of 2500 mm. Below this boundary, the average temperature remains between 35 °C and 45 °C, which is insufficient to trigger high-temperature aging. Therefore, in the axial partition aging model, a two-region approximation was used: the upper high-temperature region was assigned dielectric parameters according to the corresponding aging stage, while the lower straight section was assumed to remain unaged (i.e., 0 days of aging).

Figure 13 presents the simulation results for the real and imaginary parts of the complex capacitance under the two aging schemes. The real part of the capacitance shows a rapid decrease with increasing frequency and tends to stabilize at higher frequencies. With increased thermal aging, the real part of the low-frequency capacitance rises significantly, while the influence of aging becomes negligible above 1 Hz. The imaginary part exhibits a typical dielectric relaxation behavior, decreasing and then increasing within the 10⁻³ to 10³ Hz range, indicating a shift in the dielectric loss peak. Comparative analysis reveals that across the entire frequency spectrum, the simulated real and imaginary parts of the complex capacitance from cases 1-5 are consistently higher than those from CASES 1-5. These differences are most pronounced in the low-medium frequency band and increase with the aging level. This demonstrates that models neglecting axial aging variation tend to systematically overestimate the overall dielectric loss and polarization capability of the main insulation, potentially leading to overly optimistic insulation health assessments when using FDS. The discrepancy becomes more significant as the insulation ages, validating the “local hotspot dominates global response” mechanism of non-uniform aging.

Having identified the deviation patterns between the two simulation schemes, further validation of the axial partition model was carried out by comparing the simulated results from CASES 1-5 with FDS test data obtained from the full-scale prototype at various aging stages.Figure 14a–e illustrates the comparison between the simulated and measured FDS across five different aging stages. ${\mathsf{\epsilon }}_{\mathrm{mea}}^{\prime }$ and ${\mathsf{\epsilon }}_{\mathrm{mea}}^{″}$ refer to the measured real and imaginary parts of the complex relative permittivity obtained directly from the prototype at various aging stages; ${\mathsf{\epsilon }}_{\mathrm{sim}}^{\prime }$ and ${\mathsf{\epsilon }}_{\mathrm{sim}}^{″}$ refer to the simulated values derived from the FEM model. Figure 14f further presents the frequency dependence of the real part ${\mathsf{\epsilon }}^{\prime }$ for all five aging states in a unified plot. The results show significant overlap throughout the entire test frequency range, indicating that the model can effectively capture the spectral response characteristics of the OIP insulation under axial aging variation.

The relative error values were used to quantify the deviation between simulation and measurement.

Table 5. Average relative error at different aging stages.

Average Relative Error	Aging Stages
	0 d	20 d	55 d	80 d	100 d
RE′	4.8%	4.49%	4.27%	3.74%	3.41%
RE″	8.67%	9.22%	6.84%	6.48%	6.93%

summarizes the average relative errors of the simulated real and imaginary parts of the complex relative permittivity for different aging stages. Here, RE^′ denotes the relative error of the real part, and RE″ denotes that of the imaginary part. The results show that the average RE′ and RE″ across all aging stages do not exceed 4.8% and 9.22%, respectively. The imaginary part tends to show a slightly larger error, primarily because of its higher sensitivity to variations. Since the imaginary part reflects dielectric losses, it is more strongly affected by parameters such as conductivity and dielectric loss tangent, which are, in turn, influenced by environmental factors and aging conditions. Therefore, it is more susceptible to measurement deviations. The above comparison and error analysis demonstrate the high reliability of the proposed finite element FDS model that accounts for the axial partition in insulation aging.

Although the simulation results show good agreement with experimental data, the accuracy of the model heavily depends on the precision of the input parameters, such as the relative permittivity and conductivity of the oil-impregnated paper. These parameters may be affected by measurement errors, moisture content variations, and other factors. Therefore, it is necessary to conduct a sensitivity analysis to assess the reliability of the model results. We selected the relative permittivity from the input parameters as a key variable. Apart from measurement errors caused by equipment, the main factor leading to errors in this input parameter is moisture absorption by the insulating material. During laboratory measurements, the insulating material is inevitably influenced by ambient humidity, which perturbs its dielectric properties. An increase in moisture content typically manifests as an increase in the effective permittivity. Thus, in engineering practice, such errors are more likely to present as positive deviations. As an example, a 10% positive perturbation was applied to the parameters under different aging conditions in the original FEM model. Figure 15a,b show the comparison of the model outputs under this 10% positive perturbation. ${\mathsf{\epsilon }}_{\mathrm{orig}}^{\prime }$ and ${\mathsf{\epsilon }}_{\mathrm{orig}}^{″}$ represent the original output results and ${\mathsf{\epsilon }}_{\mathrm{pert}}^{\prime }$ and ${\mathsf{\epsilon }}_{\mathrm{pert}}^{″}$ represent the perturbed output results. It can be observed that the curves under the 10% positive perturbation generally shift slightly upward compared with the original curves across different aging states. The difference is more pronounced at higher aging levels, likely because the baseline parameter values are higher at advanced aging stages, resulting in larger absolute errors under the same perturbation. However, the relative sensitivities across different aging stages remain essentially consistent. Furthermore, the ordering of the curves for different aging states is maintained, and the overall aging trend remains consistent. Therefore, the model’s ability to distinguish between aging stages is not compromised. In conclusion, when key input parameters experience reasonable perturbations, the frequency–domain response of the model remains reliable.

5.2. Model Application Validation Using In-Service CT

To further validate the engineering applicability and predictive capability of the proposed finite element model that accounts for axial aging differences, the model was applied to a 500 kV oil-immersed inverted CT. By comparing field-measured FDS data with simulation responses, we provide technical support for insulation condition assessment and maintenance strategies.

A CT operating in a 500 kV substation was selected for verification. The structure of the tested CT was consistent with that of the prototype and the developed finite element model, adopting a capacitive main insulation system. The transformer had been in operation for over 13 years, with an average annual ambient temperature of approximately 13–22 °C and peak load utilization ranging from 70% to 90% of its rated capacity, exhibiting insulation aging characteristics typical of standard service conditions. To assess the current dielectric state of its main insulation, field FDS measurements were performed using a DIRANA dielectric response analyzer. The test frequency range was 1 mHz to 1 kHz, and the connection configuration matched that of the prototype to ensure data comparability. Due to significant uncertainties in operational temperature, loading conditions, and aging environments across different equipment, this study did not attempt to directly map the aging time observed in experiments to the actual service life of the in-service transformer. In this context, the model was validated by applying material parameters from different aging stages (as described in Section 3.2) to the axial partition aging model, and the resulting FDS responses were compared with the measured data. The same “older at the top, newer at the bottom“ axial aging distribution strategy was adopted to simulate multiple sets of FDS response curves. These were then compared with the measured field response curves. The best-matching results are presented in Figure 16, where ${\mathsf{\epsilon }}_{\mathrm{sim}}^{\prime }$ and ${\mathsf{\epsilon }}_{\mathrm{sim}}^{″}$ denote the real and imaginary parts of the simulated dielectric spectra and ${\mathsf{\epsilon }}_{\mathrm{CT}}^{\prime }$ and ${\mathsf{\epsilon }}_{\mathrm{CT}}^{″}$ denote the corresponding measured values from the in-service current transformer.

The comparison shows that, within the frequency range of 1 mHz to 1000 Hz, the simulated and measured real and imaginary parts of the dielectric spectra exhibit a high degree of agreement. Figure 17 presents the relative error across different frequency points. The results indicate that the maximum error in the real part does not exceed 16.8%, while the error in the imaginary part remains within 28%. These values fall within acceptable engineering tolerances, confirming that the proposed axial partition aging model is not only effective in controlled test environments but can also be successfully generalized to field operating conditions.

6. Conclusions

This study proposed a finite element modeling framework for FDS that integrates axial partition-based aging variations in the OIP insulation of oil-immersed inverted CTs. The reliability and applicability of the proposed model were verified through temperature field simulation, full-scale accelerated thermal aging tests, periodic FDS measurements, and practical engineering validation. The major conclusions are summarized as follows:

Temperature field simulation revealed a pronounced axial thermal gradient in the main insulation of the oil-immersed inverted CT. The peak temperature in the head region reached 76.1 °C, forming a temperature difference of approximately 30 °C compared with the straight section. The temperature–height curve exhibited a distinct change in slope at approximately 2500 mm from the base, clearly delineating the boundary between the high-temperature aging zone and the slow-aging region. This provides a theoretical basis for spatially assigning aging-related material parameters.

A full-lifetime accelerated thermal aging experiment was conducted using an oil-immersed inverted CT prototype. Periodic FDS measurements were performed on both the prototype and the insulation samples embedded in its oil conservator. The dielectric parameters of samples at different aging stages were extracted and assigned to the finite element model using corresponding spatial strategies. The results showed that compared with traditional uniform aging modeling approaches, the proposed axial partition model more accurately reproduced the dielectric response across various aging stages. In contrast, ignoring axial aging variations tended to systematically overestimate the overall insulation aging level. In the proposed model, the average relative errors of the real and imaginary parts of the complex relative permittivity were below 4.8% and 9.22%, respectively, confirming the accuracy of the modeling approach.

The model was further applied to a 500 kV in-service CT that had been operational for over 13 years, successfully predicting its aging condition. The simulated FDS curves from the axial partition model exhibited a high degree of consistency with field measurement data. The maximum error in the real part did not exceed 16.8%, and the imaginary part remained within a 28% error range. These results demonstrate that the proposed model is not only effective in laboratory settings but also exhibits strong generalizability for practical engineering applications. In future work, efforts will be made to enhance the adaptability of this model by extending it to other types of current transformers, such as 220 kV or dry-type CTs. Moreover, this modeling framework holds promise for integration into intelligent monitoring systems, enabling predictive maintenance scheduling and data-driven diagnostics in smart grid environments. Overall, the findings of this study offer a more accurate modeling solution for the dielectric response analysis and aging assessment of insulation in current transformers.