Design and Development of a New Long-Pulse-Width Power Supply

Abstract

In order to achieve a long-pulse-width output, a new long-pulse-width modulator based on the charging power supply of LCC-type high-frequency resonant converters and the pulse-generating unit in series IGBT switching technology has been designed. The relationship between the resonant cavity gain and the switching frequency has been derived. In the charging phase, the critical intermittent control mode is used to increase the charging speed, and in the voltage stabilization phase, the hysteresis burst control strategy is used to improve voltage accuracy. The simulation results show that the output pulse amplitude is 10 kV, the pulse width can reach 650 μs, and the top-drop is about 12%. Thus, a long pulse width modulator is developed. The output pulse voltage can reach 4 kV, and the output pulse width is 650 μs. The power supply reduces the capacity of the energy storage capacitor, which has industrial application value.

1. Introduction

1.1. Background

With the progression of semiconductor technology, especially the breakthrough of high-voltage and high-power IGBT devices, the proportion of magnetic flux superposition (linear transformer driver, LTD, Tomsk, Russia) and voltage superposition (Marx generator, Marx) pulse modulators with solid-state switch architecture used in industrial applications has increased significantly. The Marx generator is based on the principle of cascade discharge from capacitor energy storage, and voltage multiplication is achieved through the control of the timing of parallel charging and series discharge [1]. During the charging phase, multi-level capacitors are fed with energy simultaneously. During discharge, the capacitor is in series topology through synchronous triggering of the switch. The output voltage is the product of the single-stage voltage modulator and the number of stages, and its core depends on the energy stored in the capacitor and the synchronization of the switch. LTD uses distributed magnetic energy coupling technology and is composed of multiple independent power modules in parallel. Each module contains an energy storage capacitor, a switch, and a pulse transformer with primary winding [2]. The energy in each module is electromagnetically superimposed in the secondary winding through magnetic core coupling. The output voltage is determined by the ratio of the module voltage to the number of secondary winding turns, which is essentially a process of space energy synthesis. HV stands for high voltage. The Marx generator is shown in Figure 1. The red and blue colors represent IGBT switches.

However, due to the increase in the volume of energy storage capacitors and inductors in the Marx generator and LTD under the output scenario of a long pulse width and high power, the large-energy-storage components are prone to sparking and damaging the load under high voltages. At the same time, the controllability of pulse top-drop and pulse repetition is poor, and the power density is low. In view of the existing problems in the above modulator circuit, if you want to achieve a long-pulse-width controllable top-drop pulse output, one method is to add a top-drop compensation circuit to the Marx generator circuit, and another method is to use a series IGBT as a solid-state switch and use a high-frequency resonant fast-charging power supply as an auxiliary output pulse with a long pulse width and high top-drop controllability.

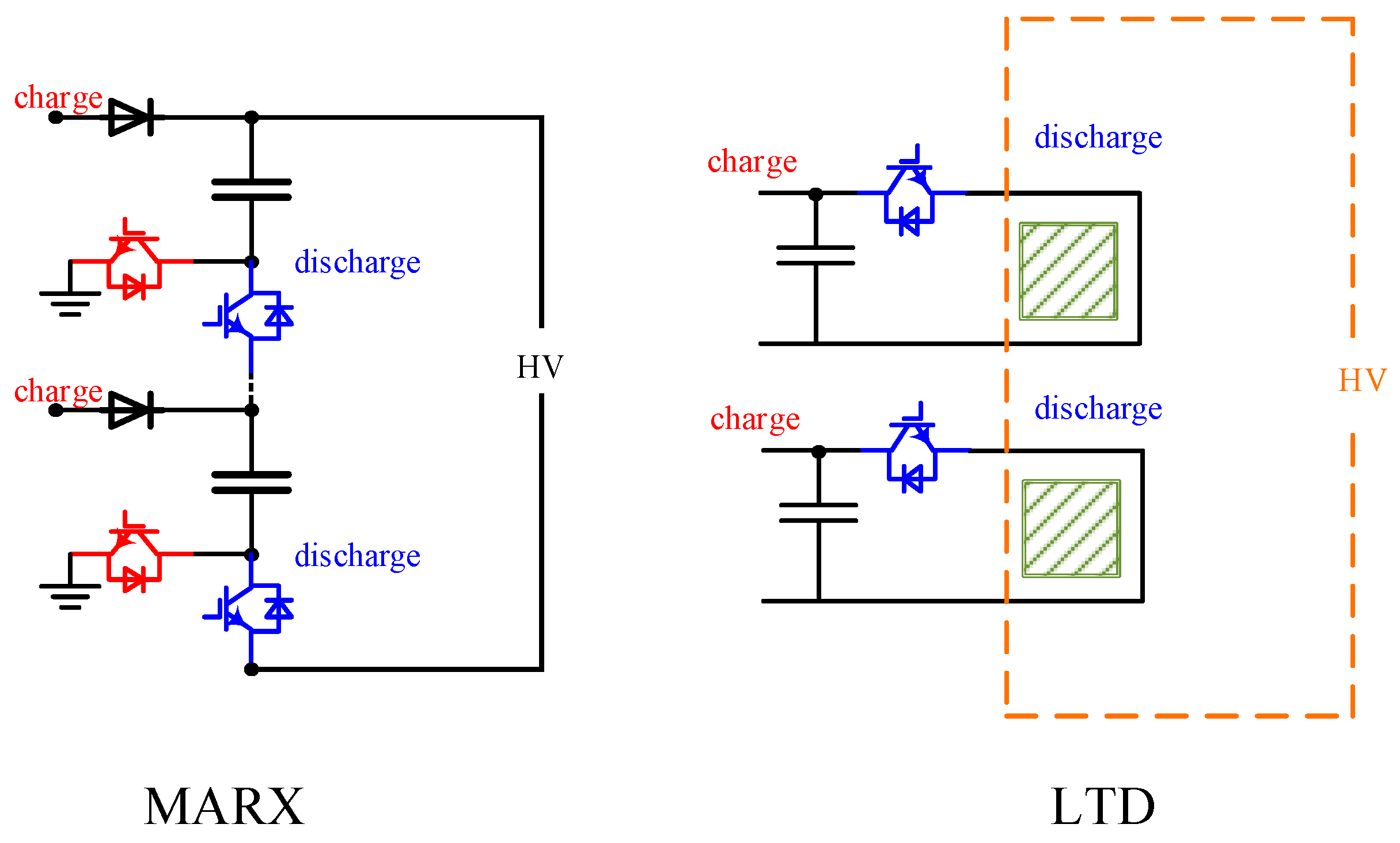
1.2. Related Works

In 2007, Toshiba Mitsubishi Electric (Tokyo, Japan) developed a 40 kV IGBT switch, including thirty-six series IGBT devices for the main switch and six series IGBT devices for transient voltage regulation. The IGBT switch can not only achieve switching between DC 40 kV and 180 A but can also quickly turn off the short-circuit current and conductors. In addition, a protection circuit was developed to prevent arc and other dangerous situations caused by an IGBT open-circuit fault [3].

In 2014, American scholars designed a solid-state high-voltage modulator using an insulated gate bipolar transistor (IGBT) to control the output voltage in series. It was able to meet the power requirements of the collector gyrotron used in the experimental fusion energy device in an electron gyrotron system. According to the specific gyrotron, the output voltage variation is required to be up to 80 kV, the current should be up to 100 A, and a square wave modulation frequency up to 1 kHz is required. Four IGBTs were configured as 2.4 kV IGBT modules, and the number of IGBT modules in series was adjusted to meet the requirements of the output voltage [4].

In 2021, Iranian scholars proposed a high-voltage short-circuit fault current limiter that can essentially limit the short-circuit energy in a system. The proposed structure is activated automatically when the current exceeds a predetermined value. Therefore, the demand for fault detection units is minimized. The short-circuit fault current limiter was fabricated based on series IGBTs. Normal operation of the proposed short-circuit fault current limiter was evaluated using a simulation and an experimental prototype [5].

In 2018, a Portuguese scholar proposed a resonant top-drop compensation scheme for a bipolar half-bridge solid-state Marx generator without an auxiliary power supply. Under the conditions of a 10 Hz repetition rate and a 100 μs pulse width, the top-drop of a 3 kV output pulse voltage was successfully compensated to within 16%. However, the scheme requires numerous switching devices and exhibits high control complexity in high-power mode, which limits its application range [6].

In 2019, a German scholar proposed a pulse top-drop compensation method based on a delay compensation stage. In this scheme, a delay compensation stage was added at the end of the traditional Marx generator, and top-drop compensation was achieved through delayed discharge. Experimental results showed that the proposed method successfully compensated for a peak drop of approximately 20 kV under the conditions of a 120 kV output voltage and a 20 μs pulse width. However, due to the delay conduction strategy, the output waveform became zigzagged and lacked flatness [7].

In 2024, Chinese scholars proposed a new type of all-solid-state boosted Marx pulse generator. Based on the classic pulse-forming Marx circuit, a new switch was introduced to isolate the energy storage and recovery of the inductor without changing the voltage level of each voltage module, thereby achieving the output of high-voltage nanosecond pulses. The structure is well-suited for use in modular high-voltage pulse generators and can output 18 kV pulses with durations of 200–1200 ns, achieving a gain of up to 36 times [8].

In terms of pulse modulator control strategies, some scholars proposed a hybrid pulse power supply (HPPS) based on the Marx–PFN hybrid distributed power supply topology and investigated its control strategy for underwater nonlinear time-varying filamentary electric explosion loads, achieving precise energy output control under complex operating conditions [9].

A current-reference feedforward control scheme was proposed by Chinese scholars to improve the tracking performance of ACC terminal current. A prototype with an output power of 2 kW, a load power of 300 W, and a pulse repetition frequency (PRF) of 150–300 Hz was developed and tested to validate the effectiveness of the proposed pulse power supply (PPS) and control scheme [10].

1.3. Contributions and Addressed Gaps

The output pulse width of traditional pulse modulators is usually limited to tens of microseconds, making it difficult to meet the technical requirements of high-power klystrons for long-pulse-width and low top-drop pulse outputs in radar transmitters, particle accelerators, and other applications. The traditional approach expands the pulse width by increasing the capacity of the energy storage capacitor. However, this method not only leads to increased system volume and reduced power density but also significantly decreases charging efficiency and equipment reliability due to thermal accumulation caused by the capacitor’s equivalent series resistance [11]. To overcome these technical limitations, this study proposes a novel long-pulse-width modulator architecture based on an LCC high-frequency resonant converter and a series IGBT switch array, aiming to achieve controllable pulse outputs with long pulse widths and low top-drop.

This study replaces the traditional LC series resonant topology with an LCC resonant network for energy transmission, achieving high-frequency energy transfer through the gain characteristics of the resonant cavity. A dual-mode hybrid control strategy is proposed [12]. During the charging phase, a critical intermittent mode is used, and a frequency-tracking algorithm maintains zero-current turn-off to shorten the charging time to less than 3 ms. In the voltage stabilization stage, hysteresis burst control dynamically adjusts the pulse group density to accurately suppress output voltage ripple. During the discharge phase, both control methods are applied to achieve a pulse output. This strategy effectively improves the system dynamic performance and voltage accuracy. For the series IGBTs, RCD voltage sharing control is employed to ensure device reliability and address voltage imbalance in high-voltage applications [13].

The system model is built and experimentally verified using the Matlab simulation platform. The key results are as follows: Under light load, a 4 kV pulse voltage with a 30 ms pulse width is achieved without noticeable pulse top-drop, reducing the required energy storage capacitor capacity to 2 μF and supporting adjustable repetition rates. When connected to a 400 Ω load, the pulse width is set to 650 μs, with a 160 μs rise time at the pulse front edge. No obvious pulse top-drop occurs, and the energy storage capacitor continues charging during pulse output.

1.4. Paper Outline

The main sections of this paper are arranged as follows:

Section 1 introduces the research background and significance of this paper and analyzes the technical difficulties faced by the solid-state pulse modulator and the current situation at home and abroad. High-frequency resonance and series IGBTs are proposed to deal with the current technical problems.

Section 2 analyzes the working mode and parameter optimization of LCC resonant converters and designs the control scheme of an LCC resonant converter and the parameters of each module.

Section 3 presents a simulation in the Simulink simulation platform and build an experimental platform for testing, verifying the rationality and feasibility of the proposed control scheme.

Section 4 summarizes the content of the entire text, analyzes the shortcomings, and looks at areas that need improvement in the future.

2. Methodology

2.1. Operating Characteristics of LCC Resonant Converter

Since the 1990s, with the development of wide-bandgap semiconductor switching devices such as silicon carbide and gallium nitride, power converters have been able to operate at higher frequencies, resulting in improved efficiency and power density [14]. This approach employs a series of high-frequency pulses to charge the energy storage capacitor, significantly enhancing charging accuracy and stability. Currently, the main mature applications include flyback converter-based charging power supplies, push–pull converter-based charging power supplies, and LC resonant charging power supplies [15].

The flyback converter charging power supply offers several advantages, including simple circuit topology, low cost, high reliability, and the ability to achieve zero-current turn-on for the switch and zero-voltage turn-off for the diode. It typically operates in discontinuous conduction mode (DCM) [16]. When controlled at a constant frequency, the converter stores a fixed amount of energy during each switching cycle, thereby enabling constant power output. However, the flyback converter experiences significant current ripple and is only suitable for low-power applications. Compared to the flyback converter, the push–pull converter utilizes a bidirectionally excited transformer, allowing the transformer to be smaller and more efficient at the same output power level [17]. However, the push–pull topology encounters a magnetic bias issue, requiring an anti-bias capacitor connected in series on the primary side. Since the primary side operates at low voltage and high current, implementing this capacitor is technically challenging and results in increased transformer losses and higher system costs.

As the most widely adopted charging topology, the LC series resonant converter provides constant current output, excellent charging linearity, short-circuit load tolerance, and ease of achieving soft switching, making it an ideal choice for capacitor charging power supplies. However, in practical applications, the parasitic capacitance of high-voltage, high-frequency transformers alters the behavior of the converter, effectively transforming it into an LCC series–parallel resonant converter [18]. Therefore, this paper focuses on the LCC series–parallel resonant converter as the primary research subject. It is worth noting that the commonly used LLC-type charging topology demands stricter resonance parameters and places stringent requirements on transformer design, making it less suitable than the LCC topology for high-voltage, low-current circuits.

The LCC resonant converter operates in either continuous conduction mode (CCM) or discontinuous conduction mode (DCM), depending on whether the resonant current is continuous. When the full-bridge switching frequency exceeds half of the series resonant frequency, the converter operates in CCM; otherwise, it functions in DCM. The LCC resonant converter integrates the transformer’s leakage inductance and distributed capacitance into its operation, enabling simultaneous zero-voltage switching (ZVS) and zero-current switching (ZCS) of power devices [19,20,21], which helps reduce switching losses and increase power density.

However, in CCM, the converter cannot achieve zero-current turn-off of the switches. The current tailing of the IGBT during turn-off leads to excessive losses and significant heating under high-frequency operation. Therefore, when using IGBTs in a full-bridge configuration, the switching frequency is typically set below half the series resonant frequency to operate in DCM, enabling zero-current turn-off and reducing losses.

In DCM, zero-current switching of the primary switches can be realized. For low-frequency, high-power applications using IGBTs, the resonant converter usually operates in intermittent current mode to minimize turn-off losses caused by current tailing. This paper focuses on analyzing the LCC resonant converter operating in DCM.

Figure 2 shows the topology of the LCC resonant converter in DCM. U_in represents the input voltage, i_n represents the input current, i_lr represents the resonant current, T_r is the transformer ratio, i_Cp represents the current flowing through the distributed capacitor of the transformer, i_p is the primary current of transformer, u_cr⁺ is the voltage across the resonant capacitor, i_o is the output current, U_o is the output voltage. Q₁ to Q₄ are the primary-side IGBT switches, and D₁ to D₄ are their body diodes. Points A and B represent the midpoint of the full-bridge converter arms. The transformer turns ratio is 1:n, where L_r is the series resonant inductance including leakage inductance, C_r is the series resonant capacitance, and C_p is the parallel resonant capacitance, including the winding capacitance referring to the primary side. D_r1 to D_r4 are the secondary-side high-voltage silicon rectifier stacks, C_O is the output filter capacitor, and R_L is the load. Switch pairs Q₁ and Q₄, and Q₂ and Q₃ are switched on and off simultaneously, with complementary switching within each bridge arm at 180° phase difference.

For analysis purposes, the following definitions are given: the transformer transformation ratio is n; the output voltage of the secondary side is equivalent to that of the primary side, $Ue=Uo/n$; voltage gain is $G=Ue/Uin$; the ratio of parallel resonant capacitance C_p to series resonant capacitance C_r is $k=Cp/Cr$; the angular frequency in series resonance is ${\omega }_r=1/\sqrt{L_r{C}_r}$, and characteristic impedance is $Z_r=\sqrt{L_r/C_r}$.

2.2. Working Mode Analysis of LCC Converter

Figure 3a,b show the voltage and current waveforms in DCM1 and DCM2. The red box in the figure indicates the time needed to achieve ZCS. According to whether the voltage U_CP on the parallel resonant capacitor can be reduced from U_e to −U_e when the resonant current is reversed, the LCC converter is divided into DCM1 and DCM2 [22]. In DCM1, the resonance time of the resonance current in the forward period is a fixed value, which is related to the parameters of the series resonance capacitance and series resonance inductance. However, in DCM2, the forward time of resonant current is composed of two parts, and the change in conduction time is determined by several parameters. Therefore, DCM1 allows for more easily achieving ZCS than DCM2. In DCM1, ZCS can be achieved by turning off the switch within [t₁, t₃] time. In DCM2, ZCS can be achieved by turning off the switch within [t₂, t₃] time. t_0–7 represents the conduction time of the switch tubes.

The duration of each moment in the circuit is explained below:

The duration of period 1 is $t_{01}=\pi /{\omega }_r$. At the same time, the voltage of the series resonant capacitor at t₁ is

$$u_{Cr}\left(t_1\right)=2\left(U_{in}-U_e\right)-u_{Cr}\left(t_0\right)$$

(1)

At time t₂, the parallel resonant capacitor C_P is charged in reverse to and clamped by the output voltage, then period 2 ends, and its duration can be calculated as

$$t_{12}={\displaystyle \frac{1}{{\omega }_{sr}}}\mathrm{a}\mathrm{r}\mathrm{c}\mathrm{c}\mathrm{o}\mathrm{s} (1+{\displaystyle \frac{2\left(1+k\right)U_e}{U_e+u_{Cr}\left(t_0\right)-U_{in}}})$$

(2)

At the same time, the series resonant capacitor voltage and the series resonant inductance voltage at t₂ are

$$\left\{\begin{array}{c}{i}_{Lr}\left(t_2\right)=-{\displaystyle \frac{2}{Z_{sr}}}\sqrt{(1+k)U_e(U_{in}-\left(2+k\right)U_e-u_{Cr}))}\\ u_{Cr}\left(t_2\right)=2U_{in}-2\left(1+k\right)U_e-u_{Cr}\left(t_0\right)\end{array}\right.$$

(3)

Similarly, the duration t₂₃ of period 3 is

$$t_{23}={\displaystyle \frac{1}{{\omega }_r}}\mathrm{a}\mathrm{r}\mathrm{c}\mathrm{t}\mathrm{a}\mathrm{n} \left({\displaystyle \frac{Z_r{i}_{Lr}\left(t_2\right)}{U_{in}-\left(3+2k\right)U_e-u_{Cr}\left(t_0\right)}}\right)$$

(4)

2.3. Control Scheme

The operating state of the system is illustrated in Figure 4. In the charging mode, the control board sends a trigger signal that tracks the critical intermittent switching frequency in real time, enabling the energy storage capacitor to be rapidly charged to the target voltage gain [23]. After the charging phase, burst hysteresis control is employed to maintain voltage stability across the energy storage capacitor. By comparing the real-time sampled output voltage with the preset target voltage, the control logic determines the switching behavior: if the voltage is below the acceptable ripple range, the switch is turned on; if it exceeds the range, the switch is turned off. This process is repeated continuously until the voltage ripple falls within the design tolerance.

Given that the pulse discharge duration is 650 μs, as defined by the design requirements, the voltage stabilization time is set to 10 μs. After the voltage has stabilized, the pulse discharge phase begins. During the intervals between pulse discharges, the charging and voltage regulation of the energy storage capacitor continue.

The critical switching frequency control mode minimizes the interruption time of the resonant current, thereby enhancing the average output current and charging speed and reducing the peak voltage drop during pulse discharge.

When the voltage gain of the traditional constant frequency output scheme increases, the switching frequency does not change, and the intermittent duration of the resonant current increases. If the critical intermittent control scheme is adopted, the critical intermittent switching frequency is taken as the actual switching frequency [24]. When the switching frequency is equal to twice the resonant period, the switching frequency can be calculated as

$$f_s={\displaystyle \frac{1}{2(t_{01}+t_{12}+t_{23}+t_{34})}}$$

(5)

When there is no t₃₄ during the operation of the converter, the resonant current is in the critical state of continuous and intermittent, and the corresponding switching frequency is defined as the critical intermittent switching frequency [25]. Simultaneously using Formulas (1)–(4) in DCM1, the critical intermittent switching frequency can be normalize to the initial resonant frequency as follows:

$$\begin{array}{c}{f}_{scr{i}_n}={\displaystyle \frac{f_{scri}}{f_r}}={\displaystyle \frac{\pi \sqrt{L_r{C}_r}}{t_{01}+t_{12}+t_{23}}}\hfill \\ ={\displaystyle \frac{\pi }{\pi +\sqrt{\frac{k}{1+k}\arccos \left(1+\frac{2\left(1+k\right)G-\left(k+1\right)G^2-1}{\left(k+1\right)G^2-1}\right)+\mathrm{a}\mathrm{r}\mathrm{c}\mathrm{c}\mathrm{o}\mathrm{s} \left(\frac{2\left(1+k\right)G-\left(1+k\right)G^2-1}{1+\left(k+1\right)G^2-2G}\right)}}} \hfill \end{array}$$

(6)

The normalized output average current curve is drawn as shown in Figure 5.

As shown in the figure, under critical intermittent mode, when the voltage gain remains constant, an increase in the coupling coefficient k leads to a decrease in the average output current. However, as the voltage gain increases, the rate of current attenuation decreases, and a constant current region becomes evident. Compared to the constant frequency control mode, the critical intermittent mode allows the switching frequency to track the critical intermittent switching frequency in real time, thereby reducing the interruption time of the resonant current and enhancing both the average output current and charging speed.

Since the normalized expression of the critical discontinuous switching frequency involves an inverse trigonometric function, direct computation on the control chip may result in calculation errors. Therefore, it is necessary to apply piecewise linear fitting to approximate the expression of the critical intermittent switching frequency, as shown in Equation (7):

$$f_{scri}=\left\{\begin{array}{c}{a}_{1}G+b_{1 } 0\le G\le x_1\\ \dots \\ a_{n}G+b_{n } x_{n-1}\le G\le 1/(1+k)\end{array}\right.$$

(7)

where a_n and b_n are the curve coefficients after segmentation and x_n is the boundary value of the segmented interval. The more the interval, the better the fitting effect of the linear equation. Since the critical frequency changes greatly after the gain is 0.4, the interval of curve division can be increased after 0.4 for more accurate fitting. Take k = 0.2 to obtain the specific linear fitting function, as shown in Equation (8):

$$f_{scri}=\left\{\begin{array}{c}0.027G+0.4998 0.000\le x\le 0.075 0.193G+0.4582 0.375\le x\le 0.450\\ 0.054G+0.4979 0.075\le x\le 0.150 0.257G+0.4292 0.450\le x\le 0.525\\ 0.078G+0.4942 0.150\le x\le 0.225 0.342G+0.3840 0.525\le x\le 0.600\\ 0.107G+0.4979 0.225\le x\le 0.300 0.451G+0.3185 0.600\le x\le 0.675\\ 0.144G+0.4768 0.300\le x\le 0.375 0.567G+0.2401 0.675\le x\le 0.750\end{array}\right.$$

(8)

For the implementation of critical frequency control using FPGA, a look-up table is employed to store pre-calculated critical frequency values, thereby avoiding the complexity of real-time calculations and improving the resolution of frequency control. The critical frequency retrieved from the look-up table is then filtered using a simple moving average filter with a coefficient of 0.25—meaning that the new value contributes 25%, while the historical value contributes 75%. This filtering technique effectively smooths abrupt changes in the frequency, resulting in a more stable system response. The total system delay introduced by this method is approximately 40 ns, which is negligible for a kHz level system. Additionally, it provides effective noise suppression and ensures that the parameters are well-suited for burst mode operation.

2.4. Prototype Design and Simulation Analysis

The overall structure of the system is shown in Figure 6. After rectification and filtering, the input three-phase voltage outputs the DC bus voltage through the DC–DC voltage-regulating circuit. After rectification and filtering, the DC bus voltage of the three-phase voltage is about 513 V. The input power supply operates in the constant-voltage current-limiting mode, and its output power is 15 kW. As the input voltage of the LCC resonant converter, the DC bus voltage outputs high voltage through the inverter bridge, resonant cavity, high-frequency transformer, and rectifier filter unit. Finally, pulse power is released to the load through the series IGBT conduction discharge in the pulse-forming unit. The FPGA control system outputs a digital PWM drive signal after algorithm processing from the analog sampling input signal [26]. ABC represents three-phase voltage, LN represents live and neutral wires. The red arrow indicates outflow, and the blue arrow indicates inflow.

See

Table 1. Design target parameters.

Parameter	Target Value
Input voltage/V	500
Output voltage/kV	10
Ratio of transformer	1:30
Pulse width/μs	650
Pulse frequency/Hz	20

for the design target parameters.

2.5. Component Parameter Design and Selection

Based on the above analysis, the peak resonant current reaches approximately 400 A, and the collector–emitter voltage withstand of the IGBT is approximately equal to the DC bus voltage. Taking into account a safety margin and the minimum switching delay, the IGBT model FZ600R17KE4 from Infineon Technologies (Neubiberg, Germany) is selected for the design.

Due to the high output voltage of the high-frequency transformer, a single rectifier diode cannot satisfy the voltage withstand requirements on the secondary side. Therefore, multiple diodes are connected in series as the secondary-side rectifiers. Given that the output winding is divided into three groups and the rated output voltage is 10 kV, an appropriate margin is reserved. For each winding group, three fast-recovery diodes (MEO450-12DA) from IXYS are connected in series to form the rectifier stack.

At the DCM1 stage, the time of forward resonance is fixed. The resonant inductance can be measured by using the resonant frequency and forward resonance time. The transformer leakage inductance L_K can be obtained by subtracting the auxiliary inductance L_s from the resonant inductance L_r.

$$L_k={\displaystyle \frac{1}{C_r}}{\left({\displaystyle \frac{t_{01}}{\pi }}\right)}^2-L_s$$

(9)

When an LCC resonant converter works in DCM, it should meet the relationship fs < 0.5 fr and adjust the desired voltage gain by adjusting the switching frequency. Combined with the IGBT process, and voltage and current capacity, the switching frequency of IGBT is about 15 kHz. Assuming that the distributed capacitance of the transformer is 0.61 μF, in DCM1, the resonant current is first generated by the series resonance of C_r and L_r, and then, the series parallel resonance of C_r, L_r, and C_p generates the reverse resonant current, and finally, C_r and L_r generate the reverse resonant current and resonate to the zero crossing point. Due to the large characteristic impedance at the forward resonance, the peak resonant current occurs at the forward resonance stage.

$$I_{Lr\_max}={\displaystyle \frac{U_{in}}{Z_r}}\left({\displaystyle \frac{1-k{G_1}^2-{G_1}^2}{1-G_1}}\right)$$

(10)

The K value of the average output current and the current stress of the switch is about 0.2. The series resonant capacitance C_r is 3.05 μF. When the resonant frequency is 34 kHz, the resonant inductance can be determined to be about 11 μH by $L=1//{{\left(2\pi f_s\right)}^2}_s{C}_r$. At the same time, considering the size of the load-side energy storage and the final output top-drop, when only considering the discharge of the energy storage capacitor to the load, the output filter capacitor can be calculated to be 2 μF when the top-drop is designed to be 30%.

2.6. Design and Measurement of High-Frequency Transformer

A high-frequency transformer is the core of an LCC resonant converter. Its leakage inductance and distributed capacitance, as the components of the resonant unit, undertake the functions of power transfer and voltage conversion. Ferrite core has the advantages of high permeability and low high-frequency loss. It is the most widely used core material in power electronic converters [27,28].

A high-frequency transformer is usually manufactured following the AP method (area product). The input voltage of the resonant cavity of an LCC resonant converter is 500 V, the output voltage is 15 kV, the rated power is 15 kW, the working frequency is 40 kHz, the magnetic flux density BM is obtained as 0.2 T, the winding current density is taken as J = 100 A/cm², the utilization coefficient K_u of the magnetic core window is taken as 0.06, and the waveform coefficient K_f is taken as 4 for the square wave [29].

$$A_p={\displaystyle \frac{2P·{10}^4}{B_m·K_f·K_u·J·f}}=1562 {\mathrm{c}\mathrm{m}}^4$$

(11)

PC95 ferrite core material is selected. Its saturation flux density B_s is 530 mT, residual flux density B_r is 85 mT, and coercivity H_c is 9.5. The structure of the magnetic core is UU type 120/90/40, with an effective cross-sectional area A_e of 2400 mm² and a window area A_w of 7080 mm². The product is greater than the AP value in the formula, so the structure and material selection of the core meet the requirements.

Ensure that the winding space of the magnetic core is sufficient and a large margin is reserved, and the effective cross-sectional area A_e of the magnetic core is 2400 mm². It can be calculated that the number of primary turns N₁ is

$$N_1={\displaystyle \frac{V_{AB}}{B_m·K_f·f·A_e}}\approx 7$$

(12)

The number of turns on the secondary side is 210, and the secondary side winding is divided into three groups, with 70 turns in each group. High-voltage insulation should be considered for each secondary winding, and insulating materials should be added to each winding device [30]. The cross-sectional area of the primary side conductor is

$$S_p={\displaystyle \frac{I_p}{J}}=30 {\mathrm{m}\mathrm{m}}^2$$

(13)

The primary is wound with 0.1 mm × 1000 high-frequency wire strands made of enamel, with a cross-sectional area of 31.4 mm². The sectional area of the secondary side conductor is

$$S_s={\displaystyle \frac{I_s}{J}}=1 {\mathrm{m}\mathrm{m}}^2$$

(14)

The secondary is wound with 0.15 mm × 70 high-frequency wire strands made of enamel, with a cross-sectional area of 1.24 mm². The wire package adopts the epoxy potting process to meet the voltage withstand with secondary to iron core ≥ 30 kV and primary to iron core ≥ 1 kV.

2.7. EMI/EMC Performance Analysis and Series IGBT Design

To mitigate EMI/EMC issues in the circuit, a high-power, low-noise regulated power supply is used as the input bus voltage source. An EMI filter is added at the input to further suppress conducted emissions. Additionally, magnetic beads are placed in the circuits of the transformer, capacitor, inductor, and sampling board, and a metal shield is implemented to address EMC concerns. The IGBT drive lines are wound using twisted pair wires to reduce signal interference. The frequency control utilizes a first-order IIR filtering algorithm, and the IGBT is connected in series with an RCD snubber circuit to suppress voltage spikes.

The model of the series-connected IGBT module is K50H603, with a rated collector–emitter voltage (U_CE) of 600 V, a rated collector current (I_C) of 100 A, an on-delay time (T_on) of 23 ns, an off-delay time (T_off) of 235 ns, and a leakage current (I_D) of 40 μA. The voltage equalization circuit for the series IGBTs adopts an RCD-based scheme. Based on the IGBT turn-off time, load current, and output voltage, the calculated capacitance value in the RCD snubber circuit is 8 nF. A total of eight IGBTs are connected in series to generate a pulse output, and a magnetic isolation driving method using a series core magnetic ring is employed. According to the circuit design, a pulse voltage of 4.8 kV can be achieved. The voltage divider board adopts an RC voltage divider circuit to ensure full-band signal transmission without phase distortion. A 2.2 MΩ high-voltage resistor is selected, with a voltage division ratio of 1:10,000.

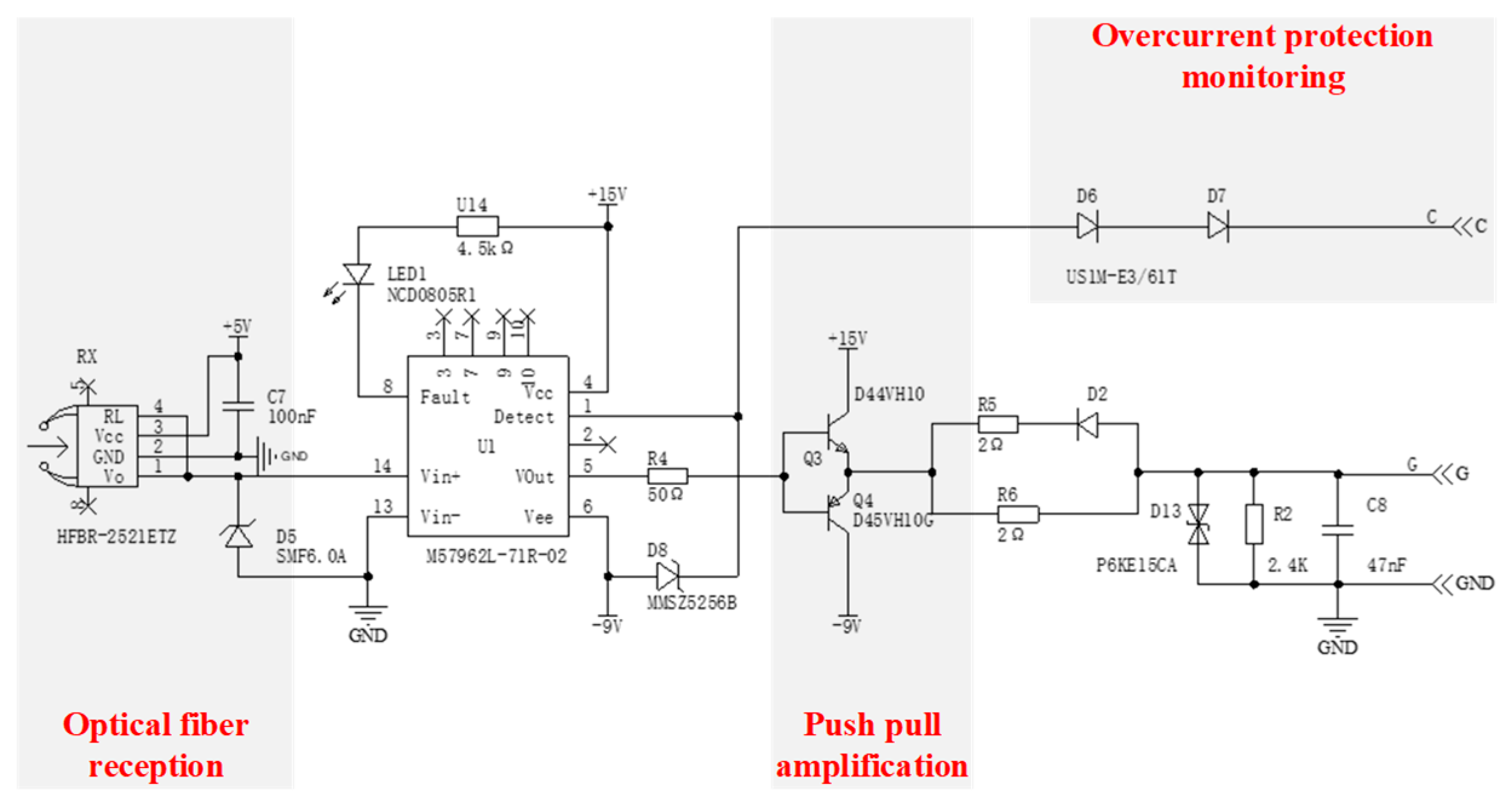
2.8. Optical Fiber Isolation Drive Design

A schematic diagram of the Optical Fiber Isolation Drive Design is shown in Figure 7. The optical fiber-receiving module converts the optical signal into an electrical signal, inputs the driving signal into the push–pull amplifier circuit, and drives the IGBT module after raising the driving power to the driving level of the IGBT module. HFBR-1414TZ is selected as the optical fiber transmitting module, and HFBR-2412TZ is selected as the optical fiber receiving module. D44VH10 and D45VH10 are selected to form a push–pull amplifier circuit. The drive chip adopts the special drive module M57962AL for IGBT produced by Mitsubishi Corporation. At the same time, 4 V is selected as the short-circuit protection threshold of IGBT. The fiber optic head is powered by 5V, while the driver chip and push-pull chip are powered by 15V. Resistors, capacitors, diodes, and LED lights in the circuit are selected according to the chip manual.

3. Results

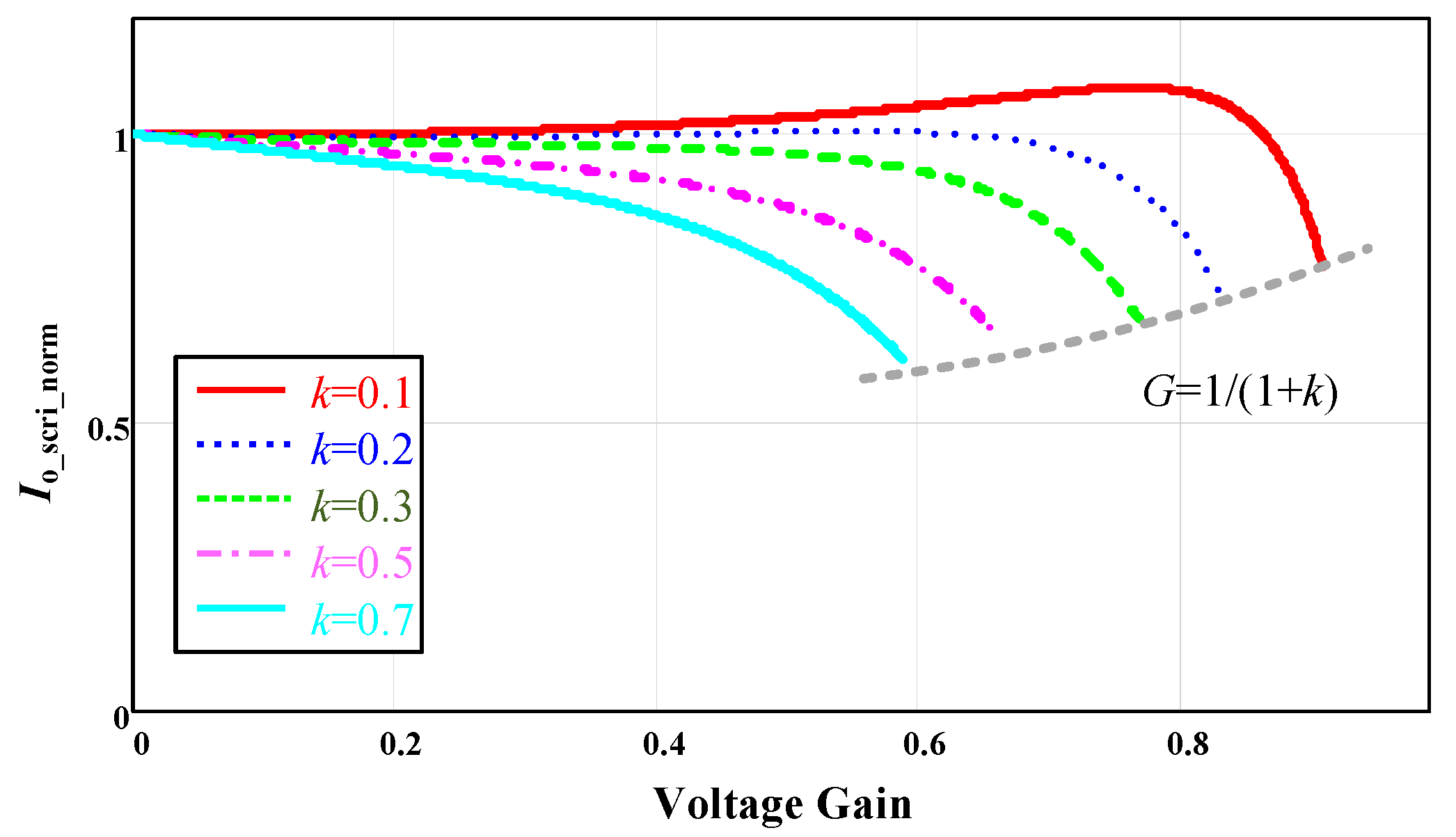
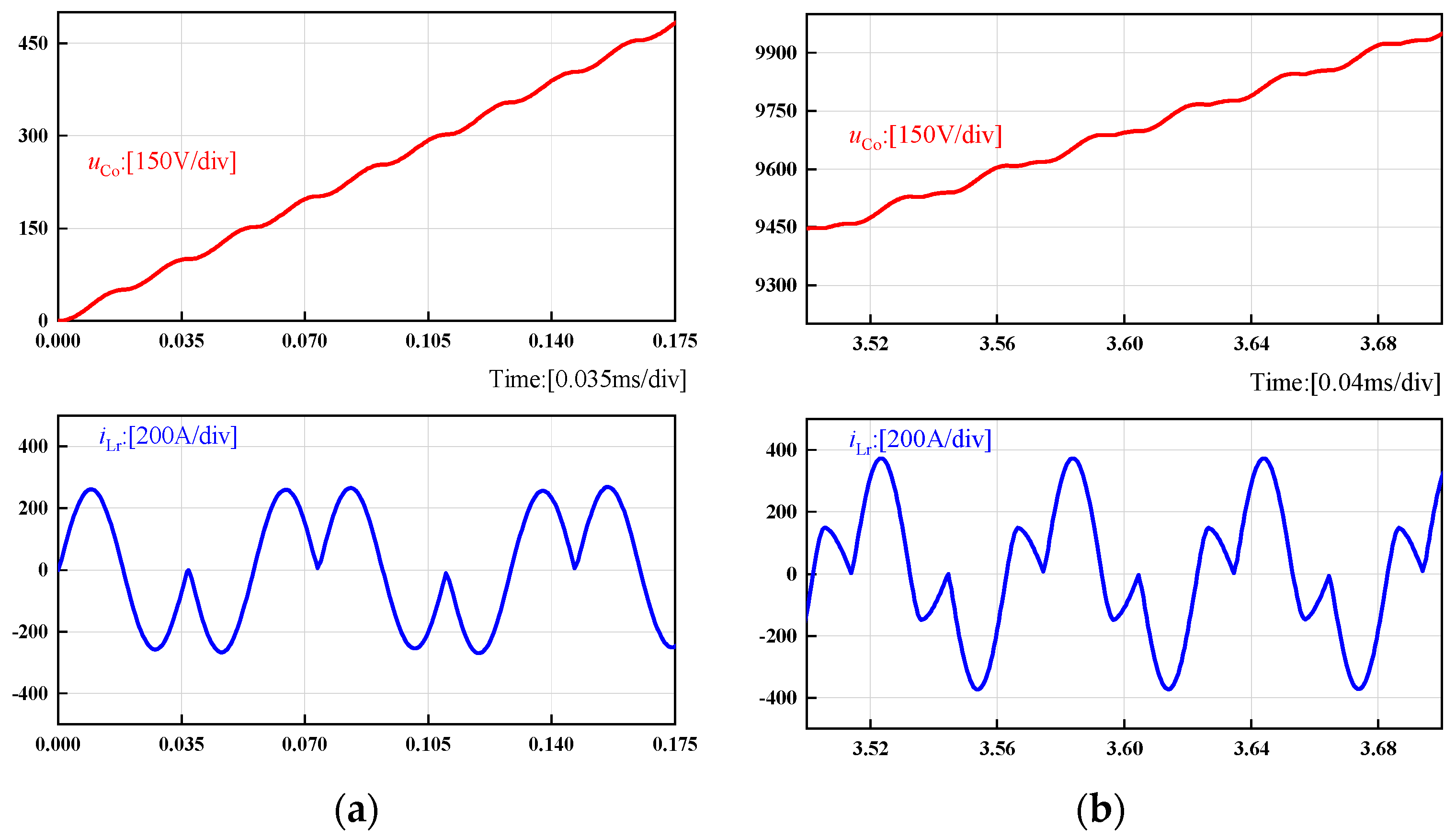
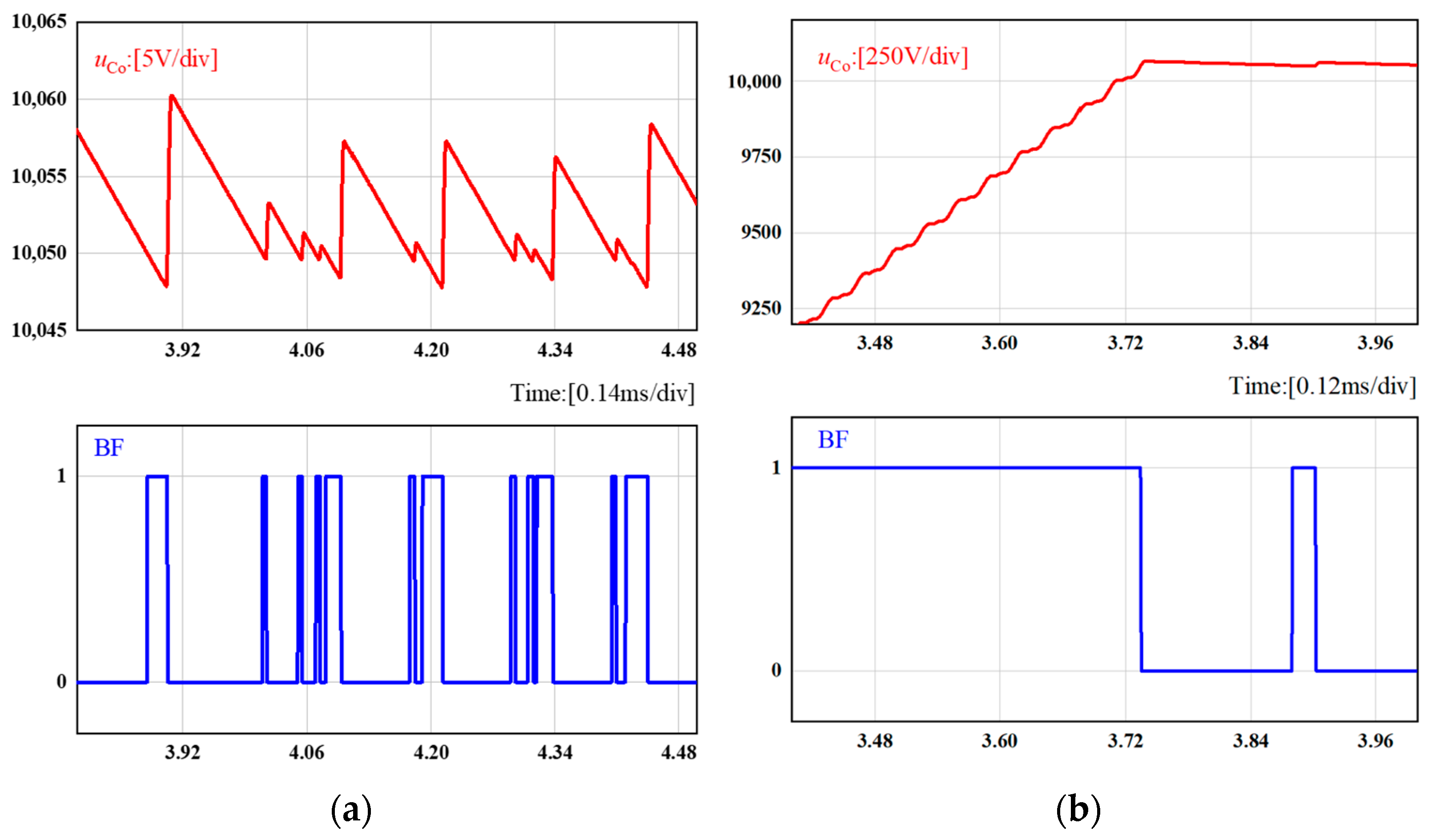
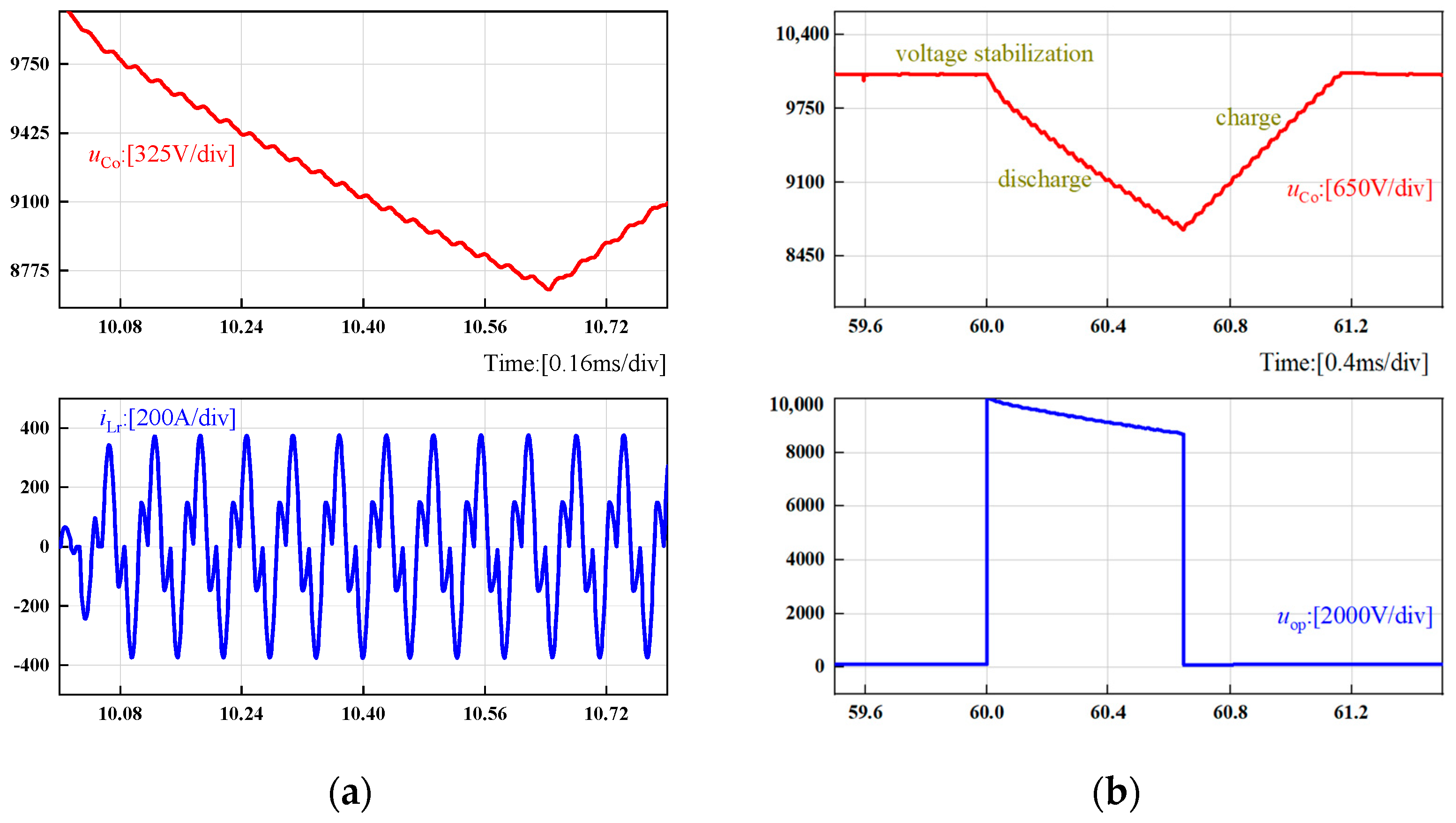
3.1. Simulation Analysis

The simulation model is built in Simulink, and the simulation step is set to 5 ns. In the constant frequency mode, the waveforms of the energy storage capacitor voltage and the primary side resonant current during the pulse discharge period are shown in Figure 8a. There are current interruptions during the pulse discharge period and at the end of the charging period. The energy storage capacitor voltage drops from 10 kV to 8.46 kV during the pulse discharge period, with a top-drop of about 15.4%. The relationship between the two at the end of charging is shown in Figure 8b. The increase in the intermittent interval of the resonant current attenuates the average output current, and the intermittent duration is about 5 μs, which reduces the charging speed.

It is observed that the resonant current is in the critical intermittent mode after using the critical frequency control mode. It is observed from Figure 9a,b that the resonant current is in the critical continuous state at the beginning and end of charging. The critical continuous frequency calculated by a simulation well tracks the actual critical continuous frequency. The peak resonant current is about 370 A.

During the voltage stabilization phase, it can be observed that the relationship between the output voltage ripple and the burst flag of burst hysteresis control is as shown in Figure 10a. When the output voltage amplitude is greater than 10.05 kV, the hysteresis control flag is set to 0 and the output voltage drops. When the output voltage amplitude is less than 10.05 kV, the hysteresis control flag is set to 1, the output voltage increases, and the output voltage ripple is controlled at about 10 V. At the end of the charging phase, it is found from Figure 10b that the hysteresis control flag is set to 1.

During the pulse output phase, it can be observed that the waveform of the energy storage capacitor voltage and resonant current is as shown in Figure 11a. During the pulse discharge, the voltage drops from 10 kV to 8.68 kV, and the top-drop is about 13.2%. The resonant current maintains critical continuity during the discharge, reducing the output pulse top-drop. From Figure 11b, the voltage of the energy storage capacitor and the output pulse voltage waveform of the load can be observed. The voltage of the energy storage capacitor has three stages: charging, stabilizing and discharging. The charging phase lasts about 1 ms, the repetition rate is 20 Hz, and the voltage ripple in the voltage stabilization phase is about 0.1%, which meets the design requirements in the previous article. A pulse output with a long pulse width, small ripples, and a low top-drop is achieved.

The simulation results show that the circuit can output a high-voltage pulse with a pulse width of 650 μs, a pulse amplitude of 10 kV, a top-drop of approximately 12%, and a voltage ripple of 0.1%. During the charging phase, the charging speed is improved by real-time tracking of the critical intermittent switching frequency. Zero-current switching (ZCS) of the IGBT is achieved across the full range, thereby reducing switching losses. During the voltage stabilization phase, burst hysteresis control is employed to enhance voltage accuracy. In the pulse discharge phase, the energy storage capacitor is continuously charged, effectively reducing the pulse top-drop.

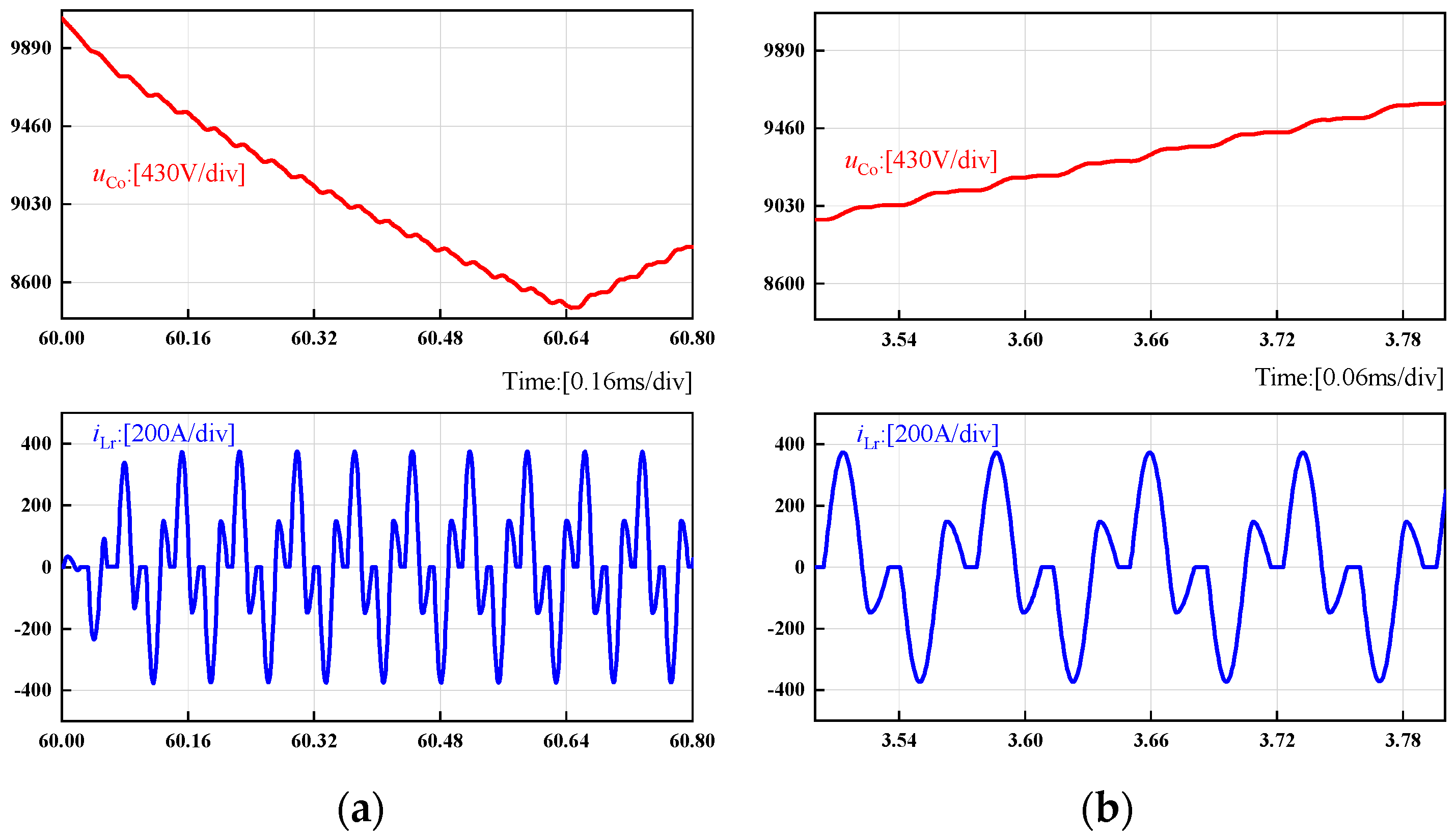
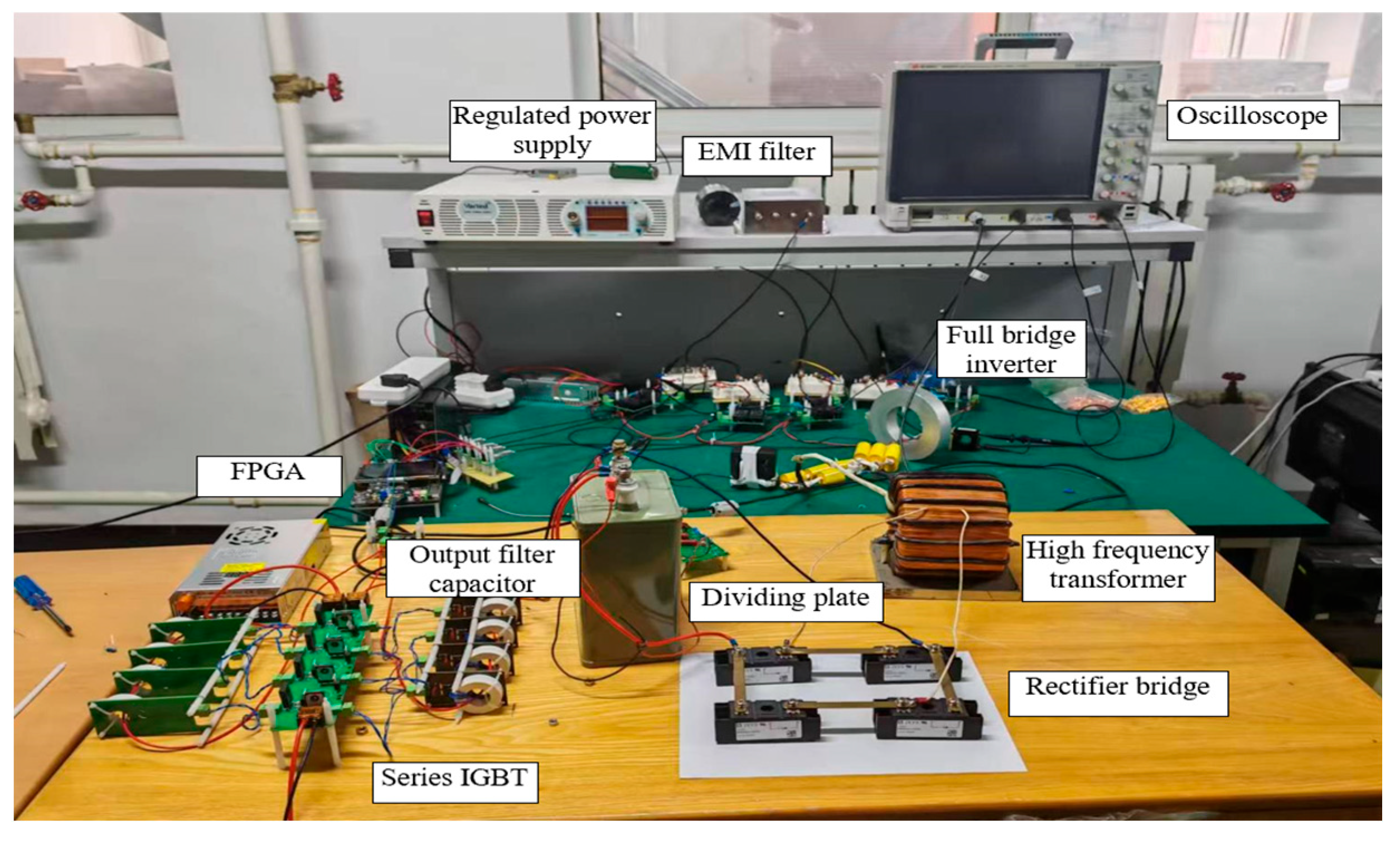
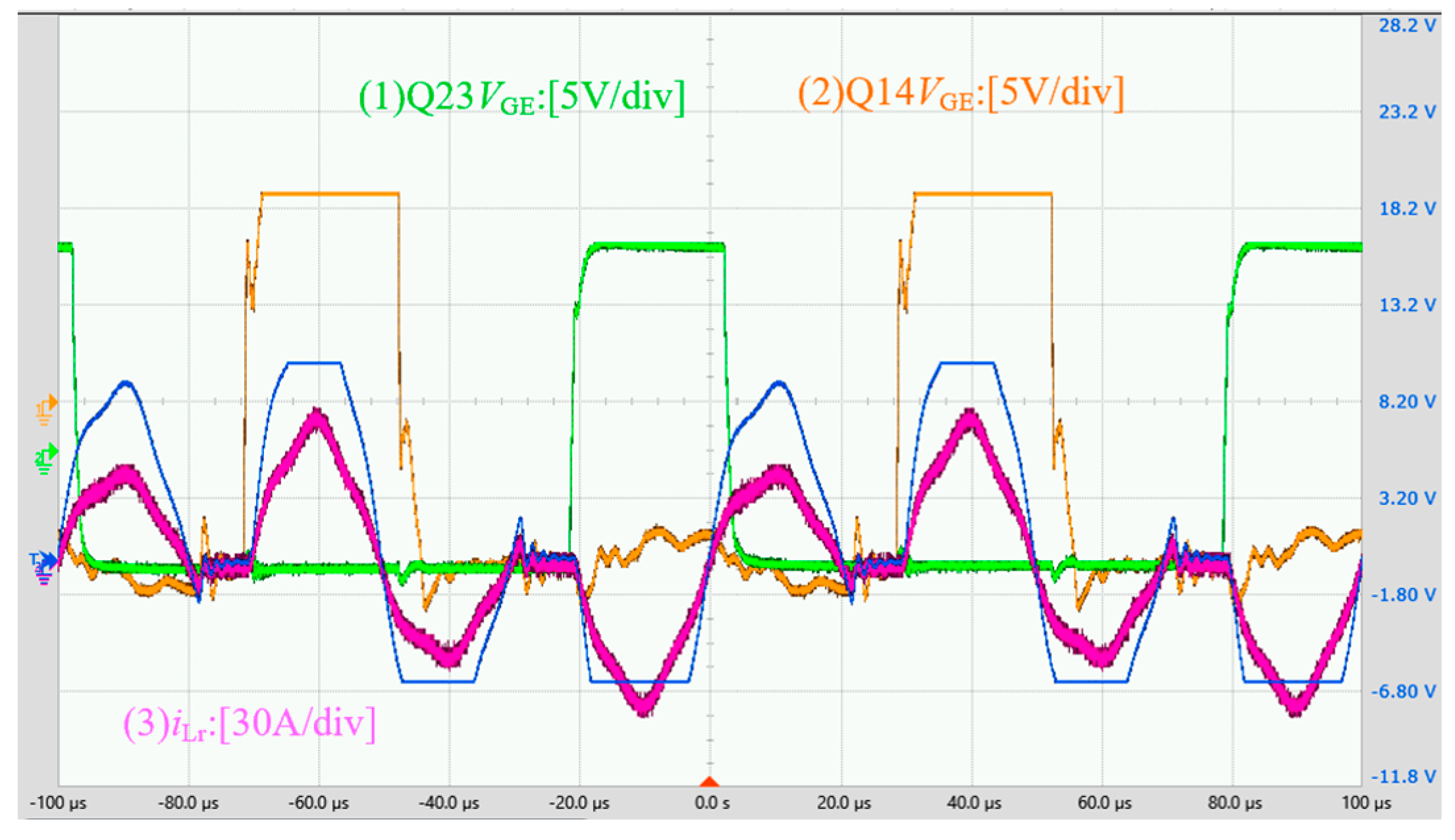
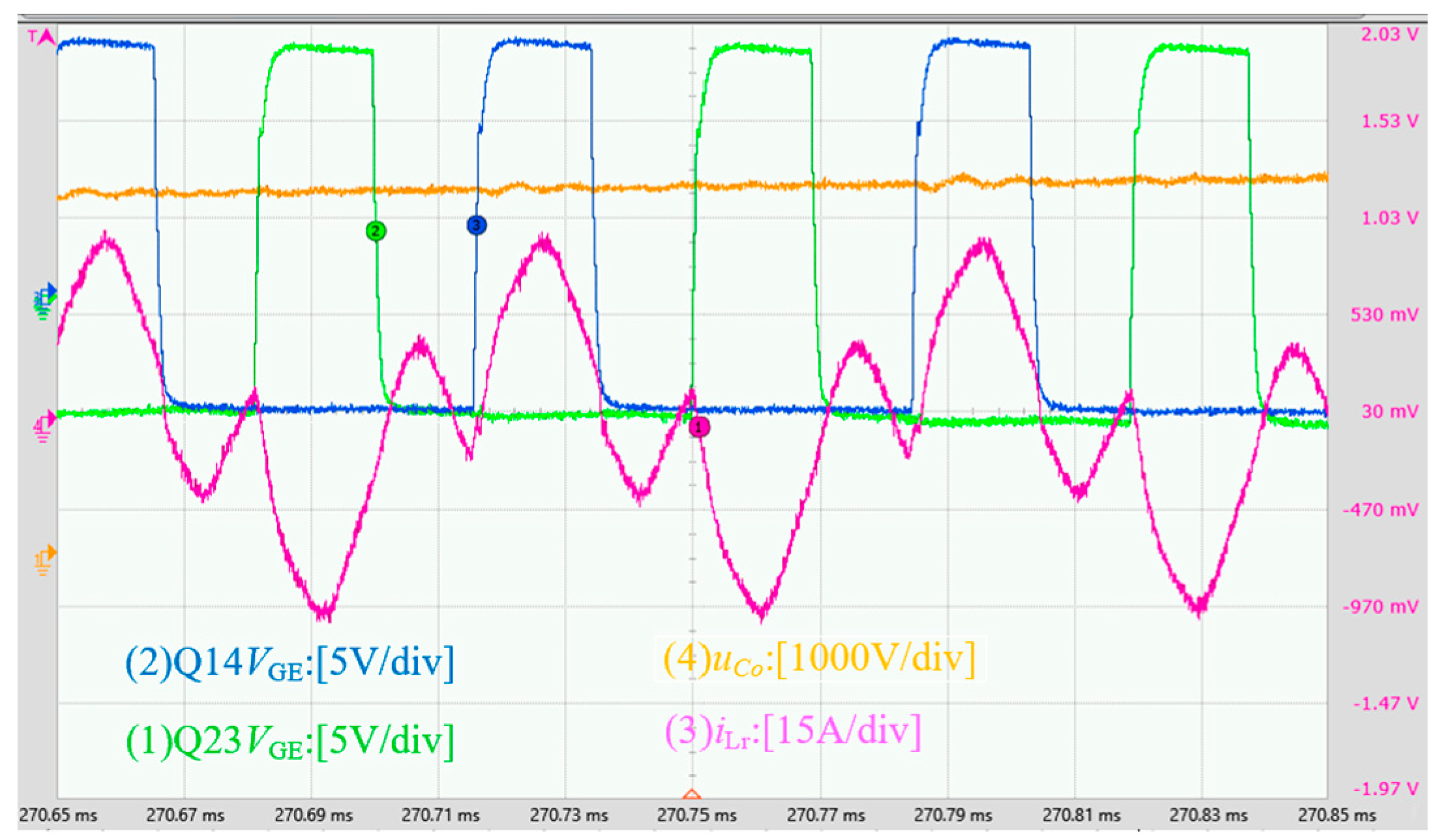
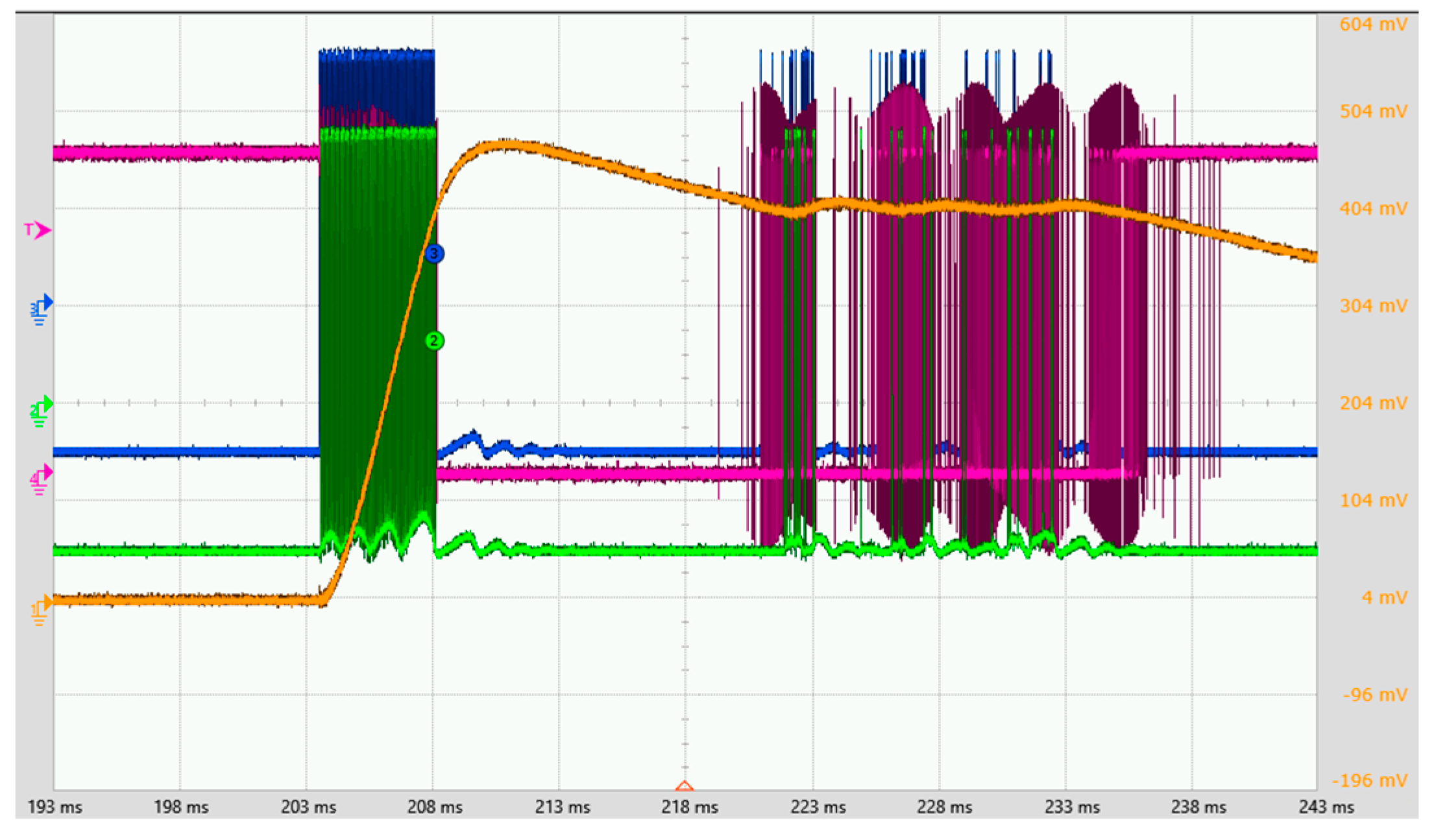
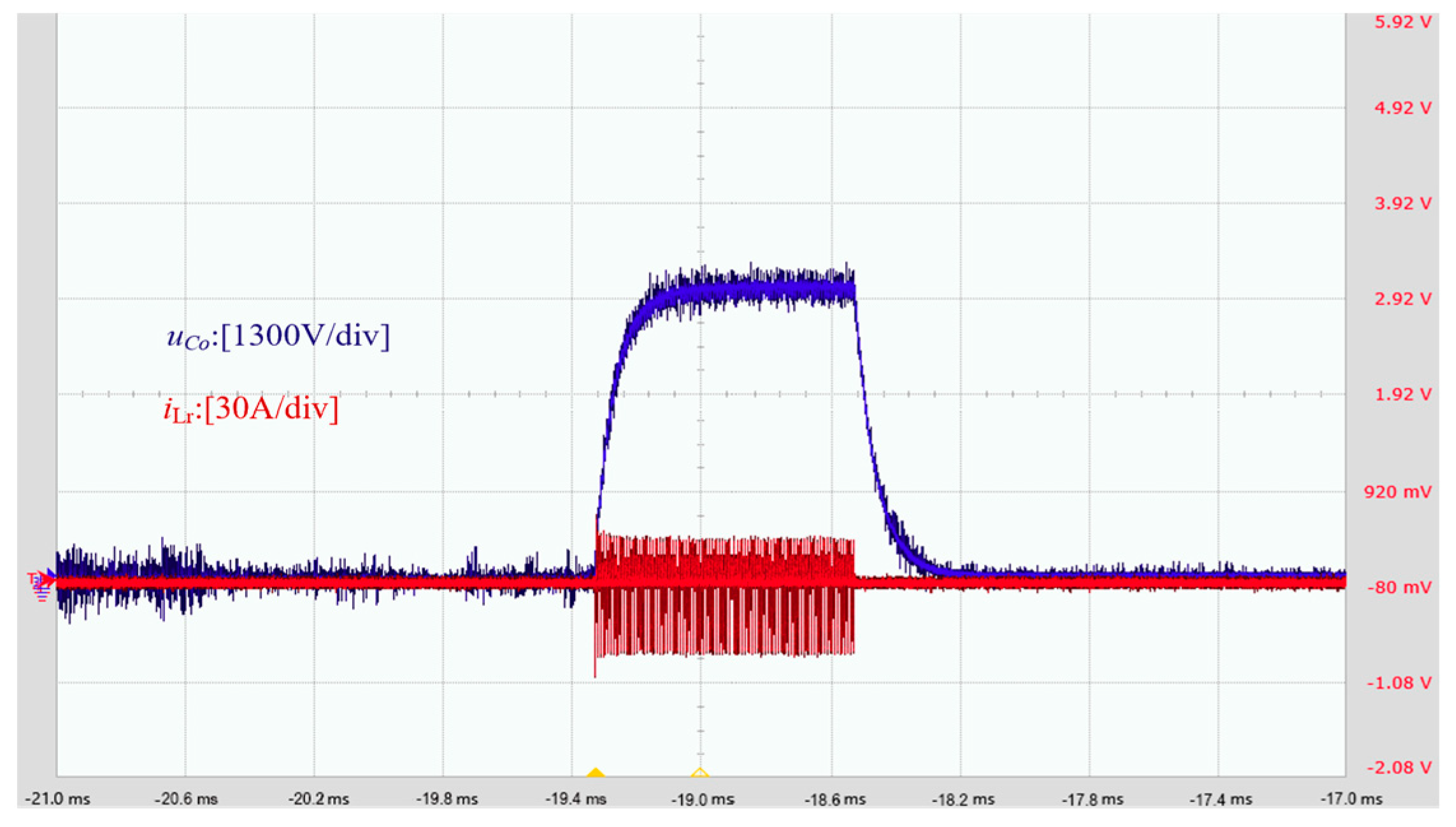
3.2. Experimental Test and Verification

According to the previous design, a solid-state pulse modulator prototype based on an LCC resonant converter with critical frequency control was constructed. The prototype was tested under low-power conditions to verify the rationality of the control algorithm and evaluate the output pulse quality. The input power source was a 5 kW regulated power supply, with an input bus voltage of 250 V, and the initial full-bridge switching frequency was set to 13 kHz. The parallel resonant capacitor was composed of multiple 0.47 μF high-voltage film capacitors arranged in parallel and series. The series resonant inductance was 7.2 μH, and the series resonant capacitance was 3.01 μF.

The actual experimental setup is shown in Figure 12.

The load is composed of multiple solenoid resistors in series, and a picture of the load is shown in the Figure 13. The load needs to keep the lead inductance small and the output power of the current modulator needs to be maintained.

First, the reliability of the whole bridge is tested. The actual circuit of the whole bridge is shown in the Figure 14.

First, as shown in Figure 15, when the critical switching frequency is not adopted, the switching frequency is fixed at 10 kHz, the input bus voltage is set to 100 V, and the peak resonant current reaches 60 A. At the end of the charging phase, the resonant current exhibits intermittent behavior, the charging duration exceeds 1 ms, and the resonant current fails to achieve critical continuity. The IGBT achieves zero-current turn-off after the series resonance ends. The series resonance lasts approximately 19 μs, and the total resonance duration is about 40 μs, which aligns with the resonance parameters specified in the design. The resonance interruption time is about 8 μs, during which the voltage across the energy storage capacitor is maintained around 350 V. Throughout the process, the LCC resonant converter remains in the active state, with the resonant current continuously charging the filter capacitor. The blue waveform represents the current measurement obtained using an auxiliary current transformer. The yellow and green waveforms represent the driving voltage waveforms of the switching tube. The pink waveform represents the resonant current waveform.

As shown in Figure 16, the output voltage of the energy storage capacitor is connected by the dividing plate. After sampling, the closed-loop test is carried out. The action voltage of a burst is set to 4 kV and the pulse repetition rate is 10 Hz in the FPGA program. When the charging voltage of the energy storage capacitor reaches 4 kV and the driving signal is closed, the filtering energy storage capacitor will stop charging. At the end of charging, the resonant current frequency rises from 12.5 kHz to 15 kHz, the peak value of the resonant current is 30 A, the resonant current is not interrupted obviously, and the corresponding gain is about 0.48, which is in line with the critical frequency model designed above.

Under light-load conditions, the pulse duration reaches 30 ms, and the charging time is approximately 4 ms. The overall operating waveforms of the system in light-load mode are shown in Figure 17. In this figure, the yellow waveform represents the charging voltage, the blue-green waveform indicates the drive voltage, and the pink waveform corresponds to the resonant current. During the charging process, the resonant current exhibits a continuous increasing trend, and charging ceases once the output voltage reaches the predefined action threshold. Subsequently, the voltage across the filter capacitor is maintained near the action voltage.

When the system is connected to a 400 Ω load, it operates in heavy-load mode. The pulse width is set to 650 μs, and the overall operating waveform under heavy-load conditions is shown in Figure 18. The pulse leading edge is approximately 160 μs. During pulse discharge, the resonant circuit continuously charges the energy storage capacitor, and the output waveform exhibits no significant top-drop. The output voltage can reach 4 kV, with a corresponding output power of up to 3 kW.

3.3. Cost Assembly Complexity Analysis

The cost of the devices used is analyzed based on the experimental platform, and the difficulty of implementation is comprehensively considered and compared with the traditional solutions, as shown in

Table 2. Economic analysis.

Component	LCC + Series IGBT	Marx Generator	LTD
Energy Storage Capacitors	Medium	Low	Medium–High
Magnetic Components	Medium	Medium–High	Medium
Switching Devices	High	Low	Medium
Drive & Control Complexity	Medium–High	High	Medium
Voltage Balancing Network	High	Low	Very Low
Assembly Complexity	Medium–High	High	Medium
Debugging & Maintenance	Medium	High	Medium–High
Overall Cost Evaluation	Medium	High	High

. The results show that the cost of this solution is low and has application value.

4. Conclusions

A low-power, light-load test was conducted on the LCC resonant converter with critical frequency control, using a 250 V bus input, a 1 Hz repetition rate, and a 4 kV pulse output. The test results show that the charging time was approximately 4 ms, and the pulse duration reached 30 ms. After connecting a 400 Ω load, the pulse width was set to 650 μs, and the leading edge of the output pulse was 160 μs, with no significant pulse top- drop observed. During the pulse output, the resonant current continuously charged the energy storage capacitor.

Although the experimental results did not fully meet the design specifications due to limitations in laboratory conditions, they validated the feasibility of the proposed technical scheme. Further experiments will be conducted in future studies, and the technical results obtained can be applied to long-pulse, high-power electron irradiation accelerators.