Numerical Study on the Influence of Cooling-Fin Geometry on the Aero-Thermal Behavior of a Rotating Tire
Abstract
1. Introduction
2. Methodology
2.1. Geometry and Computational Domain
2.2. Numerical Method
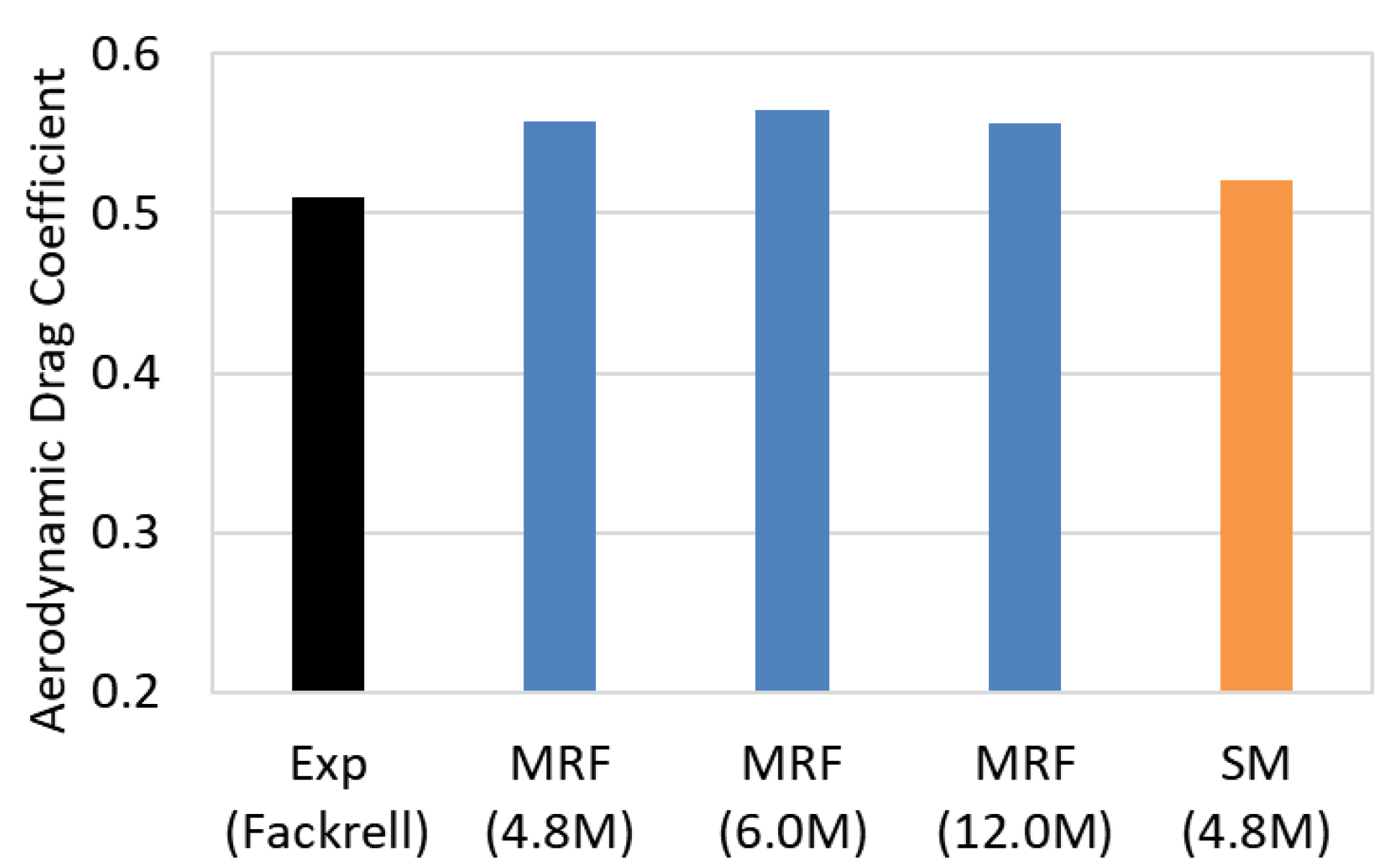
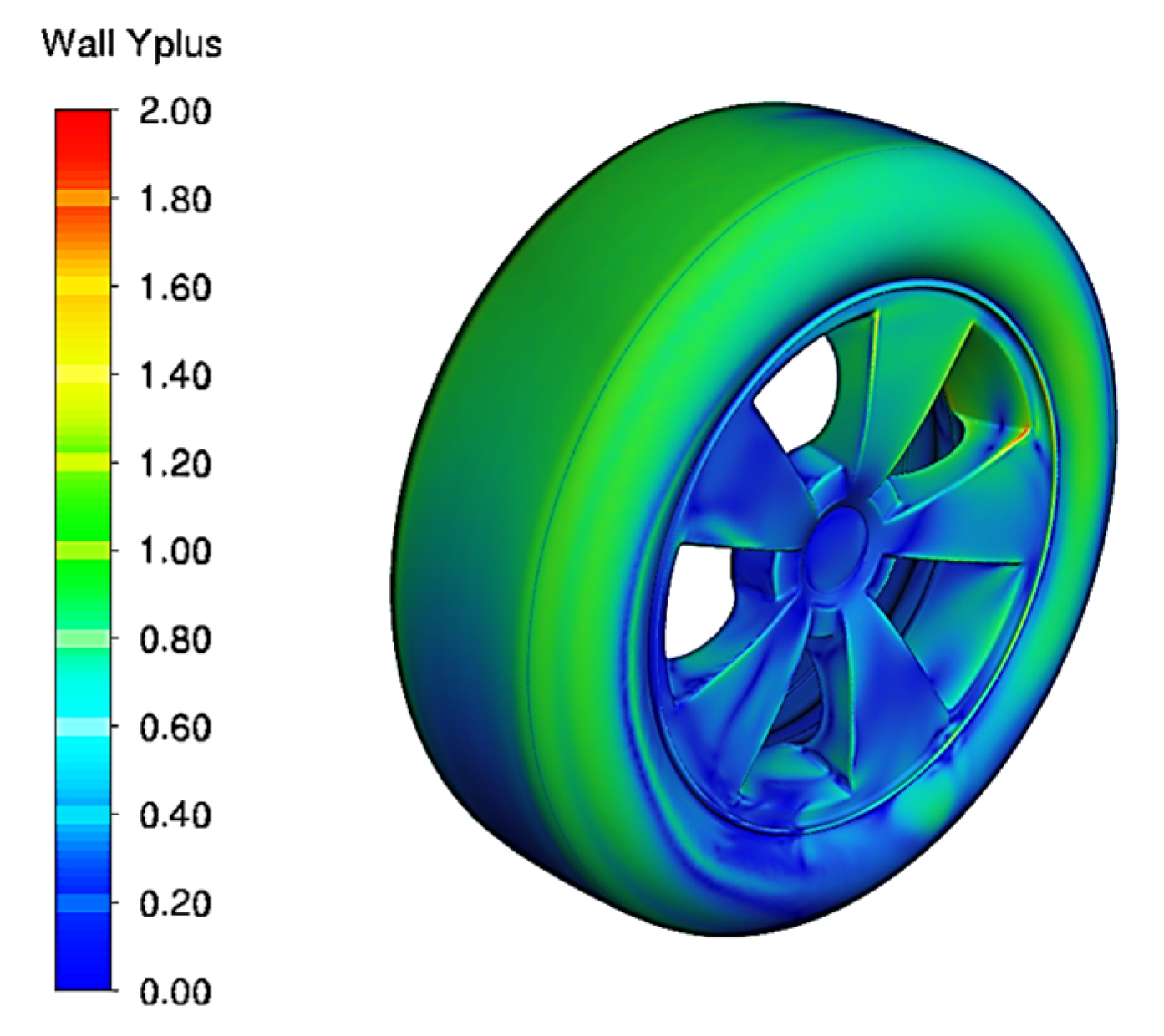
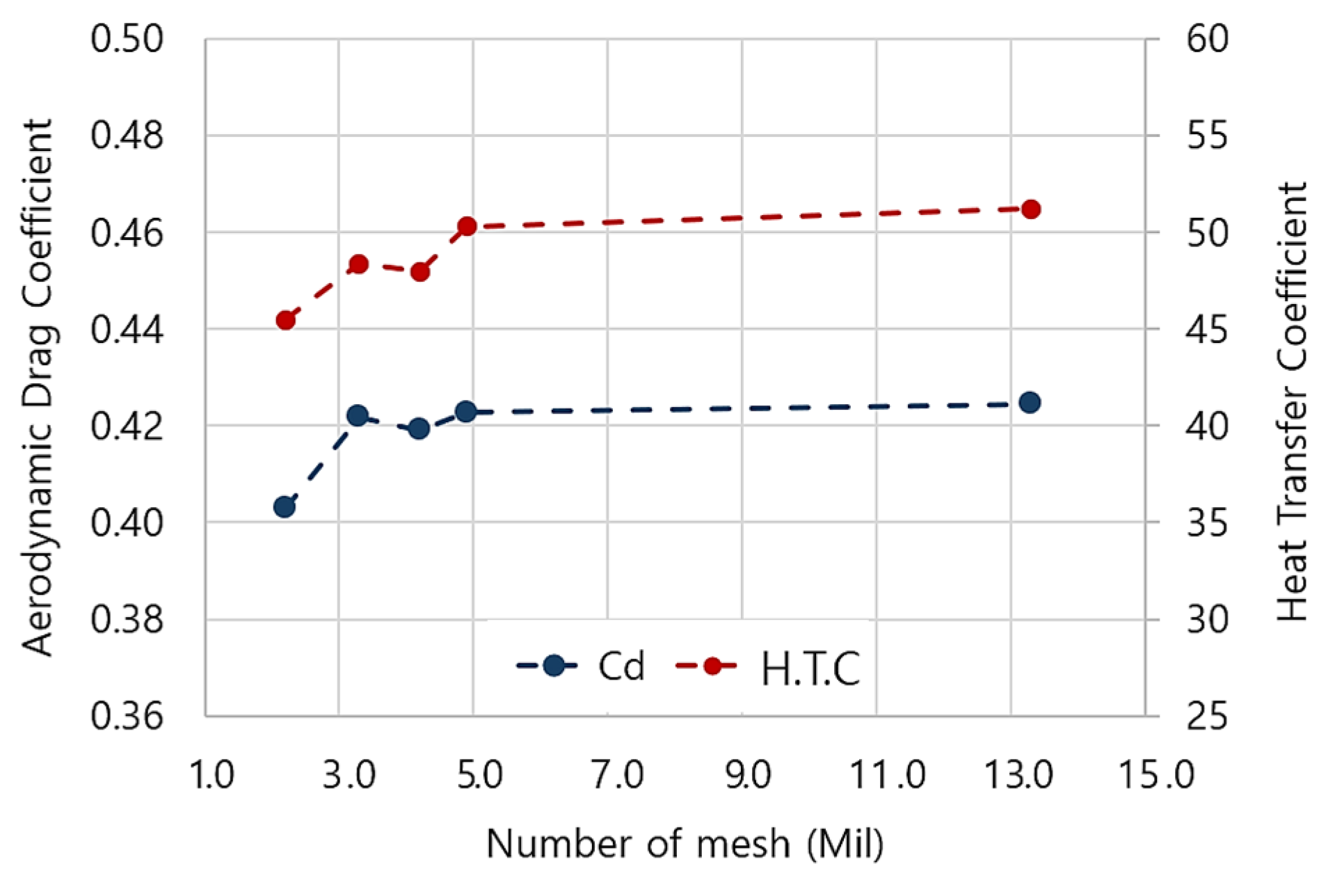
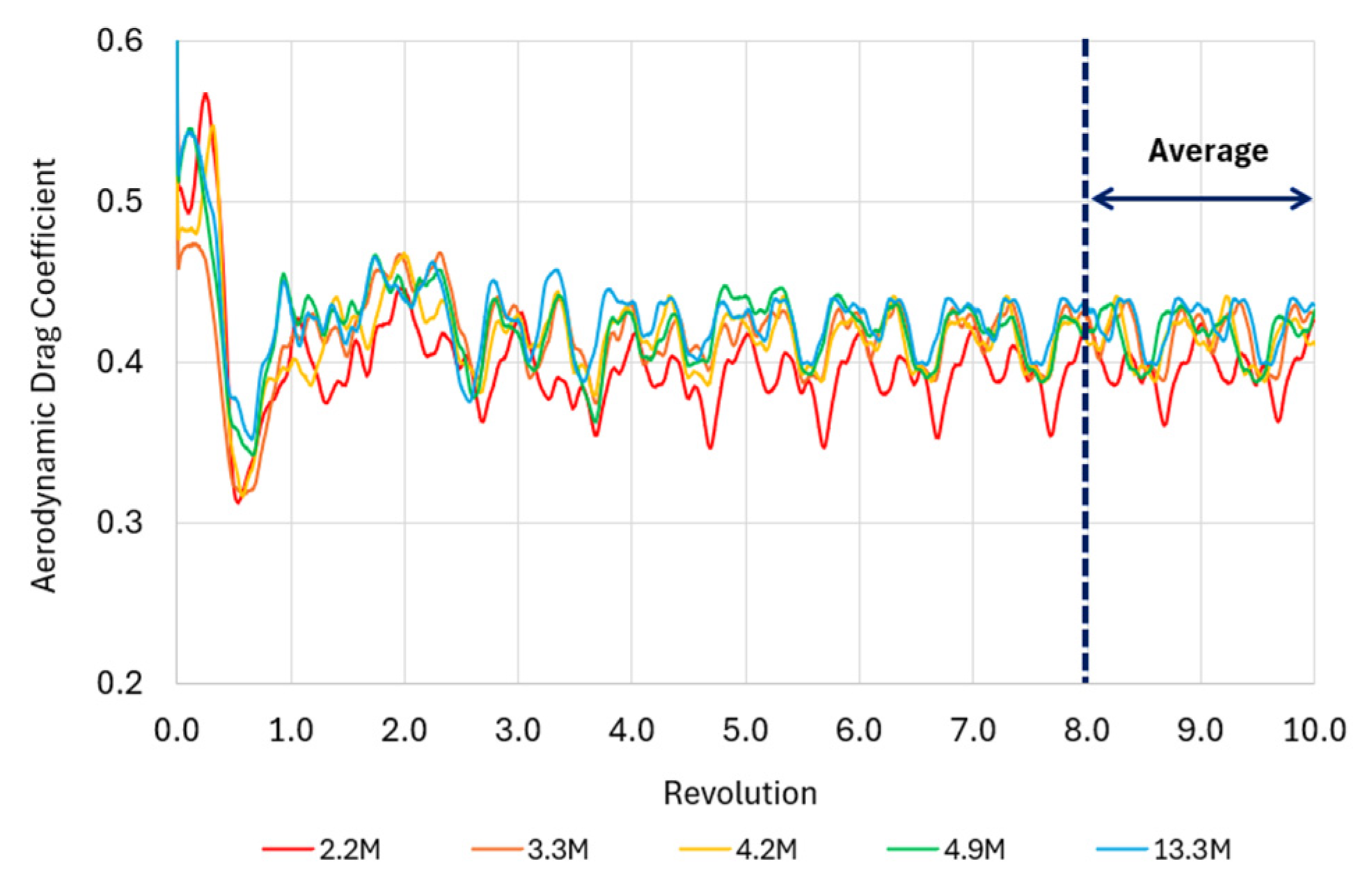
2.3. Mesh Generation and Mesh Sensitivity Analysis
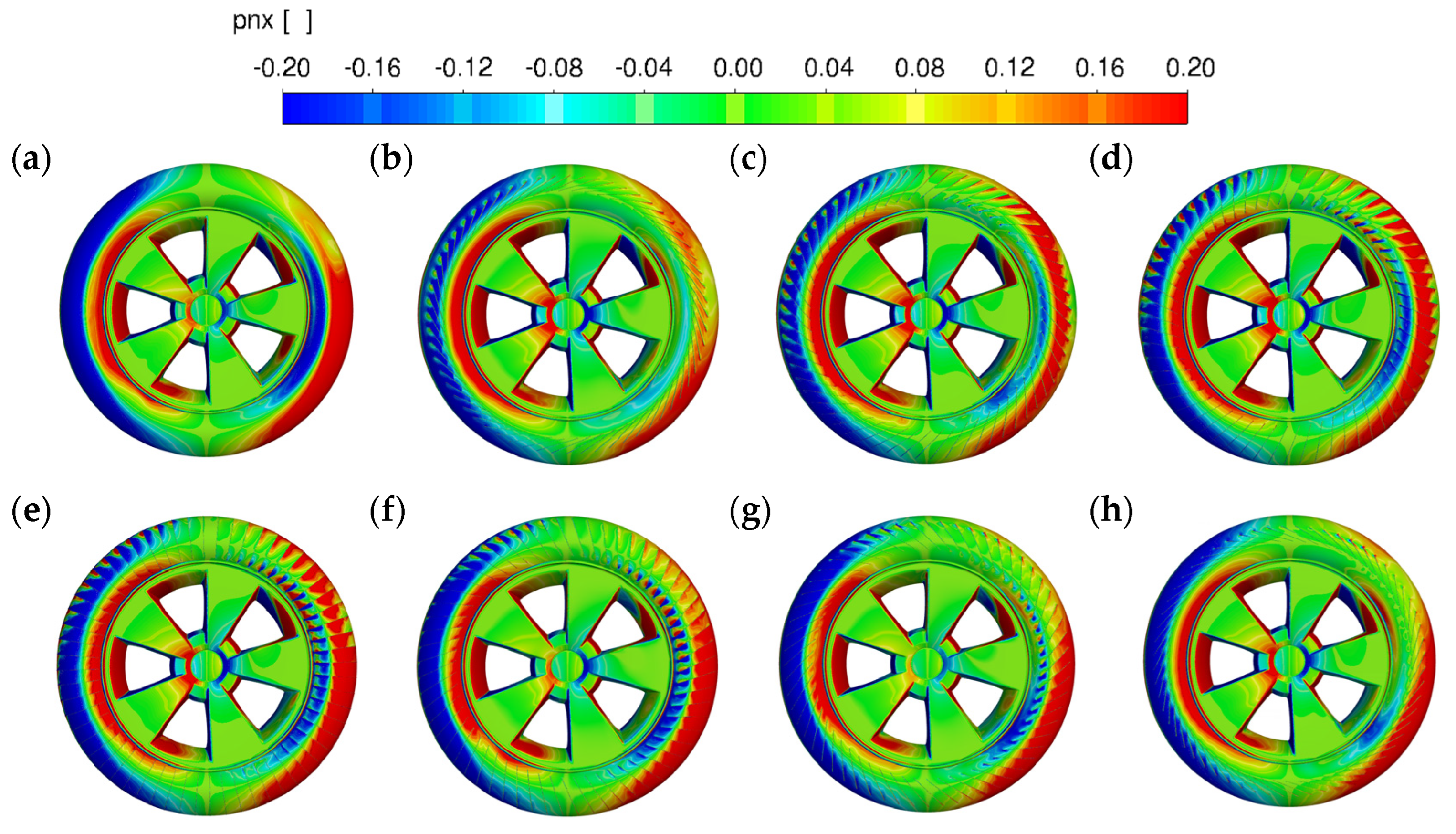
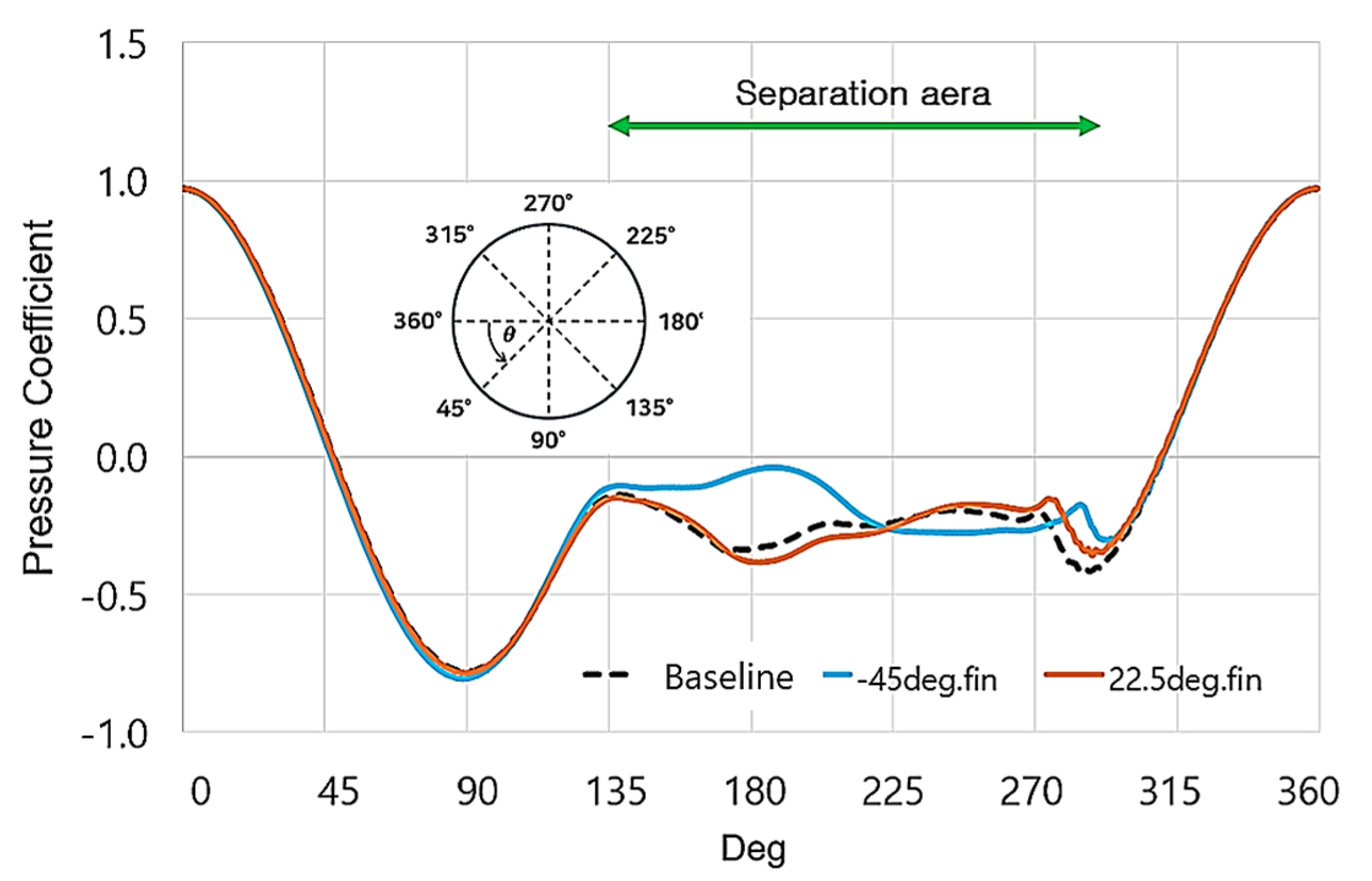
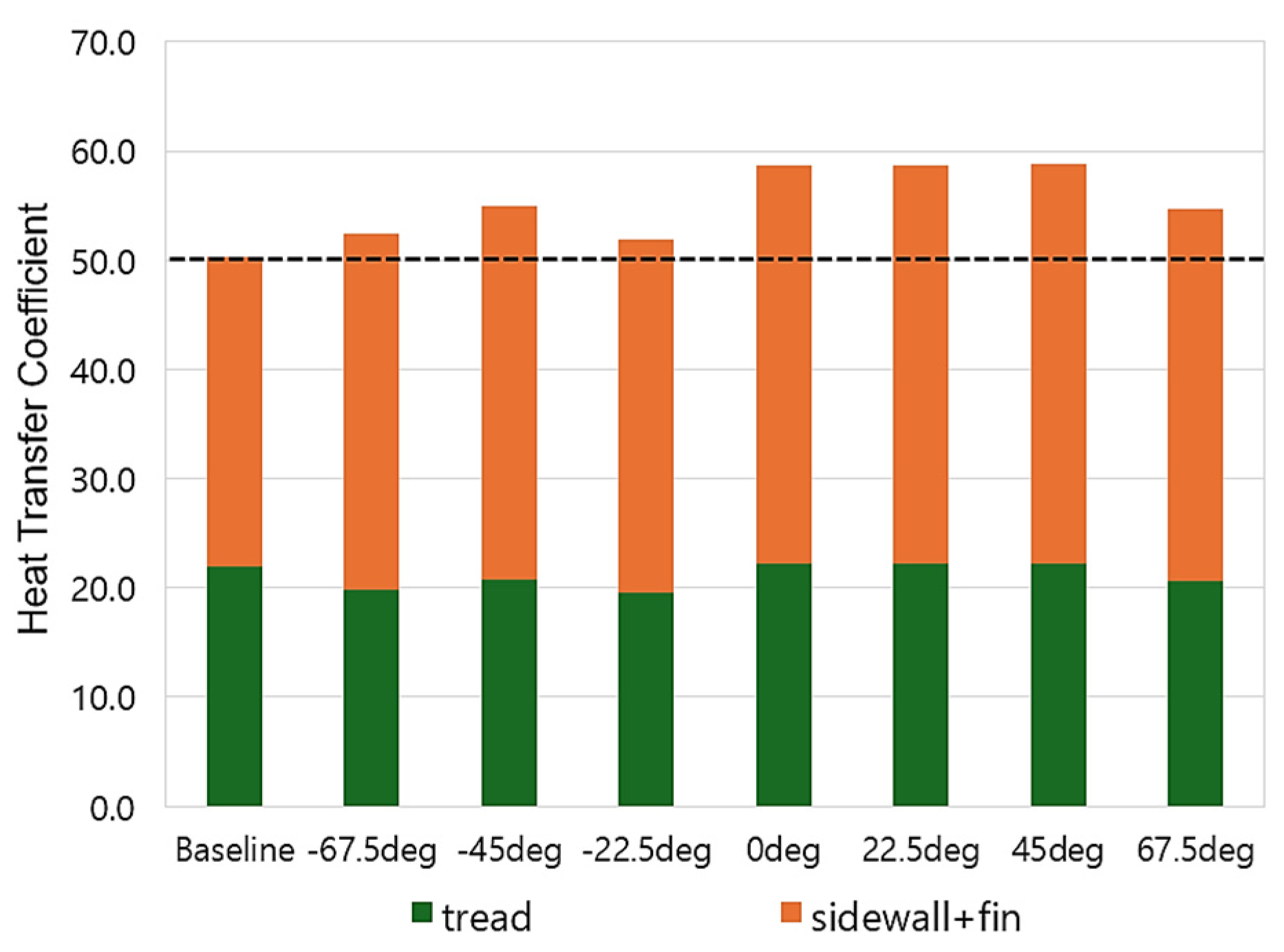
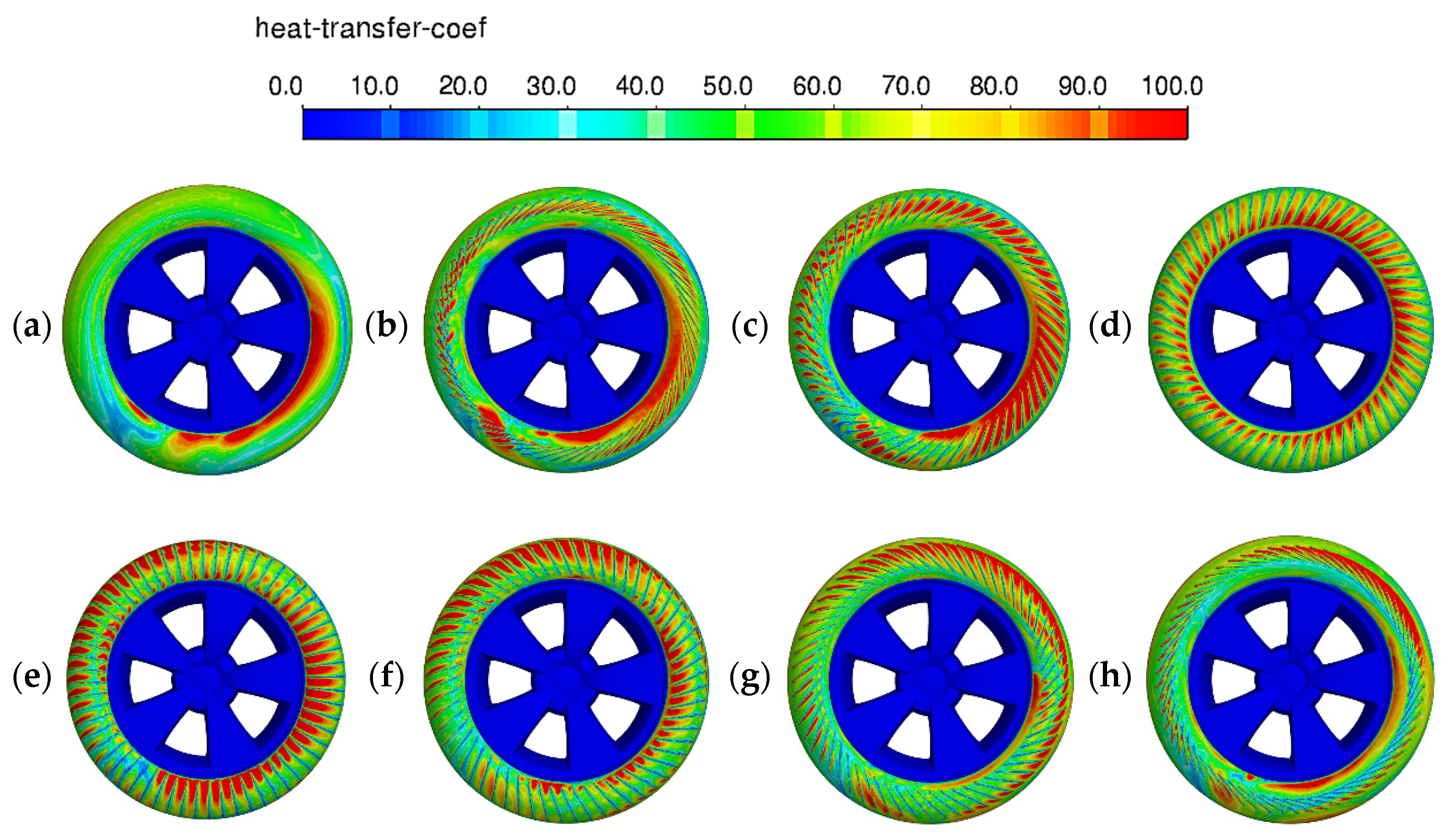
3. Results
3.1. Without Ground Contact
3.2. With Ground Contact
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| Cd | Aerodynamic drag coefficient |
| CFD | Computational fluid dynamics |
| Cp | Surface pressure coefficient |
| DES | Detached eddy simulation |
| Drag force | |
| HTC | Heat transfer coefficient |
| MRF | Multiple reference frame |
| X-directional surface normal vector | |
| p | Static pressure |
| Static pressure of freestream | |
| Pnx | X-directional pressure distribution |
| q″ | Heat flux |
| S | Projection area |
| SM | Sliding mesh |
| SST k-ω | Shear stress transport k-w turbulence model |
| T | Temperature |
| Surface temperature | |
| Fluid temperature | |
| uRANS | Unsteady Reynolds-averaged Navier–Stokes |
| Freestream velocity | |
| y+ | Non-dimensional wall distance |
| ρ | Air density |
| μ | Dynamic viscosity |
| κ | Thermal conductivity |
Appendix A

References
- Farroni, F.; Mancinelli, N.; Timpone, F. A Real-Time Thermal Model for the Analysis of Tire/Road Interaction in Motorcycle Applications. Appl. Sci. 2020, 10, 1604. [Google Scholar] [CrossRef]
- Kang, S.; Jeong, K.; Kim, K.; Chang, D. Numerical estimation of rolling resistance and temperature distribution of 3-D periodic patterned tire. Int. J. Solids Struct. 2013, 50, 86–96. [Google Scholar]
- Jeong, K.; Kang, S.; Park, W.; Kim, H.; Kim, K. Finite Element Analysis for Temperature Distribution Prediction of Steady Rolling Tires with Detailed Tread Pattern. Trans. Korean Soc. Automot. Eng. 2014, 22, 117–125. [Google Scholar] [CrossRef]
- Zhou, H.; Jiang, Z.; Wang, G.; Zhang, S. Aerodynamic characteristics of isolated loaded tires with different tread patterns: Experiment and simulation. Chin. J. Mech. Eng. 2021, 34, 6. [Google Scholar] [CrossRef]
- Cattani, P.; Cattani, L.; Magrini, A. Tyre–Road Heat Transfer Coefficient Equation Proposal. Appl. Sci. 2023, 13, 11996. [Google Scholar] [CrossRef]
- Teodosio, L.; Alferi, G.; Genovese, A.; Farroni, F.; Mele, B.; Timpone, F.; Sakhnevych, A. A numerical methodology for thermo-fluid dynamic modelling of tyre inner chamber: Towards real time applications. Meccanica 2021, 56, 549–567. [Google Scholar] [CrossRef]
- Yamaguchi, M.; Makoto, T.; Kenshiro, K. Experimental and CFD Analysis of Tire Cooling Sidewall. SAE Int. J. Passeng. Cars-Mech. Syst. 2008, 1, 1–8. [Google Scholar] [CrossRef]
- Lee, J.; Park, S.; Kim, M.; Kim, Y.; Oh, B. Vehicle aerodynamic drag for tire shape parameters using numerical analysis. Int. J Automot. Technol. 2020, 23, 335–344. [Google Scholar] [CrossRef]
- Josefsson, E.; Hobeika, T.; Sebben, S. Evaluation of wind tunnel interference on numerical prediction of wheel aerodynamics. J. Wind Eng. Ind. Aerodyn. 2022, 224, 104945. [Google Scholar] [CrossRef]
- Leśniewicz, P.; Kulak, M.; Karczewski, M. Aerodynamic analysis of an isolated vehicle wheel. J. Phys. Conf. Ser. 2014, 530, 012064. [Google Scholar] [CrossRef]
- Brandt, A.; Berg, H.; Bolzon, M.; Josefsson, L. The effects of wheel design on the aerodynamic drag of passenger vehicles. SAE Int. J. Adv. Curr. Pract. Mobil. 2019, 1, 1279–1299. [Google Scholar] [CrossRef]
- Skea, A.; Bullen, P.; Qiao, J. CFD Simulations and Experimental Measurements of the Flow over a Rotating Wheel in a Wheel Arc; SAE Technical Paper; SAE: Warrendale, PA, USA, 2000. [Google Scholar]
- Corner, E.; Mothay, G.; Socit, C.; Bezard, H. Aerodynamic analysis of an isolated wheel wake. In Proceedings of the Conference on Modelling Fluid Flow (CMFF’12), 15th International Conference on Fluid Flow Technologies, Budapest, Hungary, 4–7 September 2012. [Google Scholar]
- Haag, L.; Blacha, T.; Indinger, T. Experimental investigation on the aerodynamics of isolated rotating wheels and evaluation of wheel rotation models using CFD. Int. J. Autom Eng 2017, 8, 7–14. [Google Scholar] [CrossRef] [PubMed]
- Aultman, M.; Auza-Gutierrez, R.; Disotell, K.; Duan, L. Effects of Wheel Rotation on Long-Period Wake Dynamics of the DrivAer Fastback Model. Fluids 2022, 7, 19. [Google Scholar] [CrossRef]
- Yu, X.; Jia, Q.; Yang, Z. Comprehensive Study of the Aerodynamic Influence of Ground and Wheel States on the Notchback DrivAer. Energies 2022, 15, 1124. [Google Scholar] [CrossRef]
- Heft, A.; Indinger, T.; Adams, N. Experimental and Numerical Investigation of the DrivAer Model. In Fluids Engineering Division Summer Meeting; American Society of Mechanical Engineers: New York, NY, USA, 2012; pp. 41–51. [Google Scholar]
- Cho, S.; Lee, S. Aerodynamic performance analysis on various wheel configurations of commercial vehicle. Microsyst. Technol. 2025, 31, 1147–1159. [Google Scholar] [CrossRef]
- ANSYS Inc. ANSYS Fluent User’s Guide; ANSYS Inc.: Canonsburg, PA, USA, 2023. [Google Scholar]
- Yang, Y.; Wang, C.; Guo, R.; Zhang, M. Numerical analyses of the flow past a short rotating cylinder. J. Fluid Mech. 2023, 975, A15. [Google Scholar] [CrossRef]
- John, A.; Gianluca, I. An Aerodynamic Investigation of an Isolated Rotating Formula 1 Wheel Assembly. J. Fluids Eng. 2012, 134, 121101. [Google Scholar]
- Qin, P.; Ricci, A.; Blocken, B. CFD simulation of aerodynamic forces on the DrivAer car model: Impact of computational parameters. J. Wind Eng. Ind. Aerodyn. 2024, 248, 105711. [Google Scholar] [CrossRef]
- Josefsson, E.; Hobeika, T.; Sebben, S.; Urquhart, M. Investigation of Tyre Pattern Effect on the Aerodynamics of a Passenger Vehicle. ASME J. Fluids Eng. 2022, 144, 111209. [Google Scholar] [CrossRef]
- Baek, S.; Lee, S. Aerodynamic drag reduction on a realistic vehicle using continuous blowing. Microsyst. Technol. 2020, 26, 11–23. [Google Scholar] [CrossRef]
- Lin, S.; Huang, C. An integrated experimental and numerical study of forward-curved centrifugal fan. Exp. Therm. Fluid Sci. 2002, 26, 421–434. [Google Scholar] [CrossRef]
- Fackrell, J.; Harvey, J. The Aerodynamics of an Isolated Road Wheel. In Proceedings of the Second AIAA Symposium of Aerodynamics of Sports and Competition Automobiles, Los Angeles, CA, USA, 11 May 1975. [Google Scholar]
- Jan, R.; Haag, L.; Indinger, T. CFD investigation on fully detailed and deformed car tires. Int. J. Automot. Eng. 2019, 10, 324–331. [Google Scholar]
- Nakata, A.; Okamoto, S.; Morikawa, Y.; Nakashima, T. Effects of detailed tire geometry and wheel rotation on the aerodynamic performance of deflectors. Int. J. Automot. Eng. 2023, 14, 84–91. [Google Scholar] [CrossRef] [PubMed]






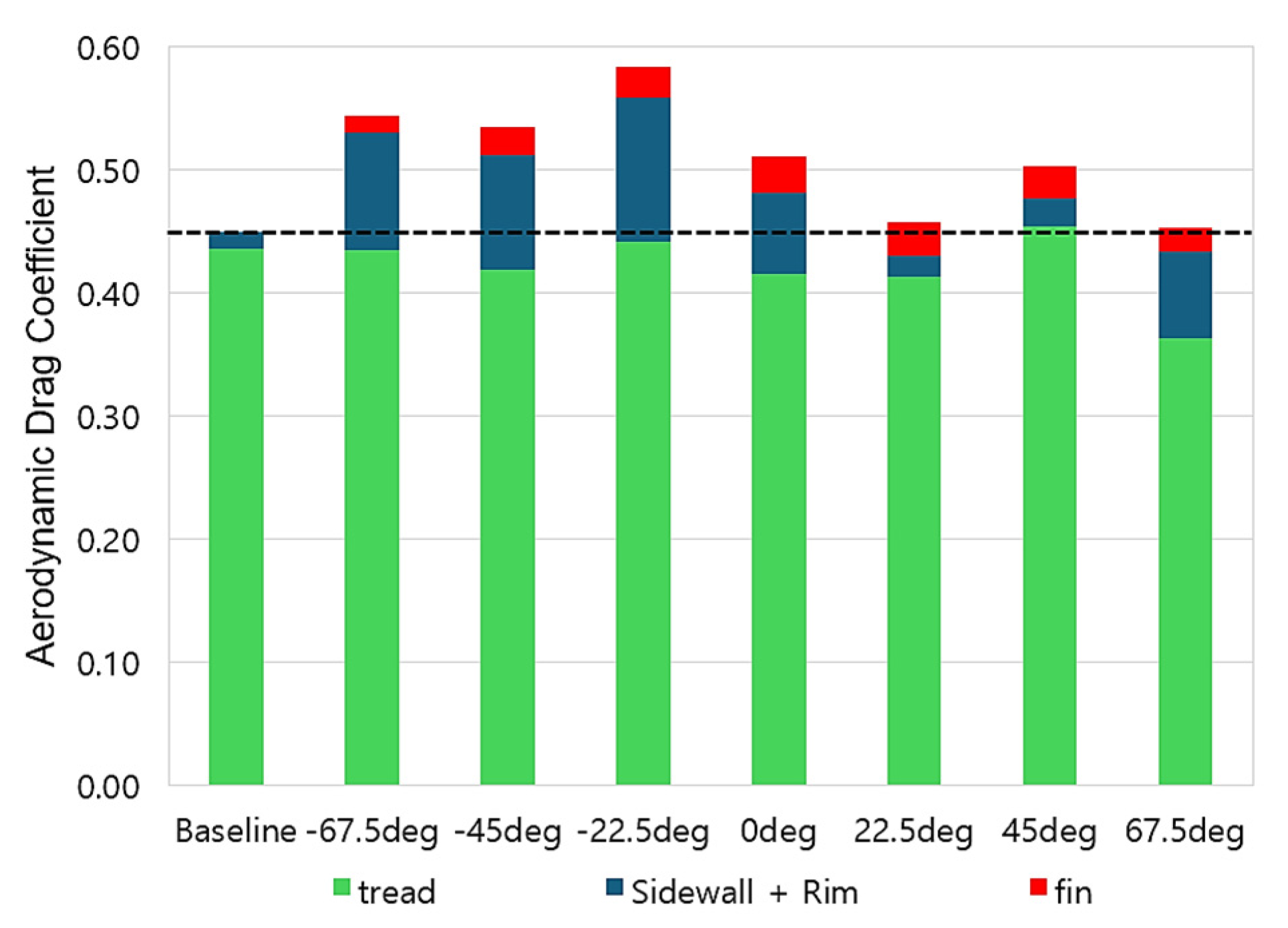

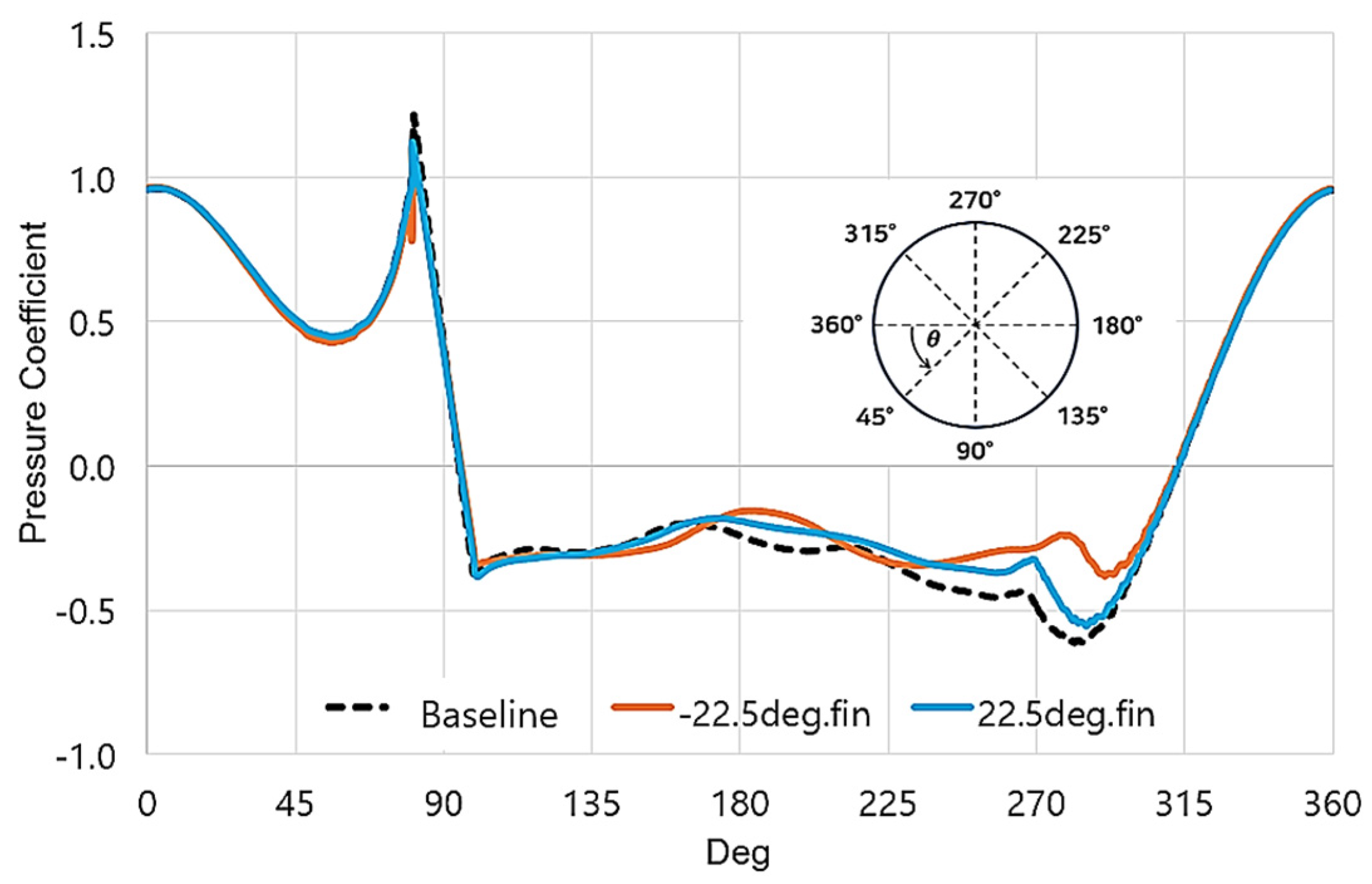

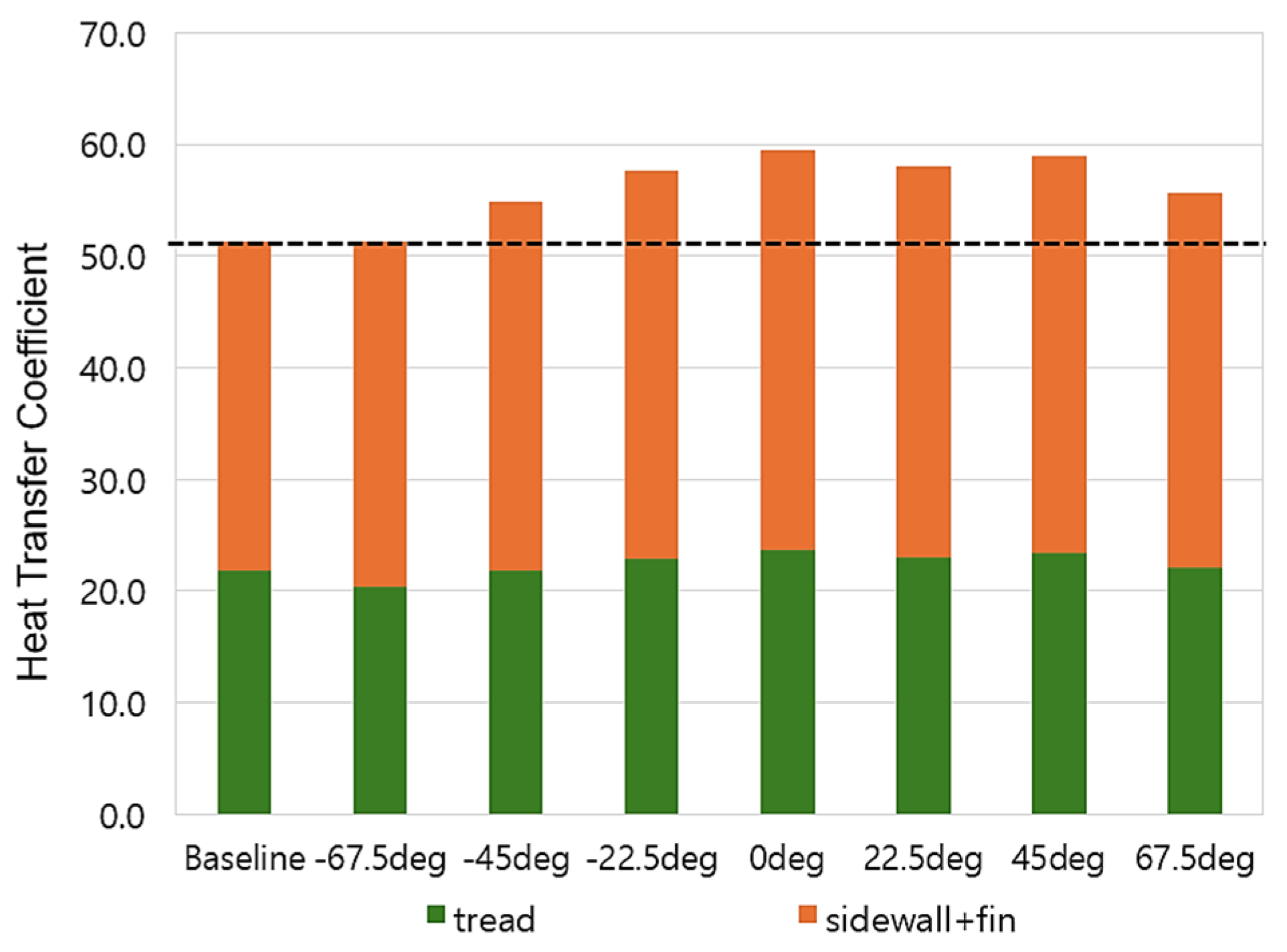
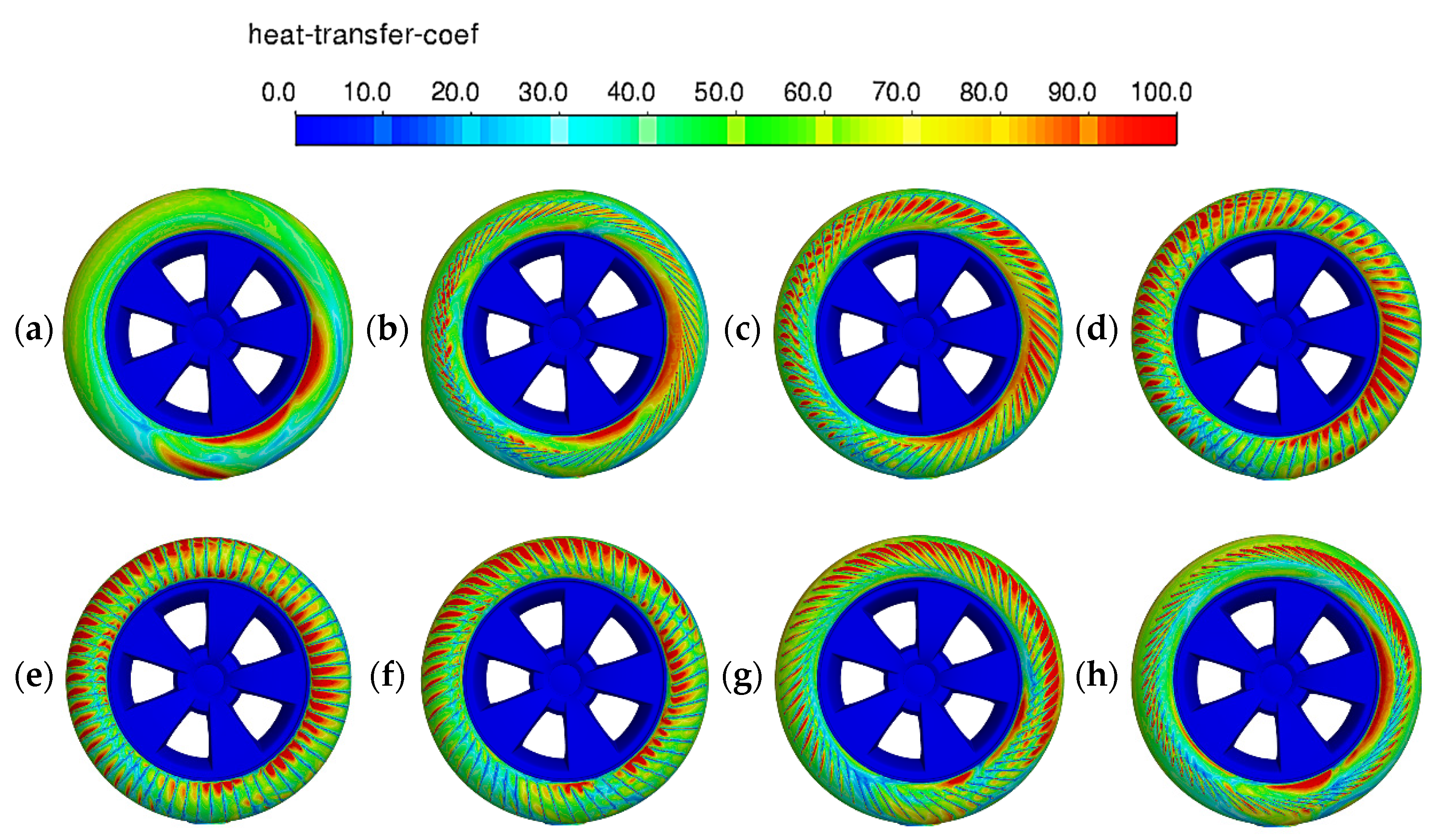
| Fin Angle | ∆ Drag Coefficient | ∆ Average HTC |
|---|---|---|
| −67.5 deg | 3.05% | 4.26% |
| −45.0 deg | −2.92% | 9.27% |
| −22.5 deg | 3.33% | 3.15% |
| 0.0 deg | 11.82% | 16.76% |
| 22.5 deg | 16.23% | 16.67% |
| 45.0 deg | 2.70% | 16.77% |
| 67.5 deg | 2.80% | 8.60% |
| Fin Angle | ∆ Drag Coefficient | ∆ Average HTC |
|---|---|---|
| −67.5 deg | 20.98% | −0.09% |
| −45.0 deg | 18.91% | 6.93% |
| −22.5 deg | 29.93% | 8.29% |
| 0.0 deg | 13.50% | 15.94% |
| 22.5 deg | 1.74% | 13.07% |
| 45.0 deg | 11.83% | 14.83% |
| 67.5 deg | 21.84% | 8.27% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yu, K.; Lee, S. Numerical Study on the Influence of Cooling-Fin Geometry on the Aero-Thermal Behavior of a Rotating Tire. Energies 2025, 18, 3133. https://doi.org/10.3390/en18123133
Yu K, Lee S. Numerical Study on the Influence of Cooling-Fin Geometry on the Aero-Thermal Behavior of a Rotating Tire. Energies. 2025; 18(12):3133. https://doi.org/10.3390/en18123133
Chicago/Turabian StyleYu, Kyoungmi, and SangWook Lee. 2025. "Numerical Study on the Influence of Cooling-Fin Geometry on the Aero-Thermal Behavior of a Rotating Tire" Energies 18, no. 12: 3133. https://doi.org/10.3390/en18123133
APA StyleYu, K., & Lee, S. (2025). Numerical Study on the Influence of Cooling-Fin Geometry on the Aero-Thermal Behavior of a Rotating Tire. Energies, 18(12), 3133. https://doi.org/10.3390/en18123133





