Comprehensive Evaluation of Cogeneration Biogas Multiple Supply System for Rural Communities in Northwest China
Abstract
1. Introduction
2. Materials and Methods
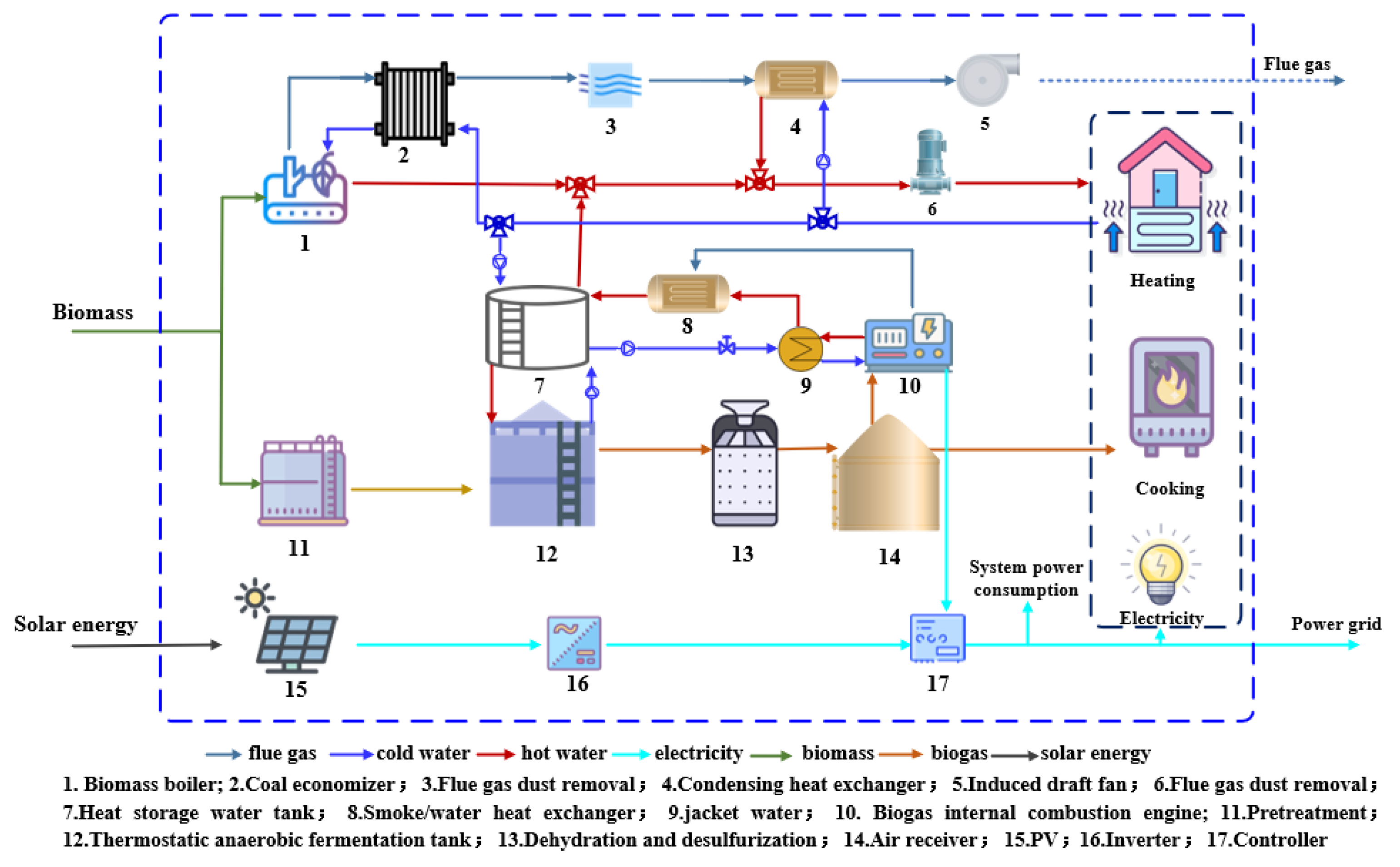
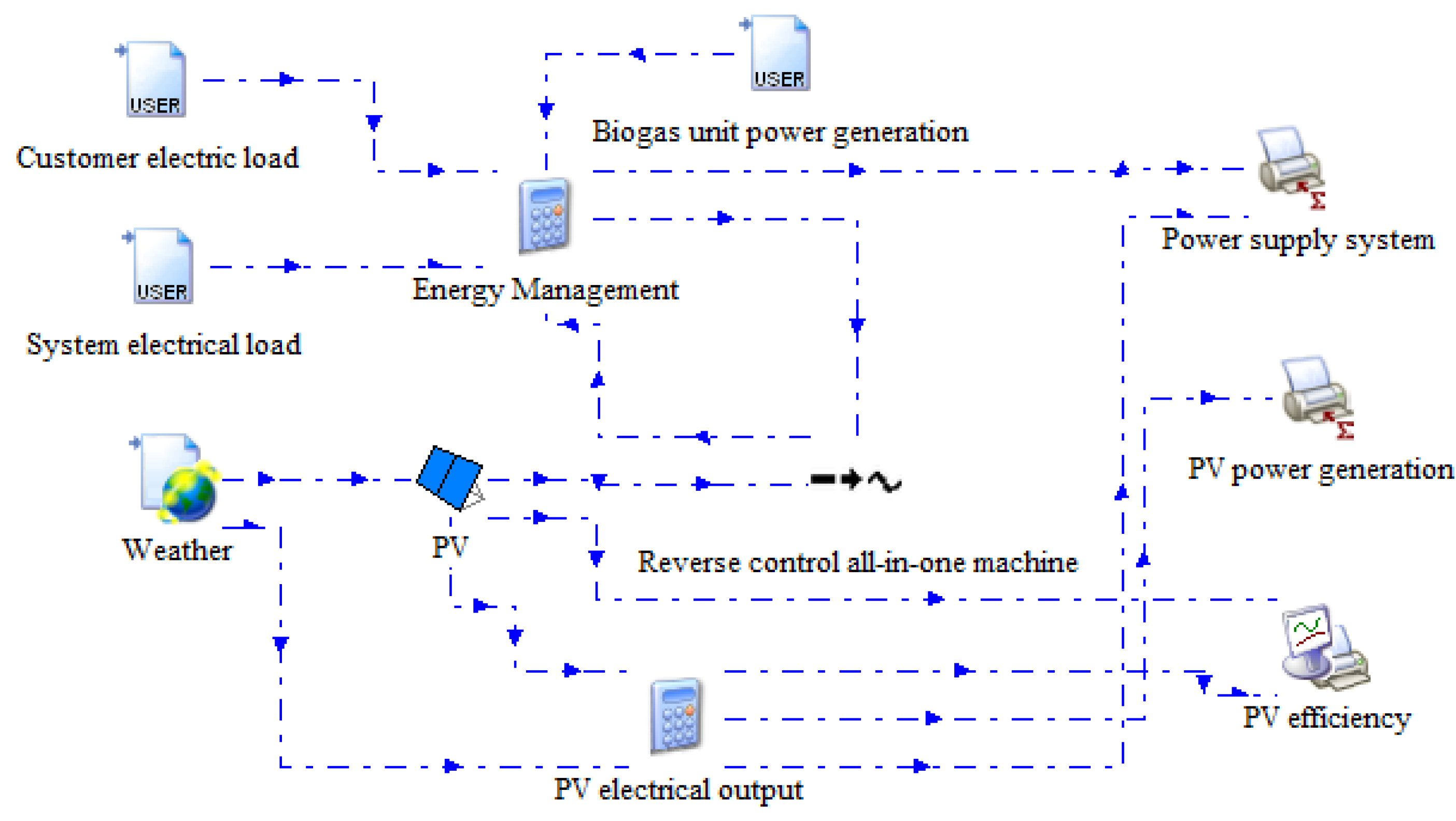
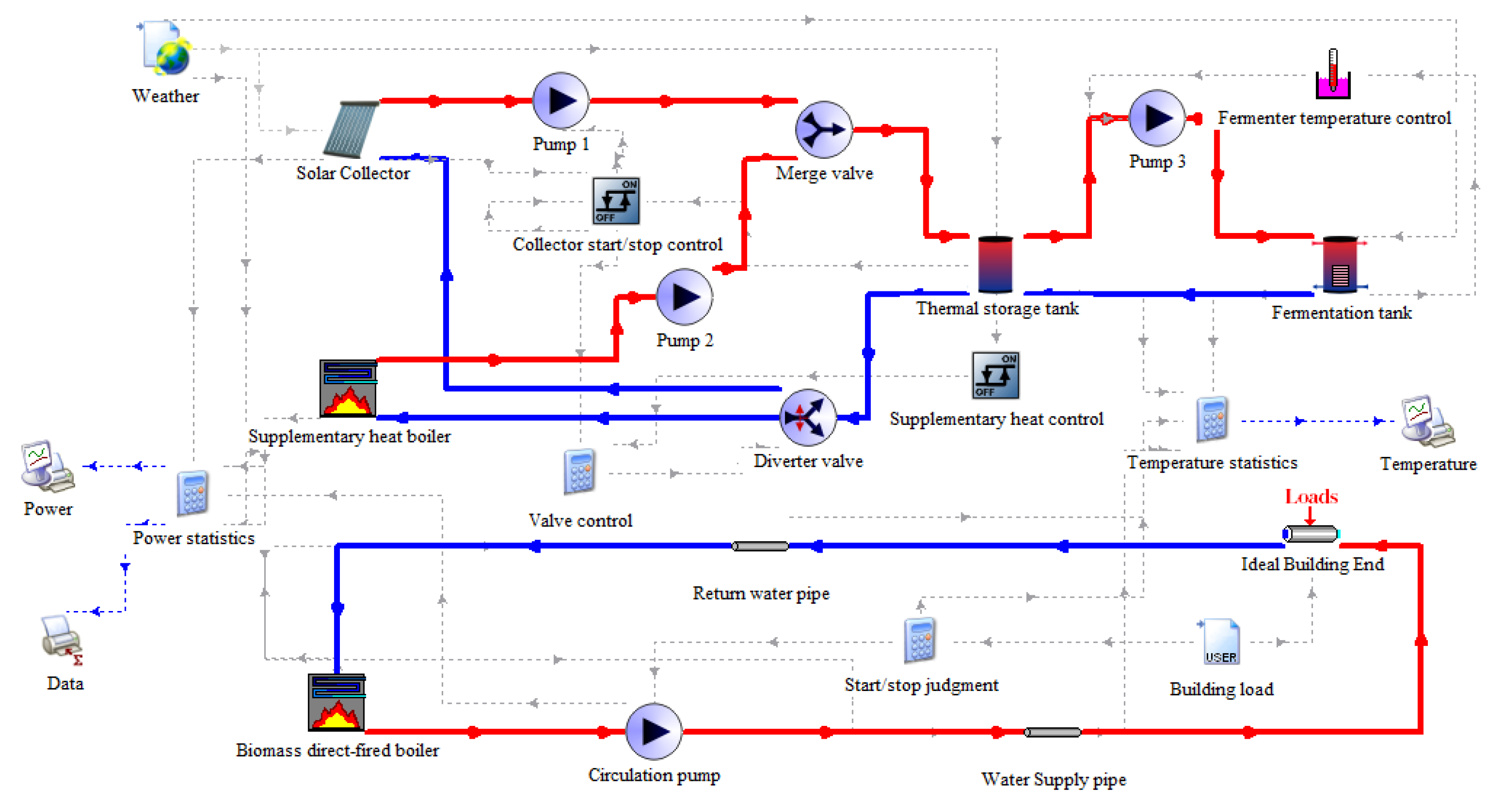
2.1. System Description
2.2. Mathematical Model of the Main Equipment in the System
2.2.1. Constant Temperature Anaerobic Reactor
2.2.2. Biomass Direct-Fired Boilers
2.2.3. Biogas Internal Combustion Generator Sets
2.2.4. PV Power Generation Module
2.2.5. Thermal Storage Tank
2.2.6. Condensing Heat Exchanger
2.3. System Evaluation
2.3.1. Energy Evaluation
2.3.2. Environmentality Evaluation
2.3.3. Economic Evaluation
3. System Model Establishment
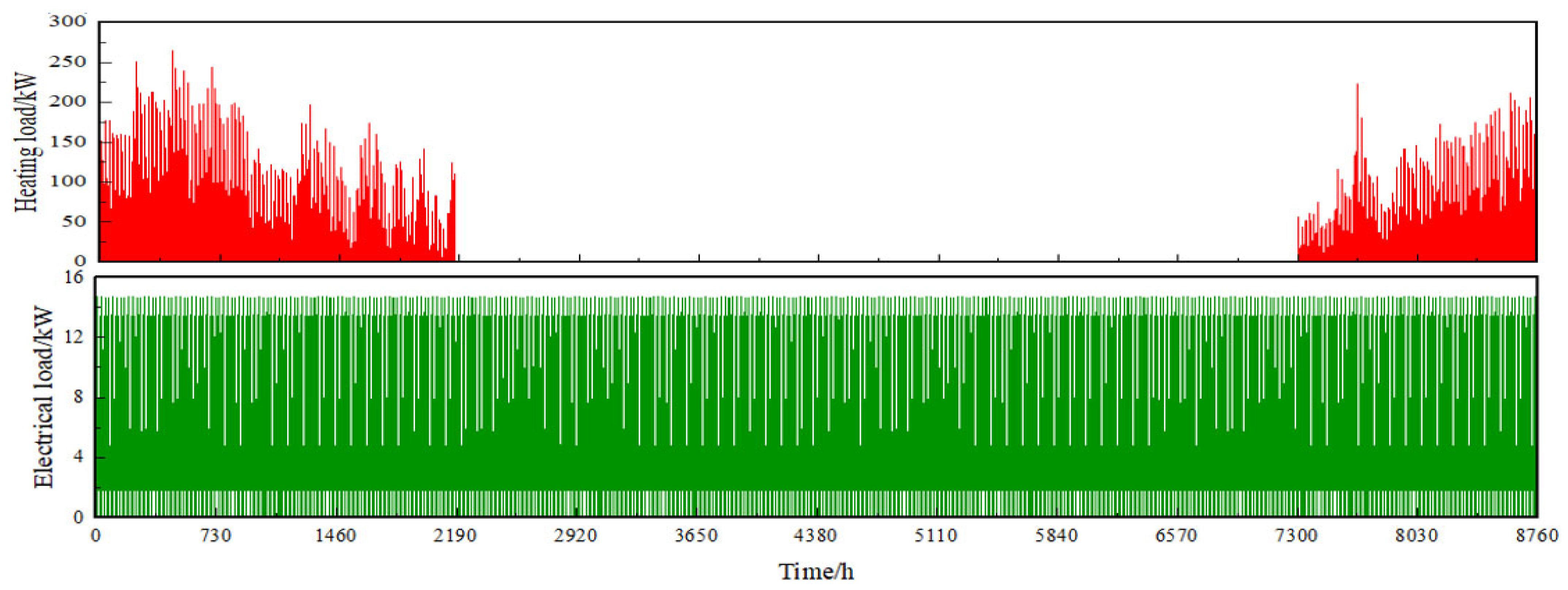
3.1. Thermoelectric Load Calculation
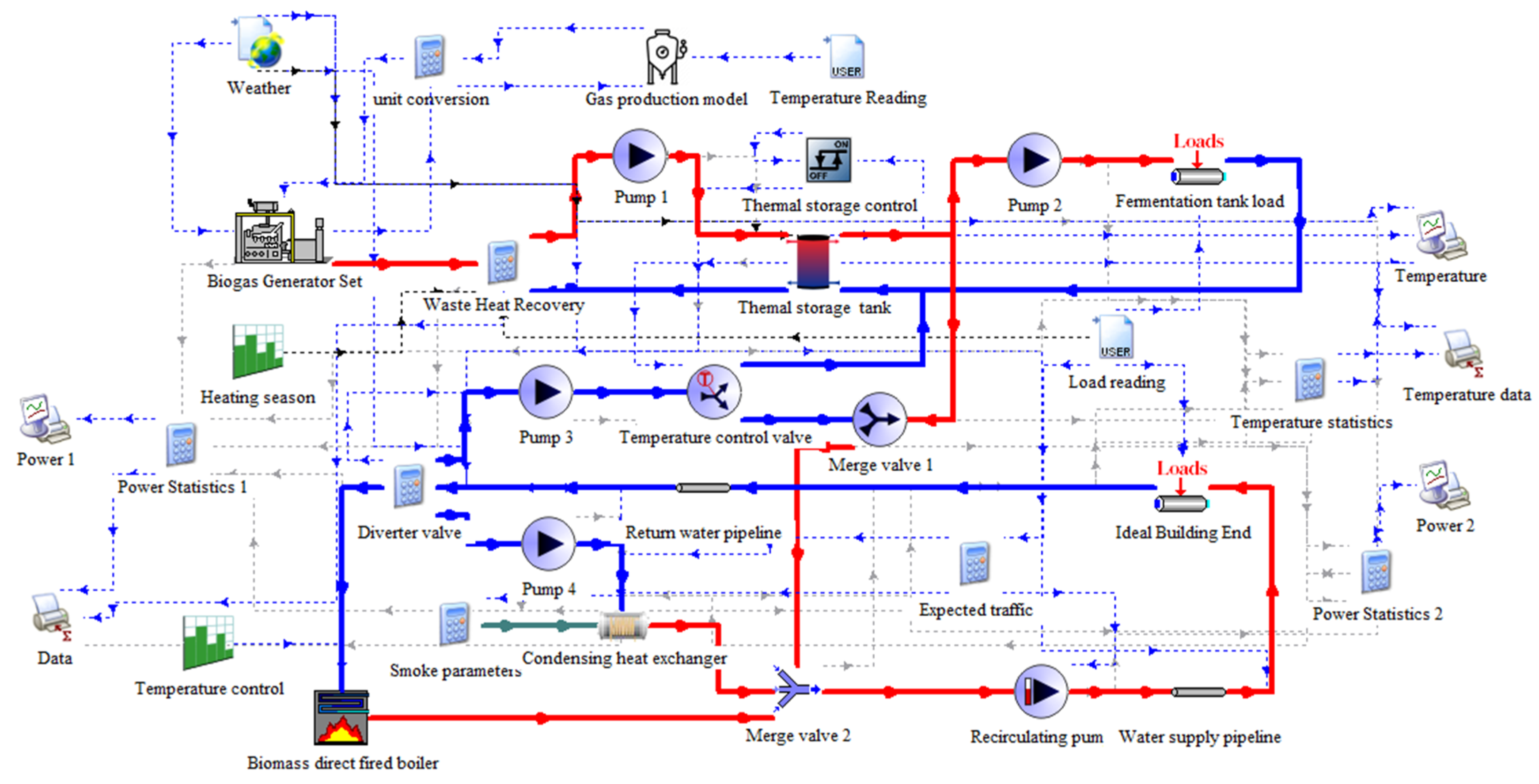
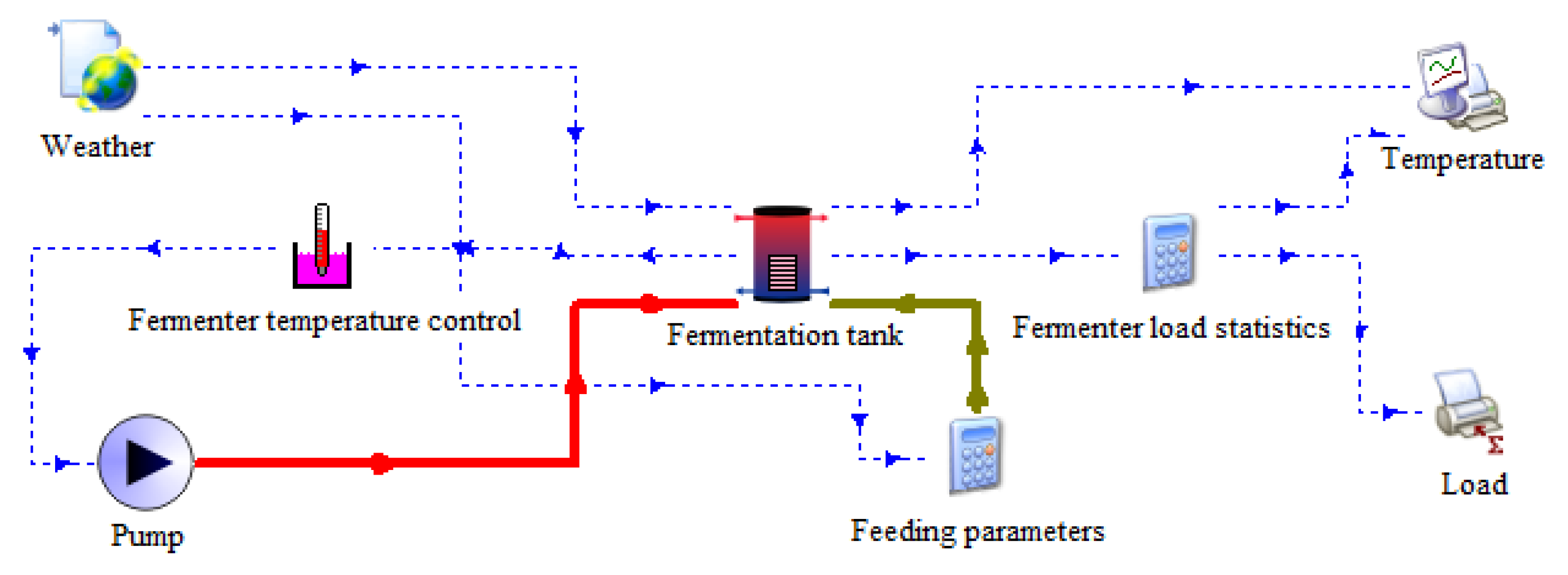
3.2. TRNSYS Simulation Modeling
3.3. System Control Method
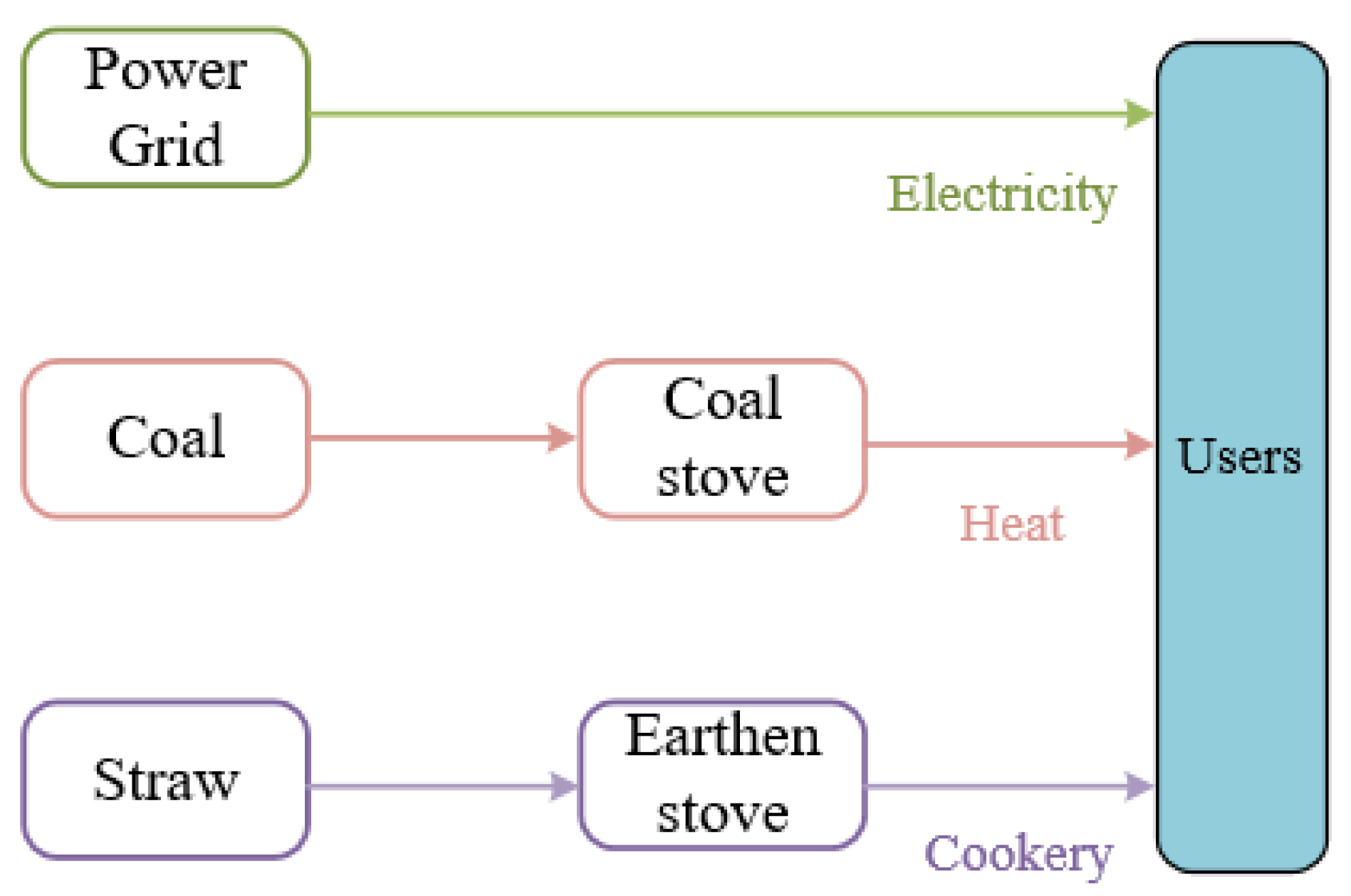
3.4. Original Energy Supply System Model
4. Results and Discussion
4.1. Typical Day System Performance
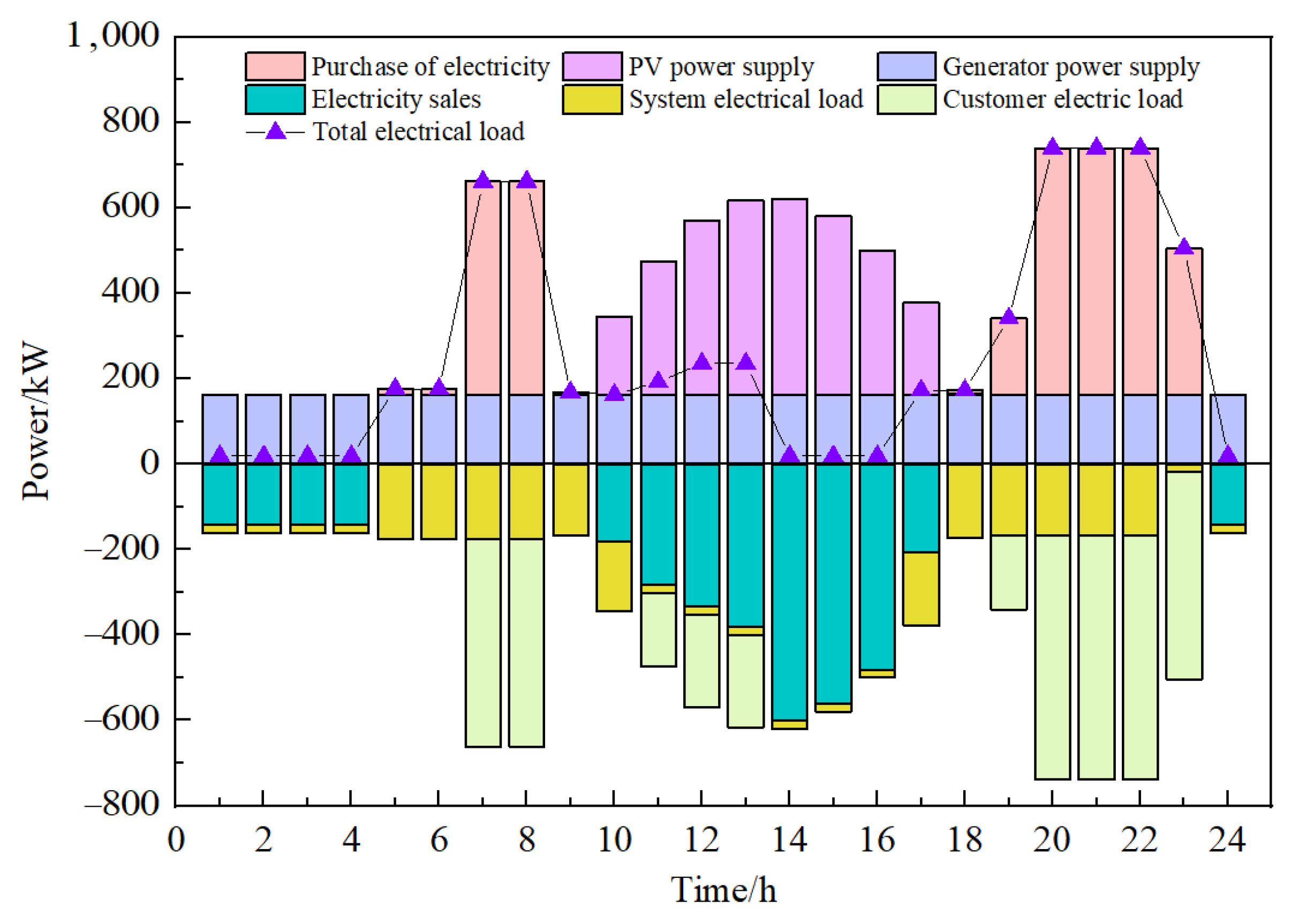
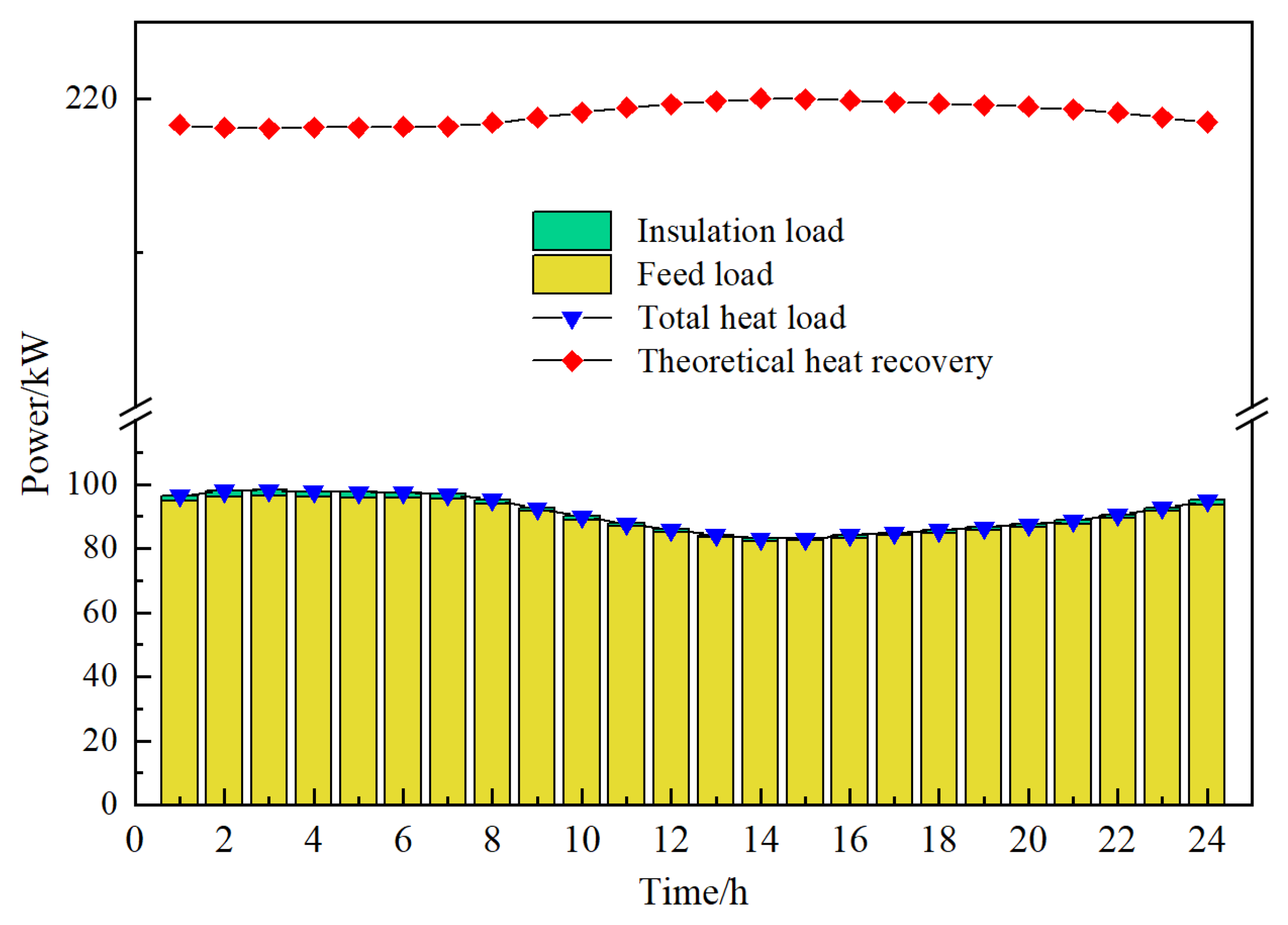
4.1.1. Typical Day During the Heating Season
4.1.2. Typical Day During the Non-Heating Season
4.2. Benefit Analysis
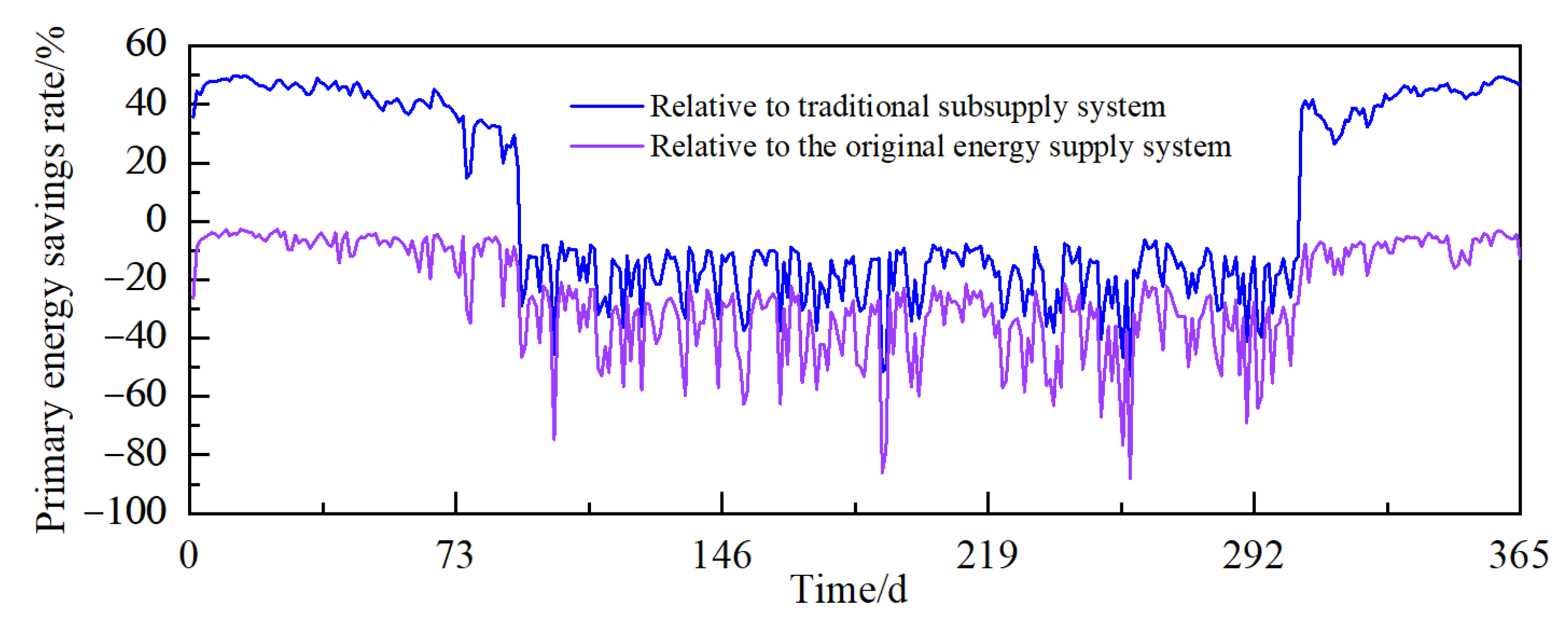
4.2.1. Energy Analysis of the System
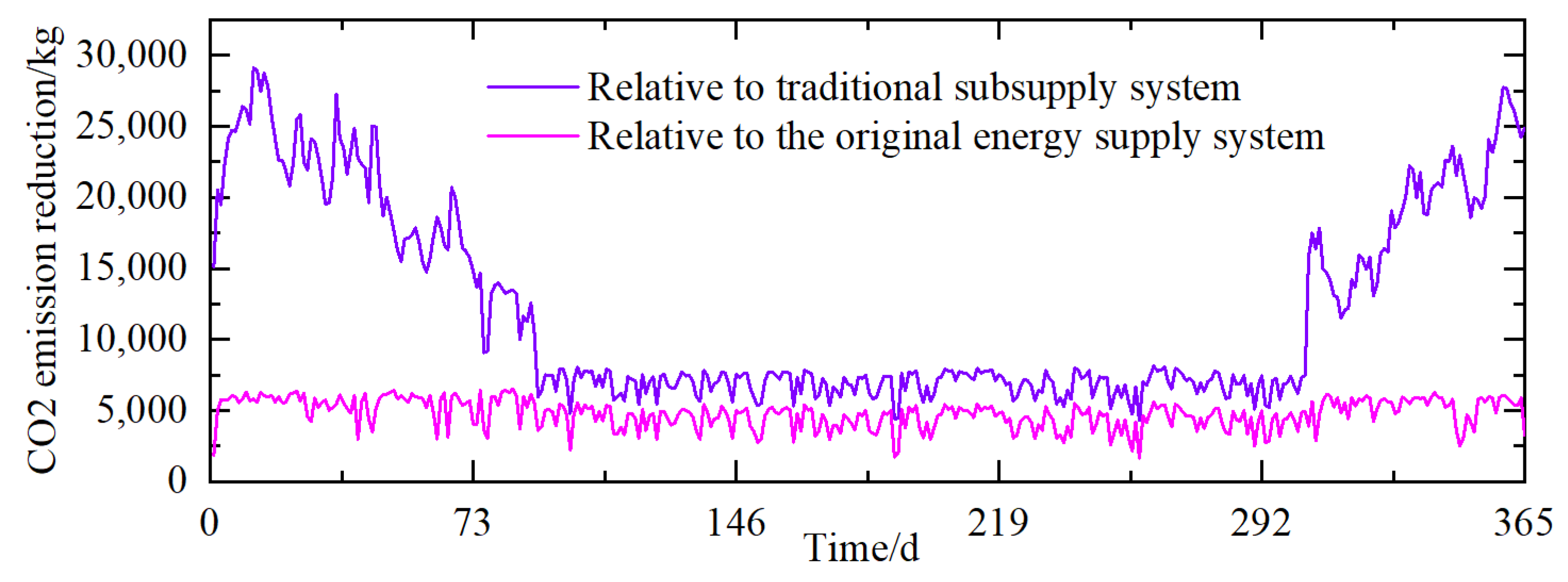
4.2.2. Environmental Benefits of the System
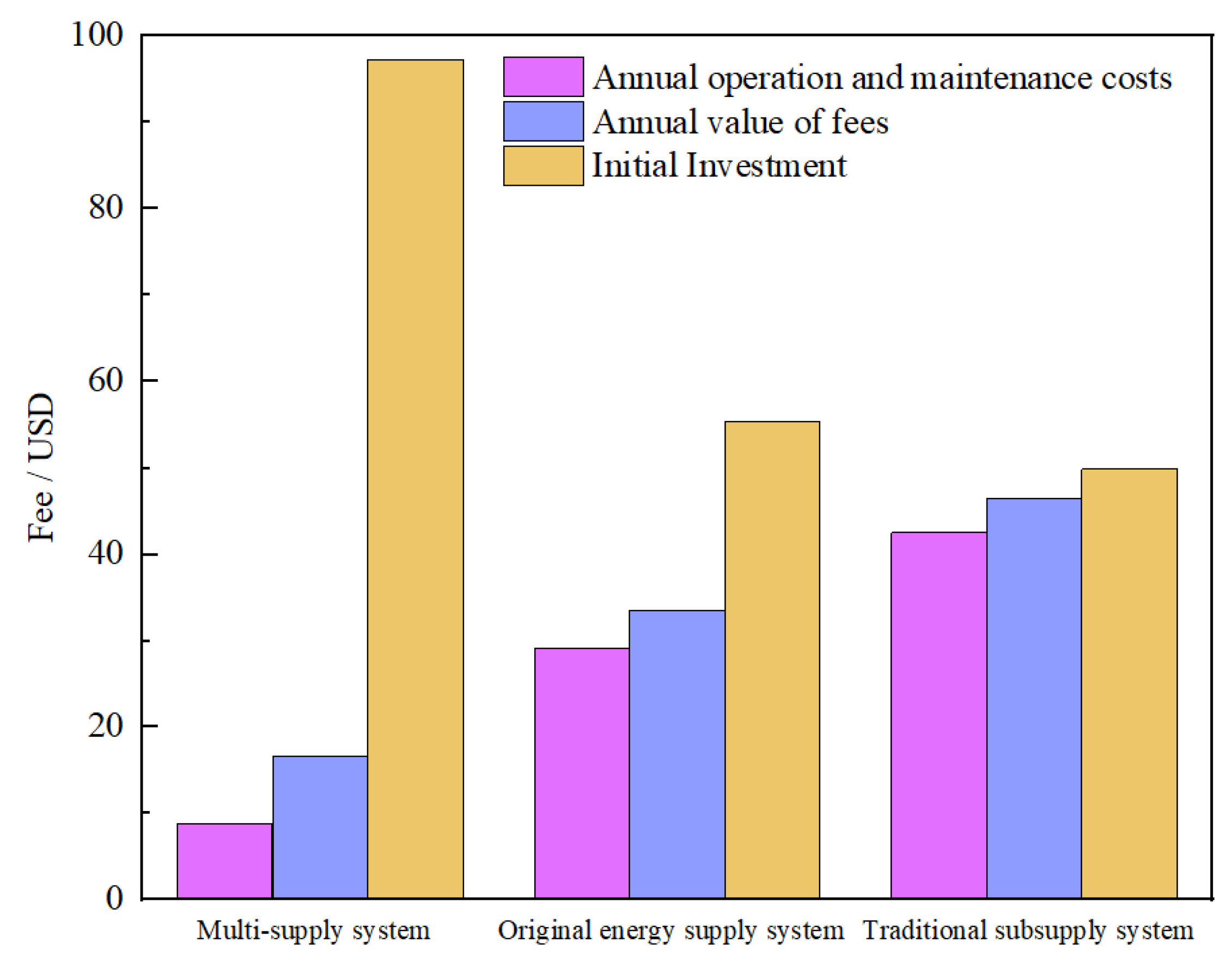
4.2.3. Economic Analysis of the System
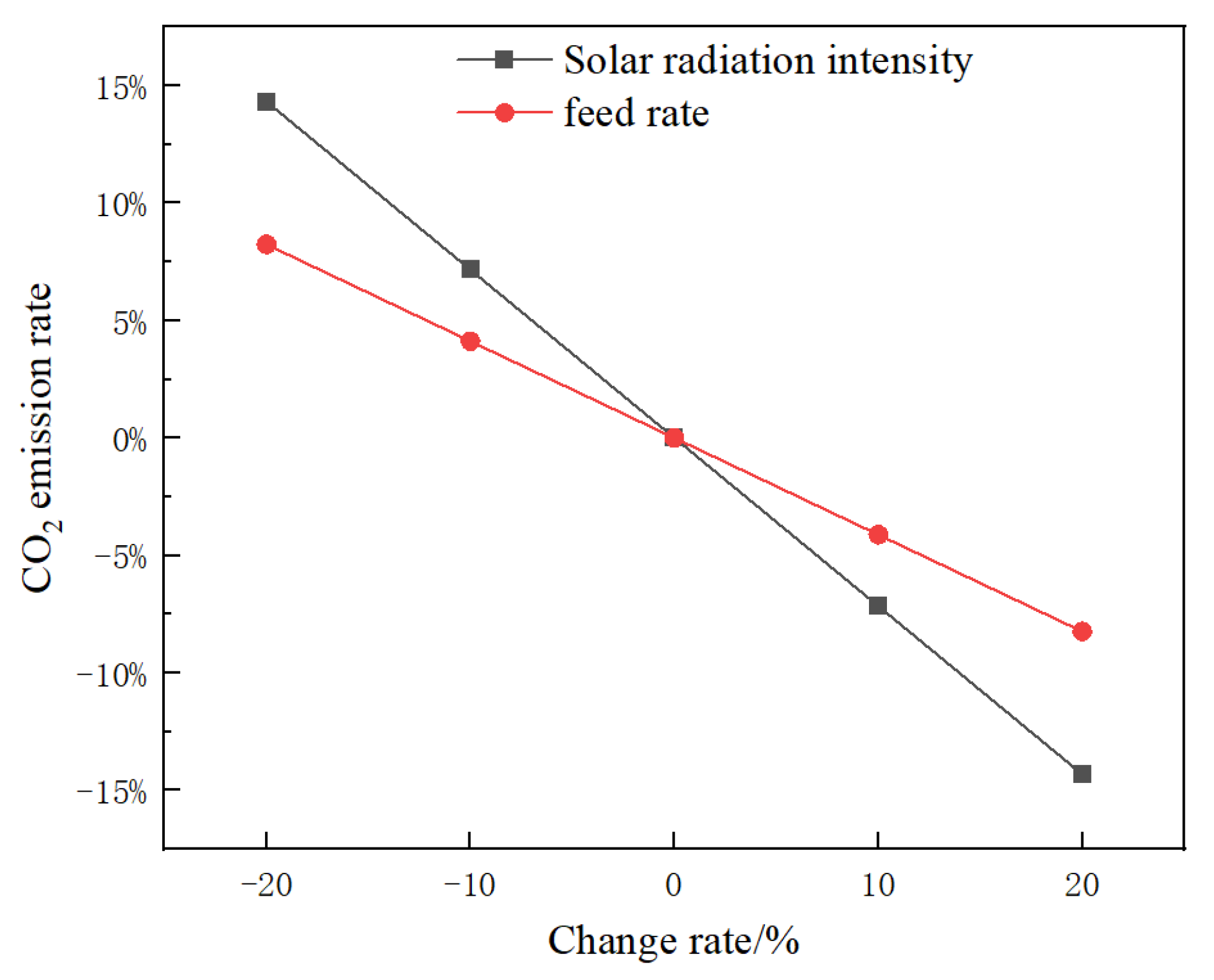
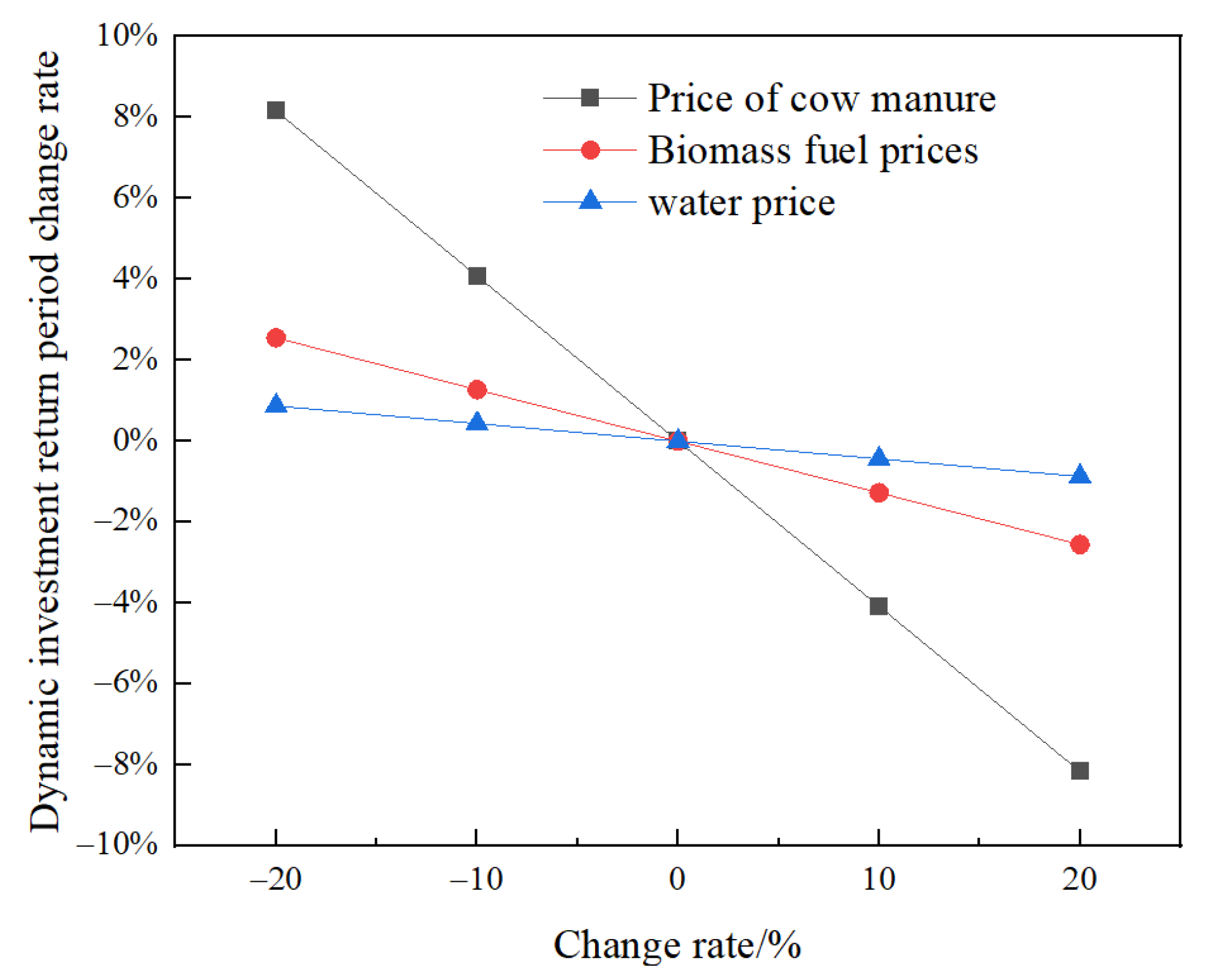
4.3. Sensitivity Analysis
5. Conclusions
- (1)
- During the heating season, the average primary energy utilization rate of multi-generation systems is 58.60%. Compared with traditional distribution systems and primary energy supply systems, the average primary energy saving of multi-generation systems is 41.52% and −9.87%, respectively.
- (2)
- The total CO2 emissions from the multi-generation system is 2,432,387.20 kg. Compared with the primary energy supply system and the traditional secondary supply system, the total CO2 emissions reduction of the multi-generation system is 1,742,264.91 kg and 4,409,442.88 kg, respectively, with an average daily CO2 reduction rate of 48.15% and 66.86%, respectively.
- (3)
- The initial investment in the multi-supply system is USD 973,100, the annual operating cost is USD 251,800, and the annual income is USD 594,400. Compared with the original energy supply system and the traditional subsupply system, the annual cost savings of the multi-supply system are 50.35% and 64.19%, respectively. Within the service life of the multi-generation system, the net present value is USD 3.2964 million, and the dynamic investment payback period is 3.14 years, which is economically feasible.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Li, S.; Zhang, L.; Su, L.; Nie, Q. Exploring the coupling coordination relationship between eco-environment and renewable energy development in rural areas: A case of China. Sci. Total Environ. 2023, 880, 163229. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.; Zhi, G.; Jin, W.; Xu, P.; Li, Z.; Kong, Y.; Zhang, H.; Shen, Y.; Hu, J. Identifying the fundamental drives behind the 10-year evolution of northern China’s rural household energy and emission: Implications for 2030 and beyond. Sci. Total Environ. 2023, 865, 161053. [Google Scholar] [CrossRef] [PubMed]
- Li, S.; Zhang, L.; Wang, X.; Zhu, C. A decision-making and planning optimization framework for multi-regional rural hybrid renewable energy system. Energy Convers. Manag. 2022, 273, 116402. [Google Scholar] [CrossRef]
- Wang, Y.; Song, M.; Jia, M.; Li, B.; Fei, H.; Zhang, Y.; Wang, X. Multi-objective distributionally robust optimization for hydrogen-involved total renewable energy CCHP planning under source-load uncertainties. Appl. Energy 2023, 342, 121212. [Google Scholar] [CrossRef]
- Zeng, L.; Xu, J.; Wu, M.; Tang, J.; Wu, Q.; Wang, Q.; Fan, G. Day-ahead interval optimization for CCHP system considering uncertainty of wind power and PV. Int. J. Electr. Power Energy Syst. 2022, 138, 107895. [Google Scholar] [CrossRef]
- Yan, R.; Wang, J.; Wang, J.; Tian, L.; Tang, S.; Wang, Y.; Zhang, J.; Cheng, Y.; Li, Y. A two-stage stochastic-robust optimization for a hybrid renewable energy CCHP system considering multiple scenario-interval uncertainties. Energy 2022, 247, 123498. [Google Scholar] [CrossRef]
- Stanek, W.; Gazda, W.; Kostowski, W. Thermo-ecological assessment of CCHP (combined cold-heat-and-power) plant supported with renewable energy. Energy 2015, 92, 279–289. [Google Scholar] [CrossRef]
- Deymi-Dashtebayaz, M.; Norani, M. Sustainability assessment and emergy analysis of employing the CCHP system under two different scenarios in a data center. Renew. Sustain. Energy Rev. 2021, 150, 111511. [Google Scholar] [CrossRef]
- Xu, X.; Zhang, Z.; Yuan, J.; Shao, J. Design and multi-objective comprehensive evaluation analysis of PV-WT-BG-Battery hybrid renewable energy systems in urban communities. Energy Convers. Manag. X 2023, 18, 100357. [Google Scholar] [CrossRef]
- Li, J.; Xu, W.; Feng, X.; Lu, H.; Qiao, B.; Gu, W.; Zhang, G.; Jiao, Y. Comprehensive evaluation system for optimal configuration of multi-energy systems. Energy Build. 2021, 252, 111367. [Google Scholar] [CrossRef]
- Chen, X.; Long, S.; Wang, C.; Chai, F.; Li, L.; Duan, P.; Li, S.; Wan, Z.; Qu, Z. Comprehensive assessment on a hybrid PEMFC multi-generation system integrated with solar-assisted methane cracking. Int. J. Hydrogen Energy 2023, 48, 14025–14037. [Google Scholar] [CrossRef]
- Ren, H.; Quan, Z.; Wang, Z.; Wang, L.; Jing, H.; Zhao, Y. Performance simulation and analysis of a multi-energy complementary energy supply system for a novel BIPVT nearly zero energy building. Energy Convers. Manag. 2023, 282, 116879. [Google Scholar] [CrossRef]
- Zhao, X.; Gao, W.; Qian, F.; Li, Y.; Ushifusa, Y.; Yang, Z.; Yin, W.; Ge, J. Economic performance of multi-energy supply system in a zero-carbon house. Energy Build. 2020, 226, 110363. [Google Scholar] [CrossRef]
- Ge, Y.; Ma, Y.; Wang, Q.; Yang, Q.; Xing, L.; Ba, S. Techno-economic-environmental assessment and performance comparison of a building distributed multi-energy system under various operation strategies. Renew. Energy 2023, 204, 685–696. [Google Scholar] [CrossRef]
- Zhu, Y.; Shao, B.; Tong, Q.L.; Li, Y.X.; Yan, X.X.; Wu, N.; Du, T. Analysis of Carbon Reduction Strategy on Distributed Combined Cooling, Heating and Power (CCHP) Systems Design in Rural Area. IOP Conf. Ser. Earth Environ. Sci. 2018, 146, 012053. [Google Scholar] [CrossRef]
- Zhang, D.; Zhang, R.; Zheng, Y.; Zhang, B.; Jiang, Z.Y.; An, Z.J.; Bai, J.H. Carbon emission reduction analysis of CHP system driven by biogas based on emission factors. Energy Built Environ. 2022, 4, 576–588. [Google Scholar] [CrossRef]
- Zhang, D.; Zhang, B.; Zheng, Y.; Zhang, R.; Liu, P.F.; An, Z.J. Economic assessment and regional adaptability analysis of CCHP system coupled with biomass-gas based on year-round performance. Sustain. Energy Technol. Assess. 2021, 45, 101141. [Google Scholar] [CrossRef]
- Das, B.K.; Al-Abdeli, Y.M.; Kothapalli, G. Integrating renewables into stand-alone hybrid systems meeting electric, heating, and cooling loads: A case study. Renew. Energy 2021, 180, 1222–1236. [Google Scholar] [CrossRef]
- Yousefi, H.; Ghodusinejad, M.H.; Kasaeian, A. Multi-objective optimal component sizing of a hybrid ICE+ PV/T driven CCHP microgrid. Appl. Therm. Eng. 2017, 122, 126–138. [Google Scholar] [CrossRef]
- Yousefi, H.; Ghodusinejad, M.H.; Noorollahi, Y. GA/AHP-based optimal design of a hybrid CCHP system considering economy, energy and emission. Energy Build. 2017, 138, 309–317. [Google Scholar] [CrossRef]
- Al Moussawi, H.; Fardoun, F.; Louahlia, H. 4-E based optimal management of a SOFC-CCHP system model for residential applications. Energy Convers. Manag. 2017, 151, 607–629. [Google Scholar] [CrossRef]
- Song, X.; Liu, L.; Zhu, T.; Zhang, T.; Wu, Z. Comparative analysis on operation strategies of CCHP system with cool thermal storage for a data center. Appl. Therm. Eng. 2016, 108, 680–688. [Google Scholar] [CrossRef]
- Wang, X.; Xu, Y.; Fu, Z.; Guo, J.; Bao, Z.; Li, W.; Zhu, Y. A dynamic interactive optimization model of CCHP system involving demand-side and supply-side impacts of climate change. Part II: Application to a hospital in Shanghai, China. Energy Convers. Manag. 2022, 252, 115139. [Google Scholar] [CrossRef]
- Huang, Y.; Wang, Y.D.; Chen, H.; Zhang, X.; Mondol, J.; Shah, N.; Hewitt, N.J. Performance analysis of biofuel fired trigeneration systems with energy storage for remote households. Appl. Energy 2017, 186, 530–538. [Google Scholar] [CrossRef]
- Lombardo, W.; Sapienza, A.; Ottaviano, S.; Branchini, L.; De Pascale, A.; Vasta, S. A CCHP system based on ORC cogenerator and adsorption chiller experimental prototypes: Energy and economic analysis for NZEB applications. Appl. Therm. Eng. 2021, 183, 116119. [Google Scholar] [CrossRef]
- Zhang, D.; Zheng, Y.; Wu, J.; Li, B.; Li, J. Annual energy characteristics and thermodynamic evaluation of combined heating, power and biogas system in cold rural area of Northwest China. Energy 2020, 192, 116522. [Google Scholar] [CrossRef]
- Pal, A.; Bhattacharjee, S. Effectuation of biogas based hybrid energy system for cost-effective decentralized application in small rural community. Energy 2020, 203, 117819. [Google Scholar] [CrossRef]
- Wang, J.J.; Yang, Y. Energy, exergy and environmental analysis of a hybrid combined cooling heating and power system uti-lizing biomass and solar energy. Energy Convers. Manag. 2016, 124, 566–577. [Google Scholar] [CrossRef]
- Murugaperumal, K.; Raj, P.A.D.V. Feasibility design and techno-economic analysis of hybrid renewable energy system for rural electrification. Sol. Energy 2019, 188, 1068–1083. [Google Scholar] [CrossRef]
- Moaleman, A.; Kasaeian, A.; Aramesh, M.; Mahian, O.; Sahota, L.; Tiwari, G.N. Simulation of the performance of a solar concentrating photovoltaic-thermal collector, applied in a combined cooling heating and power generation system. Energy Convers. Manag. 2018, 160, 191–208. [Google Scholar] [CrossRef]
- Maqbool, U.; Tyagi, A.; Tyagi, V.V.; Kothari, R. Optimization of the renewable-energy-based micro-grid for rural electrification in northern region of India. Clean Technol. Environ. Policy 2020, 579–590. [Google Scholar] [CrossRef]
- Wang, L.; Lin, J.; Dong, H.; Wang, Y.; Zeng, M. Demand response comprehensive incentive mechanism-based multi-time scale optimization scheduling for park integrated energy system. Energy 2023, 270, 126893. [Google Scholar] [CrossRef]
- Nikitin, A.; Deymi-Dashtebayaz, M.; Baranov, I.V.; Sami, S.; Nikitina, V.; Abadi, M.K.; Rumiantceva, O. Energy, exergy, economic and environmental (4E) analysis using a renewable multi-generation system in a near-zero energy building with hot water and hydrogen storage systems. J. Energy Storage 2023, 62, 106794. [Google Scholar] [CrossRef]
- Mohsenipour, M.; Ebadollahi, M.; Rostamzadeh, H.; Amidpour, M. Design and evaluation of a solar-based trigeneration system for a nearly zero energy greenhouse in arid region. J. Clean. Prod. 2020, 254, 119990. [Google Scholar] [CrossRef]
- Ma, Z.; Dong, F.; Wang, J.; Zhou, Y.; Feng, Y. Optimal design of a novel hybrid renewable energy CCHP system considering long and short-term benefits. Renew. Energy 2023, 206, 72–85. [Google Scholar] [CrossRef]
- Li, J.; Liu, P.; Li, Z. Optimal design and techno-economic analysis of a solar-wind-biomass off-grid hybrid power system for remote rural electrification: A case study of west China. Energy 2020, 208, 118387. [Google Scholar] [CrossRef]
- Li, C.; Yang, H.; Shahidehpour, M.; Xu, Z.; Zhou, B.; Cao, Y.; Zeng, L. Optimal planning of islanded integrated energy system with solar-biogas energy supply. IEEE Trans. Sustain. Energy 2019, 11, 2437–2448. [Google Scholar] [CrossRef]
- Das, H.S.; Tan, C.W.; Yatim, A.H.M.; Lau, K.Y. Feasibility analysis of hybrid photovoltaic/battery/fuel cell energy system for an indigenous residence in East Malaysia. Renew. Sustain. Energy Rev. 2017, 76, 1332–1347. [Google Scholar] [CrossRef]
- Villarroel-Schneider, J.; Balderrama, S.; Sanchez, C.; Cardozo, E.; Malmquist, A.; Martin, A. Open-source model applied for techno-economic optimization of a hy-brid solar PV biogas-based polygeneration plant: The case of a dairy farmers’ association in central Bolivia. Energy Conver-Sion Manag. 2023, 291, 117223. [Google Scholar] [CrossRef]
- Hashimoto, A.G. Methane from cattle waste: Effects of temperature, hydraulic retention time, and influent substrate concentration on kinetic parameter (k). Biotechnol. Bioeng. 1982, 24, 2039–2052. [Google Scholar] [CrossRef]
- Chen, Y.R.; Hashimoto, A.G. Substrate utilization kinetic model for biological treatment process. Biotechnol. Bioeng. 1980, 22, 2081–2095. [Google Scholar] [CrossRef] [PubMed]
- Teng, J.; Wang, W.; Mu, X. A novel economic analyzing method for CCHP systems based on energy cascade utilization. Energy 2020, 207, 118227. [Google Scholar] [CrossRef]
- Li, N.; Zhao, X.; Shi, X.; Pei, Z.; Mu, H.; Taghizadeh-Hesary, F. Integrated energy systems with CCHP and hydrogen supply: A new outlet for curtailed wind power. Appl. Energy 2021, 303, 117619. [Google Scholar] [CrossRef]
- Wang, Z.; Cai, W.; Tao, H.; Wu, D.; Meng, J. Research on capacity and strategy optimization of combined cooling, heating and power systems with solar photovoltaic and multiple energy storage. Energy Convers. Manag. 2022, 268, 115965. [Google Scholar] [CrossRef]
- Klein, S. TRNSYS 17: A Transient System Simulation Program; University of Wisconsin: Madison, WI, USA, 2010. [Google Scholar]






| Equipment | Numerical Value | Unit |
|---|---|---|
| PV | 504.21 | kWp |
| Biogas generator set | 180 | kW |
| Condensing heat exchanger | 115 | m2 |
| Anaerobic fermenter | 2000 | m3 |
| Thermal storage tank | 34.28 | m3 |
| Biomass direct-fired boilers | 7 | MW |
| Circulation pumps | 375 | m3/h |
| Module | Name | Parameter | Number | Parameter | Number |
|---|---|---|---|---|---|
 | Meteorological data module | Surface inclination angle | 37.93° | ||
 | Biomass boiler | Customized heat | 7000 kW | Thermal efficiency | 85% |
| Combustion efficiency | 92% | ||||
 | Anaerobic fermentation tank | Fermentation tank capacity | 1000 m3 | Height | 10 m |
| Specific heat capacity of fermentation broth | 4.1667 kJ/(kg·k) | Feed quality flow rate | 1784.88 kg/h | ||
 | Biogas generator module | Installed capacity | 180 kW | Gas flow | 1300 kg/h |
| Inlet temperature of water on the cylinder liner | 86 °C | Cylinder liner water outlet temperature | 91.26 °C | ||
| Cylinder liner water flow rate | 15,000 kg/h, | Exhaust gas temperature | 100 °C. | ||
 | Heat storage water tank | Volume | 34.28 m3 | Height | 2 m |
| Heat loss coefficient | 2.5 kJ/(h·m2·K) | ||||
 | Anaerobic fermentation gas production module | TS | 10% | Dry cow manure gas production factor | 0.3 m3/(kg⸱TS) |
| HRT | 20 days | Temperature | 35 °C | ||
 | PV | Open-circuit voltage | 44.4 V | Short-circuit current | 8.64 A |
| Maximum power point voltage | 35.9 V | Maximum power point current | 8.08 A |
| Price | Symbols | Numerical Values | Unit |
|---|---|---|---|
| Anaerobic fermentation system | 333,600 | USD | |
| Biomass direct-fired boiler heating system | 221,371 | USD | |
| PV power generation system | 0.579 | USD/Wp | |
| Biogas cogeneration system | 614.29 | USD/kW | |
| Condensing heat exchanger | 114.29 | USD/m2 | |
| Thermal storage tank | 121.43 | USD/m3 | |
| Coal stove | 142.86 | USD/each | |
| Earthen stove | 285.71 | USD/each | |
| Dried cow dung | 0.043 | USD/kg | |
| Biomass fuel | 71.429 | USD/t | |
| Running water | 0.554 | USD/t | |
| Electricity grid | 0.079 | USD/kW·h | |
| Heating | 3.571 | USD/(m2·a) | |
| Gas supply | 0.257 | USD/m3 | |
| Slurry | 0.002 | USD/kg | |
| Residue | 0.034 | USD/kg | |
| Standard coal | 0.117 | USD/kg | |
| Straw | 0.040 | USD/kg |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, J.; Han, X. Comprehensive Evaluation of Cogeneration Biogas Multiple Supply System for Rural Communities in Northwest China. Energies 2025, 18, 3124. https://doi.org/10.3390/en18123124
Li J, Han X. Comprehensive Evaluation of Cogeneration Biogas Multiple Supply System for Rural Communities in Northwest China. Energies. 2025; 18(12):3124. https://doi.org/10.3390/en18123124
Chicago/Turabian StyleLi, Jinping, and Xiaotong Han. 2025. "Comprehensive Evaluation of Cogeneration Biogas Multiple Supply System for Rural Communities in Northwest China" Energies 18, no. 12: 3124. https://doi.org/10.3390/en18123124
APA StyleLi, J., & Han, X. (2025). Comprehensive Evaluation of Cogeneration Biogas Multiple Supply System for Rural Communities in Northwest China. Energies, 18(12), 3124. https://doi.org/10.3390/en18123124




