Abstract
To enhance the steam parameters of steam injection boilers during the thermal recovery of heavy oil while ensuring the safe and stable operation of boiler pipelines, this study conducted two-phase flow boiling numerical simulations in a horizontal heated tube with an inner diameter of 65 mm, using water and water vapor as working fluids. The analysis focused on the gas–liquid phase distribution, temperature profiles, near-wall fluid velocity, and pressure drop along both the axial and radial directions of the tube. Furthermore, the effects of heat flux density, mass flow rate, and inlet subcooling on these parameters were systematically investigated. The results reveal that higher heat fluxes intensify the velocity difference between the upper and lower tube walls and enlarge the temperature gradient across the wall surface. A reduction in mass flow rate increases the gas phase fraction within the tube and causes the occurrence of identical flow patterns at earlier axial positions. Additionally, the onset of nucleate boiling shifts upstream, accompanied by an increase and upstream movement of the wall’s maximum temperature. An increase in inlet subcooling prolongs the time required for the working fluid mixture to reach saturation, thereby decreasing the gas phase fraction and delaying the appearance of the same flow patterns. Finally, preventive and control strategies for ensuring the safe operation of steam injection boiler pipelines during heavy oil recovery are proposed from the perspective of flow pattern regulation.
1. Introduction
Heavy oil reservoirs constitute a significant portion of global oil reserves [1]. The annual production of heavy oil is steadily increasing worldwide, while traditional cold water flooding methods are no longer effective in achieving satisfactory recovery rates in these fields [2,3]. Consequently, thermal recovery methods are required to enhance the fluidity and recovery of heavy oil. As the development of heavy oil reservoirs progresses, conventional methods, such as injecting wet saturated steam with typical dryness levels, are no longer sufficient, particularly in the later stages of extraction [4,5]. For the same volume of steam injection, achieving higher steam dryness at the outlet of the steam injection boiler is both advantageous and essential for improving oil recovery efficiency [6]. However, this process poses challenges, such as the deterioration of flow boiling heat transfer in horizontal tubes, which can lead to safety risks, including tube wall overheating [7,8]. In addition, in steam injection boilers, the horizontal tube section serves as a critical heating surface. As it is part of the furnace’s radiant heating zone, the working fluid in this section absorbs approximately 60% of the total heat input. Therefore, investigating the boiling heat transfer characteristics of water–steam two-phase flow in horizontal tubes is of great practical importance for ensuring boiler safety and enhancing oil recovery efficiency.
So far, a large number of experimental studies have been carried out on two-phase flow and heat transfer characteristics in horizontal tubes [9,10,11,12]. Yin et al. [13] experimentally investigated the flow patterns of boiling water in a horizontally heated tube and developed a flow regime map to predict the corresponding flow behavior. Loh et al. [14] experimentally investigated the effect of pressure on the transition of gas–liquid flow from stratified to droplet flow in a 108.2 mm horizontal pipe. Vuong et al. [15] conducted experimental investigations using a high-pressure apparatus with an inner diameter of 152.4 mm to evaluate the effects of high operating pressure and surface velocity on droplet entrainment in horizontal oil–gas two-phase flow under low liquid loading conditions. Kong et al. [16] experimentally investigated various flow structures and transition mechanisms in horizontal gas–water two-phase flow through a pipe with an inner diameter of 101.6 mm. However, experimental studies may be limited by factors such as the environment, equipment, and other constraints. Experimental visualization techniques exhibit constrained spatial coverage, restricting comprehensive documentation of bubble dynamics and evolutionary flow patterns within two-phase systems. A growing cohort of investigators is employing computational fluid dynamics (CFD) to probe flow boiling phenomena, aiming to unravel the inherent mechanisms governing fluid dynamics and thermal transfer processes [17,18,19,20]. Some studies have achieved accurate simulations of pool boiling, with particular emphasis on film boiling [21,22]. Liu et al. [23] developed a CFD model capable of predicting heat flux during the film boiling stage. Ahammad et al. [24] conducted CFD simulations of low-temperature film boiling, which, when combined with a first-principles model, can be used to estimate the wall heat flux. Some studies have also improved CFD models for subcooled boiling in flow boiling conditions [25,26,27]. Typically, refrigerants are used as working fluids in these studies, with common examples including R1234ze(E)/R152a [28,29], R141B [30], R417A, and R410A [31].
Additionally, some researchers have begun conducting numerical simulations of gas–liquid two-phase flow in horizontal pipes. Ghorai et al. [32] conducted a numerical simulation of gas–liquid two-phase flow with low liquid content in a horizontal pipe using CFD methods. The study investigated the liquid phase volume fraction, pressure gradient, and interfacial roughness and derived a relationship between the interfacial friction coefficient and the wall friction coefficient. Verdin et al. [33] employed a steady-state CFD simulation to examine the flow characteristics of low liquid content gas–liquid two-phase laminar flow in a horizontal pipe with a diameter of 965.2 mm. Their findings revealed that the liquid film is thicker at the bottom of the pipe, with the highest droplet concentration in this region. Secondary flow occurs when the roughness varies along the pipe wall’s perimeter, and the surface tension of the gas–liquid phase influences the entrainment rate. Pineda et al. [34] used the VOF model in FLUENT software to perform numerical simulations of gas–liquid two-phase flow in a horizontal pipe. The study analyzed the liquid holding rate, flow patterns, and wall shear stress for liquid viscosities ranging from 161 mPa·s to 567 mPa·s. The observed flow patterns included wave-stratified flow and segmented plug flow.
Currently, most studies on two-phase flow boiling have primarily focused on the pressure drop and average heat transfer coefficient, while relatively little attention has been given to simulating the evolution of flow patterns. Moreover, there is a lack of research on water-steam two-phase boiling heat transfer at high operating pressures in large-diameter horizontal tubes typical of heavy oil thermal recovery steam boilers. Under these conditions, key factors such as heat flux, mass flow rate, and inlet subcooling can have a significant impact on the heat transfer characteristics of gas–liquid two-phase flows. Research that systematically summarizes these influencing factors and provides recommendations for improving steam dryness while ensuring the safe and stable operation of steam injection boiler pipelines under heavy oil extraction conditions remains particularly scarce.
In this study, CFD simulations were conducted on the boiling two-phase flow of water and steam within a 65 mm horizontal tube of a heavy oil thermal recovery steam boiler. The flow field distribution characteristics of boiling flow inside the horizontal tube were comprehensively analyzed. In addition, the effects of heat flux density, mass flow rate, and inlet subcooling on key parameters such as gas–liquid volume distribution, temperature, and near-wall fluid velocity are systematically investigated. Finally, preventive and control measures for ensuring the safe operation of steam injection boiler pipelines during heavy oil extraction are proposed from the perspective of flow pattern regulation. This study provides an in-depth analysis of the two-phase boiling flow process, which could offer insights to support the stable operation of steam injection boilers under conditions of increased steam dryness.
2. Model Foundation
2.1. Geometric Model
In this study, the physical model was developed based on a representative segment of the water-cooled wall in a steam injection boiler, which was idealized as a horizontal smooth-walled tube, with a focus on investigating the internal flow boiling heat transfer processes of water within the tube. Constructed from 15 CrMo alloy, the tubular specimen features geometric parameters of 89 mm (outer)/65 mm (inner) diametral dimensions, extending to 30,000 mm longitudinally. Under the boiler’s rated operating conditions, the steam produced is wet steam at a pressure of 12.354 MPa. The physical properties of water under these conditions are presented in Table 1. The computational domain model was established using the pre-processing software ICEM CFD, as illustrated in Figure 1.

Table 1.
Physical parameters of water.
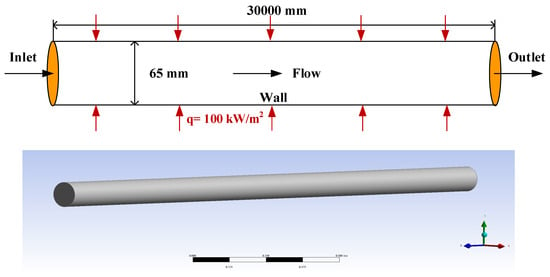
Figure 1.
Horizontal pipe geometry model and 3D model schematic drawing.
2.2. Numerical Method
The Volume of Fluid (VOF) model was selected as the multiphase flow model for the numerical simulations. The Lee formulation was implemented to quantify coupled thermal and material fluxes across phase boundaries. Surface tension was modeled as a volumetric force using the Continuum Surface Force (CSF) model. The Shear Stress Transport (SST) k-ω model was adopted for the turbulence calculations.
2.2.1. Multiphase Flow Model
In this study, the VOF model is selected as the multiphase flow model for numerical simulation. Tracing gas–liquid interfaces by the Geometric Reconstruction Scheme. The parameters are defined as constant physical properties for an incompressible Newtonian fluid, with viscous dissipation and minor source terms from volumetric forces being neglected. Consequently, for immiscible incompressible Newtonian fluids, the conservation equations for mass, momentum, and energy within the computational domain can be simplified and expressed as follows:
where is the density, kg m−1; denotes time, s; , , represent velocities in the , , and directions, m s−1.
where is the pressure on the fluid element, Pa; denotes the gravitational body force acting on the fluid element, m s−2; is the dynamic viscosity, kg m−1 s−1; represents the external body force that includes interfacial interaction forces, N m−3.
where represents the total energy of the fluid element, which is the sum of kinetic and internal energy, J; represents the effective thermal conductivity, W m−1 K−1; denotes the energy source term, J.
The VOF method employs a unified set of equations applicable to both gas and liquid phases across the entire fluid domain. Phase differentiation is achieved through a distinct volume fraction variable, α. The physical properties in these equations are typically determined using a volume fraction-weighted average approximation, as illustrated below:
where v and 1 represent the gas phase and the liquid phase, respectively.
2.2.2. Evaporation-Condensation Mechanism
Flow boiling is a complex thermofluidic phenomenon characterized by gas–liquid two-phase dynamics, involving simultaneous mass and energy transfer. The LEE model features a simple and easily implementable formulation. Its definition allows the source terms to be generated beyond the gas–liquid interface region (0 < α < 1), making it widely applicable in the numerical simulation of both boiling and condensation processes [35]. It is particularly suitable for modeling condensation and nucleate boiling flows with continuously generated dense vapor cores [30]. Therefore, the LEE model is employed in this study to compute the mass transfer source terms associated with phase change processes. The energy source term equation of the LEE model assumes that the fluid phase transition occurs in a constant-pressure, quasi-equilibrium environment, with the expression for the mass source term, m, given as follows:
where is the saturation temperature, K; represents the phase transition factor in the LEE model. In this study, is set to 1000 (dimensionless).
The energy source term Q is calculated based on the latent heat of vaporization h and the mass source term m:
In addition, in this paper, surface tension is modeled as a volumetric force based on the CSF model. The static contact angle model is applied, with the contact angle (θ) set to 106.6°. This study involves turbulent gas–liquid two-phase flow with phase change, for which the SST k-ω turbulence model is employed [36]. This model combines the original k-ω formulation in the near-wall region with the standard k-ε model in the outer boundary layer and free shear flow regions, making it suitable for the present investigation. The near-wall mesh design was informed by preliminary simulations to estimate the friction velocity under single-phase flow conditions. The first layer thickness was set to 0.01 mm to ensure that y+ remains below 1 along the entire heated wall, in accordance with the SST k-ω model’s requirement for resolving the viscous sublayer. A total of 14 inflation layers with a growth rate of 1.2 were employed to adequately capture the estimated thickness of the turbulent boundary layer. A velocity inlet is specified for the working fluid inlet, the horizontal pipe is modeled with a no-slip wall condition, and the pipe wall is set with a constant heat flux boundary condition. The outlet for the working fluid is modeled with a pressure outlet boundary condition.
2.3. Model Setup and Grid Independence Verification
2.3.1. Boundary Condition
The inlet boundary condition is specified as a velocity inlet, with a fully developed turbulent velocity profile imposed via a user-defined function (UDF). This approach ensures that the inlet flow conforms to the theoretical logarithmic law of the wall for turbulent flows. The pipe has a total length-to-diameter ratio of 461.5, which is substantially greater than the typical flow development length (approximately 20 times the pipe diameter). Therefore, the influence of inlet effects on the overall flow field is negligible. The flow direction is aligned with the length of the pipe, corresponding to the positive x-axis. Given the integrated thermal transfer mechanisms, the inflow thermal state requires precise definition through equilibrium parameters matching phase-change thresholds under modeled operational parameters.
For the outlet boundary condition, Outflow is initially used in the calculation. If backflow occurs during the simulation and persists in later stages, the boundary condition is switched to Pressure Outlet, with the backflow direction assumed to be perpendicular to the boundary. The Backflow Total Temperature is set to the saturation temperature.
For the wall boundary conditions, a constant heat flux is defined as the thermodynamic boundary condition, and the Wall Thickness is not considered. The wall material is 15CrMo steel, with its physical properties editable in FLUENT 2022R1. The wall is defined as a Stationary Wall, and the gas shear force on the gas–liquid interface is neglected. In shear-dominated flow regimes, the solid boundaries enforce no-slip conditions with surface roughness parameters configured as zero magnitude height and a standard 0.5 roughness coefficient. In addition, Standard Initialisation was used to select all zones to initialize the flow field.
For transient simulations, the time step size, number of time steps, and maximum number of inner iterations must be specified. In this study, the time step size is set to 0.0005 s, and the maximum number of inner iterations is set to 50. Convergence criteria for the residuals of all governing equations are also defined: the energy equation is assigned a residual tolerance of 10−6, while all other equations are set to 10−4, serving as part of the convergence criteria. In addition, parameters such as the gas volume fraction at the outlet section, average wall temperature, and outlet wall temperature are monitored throughout the simulation to determine whether a steady-state condition has been reached during the flow boiling process inside the tube.
Given the inherent intricacies of flow boiling mechanisms, the model is simplified to represent the actual boiling heat transfer within the tube. The following assumptions are made:
- (1)
- The fluid is treated as an incompressible Newtonian fluid and is considered a continuous medium.
- (2)
- Owing to limited fluctuations in the material properties of intratubular fluids under varying operational scenarios, the gas–liquid phase composite is hypothesized to maintain constant thermophysical parameters.
- (3)
- Based on the simulation conditions, the Reynolds number is calculated to be greater than 2300, indicating that the flow within the tube is fully developed turbulent flow.
- (4)
- The effect of non-condensable gases is neglected in the boiling heat transfer process.
- (5)
- The pipe wall is treated as a constant heat flux boundary condition.
2.3.2. Grid Independence Verification
O-grid block meshing is commonly used for geometries with curved structures (e.g., circles, spheres, cylinders). In this study, ICEM CFD is used to generate a structured O-grid mesh on the cylindrical channel of the geometric model. Additionally, significant velocity and temperature gradients exist in the near-wall region. To accurately capture the flow pattern changes in the boiling process of the mixed-phase flow in this region, a boundary layer mesh is applied. The mesh configuration for the smooth tube is shown in Figure 2.

Figure 2.
Round tube cross-section grid.
The values of pressure drop between each point and the inlet of the working fluid in the tube on the median axis are selected for grid-independence verification. As shown in Figure 3, increasing the number of grids from 1.02 million to 1.85 million yields consistent pressure drop trends along the tube. According to Table 2, when the relative error is calculated using the results of 1.85 million grids as the standard, the difference in pressure drop values is 1.24% when the grid is increased from 1.02 million to 1.85 million. Additionally, grid independence was further assessed for near-wall temperatures and cross-sectional average gas volume fractions. When the grid count was increased from 1.02 million to 1.85 million, the maximum deviation in the near-wall temperature on the upper wall occurred 7.5 m downstream of the inlet, with errors of 1.63% for the 1.02 million grid and 0.39% for the 1.51 million grids. For the lower wall, the largest deviation was observed at 9.2 m from the inlet, with corresponding errors of 1.88% and 0.41%, respectively. The maximum difference in the cross-sectional average gas volume fraction appeared at 8 m from the inlet, with errors of 1.29% for the 1.02 million grid and 0.28% for the 1.51 million grids. These results indicate that increasing the grid density no longer affects the simulation results. Considering the calculation accuracy and simulation time, 1.51 million grids are used for calculation in this study.
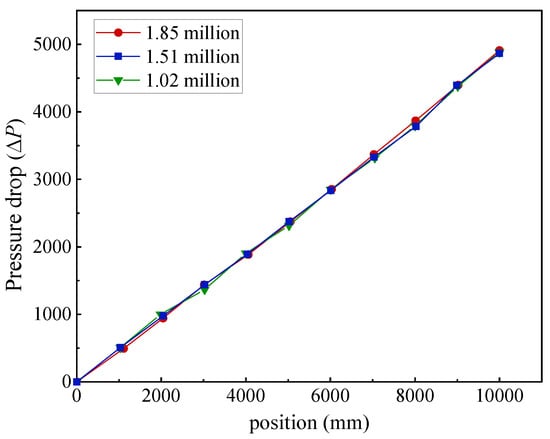
Figure 3.
Comparison of pressure drop variation with position under different mesh densities.

Table 2.
Relative error calculated using 1.85 million grid inlet and outlet pressure drops as the standard.
2.4. Model Validation
To assess the dependability and correctness of the numerical model presented in this study, simulations are conducted for the experimental conditions from a previous study [37] using the proposed computational methods. The two-phase flow boiling experiments in a horizontal tube were conducted in a tube with a hydraulic diameter of 5 mm and a heated length of 3 m. The inlet temperature was 92 °C, the inlet pressure was 4 bar, and the heat flux was 63.7 kW/m2. The outlet pressures ranged from 3.39 to 3.86 bar, while the outlet temperatures varied between 145.5 °C and 154.7 °C. Numerical simulations of flow boiling heat transfer were performed for different water flow rates within the tube. The simulated flow patterns, outlet temperatures, and pressures were validated against experimental measurements from previous studies, as shown in Figure 4, Figure 5 and Figure 6.

Figure 4.
Comparison of flow patterns between the numerical simulation results (upper panel) and the experimental results from a previous study (lower panel) for the horizontal pipe.
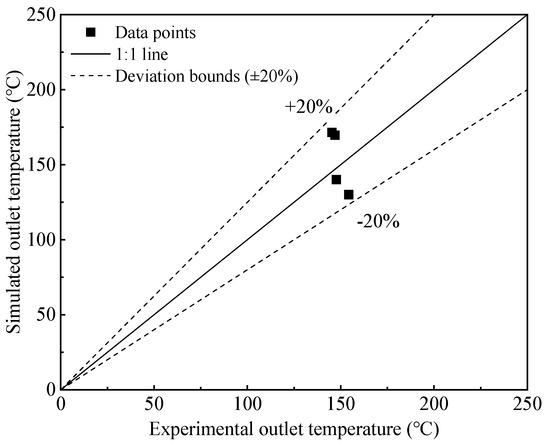
Figure 5.
Comparison of experimental and simulated outlet temperatures.
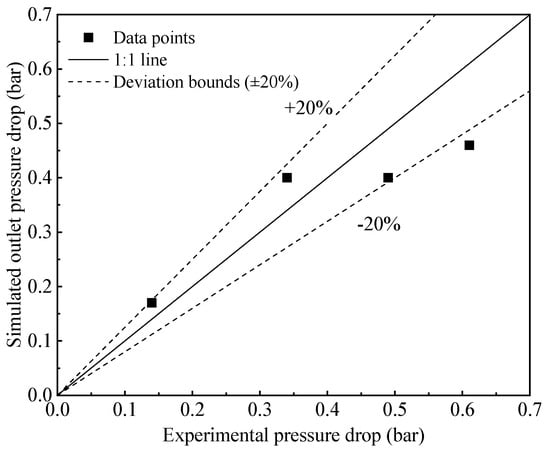
Figure 6.
Comparison of experimental and simulated outlet pressure drop.
Under the calculated operating conditions, bubbly flow, slug flow, annular flow, and stratified flow occurred sequentially within the pipe, which is generally consistent with the experimental results. The relative error between the simulated and experimental outlet temperatures is within ±20%. For the outlet pressure drop, the relative errors between the simulated and experimental values are all within ±20%, except for one data point, where the relative error is 24.6%. This indicates that the calculated results are in good agreement with the experimental measurements. The primary source of the error may be attributed to:
- (1)
- In the simulation, the wall boundary condition is set to a constant heat flow density, but in the experiment, the pipe absorbs heat from the hot water in the thermostatic tank, which is localized and unstable, thus causing errors.
- (2)
- In the computational model, both the inlet-to-outlet pressure gradient and outlet thermal state evaluations adopt cross-sectionally averaged quantities, contrasting with experimental recordings of point-specific measurements.
- (3)
- The horizontal tube in the simulation is assumed to be smooth, whereas the horizontal tube in the experiment has a certain roughness, which affects the generation and development of bubbles.
- (4)
- Non-condensable gases are neglected in the assumptions. In practice, they accumulate near the gas–liquid interface, forming a thermal barrier that increases interfacial resistance and lowers the heat transfer coefficient. They also occupy part of the total pressure, reducing the vapor’s partial pressure.
- (5)
- In simulations of convective boiling in horizontal tubes, assuming constant thermophysical properties tends to underestimate the pressure drop and phase change rate, while overestimating the heat transfer coefficient. However, during experiments, the thermophysical properties of water vary with increasing temperature.
3. Results and Discussion
Based on the geometric model, numerical method, and boundary conditions established above, the characteristics of gas volume fraction distribution, temperature field distribution, and velocity field distribution are analyzed under the conditions of an inner tube diameter of 65 mm, a heat flux density of 100 kW/m2, a flow rate of 30 t/h, and an inlet fluid subcooling of 0. Additionally, the effect of heat flux density on boiling flow within the horizontal tube is examined.
3.1. Flow Field Distribution Characteristics of Flow Boiling in a Horizontal Tube
3.1.1. Gas Volume Fraction Distribution
Figure 7 and Figure 8 illustrate the cloud plots of gas volume fraction distribution along the tube’s longitudinal direction (xy plane) and at each meter’s cross-section (yz plane). Higher values in the graph indicate a higher gas content and a lower liquid content. The figures reveal that the gas volume fraction progressively increases along the tube length. The predominant flow patterns observed include single-phase flow, bubbly flow, slug flow, annular flow, and stratified flow. Additionally, in the horizontal tube, the vapor-liquid two-phase fluid exhibits an asymmetric flow structure due to buoyancy forces, causing the vapor to predominantly accumulate in the upper region of the tube.

Figure 7.
Contour plot of flow pattern distribution along the tube in the xy-plane.

Figure 8.
Contour plots of gas volume fraction distribution across different cross-sections (yz-planes) along the length of the tube.
When the vapor content in the gas–liquid two-phase flow is low, small vapor bubbles form and detach from nucleation sites on the tube wall. These bubbles are dispersed within the liquid phase, distributed across the entire cross-section of the tube, and move upward. Given the use of a smooth horizontal tube in the simulation, the exact location of the vaporization core is not well-defined; thus, the temperature of each computational cell is used as a criterion for determining bubble formation. As depicted in Figure 7 and Figure 8, the bubbling points in the inlet section are discontinuous, with the earliest bubbling observed at 1.7 m under the given conditions. As the vapor content increases, small bubbles within the tube coalesce into larger bubbles. While small bubble departure enhances near-wall micro-convection and increases the heat transfer coefficient, large bubble detachment removes considerable latent heat, though it may lead to flow instabilities and localized overheating. Additionally, due to the high steam velocity, these bubbles frequently collide and fragment into irregularly shaped vapor masses. As observed in Figure 7, this flow pattern deviates from the classic slug flow, where gas bubbles typically present a spherical front and a flattened rear, similar to a bullet shape. This deviation is primarily due to the low surface tension at the vapor-water interface under the calculated working pressure of 12.354 MPa. However, in the absence of a water film in the upper section, the upper pipe wall experiences periodic wetting, resembling the characteristics of slug flow. Therefore, it is classified as slug flow. As the liquid film surface vaporizes, large bubbles gradually coalesce, forming a vapor column in the middle of the tube surrounded by a liquid film, which is thicker at the bottom. Consequently, annular flow develops within the tube. With further increases in vapor content, a more distinct vapor-liquid phase interface emerges in the exit section of the horizontal tube, characterized by vapor occupying the upper part and liquid remaining at the bottom, resulting in a stratified flow pattern. The average gas volume fraction at the exit section of the horizontal tube is 0.42.
3.1.2. Temperature Field Distribution
Figure 9 depicts the thermal distribution at multiple cross-sectional planes (yz-orientation) along the axial length of the tubular structure. Due to the density difference between the vapor and liquid, the upper surface, which is in contact with the vapor, exhibits a higher temperature. Overall, the temperature inside the tube is lower, with a maximum wall temperature of 630.7 K, reflecting an increase of 32.7 K. The temperature is higher at the top surface compared to the bottom surface.

Figure 9.
Temperature distribution across different cross-sections (yz-planes) along the length of the tube.
Figure 10a delineates thermal gradients across superior and inferior boundary interfaces parallel to the flow vector (xy-plane) in the tubular domain. It is evident from the figure that the temperature of the upper wall is significantly higher than that of the lower wall. This disparity is attributed to gravitational effects, which cause an uneven distribution of the vapor and liquid phases along the gravitational direction inside the tube. The temperature of the lower wall remains relatively stable, except at the 10 m mark, where it is approximately 3 K higher than at other locations. This increase is primarily due to the lower wall undergoing nucleate boiling, resulting in localized temperature elevations. Conversely, the temperature of the upper wall decreases slightly along the flow direction, with a reduction of about 4 K from 10 m to 29 m. This is mainly because, beyond 10 m, vapor-liquid stratification occurs, leading to an increase in vapor flow velocity as the temperature rises, thereby enhancing the convective heat transfer coefficient and reducing the temperature. Nonetheless, due to the low thermal conductivity of steam and the continuous contact of the upper wall with the vapor, the upper wall maintains a relatively higher temperature.

Figure 10.
Temperature variation with position within the tube across different planes.
Figure 10b illustrates the temperature variation along the tube diameter (yz-plane). The figure shows that the temperature increases from the lower wall surface to the upper wall surface. The temperature rise from the lower wall surface to the central axis is minor, with changes in less than 1 K, whereas the increase from the central axis to the upper wall surface is more pronounced, corresponding to the volume fraction distribution field. Since the tube wall is heated by a constant heat flux, the temperature of the working fluid near the wall surface is higher than the mainstream temperature. Additionally, the temperature gradient near the wall is greater than that of the mainstream.
3.1.3. Velocity Field Distribution
Figure 11 presents velocity distribution contour diagrams for various cross-sections (yz-plane) along the length of the tube. The figure reveals that the velocity distribution of the mixed fluid is non-uniform, with the regions of higher velocity gradually shifting towards the upper wall. In the cross-sections at 5 m and 6 m, the highest velocities are observed near the central axis. Subsequently, regions of high velocity appear closer to the upper surface, with the maximum velocity reaching approximately 7.5 m/s. This behavior is associated with the distribution of the gas volume fraction.

Figure 11.
Velocity distribution contours for various cross-sections (yz-plane) along the tube length.
Figure 12a illustrates the variation in velocity with position in the tube along the flow direction (xy plane) near the upper and lower walls (±30 mm). The figure indicates a gradual increase in velocity along the tube length. The velocity increment differs between the gas and liquid phases, with the liquid near the lower wall experiencing an 18.4% increase, while the vapor near the upper wall shows an 86.8% increase. Figure 12b presents the velocity variation along the tube diameter direction (yz plane). The relative velocity difference between the gas and liquid phases at the cross-section grows progressively larger, with a difference of 22.1% at 10 m and 45.7% at the outlet (30 m). This increasing shear between the two phases can result in a marked rise in pressure loss.

Figure 12.
Velocity variation with position within the tube across different planes.
In addition, the variation in pressure drop along the tube length was analyzed, as shown in Figure 13. The figure reveals that the pressure drop increases progressively as the boiling flow advances. Initially, up to 18 m, the pressure drop increases linearly; beyond 18 m, the rate of increase accelerates. This behavior is attributed to the different flow regimes: in the initial section, the flow is characterized by a bubble flow regime, where flow disturbances are minimal, resulting in relatively stable resistance losses. As the flow progresses and dryness increases within the tube, the liquid phase gradually converts to the gas phase, leading to an increase in gas volume. Consequently, the relative velocity difference between the gas and liquid phases at the same location grows, intensifying the inter-phase shear forces and significantly elevating the pressure drop.

Figure 13.
Pressure drop variation along the tube length.
3.2. The Impact of Heat Flux Density on Flow Boiling in the Horizontal Tube
The heat flux density plays a crucial role in determining the behavior of two-phase flow in boiling systems, particularly in horizontal tubes. Understanding its influence is essential for optimizing heat transfer, flow patterns, and pressure drop in such systems. In boiling water, as heat flux density increases, it significantly affects the distribution of gas and liquid phases, the temperature profiles, and the velocity of the working fluid near the walls, all of which contribute to changes in flow regimes and pressure loss. The water undergoes heat exchange with the flue gas in the convection and transition sections, where it boils inside the tube, causing the flue gas temperature to gradually decrease. In this study, the process is simplified by assuming a constant heat flux on the horizontal pipe wall. This section examines the impact of different heat flux densities (100 kW/m2, 200 kW/m2, and 300 kW/m2) on the boiling process inside the tube under the original operating conditions.
3.2.1. The Impact of Heat Flux Density on the Gas Distribution in the Horizontal Tube
Figure 14 and Figure 15 present the gas volume fraction distribution contours under different heat flux conditions. As shown in the figures, the rate of bubble growth is dependent on the heat flux density. Additionally, under varying heat flux conditions, the flow patterns during the boiling process inside the tube differ. The primary flow regimes observed include single-phase flow, bubbly flow, slug flow, annular flow, and stratified flow. From Figure 14, it can be seen that as the heat flux density increases, the number of vaporization cores on the tube wall increases, which significantly accelerates the growth and detachment rates of the bubbles. This, in turn, speeds up the transition of the mixed-phase fluid from liquid to gas. With the increasing gas phase fraction, the shear between the gas and liquid phases intensifies, enhancing the disturbance and accelerating the transition between flow patterns. Figure 15 reveals that the gas volume fraction at the same position in the pipe increases with the rise in heat flux density. Specifically, at an outlet cross-section with a heat flux density of 100 kW/m2, the gas volume fraction is 0.42, while at 300 kW/m2, it increases to 0.59. However, at the inlet positions of 5 m and 10 m, the gas volume fraction at 300 kW/m2 is lower. As shown in Table 3, at the 3 m and 8 m positions, the gas volume fraction at 300 kW/m2 is 0.19 and 0.25, respectively, both higher than those at 200 kW/m2. This difference is due to the flow regime being “slug flow” between 2 m and 12 m, where the gas volume fraction varies periodically across the cross-section.

Figure 14.
Effect of heat flux density on the flow pattern in the inlet section (xy-plane).
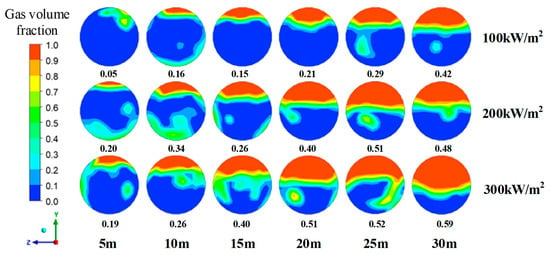
Figure 15.
Effect of heat flux density on the gas volume fraction distribution (yz-plane).

Table 3.
Gas volume fraction at various cross-sectional positions.
3.2.2. The Impact of Heat Flux Density on the Temperature of the Horizontal Tube
Figure 16 shows the temperature profile of the working fluid at the upper wall (di = ±32.5 mm) under different heat flux density conditions. As seen in Figure 16a, when the heat flux density increases by 100 kW/m2, the average temperature of the mixed working fluid at the lower wall rises by approximately 5 K. However, when the heat flux density increases to 300 kW/m2, the temperature of the working fluid varies significantly along the length of the tube. At 22 m, the temperature of the working fluid at the lower wall reaches its maximum value of 628.5 K. Due to gravity, the vapor bubbles move upward, and the lower tube wall primarily contacts the liquid-phase water, leading to a subsequent decrease in temperature. Furthermore, as the heat flux density increases, the number of vaporization cores also increases, resulting in the production of more vapor bubbles at the lower wall, which in turn raises the temperature. In addition, it is observed that the wall temperature at 10 m near the lower wall is higher under a heat flux of 200 kW/m2 than under 300 kW/m2. Combined with Table 3, which presents the gas volume fractions at the 10 m cross-section, it is evident that the gas volume fraction is higher at 200 kW/m2 than at 300 kW/m2. This suggests that the flow regime in this region is characterized by slug flow, where alternating gas and liquid plugs intermittently disrupt local heat transfer, resulting in a temporary rise in wall temperature. Once the liquid plug re-wets the wall, heat transfer is restored, and the temperature subsequently decreases.

Figure 16.
Effect of heat flux density on the wall fluid temperature.
As shown in Figure 16b, for different heat flux densities, the temperature of the mixed fluid in the tube first increases and then decreases along the length of the tube. As the heat flux density increases, the magnitude of the temperature change also increases. When the heat flux density is 100 kW/m2, the temperature of the mixed fluid gradually decreases after 10 m, with a total decrease of 6.3 K at the outlet, corresponding to a 0.9% drop. When the heat flux density is 300 kW/m2, the temperature of the mixed fluid decreases after 6 m, with a total decrease of 27.1 K at the outlet, corresponding to a 4.0% drop. Additionally, the temperature at the same position in the tube increases with the heat flux density, although the rate of increase decreases after 8 m. As shown in Table 4, at a distance of 16 m from the inlet, the temperature increases by 18.2 K when the heat flux density rises from 100 kW/m2 to 200 kW/m2, and by 16.4 K when it increases from 200 kW/m2 to 300 kW/m2. This is related to the increase in fluid velocity caused by the rise in heat flux density. According to Figure 16 and Table 4, at 6 m from the inlet, the temperature difference between the upper and lower wall surfaces is 24.9 K when the heat flux density is 100 kW/m2. When the heat flux density increases to 300 kW/m2, the temperature difference increases by a factor of 2.7. This indicates that the temperature difference between the upper and lower wall surfaces increases with the increase in heat flux density.

Table 4.
Effect of heat flux density variation on the temperature at the wall surface of the horizontal tube.
3.2.3. The Impact of Heat Flux Density on the Near-Wall Fluid Velocity of the Horizontal Tube
Table 5 presents the effect of heat flux density on the fluid velocity near the wall (di = ±30 mm). As shown in the table, when the heat flux density is 100 kW/m2, at 10 m from the inlet, the fluid velocity near the lower wall is 3.7 m/s, while the velocity near the upper wall is 4.7 m/s, resulting in a velocity difference of 1.0 m/s. At the same position in the tube, when the heat flux density increases to 300 kW/m2, the fluid velocity near the lower wall increases to 4.3 m/s, a 16.2% increase, while the velocity near the upper wall increases to 6.6 m/s, a 40.4% increase, with a velocity difference of 2.3 m/s. The results indicate that, at the same position in the horizontal tube, a higher heat flux density leads to a greater velocity difference between the fluid near the upper and lower walls.

Table 5.
Effect of heat flux density on the velocity of the near-wall fluid.
Additionally, when the heat flux density is 100 kW/m2, at 26 m from the inlet, the fluid velocity near the lower wall is 4.1 m/s, which is a 10.8% increase compared to the velocity at 10 m; the fluid velocity near the upper wall is 10.1 m/s, a 53.0% increase compared to the velocity at 10 m. The results indicate that, in the flow direction, the velocity of the fluid near both the upper and lower walls increases with the increase in heat flux density, and the velocity difference also increases progressively. This is due to the fact that the upper wall is in the vapor phase, while the lower wall is in the liquid phase. Therefore, it can be concluded that the increase in heat flux density accelerates the velocity of the gas–liquid phase, but the increase in vapor phase velocity is significantly larger than that in the liquid phase velocity.
3.2.4. The Impact of Heat Flux Density on the Pressure Drop of the Horizontal Tube
Figure 17 illustrates the effect of heat flux density on the pressure drop. As shown in the figure, the impact of increasing heat flux density on the pressure drop is minimal up to 5 m from the inlet. However, the pressure drop increases as the distance from the inlet grows. When the heat flux density is 100 kW/m2, the pressure drop between the inlet and outlet is 27,458 Pa. In contrast, at a heat flux density of 300 kW/m2, the pressure drop increases to 42,254 Pa, representing a 53.9% increase. This result can be attributed to the differential effect of heat flux density on the velocities of the gas and liquid phases, which exacerbates the interphase shear force and leads to a significant increase in pressure loss.

Figure 17.
Effect of heat flow density on pressure drop (di = 0).
3.3. The Impact of Mass Flow Rate on Flow Boiling in the Horizontal Tube
The rated mass flow rate of the steam injection boiler in this study is 30 t/h, which may be reduced based on actual process needs. A decrease in flow rate could lead to increasingly adverse operating conditions within the horizontal tube. Therefore, this section examines the impact of different mass flow rates (10 t/h, 15 t/h, and 30 t/h) on the boiling process inside the tube under the original operating conditions.
3.3.1. The Impact of Mass Flow Rate on the Gas Distribution in the Horizontal Tube
Figure 18 and Figure 19 illustrate the effect of mass flow rate on the distribution of gas volume fraction in the xy-plane and yz-plane. It can be observed that as the mass flow rate decreases, the gas volume fraction at the same cross-sectional location of the horizontal tube increases. Additionally, the flow pattern inside the tube changes with varying mass flow rates. Table 6 presents the influence of mass flow rate on the flow pattern, showing that as the mass flow rate decreases, the gas phase fraction in the tube increases, and the onset of the same flow pattern occurs earlier. This is primarily because, under constant heat flux density, a reduction in mass flow rate leads to a decrease in the velocity of the mixed working fluid inside the tube. Consequently, the amount of heat absorbed by the mixed fluid per unit length increases, resulting in a rise in temperature at the same location within the tube.

Figure 18.
Effect of mass flow rate on the flow pattern (xy-plane).
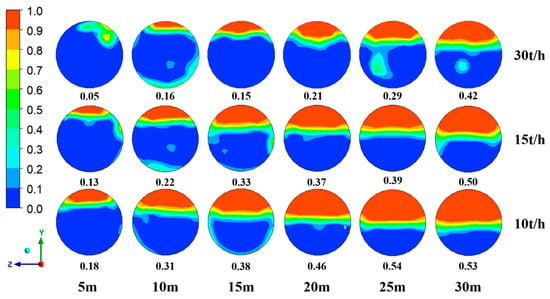
Figure 19.
Effect of mass flow rate on the flow pattern (yz-plane).

Table 6.
Effect of mass flow rate on flow pattern.
3.3.2. The Impact of Mass Flow Rate on the Temperature and Near-Wall Fluid Velocity of the Horizontal Tube
Table 7 presents the effect of mass flow rate on the bubbling point, maximum wall temperature, and their respective locations during boiling in the horizontal tube. As shown in the table, with a decrease in mass flow rate, the position of the boiling point inside the tube gradually shifts upstream. This is because a higher mass flow rate results in a higher fluid inlet velocity, and the heat transferred by the pipe wall per unit length is insufficient to induce phase change, causing the boiling point to occur further downstream. Additionally, a reduction in mass flow rate leads to an increase in the maximum wall temperature, which occurs earlier. In practical operation, the steam injection boiler can adjust its mass flow rate to meet varying oil recovery demands. When the mass flow rate is reduced to one-third of the rated value (10 t/h), the maximum temperature of the horizontal tube wall approaches the upper operating temperature limit of the tube material 15CrMo (773–823 K), significantly increasing the risk of tube rupture.

Table 7.
Effect of mass flow rate on boiling in a horizontal tube.
Figure 20 presents the temperature at the wall surface (±32.5 mm) and the velocity variation curve of the working fluid near the wall surface (±30 mm) for different mass flow rates. As shown in Figure 20a, when the mass flow rate is 30 t/h, the average temperature of the lower wall is approximately 602 K. When the mass flow rate is reduced to 10 t/h, the average temperature increases by about 4 K. This indicates that changes in mass flow rate have a relatively small impact on the temperature variation in the working fluid at the lower wall. Higher temperatures at certain positions along the tube length are associated with the formation of a vapor core. Additionally, for different mass flow rates, the temperature of the working fluid decreases along the tube length, which is related to the change in velocity. From the velocity curves in Figure 20c, it can be observed that the inlet and outlet velocities of the horizontal tube increase by 18.4% when the mass flow rate is 30 t/h, whereas the inlet and outlet velocities increase by 69.2% when the mass flow rate is 10 t/h. This indicates that the smaller the mass flow rate, the more significant the change in the inlet and outlet velocities of the working fluid near the lower wall.

Figure 20.
Effect of mass flow rate on wall work temperature and near-wall velocity.
Figure 20b presents the temperature variation in the working fluid on the upper wall. It can be observed that as the mass flow rate decreases, the temperature of the working fluid increases. Additionally, the temperature trend along the length of the tube is consistent under different mass flow rates, with the temperature initially rising and then falling. When the mass flow rate is 10 t/h, the temperature reaches 678.3 K at 2 m, after which it gradually decreases along the tube length, with a 37.3 K drop at 28 m. In contrast, for mass flow rates of 15 t/h and 30 t/h, the temperature shows minimal reduction after 10 m, remaining around 630 K and 622 K, respectively. From the velocity profile shown in Figure 20d, it is evident that when the mass flow rate is 10 t/h, the velocity near the upper wall is the smallest, and the inlet and outlet velocities increase by approximately 1.9 times along the flow direction. At a mass flow rate of 20 t/h, the inlet and outlet velocities increase by about 1.4 times, while for 30 t/h, the increase is only around 0.7 times. This indicates that as the mass flow rate decreases, the change in inlet and outlet velocities becomes more pronounced. With decreasing mass flow rate, the fluid velocity reduces, leading to a decrease in the convective heat transfer coefficient. When the heat flux density is held constant, this results in an increase in the pipe wall temperature and a rise in the fluid temperature. In practical operation, reducing the mass flow rate significantly raises the associated risks.
3.4. The Impact of Inlet Subcooling on Flow Boiling in the Horizontal Tube
As the water enters the transition section of the steam injection boiler, it is in either a saturated or subcooled state. Thus, the impact of subcooling on the flow pattern warrants investigation. Therefore, this section examines the effect of varying inlet subcooling degrees on boiling within the tube under the initial conditions.
3.4.1. The Impact of Inlet Subcooling on the Gas Distribution in the Horizontal Tube
Figure 21 and Table 8 illustrate the effect of inlet subcooling degree on the gas volume fraction distribution. It can be observed that, under the same operating conditions, an increase in the inlet subcooling degree reduces the conversion of the liquid phase to the gas phase. When the inlet subcooling degree is 10 K, the flow within the horizontal tube is predominantly single-phase, with the gas volume fraction at the outlet section being only 0.05. When the inlet subcooling degree is 5 K, bubbly flow appears between 13.9 and 18.5 m inside the tube, and slug flow occurs between 18.5 and 22.8 m, indicating that both bubbly and slug flows appear further downstream in the tube. Additionally, annular flow emerges between 22.8 and 30 m, while no stable stratified flow is observed. When the inlet subcooling degree is 10 K, the single-phase flow length extends to 28.1 m, with bubbly flow appearing only between 28.1 and 30 m. From the distribution of flow patterns described above, it is evident that an increase in inlet subcooling reduces the gas phase proportion in the tube and shifts the onset of the same flow patterns to later positions. This is primarily because, at constant heat flux density, an increase in inlet subcooling extends the time required for the mixed fluid in the tube to reach the saturation temperature.

Figure 21.
Effect of inlet subcooling on the flow pattern (yz-plane).

Table 8.
Effect of inlet subcooling on flow pattern.
3.4.2. The Impact of Inlet Subcooling on the Temperature and Near-Wall Fluid Velocity of the Horizontal Tube
Table 9 presents the effects of inlet subcooling on the onset of nucleate boiling, the maximum wall temperature, and its corresponding axial location during flow boiling in a horizontal tube. When the inlet subcooling is 0 K, nucleation occurs at a distance of 1.7 m from the tube inlet. As the inlet subcooling increases to 5 K, the nucleation point shifts downstream to 13.9 m. This trend indicates that a lower inlet subcooling advances the onset of boiling along the tube. The reason is that with lower subcooling, the working fluid undergoes only a boiling process, and the heat transferred from the tube wall over a unit length is sufficient to induce phase change, thereby causing earlier bubble formation. In contrast, at higher subcooling levels, both evaporation and condensation processes coexist. The vapor generated near the wall may subsequently condense back into liquid in the core flow region due to the lower bulk fluid temperature. Furthermore, when the inlet subcooling is 5 K, the maximum wall temperature appears at 21.9 m and reaches 630.4 K, which is 32.4 K higher than the inlet fluid temperature. At 10 K subcooling, the peak wall temperature is observed at 29.5 m, measuring 630.5 K–36.5 K above the inlet temperature. These observations suggest that as the inlet subcooling increases, the location of the maximum wall temperature shifts further downstream, while the peak temperature itself remains nearly constant.

Table 9.
Effect of inlet subcooling on boiling in a horizontal tube.
Figure 22 illustrates the influence of inlet subcooling on the wall temperature of the working fluid and the near-wall velocity. As shown in Figure 22a, when the inlet subcooling is 10 K, the temperature along the lower wall increases linearly and reaches the saturation temperature of 598 K at a distance of 18 m. In contrast, at an inlet subcooling of 5 K, the lower wall temperature continues to rise up to 20 m, after which it exhibits noticeable fluctuations. These fluctuations are associated with the onset of bubble generation, as previously observed in Figure 21. Figure 22c displays the near-wall velocity profile, indicating a significant increase in fluid velocity following the onset of vapor formation at an inlet subcooling of 5 K. Figure 22b shows the temperature distribution along the upper wall. When the inlet subcooling is 10 K, the upper wall temperature also increases linearly. However, for an inlet subcooling of 5 K, temperature fluctuations begin to occur at around 16 m, which is earlier than the fluctuations observed along the lower wall. The velocity profile in Figure 22d exhibits a similar trend to that of the lower wall. Overall, these results suggest that vapor bubble generation induces temperature fluctuations and significantly enhances local fluid velocity.
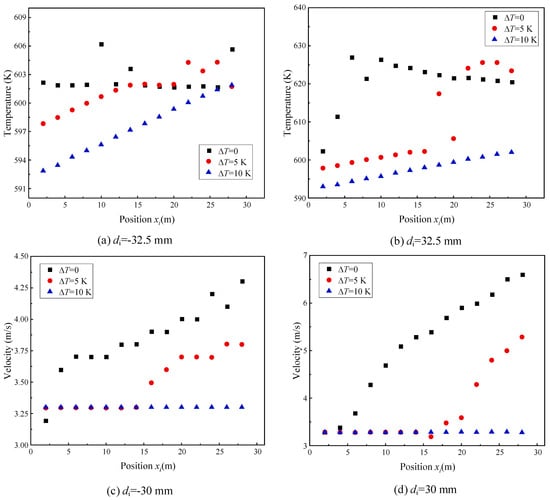
Figure 22.
Effect of inlet subcooling on wall work temperature and near-wall velocity.
4. Conclusions
To enhance the steam quality of steam injection boilers used in the thermal recovery of heavy oil while ensuring the safe and stable operation of boiler pipelines, this study conducted a numerical simulation of two-phase flow boiling within a horizontal heating tube (inner diameter: 65 mm) of a steam injection boiler, using water and steam as working fluids. Under specified operating conditions, the two-phase flow distribution patterns were analyzed. Furthermore, the effects of heat flux, mass flow rate, and inlet subcooling on key parameters such as gas phase distribution, temperature, and near-wall mass velocity were systematically investigated. The main conclusions are as follows:
(1) The gas volume fraction increases progressively along the length of the tube, with the predominant flow patterns observed being single-phase flow, bubbly flow, slug flow, annular flow, and stratified flow. Bubble formation was first observed at 1.7 m, and the average gas volume fraction at the outlet cross-section of the horizontal tube reached 0.42. Similarly to the findings in [38], owing to the density difference between the gas and liquid phases, the upper wall of the tube remains in contact with the vapor phase, resulting in a higher wall temperature compared to the average fluid temperature within the tube—a difference of 32.7 K. The phase velocities exhibited distinct growth rates: the liquid velocity near the lower wall increased by 18.4%, whereas the vapor velocity near the upper wall increased by 86.8%.
(2) With increasing heat flux density, both the bubble growth rate and detachment rate at the tube wall are accelerated, leading to a higher gas volume fraction at the same axial position within the tube. At a given location in the horizontal tube, a higher heat flux density results in a greater velocity difference between the fluids near the upper and lower walls. Although the velocities of both gas and liquid phases increase with rising heat flux, the velocity increment of the gas phase is significantly greater than that of the liquid phase. While literature [31,39] suggests that variations in heat flux have a limited direct impact on the overall heat transfer coefficient, the phenomenon observed in this study is attributed to the transition to an annular/stratified flow pattern (associated with an increase in void fraction) and the enhanced gas–liquid velocity difference, which modifies the heat transfer mechanism.
(3) As the mass flow rate decreases, the proportion of the gas phase within the tube increases, consistent with the observations in study [40]. Additionally, the onset of each characteristic flow pattern occurs earlier, with the bubble inception point moving upstream and the maximum tube wall temperature increasing and shifting forward. When the mass flow rate is reduced to one-third of the rated value (10 t/h), the maximum temperature of the horizontal tube wall approaches the upper limit of the operating temperature range for the tube material 15CrMo, significantly increasing the risk of tube rupture.
(4) When the subcooling of the water at the inlet of the boiler’s convection section increases to 10 K, the time required for the working fluid inside the tube to reach saturation temperature is prolonged. This leads to a reduced gas phase fraction and delays the onset of the same flow patterns, making it difficult to achieve the required dryness at the tube outlet. Therefore, in practical operation, the subcooling at the convection section inlet should be minimized.
The above findings indicate that increasing the heat flux, reducing the mass flow rate, and lowering the subcooling of the water at the inlet of the boiler’s convection section can effectively enhance the steam dryness at the transition section outlet. However, under these conditions, the dominant flow patterns near the location of the maximum tube wall temperature are slug flow and stratified flow. Since the upper wall is in contact only with steam, the local convective heat transfer coefficient is significantly reduced, resulting in insufficient wall cooling and a higher risk of tube rupture. Therefore, it is necessary to adopt flow pattern control strategies to promote flow regimes that enhance heat transfer and mitigate the risk of localized overheating [41]:
(1) For the design and construction of new steam injection boilers, internally finned (or internally threaded) tubes can be used to replace smooth tubes. These structures induce spiral or secondary flows, which enhance flow disturbance, disrupt the thermal boundary layer, and effectively reduce the tube wall temperature. In the subcritical pressure region, annular flow becomes the dominant pattern when using internally finned tubes [42], which significantly mitigates the risk of heat transfer deterioration.
(2) For existing steam injection boilers, vortex generators or similar flow-disturbing devices can be installed inside the tubes to disrupt boundary layer development and thereby prevent heat transfer deterioration. For instance, embedding a metallic mesh insert within the tube can promote the transition from slug or stratified flow to annular flow [43,44]. This ensures continuous contact between the tube wall and the liquid film, thereby significantly reducing the risk of tube rupture.
In addition, the model used in this study has certain limitations. It assumes smooth, corrosion- and scale-free inner pipe walls, whereas in practice, long-term operation of steam injection boiler pipelines may lead to surface roughness changes or deposition, which can influence two-phase flow distribution and heat transfer efficiency. Furthermore, the simulation employs pure water and steam as the working fluid, while the actual injected fluid during heavy oil thermal recovery may contain dissolved gases or trace impurities, potentially altering the onset of boiling and phase change kinetics. Incorporating these factors into the model might lead to more accurate simulation results.
Author Contributions
Methodology, Z.W. and C.W.; Software, C.W.; Validation, Z.W.; Investigation, G.G.; Data curation, G.L.; Writing—original draft, G.G.; Writing—review & editing, L.D.; Supervision, G.L. and L.D. All authors have read and agreed to the published version of the manuscript.
Funding
This work acknowledges financial support from the Research on the Characteristics of Salt Deposition in Furnace Water During the Evaporation Process of Steam-Injected Boilers and Analysis of Steam Salt-Carrying Capacity (2024XJZD09032).
Data Availability Statement
The original contributions presented in this study are included in the article. Further inquiries can be directed to the corresponding author.
Conflicts of Interest
Authors Genying Gao, Zicheng Wang and Gaoqiao Li were employed by PetroChina Xinjiang Oilfield Company. The remaining authors declare that this research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Nomenclature
| Symbols | |
| Energy (J) | |
| External body force (N m−3) | |
| Gravitational body force (m s−2) | |
| m | Mass flow rate (kg s−1) |
| Pressure (Pa) | |
| SE | Energy source term (J) |
| Time (s) | |
| Saturation temperature (K) | |
| Outlet temperature (K) | |
| Dynamic viscosity (kg m−1 s−1) | |
| Density (kg m−1) | |
| Thermal conductivity (W m−1 K−1) | |
| Gas phase volume fraction (%) | |
| Liquid phase volume fraction (%) |
References
- Liu, Z.; Wang, H.; Blackbourn, G.; Ma, F.; He, Z.; Wen, Z.; Wang, Z.; Yang, Z.; Luan, T.; Wu, Z. Heavy oils and oil sands: Global distribution and resource assessment. Acta Geol. Sin.-Engl. Ed. 2019, 93, 199–212. [Google Scholar] [CrossRef]
- Wang, L.; Guo, J.X.; Li, C.; Xiong, R.Y.; Chen, X.W.; Zhang, X.J. Advancements and future prospects in in-situ catalytic technology for heavy oil reservoirs in China: A review. Fuel 2024, 374. [Google Scholar] [CrossRef]
- Shi, Q.; Zhao, S.Q.; Zhou, Y.S.; Gao, J.S.; Xu, C.M. Development of heavy oil upgrading technologies in China. Rev. Chem. Eng. 2020, 36, 1–19. [Google Scholar] [CrossRef]
- Zhao, Q.; Niu, J.; Dong, Y.; Song, Z.; Ke, B.; An, P.; Jin, H.; Guo, L. Sub- and supercritical water upgrading of heavy oil: A review of laboratory-scale research on upgrading performance and physicochemical mechanism. Chem. Eng. J. 2024, 500, 157376. [Google Scholar] [CrossRef]
- He, X.; Zhao, L.; Lu, X.; Ding, F.; Wang, Z.; Han, R.; Liu, P. A Critical Review Using CO2 and N2 of Enhanced Heavy-Oil-Recovery Technologies in China. Appl. Sci. 2022, 12, 12585. [Google Scholar] [CrossRef]
- Pei, H.H.; Zhang, G.C.; Ge, J.J.; Tang, M.G.; Zheng, Y.F. Comparative effectiveness of alkaline flooding and alkaline-surfactant flooding for improved heavy-oil recovery. Energy Fuels 2012, 26, 2911–2919. [Google Scholar] [CrossRef]
- Xiao, Y.; Hu, Z.X.; Chen, S.; Gu, H.Y. Experimental investigation of boiling heat transfer in helically coiled tubes at high pressure. Ann. Nucl. Energy 2018, 113, 409–419. [Google Scholar] [CrossRef]
- Zhang, K.; Hou, Y.D.; Tian, W.X.; Fan, Y.Q.; Su, G.H.; Qiu, S.Z. Experimental investigations on single-phase convection and steam-water two-phase flow boiling in a vertical rod bundle. Exp. Therm. Fluid Sci. 2017, 80, 147–154. [Google Scholar] [CrossRef]
- Gawas, K.; Karami, H.; Pereyra, E.; Al-Sarkhi, A.; Sarica, C. Wave characteristics in gas-oil two phase flow and large pipe diameter. Int. J. Multiph. Flow 2014, 63, 93–104. [Google Scholar] [CrossRef]
- Badie, S.; Hale, C.P.; Lawrence, C.J.; Hewitt, G.F. Pressure gradient and holdup in horizontal two-phase gas-liquid flows with low liquid loading. Int. J. Multiph. Flow 2000, 26, 1525–1543. [Google Scholar] [CrossRef]
- Ge, M.; Zhang, G.; Petkovšek, M.; Long, K.; Coutier-Delgosha, O. Intensity and regimes changing of hydrodynamic cavitation considering temperature effects. J. Clean. Prod. 2022, 338, 130470. [Google Scholar] [CrossRef]
- Ge, M.M.; Manikkam, P.; Ghossein, J.; Subramanian, R.K.; Coutier-Delgosha, O.; Zhang, G.J. Dynamic mode decomposition to classify cavitating flow regimes induced by thermodynamic effects. Energy 2022, 254, 124426. [Google Scholar] [CrossRef]
- Yin, S.W.; Zhang, J.X.; Tong, L.G.; Yao, Y.; Wang, L. Experimental study on flow patterns for water boiling in horizontal heated tubes. Chem. Eng. Sci. 2013, 102, 577–584. [Google Scholar] [CrossRef]
- Loh, W.L.; Hernandez-Perez, V.; Tam, N.D.; Wan, T.T.; Zhao, Y.Q.; Premanadhan, V.K. Experimental study of the effect of pressure and gas density on the transition from stratified to slug flow in a horizontal pipe. Int. J. Multiph. Flow 2016, 85, 196–208. [Google Scholar]
- Vuong, D.H.; Sarica, C.; Pereyra, E.; Al-Sarkhi, A. Liquid droplet entrainment in two-phase oil-gas low-liquid-loading flow in horizontal pipes at high pressure. Int. J. Multiph. Flow 2018, 99, 383–396. [Google Scholar] [CrossRef]
- Kong, R.; Rau, A.; Lu, C.; Gamber, J.; Kim, S.; Bajorek, S.; Tien, K.; Hoxie, C. Experimental study of interfacial structure of horizontal air-water two-phase flow in a 101.6 mm ID pipe. Exp. Therm. Fluid Sci. 2018, 93, 57–72. [Google Scholar] [CrossRef]
- Sardeshpande, M.V.; Raymond, B.; Ranade, V.V. Two-phase flow boiling in 19mm tube: Experiments and CFD modelling. Can. J. Chem. Eng. 2016, 94, 872–885. [Google Scholar] [CrossRef]
- Rabhi, A.; Aslanidou, I.; Kyprianidis, K.; Fdhila, R.B. Onset of nucleate boiling model for rectangular upward narrow channel: CFD based approach. Int. J. Heat Mass Transf. 2021, 165, 120715. [Google Scholar] [CrossRef]
- Lo, S.; Osman, J. CFD Modeling of Boiling Flow in PSBT 5x5 Bundle. Sci. Technol. Nucl. Install. 2012, 2012, 795935. [Google Scholar] [CrossRef]
- Xu, Y.; Tian, J.; Wang, Z.; Zhang, J.; Li, S.; Yan, Y.; Ge, M. A comprehensive study on the flow field of cylindrical cavitation nozzle jet under different turbulence models. Ocean. Eng. 2025, 315, 119596. [Google Scholar] [CrossRef]
- Sato, Y.; Niceno, B. Pool boiling simulation using an interface tracking method: From nucleate boiling to film boiling regime through critical heat flux. Int. J. Heat Mass Transf. 2018, 125, 876–890. [Google Scholar] [CrossRef]
- Petrovic, M.M.; Stevanovic, V.D. Pool boiling simulation with two-fluid and grid resolved wall boiling model. Int. J. Multiph. Flow 2021, 144, 103806. [Google Scholar] [CrossRef]
- Liu, Y.; Olewski, T.; Véchot, L.N. Modeling of a cryogenic liquid pool boiling by CFD simulation. J. Loss Prev. Process Ind. 2015, 35, 125–134. [Google Scholar] [CrossRef]
- Ahammad, M.; Olewski, T.; Véchot, L.N.; Mannan, S. A CFD based model to predict film boiling heat transfer of cryogenic liquids. J. Loss Prev. Process Ind. 2016, 44, 247–254. [Google Scholar] [CrossRef]
- Shaparia, N.; Pelay, U.; Bougeard, D.; Levasseur, A.; Francois, N.; Russeil, S. Investigation of wall boiling closure, momentum closure and population balance models for refrigerant gas-liquid subcooled boiling flow in a vertical pipe using a two-fluid eulerian CFD model. Energies 2024, 17, 4225. [Google Scholar] [CrossRef]
- Gilman, L.; Baglietto, E. A self-consistent, physics-based boiling heat transfer modeling framework for use in computational fluid dynamics. Int. J. Multiph. Flow 2017, 95, 35–53. [Google Scholar] [CrossRef]
- Li, Q.; Jiao, Y.; Avramova, M.; Chen, P.; Yu, J.; Chen, J.; Hou, J. Development, verification and application of a new model for active nucleation site density in boiling systems. Nucl. Eng. Des. 2018, 328, 1–9. [Google Scholar] [CrossRef]
- Wang, L.L.; Dai, Y.D.; Wu, J.H.; Li, B. Experimental investigation on flow boiling heat transfer characteristics of R1234ze(E)/R152a in 6-mm ID horizontal smooth tube. Exp. Heat Transf. 2021, 34, 342–355. [Google Scholar] [CrossRef]
- Wu, J.H.; Wang, L.L.; Li, B.A.; Dai, Y.D. Flow boiling heat transfer performances of R1234ze(E)/R152a in a horizontal micro-fin tube. Exp. Heat Transf. 2022, 35, 381–398. [Google Scholar] [CrossRef]
- Yang, Z.; Peng, X.F.; Ye, P. Numerical and experimental investigation of two phase flow during boiling in a coiled tube. Int. J. Heat Mass Transf. 2008, 51, 1003–1016. [Google Scholar] [CrossRef]
- Shao, Y.; Deng, S.; Lu, P.; Zhao, D.; Zhao, L.; Su, W.; Ma, M. A numerical study on heat transfer of R410A during flow boiling. Energy Procedia 2019, 158, 5414–5420. [Google Scholar] [CrossRef]
- Ghorai, S.; Nigam, K.D.P. CFD modeling of flow profiles and interfacial phenomena in two-phase flow in pipes. Chem. Eng. Process.-Process Intensif. 2006, 45, 55–65. [Google Scholar] [CrossRef]
- Verdin, P.G.; Thompson, C.P.; Brown, L.D. CFD modelling of stratified/atomization gas-liquid flow in large diameter pipes. Int. J. Multiph. Flow 2014, 67, 135–143. [Google Scholar] [CrossRef]
- Pineda-Pérez, H.; Kim, T.; Pereyra, E.; Ratkovich, N. CFD modeling of air and highly viscous liquid two-phase slug flow in horizontal pipes. Chem. Eng. Res. Des. 2018, 136, 638–653. [Google Scholar] [CrossRef]
- Luo, Y.; Li, W.; Zhou, K.; Sheng, K.; Shao, S.; Zhang, Z.; Du, J.; Minkowycz, W.J. Three-dimensional numerical simulation of saturated annular flow boiling in a narrow rectangular microchannel. Int. J. Heat Mass Transf. 2020, 149, 119246. [Google Scholar] [CrossRef]
- van Hooff, T.; Blocken, B.; Tominaga, Y. On the accuracy of CFD simulations of cross-ventilation flows for a generic isolated building: Comparison of RANS, LES and experiments. Build. Environ. 2017, 114, 148–165. [Google Scholar] [CrossRef]
- Temraz, A.; Alobaid, F.; Lanz, T.; Elweteedy, A.; Epple, B. Operational flexibility of two-phase flow test rig for investigating the dynamic instabilities in tube boiling systems. Front. Energy Res. 2020, 8, 517740. [Google Scholar] [CrossRef]
- Parvareh, A.; Rahimi, M.; Alizadehdakhel, A.; Alsairafi, A.A. CFD and ERT investigations on two-phase flow regimes in vertical and horizontal tubes. Int. Commun. Heat Mass Transf. 2010, 37, 304–311. [Google Scholar] [CrossRef]
- Yu, J.W.; Ma, H.Q.; Jiang, Y.Q. A numerical study of heat transfer and pressure drop of hydrocarbon mixture refrigerant during boiling in vertical rectangular minichannel. Appl. Therm. Eng. 2017, 112, 1343–1352. [Google Scholar] [CrossRef]
- Mahmood, R.A.; Saleh, K.; Musa, V.A.; Massoud, E.; Sharifian-Barforoush, A.; Abdulkareem, L.A. Two-phase flow development of R134a in a horizontal pipe: Computational investigation. Int. J. Heat Technol. 2021, 39, 1532–1540. [Google Scholar] [CrossRef]
- Niu, Z.Y. Experimental Investigations on Heat Transfer Enhancement of Flow Boiling Inside a Horizontal Tube Based on Flow Pattern Modulation. Ph.D. Thesis, North China Electric Power University, Beijing, China, 2014. [Google Scholar]
- Huo, X.Q. Research on Decaying Mechanism of Gas-Liquid Swirl Annular Flow. Master’s Thesis, Tianjin University, Tianjin, China, 2019. [Google Scholar]
- Li, Z.X. Research on the Gas-Liquid Flow Regimes and Transition Mechanisms in Helically Coiled Tubes. Ph.D. Thesis, Tsinghua University, Beijing, China, 2018. [Google Scholar]
- Liu, S.L. Simulational and Experimental Research on Two-Phase Flow Boiling Heat Transfer in Tube Side of the Spiral-Wound Heat Exchanger. Master’s Thesis, Zhengzhou University, Zhengzhou, China, 2019. [Google Scholar]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).