Data Flow Forecasting for Smart Grid Based on Multi-Verse Expansion Evolution Physical–Social Fusion Network
Abstract
1. Introduction
- A single network cannot accurately extract the temporal and spatial features of financial flow data: The financial flow data of a power grid exhibit characteristics such as long sequences, nonlinearity, multi-scale patterns, and non-stationarity. While CNNs excel at capturing local features, they lack the ability to perceive global information. On the other hand, BiLSTMs can handle forward and backward dependencies in time series but show limitations in modeling nonlinear and complex patterns. Existing standalone networks cannot effectively integrate the spatial and temporal features of financial flow data, leading to lower forecasting accuracy for power grid financial flows [16].
- The ineffective training of model parameters increases the risk of the optimization process converging to local optima: Deep learning models like CNNs and BiLSTMs involve numerous parameters that significantly affect their forecasting performance. Current approaches for parameter optimization in deep learning models fail to achieve global parameter search, causing models to frequently converge to local optima during training. This limitation severely affects the efficiency and accuracy of financial flow forecasting in power grids.
- A financial flow data feature extraction model for power grid based on STFN is proposed: This model organically combines the associative feature extraction capabilities of CNN with the temporal sequence modeling capabilities of BiLSTM. CNN effectively extracts features from the financial flow data of power grid companies, while BiLSTM captures the contextual temporal relationships. The complementary strengths of CNN and BiLSTM are leveraged, significantly improving the accuracy of power-grid financial flow data forecasting.
- A fine-tuning method for STFN based on MVE2 is proposed: Leveraging the global search capability and fast convergence of MVE2, it is employed to optimize the parameters of STFN. The proposed algorithm effectively mitigates the issue of traditional methods falling into local optima during model training, accelerates convergence, and significantly enhances both the efficiency and accuracy of financial flow forecasting models.
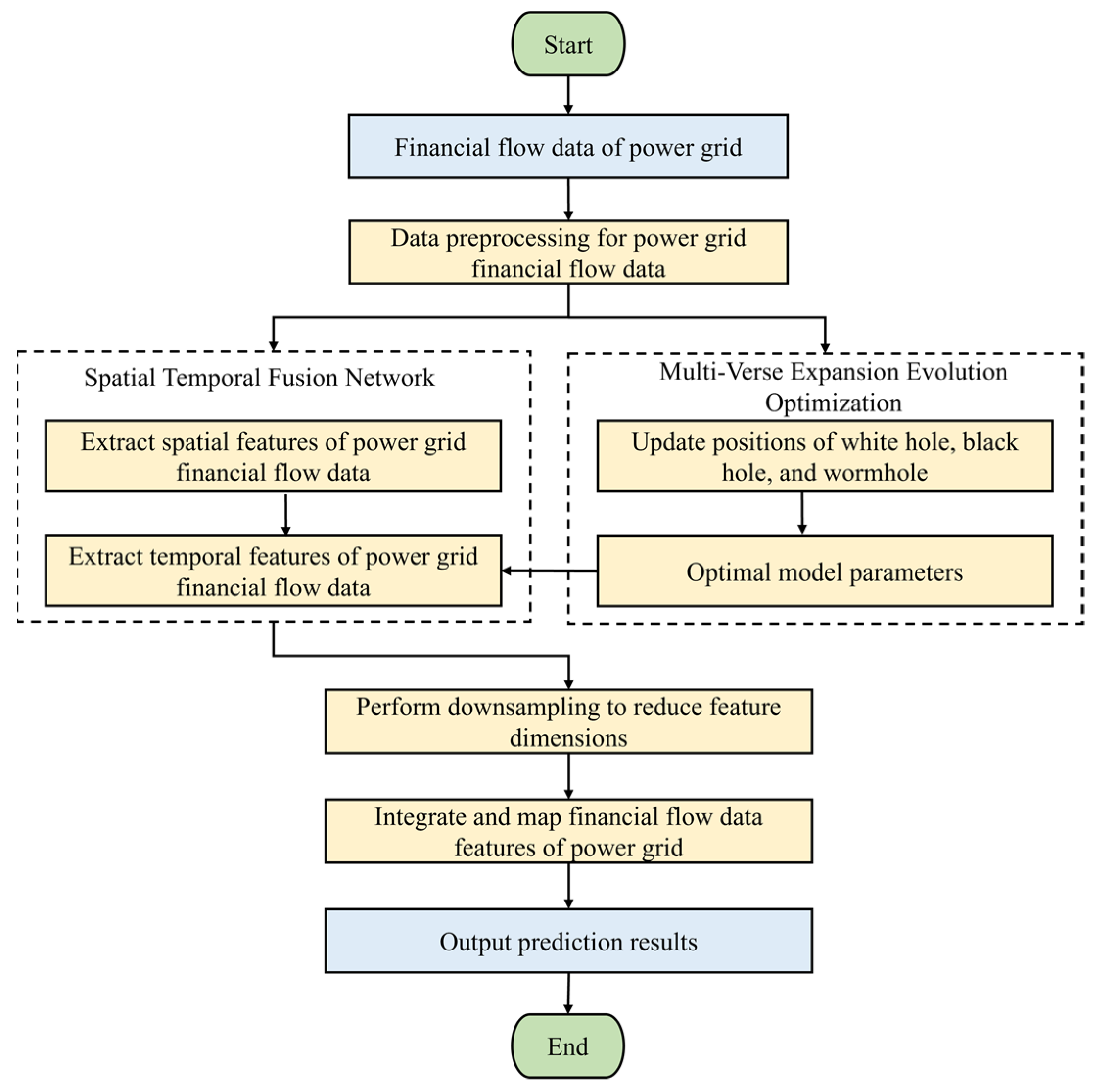
2. Data Preprocessing for Power Grid Financial Flow Data Based on ARIMA Model
2.1. Data Cleaning and Normalization Processing
2.2. Construction of Financial Flow Data Forecasting Dataset Based on ARIMA Model
2.2.1. White Noise Test and Removal
2.2.2. ARIMA Model-Based Financial Flow Data Forecasting and Dataset Construction
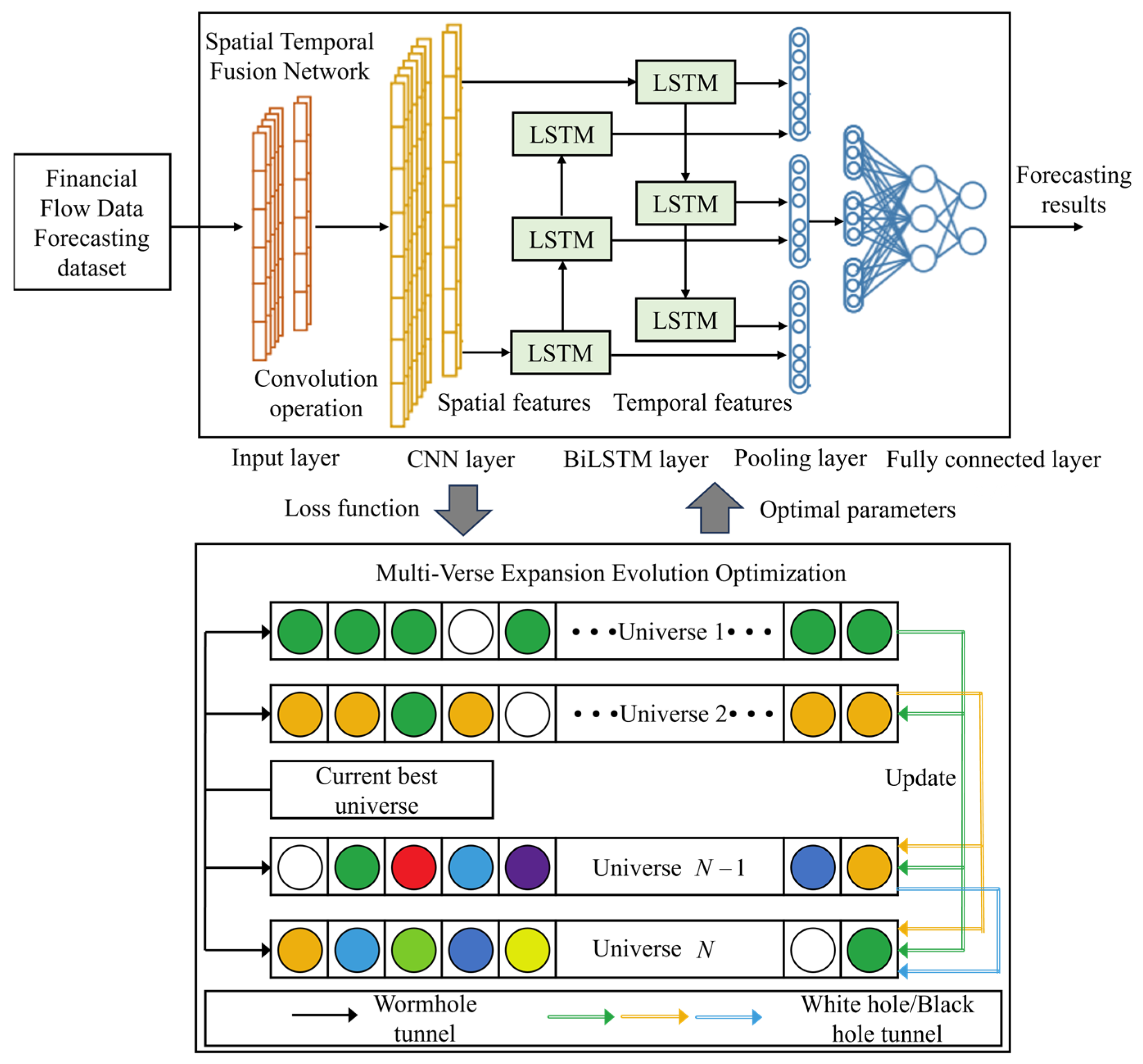
3. Financial Flow Data Forecasting Based on MVE2-STFN
3.1. Power Grid Financial Flow Feature Extraction Model Based on STFN
3.2. Fine-Tuning Method for STFN Based on MVE2
3.3. Limitations of the Algorithm
4. Experimental Results and Analysis
4.1. Evaluation Metrics
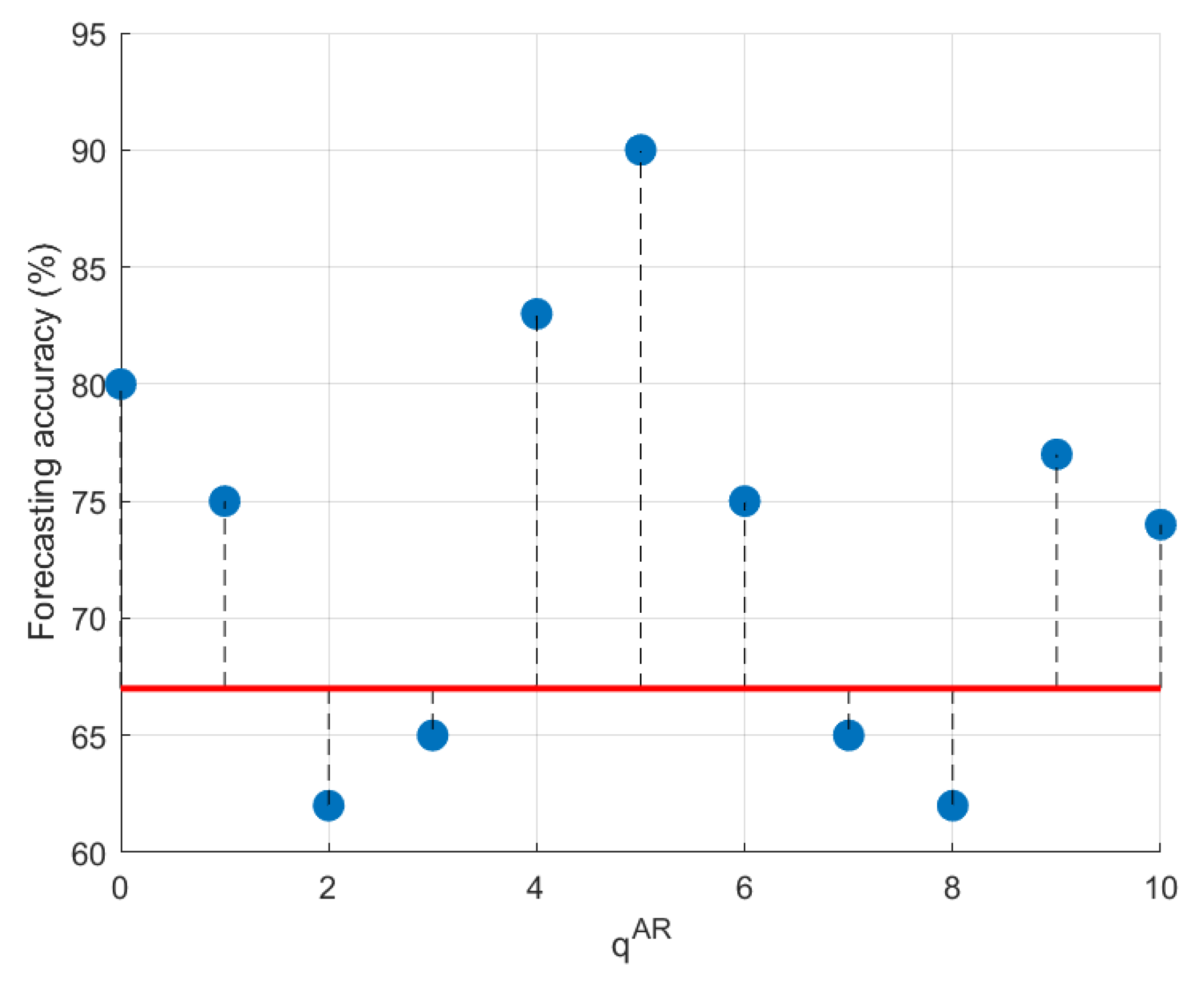
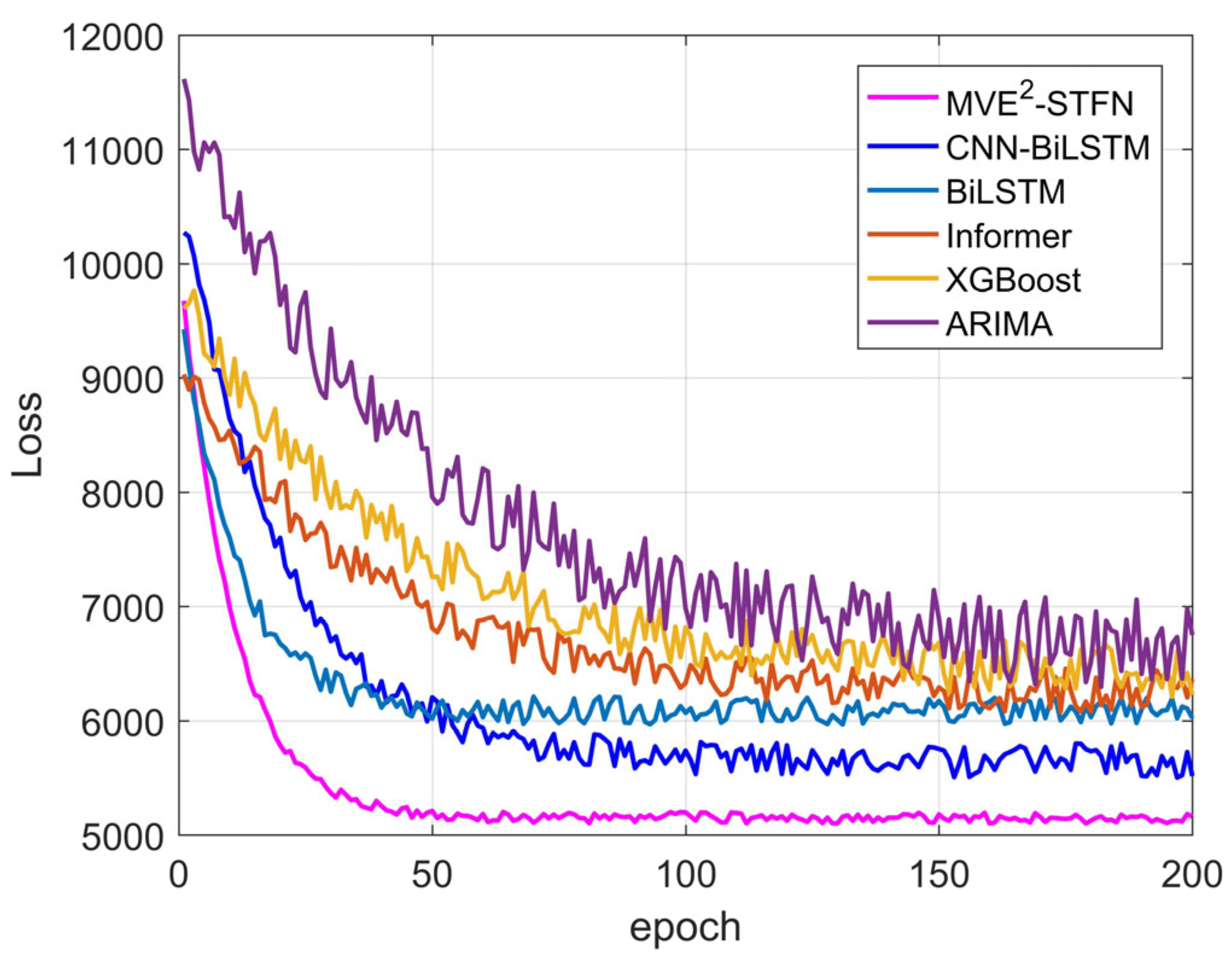
4.2. Experimental Results
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Wang, C.; Lv, Y.; Huang, H.; Zhang, J.; Li, J.; Li, Y.; Sun, W.; Chang, Y. Low Frequency Oscillation Characteristics of East China Power Grid after Commissioning of Huai-Hu Ultra-High Voltage Alternating Current Project. J. Mod. Power Syst. Clean Energy 2015, 3, 332–340. [Google Scholar] [CrossRef]
- Pokou, F.; Sadefo Kamdem, J.; Benhmad, F. Hybridization of ARIMA with learning models for forecasting of stock market time series. Comput. Econ. 2024, 63, 1349–1399. [Google Scholar] [CrossRef]
- Wang, Y.; Chen, Y.; Liu, H.; Ma, X.; Su, X.; Liu, Q. Day-Ahead Photovoltaic Power Forcasting Using Convolutional-LSTM Network. In Proceedings of the 2021 3rd Asia Energy and Electrical Engineering Symposium (AEEES), Chengdu, China, 26–29 March 2021; pp. 917–921. [Google Scholar]
- Bi, J.; Yuan, H.; Li, S.; Zhang, K.; Zhang, J.; Zhou, M. ARIMA-Based and Multiapplication Workload Prediction with Wavelet Decomposition and Savitzky–Golay Filter in Clouds. IEEE Trans. Syst. Man Cybern. Syst. 2024, 54, 2495–2506. [Google Scholar] [CrossRef]
- Yu, W.; Cheng, X.; Jiang, M. Exploitation of ARIMA and Annual Variations Model for SAR Interferometry Over Permafrost Scenarios. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2025, 18, 8938–8952. [Google Scholar] [CrossRef]
- Saba, T.; Haseeb, K.; Rehman, A.; Jeon, G. Blockchain-Enabled Intelligent IoT Protocol for High-Performance and Secured Big Financial Data Transaction. IEEE Trans. Comput. Soc. Syst. 2024, 11, 1667–1674. [Google Scholar] [CrossRef]
- Zheng, J.; Gao, Q.; Ogorzałek, M.; Lü, J.; Deng, Y. A Quantum Spatial Graph Convolutional Neural Network Model on Quantum Circuits. IEEE Trans. Neural Netw. Learn. Syst. 2025, 36, 5706–5720. [Google Scholar] [CrossRef]
- Mehtab, S.; Sen, J.; Dasgupta, S. Robust Analysis of Stock Price Time Series Using CNN and LSTM-Based Deep Learning Models. In Proceedings of the 2020 4th International Conference on Electronics, Communication and Aerospace Technology (ICECA), Coimbatore, India, 5–7 November 2020; pp. 1481–1486. [Google Scholar]
- Staffini, A. A CNN–BiLSTM Architecture for Macroeconomic Time Series Forecasting. Eng. Proc. 2023, 39, 33–34. [Google Scholar]
- Wang, Z. Application of CNN-based Financial Risk Identification and Management Convolutional Neural Networks in Financial Risk. Syst. Soft Comput. 2025, 7, 200215. [Google Scholar] [CrossRef]
- Zhang, J.; Tang, Q.; Liu, D. Research Into the LSTM Neural Network-Based Crystal Growth Process Model Identification. IEEE Trans. Semicond. Manuf. 2019, 32, 220–225. [Google Scholar] [CrossRef]
- Zhao, G.; Yuan, P. A Stock Prediction Model Based on CNN-Bi-LSTM and Multiple Attention Mechanisms. In Proceedings of the 2023 5th International Conference on Applied Machine Learning (ICAML), Dalian, China, 21–23 July 2023; pp. 214–220. [Google Scholar]
- Zhao, B.; Cheng, C.; Peng, Z.; Dong, X.; Meng, G. Detecting the Early Damages in Structures With Nonlinear Output Frequency Response Functions and the CNN-LSTM Model. IEEE Trans. Instrum. Meas. 2020, 69, 9557–9567. [Google Scholar] [CrossRef]
- Bartouli, M.; Helali, A.; Hassen, F. Applying Bayesian Optimized CNN-Bi-LSTM to Real-Time Load Forecasting Model for Smart Grids. In Proceedings of the 2024 IEEE International Conference on Advanced Systems and Emergent Technologies (ICASET)., Hammamet, Tunisia, 27–29 April 2024; pp. 1–6. [Google Scholar]
- Jian, W.; Li, J.; Akbar, M.A.; Haq, A.U.; Khan, S.; Alotaibi, R.M.; Alajlan, S.A. SA-Bi-LSTM: Self Attention With Bi-Directional LSTM-Based Intelligent Model for Accurate Fake News Detection to Ensured Information Integrity on Social Media Platforms. IEEE Access 2024, 12, 48436–48452. [Google Scholar] [CrossRef]
- Wasserbacher, H.; Spindler, M. Machine Learning for Financial Forecasting, Planning and Analysis: Recent Developments and Pitfalls. Digit. Financ. 2022, 4, 63–88. [Google Scholar] [CrossRef]
- Gao, S.; Hao, W.; Wang, Q.; Zhang, Y. Missing-Data Filling Method Based on Improved Informer Model for Mechanical-Bearing Fault Diagnosis. IEEE Trans. Instrum. Meas. 2024, 73, 1–10. [Google Scholar] [CrossRef]
- Zhang, X.; Chan, K.-W.; Li, H.; Wang, H.; Qiu, J.; Wang, G. Deep-Learning-Based Probabilistic Forecasting of Electric Vehicle Charging Load With a Novel Queuing Model. IEEE Trans. Cybern. 2021, 51, 3157–3170. [Google Scholar] [CrossRef]
- Liu, G.; Sun, Q.; Su, H.; Hu, Z. Adaptive Tracking Control for Uncertain Nonlinear Multi-Agent Systems with Partially Sensor Attack. IEEE Trans. Autom. Sci. Eng. 2025, 22, 6270–6279. [Google Scholar] [CrossRef]
- Liu, G.; Sun, Q.; Su, H.; Wang, M. Adaptive Cooperative Fault-Tolerant Control for Output-Constrained Nonlinear Multi-Agent Systems Under Stochastic FDI Attacks. IEEE Trans. Circuits Syst. I Regul. Pap. 2025, 1–12. [Google Scholar] [CrossRef]
- Fu, Y.; Zhou, M.; Guo, X.; Qi, L.; Sedraoui, K. Multiverse Optimization Algorithm for Stochastic Bi-objective Disassembly Sequence Planning Subject to Operation Failures. IEEE Trans. Syst. Man Cybern. Syst. 2022, 52, 1041–1051. [Google Scholar] [CrossRef]
- Hong, D.; Gao, L.; Yao, J.; Zhang, B.; Plaza, A.; Chanussot, J. Graph Convolutional Networks for Hyperspectral Image Classification. IEEE Trans. Geosci. Remote Sens. 2021, 59, 5966–5978. [Google Scholar] [CrossRef]
- Sattler, F.; Wiedemann, S.; Müller, K.-R.; Samek, W. Robust and Communication-Efficient Federated Learning From Non-i.i.d. Data. IEEE Trans. Neural Netw. Learn. Syst. 2020, 31, 3400–3413. [Google Scholar] [CrossRef]
- Huang, J.; Saw, S.N.; Feng, W.; Jiang, Y.; Yang, R.; Qin, Y.; Seng, L.S. A Latent Factor-Based Bayesian Neural Networks Model in Cloud Platform for Used Car Price Prediction. IEEE Trans. Eng. Manag. 2024, 71, 12487–12497. [Google Scholar] [CrossRef]
- Qu, Z.; Yang, K.; Li, Y.; Jiang, X.; Zhang, Y.; Zhao, Y.; Wu, W.; Gao, Y.; Gu, Z.; Zhao, Z. On Grain Security by Temperature Interpolation: A Deep Learning Method for Comprehensive Data Fusion in Smart Granaries. IEEE Trans. Instrum. Meas. 2024, 73, 1–20. [Google Scholar] [CrossRef]
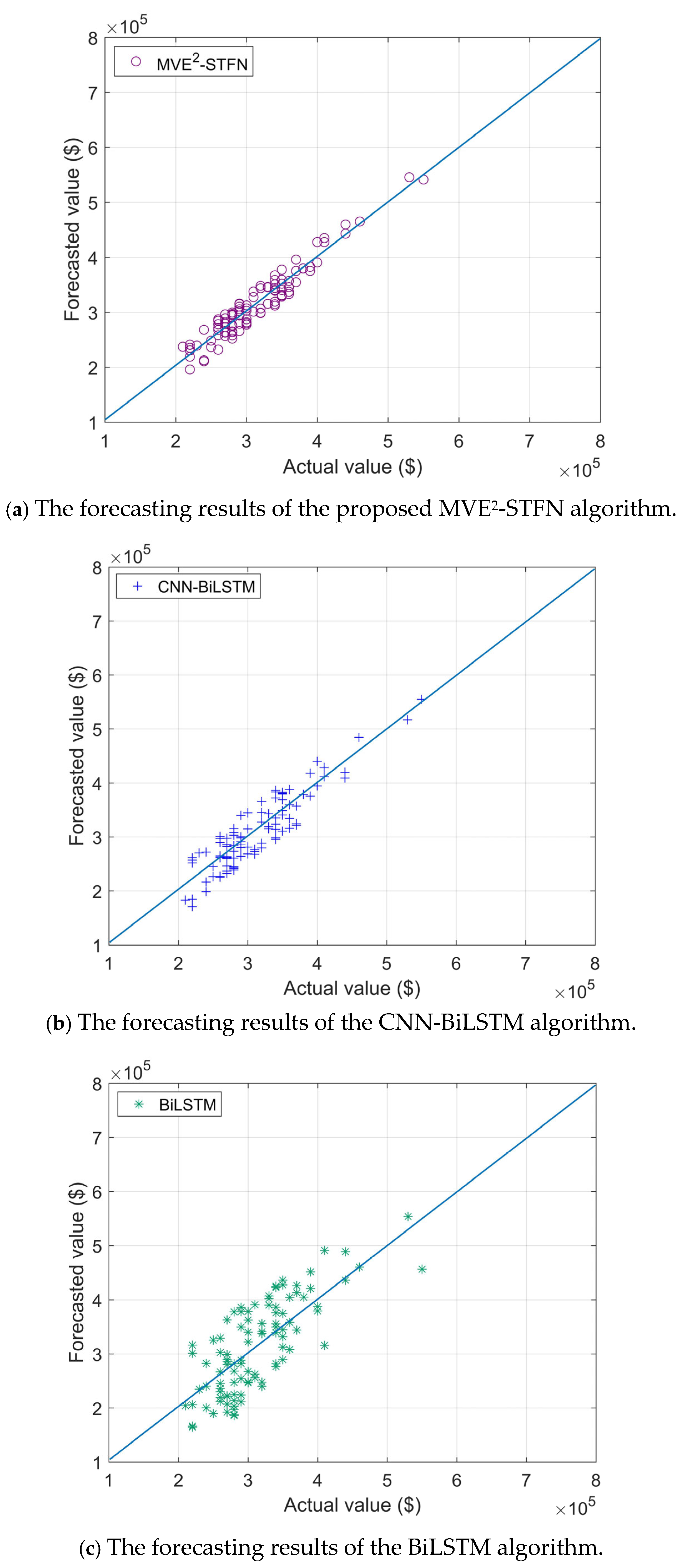
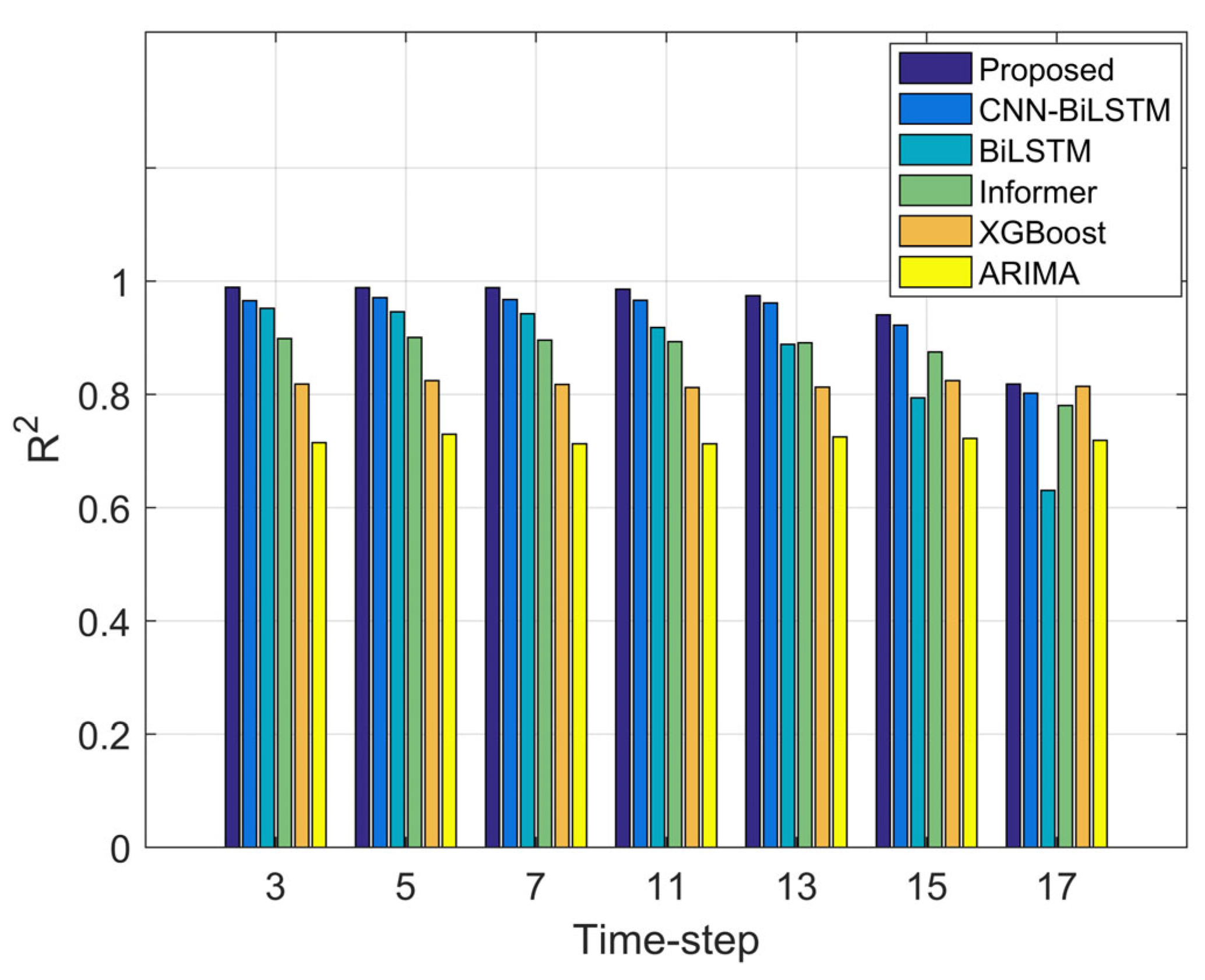
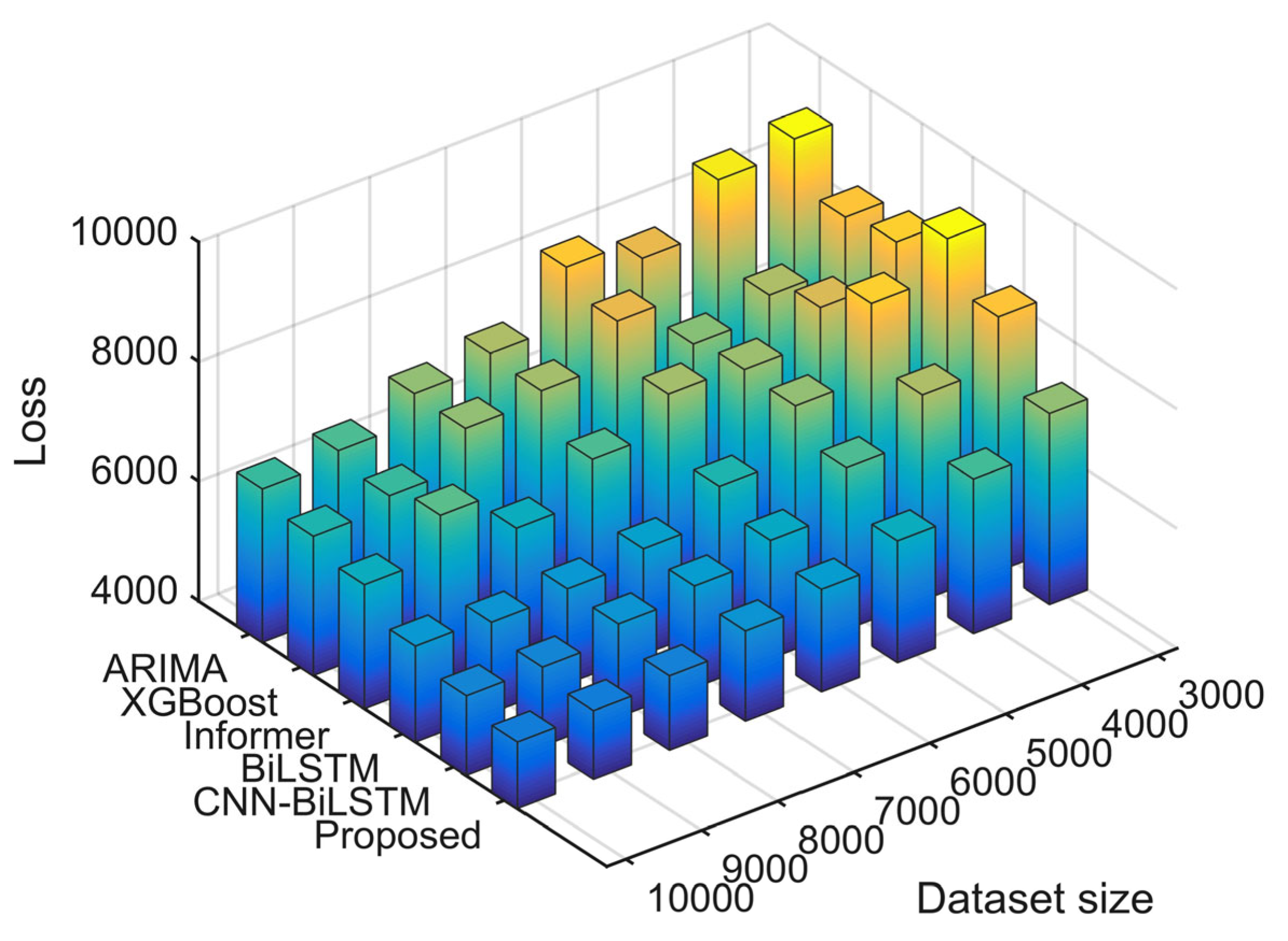
| Parameter | Value | Parameter | Value |
|---|---|---|---|
| Number of convolution kernels | 128 | Convolution kernel size | 3 |
| Training set proportion | 80% | Validation set ratio | 10% |
| Number of hidden layers | 3 | Initial learning rate | 0.001 |
| Evaluation Metrics | ||||
|---|---|---|---|---|
| MVE2-STFN | 5298.62 | 3880.15 | 0.0928 | 0.9924 |
| CNN-BiLSTM | 5612.37 | 4231.27 | 0.1194 | 0.9801 |
| BiLSTM | 6117.51 | 5011.89 | 0.1593 | 0.9359 |
| Informer | 6337.15 ± 322.46 | 4940.21 ± 294.41 | 0.1389 ± 0.0131 | 0.8802 ± 0.0056 |
| XGBoost | 6484.45 ± 342.46 | 5044.58 ± 300.65 | 0.1402 ± 0.0163 | 0.8157 ± 0.0063 |
| ARIMA | 6765.81 ± 332.46 | 5180.77 ± 243.65 | 0.1451 ± 0.0167 | 0.7143 ± 0.0071 |
| Training Time | Prediction Time | Average CPU Usage | Prediction Error | |
|---|---|---|---|---|
| MVE2-STFN | 2894.84 s | 11.98 s | 55% | 8.89% |
| CNN-BiLSTM | 3021.78 s | 12.43 s | 64% | 6.26% |
| BiLSTM | 3312.31 s | 12.58 s | 70% | 4.63% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, K.; Hu, B.; Zhang, J.; Zhang, R.; Zhang, H.; Zhang, S.; Chen, X. Data Flow Forecasting for Smart Grid Based on Multi-Verse Expansion Evolution Physical–Social Fusion Network. Energies 2025, 18, 3093. https://doi.org/10.3390/en18123093
Wang K, Hu B, Zhang J, Zhang R, Zhang H, Zhang S, Chen X. Data Flow Forecasting for Smart Grid Based on Multi-Verse Expansion Evolution Physical–Social Fusion Network. Energies. 2025; 18(12):3093. https://doi.org/10.3390/en18123093
Chicago/Turabian StyleWang, Kun, Bentao Hu, Jiahao Zhang, Ruqi Zhang, Hongshuo Zhang, Sunxuan Zhang, and Xiaomei Chen. 2025. "Data Flow Forecasting for Smart Grid Based on Multi-Verse Expansion Evolution Physical–Social Fusion Network" Energies 18, no. 12: 3093. https://doi.org/10.3390/en18123093
APA StyleWang, K., Hu, B., Zhang, J., Zhang, R., Zhang, H., Zhang, S., & Chen, X. (2025). Data Flow Forecasting for Smart Grid Based on Multi-Verse Expansion Evolution Physical–Social Fusion Network. Energies, 18(12), 3093. https://doi.org/10.3390/en18123093





