Optimization and Analysis of Sensitive Areas for Look-Ahead Electromagnetic Logging-While-Drilling Based on Geometric Factors
Abstract
1. Introduction
2. Methods
2.1. Born Geometric Factor
2.2. Look-Ahead Geometric Factor for LWD
3. Results and Discussion
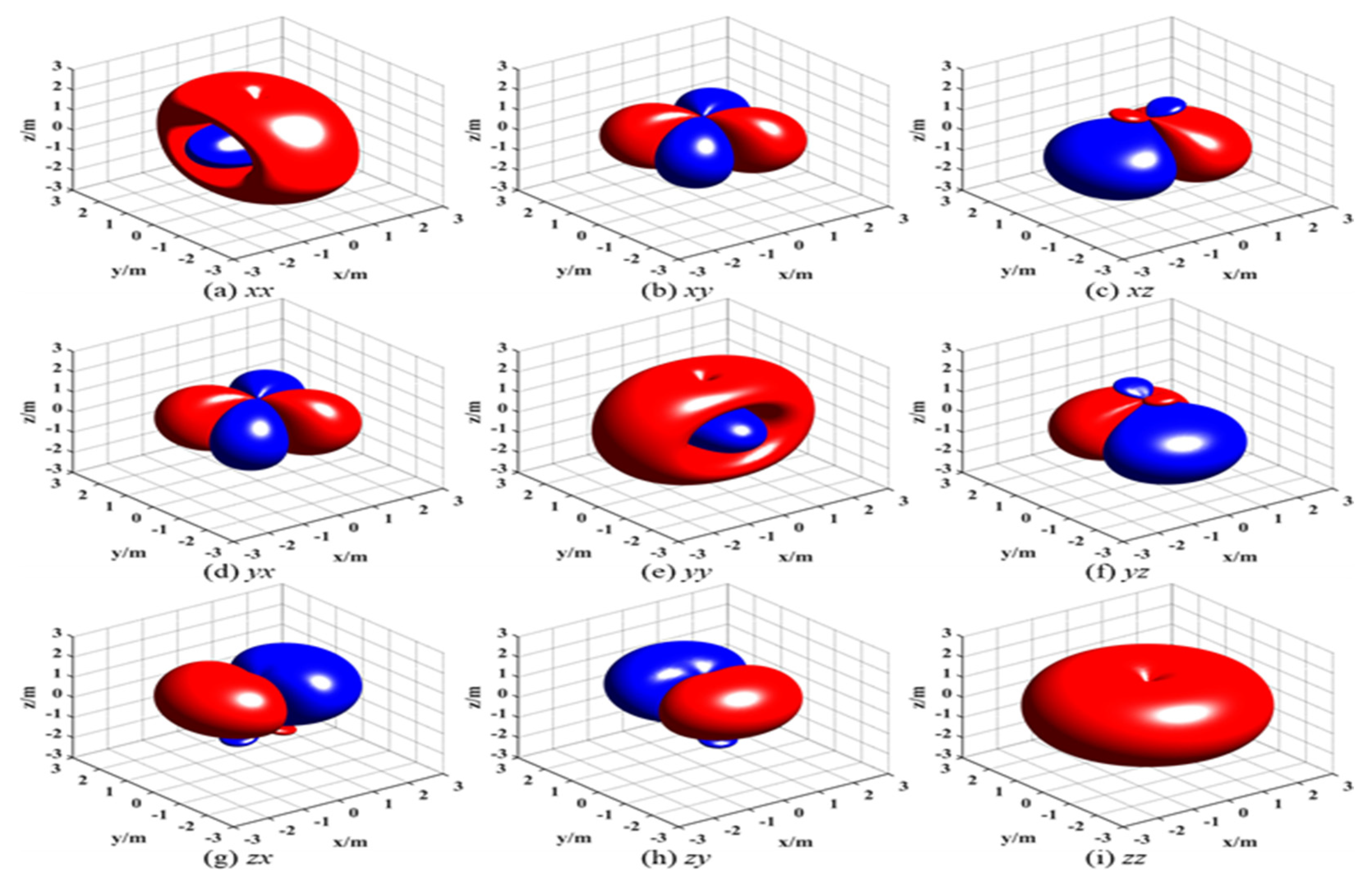
3.1. Geometric Factor Distribution Features
3.1.1. Component Geometric Factor
3.1.2. Look-Ahead Geometric Factor
3.2. Optimization of Sensitive Area
3.2.1. Optimization Method
3.2.2. Sensitivity Analysis
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Su, Y.; Dou, X.; Gao, W.; Liu, K. Discussion and prospects of the development on measurement while drilling technology in oil and gas wells. Pet. Sci. Bull. 2023, 8, 535–554. [Google Scholar]
- Passey, Q.R. Overview of high-angle and horizontal well formation evaluation: Issues, learnings, and future directions. In Proceedings of the SPWLA 46th Annual Logging Symposium, New Orleans, LA, USA, 26–29 June 2005. [Google Scholar]
- Market, J.; Quirein, J.; Pitcher, J.; Hinz, D.; Buller, D.; Al-Dammad, C.; Spain, D.; Odumosu, T. Logging-while-drilling in unconventional shales. In Proceedings of the SPE Annual Technical Conference and Exhibition, Florence, Italy, 19–22 September 2010. [Google Scholar]
- Gremillion, J.; Flowers, M.; Tvrdy, N.; Okoro, M.; Newnam, Z. Selection of logging-while-drilling measurements for geosteering of horizontal wells in unconventional reservoirs. In Proceedings of the SPE/AAPG/SEG Unconventional Resources Technology, Denver, CO, USA, 22–24 July 2019. [Google Scholar]
- Li, Y. Ultra-deep oil and gas reservoir seismic prospecting technologies progress. Oil Geophys. Prospect. 2024, 59, 915–924. [Google Scholar]
- Bittar, M.S.; Klein, J.D.; Beste, R.; Hu, G.; Wu, M.; Pitcher, J.L.; Golla, C.; Althoff, G.D.; Sitka, M.; Minosyan, V.; et al. A new azimuthal deep-reading resistivity tool for geosteering and advanced formation evaluation. SPE Reserv. Eval. Eng. 2009, 12, 270–279. [Google Scholar] [CrossRef]
- Li, S.; Chen, J.; Binford, T.L. Using new LWD measurements to evaluate formation resistivity anisotropy at any dip angle. In Proceedings of the SPWLA 55th Annual Logging Symposium, Abu Dhabi, United Arab Emirates, 18–22 May 2014. [Google Scholar]
- Hu, X.; Fan, Y. Huber inversion for logging-while-drilling resistivity measurements in high angle and horizontal wells. Geophysics 2018, 83, D113–D125. [Google Scholar] [CrossRef]
- Bittar, M.; Wu, H.H.; Ma, J.; Griffing, M.; Lozinsky, C. First lwd fully triaxial co-located antenna sensors for real-time anisotropy and dip angle determination, yielding better look-ahead detection. In Proceedings of the SPWLA 61st Annual Logging Symposium, Virtual Online Webinar, 24–29 June 2020. [Google Scholar]
- Vetsak, A.; Jablonski, B. Increase exposed bitumen reserves by optimizing wellbore placement in oil sands with extra-deep azimuthal resistivity LWD service. In Proceedings of the SPE Thermal Well Integrity and Design Symposium, Banff, AB, Canada, 27–29 November 2018. [Google Scholar]
- Larsen, D.S.; Boesing, D.; Hartmann, A.; Martakov, S.; Mumtaz, A.; Skillings, J.; Vianna, A. Boundary detection ahead of the bit–A sensitivity study of extra deep azimuthal resistivity. In Proceedings of the Offshore Technology Conference Asia, Kuala Lumpur, Malaysia, 20–23 March 2018. [Google Scholar]
- Anderson, B.I.; Druskin, V.; Lee, F.; Luling, M.G.; Schoen, F.; Tabanou, J.; Wu, F.; Davydycheva, S.; Knizhnerman, L. Modeling 3D Effects on 2-MHz LWD Resistivity Logs. In Proceedings of the SPWLA Annual Logging Symposium, Houston, TX, USA, 15–18 June 1997. [Google Scholar]
- Halliburton Sperry-Sun. Electromagnetic Wave Resistivity (EWR) Sensor Manual; Halliburton Sperry-Sun: Dubai, United Arab Emirates, 2003. [Google Scholar]
- Li, Q.; Omeragic, D.; Chou, L.; Yang, L.; Duong, K. New directional electromagnetic tool for proactive geosteering and accurate formation evaluation while drilling. In Proceedings of the SPWLA 46th Annual Logging Symposium, New Orleans, LA, USA, 26–29 June 2005. [Google Scholar]
- Bell, C.; Hampson, J.; Eadsforth, P.; Chemali, R.; Helgesen, T.; Meyer, H.; Peveto, C.; Poppitt, A.; Randall, R.; Signorelli, J.; et al. Navigating and imaging in complex geology with azimuthal propagation resistivity while drilling. In Proceedings of the SPE Annual Technical Conference and Exhibition, San Antonio, TX, USA, 24–27 September 2006. [Google Scholar]
- Antonsen, F.; De Oliveira, M.E.T.; Hermanrud, K.; Luna, C.A.; Petersen, S.A.; Metcalfe, R.W.; Constable, M.V.; Alme, A.; Vee, T.; Salim, D.; et al. Ultra-deep LWD-resistivity is essential to map reservoir structure and fluid contacts in a two-branched horizontal producer. In Proceedings of the SPE Norway One Day Seminar, Bergen, Norway, 18 April 2018. [Google Scholar]
- Seydoux, J.; Legendre, E.; Mirto, E.; Dupuis, C.; Denichou, J.-M.; Bennett, N.; Kutiev, G.; Kuchenbecker, M.; Morriss, C.; Yang, L. Full 3D deep directional resistivity measurements optimize well placement and provide reservoir-scale imaging while drilling. In Proceedings of the SPWLA Annual Logging Symposium, Abu Dhabi, United Arab Emirates, 18–22 May 2014. [Google Scholar]
- Wu, H.H.; Golla, C.; Parker, T.; Clegg, N.; Monteilhet, L. A new ultra-deep azimuthal electromagnetic LWD sensor for reservoir insight. In Proceedings of the SPWLA Annual Logging Symposium, London, UK, 2–6 June 2018. [Google Scholar]
- Hartmann, A.; Vianna, A.; Maurer, H.-M.; Sviridov, M.; Martakov, S.; Lautenschläger, U.; Antonsen, F.; Olsen, P.A.; Constable, M.V. Verification testing of a new extra-deep azimuthal resistivity measurement. In Proceedings of the SPWLA Annual Logging Symposium, Abu Dhabi, United Arab Emirates, 18–22 May 2014. [Google Scholar]
- Li, K.; Gao, J.; Zhao, X. Tool design of look-ahead electromagnetic resistivity LWD for boundary identification in anisotropic formation. J. Pet. Sci. Eng. 2020, 184, 106537. [Google Scholar] [CrossRef]
- Hou, L.; Yang, H.; Zhao, P.; Yu, X.; Cui, Y. Development of looking forward and looking around technology while drilling. World Pet. Ind. 2020, 27, 35–41. [Google Scholar]
- Zhang, P.; Deng, S.; Hu, X.; Wang, L.; Yuan, X. Detection performance and sensitivity of logging-while-drilling extra-deep azimuthal resistivity measurement. Chin. J. Geophys. 2021, 64, 2210–2219. [Google Scholar]
- Qin, Z.; Tang, B.; Wu, D.; Luo, S.; Ma, X.; Huang, K.; Deng, C.; Yang, H.; Pan, H.; Wang, Z. A qualitative characteristic scheme and a fast distance prediction method of multi-probe azimuthal gamma-ray logging in geosteering. J. Pet. Sci. Eng. 2021, 199, 1–10. [Google Scholar] [CrossRef]
- Ma, J.; Riofrio, K.; Clegg, N.; Sinha, S.; Wu, H.-H.; Kotwicki, A.; Skorve, T.; Johansen, Y.B. Successful geostopping using a recently developed LWD look-ahead ultra-deep EM resistivity tool. In Proceedings of the ADIPEC, Abu Dhabi, United Arab Emirates, 31 October–3 November 2022. [Google Scholar]
- Upchurch, E.R.; Saleem, S.; Russell, K.; Viandante, M.G. Geo-stopping using deep directional resistivity LWD: A new method for well bore placement using below-the-bit resistivity mapping. In Proceedings of the SPE/IADC Drilling Conference and Exhibition, London, UK, 17–19 March 2015. [Google Scholar]
- Constable, M.V.; Antonsen, F.; Stalheim, S.O.; Eikenes, S.; Aarflot, H.; Haldorsen, K.; Digranes, G.; Seydoux, J.; Thiel, M.; Davydyche, A.; et al. Looking ahead of the bit while drilling: From vision to reality. In Proceedings of the SPWLA Annual Logging Symposium, Reykjavik, Iceland, 25–29 June 2016. [Google Scholar]
- Thiel, M.; Omeragic, D.; Seydoux, J. Enhancing the look-ahead-of-the-bit capabilities of deep-directional resistivity measurements while drilling. In Proceedings of the SPWLA Annual Logging Symposium, The Woodlands, TX, USA, 15–19 June 2019. [Google Scholar]
- Hagiwara, T. Detection sensitivity and new concept of deep reading look-ahead look-around geosteering tool. In Proceedings of the SEG International Exposition and Annual Meeting, Anaheim, CA, USA, 14–19 October 2018. [Google Scholar]
- Li, S. System and Methodology of Look Ahead and Look Around LWD Tool. U.S. Patent 10,605,073, 31 March 2020. [Google Scholar]
- Wang, L.; Li, S.; Fan, Y. An all-new ultradeep detection method based on hybrid dipole antennas in electromagnetic logging while drilling. IEEE Trans. Geosci. Remote Sens. 2019, 58, 2124–2134. [Google Scholar] [CrossRef]
- Wu, J.; Gao, Z. Parameter design and response research of ahead detection half-coil induction logging. In Proceedings of the 2022 4th International Conference on Intelligent Control, Measurement and Signal Processing (ICMSP), Hangzhou, China, 8–10 July 2022. [Google Scholar]
- Gianzero, S.; Anderson, B.I. A new look at skin effect. Log Anal. 1982, 23, 93–104. [Google Scholar]
- Moran, J.H. Induction logging-geometrical factors with skin effect. Log Anal. 1982, 23, 4–10. [Google Scholar]
- Zhang, G.J.; Zhang, Z.Q. Application of successive approximation method to the computation of the Green’s function in axisymmetric inhomogeneous media. IEEE Trans. Geosci. Remote Sens. 1998, 36, 732–737. [Google Scholar] [CrossRef]
- Howard, A.Q.; Chew, W.C.; Moldoveanu, M.C. A new correction to the Born approximation. IEEE Trans. Geosci. Remote Sens. 1990, 28, 394–399. [Google Scholar] [CrossRef]
- Barber, T.; Anderson, B.; Abubakar, A.; Broussard, T.; Chen, K.-C.; Davydycheva, S.; Druskin, V.; Habashy, T.; Homan, D.; Minerbo, G.; et al. Determining formation resistivity anisotropy in the presence of invasion. In Proceedings of the SPE Annual Technical Conference and Exhibition, Houston, TX, USA, 26–29 September 2004. [Google Scholar]












Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, G.; Wu, Z.; Liao, X.; Yue, X.; Zhang, X.; Liu, T.; Zeng, Y. Optimization and Analysis of Sensitive Areas for Look-Ahead Electromagnetic Logging-While-Drilling Based on Geometric Factors. Energies 2025, 18, 3014. https://doi.org/10.3390/en18123014
Li G, Wu Z, Liao X, Yue X, Zhang X, Liu T, Zeng Y. Optimization and Analysis of Sensitive Areas for Look-Ahead Electromagnetic Logging-While-Drilling Based on Geometric Factors. Energies. 2025; 18(12):3014. https://doi.org/10.3390/en18123014
Chicago/Turabian StyleLi, Guoyu, Zhenguan Wu, Xiaoqiao Liao, Xizhou Yue, Xiang Zhang, Tianlin Liu, and Yunxin Zeng. 2025. "Optimization and Analysis of Sensitive Areas for Look-Ahead Electromagnetic Logging-While-Drilling Based on Geometric Factors" Energies 18, no. 12: 3014. https://doi.org/10.3390/en18123014
APA StyleLi, G., Wu, Z., Liao, X., Yue, X., Zhang, X., Liu, T., & Zeng, Y. (2025). Optimization and Analysis of Sensitive Areas for Look-Ahead Electromagnetic Logging-While-Drilling Based on Geometric Factors. Energies, 18(12), 3014. https://doi.org/10.3390/en18123014





