Techno-Economic Enhancement of Distribution Network by Optimal DG Allocation Along with Network Reconfiguration Considering Different Load Models and Levels
Abstract
1. Introduction
- The objective of minimizing CAEL is considered for the first time for solving the simultaneous DG allocation and NR problem with multiple load models.
- This work incorporates a variety of PFs, like the zero power factor (ZPF), unity power factor (UPF), and optimal power factor (OPF), under multiple load models (CP, CI, CZ, and ZIP).
- The investigation entails a comprehensive comparison of several cases with multiple loading scenarios to assess the efficacy of the proposed strategies.
- The HOA methodology is employed for the first time for the strategic planning of DG units with NR in an IEEE 33-Bus DN. The HOA effectively balances exploration and exploitation through adaptive movement strategies. It can be applied to both continuous and discrete optimization problems and even hybrid ones like DG allocation with network reconfiguration.
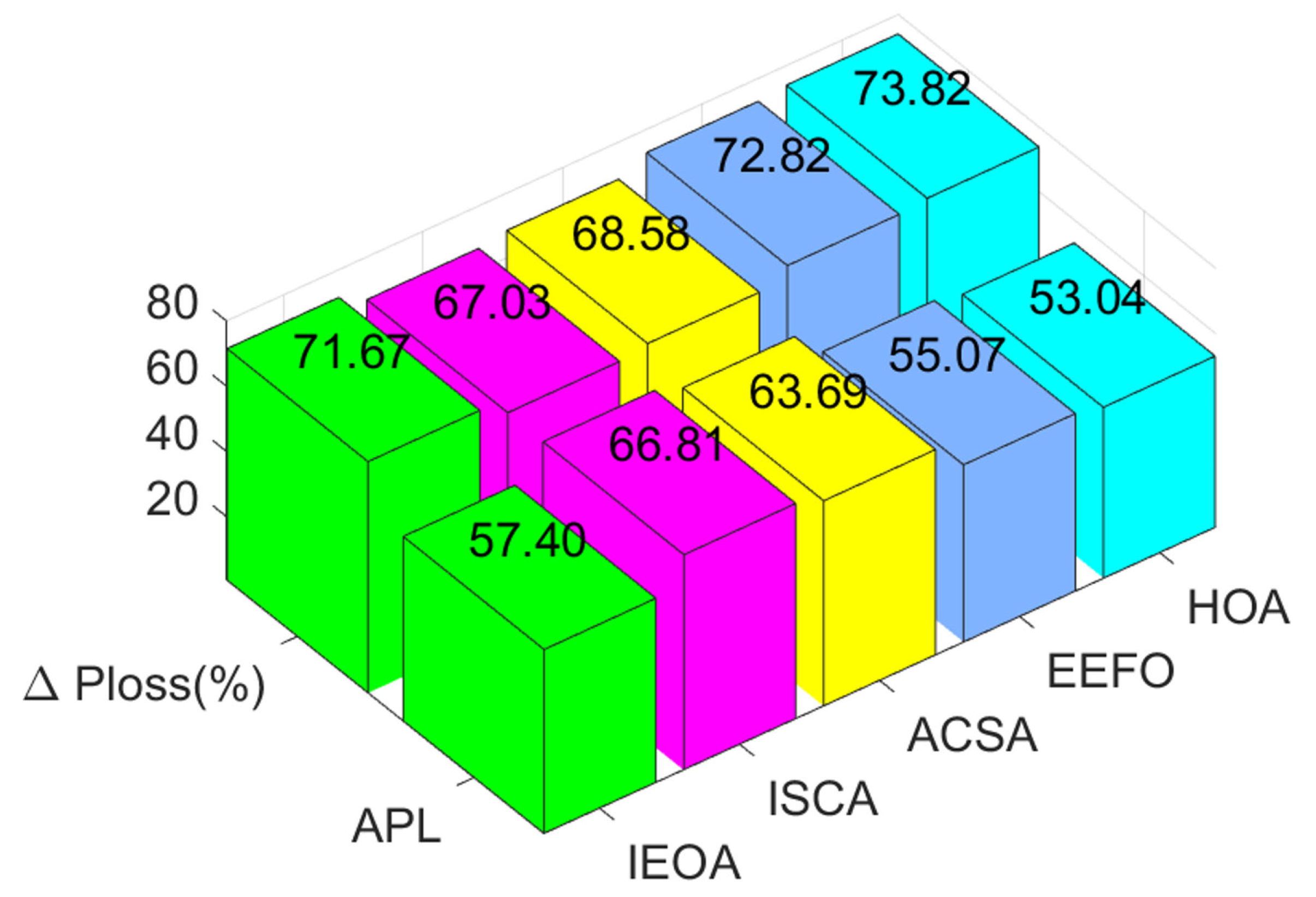
- The suitability of the HOA for the optimal DG allocation problem is examined through a comparative analysis between the HOA and other contemporary methods like the IEOA, improved sine cosine algorithm (ISCA), and electric eel foraging optimization (EEFO), as reported in the literature.
2. Mathematical Formulation
2.1. Objective Functions
2.1.1. APL Minimization
2.1.2. CAEL Minimization
2.2. Constraints
2.2.1. Power Balance
2.2.2. Bus Voltage
2.2.3. DG Size and Power Factor
2.2.4. DG Location
2.2.5. Radial Topology
2.3. Load Modeling
2.4. DG Modeling
3. HOA Algorithm
- Step 1:
- InitializationFor initializing the hiker with a random position in the search space, the following equation is used:where is the jth dimension of the ith hiker and is a uniformly distributed number ranging between 0 and 1. and are the upper bound and lower bound of the jth decision variable, respectively.
- Step 2:
- Velocity EvaluationThe HOA’s mathematical foundation is derived from Waldo Tobler’s hiking function. The exponential function to determine the hiker’s speed is as follows:where and are the terrain slope and velocity of the ith hiker at the tth iteration, respectively. can be defined as follows:While hiking, the and denote the distance covered by the hiker in the horizontal and vertical dimensions, respectively. Accordingly, for the ith hiker is updated in the tth iteration; it ranges between and . It is worth mentioning that a higher value of drags the HOA into the exploration phase, while a lower value tends towards the exploitation phase.
- Step 3:
- UpdateThe updated velocity of hiker i, utilizing group social thinking and individual cognitive abilities, can be determined using the following equation:Here, is a uniformly distributed number range between 0 and 1. Similarly, varies between 1 and 3, and its value decreases with the iteration count to shift the search mechanism from exploration to exploitation. and are the positions of the ith hiker and lead hiker in the tth iteration, respectively.The updated position of hiker i based on the updated velocity is evaluated as follows:
4. Results and Discussion
4.1. Base Case: System Analysis Without DG and NR
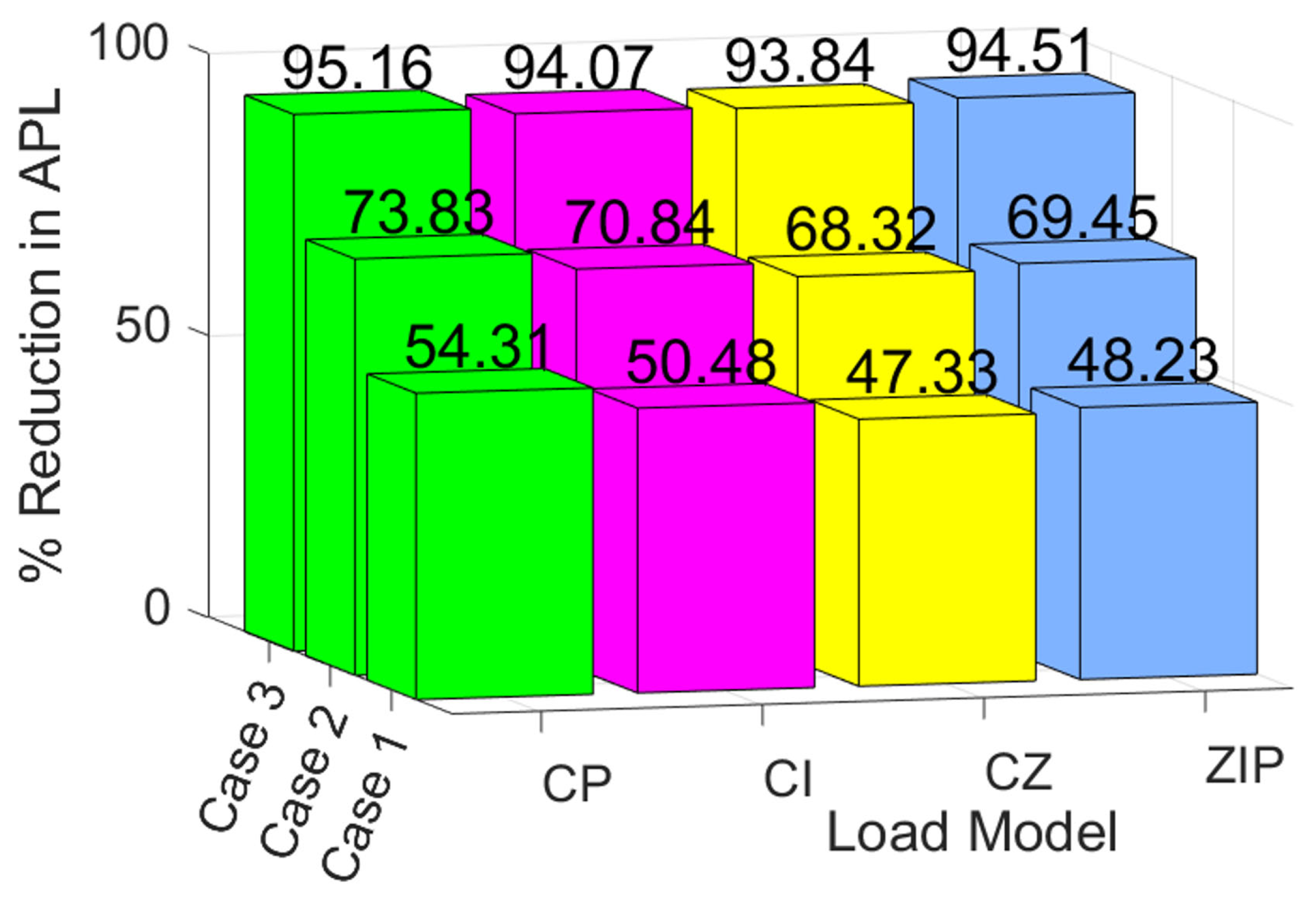
4.2. Case 1: Minimization of Power Loss at the ZPF Considering Different Load Models
4.3. Case 2: Minimization of Power Loss at the UPF Considering Different Load Models
4.4. Case 3: Minimization of Power Loss at the OPF with Consideration of Different Load Models
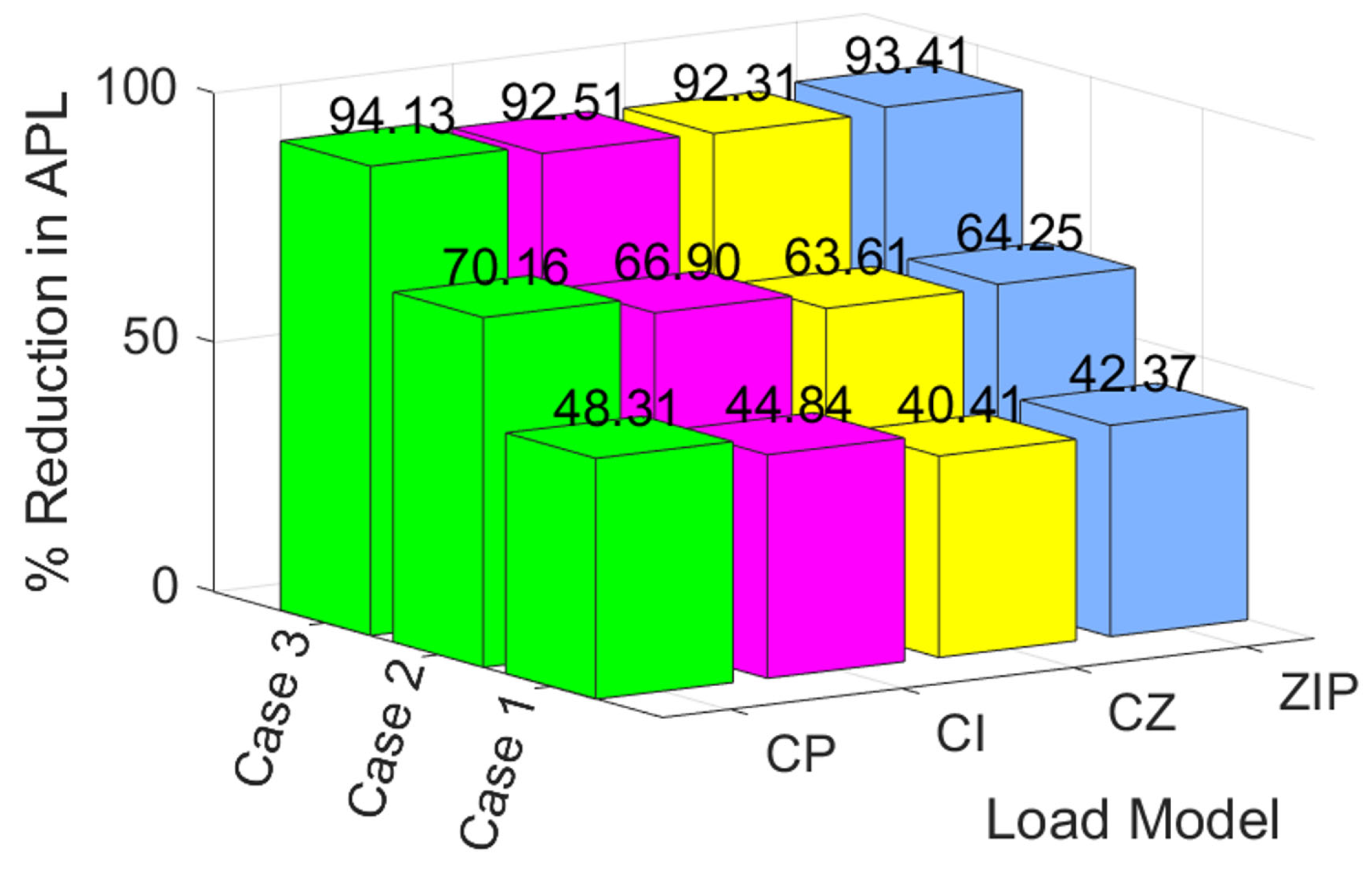
4.5. Case 4: CAEL Minimization at the ZPF Considering Both Different Load Models and Load Levels
4.6. Case 5: CAEL Minimization at the UPF Considering Both Different Load Models and Load Levels
4.7. Case 6: CAEL Minimization at the OPF Considering Both Different Load Models and Load Levels
5. Parameter Sensitivity Analysis
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| DG | Distributed generation |
| DN | Distribution network |
| NR | Network reconfiguration |
| APL | Active power loss |
| CAEL | Cost of annual energy loss |
| HOA | Hiking optimization algorithm |
| PF | Power factor |
| VP | Voltage profile |
| WT | Wind turbine |
| PV | Photovoltaic |
| LSF | Loss sensitivity factor |
| ESS | Energy storage system |
| MILP | Mixed-integer linear programming |
| MOGWO | Multi-objective grey wolf optimization |
| BA | Bat algorithm |
| DSTATCOM | Distribution static compensator |
| OLTC | On-load tap changer |
| SC | Shunt capacitor |
| DERs | Distributed energy resources |
| SOS | Symbiotic organism search |
| EOA | Equilibrium optimization algorithm |
| CP | Constant power |
| CI | Constant current |
| CZ | Constant impedance |
| ZPF | Zero power factor |
| UPF | Unity power factor |
| OPF | Optimal power factor |
| BVD | Bus voltage deviation |
| ACA | Ant colony algorithm |
| BPSO | Binary particle swarm optimization |
| EEFO | Electric eel foraging optimization |
| IEOA | Improved equilibrium optimization algorithm |
| ISCA | Improved sine cosine algorithm |
| ACSA | Adaptive cuckoo search algorithm |
| DNPL-GA | Dynamic Node Priority List Genetic Algorithm |
| CMSO | Corrected Moth Search Optimization |
| MA-SCA | Multi-Agent Sine-Cosine Algorithm |
| WOA | Whale Optimization Algorithm |
| NSGA | Non-dominated sorting genetic algorithm |
References
- Maurya, P.; Tiwari, P.; Pratap, A. Electric eel foraging optimization algorithm for distribution network reconfiguration with distributed generation for power system performance enhancement considerations different load models. Comput. Electr. Eng. 2024, 119, 109531. [Google Scholar] [CrossRef]
- Badran, O.; Mekhilef, S.; Mokhlis, H.; Dahalan, W. Optimal reconfiguration of distribution system connected with distributed generations: A review of different methodologies. Renew. Sustain. Energy Rev. 2017, 73, 854–867. [Google Scholar] [CrossRef]
- Kandasamy, M.; Thangavel, R.; Arumugam, T.; Jayaram, J.; Kim, W.; Geem, Z. Performance enhancement of radial power distribution networks using network reconfiguration and optimal planning of solar photovoltaic- based distributed generation and shunt capacitors. Sustainability 2022, 14, 11480. [Google Scholar]
- Jayabarathi, T.; Raghunathan, T.; Mithulananthan, N.; Cherukuri, S.; Loknath Sai, G. Enhancement of distribution system performance with reconfiguration, distributed generation and capacitor bank deployment. Heliyon 2024, 10, e26343. [Google Scholar] [CrossRef]
- Gao, H.; Wang, R.; He, S.; Wang, L.; Liu, J.; Chen, Z. A Cloud-Edge Collaboration Solution for Distribution Network Reconfiguration Using Multi-Agent Deep Reinforcement Learning. IEEE Trans. Power Syst. 2024, 39, 3867–3879. [Google Scholar] [CrossRef]
- Kashyap, M.; Kansal, S.; Verma, R. Sizing and allocation of DGs in a passive distribution network under various loading scenarios. Electr. Power Syst. Res. 2022, 209, 108046. [Google Scholar] [CrossRef]
- Iyer, A.; Patel, C. Optimal placement of distributed energy resources and shunt capacitors with consideration of existing on-line tap changer using honey badger optimization. In Proceedings of the 2023 Third International Conference on Advances in Electrical, Computing, Communication and Sustainable Technologies (ICAECT), Bhilai, India, 5–6 January 2023; pp. 1–6. [Google Scholar]
- Nematollahi, A.; Rahiminejad, A.; Vahidi, B. A novel multi-objective optimization algorithm based on Lightning Attachment Procedure Optimization algorithm. Appl. Soft Comput. 2019, 75, 404–427. [Google Scholar] [CrossRef]
- Adegoke, S.; Sun, Y.; Adegoke, A.; Ojeniyi, D. Optimal placement of distributed generation to minimize power loss and improve voltage stability. Heliyon 2024, 10, e39298. [Google Scholar] [CrossRef]
- Saxena, V.; Manna, S.; Rajput, S.; Kumar, P.; Sharma, B.; Alsharif, M.; Kim, M. Navigating the complexities of distributed generation: Integration, challenges, and solutions. Energy Rep. 2024, 12, 3302–3322. [Google Scholar] [CrossRef]
- Azad, S.; Amiri, M.; Heris, M.; Mosallanejad, A.; Ameli, M. A novel analytical approach for optimal placement and sizing of distributed generations in radial electrical energy distribution systems. Sustainability 2021, 13, 10224. [Google Scholar] [CrossRef]
- Prakash, P.; Meena, D.; Malik, H.; Alotaibi, M.; Khan, I. A novel analytical approach for optimal integration of renewable energy sources in distribution systems. Energies 2022, 15, 1341. [Google Scholar] [CrossRef]
- Wu, X.; Yang, C.; Han, G.; Ye, Z.; Hu, Y. Energy loss reduction for distribution networks with energy storage systems via loss sensitive factor method. Energies 2022, 15, 5453. [Google Scholar] [CrossRef]
- Bendriss, B.; Sayah, S.; Hamouda, A. Efficient multi-objective optimization approach for solving optimal DG placement and sizing problem in distribution systems. J. Eng. Res. 2024. [Google Scholar] [CrossRef]
- Pareja, G.; Luis, A.; López-Lezama Jesús, M.; Gómez Carmona, O. A mixed-integer linear programming model for the simultaneous optimal distribution network reconfiguration and optimal placement of distributed generation. Energies 2022, 15, 3063. [Google Scholar] [CrossRef]
- El-Ela, A.; El-Sehiemy, R.; Shaheen, A.; Ellien, A. Optimal allocation of distributed generation units correlated with fault current limiter sites in distribution systems. IEEE Syst. J. 2020, 15, 2148–2155. [Google Scholar] [CrossRef]
- Khenissi, I.; Guesmi, T.; Alshammari, B.; Alqunun, K.; Almalaq, A.; Alturki, M.; Neji, R. A hybrid chaotic bat algorithm for optimal placement and sizing of dg units in radial distribution networks. Energy Rep. 2024, 12, 1723–1741. [Google Scholar] [CrossRef]
- Neda, O. Optimal amalgamation of DG units in radial distribution system for techno-economic study by improved SSA: Practical case study. Electr. Power Syst. Res. 2025, 241, 111365. [Google Scholar] [CrossRef]
- Dash, S.; Mishra, S.; Abdelaziz, A.; Hong, J.; Geem, Z. Optimal planning of multitype DGs and D-STATCOMs in power distribution network using an efficient parameter free metaheuristic algorithm. Energies 2022, 15, 3433. [Google Scholar] [CrossRef]
- Ramshanker, A.; Isaac, J.; Jeyeraj, B.; Swaminathan, J.; Kuppan, R. Optimal DG placement in power systems using a modified flower pollination algorithm. Energies 2022, 15, 8516. [Google Scholar] [CrossRef]
- Ganguly, S.; Samajpati, D. Distributed generation allocation with on-load tap changer on radial distribution networks using adaptive genetic algorithm. Appl. Soft Comput. 2017, 59, 45–67. [Google Scholar] [CrossRef]
- Singh, P.; Bishnoi, S.; Meena, N. Moth search optimization for optimal DERs integration in conjunction to OLTC tap operations in distribution systems. IEEE Syst. J. 2019, 14, 880–888. [Google Scholar] [CrossRef]
- Sunil, A.; Venkaiah, C. Multi-objective adaptive fuzzy campus placement based optimization algorithm for optimal integration of DERs and DSTATCOMs. J. Energy Storage 2024, 75, 109682. [Google Scholar] [CrossRef]
- Mahdavi, E.; Asadpour, S.; Macedo, L.; Romero, R. Reconfiguration of Distribution Networks with Simultaneous Allocation of Distributed Generation Using the Whale Optimization Algorithm. Energies 2023, 16, 4560. [Google Scholar] [CrossRef]
- Prasad, K.; Kollu, R.; Ramkumar, A.; Ramesh, A. A multi-objective strategy for optimal DG and capacitors placement to improve technical, economic, and environmental benefits. Int. J. Electr. Power Energy Syst. 2025, 165, 110491. [Google Scholar] [CrossRef]
- Huy, T. Enhancing distribution system performance via distributed generation placement and reconfiguration based on improved symbiotic organisms search. J. Control Sci. Eng. 2023, 2023, 6081991. [Google Scholar] [CrossRef]
- Shaheen, A.; Elsayed, A.; El-Sehiemy, R.; Abdelaziz, A. Equilibrium optimization algorithm for network reconfiguration and distributed generation allocation in power systems. Appl. Soft Comput. 2021, 98, 106867. [Google Scholar] [CrossRef]
- Oladejo, S.; Ekwe, S.; Mirjalili, S. The Hiking Optimization Algorithm: A novel human-based metaheuristic approach. Knowl.-Based Syst. 2024, 296, 111880. [Google Scholar] [CrossRef]
- Huy, T.; Van Tran, T.; Vo, D.; Nguyen, H. An improved metaheuristic method for simultaneous network reconfiguration and distributed generation allocation. Alex. Eng. J. 2022, 61, 8069–8088. [Google Scholar] [CrossRef]
- Kasaei, M.; Gandomkar, M. Loss reduction in distribution network using simultaneous capacitor placement and reconfiguration with ant colony algorithm. In Proceedings of the 2010 Asia-Pacific Power And Energy Engineering Conference, Chengdu, China, 28–31 March 2010; pp. 1–4. [Google Scholar]
- Raut, U.; Mishra, S. An improved sine–cosine algorithm for simultaneous network reconfiguration and DG allocation in power distribution systems. Appl. Soft Comput. 2020, 92, 106293. [Google Scholar] [CrossRef]
- Nguyen, T.; Truong, A.; Phung, T. A novel method based on adaptive cuckoo search for optimal network reconfiguration and distributed generation allocation in distribution network. Int. J. Electr. Power Energy Syst. 2016, 78, 801–815. [Google Scholar] [CrossRef]
- Meena, N.; Swarnkar, A.; Gupta, N.; Niazi, K. Optimal integration of DERs in coordination with existing VRs in distribution networks. IET Gener. Transm. Distrib. 2018, 12, 2520–2529. [Google Scholar] [CrossRef]
- Patel, C.; Tailor, T. Multi-agent based sine–cosine algorithm for optimal integration of DERs with consideration of existing OLTC in distribution networks. Appl. Soft Comput. 2022, 117, 108387. [Google Scholar] [CrossRef]


| Load Level | Multiplying Factor | Duration (H) | Energy Price (USD/MWh) |
|---|---|---|---|
| Low (L) | 0.5 | 2000 | 55 |
| Normal (N) | 1.0 | 5260 | 72 |
| Peak (P) | 1.6 | 1500 | 120 |
| Case No. | Objective | Power Factor | Load Model | Loading Scenario |
|---|---|---|---|---|
| 1 | Power loss minimization | ZPF | CP, CI, CZ, ZIP | Normal |
| 2 | Power loss minimization | UPF | CP, CI, CZ, ZIP | Normal |
| 3 | Power loss minimization | OPF | CP, CI, CZ, ZIP | Normal |
| 4 | CAEL minimization | ZPF | CP, CI, CZ, ZIP | Low, normal, high |
| 5 | CAEL minimization | UPF | CP, CI, CZ, ZIP | Low, normal, high |
| 6 | CAEL minimization | OPF | CP, CI, CZ, ZIP | Low, normal, high |
| Load Model | (MW) | (MVAr) | BVD |
|---|---|---|---|
| CP | 202.66 | 135.1 | 1.7009 |
| CI | 176.6 | 117.5 | 1.5847 |
| CZ | 156.9 | 104.2 | 1.4907 |
| ZIP | 162.6 | 108 | 1.5184 |
| CP | CI | CZ | ZIP | |
|---|---|---|---|---|
| Open switch | 9, 14, 37, 32, 7 | 14, 37, 9, 7, 36 | 9, 37, 14, 7, 32 | 7, 14, 9, 36, 37 |
| DG location | 30, 8, 24 | 24, 22, 30 | 8, 24, 30 | 30, 24, 12 |
| DG size (kVAr) | 962.85, 445.62, 523.94 | 509.03, 463.64, 981.67 | 391.58, 501.36, 925.93 | 969.09, 506.04, 339.59 |
| APL (kW) | 92.59 | 87.46 | 82.64 | 84.17 |
| RPL (kVAr) | 69.83 | 64.81 | 62.09 | 62.24 |
| BVD (pu) | 0.8238 | 0.7945 | 0.7958 | 0.7864 |
| Vmin (pu) | 0.9595 | 0.9598 | 0.9610 | 0.9604 |
| CP | CI | CZ | ZIP | |
|---|---|---|---|---|
| Open switch | 14, 27, 9, 31, 7 | 14, 28, 31, 7, 9 | 9, 14, 7, 27, 31 | 7, 14, 27, 30, 9 |
| DG location | 12, 25, 18 | 33, 12, 25 | 18, 22, 25 | 25, 18, 12 |
| DG size (kW) | 568.59, 1445.65, 642.61 | 615.95, 571.45, 1365.37 | 590.10, 733.32, 1378.06 | 1245.70, 776.81, 558.50 |
| APL (kW) | 53.04 | 51.49 | 49.70 | 49.67 |
| RPL (kVAr) | 40.32 | 38.89 | 37.92 | 38.61 |
| BVD (pu) | 0.4705 | 0.4728 | 0.4811 | 0.5073 |
| Vmin (pu) | 0.9766 | 0.9769 | 0.9766 | 0.9705 |
| CP | CI | CZ | ZIP | |
|---|---|---|---|---|
| Open switch | 13, 33, 21, 17, 26 | 25, 36, 21, 11, 33 | 5, 11, 26, 15, 35 | 13, 35, 20, 23, 15 |
| DG location | 30, 24, 9 | 24, 30, 15 | 25, 32, 8 | 32, 8, 25 |
| DG size (kW) | 1090.00, 897.64, 1065.23 | 980.75, 1011.96, 940.99 | 1122.05, 747.43, 1122.98 | 745.60, 1190.64, 1149.23 |
| DG OPF | 0.7255, 0.8997, 0.9042 | 0.9129, 0.7000, 0.9047 | 0.8062, 0.7967, 0.9024 | 0.8001, 0.8915, 0.8207 |
| APL (kW) | 9.81 | 10.48 | 9.67 | 8.92 |
| RPL (kVAr) | 7.93 | 8.80 | 8.01 | 7.12 |
| BVD (pu) | 0.1056 | 0.1096 | 0.1071 | 0.0895 |
| Vmin (pu) | 0.9934 | 0.9927 | 0.9874 | 0.9920 |
| CP | CI | CZ | ZIP | |
|---|---|---|---|---|
| Open switch | 9, 7, 14, 36, 37 | 32, 7, 14, 37, 9 | 7, 9, 28, 14, 36 | 10, 37, 7, 14, 36 |
| DG location | 31, 30, 9 | 30, 32, 9 | 31, 16, 25 | 33, 16, 30 |
| DG size (kVAr) | [105.38, 422.90, 170.98] L; [211.60, 852.08, 349.83] N; [1291.87, 591.04, 616.37] P | [386.61, 100.00, 185.89] L; [864.22, 138.32, 370.02] N; [943.61, 641.76, 884.36] P | [258.47, 117.88, 390.85] L; [502.58, 226.15, 777.83] N; [1059.75, 344.49, 1002.88] P | [100.00, 123.97, 419.89] L; [142.00, 239.64, 886.57] N; [842.98, 473.03, 1119.36] P |
| APL (kW) | 23.34 L, 96.38 N, 264.95 P | 22.62 L, 90.55 N, 236.73 P | 22.34 L, 87.00 N, 216.65 P | 22.44 L, 88.10 N, 228.81 P |
| CAEL (USD) | 86,759.06 | 79,391.2 | 74,403.96 | 77,018.28 |
| Vmin (pu) | 0.98 L, 0.96 N, 0.95 P | 0.98 L, 0.96 N, 0.95 P | 0.98 L, 0.95 N, 0.95 P | 0.98 L, 0.96 N, 0.95 P |
| CP | CI | CZ | ZIP | |
|---|---|---|---|---|
| Open switch | 28, 11, 33, 34, 31 | 33, 11, 30, 14, 28 | 31, 11, 33, 34, 28 | 34, 11, 28, 33, 31 |
| DG location | 30, 33, 26 | 8, 33, 25 | 29, 33, 7 | 18, 29, 8 |
| DG size (kW) | [518.69, 351.09, 488.43] L; [1046.26, 704.18, 984.97] N; [1224.25, 1034.16, 1456.59] P | [481.89, 265.99, 627.98] L; [967.73, 529.32, 1254.05] N; [1308.18, 906.66, 1499.48] P | [554.63, 348.74, 489.11] L; [1099.69, 685.88, 974.36] N; [1485.48, 1048.61, 1180.88] P | [357.95, 571.58, 414.77] L; [710.51, 1130.57, 828.0] N; [1105.99, 1500.0, 1109.01] P |
| APL (kW) | 13.35 L, 54.70 N, 151.54 P | 13.13 L, 52.65 N, 136.63 P | 12.32 N, 48.62 L, 126.25 P | 12.47 L, 49.47 N, 128.36 P |
| CAEL (USD) | 49,461.38 | 45,976.84 | 42,495.25 | 43,211.8 |
| Vmin (pu) | 0.99 L, 0.97 N, 0.95 P | 0.99 L, 0.97 N, 0.95 P | 0.99 L, 0.98 N, 0.96 P | 0.99 L, 0.98 N, 0.96 P |
| CP | CI | CZ | ZIP | |
|---|---|---|---|---|
| Open switch | 27, 35, 14, 33, 15 | 35, 33, 26, 13, 16 | 11, 15, 27, 13, 33 | 33, 35, 10, 37, 32 |
| DG location | 25, 9, 32 | 32, 29, 9 | 32, 25, 8 | 30, 25, 15 |
| DG size (kW) | [604.13, 455.80, 323.36] L; [1102.24, 916.34, 752.80] N; [1496.75, 1019.16, 1199.09] P | [309.08, 558.42, 477.24] L; [615.21, 1095.03, 957.73] N; [891.28, 1486.31, 1337.40] P | [369.71, 541.68, 474.80] L; [739.21, 1088.25, 952.04] N; [1072.57, 1499.95, 1142.49] P | [478.83, 423.54, 455.71] L; [955.48, 845.95, 908.74] N; [1415.81, 923.61, 1375.58] P |
| DG OPF | [0.86, 0.90, 0.70] L; [0.80, 0.90, 0.80] N; [0.75, 0.82, 0.80] P | [0.82, 0.78, 0.90] L; [0.82, 0.77, 0.90] N; [0.81, 0.70, 0.88] P | [0.80, 0.80, 0.90] L; [0.79, 0.80, 0.90] N; [0.76, 0.76, 0.84] P | [0.71, 0.90, 0.90] L; [0.70, 0.90, 0.90] N; [0.70, 0.81, 0.88] P |
| APL (kW) | 2.77 L, 10.87 N, 35.64 P | 2.75 L, 10.97 N, 32.43 P | 2.56 L, 10.21 N, 31.24 | P 2.73 L, 10.87 N, 32.56 P |
| CAEL (USD) | 10,837.91 | 10,294.22 | 9770.612 | 10,277.72 |
| Vmin (pu) | 1.00 L, 0.99 N, 0.98 P | 1.00 L, 0.99 N, 0.99 P | 1.00 L, 0.99 N, 0.99 P | 1.00 L, 0.99 N, 0.99 P |
| DNPL-GA | CMSO | MASCA | HOA | |
|---|---|---|---|---|
| Case 5 | 68,753 | 64,820 | 63,965 | 49,461.38 |
| Case 6 | 18,033 | 16,906 | 13,961 | 10,837.9 |
| Comb1 Npop = 10 Niter = 1500 | Comb2 Npop = 20 Niter = 750 | Comb3 Npop = 30 Niter = 500 | Comb4 Npop = 40 Niter = 375 | Comb5 Npop = 50 Niter = 300 | ||
|---|---|---|---|---|---|---|
| Case 1 | Best | 95.08 | 94.13 | 92.59 | 93.30 | 94.91 |
| Worst | 107.89 | 102.47 | 96.88 | 100.38 | 101.10 | |
| Average | 99.49 | 97.79 | 94.86 | 97.00 | 97.13 | |
| Standard deviation | 3.456 | 2.169 | 1.189 | 1.980 | 1.792 | |
| Case 4 | Best | 90,068.41 | 88,399.45 | 86,759.06 | 88,739.63 | 89,895.84 |
| Worst | 101,368.35 | 100,388.47 | 90,150.75 | 97,217.11 | 98,384.57 | |
| Average | 93,802.98 | 92,610.89 | 88,636.56 | 91,303.83 | 93,696.51 | |
| Standard deviation | 3379.80 | 3344.56 | 1079.50 | 2517.44 | 2700.61 |
| Comb3 vs. | Comb1 | Comb2 | Comb4 | Comb5 |
|---|---|---|---|---|
| Case 1 | 3.05 × 10−6 | 7.54 × 10−6 | 7.93 × 10−6 | 1.92 × 10−4 |
| Case 4 | 4.13 × 10−6 | 4.22 × 10−6 | 4.22× 10−6 | 4.14 × 10−6 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Patel, C.D.; Tailor, T.K.; Shah, S.S.; Sharma, G.; Bokoro, P.N. Techno-Economic Enhancement of Distribution Network by Optimal DG Allocation Along with Network Reconfiguration Considering Different Load Models and Levels. Energies 2025, 18, 3005. https://doi.org/10.3390/en18123005
Patel CD, Tailor TK, Shah SS, Sharma G, Bokoro PN. Techno-Economic Enhancement of Distribution Network by Optimal DG Allocation Along with Network Reconfiguration Considering Different Load Models and Levels. Energies. 2025; 18(12):3005. https://doi.org/10.3390/en18123005
Chicago/Turabian StylePatel, Chintan D., Tarun Kumar Tailor, Samyak S. Shah, Gulshan Sharma, and Pitshou N. Bokoro. 2025. "Techno-Economic Enhancement of Distribution Network by Optimal DG Allocation Along with Network Reconfiguration Considering Different Load Models and Levels" Energies 18, no. 12: 3005. https://doi.org/10.3390/en18123005
APA StylePatel, C. D., Tailor, T. K., Shah, S. S., Sharma, G., & Bokoro, P. N. (2025). Techno-Economic Enhancement of Distribution Network by Optimal DG Allocation Along with Network Reconfiguration Considering Different Load Models and Levels. Energies, 18(12), 3005. https://doi.org/10.3390/en18123005






