Modeling Homogeneous, Stratified, and Diffusion Combustion in Hydrogen SI Engines Using the Wiebe Approach
Abstract
1. Introduction
2. Research Methodology
2.1. A Mathematical Zero-Dimensional Model of the Engine Power Cycle
2.2. Base Combustion Model
2.3. Evaluation of Combustion Duration from Experimental Data
2.4. Engines, Operating Modes, and Modeling Features
3. Results and Discussion
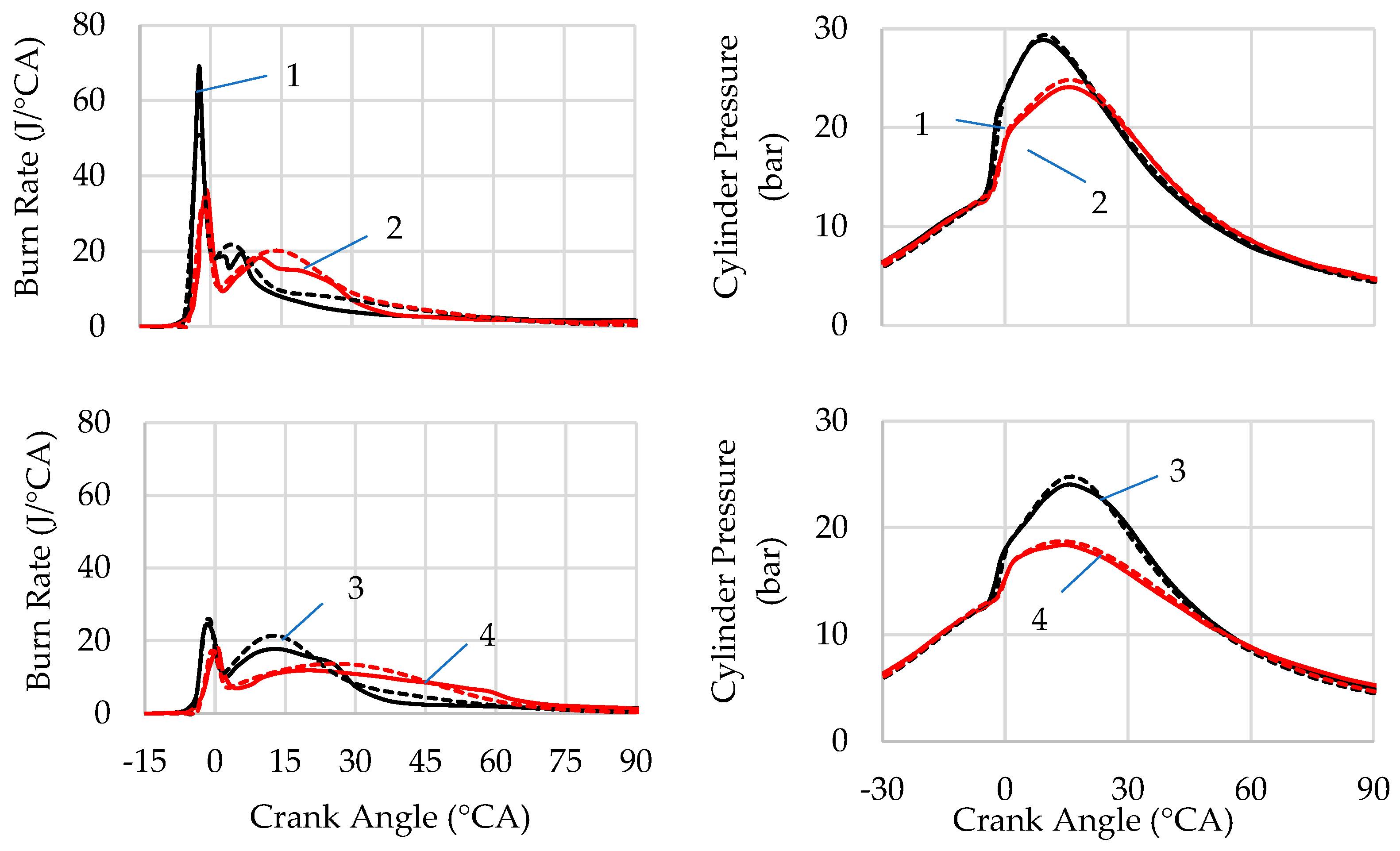
3.1. The Influence of Mixture Composition and Engine Speed on the Hydrogen Combustion
3.2. The Influence of Mixture Stratification on the Hydrogen Combustion
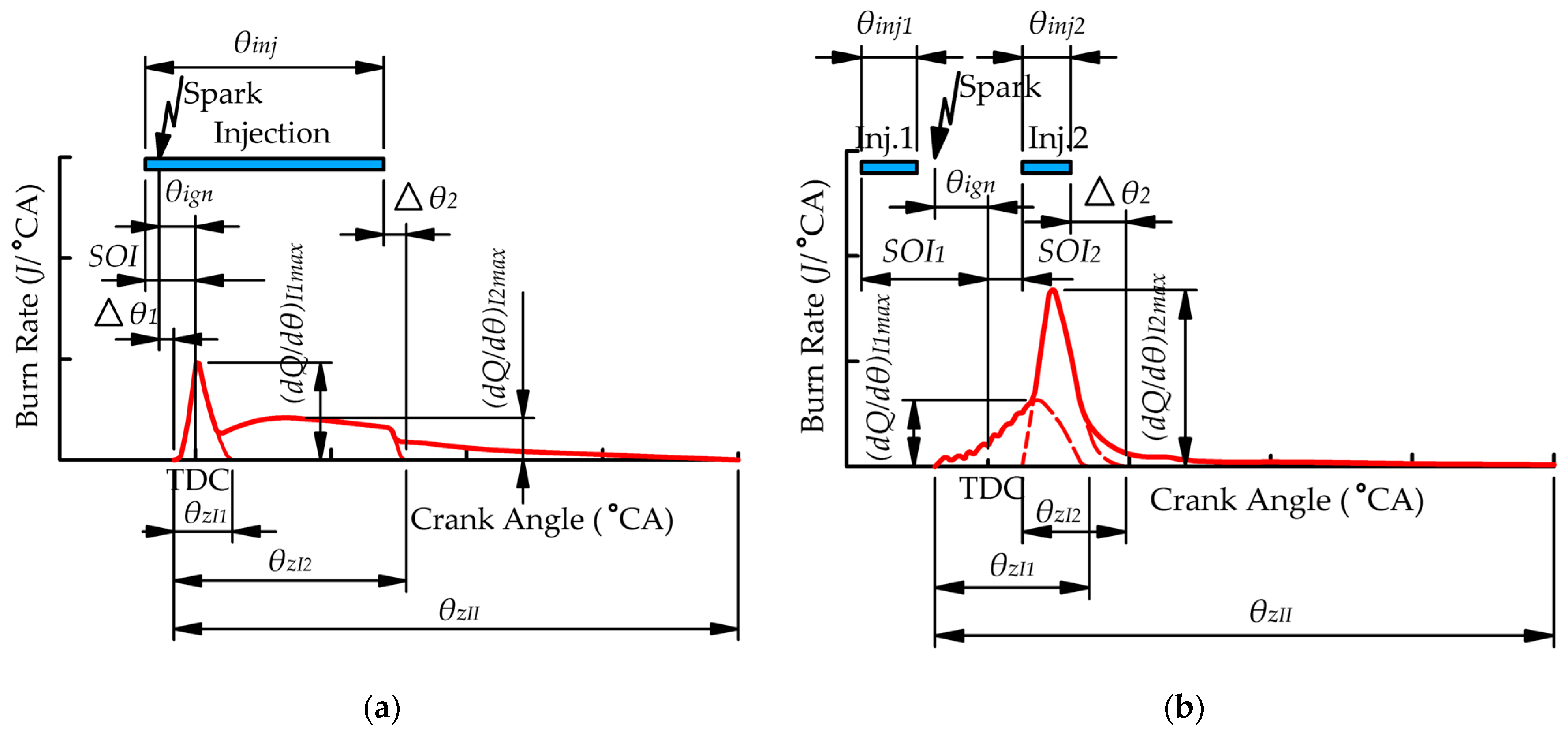
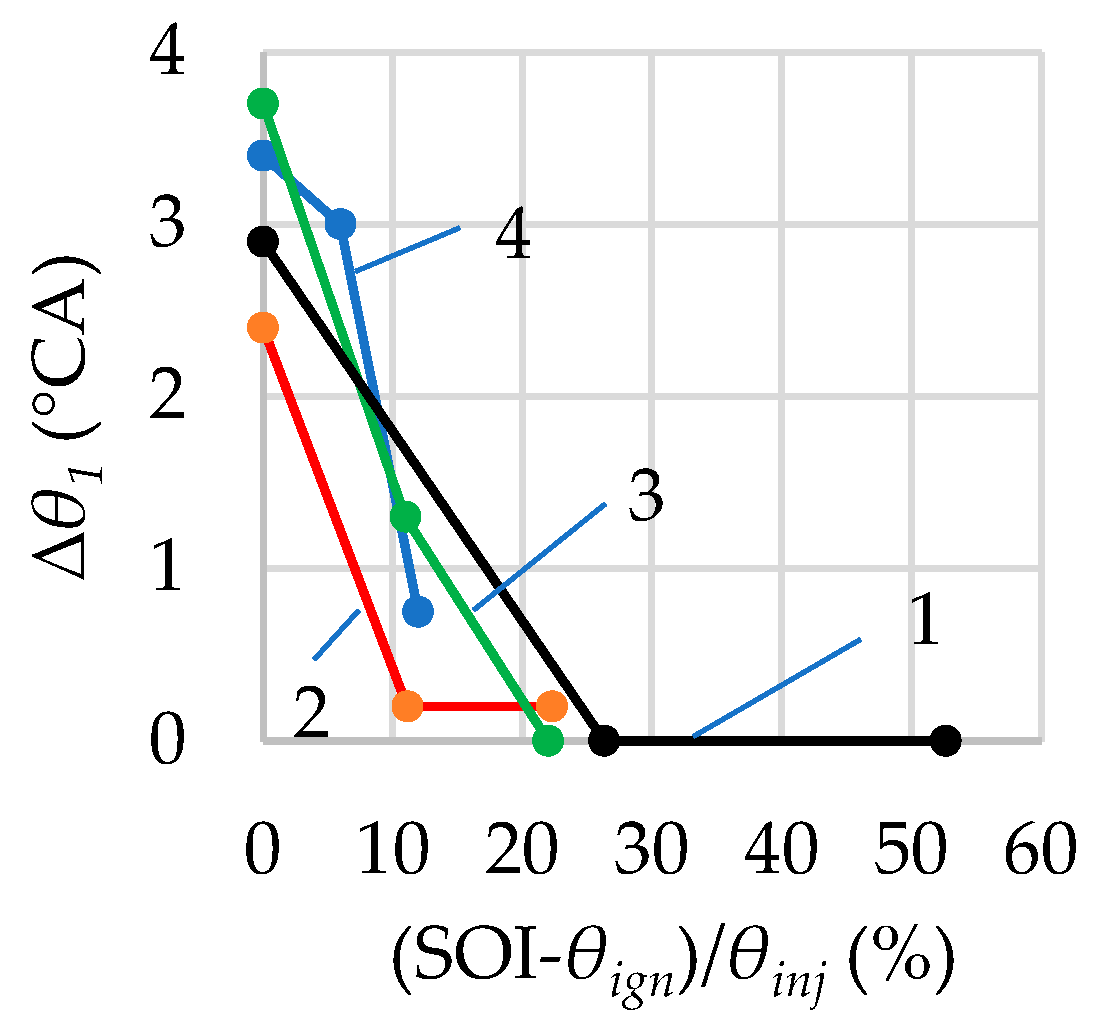
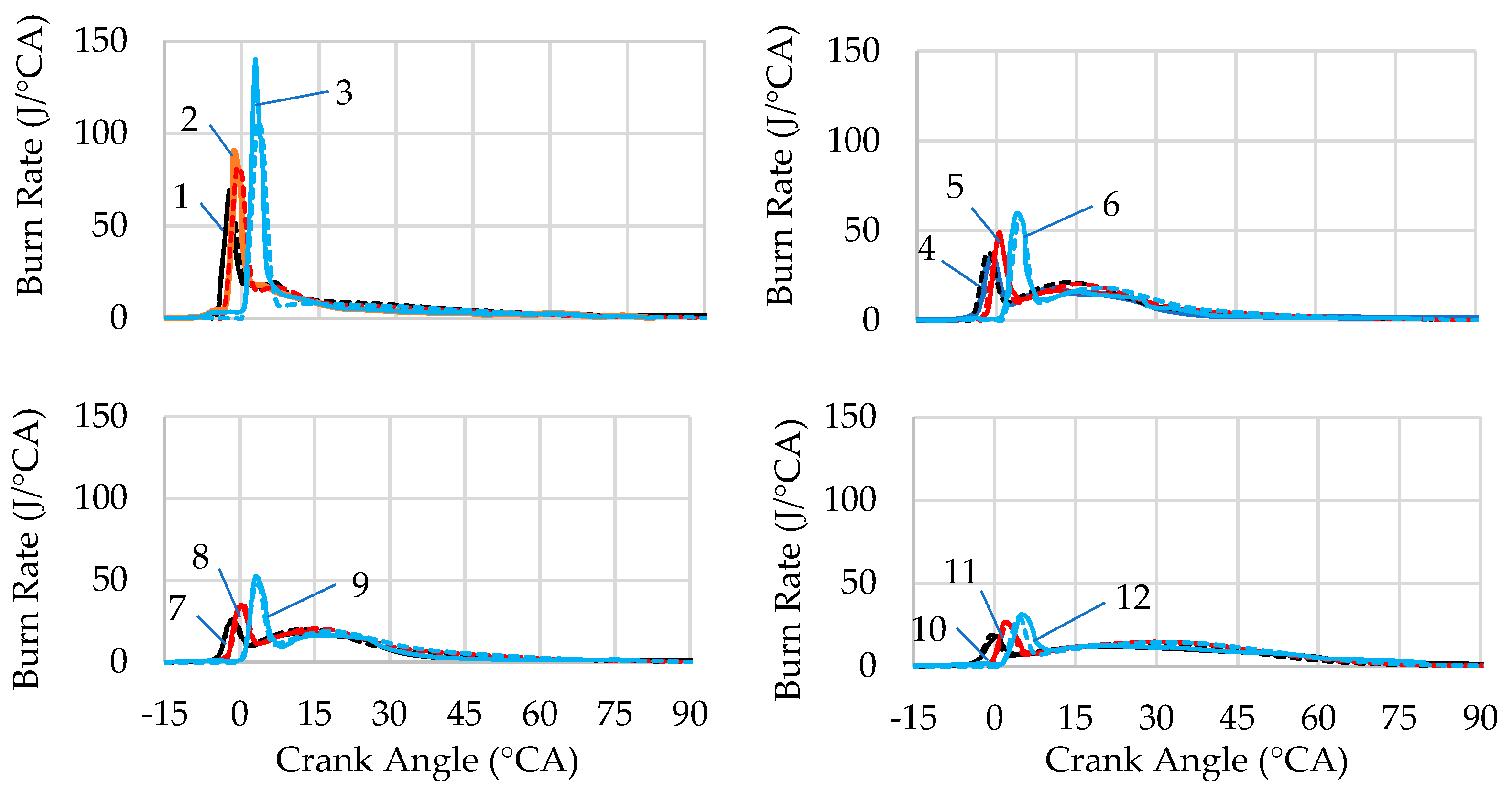
3.3. Influence of Single Injection and Ignition Parameters on Hydrogen Combustion in Jet-Guided Operation
3.4. Influence of Dual Injection and Ignition Parameters on Hydrogen Combustion
3.5. The Scope of Application of the Developed Combustion Model and Directions for Its Further Development
4. Conclusions
- An approach to determining the duration of premixed and diffusion combustion based on experimental combustion characteristics using the Wiebe function is proposed.
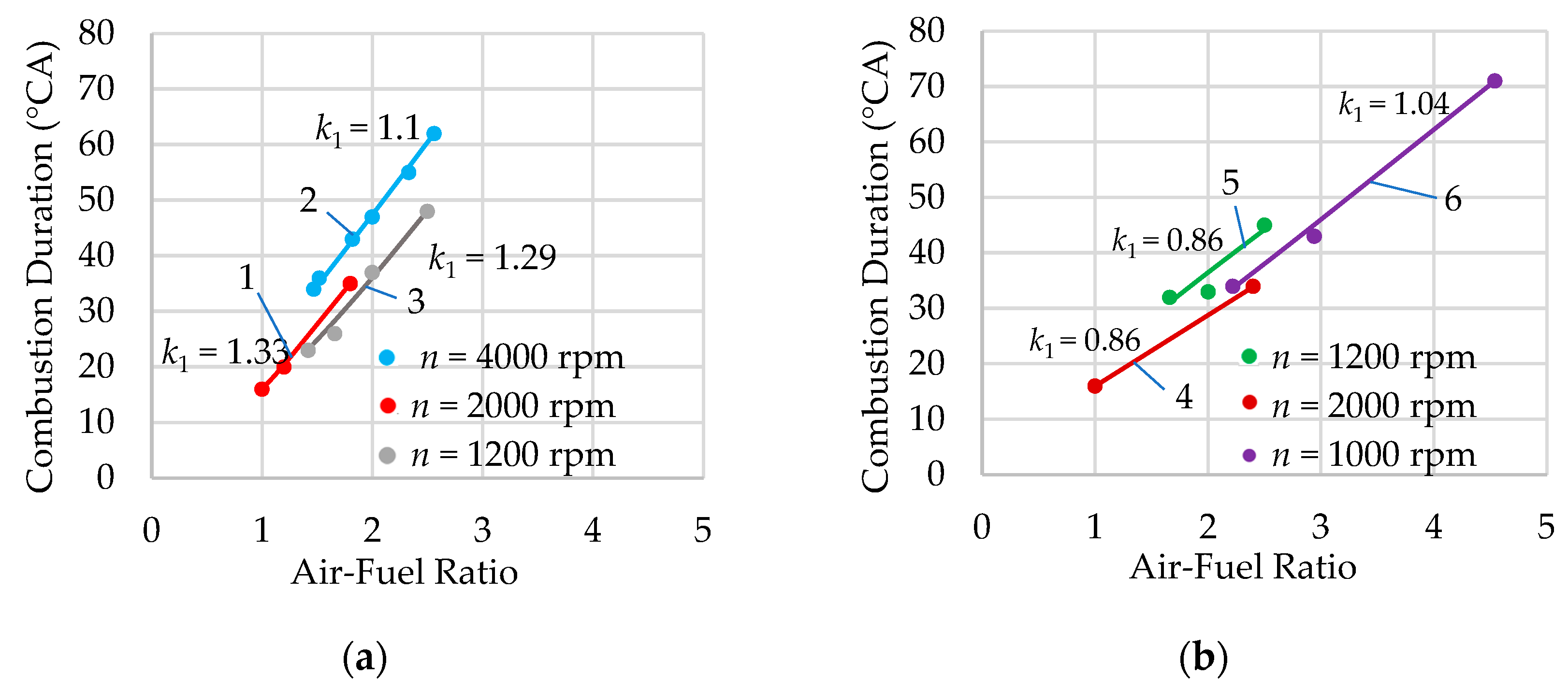
- It was found that the influence of mixture composition on fuel combustion duration in PFI engines is greater at low engine speeds than at high engine speeds. This influence can be accounted for in the model by selecting the coefficient k1 in Formula (4) from the proposed range or by using the empirical Equation (5).
- For two different hydrogen engines, the influence of engine speed on the duration of stoichiometric mixture combustion is approximately the same. Accordingly, the model coefficient k2, which accounts for this parameter, does not change significantly between these two engines. This allows for the broader generalization of the obtained results.
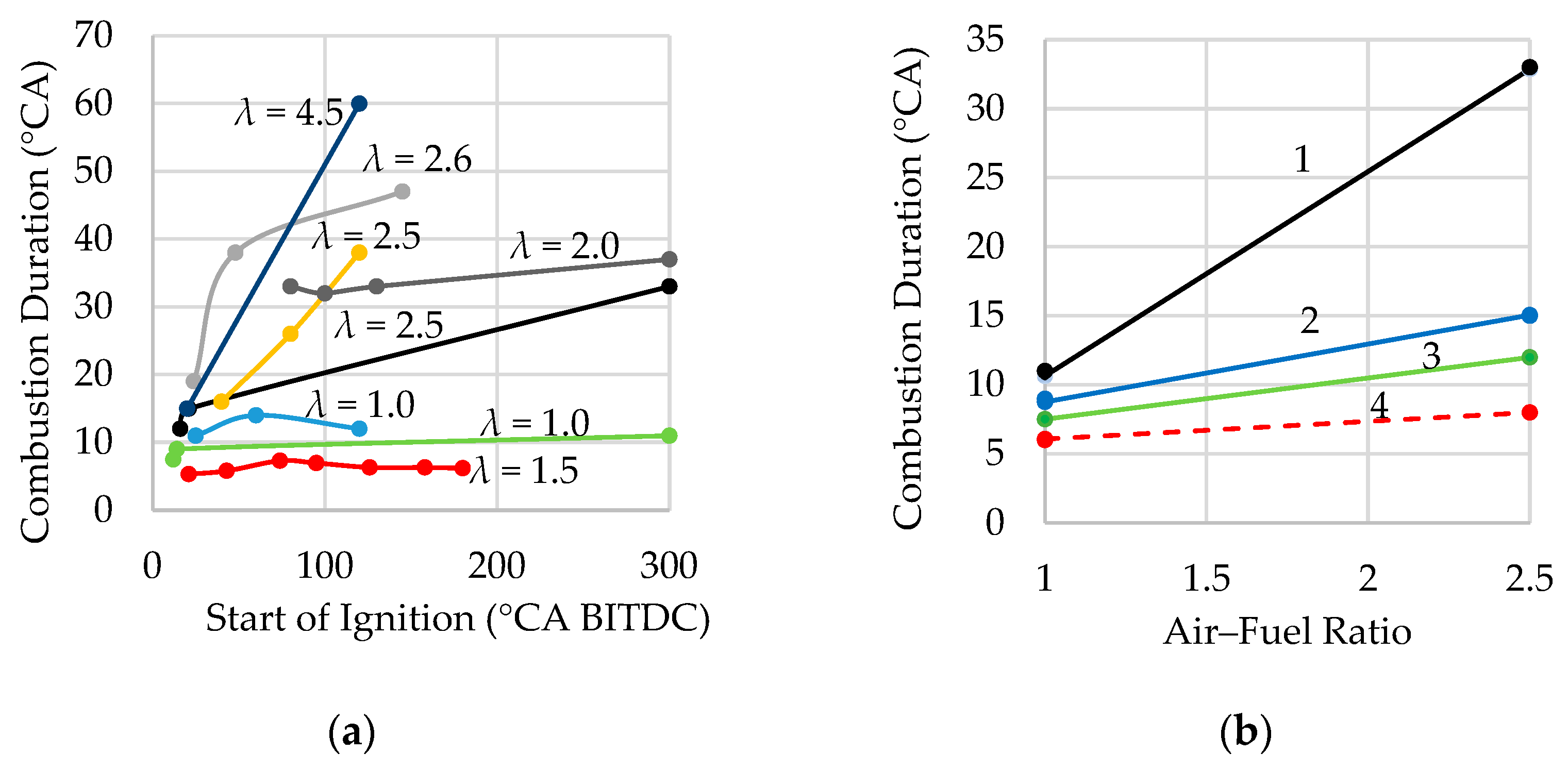
- Significant mixture stratification in DI engines occurs when injection begins later than 80° CA BTDC, and the influence of late SOI on hydrogen combustion duration increases with λ. This effect is accounted for in the combustion model by selecting lower values of the coefficient k1 for late injection from the specified range.
- Mixture stratification is sometimes accompanied by an increase in the fraction of fuel burning in lean-mixture zones. Model coefficients have been proposed to account for the kinetics of premixed combustion and relatively slow combustion.
- In single injection and jet-guided operation, strong mixture stratification occurs, and the influence of mixture composition on the combustion duration in the flame front is minimal. A methodology for determining the duration of premixed combustion and the amount of fuel burned in the flame front has been proposed.
- The duration of diffusion combustion in single injection and jet-guided operation correlates well with the fuel injection duration at various injection pressures, ignition timings, and injector needle lifts. Values or ranges for the model coefficients accounting for the kinetics of different types of combustion at this injection strategy are provided.
- In dual injection, the duration and rate of premixed combustion are determined by the SOI and the mixture composition in the cylinder at the moment of ignition, while the characteristics of diffusion combustion are mainly influenced by ignition timing and the parameters of the second fuel injection. Values or ranges for the model coefficients that account for the kinetics of different types of combustion at this injection strategy are provided.
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| BITDC | Before Ignition Top Dead Center |
| BMEP | Brake Mean Effective Pressure |
| BSFC | Brake Specific Fuel Consumption |
| BTE | Brake Thermal Efficiency |
| CA | Crank Angle |
| CFD | Computational Fluid Dynamics |
| DI | Direct Injection |
| ITE | Indicated Thermal Efficiency |
| MFB50 | 50% Mass Fraction Burned |
| NOx | Nitrogen Oxides |
| PFI | Port Fuel Injection |
| SOI | Start of Injection |
References
- Stepien, Z.A. Comprehensive Overview of Hydrogen-Fueled Internal Combustion Engines: Achievements and Future Challenges. Energies 2021, 14, 6504. [Google Scholar] [CrossRef]
- Gao, W.; Fu, Z.; Li, Y.; Li, Y.; Zou, J. Progress of Performance, Emission, and Technical Measures of Hydrogen Fuel Internal-Combustion Engines. Energies 2022, 15, 7401. [Google Scholar] [CrossRef]
- Gerke, U. Numerical Analysis of Mixture Formation and Combustion in a Hydrogen Direct-Injection Internal Combustion Engine. Ph.D. Thesis, Swiss Federal Institute of Technology, Zürich, Switzerland, 2007. [Google Scholar]
- Beyer, A.; Balmelli, M.; Merotto, L.; Wright, Y.M.; Soltic, P.; Kulzer, A. DIH2jet (DI Hydrogen Combustion Process). In 2024 Stuttgart International Symposium on Automotive and Engine Technology; Kulzer, A.C., Reuss, H.C., Eds.; Springer Vieweg: Wiesbaden, Germany, 2024; pp. 53–67. [Google Scholar]
- Beyer, A.; Berner, H.J.; Casal Kulzer, A. A Non-premixed Hydrogen Combustion Process Using a Spark-Ignited Hydrogen Jet. In Proceedings of the 2023 Conference on Powertrains with Renewable Energy Carriers, Stuttgart, Germany, 28–29 November 2023. [Google Scholar]
- Mohammadi, A.; Shioji, M.; Nakai, Y.; Ishikura, W.; Tabo, E. Performance and Combustion Characteristics of a Direct Injection SI Hydrogen Engine. Int. J. Hydrogen Energy 2007, 32, 296–304. [Google Scholar] [CrossRef]
- Spuller, C. Dieselbrennverfahren mit Wasserstoff für PKW-Anwendung. Ph.D. Thesis, Technische Universität Graz, Graz, Austria, 2011. [Google Scholar]
- Fouquet, M. Niedrigstemissionskonzept für einen Wasserstoffbetriebenen Verbrennungsmotor. Ph.D. Thesis, Technische Universität München, München, Germany, 2012. [Google Scholar]
- Wiebe, I.I. Progress in Engine Cycle Analysis: Combustion Rate and Cycle Processes; Mashgiz: Moscow, Russia, 1962. (In Russian) [Google Scholar]
- Ghojel, J.I. Review of the Development and Applications of the Wiebe Function: A Tribute to the Contribution of Ivan Wiebe to Engine Research. Int. J. Engine Res. 2010, 11, 297–312. [Google Scholar] [CrossRef]
- Takáts, M.; Macek, J.; Polášek, M.; Kovar, Z.; Beroun, S.; Schloz, C. Hydrogen-Fuelled Reciprocating Engine as an Automotive Prime Mover? In Proceedings of the FISITA World Automotive Congress, Paris, France, 25–30 September 1988.
- Ma, J.; Su, Y.; Zhou, Y.; Zhang, Z. Simulation and prediction on the performance of a vehicle’s hydrogen engine. Int. J. Hydrogen Energy 2003, 28, 77–83. [Google Scholar] [CrossRef]
- Geiler, J.N.; Springer, K.M.; Lorenz, T.; Blomberg, M.; Achenbach, J.; Bloch, P. H2 Engine Hybrid Powertrain for Future Light Commercial Vehicles. In Internationaler Motorenkongress 2023; Heintzel, A., Ed.; Springer Vieweg: Wiesbaden, Germany, 2024; pp. 53–67. [Google Scholar]
- Verhelst, S.; Sierens, R. A Quasi-Dimensional Model for the Power Cycle of a Hydrogen-Fuelled ICE. Int. J. Hydrogen Energy 2007, 32, 3545–3554. [Google Scholar] [CrossRef]
- Blizard, N.C.; Keck, J.C. Experimental and Theoretical Investigation of Turbulent Burning Model for Internal Combustion Engines. SAE Int. J. 1974, 740191. [Google Scholar] [CrossRef]
- Tabaczynski, R.J.; Ferguson, C.R.; Radhakrishnan, K. A Turbulent Entrainment Model for Spark-Ignition Engine Combustion. SAE Int. J. 1977, 70647. [Google Scholar]
- Hires, S.D.; Tabaczynski, R.J.; Novak, J.M. The Prediction of Ignition Delay and Combustion Intervals for a Homogeneous Charge, Spark Ignition Engine. SAE Int. J. 1978, 780232. [Google Scholar]
- Tabaczynski, R.J.; Trinker, F.H.; Shannon, B.A.S. Further Refinement and Validation of a Turbulent Flame Propagation Model for Spark-Ignition Engines. Combust. Flame 1980, 39, 111–121. [Google Scholar] [CrossRef]
- Millo, F.; Piano, A.; Rolando, L.; Accurso, F.; Gullino, F.; Roggio, S.; Bianco, A.; Pesce, F.; Vassallo, A.; Rossi, R. Synergetic Application of Zero-, One-, and Three-Dimensional Computational Fluid Dynamics Approaches for Hydrogen-Fuelled Spark Ignition Engine Simulation. SAE Int. J. Engines 2022, 15, 561–580. [Google Scholar] [CrossRef]
- Rezaei, R.; Hayduk, C.; Sens, M.; Fandakov, A. Hydrogen Combustion—A Puzzle Piece of Future Sustainable Transportation! In Proceedings of the SIA 2020 Digital Powertrain & Energy, Rouen, France, 16–29 November 2020.
- D’Errico, G.; Onorati, A.; Ellgas, S. 1D Thermo-Fluid Dynamic Modelling of an S.I. Single-Cylinder H2 Engine with Cryogenic Port Injection. Int. J. Hydrogen Energy 2008, 33, 5829–5841. [Google Scholar] [CrossRef]
- Gülder, Ö.L. Turbulent premixed flame propagation models for different combustion regimes. Proc. Combust. Inst. 1990, 23, 743–750. [Google Scholar] [CrossRef]
- Lipatnikov, A.N.; Chomiak, J. Turbulent flame speed and thickness: Phenomenology, evaluation, and application in multi-dimensional simulations. Prog. Energy Combust. Sci. 2002, 28, 1–74. [Google Scholar] [CrossRef]
- Zimont, V.L. Gas premixed combustion at high turbulence. Turbulent flame closure combustion model. Exp. Therm. Fluid Sci. 2000, 21, 179–186. [Google Scholar] [CrossRef]
- Peters, N. Turbulent Combustion; Cambridge University Press: Cambridge, UK, 2000. [Google Scholar]
- Changwei, J.; Jinxin, Y.; Xiaolong, L.; Bo, Z.; Shuofeng, W.; Binbin, G. A quasi-dimensional model for combustion performance prediction of an SI hydrogen-enriched methanol engine. Int. J. Hydrogen Energy 2016, 41, 17676–17686. [Google Scholar]
- Ma, F.; Deng, J.; Qi, Z.; Li, S.; Chen, R.; Yang, H.; Zhao, S. Study on the calibration coefficients of a quasi-dimensional model for HCNG engine. Int. J. Hydrogen Energy 2011, 36, 9278–9285. [Google Scholar] [CrossRef]
- Schmelcher, R.; Kulzer, A.; Gal, T.; Vacca, A.; Chiodi, M. Numerical Investigation of Injection and Mixture Formation in Hydrogen Combustion Engines by Means of Different 3D-CFD Simulation Approaches; SAE Technical Paper 2024-01-3007; SAE International: Warrendale, PA, USA, 2024. [Google Scholar] [CrossRef]
- Li, J.; Gao, W.; Zhang, P.; Ye, Y.; Wei, Z. Effects study of injection strategies on hydrogen-air formation and performance of hydrogen direct injection internal combustion engine. Int. J. Hydrogen Energy 2019, 44, 26000–26011. [Google Scholar] [CrossRef]
- Wallner, T.; Scarcelli, R.; Nande, A.; Naber, J. Assessment of multiple injection strategies in a direct injection hydrogen research engine. SAE Int. J. Engines 2009, 2, 1701–1709. [Google Scholar] [CrossRef]
- Verhelst, S.; Wallner, T. Hydrogen-fueled internal combustion engines. Prog. Energy Combust. Sci. 2009, 35, 490–527. [Google Scholar] [CrossRef]
- Convergent Science. CONVERGE Manual, v3.0; Convergent Science: Madison, WI, USA, 2020. [Google Scholar]
- Givler, S.; Raju, M.; Pomraning, E.; Senecal, P.; Salman, N.; Reese, R. Gasoline Combustion Modeling of Direct and Port-Fuel Injected Engines Using a Reduced Chemical Mechanism; SAE Technical Paper 2013-01-1098; SAE International: Warrendale, PA, USA, 2013. [Google Scholar]
- Broatch, A.; Margot, X.; Novella, R.; Gomez-Soriano, J. Combustion noise analysis of partially premixed combustion concept using gasoline fuel in a 2-stroke engine. Energy 2016, 107, 612–624. [Google Scholar] [CrossRef]
- Chiodi, M.; Tortorella, C.; Haro, E.H.; Pipolo, M.; Reuss, H.; Wagner, A. Advancing internal combustion engines and fuel innovation: A modular approach to 3D virtual prototyping for a carbon-neutral future. In 2024 Stuttgart International Symposium on Automotive and Engine Technology; Kulzer, A.C., Reuss, H.C., Eds.; Springer Vieweg: Wiesbaden, Germany, 2024; pp. 85–101. [Google Scholar]
- Srivastava, D.K.; Agarwal, A.K.; Datta, A.; Maurya, R.K. Advances in Internal Combustion Engine Research; Springer: Singapore, 2018. [Google Scholar]
- Pathak, B.; Shekh, A.; Patel, N.; Patel, V. Review analysis on CFD techniques and numerical methods for IC engines fueled with diesel and biofuels. J. Adv. Res. Fluid Mech. Therm. Sci. 2023, 110, 40–62. [Google Scholar] [CrossRef]
- Osetrov, O.; Haas, R. Simulation of Hydrogen Combustion in Spark Ignition Engines Using a Modified Wiebe Model; SAE Technical Paper 2024-01-3016; SAE International: Warrendale, PA, USA, 2024. [Google Scholar]
- Dyachenko, V.G. Theory of Internal Combustion Engines: Textbook; KhNADU: Kharkiv, Ukraine, 2009. (In Russian) [Google Scholar]
- Heywood, J.B. Internal Combustion Engine Fundamentals; McGraw-Hill: Singapore, 1988. [Google Scholar]
- Tang, X.; Kabat, D.M.; Natkin, R.J.; Stockhausen, W.F. Ford P2000 Hydrogen Engine Dynamometer Development; SAE Technical Paper 2002-01-0242; SAE International: Warrendale, PA, USA, 2002. [Google Scholar]
- Bai-gang, S.; Hua-yu, T.; Fu-shui, L. The distinctive characteristics of combustion duration in hydrogen internal combustion engine. Int. J. Hydrogen Energy 2014, 39, 14472–14478. [Google Scholar] [CrossRef]
- Grabner, P.; Eichlseder, H.; Gerbig, F.; Gerke, U. Optimisation of a hydrogen internal combustion engine with inner mixture formation. In Proceedings of the 1st International Symposium on Hydrogen Internal Combustion Engines, Graz, Austria, 28–29 September 2006. [Google Scholar]
- Tsujimura, T.; Suzuki, Y. Development of a large-sized direct injection hydrogen engine for a stationary power generator. Int. J. Hydrogen Energy 2019, 44, 11355–11369. [Google Scholar] [CrossRef]
- Tanno, S.; Ito, Y.; Michikawauchi, R.; Nakamura, M.; Tomita, H. High-efficiency and low-NOx hydrogen combustion by high pressure direct injection. SAE Int. J. Engines 2010, 3, 259–268. [Google Scholar] [CrossRef]
- Eichlseder, H.; Wallner, T.; Gerbig, F.; Fickel, H. Gemischbildungs- und Verbrennungskonzepte für den Wasserstoff-Verbrennungsmotor. In Proceedings of the 7th Symposium ‘Entwicklungstendenzen bei Ottomotoren’, Technische Akademie Esslingen, Ostfildern, Germany, 12–13 December 2004. [Google Scholar]
- Huang, Z.; Wang, L.; Pan, H.; Li, J.; Wang, T.; Wang, L. Experimental study on the impact of hydrogen injection strategy on combustion performance in internal combustion engines. ACS Omega 2023, 8, 39427–39436. [Google Scholar] [CrossRef]
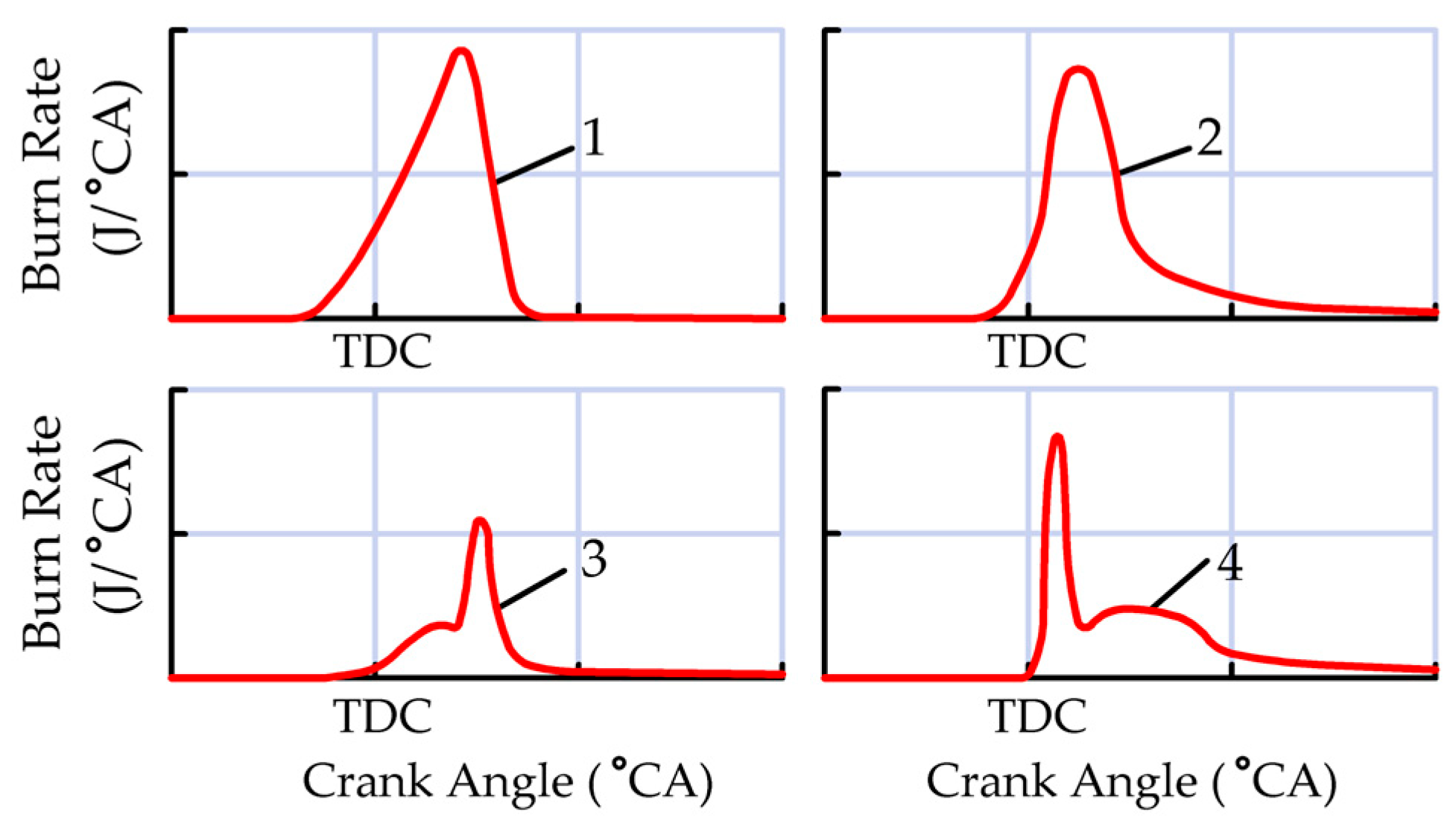








| Parameter | Value [41] | Value [4,5] | Value [3] | Value [7] |
|---|---|---|---|---|
| Number of Cylinders | 4 | 1 | 1 | 1 |
| Bore (mm) | 84 | 83 | 84 | 84 |
| Stroke (mm) | 88 | 92.4 | 90 | 90 |
| Compression Ratio | 12.5 | 10 | 10 | 17.5 |
| Valve Number | 16 | 4 | 4 | 4 |
| Hydrogen Injection Method | PFI | DI | DI | DI |
| Mode | Source | IMEP (bar) | Speed (rpm) | Air–Fuel Ratio | Spark Timing (° CA BITDC) | SOI1 (° CA BITDC) | SOI2 (° CA BITDC) | Fuel Mass Share: First Injection/Second Injection (%/%) | Injection Pressure (bar) | Injector Needle Lift |
|---|---|---|---|---|---|---|---|---|---|---|
| 1 | [4] | 5 | 1500 | 1 | −1 | 300 | - | 100/0 | 200 | - |
| 2 | [4] | 5 | 1500 | 1 | −1 | 14 | - | 100/0 | 200 | - |
| 3 | [4] | 5 | 1500 | 1 | −1 | 12 | - | 100/0 | 200 | - |
| 4 | [4] | 5 | 1500 | 1 | 9 | 12 | - | 100/0 | 200 | - |
| 5 | [4] | 10 | 1500 | 2.5 | 8 | 300 | - | 100/0 | 200 | - |
| 6 | [4] | 10 | 1500 | 2.5 | −1 | 21 | - | 100/0 | 200 | - |
| 7 | [4] | 10 | 1500 | 2.5 | −3 | 16 | - | 100/0 | 200 | - |
| 8 | [4] | 10 | 1500 | 2.5 | 8 | 12 | - | 100/0 | 200 | - |
| 9 | [5] | 4.84 | 1500 | 1 | 8 | 8 | - | 100/0 | 190 | low |
| 10 | [5] | 4.84 | 1500 | 1 | 4 | 8 | - | 100/0 | 190 | low |
| 11 | [5] | 4.84 | 1500 | 1 | 0 | 8 | - | 100/0 | 190 | low |
| 12 | [5] | 4.98 | 1500 | 1 | 8 | 8 | - | 100/0 | 190 | high |
| 13 | [5] | 4.98 | 1500 | 1 | 4 | 8 | - | 100/0 | 190 | high |
| 14 | [5] | 4.98 | 1500 | 1 | 0 | 8 | - | 100/0 | 190 | high |
| 15 | [5] | 5.18 | 1500 | 1 | 8 | 8 | - | 100/0 | 80 | low |
| 16 | [5] | 5.18 | 1500 | 1 | 4 | 8 | - | 100/0 | 80 | low |
| 17 | [5] | 5.18 | 1500 | 1 | 0 | 8 | - | 100/0 | 80 | low |
| 18 | [5] | 4.7 | 1500 | 1 | 8 | 8 | - | 100/0 | 80 | high |
| 19 | [5] | 4.7 | 1500 | 1 | 4 | 8 | - | 100/0 | 80 | high |
| 20 | [5] | 4.7 | 1500 | 1 | 0 | 8 | - | 100/0 | 80 | high |
| 21 | [7] | 6.3 | 2000 | 2.5 | 11 | 27 | −8 | 60/40 | 200 | - |
| 22 | [7] | 7.1 | 1100 | 2 | 10 | 27 | −10 | 50/50 | 200 | - |
| 23 | [3] | 10 | 2000 | 1 | 13 | 120 | 5 | 45/55 | 150 | - |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Osetrov, O.; Haas, R. Modeling Homogeneous, Stratified, and Diffusion Combustion in Hydrogen SI Engines Using the Wiebe Approach. Energies 2025, 18, 3004. https://doi.org/10.3390/en18123004
Osetrov O, Haas R. Modeling Homogeneous, Stratified, and Diffusion Combustion in Hydrogen SI Engines Using the Wiebe Approach. Energies. 2025; 18(12):3004. https://doi.org/10.3390/en18123004
Chicago/Turabian StyleOsetrov, Oleksandr, and Rainer Haas. 2025. "Modeling Homogeneous, Stratified, and Diffusion Combustion in Hydrogen SI Engines Using the Wiebe Approach" Energies 18, no. 12: 3004. https://doi.org/10.3390/en18123004
APA StyleOsetrov, O., & Haas, R. (2025). Modeling Homogeneous, Stratified, and Diffusion Combustion in Hydrogen SI Engines Using the Wiebe Approach. Energies, 18(12), 3004. https://doi.org/10.3390/en18123004





