Intelligent Fuzzy Multi-Criteria Decision-Making for Energy-Saving Building Designs in Construction

Abstract

The transition toward sustainable construction practices has intensified the demand for intelligent and energy-efficient building components, particularly smart window technologies. While numerous innovations exist, the selection of the most optimal smart window solution is difficult due to the trade-offs among conflicting criteria such as energy performance, economic feasibility, environmental impact, and user comfort. This study proposes an integrated Fuzzy Multi-Criteria Decision-Making (FMCDM) framework for selecting smart window technologies. The methodology combines the Fuzzy Analytic Hierarchy Process (FAHP) to determine criterion weights and the Technique for Order of Preference by Similarity to Ideal Solution (TOPSIS) to rank alternatives. Nine sustainability-related criteria across the environmental, economic, and social dimensions were evaluated using expert input. The results identify thermochromic smart windows as the optimal choice. This research contributes a structured, adaptable, and scalable FMCDM framework for sustainable technology selection, with broader applicability to green product design and decision-making in the construction and energy sectors.

1. Introduction

Climate change remains one of the most critical challenges worldwide, primarily driven by greenhouse gas emissions from human activity. To mitigate these effects, integrating renewable energy sources with energy conservation measures is essential for reducing emissions and minimizing the negative impacts of climate change on society [1]. Buildings are among the leading contributors to global energy consumption, accounting for nearly 40% of the total energy usage, with nearly half dedicated to heating and cooling. Windows, as the primary interface for energy exchange between indoor and outdoor environments, are responsible for 20–40% of the energy losses. This highlights the urgent need for energy-efficient solutions in building designs. One promising approach to address this challenge is the development of smart windows, which minimize energy consumption while maintaining natural light and aesthetics. These advanced windows, also known as switchable or dynamic windows, leverage cutting-edge materials and technologies to adjust their visual properties in response to external factors such as light, heat, and voltage. By optimizing indoor climate conditions and reducing reliance on artificial heating and cooling systems, smart windows play a crucial role in promoting sustainable, energy-efficient buildings. 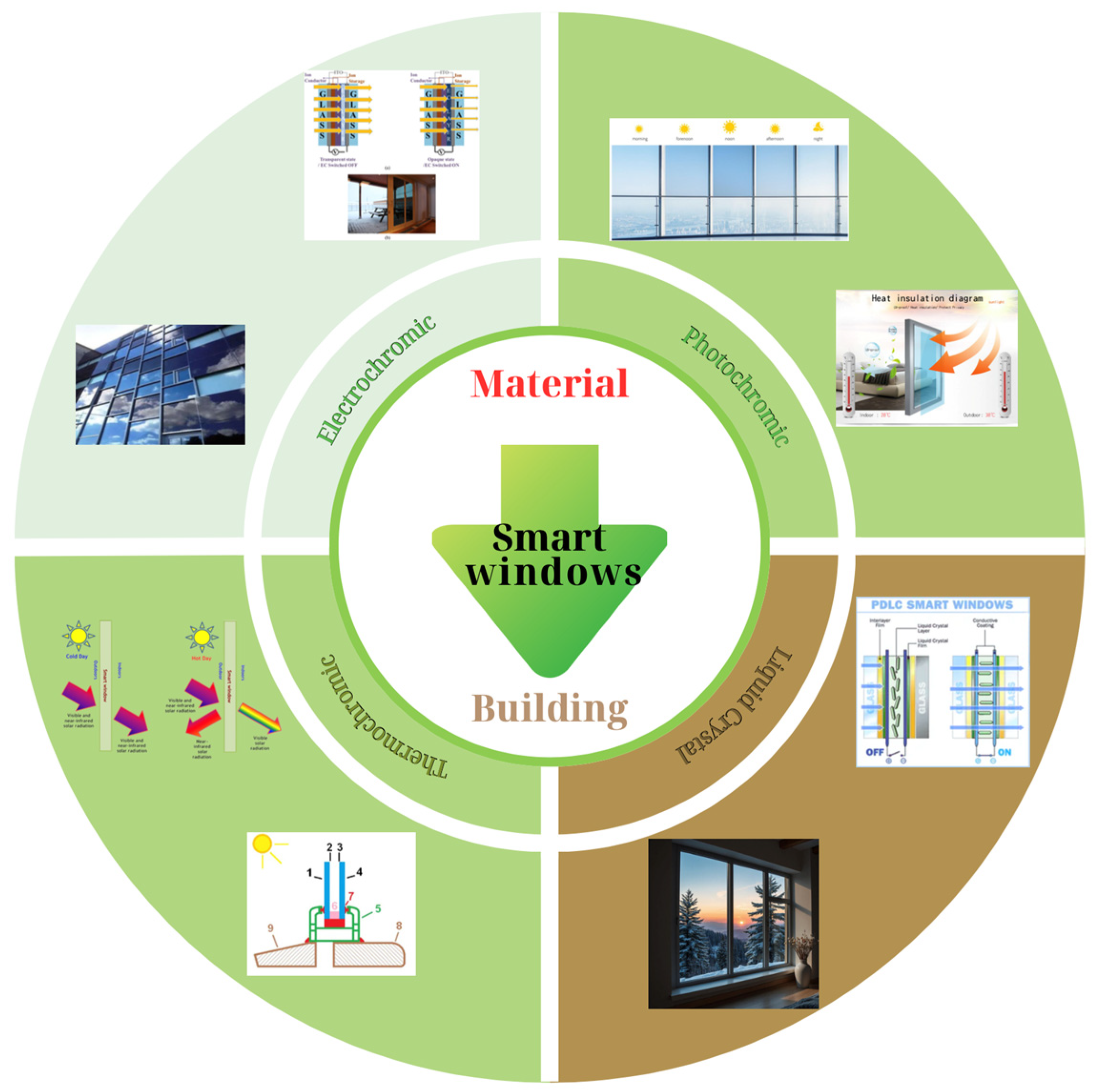In modern architectural design, smart windows are highly valued for their ability to improve energy efficiency, enhance occupant comfort, and contribute to building sustainability [2]. Smart windows have been developed in various types (Figure 1), depending on the technology and functionality to meet diverse practical needs.

Electrochromic Smart Windows (ESWs) use electrochromic materials that can change their light transmission properties (transmittance) under an electric voltage, allowing for control over the amount of light and heat passing through. As electrochromic smart window systems enable users to adjust light levels as desired, they are now effectively used for energy-saving purposes in buildings, achieving energy savings of up to 48%. Electrochromic smart windows also provide comfort in terms of light and temperature, such as glare reduction and heat mitigation, while enhancing aesthetics and offering visual comfort to occupants [3,4].

Photochromic Smart Windows (SPWs) provide a promising foundation for designing Energy-Saving Buildings (ESBs) due to their distinctive characteristics. SPWs can regulate solar energy through dynamic color-switching in response to external stimuli while simultaneously generating electricity by harvesting solar energy [5]. These smart windows function as both regular windows and renewable energy sources. The key advantage of photovoltaic glass lies in its ability to generate clean energy, reduce dependence on traditional power grids, and lower the long-term energy costs. Moreover, integrating renewable energy into glass enhances the efficiency of construction spaces, particularly in modern and sustainable urban projects.

Thermochromic Smart Windows (TSWs) are optical systems capable of dynamically adjusting their light transmission properties in response to changes in external temperature, helping to reduce heat radiation and control the temperature inside a building [6]. TSWs operate completely automatically without requiring an external power source, providing convenience and suitability for areas with significant temperature fluctuations. In addition to saving energy, TSWs enhance user comfort, making them an ideal solution for modern and sustainable construction projects.

Liquid Crystal Smart Windows (LSWs), which adjust optical transmittance in response to external stimuli to control natural light, have emerged as an effective solution for reducing energy consumption in buildings [7,8]. LSWs have many advantages, such as the ability to flexibly adjust light from transparent to opaque, energy-saving features, enhanced privacy without the need for curtains, and easy control via electronic devices. With a long lifespan, modern aesthetics, and versatile applications in various spaces, this type of window not only improves energy efficiency but also contributes to the development of sustainable and environmentally friendly structures.

Each type of smart window offers unique advantages, providing diverse and sustainable solutions for architecture, transportation, and other industries. Thus, Choosing the most appropriate smart window solution is a challenging decision-making task due to the presence of conflicting criteria, such as energy efficiency, durability, cost, environmental impact, and technological feasibility. This complexity is further compounded by the inherent uncertainty and subjectivity in evaluating these criteria, as decision-makers must consider varying priorities and expert opinions on the matter.

This research is focused on establishing FMCDM-driven frameworks to support the selection of smart window technologies. FMCDM integrates fuzzy logic to handle an uncertain environment, making it a robust approach for evaluating alternatives against multiple conflicting criteria. This research utilizes FMCDM to develop a systematic and flexible framework for selecting smart glass that meets both functional and sustainability objectives.

This article is organized into five sections. The introduction presents the context, research problem, and objective of proposing a spherical fuzzy MCDM model for smart window technology selection. The Literature Review analyzes related studies on technology evaluation and selection, as well as fuzzy MCDM methods. The Methodology section introduces the application of fuzzy AHP to determine the weights of criteria and the TOPSIS model to rank design alternatives based on criteria. Results and Discussion present the analysis results, emphasizing the importance of the criteria and evaluating the optimal alternatives. Finally, the Conclusion summarizes the findings and suggests future directions.

2. Literature Review

The application of Fuzzy Multi-Criteria Decision-Making (FMCDM) models has gained significant traction in sustainable technology selection across domains such as renewable energy, green materials, and smart infrastructure. However, within the specific context of ranking smart window alternatives (a critical component in green building design), the integration of fuzzy logic and MCDM remains underexplored. Existing studies often address individual criteria, such as energy efficiency or cost, and while some adopt MCDM approaches, they rarely incorporate fuzzy theory to capture the inherent uncertainty in expert evaluations. This paper contributes to bridging that gap by proposing a tailored hybrid FMCDM framework for smart window strategy selection. By combining fuzzy theory with structured decision-making, the model enhances the robustness and reliability of the ranking process, especially when dealing with imprecise, linguistically expressed expert judgments.

Gülçin Büyüközkan and Merve Güler [9] present an integrated method combining the fuzzy hesitant linguistic term set (HFLTS), the ordered weighted average (OWA) operator, and the TOPSIS technique in a fuzzy hesitant environment to evaluate smart glass technology. This study demonstrates the potential of the proposed model to support managers in effectively selecting smart glass technology while considering technical performance and sustainability factors. Mohamed Alzarooni et al. [10] proposed an integrated fuzzy MCDM approach combining FAHP and TOPSIS to select solar window film sheets aimed at enhancing energy efficiency in buildings. The proposed method enables decision-makers to evaluate and select optimal alternatives by considering multiple criteria, including energy efficiency, cost, durability, and environmental impact. Elaheh Jalilzadehazhari et al. [11] introduced a MCDM model by integrating non-dominated sorting genetic algorithm-II and the AHP model to select window and blind designs by evaluating trade-offs among visual comfort, thermal comfort, energy consumption, and lifecycle cost.

Hamza Hamida et al. [12] developed a model to streamline the evaluation and selection processes for curtain wall systems in office buildings. Amirhossein Balali et al. [13] conducted a comprehensive study to identify and prioritize the most suitable smart materials for building facades based on the sustainable development goals (SDGs). Mohammad Seraj et al. [14] evaluated alternative solutions for building sustainable green structures through the application of advanced scientific techniques. This research identified 10 key challenges hindering operational efficiency in the construction industry and utilized the AHP method to rank the most optimal solutions. This tool demonstrated its capability to accurately assess energy management equipment options for green buildings, ensuring objectivity in addressing MCDM challenges in the future. Fahimeh Aliakbari Nouri et al. [15] conducted a study focusing on the development of a comprehensive model for technology evaluation and selection. The author proposed a hybrid approach combining the FANP model, which accounts for interrelated criteria, and Fuzzy TOPSIS, which ranks alternatives based on their closeness to the ideal. Through a real-life case study, the authors validated the applicability of the proposed model for supporting technology adoption decisions in manufacturing firms. Fatemeh Parvaneh et al. [16] used a combined MCDM model to rank power generation technologies.

Gigih Rahmandhani Setyantho et al. [17] established a multi-criteria assessment approach incorporating AHP and PRO-METHEE II for evaluating semi-transparent photovoltaic windows across different climate contexts. The key findings of this research are to provide valuable insights for decision-making in energy-efficient building design. M Gülçin Büyüközkan et al. [18] proposed an evaluation framework based on the Hesitant Fuzzy MCDM approach to jointly account for the various factors influencing the final decision. Carman-Ka-Man Lee et al. [19] proposed an MCDM approach to design and select an optimal new product development (NPD) project portfolio. In the first phase, the available market product features are identified and ranked to highlight promising NPD projects. In the second phase, these projects are evaluated using the Sustainable Supply Chain Operation Reference (SustainableSCOR) model to determine the most sustainable NPD project for implementation. To address uncertainty in selecting waste to energy distributed generation systems, Moshood Akanni Alao et al. [20] developed a new fuzzy-integrated MCDM model. Junfei Chu et al. [21] developed a novel approach for selecting advanced manufacturing technologies by integrating a common-weight MCDM method into the Data Envelopment Analysis (DEA) framework. Recent research emphasizes the importance of adopting a structured decision-making approach to support technology selection within ITs. In particular, Mladen Krstić et al. [22] developed a comprehensive framework for evaluating and selecting suitable technologies for intermodal terminal subsystems. This study proposes a novel hybrid MCDM model that integrates the Fuzzy Factor Relationship (FFARE) method for determining criterion weights and the Fuzzy Combinative Distance-based Assessment (FCODAS) method for evaluating and ranking alternative technologies.

Petrović et al. [23] analyzed and compared three fuzzy MCDM methods to solve the supplier selection problem, highlighting their critical role in supporting effective decision-making. Sharma and Tripathy [24] introduced an integrated approach combining Quality Function Deployment (QFD) and the TOPSIS model for supplier evaluation and selection, showcasing the potential of fuzzy MCDM in improving decision outcomes. In addition, Zhao et al. [25] demonstrated the utility of fuzzy MCDM techniques by applying an extended VIKOR method with intuitionistic fuzzy sets to the supplier selection process. Chang et al. [26] proposed a fuzzy optimization model for supply chain decision-making, showcasing how green criteria can be integrated into fuzzy MCDM approaches to enhance sustainable supplier selection. Yücesan et al. [27] proposed an integrated fuzzy MCDM method based on various decision-making techniques for evaluating green suppliers, underscoring the versatility of fuzzy MCDM in addressing diverse supplier selection criteria. Moreover, Mohamed and Mohamed [28] introduced a fuzzy MCDM method for selecting green suppliers, providing insights into the practical application of such methods in real-world scenarios. Nguyen et al. [29] proposed a spherical fuzzy MCDM model for wind turbine supplier selection, highlighting its flexibility in uncertain decision-making environments.

In summary, while a broad spectrum of studies has explored the use of FMCDM models across various sustainability-driven domains, very few have specifically addressed the ranking of smart window alternatives using a combined fuzzy and multi-criteria decision-making approach. Most prior works either focused on generic smart materials or adopted MCDM methods in isolation without incorporating fuzzy logic to capture uncertainty in stakeholder evaluations. Even studies that apply fuzzy methods tend to prioritize broader technological categories rather than the nuanced decision-making required for facade-integrated smart glass systems. This reveals a clear research gap in the application of integrated FMCDM models tailored to smart window selection, where multiple, often conflicting criteria must be evaluated under uncertainty. This paper aims to fill this gap by introducing a novel hybrid FMCDM framework that not only addresses the complexity of sustainability-driven decisions but also improves the robustness and transparency of the ranking process for smart window technologies.

3. Methodology

A fuzzy MCDM model incorporating fuzzy AHP and TOPSIS is developed in this study to determine the best smart window technology. These methods were selected due to their proven effectiveness in managing complex decision-making scenarios under uncertain conditions. FAHP is employed for its ability to systematically incorporate expert judgment while managing vagueness and subjectivity through fuzzy logic, offering more nuanced and reliable weight assessments than conventional AHP. This is particularly crucial in sustainability-related evaluations, where qualitative judgments and imprecise data are often prevalent. TOPSIS, on the other hand, is selected for its computational efficiency, straightforward logic, and its intuitive capability to rank alternatives by comparing their relative distances to an ideal and a negative ideal solution. 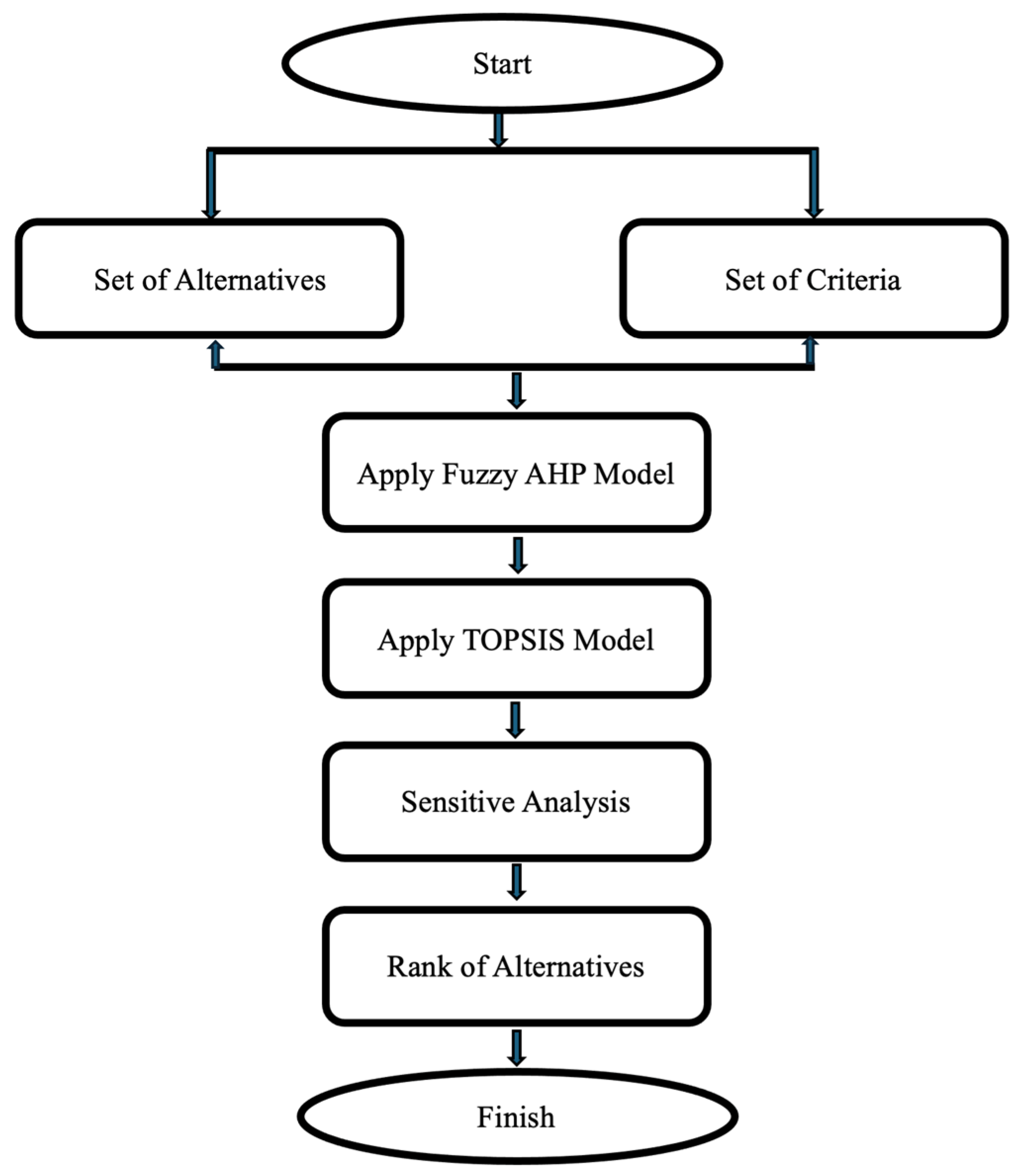Despite being introduced over four decades ago, TOPSIS has maintained its relevance and popularity, as evidenced by numerous recent studies [30,31,32]. Its strength lies in its clarity, replicability, and adaptability to a wide range of decision-making contexts. Both FAHP and TOPSIS are considered classical MCDM techniques, valued for their ease of implementation, interpretability of results, and compatibility with the available computational tools. While newer, more advanced algorithms, such as hybrid metaheuristics or AI-driven models, may offer additional precision or complexity, their adoption often entails steep learning curves, extensive data requirements, and reduced transparency. In contrast, the FAHP−TOPSIS combination strikes a practical balance between methodological rigor and operational feasibility—making it particularly suitable for real-world applications in sustainable construction technology selection. The three primary steps of the research process are illustrated in Figure 2.

Step 1: Conduct comprehensive expert interviews and an extensive review of the relevant literature to identify all key criteria that influence the selection process for smart window technology. This step ensures a thorough understanding of the factors impacting decision-making, incorporating both practical insights from industry experts and theoretical frameworks from academic studies.

Step 2: Utilize the FAHP approach to compute the importance of each criterion. This method leverages expert opinions while accounting for uncertainty and fuzziness in the evaluation process, ensuring precise and reliable weight calculations for each criterion.

Step 3: Use the TOPSIS model to evaluate and rank smart window technology options. This ranking provides a clear and actionable prioritization, enabling decision-makers to make informed, objective, and data-driven choices during the selection process.

The FAHP method is utilized to derive the fuzzy weights of the evaluation criteria, effectively addressing the uncertainty and subjectivity inherent in expert judgments by incorporating fuzzy logic. This approach enables a more refined and realistic evaluation of the relative significance of each criterion. Following the determination of these weights, the TOPSIS technique is employed to rank the smart window alternatives. By assessing the relative closeness of each option to an ideal solution, TOPSIS offers a structured and objective ranking process. The integration of FAHP and TOPSIS forms a comprehensive decision-making framework that accommodates both the ambiguity of human perceptions and the requirement for systematic alternative prioritization.

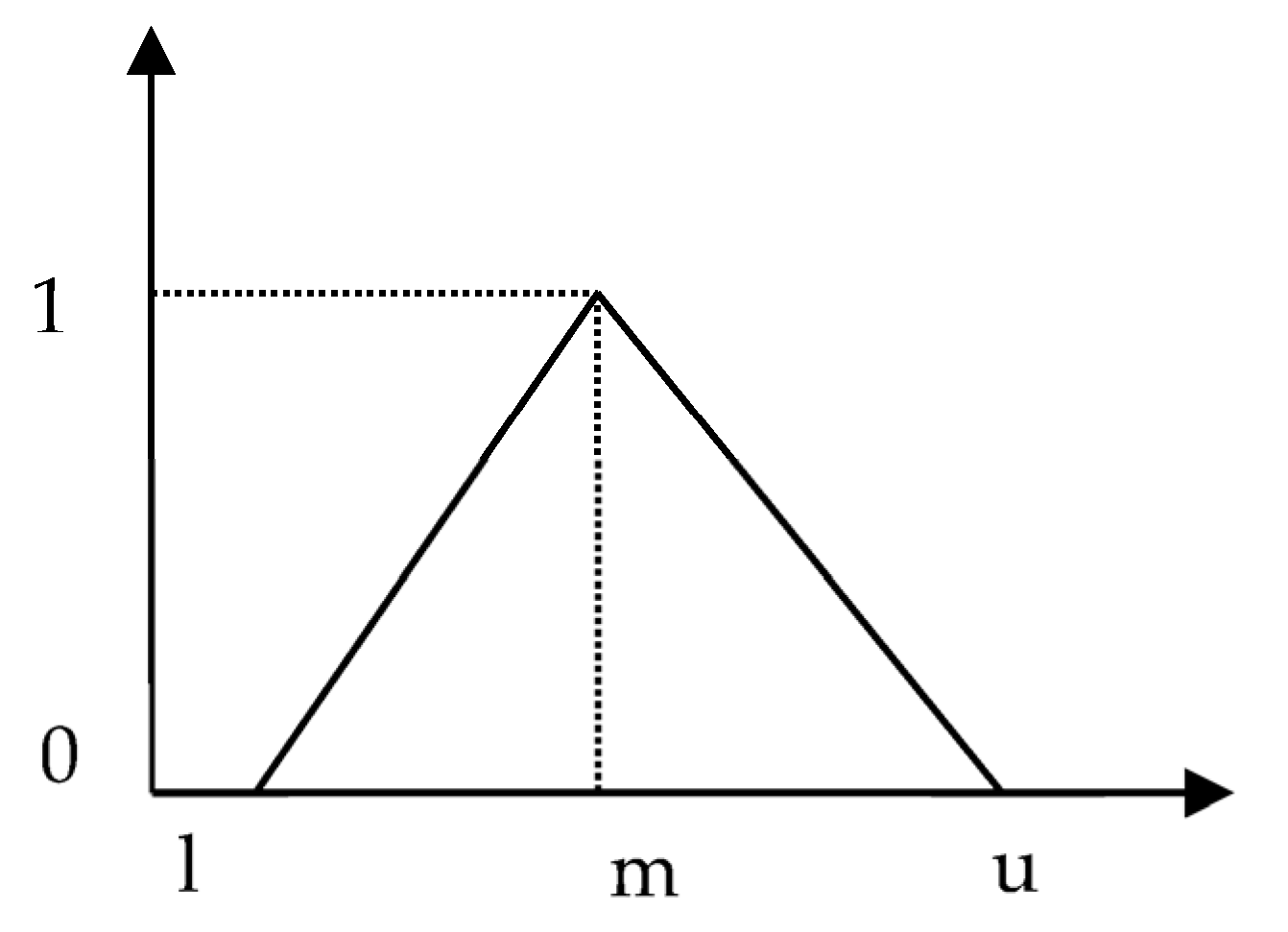
3.1. Traingular Fuzzy Number

Zadeh originally introduced fuzzy set theory, which later led to the development of various types of fuzzy numbers. Among these, triangular fuzzy numbers (TFNs) are widely adopted for their simplicity and ease of application. Figure 3 depicts the structure of a typical TFN.

A triangular fuzzy number $\tilde{A}$ is commonly expressed as a triplet (l,m,u), where:

$$\mathsf{\mu }\left(x\right)=\left\{\begin{array}{c}\begin{array}{c}\begin{array}{c}0, x<1 \\ {\displaystyle \frac{x-l}{m-l}}, l\le x \le m\hfill \end{array}\\ {\displaystyle \frac{u-x}{u-m}}, m<x\le u\\ 0, x>u\end{array} \\ \end{array}\right.$$

(1)

3.2. Fuzzy Analytic Hierarchy Process (FAHP)

FAHP is an extended version of AHP designed to overcome AHP’s limitations in handling uncertainty in decision-making scenarios. Let $X=\left\{x_1, x_2,\dots .x_n\right\}$ represent the set of alternatives, and $K=\left\{k_1, k_2,\dots .k_n\right\}$ denote the set of criteria. Each alternative undergoes an extent analysis based on Chang’s extent analysis method [33]. The corresponding values are expressed as follows:

$$L_{k_i}^1,L_{k_i}^2,{\dots ,L}_{k_i}^m, i=\mathrm{1,2},\dots ,n.$$

(2)

where $L_k^j(j=\mathrm{1,2},\dots .,m)$ are the TFNs.

The fuzzy synthetic extent value for the $i^{th}$ the object is expressed as:

$$S_i=\sum _{j=1}^m{L}_{k_i}^j\otimes {\left[\sum _{i=1}^n\sum _{j=1}^m{L}_{k_i}^j\right]}^{-1}.$$

(3)

The degree of possibility that $L_1$ is greater than or equal to $L_2$ is defined as:

$$V\left(L_1\ge L_2\right)={sup}_{y\ge x}\left[min\left({\mu }_{L_1}\left(x\right),\right),\left({\mu }_{L_2}\left(y\right)\right)\right].$$

(4)

We have $V\left(L_1\ge L_2\right)=1$ if the pair $(x,y)$ exists with $x\ge y$ and ${\mu }_{L_1}\left(x\right)={\mu }_{L_2}\left(y\right)$.

Given that $L_1$ and $L_2$ are convex fuzzy numbers, the following condition applies:

$$V\left(L_1\ge L_2\right)=1, if l_1\ge l_2.$$

(5)

And

$$\left(L_2\ge L_1\right)=hgt(L_1\cap L_2)={\mu }_{L_1}\left(d\right).$$

(6)

The value of the membership function at the highest intersection points D between ${\mu }_{L_1}$ and ${\mu }_{L_2}$ is represented by d.

Point DD is calculated based on $L_1=(o_1,p_1$,$q_1)$ and $L_2=(o_2,p_2$,$q_2)$, as specified in Equation (7):

$$V\left(L_2\ge L_1\right)=hgt\left(L_1\cap L_2\right)={\displaystyle \frac{l_1-q_2}{\left(p_2-q_2\right)-\left(p_1-o_1\right)}}.$$

(7)

To compare $L_1$ and $L_2$, compute the values of $V\left(L_1\ge L_2\right)$ and $V\left(L_2\ge L_1\right)$.

Here, $L_i(i=\mathrm{1,2},\dots k)$ denotes the degree of possibility that a given convex fuzzy number is greater than each of the $k$ convex fuzzy numbers.

$$\left(L\ge L_1,L_2,\dots ,L_k\right)=V\left[\left(L\ge L_1\right) and \left(L\ge L_2\right) \right].$$

(8)

Additionally, the condition $(L\ge L_k$) is defined as the minimum of V (L $\ge L_i),i=\mathrm{1,2},\dots ,k$.

Assuming that

$$d^{\prime }\left(B_i\right)=minV\left(S_i\ge S_k\right).$$

(9)

for $k=\mathrm{1,2},\dots n \mathrm{a}\mathrm{n}\mathrm{d} k\#i$, the weight vector is computed as follows:

$$W^{\prime }={(d^{\prime }\left(B_1\right),d^{\prime }\left(B_2\right),\dots d^{\prime }\left(B_n\right))}^T.$$

(10)

Here, $B_i$ represents the number of elements, and $n$ signifies the total number of elements.

The normalized weight vectors are calculated as follows:

$$W={(d\left(B_1\right),d\left(B_2\right),\dots .,d\left(B_n\right))}^T.$$

(11)

The value of WW is a precise number.

The consistency of Saaty’s matrix is evaluated to ensure the reliability of the pairwise comparisons.

$$CR={\displaystyle \frac{CI}{RI}}={\displaystyle \frac{\overline{\lambda }-n}{\left(n-1\right)\times RI}}\le 0.1$$

(12)

3.3. TOPSIS Model

The TOPSIS model, originally proposed by Ching-Lai Hwang and Yoon in 1981 [34], was subsequently refined by Yoon [35], Hwang, and later by Lai and Liu [36]. The implementation of the TOPSIS methodology involves the following steps.

Step 1: Develop an evaluation matrix with m alternatives and n criteria, where each element $x_{ij}$ represents the performance of alternative i with respect to criterion j, forming the matrix ${\left(x_{ij}\right)}_{mxn}$.

Step 2: The matrix ${\left(x_{ij}\right)}_{mxn}$ is then normalized to obtain the matrix $R={\left(r_{ij}\right)}_{mxn}$ using an appropriate normalization technique.

$$r_{ij}={\displaystyle \frac{x_{ij}}{\sqrt{\sum _{k=1}^m{x}_{kj}^2}}},\mathrm{i}=1,2,\dots ,\mathrm{m};\mathrm{j}=1,2,\dots ,\mathrm{n}.$$

Step 3: Calculate the weighted normalized decision matrix as follows:

$$t_{ij}=r_{ij}.w_j, \mathrm{i}=\mathrm{1,2},\dots ,\mathrm{m};\mathrm{j}=\mathrm{1,2},\dots ,\mathrm{n}.$$

where $w_j={\displaystyle \frac{W_j}{\sum _{k=1}^n{W}_k}},$ j = 1,2, …,n so that $\sum _{i=1}^n{w}_j=1,$ and $W_j$ is the original weight given to the indicator $v_j,$ j = 1,2, …,n.

Step 4: Identify the worst option ($A_w)$ and the best option ($A_b)$:

$$A_w=\left\{⟨\mathrm{m}\mathrm{a}\mathrm{x}(t_{ij}|i=\mathrm{1,2},\dots ,m|j\in J_{-}⟩,⟨\mathrm{m}\mathrm{i}\mathrm{n}(t_{ij}|i=\mathrm{1,2},\dots ,m|j\in J_{+}⟩\right\}=\left\{t_{wj}|j=\mathrm{1,2}, \dots ,n\right\}$$

$$A_b=\left\{⟨\mathrm{m}\mathrm{i}\mathrm{n}(t_{ij}|i=\mathrm{1,2},\dots ,m|j\in J_{-}⟩, ⟨\mathrm{m}\mathrm{a}\mathrm{x}(t_{ij}|i=\mathrm{1,2},\dots ,m|j\in J_{+}⟩\right\}=\left\{t_{wj}|j=\mathrm{1,2}, \dots ,n\right\}$$

Step 5: Evaluate the $L^2$—distance between alternative $i$ and the worst condition $A_w$:

$$d_{iw}=\sqrt{{\sum }_{j=1}^n{(t_{ij}-t_{wj})}^2, }i=\mathrm{1,2},\dots ,m.$$

In addition, the distance between the target alternative $i$ and the least favorable solution $A_b$ is determined.

$$d_b=\sqrt{{\sum }_{j=1}^n{(t_{ij}-t_{bj})}^2, }i=\mathrm{1,2},\dots ,m.$$

Step 6: Compute the similarity to the worst condition:

$$s_{iw}={\displaystyle \frac{d_{ib}}{\left(d_{iw}+d_{ib}\right) }}i=\mathrm{1,2},\dots ,m.$$

Step 7: Ranking the alternatives in order of $s_{iw}$ ($i=\mathrm{1,2},\dots ,m)$.

4. Case Study

In a world increasingly focused on sustainable solutions to minimize negative environmental impacts and enhance the quality of life, Smart Window Technology has rapidly emerged as a breakthrough innovation in the construction sector. Smart windows not only offer aesthetic value but also incorporate advanced functionalities that optimize energy efficiency, improve living and working conditions, and support global sustainable development goals. With the ability to automatically regulate light and heat transmission through the glass surface, this technology significantly reduces energy costs, particularly for air conditioning and lighting.

One of the key advantages of smart windows is their ability to effectively conserve energy. By integrating modern technologies, such as electrochromic and thermochromic glass, they can automatically adjust to optimize natural light and temperature within indoor spaces. This reduces the strain on air conditioning systems and significantly decreases the CO₂ emissions associated with energy consumption, contributing to global climate change mitigation efforts. Moreover, this technology enhances user comfort by adapting lighting conditions to the time of day, while promoting health and productivity through a more efficient use of natural light.

However, selecting the most suitable smart window technology for specific applications remains a complex challenge. The diverse range of technologies, features, and costs associated with smart windows necessitates decision-making based on multiple criteria, including economic efficiency, technical performance, environmental impact, and practical applicability. In this context, MCDM models have proven to be invaluable tools, offering scientific and objective approaches to facilitate the decision-making process.

This study aims to apply optimization methods to the evaluation and selection of smart window technologies, with a particular focus on sustainability, as well as social, economic, and environmental considerations. To ensure the credibility and reliability of the decision-making process, expert opinions were collected from a panel of professionals with extensive experience in sustainable building technologies, facade engineering, and energy-efficient materials. A total of twelve experts were selected through purposive sampling, ensuring diversity in their academic, industrial, and technical backgrounds. All information regarding the experts is presented in

Table 1. Experts’ information.

No	Role	Number of Experts	Area of Expertise	Affiliaton Type
1	University Professors	2	Green building, sustainable materials, energy systems	Academia
2	Senior Engineers	4	Architectural design, facade systems, construction projects	Architecture and Construction Firms
3	Sustainability Consultants	4	Environmental assessment	Sustainability Consulting Firms
4	R&D Manager	2	Smart glass technology development and innovation	Smart Glass Manufacturer

.

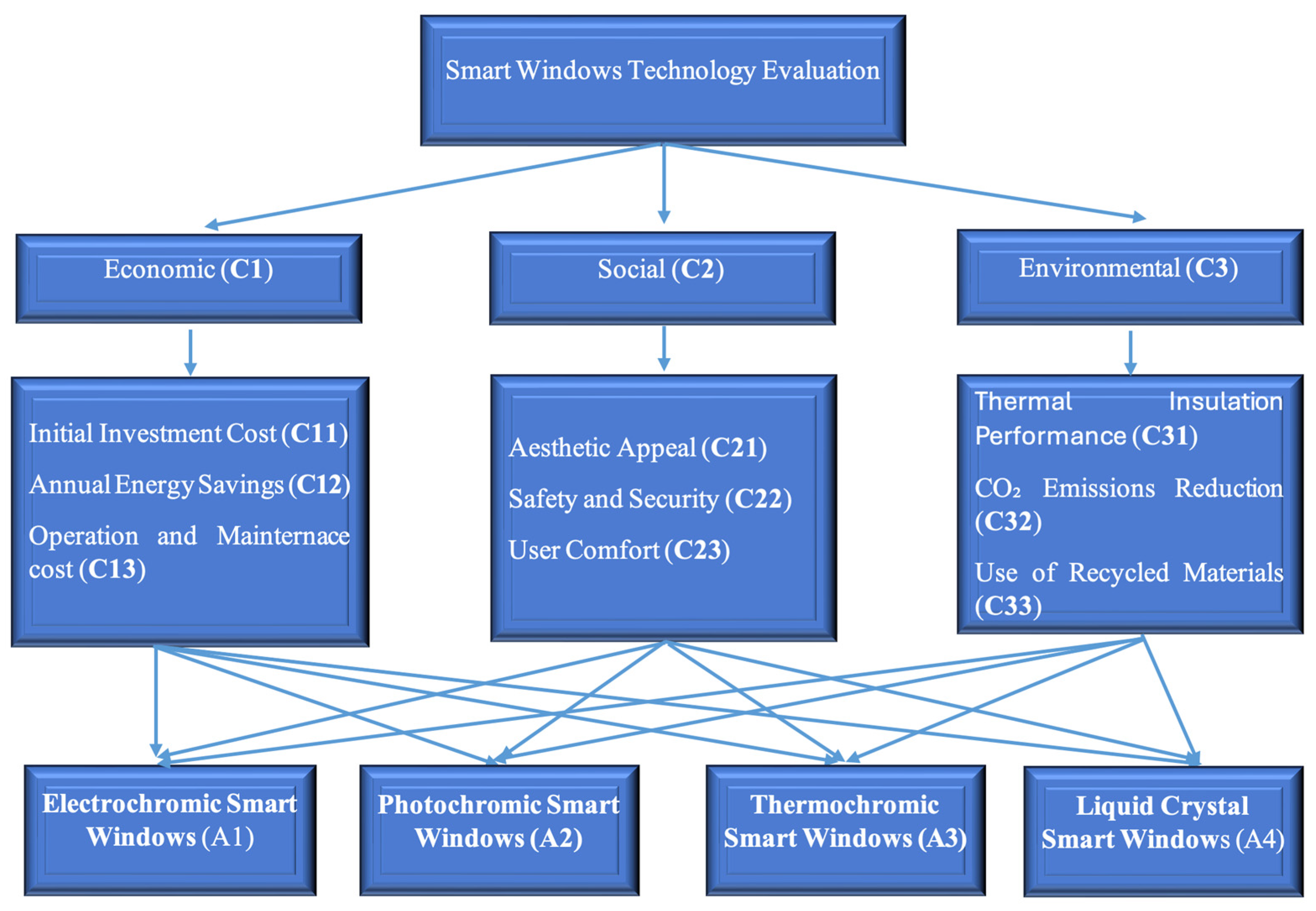
Based on a literature review and expert opinions, the general hierarchy structure of FAHP is shown in Figure 4.

The FAHP model offers a versatile and thorough method for determining weights in scenarios involving numerous uncertainties, thereby enabling decision-makers to make more precise choices. All the input data were provided by 12 experts specializing in smart window technologies. The fuzzy comparison matrix is presented in

Table 2. Fuzzy comparison matrices.

	Economic (C1)	Social (C2)	Environmental (C3)
Economic (C1)	(1, 1, 1)	(1/5, 1/4, 1/3)	(1/4, 1/3, 1/2)
Social (C2)	(3, 4, 5)	(1, 1, 1)	(2, 3, 4)
Environmental (C3)	(2, 3, 4)	(1/4, 1/3, 1/2)	(1, 1, 1)

.

Defuzzification is performed using coefficients α = 0.5 and β = 0.5, where α captures environmental uncertainty and β represents the evaluator’s viewpoint.

$${\mathrm{g}}_{0.5,0.5}\left(\overline{a_{C1,C2}}\right)=\left[\right(0.5\times 0.2)+(1-0.5)\times 0.3]=1/4$$

f_0.5(L_C1,C2) = (1/4 − 1/5) × 0.5 + 1/5 = 0.2

f_0.5(U_C1,C3) = 1/3 − (1/3 − 1/4) × 0.5 = 0.3

$${\mathrm{g}}_{0.5,0.5}\left(\overline{a_{C2,C1)}}\right)=4$$

The subsequent calculations and determination of fuzzy number priority points follow the same approach as the previous computation.

Table 3. Real number priority.

	Economic (C1)	Social (C2)	Environmental (C3)
Economic (C1)	1	1/4	1/3
Social (C2)	4	1	3
Environmental (C3)	3	1/3	1

displays the real number priorities for the pairwise comparisons of the main criteria.

The maximum value for each criterion was determined as follows:

YZ1 = (1 × 14 × 1/3)^1/3 = 0.437

YZ2 = (4 × 1 × 3)^1/3 = 2.289

YZ3 = (3 × 1/3 × 1)^1/3 = 1

$$\sum YZ=\mathrm{Y}\mathrm{Z}1+\mathrm{Y}\mathrm{Z}1+\mathrm{Y}\mathrm{Z}1=3.726$$

$${\omega }_1={\displaystyle \frac{0.437}{3.726}}=0.117$$

$${\omega }_2={\displaystyle \frac{2.289}{3.726}}=0.614$$

$${\omega }_3={\displaystyle \frac{1}{3.726}}=0.269$$

$$\left[\begin{array}{cc}1& \begin{array}{cc}1/4& 1/3\end{array}\\ \begin{array}{c}4\\ 3\end{array}& \begin{array}{cc}\begin{array}{c}1\\ 1/3\end{array}& \begin{array}{c}3\\ 1\end{array}\end{array}\end{array}\right]\times \left[\begin{array}{c}0.117\\ 0.614\\ 0.269\end{array}\right]=\left[\begin{array}{c}0.360\\ 1.889\\ 0.825\end{array}\right]$$

$$\left[\begin{array}{c}0.360\\ 1.889\\ 0.825\end{array}\right]/\left[\begin{array}{c}0.117\\ 0.614\\ 0.269\end{array}\right]=\left[\begin{array}{c}3.077\\ 3.077\\ 3.067\end{array}\right]$$

When the number of criteria is three, $n$ = 3, and λ_max and $CI$ are calculated as follows:

$${\lambda }_{max}={\displaystyle \frac{3.077+3.077+3.067}{3}}=3.074$$

$$CI={\displaystyle \frac{{\lambda }_{max}-n}{n-1}}={\displaystyle \frac{3.074-3}{3-1}}=0.037$$

For CR, with $n$ = 3, get $RI$ = 0.58

$$CR={\displaystyle \frac{CI}{RI}}={\displaystyle \frac{0.037}{0.58}}=0.064$$

Since $CR$ = 0.064 ≤ 0.1, the pairwise comparison data demonstrates consistency, eliminating the need for further reassessment. The weights assigned to the nine criteria are listed in

Table 4. Weight of criteria.

No	Criteria	Symbol	Weight
1	Initial Investment Cost	C11	0.075
2	Annual Energy Savings	C12	0.200
3	Operation and Maintenance cost	C13	0.088
4	Aesthetic Appeal	C21	0.085
5	Safety and Security	C22	0.084
6	User Comfort	C23	0.065
7	Thermal Insulation Performance	C31	0.253
8	CO2 Emissions Reduction	C32	0.093
9	Use of Recycled Materials	C33	0.057

.

In the second stage, the TOPSIS model is applied to rank the four potential technologies. The TOPSIS approach has significant advantages in supporting the MCDM model. The TOPSIS method identifies the optimal alternative by measuring the distance of each option to both the ideal and the least ideal solutions. TOPSIS is easy to apply, capable of handling both quantitative and qualitative data, and provides intuitive results, enabling decision-makers to make more rational and accurate choices. The normalized matrix of the TOPSIS model is shown in

Table 5. Normalized matrix.

Normalized Matrix	C11	C12	C13	C21	C22	C23	C31	C32	C33
A1	0.4073	0.4636	0.5298	0.4111	0.4111	0.5153	0.5774	0.4774	0.5447
A2	0.4073	0.4636	0.3974	0.4796	0.4796	0.5153	0.4491	0.4092	0.4842
A3	0.6110	0.5960	0.5298	0.5482	0.5482	0.5153	0.5132	0.6138	0.4842
A4	0.5431	0.4636	0.5298	0.5482	0.5482	0.4509	0.4491	0.4774	0.4842

and

Table 6. Normalized weighted matrices.

Normalized Weighted Matrix	C11	C12	C13	C21	C22	C23	C31	C32	C33
A1	0.0304	0.0929	0.0465	0.0350	0.0345	0.0336	0.1461	0.0445	0.0308
A2	0.0304	0.0929	0.0348	0.0408	0.0402	0.0336	0.1137	0.0382	0.0274
A3	0.0457	0.1194	0.0465	0.0467	0.0460	0.0336	0.1299	0.0572	0.0274
A4	0.0406	0.0929	0.0465	0.0467	0.0460	0.0294	0.1137	0.0445	0.0274

.

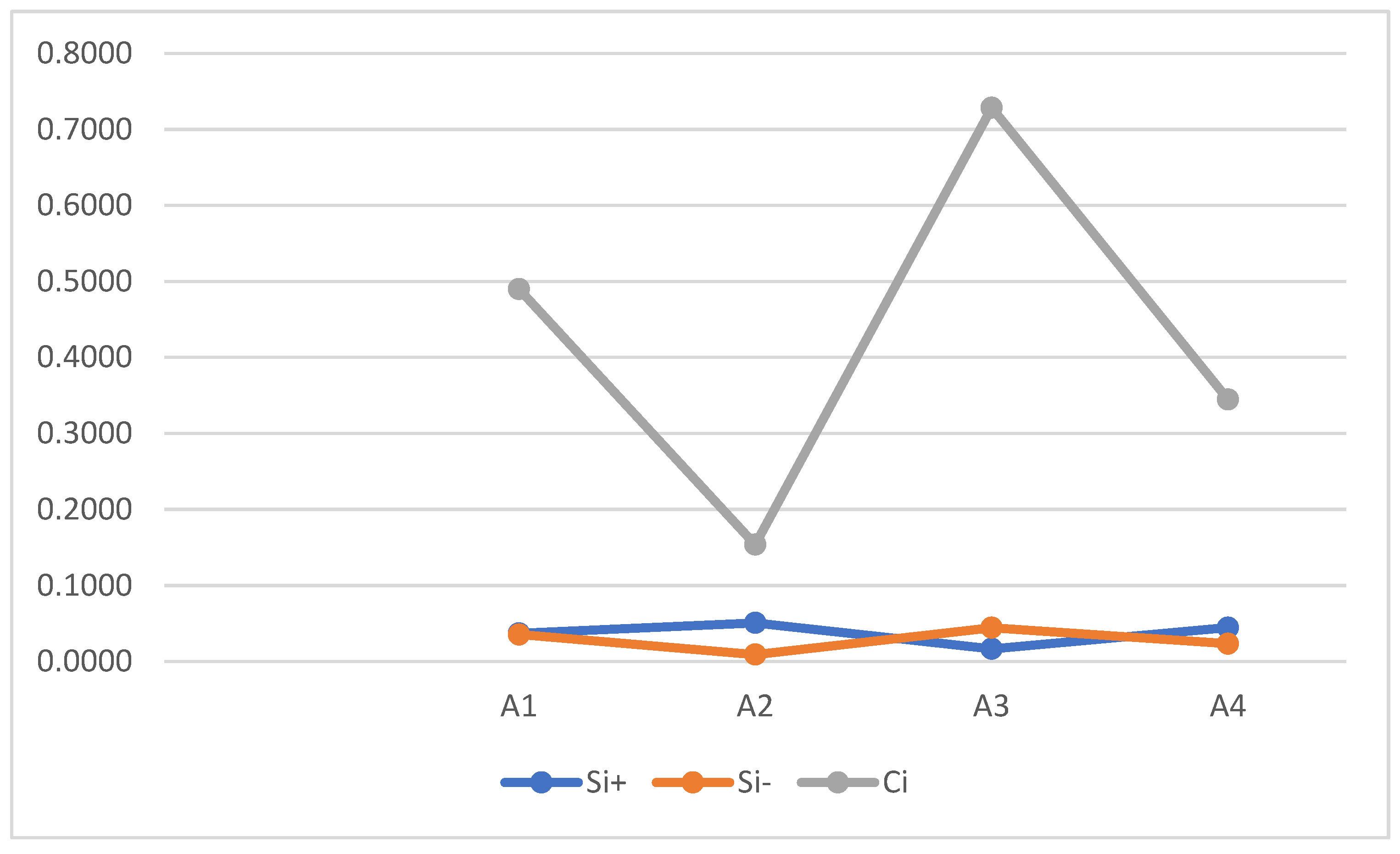
TOPSIS operates on the principle that the optimal alternative should be the one closest to the positive ideal solution (PIS) and farthest from the negative ideal solution (NIS) in terms of geometric distance. The results of the TOPSIS model are shown in

Table 7. Results of the TOPSIS model.

Alternatives	Si+	Si−	Ci	Ranking
Photochromic Smart Windows (A1)	0.0370	0.0355	0.4898	2
Photochromic Smart Windows (A2)	0.0507	0.0092	0.1537	4
Thermochromic Smart Windows (A3)	0.0166	0.0445	0.7286	1
Liquid Crystal Smart Windows (A4)	0.0445	0.0234	0.3446	3

.

Using the TOPSIS model presented in Table 7 and Figure 5, four potential technologies were evaluated and ranked, with A3-thermochromic smart windows identified as the most suitable option. The TOPSIS approach systematically assesses multiple factors by assigning scores based on how well each technology satisfies predefined criteria. This method ensures a structured and objective evaluation, aiding decision-makers in selecting the most appropriate technology for implementation.

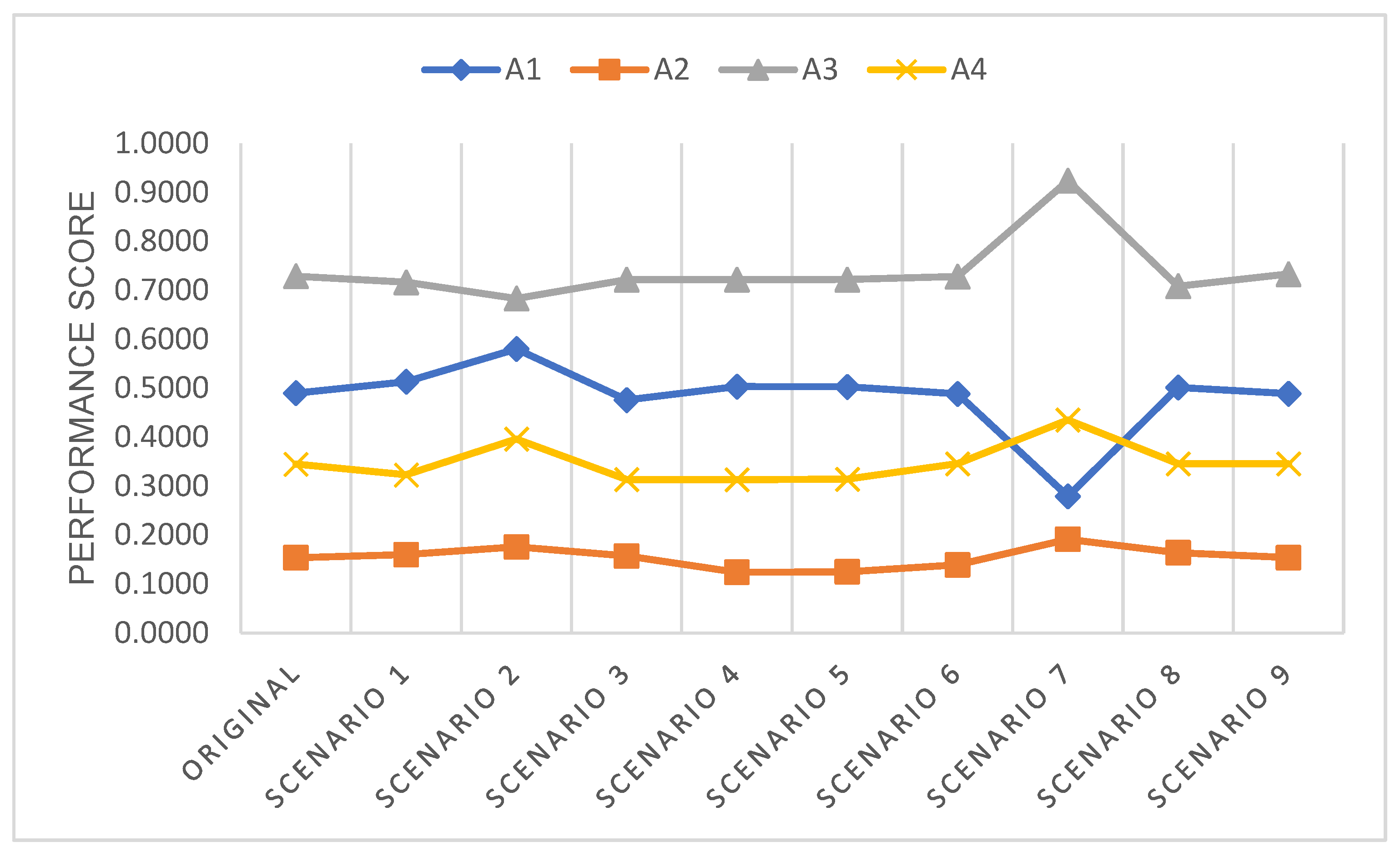
A sensitivity analysis is conducted to assess the robustness of the TOPSIS-based multi-criteria decision-making (MCDM) model by analyzing how the exclusion of each individual criterion influences the rankings and performance scores of the four alternatives (A1, A2, A3, A4). This approach aids in identifying the most influential criteria that significantly impact decision-making outcomes.

Table 8. The weights assigned to criteria across all scenarios.

Criteria	Weights of Criteria Across All Scenarios
	Original	Scenario-1	Scenario-2	Scenario-3	Scenario-4	Scenario-5	Scenario-6	Scenario-7	Scenario-8	Scenario-9
C1	0.0747	0.0000	0.0935	0.0819	0.0817	0.0816	0.0800	0.1001	0.0824	0.0792
C2	0.2004	0.2166	0.0000	0.2196	0.2190	0.2187	0.2144	0.2683	0.2210	0.2124
C3	0.0877	0.0948	0.1097	0.0000	0.0959	0.0957	0.0938	0.1174	0.0967	0.0930
C4	0.0851	0.0920	0.1065	0.0933	0.0000	0.0929	0.0911	0.1140	0.0939	0.0903
C5	0.0838	0.0906	0.1048	0.0919	0.0916	0.0000	0.0897	0.1122	0.0924	0.0889
C6	0.0653	0.0705	0.0816	0.0715	0.0713	0.0712	0.0000	0.0874	0.0720	0.0692
C7	0.2531	0.2736	0.3166	0.2775	0.2767	0.2763	0.2708	0.0000	0.2791	0.2683
C8	0.0932	0.1008	0.1166	0.1022	0.1019	0.1018	0.0998	0.1248	0.0000	0.0988
C9	0.0566	0.0611	0.0708	0.0620	0.0618	0.0618	0.0605	0.0758	0.0624	0.0000

presents the adjusted criteria weights for all nine scenarios, each reflecting the exclusion of a specific criterion.

Among all the criteria, C7 emerged as the most influential, carrying the highest weight in the original model (0.2531). When C7 was excluded (Scenario 7), a substantial redistribution of weights occurred, particularly increasing the influence of C2 (0.2683) and C3 (0.1174). The exclusion of C7 resulted in substantial alterations to the performance scores and rankings of the alternatives, underscoring its pivotal role in differentiating among options. The pronounced decline in model consistency following its removal indicates that C7 encapsulates core decision-maker priorities, likely due to its alignment with critical sustainability or performance-related dimensions. The results further highlight that ranking stability is relatively maintained when low-weight criteria (C6 or C9) are removed, while the model becomes more sensitive and less robust when high-weight criteria like C2 or C7 are excluded. This underscores the importance of carefully validating the weight assignment for key criteria during the FAHP phase to ensure the reliability of the overall decision framework.

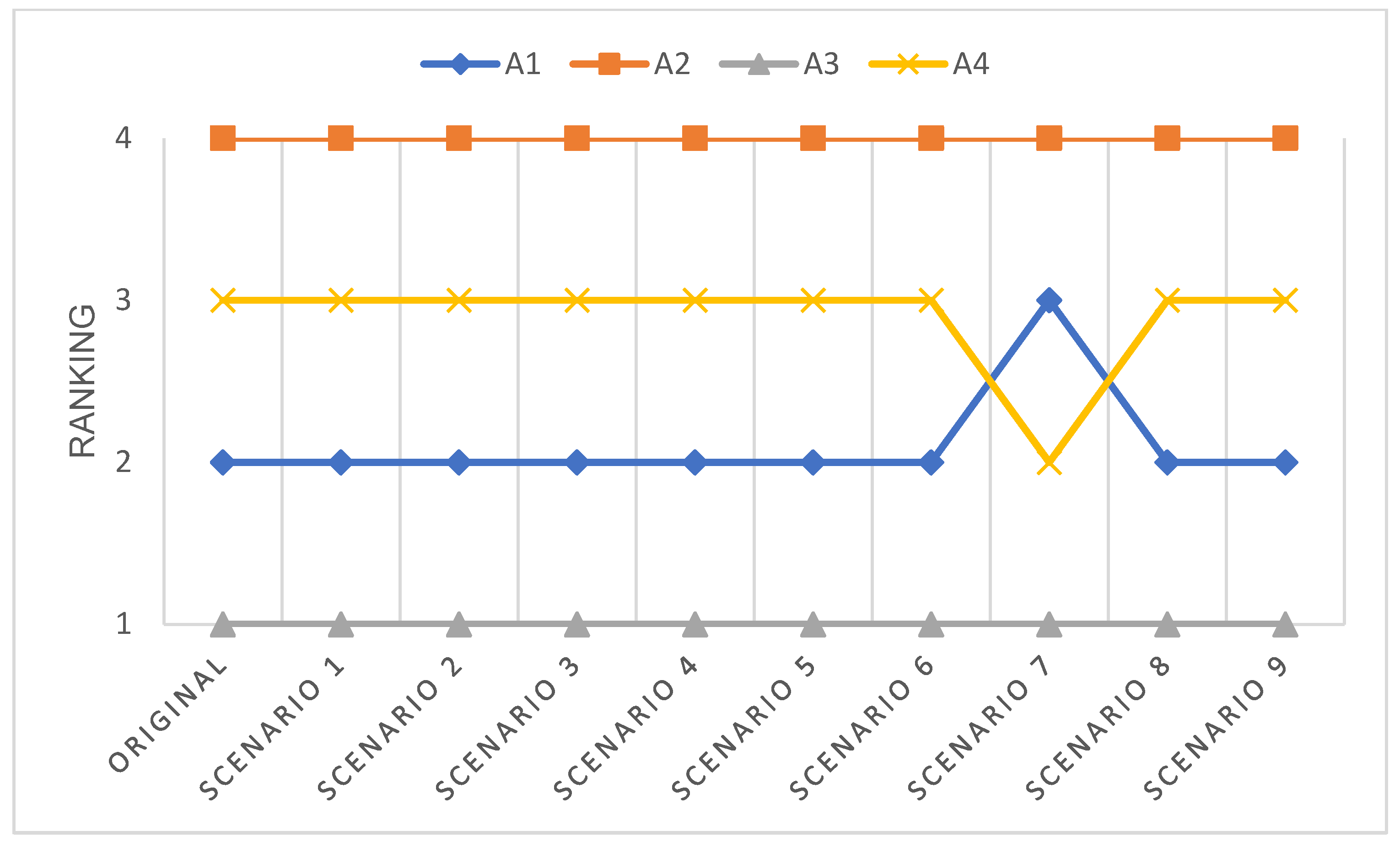
According to the results in

Table 9. Assessment results in each scenario.

Alternatives	Scores Obtained Under All Evaluated Scenarios
	Original	Scenario-1	Scenario-2	Scenario-3	Scenario-4	Scenario-5	Scenario-6	Scenario-7	Scenario-8	Scenario-9
A1	0.4898	0.5131	0.5798	0.4757	0.5030	0.5025	0.4881	0.2791	0.5015	0.4887
A2	0.1537	0.1599	0.1757	0.1572	0.1239	0.1250	0.1391	0.1913	0.1639	0.1540
A3	0.7286	0.7161	0.6831	0.7216	0.7215	0.7217	0.7277	0.9237	0.7081	0.7329
A4	0.3446	0.3229	0.3960	0.3134	0.3130	0.3141	0.3457	0.4351	0.3456	0.3453

and Figure 6, alternative A3 consistently ranks first across all scenarios, confirming its superiority in performance. Its uniform performance across the evaluation criteria allows it to retain this position regardless of criterion exclusion. A1 also shows resilience by consistently ranking second, emphasizing its reliability as an alternative.

In Scenario 7, A4 overtakes A1 as the second-best alternative, indicating a notable shift in performance. This suggests that the exclusion of a specific criterion in this scenario has a substantial impact on A4′s relative standing, improving its competitiveness compared to A1. The increase in A4′s performance score in this scenario highlights its sensitivity to the removed criterion.

The sensitivity analysis results (Figure 7) show that alternative A3 (thermochromic smart windows) consistently holds the top-ranking position across all scenarios, even when individual criteria are excluded. This indicates that A3 demonstrates a stable and well-rounded performance across most criteria, particularly those with high weights, such as thermal insulation performance and annual energy savings. The ability of A3 to maintain its leading position despite weight fluctuations confirms the stability and reliability of the FAHP–TOPSIS model in supporting the selection of sustainable and smart window technologies.

This stability also reflects the strength of the TOPSIS method in handling multi-criteria decision-making under uncertainty. Rather than relying on a single criterion, TOPSIS evaluates each alternative based on its geometric distance from both the positive and negative ideal solutions, thereby minimizing the impact of local weight changes. Furthermore, the consistency of the rankings suggests that the input data and FAHP-based weighting process are well-structured and coherent, reinforcing confidence in the overall decision-making process. This serves as a solid foundation for the practical application of the model in real-world technology selection contexts.

5. Conclusions

This study makes a significant contribution to sustainable construction decision-making by providing a transparent, structured, and practical FMCDM framework for selecting smart window technologies. Smart windows represent a key innovation in modern architecture, offering dynamic control over light and heat transmission to enhance energy efficiency and occupant comfort. Their adoption plays a critical role in reducing the energy consumption of buildings, thereby supporting global efforts to reduce greenhouse gas emissions and promote environmental sustainability.

The proposed model, integrating FAHP and the TOPSIS models, effectively evaluates and ranks smart window alternatives based on a comprehensive set of economic, social, and environmental criteria. The results show that thermochromic smart windows offer the best balance between technical performance and sustainability objectives. The model’s simplicity, scalability, and interpretability make it suitable for a wide range of real-world applications, not only in construction but also in the broader context of green product development.

In addition to its theoretical implications, this study offers practical value by equipping architects, engineers, and policymakers with a data-driven framework for evaluating and implementing sustainable technologies. The proposed decision-making model not only strengthens the feasibility and reliability of smart window integration in green building design but also has broader scientific significance. Specifically, the framework demonstrates potential universality for application across diverse sustainable technology selection contexts, thus extending its relevance beyond the studied case. Furthermore, this research contributes to the advancement of fuzzy MCDM theory by incorporating problem-specific sustainability criteria and addressing the epistemic uncertainty inherent in expert-based evaluations.

Future research should aim to enrich the proposed framework by incorporating additional criteria, such as lifecycle cost, durability, and climate adaptability. Furthermore, integration with complementary techniques like Life Cycle Assessment (LCA) or Dynamic Fuzzy Sets can enhance the applicability of the model. These advancements will contribute to a more holistic and intelligent selection process, accelerating the adoption of sustainable innovations in the built environment.