Reviews of Photovoltaic and Energy Storage Systems in Buildings for Sustainable Power Generation and Utilization from Perspectives of System Integration and Optimization
Abstract
1. Introduction
2. Photovoltaic Power Generation
2.1. Configurations of BIPV
2.1.1. PV-Roof System
2.1.2. PV-Wall System
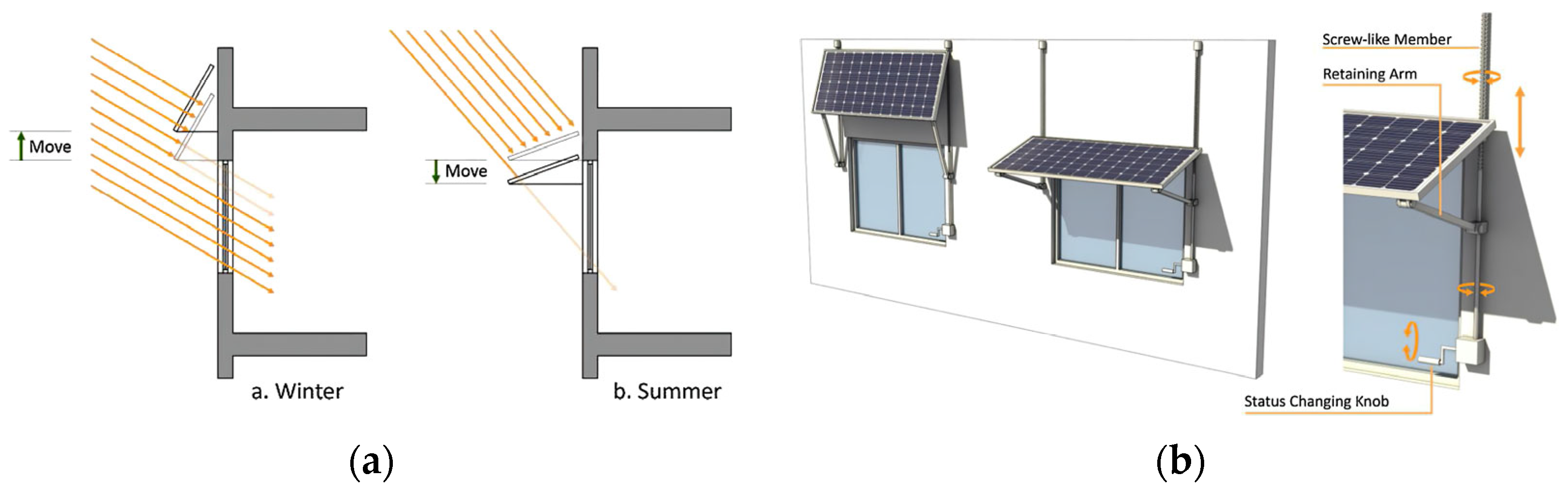
2.1.3. PV-Window System
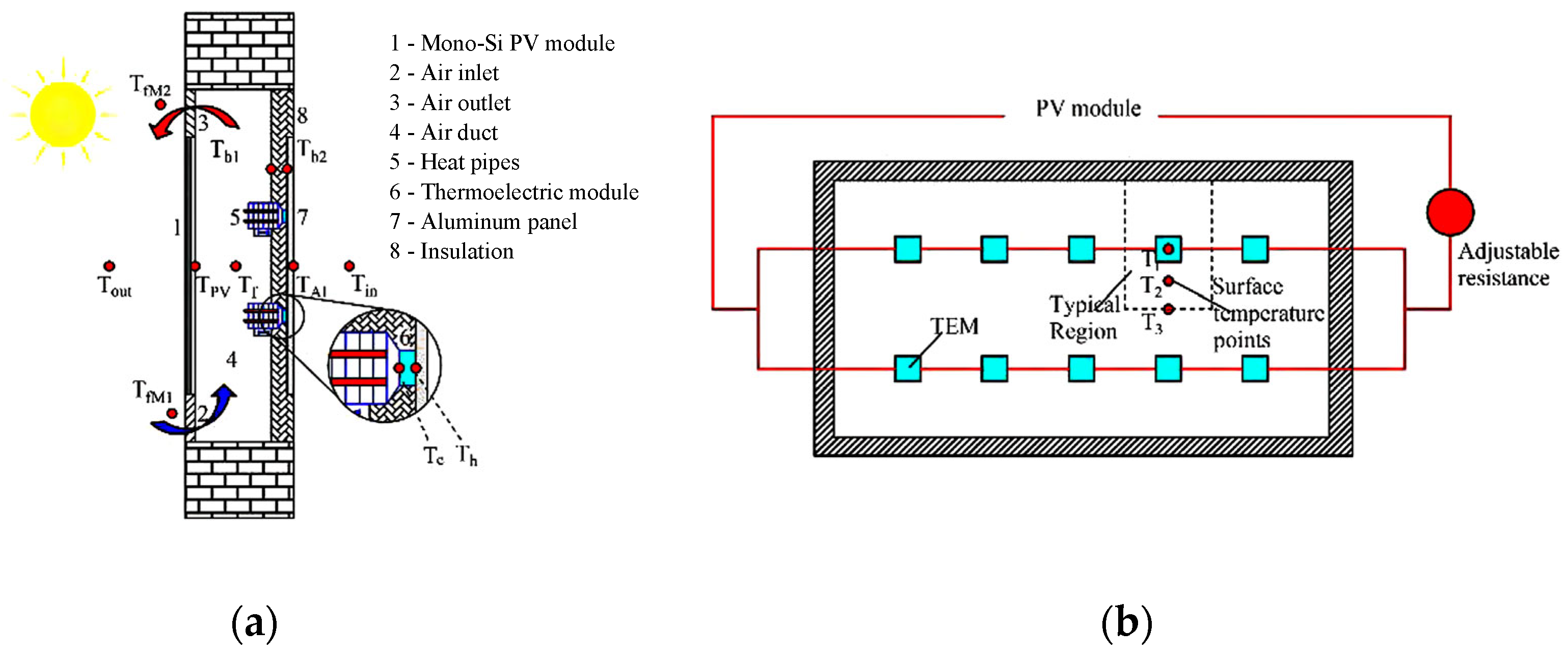
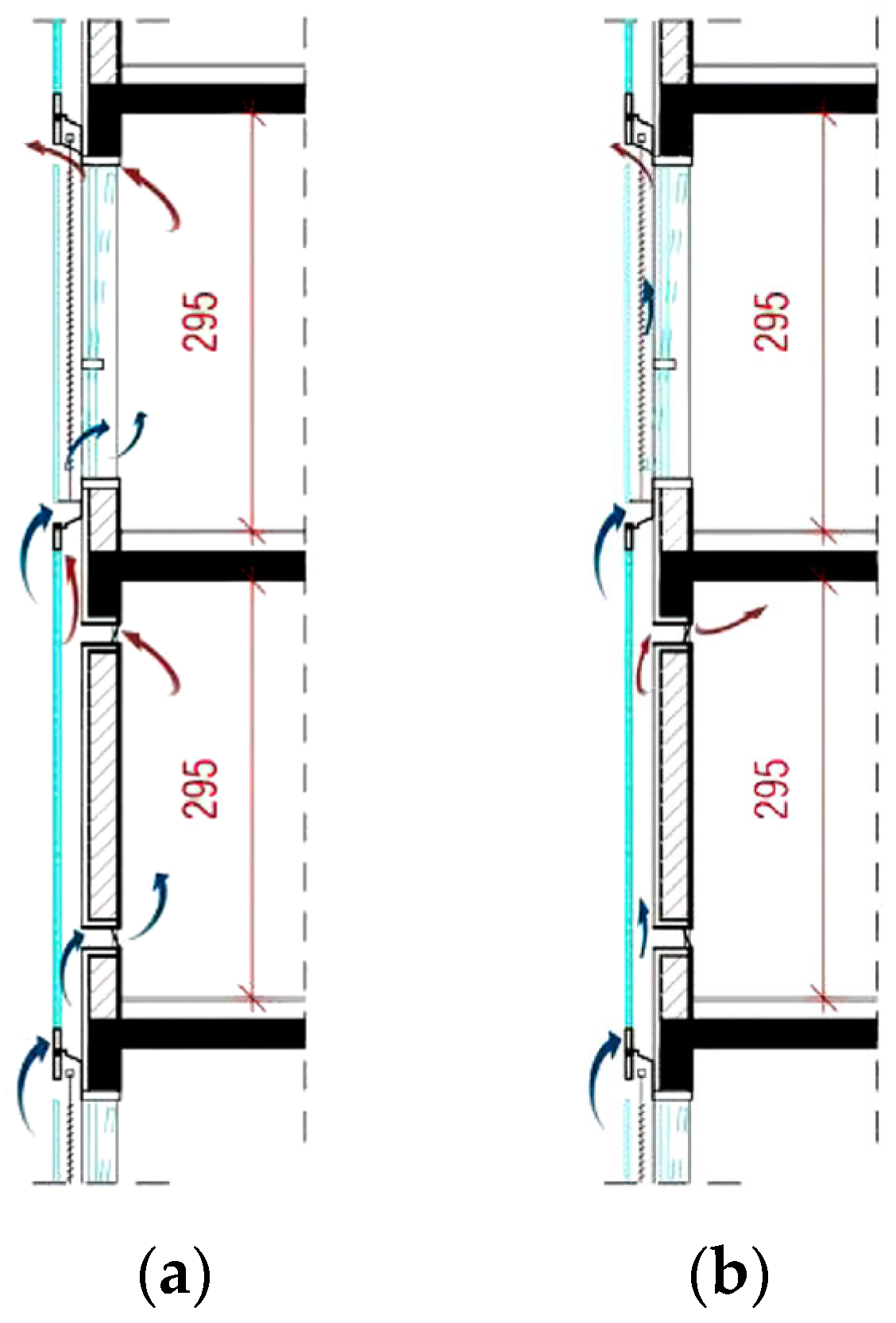
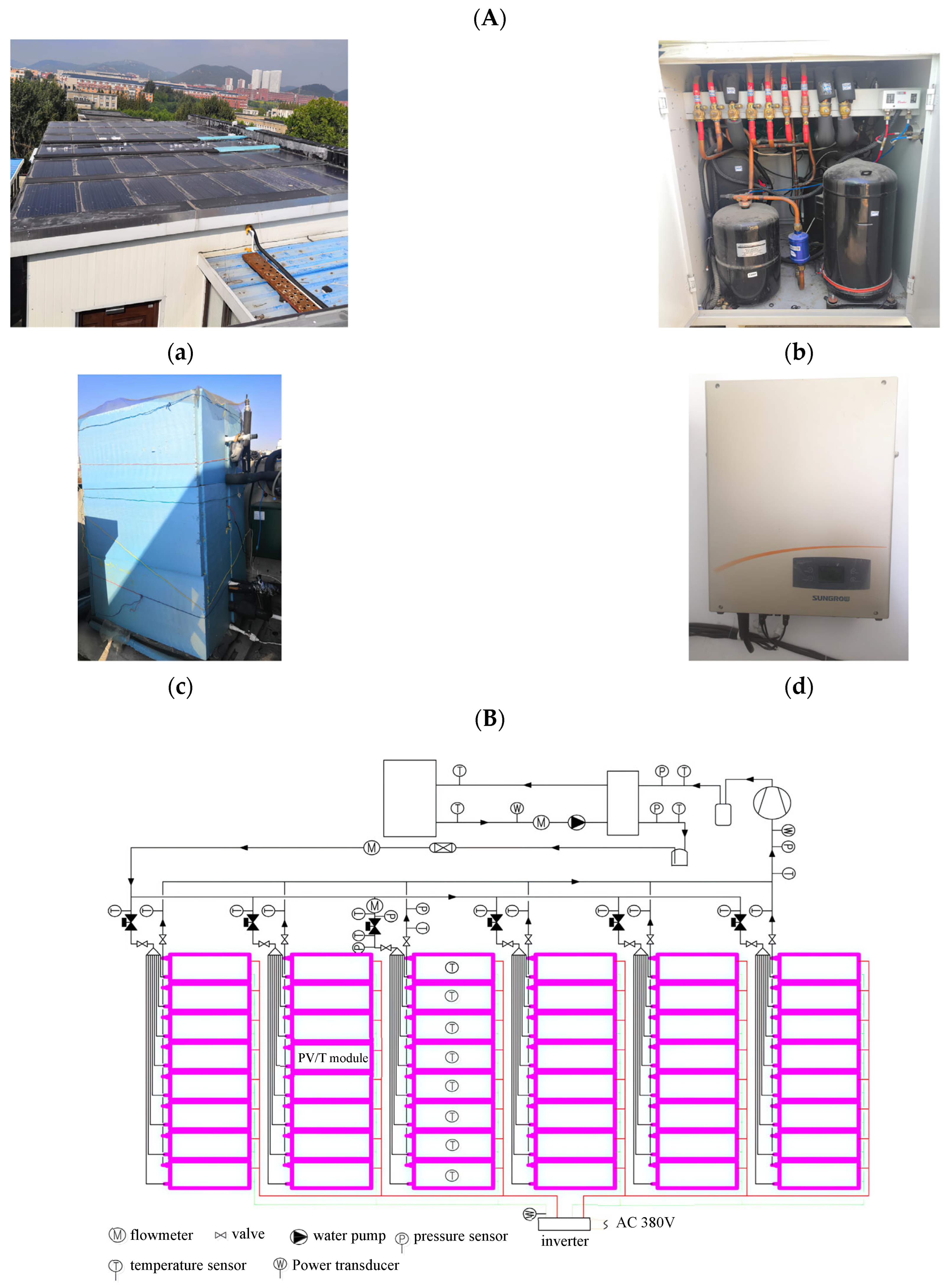
2.1.4. PV/T System
2.2. Yield of PV
2.2.1. Mathematic Models of PV Yield
2.2.2. Forecasting Models of PV Yield
2.2.3. Methods to Increase PV Yield
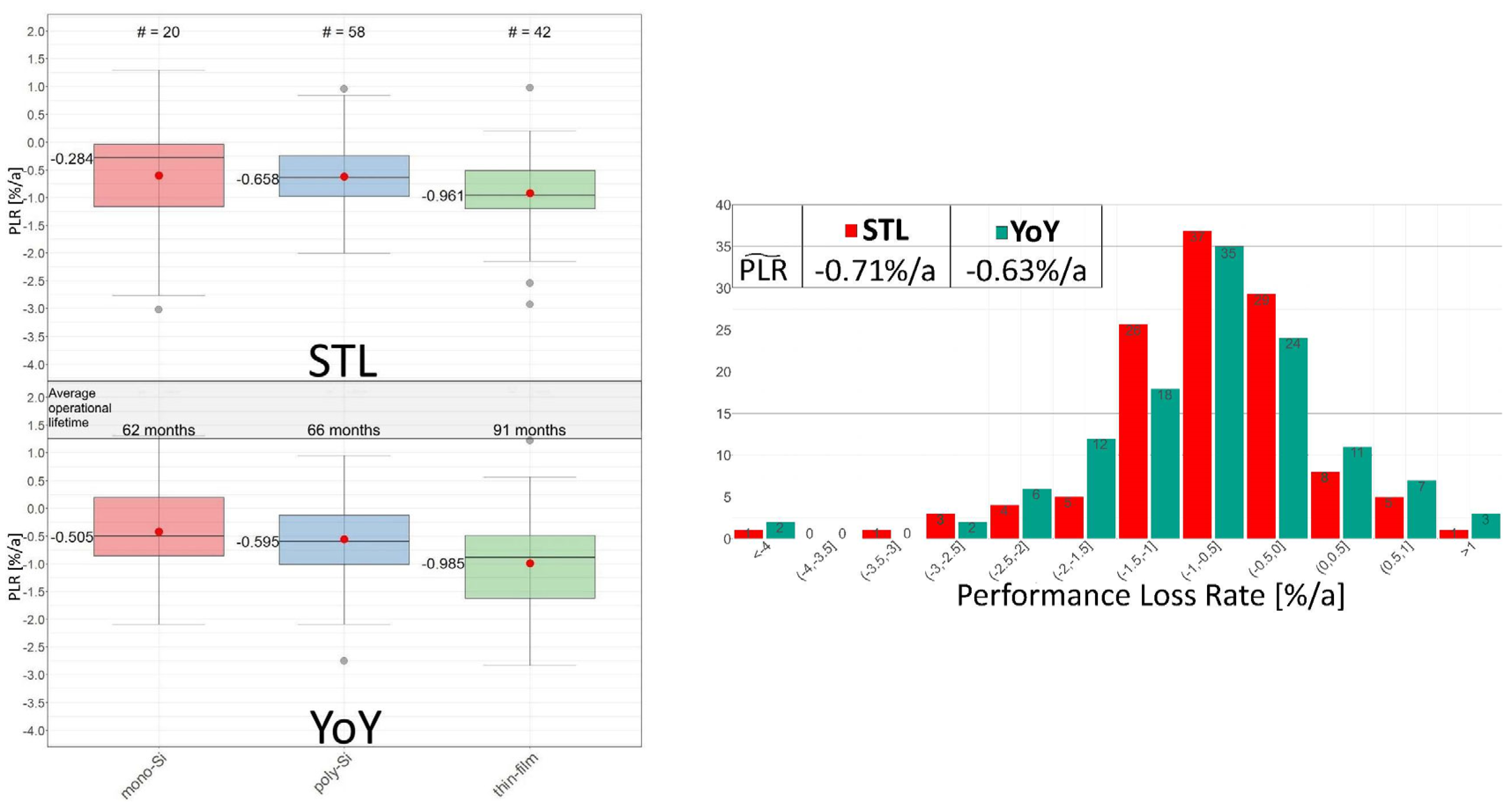
2.3. Long-Term Field Performance and Market Evolution of Building PV
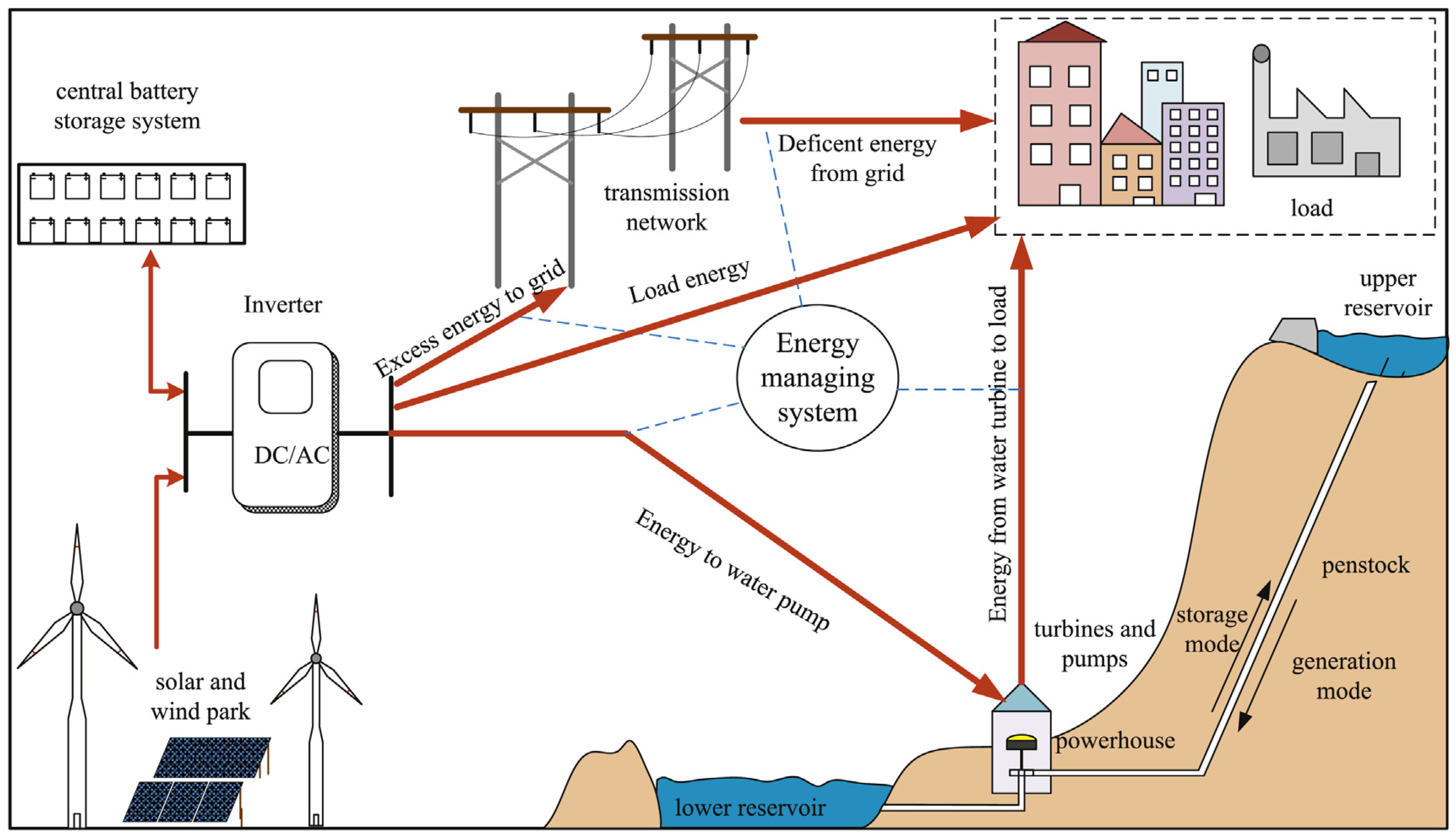
3. Energy Storage System Using Storage Battery
3.1. Working Principles of Storage Battery
3.1.1. Mathematic Model
3.1.2. Performance Influence Factors
3.1.3. Passive Techniques in PV-BESS Design
3.2. Applications
3.2.1. Centralized BESS
3.2.2. Customer-Sited Distributed BESS
3.2.3. Electrical Vehicle
3.3. Comparison Among Different Energy Storage Methods
4. Optimization of PV-BESS System’s Design Parameters
4.1. Economic Performance Indexes
4.2. Optimized Design Parameters of the System’s Components
5. Operation Optimization of the PV-BESS System in Buildings
5.1. Measures to Improve Economic Performance
5.2. Operation Optimization Process
5.3. Operation Strategies
- (1)
- Energy transfer optimization
- (2)
- Smoothing the power profiles and reducing the peaks in generation
- (3)
- Increasing power usage from PV and reducing power usage from the grid
- (4)
- Improving the humanization
- (1)
- Time-of-use: considering peak, valley, and flat power prices
- (2)
- The demand response [130]
- (3)
- Power demand forecasts
5.4. Integration of PV-BESS with CCHP Systems
6. Conclusions
- (1)
- Photovoltaic power generation systems in buildings were introduced. The power yield of PV systems was influenced by factors such as temperature, solar radiation, roof type, and panel orientation. Models to calculate or forecast PV yield were summarized, and strategies to enhance energy generation were concluded.
- (2)
- Energy Storage Systems (ESS) in buildings play a crucial role in balancing electricity generation and consumption. Mathematic models of ESS were introduced, showing that the aging of batteries was mainly related to operating temperature, depth of discharge, discharge current, and charge current. Performance degradation models and operation strategies were proposed to extend batteries’ lifespan. Applications of typical ESS, such as centralized and customer-sited distributed systems, as well as in electric vehicles, were summarized, and related operation strategies were concluded.
- (3)
- Optimizations of the PV-BESS system during design processes were summarized, from perspectives of technical, economic, and environmental performances, which is a multi-objective optimization problem. With appropriate optimization algorithms, optimal design parameters of PV-BESS can be determined, leading to a better matching between supply and demand. The ambient environment, PV system configuration, energy system location, and power consumption were found to significantly influence the values of the design parameters of the PV-BESS system.
- (4)
- Optimization methods and technologies were summarized for the operation of PV-BESS systems in buildings. Energy management strategies and optimization processes for the PV-BESS system were concluded. It is also a multi-objective optimization problem, aiming to minimize cost, maximize profit, bring the best peak shaving effects, minimize utilization of storage, maximize renewable energy consumption, minimize degradation cost, and so on. Three mainstream operation strategies as well as corresponding applications were then summarized.
Funding
Conflicts of Interest
Glossary
| Term | Definition |
| Photovoltaic (PV) Systems | Systems that convert sunlight directly into electricity using semiconductor materials. |
| Energy Storage System (ESS) | Technologies used to store energy for later use, including batteries, thermal storage, and hydrogen storage. |
| Building Integrated Photovoltaics (BIPV) | PV systems integrated into building structures (e.g., roofs, walls, windows) to serve dual purposes of energy generation and architectural function. |
| Peak Shaving | Reducing electricity consumption during periods of high demand to alleviate grid stress. |
| Valley Filling | Storing excess energy during low-demand periods for use during peak times. |
| State of Charge (SOC) | The remaining capacity of a battery as a percentage of its total capacity. |
| Depth of Discharge (DoD) | The percentage of a battery’s capacity that has been discharged relative to its total capacity. |
| Levelized Cost of Energy (LCOE) | The average cost of generating electricity over a system’s lifetime. |
| Net Present Value (NPV) | A financial metric calculating the profitability of a project by comparing present revenues and costs. |
| Internal Rate of Return (IRR) | The discount rate at which the NPV of a project equals zero, indicating breakeven profitability. |
| Self-Consumption Ratio (SCR) | The proportion of PV-generated electricity consumed on-site. |
| Self-Sufficiency Rate (SSR) | The ability of a system to meet its own energy demand without external grid support. |
| Hybrid Systems | Combined energy systems (e.g., PV + ESS + diesel generators) for improved reliability and efficiency. |
| Photovoltaic-Thermal (PV/T) System | A hybrid system generating both electricity and thermal energy from solar radiation. |
| Compressed Air Energy Storage (CAES) | Storing energy by compressing air in underground reservoirs. |
| Pumped Hydro Storage (PHS) | Storing energy by pumping water to an elevated reservoir and releasing it through turbines. |
| Time-of-Use (TOU) Pricing | Electricity pricing that varies based on demand periods (peak, off-peak). |
| Demand Response (DR) | Adjusting energy consumption patterns in response to grid signals or price incentives. |
| Maximum Power Point Tracking (MPPT) | A control algorithm to optimize PV panel output under varying conditions. |
| Vehicle-to-Grid (V2G) | Technology allowing bidirectional energy flow between electric vehicles and the grid. |
Abbreviations
| Abbreviation | Full Term |
| PV | Photovoltaic |
| ESS | Energy Storage System |
| BIPV | Building Integrated Photovoltaics |
| BESS | Battery Energy Storage System |
| SOC | State of Charge |
| DoD | Depth of Discharge |
| LCOE | Levelized Cost of Energy |
| NPV | Net Present Value |
| IRR | Internal Rate of Return |
| SCR | Self-Consumption Ratio |
| SSR | Self-Sufficiency Rate |
| CAES | Compressed Air Energy Storage |
| PHS | Pumped Hydro Storage |
| TOU | Time-of-Use |
| DR | Demand Response |
| MPPT | Maximum Power Point Tracking |
| V2G | Vehicle-to-Grid |
| EV | Electric Vehicle |
| HVAC | Heating, Ventilation, and Air Conditioning |
| LES | Local Electricity System |
| MILP | Mixed-Integer Linear Programming |
| ANN | Artificial Neural Network |
| GA | Genetic Algorithm |
| NSGA-II | Non-dominated Sorting Genetic Algorithm II |
| SAM | System Advisor Model |
| SNL | Sandia National Laboratory |
| NOCT | Nominal Operating Cell Temperature |
| CL | Cycle Life |
| FPPT | Flexible Power Point Tracking |
| EMS | Energy Management System |
| RE | Renewable Energy |
| GHG | Greenhouse Gas |
| NZEB | Net-Zero Energy Building |
| TES | Thermal Energy Storage |
| CCHP | Combined Cooling, Heating, and Power |
References
- Ikäheimo, J.; Weiss, R.; Kiviluoma, J.; Pursiheimo, E.; Lindroos, T.J. Impact of power-to-gas on the cost and design of the future low-carbon urban energy system. Appl. Energy 2022, 305, 117713. [Google Scholar] [CrossRef]
- Liu, Z.; Wang, S.; Lim, M.Q.; Kraft, M.; Wang, X. Game theory-based renewable multi-energy system design and subsidy strategy optimization. Adv. Appl. Energy 2021, 2, 100024. [Google Scholar] [CrossRef]
- United Nations Environment Programme. 2022 Global Status Report for Buildings and Construction: Towards a Zero-emissions, Efficient and Resilient Buildings and Construction Sector; United Nations Environment Programme: Nairobi, Kenya, 2022. [Google Scholar]
- Göss, S.; Lv, Y.; Yin, Y. Development of Distributed PV in Germany. In Sino-German Energy Partnership Project; Deutsche Gesellschaft für Internationale Zusammenarbeit (GIZ): Bonn, Germany, 2024. [Google Scholar]
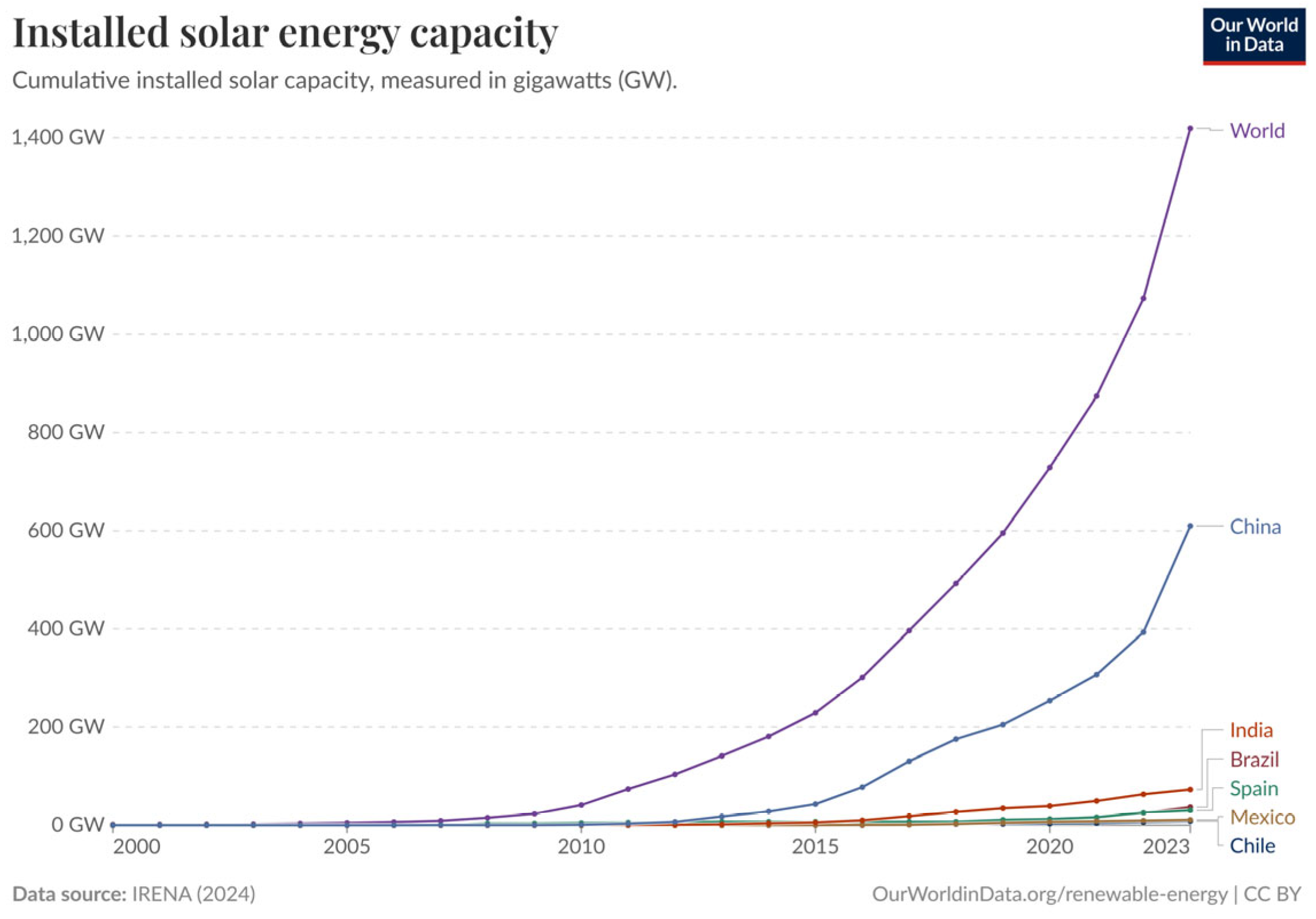
- Our World in Data. Installed Solar PV Capacity [DB/OL]. Available online: https://ourworldindata.org/grapher/installed-solar-pv-capacity (accessed on 31 December 2023).
- Wei, M.; Lee, S.H.; Hong, T.; Conlon, B.; McKenzie, L.; Hendron, B.; German, A. Approaches to cost-effective near-net zero energy new homes with time-of-use value of energy and battery storage. Adv. Appl. Energy 2021, 2, 100018. [Google Scholar] [CrossRef]
- Seck, G.S.; Krakowski, V.; Assoumou, E.; Maïzi, N.; Mazauric, V. Embedding power system’s reliability within a long-term Energy System Optimization Model: Linking high renewable energy integration and future grid stability for France by 2050. Appl. Energy 2020, 257, 114037. [Google Scholar] [CrossRef]
- Sun, H.; Heng, C.K.; Tay, S.E.R.; Chen, T.; Reindl, T. Comprehensive feasibility assessment of building integrated photovoltaics (BIPV) on building surfaces in high-density urban environments. Sol. Energy 2021, 225, 734–746. [Google Scholar] [CrossRef]
- Marqusee, J.; Becker, W.; Ericson, S. Resilience and economics of microgrids with PV, battery storage, and networked diesel generators. Adv. Appl. Energy 2021, 3, 100049. [Google Scholar] [CrossRef]
- Schleifer, A.H.; Murphy, C.A.; Cole, W.J.; Denholm, P.L. The evolving energy and capacity values of utilierty-scale PV-plus-battery hybrid system architectures. Adv. Appl. Energy 2021, 2, 100015. [Google Scholar] [CrossRef]
- Liu, J.; Chen, X.; Yang, H.; Li, Y. Energy storage and management system design optimization for a photovoltaic integrated low-energy building. Energy 2020, 190, 116424. [Google Scholar] [CrossRef]
- Liu, J.; Chen, X.; Yang, H.; Shan, K. Hybrid renewable energy applications in zero-energy buildings and communities integrating battery and hydrogen vehicle storage. Appl. Energy 2021, 290, 116733. [Google Scholar] [CrossRef]
- Xu, T.; Gao, W.; Qian, F.; Li, Y. The implementation limitation of variable renewable energies and its impacts on the public power grid. Energy 2022, 239, 121992. [Google Scholar] [CrossRef]
- Ramos, A.; Tuovinen, M.; Ala-Juusela, M. Battery Energy Storage System (BESS) as a service in Finland: Business model and regulatory challenges. J. Energy Storage 2021, 40, 102720. [Google Scholar] [CrossRef]
- Pu, G.; Zhu, X.; Dai, J.; Chen, X. Understand technological innovation investment performance: Evolution of industry-university-research cooperation for technological innovation of lithium-ion storage battery in China. J. Energy Storage 2022, 46, 103607. [Google Scholar] [CrossRef]
- Ershad, A.M.; Ueckerdt, F.; Pietzcker, R.C.; Giannousakis, A.; Luderer, G. A further decline in battery storage costs can pave the way for a solar PV-dominated Indian power system. Renew. Sustain. Energy Transit. 2021, 1, 100006. [Google Scholar] [CrossRef]
- Dougherty, A.; Billings, B.; Camacho, N.; Powell, K. Improving the economics of battery storage for industrial customers: Are incentives enough to increase adoption? The Electricity Journal 2021, 34, 107027. [Google Scholar] [CrossRef]
- Karamov, D.N.; Suslov, K.V. Storage battery operation in autonomous photovoltaic systems in Siberia and the Russian Far East. Practical operating experience. Energy Rep. 2022, 8, 649–655. [Google Scholar] [CrossRef]
- Chen, S.; Li, Z.; Li, W. Integrating high share of renewable energy into power system using customer-sited energy storage. Renew. Sustain. Energy Rev. 2021, 143, 110893. [Google Scholar] [CrossRef]
- de la Nieta, A.A.S.; Ilieva, I.; Gibescu, M.; Bernt, B.; Stig, S.; Eivind, G. Optimal midterm peak shaving cost in an electricity management system using behind customers’smart meter configuration. Appl. Energy 2021, 283, 116282. [Google Scholar] [CrossRef]
- Zimmermann, F.; Sauer, A. Sizing electric storage systems for industrial peak shaving applications. Procedia CIRP 2020, 90, 666–671. [Google Scholar] [CrossRef]
- Meimand, M.; Jazizadeh, F. A personal touch to demand response: An occupant-centric control strategy for HVAC systems using personalized comfort models. Energy Build. 2024, 303, 113769. [Google Scholar] [CrossRef]
- Hossain, J.; Saeed, N.; Manojkumar, R.; Marzband, M.; Sedraoui, K.; Al-Turki, Y. Optimal peak-shaving for dynamic demand response in smart Malaysian commercial buildings utilizing an efficient PV-BES system. Sustain. Cities Soc. 2024, 101, 105107. [Google Scholar] [CrossRef]
- Zahari, N.E.M.; Mokhlis, H.; Mubarak, H.; Mansor, N.N.; Sulaima, M.F.; Ramasamy, A.K. Integrating Solar PV, Battery Storage, and Demand Response for Industrial Peak Shaving: A Systematic Review on Strategy, Challenges and Case Study in Malaysian Food Manufacturing. IEEE Access 2024, 12, 106832–106856. [Google Scholar] [CrossRef]
- Zhang, Y.; Campana, P.E.; Lundblad, A.; Yan, J. Comparative study of hydrogen storage and battery storage in grid connected photovoltaic system: Storage sizing and rule-based operation. Appl. Energy 2017, 201, 397–411. [Google Scholar] [CrossRef]
- Cao, S.; Alanne, K. The techno-economic analysis of a hybrid zero-emission building system integrated with a commercial-scale zero-emission hydrogen vehicle. Appl. Energy 2018, 211, 639–661. [Google Scholar] [CrossRef]
- Mayyas, A.; Wei, M.; Levis, G. Hydrogen as a long-term, large-scale energy storage solution when coupled with renewable energy sources or grids with dynamic electricity pricing schemes. Int. J. Hydrogen Energy 2020, 45, 16311–16325. [Google Scholar] [CrossRef]
- Weimann, L.; Gabrielli, P.; Boldrini, A.; Kramer, G.J.; Gazzani, M. Optimal hydrogen production in a wind-dominated zero-emission energy system. Adv. Appl. Energy 2021, 3, 100032. [Google Scholar] [CrossRef]
- Pascual, J.; Arcos-Aviles, D.; Ursúa, A.; Sanchis, P.; Marroyo, L. Energy management for an electro-thermal renewable–based residential microgrid with energy balance forecasting and demand side management. Appl. Energy 2021, 295, 117062. [Google Scholar] [CrossRef]
- Galvan, E.; Mandal, P.; Sang, Y. Networked microgrids with roof-top solar PV and battery energy storage to improve distribution grids resilience to natural disasters. Int. J. Electr. Power Energy Syst. 2020, 123, 106239. [Google Scholar] [CrossRef]
- Schardt, J.; te Heesen, H. Performance of roof-top PV systems in selected European countries from 2012 to 2019. Sol. Energy 2021, 217, 235–244. [Google Scholar] [CrossRef]
- Zhou, X.; Zhang, Y.; Ma, X.; Li, G.; Wang, Y.; Hu, C.; Liang, J.; Li, M. Performance characteristics of photovoltaic cold storage under composite control of maximum power tracking and constant voltage per frequency. Applied Energy 2022, 305, 117840. [Google Scholar] [CrossRef]
- Ritzen, M.J.; Vroon, Z.A.E.P.; Rovers, R.; Geurts, C.P.W. Comparative performance assessment of a non-ventilated and ventilated BIPV rooftop configurations in the Netherlands. Sol. Energy 2017, 146, 389–400. [Google Scholar] [CrossRef]
- Do, M.-T.; Soubdhan, T.; Robyns, B. A study on the minimum duration of training data to provide a high accuracy forecast for PV generation between two different climatic zones. Renew. Energy 2016, 85, 959–964. [Google Scholar] [CrossRef]
- Agathokleous, R.A.; Kalogirou, S.A. PV roofs as the first step towards 100% RES electricity production for Mediterranean islands: The case of Cyprus. Smart Energy 2021, 4, 100053. [Google Scholar] [CrossRef]
- Castro, J.B.; Schweiger, M.; Moser, D.; Tanahashi, T.; King, B.h.; Friesen, G.; Haitao, L.; French, R.; Bruckman, L.S.; Müller, B.; et al. Climatic Rating of Photovoltaic Modules: Different Technologies for Various Operating Conditions; IEA PVPS: Sydney, Australia, 2020. [Google Scholar]
- Zomer, C.; Custódio, I.; Antoniolli, A.; Rüther, R. Performance assessment of partially shaded building-integrated photovoltaic (BIPV) systems in a positive-energy solar energy laboratory building: Architecture perspectives. Sol. Energy 2020, 211, 879–896. [Google Scholar] [CrossRef]
- Amara, H.B.; Bouadila, S.; Fatnassi, H.; Arici, M.; Guizani, A.A. Climate assessment of greenhouse equipped with south-oriented PV roofs: An experimental and computational fluid dynamics study. Sustain. Energy Technol. Assess. 2021, 45, 101100. [Google Scholar]
- Al-Saqlawi, J.; Madani, K.; Mac Dowell, N. Techno-economic feasibility of grid-independent residential roof-top solar PV systems in Muscat, Oman. Energy Convers. Manag. 2018, 178, 322–334. [Google Scholar] [CrossRef]
- Celik, B.; Karatepe, E.; Silvestre, S.; Gokmen, N.; Chouder, A. Analysis of spatial fixed PV arrays configurations to maximize energy harvesting in BIPV applications. Renew. Energy 2015, 75, 534–540. [Google Scholar] [CrossRef]
- Scherba, A.; Sailor, D.J.; Rosenstiel, T.N.; Wamser, C.C. Modeling impacts of roof reflectivity, integrated photovoltaic panels and green roof systems on sensible heat flux into the urban environment. Build. Environ. 2011, 46, 2542–2551. [Google Scholar] [CrossRef]
- Cavadini, G.B.; Cook, L.M. Green and cool roof choices integrated into rooftop solar energy modelling. Appl. Energy 2021, 296, 117082. [Google Scholar] [CrossRef]
- Mühleisen, W.; Loeschnig, J.; Feichtner, M.; Burgers, A.R.; Bende, E.E.; Zamini, S.; Yerasimou, Y.; Kosel, J.; Hirschl, C.; Georghiou, G.E. Energy yield measurement of an elevated PV system on a white flat roof and a performance comparison of monofacial and bifacial modules. Renew. Energy 2021, 170, 613–619. [Google Scholar] [CrossRef]
- Shukla, N.; Watts, A.; Honeker, C.; Hill, M.; Kośny, J. Thermal impact of adhesive-mounted rooftop PV on underlying roof shingles. Sol. Energy 2018, 174, 957–966. [Google Scholar] [CrossRef]
- Shao, N.; Ma, L.; Zhang, J. Experimental study on electrical and thermal performance and heat transfer characteristic of PV/T roof in summer. Appl. Therm. Eng. 2019, 162, 114276. [Google Scholar] [CrossRef]
- Skandalos, N.; Karamanis, D. An optimization approach to photovoltaic building integration towards low energy buildings in different climate zones. Appl. Energy 2021, 295, 117017. [Google Scholar] [CrossRef]
- Theokli, C.; Elia, C.; Markou, M.; Vassiliades, C. Energy renovation of an existing building in Nicosia Cyprus and investigation of the passive contribution of a BIPV/T double façade system: A case-study. Energy Rep. 2021, 7, 8522–8533. [Google Scholar] [CrossRef]
- Tina, G.M.; Scavo, F.B.; Aneli, S.; Gagliano, A. Assessment of the electrical and thermal performances of building integrated bifacial photovoltaic modules. J. Clean. Prod. 2021, 313, 127906. [Google Scholar] [CrossRef]
- Shirazi, A.M.; Zomorodian, Z.S.; Tahsildoost, M. Techno-economic BIPV evaluation method in urban areas. Renew. Energy 2019, 143, 1235–1246. [Google Scholar] [CrossRef]
- Luo, Y.; Zhang, L.; Liu, Z.; Yu, J.; Xu, X.; Su, X. Towards net zero energy building: The application potential and adaptability of photovoltaic-thermoelectric-battery wall system. Appl. Energy 2020, 258, 114066. [Google Scholar] [CrossRef]
- Chen, M.; Zhang, W.; Xie, L.; Ni, Z.; Wei, Q.; Wang, W.; Tian, H. Experimental and numerical evaluation of the crystalline silicon PV window under the climatic conditions in southwest China. Energy 2019, 183, 584–598. [Google Scholar] [CrossRef]
- Yang, S.; Fiorito, F.; Prasad, D.; Sproul, A.; Cannavale, A. A sensitivity analysis of design parameters of BIPV/T-DSF in relation to building energy and thermal comfort performances. J. Build. Eng. 2021, 41, 102426. [Google Scholar] [CrossRef]
- Chen, L.; Zheng, X.; Yang, J.; Yoon, J.H. Impact of BIPV windows on building energy consumption in street canyons: Model development and validation. Energy Build. 2021, 249, 111207. [Google Scholar] [CrossRef]
- Salameh, T.; Assad, M.E.H.; Tawalbeh, M.; Ghenai, C.; Merabet, A.; Öztop, H.F. Analysis of cooling load on commercial building in UAE climate using building integrated photovoltaic façade system. Sol. Energy 2020, 199, 617–629. [Google Scholar] [CrossRef]
- te Heesen, H.; Herbort, V.; Rumpler, M. Performance of roof-top PV systems in Germany from 2012 to 2018. Sol. Energy 2019, 194, 128–135. [Google Scholar] [CrossRef]
- Chialastri, A.; Isaacson, M. Performance and optimization of a BIPV/T solar air collector for building fenestration applications. Energy Build. 2017, 150, 200–210. [Google Scholar] [CrossRef]
- Paydar, M.A. Optimum design of building integrated PV module as a movable shading device. Sustain. Cities Soc. 2020, 62, 102368. [Google Scholar] [CrossRef]
- Shao, N.; Ma, L.; Zhang, J. Experimental investigation on the performance of direct-expansion roof-PV/T heat pump system. Energy 2020, 195, 116959. [Google Scholar] [CrossRef]
- Khordehgah, N.; Guichet, V.; Lester, S.P.; Jouhara, H. Computational study and experimental validation of a solar photovoltaics and thermal technology. Renew. Energy 2019, 143, 1348–1356. [Google Scholar] [CrossRef]
- Li, Z.; Ji, J.; Yuan, W.; Song, Z.; Ren, X.; Uddin, M.M.; Luo, K.; Zhao, X. Experimental and numerical investigations on the performance of a G-PV/T system comparing with A-PV/T system. Energy 2020, 194, 116776. [Google Scholar] [CrossRef]
- Wang, C.; Ji, J.; Yu, B.; Xu, L.; Wang, Q.; Tian, X. Investigation on the operation strategy of a hybrid BIPV/T façade in plateau areas: An adaptive regulation method based on artificial neural network. Energy 2022, 239, 122055. [Google Scholar] [CrossRef]
- Rounis, E.D.; Athienitis, A.K.; Stathopoulos, T. BIPV/T curtain wall systems: Design, development and testing. J. Build. Eng. 2021, 42, 103019. [Google Scholar] [CrossRef]
- Hasan, J.; Fung, A.S.; Horvat, M. A comparative evaluation on the case for the implementation of building integrated photovoltaic/thermal (BIPV/T) air based systems on a typical mid-rise commercial building in Canadian cities. J. Build. Eng. 2021, 44, 103325. [Google Scholar] [CrossRef]
- Gao, Y.; Ji, J.; Han, K.; Zhang, F. Experimental and numerical study of a PV/T direct-driven refrigeration/heating system. Energy 2021, 230, 120793. [Google Scholar] [CrossRef]
- Mao, M.; Yu, S.; Su, J. Versatile Matlab Simulation Model for Photovoltaic Array with MPPT Function. J. Syst. Simul. 2005, 17, 1248–1251. [Google Scholar]
- Kumar, N.M.; Gupta, R.P.; Mathew, M.; Jayakumar, A.; Singh, K.N. Performance, energy loss, and degradation prediction of roof-integrated crystalline solar PV system installed in Northern India. Case Stud. Therm. Eng. 2019, 13, 100409. [Google Scholar] [CrossRef]
- Qu, Y.; Xu, J.; Sun, Y.; Liu, D. A temporal distributed hybrid deep learning model for day-ahead distributed PV power forecasting. Appl. Energy 2021, 304, 117704. [Google Scholar] [CrossRef]
- Hossain, M.; Mekhilef, S.; Danesh, M.; Olatomiwa, L.; Shamshirband, S. Application of extreme learning machine for short term output power forecasting of three grid-connected PV systems. J. Clean. Prod. 2017, 167, 395–405. [Google Scholar] [CrossRef]
- Kumari, P.; Toshniwal, D. Long short term memory–convolutional neural network based deep hybrid approach for solar irradiance forecasting. Appl. Energy 2021, 295, 117061. [Google Scholar] [CrossRef]
- Ren, H.; Xu, C.; Ma, Z.; Sun, Y. A novel 3D-geographic information system and deep learning integrated approach for high-accuracy building rooftop solar energy potential characterization of high-density cities. Appl. Energy 2022, 306, 117985. [Google Scholar] [CrossRef]
- Tang, P.; Li, Q. Evaluation of the observation methods of outdoor mean radiant temperature in a subtropical city. Build. Environ. 2022, 207, 108462. [Google Scholar] [CrossRef]
- D’orazio, M.; Di Perna, C.; Di Giuseppe, E. Experimental operating cell temperature assessment of BIPV with different installation configurations on roofs under Mediterranean climate. Renew. Energy 2014, 68, 378–396. [Google Scholar] [CrossRef]
- Kaplanis, S.; Kaplani, E.; Kaldellis, J.K. PV temperature and performance prediction in free-standing, BIPV and BAPV incorporating the effect of temperature and inclination on the heat transfer coefficients and the impact of wind, efficiency and ageing. Renew. Energy 2022, 181, 235–249. [Google Scholar] [CrossRef]
- Vaka, A.S.; Talukdar, P. Novel inverse heat transfer technique for estimation of properties and location-specific process parameters of roof-mounted solar PV plants. Therm. Sci. Eng. Prog. 2020, 19, 100657. [Google Scholar] [CrossRef]
- Amabile, L.; Bresch-Pietri, D.; El Hajje, G.; Labbé, S.; Petit, N. Optimizing the self-consumption of residential photovoltaic energy and quantification of the impact of production forecast uncertainties. Adv. Appl. Energy 2021, 2, 100020. [Google Scholar] [CrossRef]
- Li, S. Research on Coordinated Scheduling Strategy for Large-Scale Energy Storage and High-Permeability New Energy. Master’s Thesis, Lanzhou Jiaotong University, Lanzhou, China, 2019. [Google Scholar]
- Mehrjerdi, H.; Iqbal, A.; Rakhshani, E.; Torres, J.R. Daily-seasonal operation in net-zero energy building powered by hybrid renewable energies and hydrogen storage systems. Energy Convers. Manag. 2019, 201, 112156. [Google Scholar] [CrossRef]
- Cervone, G.; Clemente-Harding, L.; Alessandrini, S.; Delle Monache, L. Short-term photovoltaic power forecasting using Artificial Neural Networks and an Analog Ensemble. Renew. Energy 2017, 108, 276–286. [Google Scholar] [CrossRef]
- Chen, L.; Yang, J.; Li, P. Modelling the effect of BIPV window in the built environment: Uncertainty and sensitivity. Build. Environ. 2022, 208, 108605. [Google Scholar] [CrossRef]
- Zhang, J.; Ji, W. Optimal allocation of energy storage in photovoltaic system based on improved genetic algorithm. China Meas. Test 2021, 47, 160–168. [Google Scholar]
- González-Ordiano, J.Á.; Mühlpfordt, T.; Braun, E.; Liu, J.; Çakmak, H.; Kühnapfel, U.; Düpmeier, C.; Waczowicz, S.; Faulwasser, T.; Mikut, R.; et al. Probabilistic forecasts of the distribution grid state using data-driven forecasts and probabilistic power flow. Appl. Energy 2021, 302, 117498. [Google Scholar] [CrossRef]
- Thorey, J.; Chaussin, C.; Mallet, V. Ensemble forecast of photovoltaic power with online CRPS learning. Int. J. Forecast. 2018, 34, 762–773. [Google Scholar] [CrossRef]
- Kumar, N.M.; Samykano, M.; Karthick, A. Energy loss analysis of a large scale BIPV system for university buildings in tropical weather conditions: A partial and cumulative performance ratio approach. Case Stud. Therm. Eng. 2021, 25, 100916. [Google Scholar] [CrossRef]
- Azami, A.; Sevinç, H. Environment. The energy performance of building integrated photovoltaics (BIPV) by determination of optimal building envelope. Build. Environ. 2021, 199, 107856. [Google Scholar] [CrossRef]
- Sharma, M.K.; Kumar, D.; Dhundhara, S.; Gaur, D.; Verma, Y.P. Optimal tilt angle determination for PV panels using real time data acquisition. Glob. Chall. 2020, 4, 1900109. [Google Scholar] [CrossRef]
- Poulek, V.; Matuška, T.; Libra, M.; Kachalouski, E.; Sedláček, J. Influence of increased temperature on energy production of roof integrated PV panels. Energy Build. 2018, 166, 418–425. [Google Scholar] [CrossRef]
- Khordehgah, N.; Żabnieńska-Góra, A.; Jouhara, H. Analytical modelling of a photovoltaics-thermal technology combined with thermal and electrical storage systems. Renew. Energy 2021, 165, 350–358. [Google Scholar] [CrossRef]
- Kong, M.; Joo, H.; Kwak, H. Experimental identification of effects of using dual airflow path on the performance of roof-type BAPV system. Energy Build. 2020, 226, 110403. [Google Scholar] [CrossRef]
- Alsaigh, R.E.; Bauer, R.; Lavery, M.P.J. Multi-layer light trap** structures for enhanced solar collection. Opt. Express 2020, 28, 31714–31728. [Google Scholar] [CrossRef]
- Kim, J.; Rivera, J.L.; Meng, T.Y.; Laratte, B.; Chen, S. Review of life cycle assessment of nanomaterials in photovoltaics. Sol. Energy 2016, 133, 249–258. [Google Scholar] [CrossRef]
- French, R.H.; Bruckman, L.S.; Moser, D.; Lindig, S.; van Iseghem, M.; Müller, B.; Stein, J.S.; Richter, M.; Herz, M.; Sark, W.V.; et al. Assessment of Performance Loss Rate of PV Power Systems; IEA PVPS: Sydney, Australia, 2021. [Google Scholar]
- Sevilla, F.R.S.; Parra, D.; Wyrsch, N.; Patel, M.K.; Kienzle, F.; Korba, P. Techno-economic analysis of battery storage and curtailment in a distribution grid with high PV penetration. J. Energy Storage 2018, 17, 73–83. [Google Scholar] [CrossRef]
- Kumar, A.R.; Shrimali, G. Role of policy in the development of business models for battery storage deployment: Hawaii case study. Energy Policy 2021, 159, 112605. [Google Scholar] [CrossRef]
- Furubayashi, T. Design and analysis of a 100% renewable energy system for Akita prefecture, Japan. Smart Energy 2021, 2, 100012. [Google Scholar] [CrossRef]
- Zheng, S.; Huang, G.; Lai, A.C. Techno-economic performance analysis of synergistic energy sharing strategies for grid-connected prosumers with distributed battery storages. Renew. Energy 2021, 178, 1261–1278. [Google Scholar] [CrossRef]
- Nordelöf, A.; Messagie, M.; Tillman, A.-M.; Söderman, M.L.; Mierlo, J.V. Environmental impacts of hybrid, plug-in hybrid, and battery electric vehicles—What can we learn from life cycle assessment. Int. J. Life Cycle Assess. 2014, 19, 1866–1890. [Google Scholar] [CrossRef]
- Omar, N.; Monem, M.A.; Firouz, Y.; Salminen, J.; Smekens, J.; Hegazy, O.; Gaulous, H.; Mulder, G.; Van den Bossche, P.; Coosemans, T.; et al. Lithium iron phosphate based battery–Assessment of the aging parameters and development of cycle life model. Appl. Energy 2014, 113, 1575–1585. [Google Scholar] [CrossRef]
- Shao, Y.Q.; Liu, H.L.; Shao, X.D.; Sang, L.; Chen, Z. An all coupled electrochemical-mechanical model for all-solid-state Li-ion batteries considering the effect of contact area loss and compressive pressure. Energy 2022, 239, 121929. [Google Scholar] [CrossRef]
- Wang, Y.; Sun, Y.; Zhang, Y.; Chen, X.; Shen, H.K.; Liu, Y.; Zhang, X.Y.; Zhang, Y.X. Optimal modeling and analysis of microgrid lithium iron phosphate battery energy storage system under different power supply states. J. Power Sources 2022, 521, 230931. [Google Scholar] [CrossRef]
- Moy, K.; Lee, S.B.; Harris, S.; Onori, S. Design and Validation of Synthetic Duty Cycles for Grid Energy Storage Dispatch Using Lithium-ion Batteries. Adv. Appl. Energy 2021, 4, 100065. [Google Scholar] [CrossRef]
- Gräf, D.; Marschewski, J.; Ibing, L.; Huckebrink, D.; Fiebrandt, M.; Hanau, G.; Bertsch, V. What drives capacity degradation in utility-scale battery energy storage systems? The impact of operating strategy and temperature in different grid applications. J. Energy Storage 2022, 47, 103533. [Google Scholar] [CrossRef]
- Guo, M.; Mu, Y.; Jia, H.; Deng, Y.; Xu, X.; Yu, X. Electric/thermal hybrid energy storage planning for park-level integrated energy systems with second-life battery utilization. Adv. Appl. Energy 2021, 4, 100064. [Google Scholar] [CrossRef]
- Loukatou, A.; Johnson, P.; Howell, S.; Duck, P. Optimal valuation of wind energy projects co-located with battery storage. Appl. Energy 2020, 283, 116247. [Google Scholar] [CrossRef]
- Song, M.; Choe, S.Y. Parameter sensitivity analysis of a reduced-order electrochemical-thermal model for heat generation rate of lithium-ion batteries. Appl. Energy 2022, 305, 117920. [Google Scholar] [CrossRef]
- Solntsev, A.; Asoyan, A.; Nikitin, D.; Bagrin, V.; Fediushkina, O.; Evtykov, S.; Marusin, A. Influence of temperature on the performance and life cycle of storage batteries. Transp. Res. Procedia 2021, 57, 652–659. [Google Scholar] [CrossRef]
- Yang, Q.; Li, J.; Yang, R.; Zhu, J.; Wang, X.C.; He, H.W. New hybrid scheme with local battery energy storages and electric vehicles for the power frequency service. eTransportation 2021, 11, 100151. [Google Scholar] [CrossRef]
- Sepúlveda-Mora, S.B.; Hegedus, S. Making the case for time-of-use electric rates to boost the value of battery storage in commercial buildings with grid connected PV systems. Energy 2021, 218, 119447. [Google Scholar] [CrossRef]
- Vonsien, S.; Madlener, R. Li-ion battery storage in private households with PV systems: Analyzing the economic impacts of battery aging and pooling. J. Energy Storage 2020, 29, 101407. [Google Scholar] [CrossRef]
- Su, D.; Lei, Z. Optimal configuration of battery energy storage system in primary frequency regulation. Energy Rep. 2021, 7, 157–162. [Google Scholar] [CrossRef]
- Lee, J.O.; Kim, Y.S. Novel battery degradation cost formulation for optimal scheduling of battery energy storage systems. Int. J. Electr. Power Energy Syst. 2022, 137, 107795. [Google Scholar] [CrossRef]
- Angenendt, G.; Zurmühlen, S.; Axelsen, H.; Sauer, D.U. Comparison of different operation strategies for PV battery home storage systems including forecast-based operation strategies. Appl. Energy 2018, 229, 884–899. [Google Scholar] [CrossRef]
- Liu, X.; Xu, X.; Wu, Q.; Chen, X.; Wen, J.Y.; Wang, W.; Zhang, K.J.; Li, C.B.; Chen, X.Y. SoC threshold optimization for battery storage in frequency regulation considering uncertainty of SoC measurement and automatic generation control fatigue loss of thermal power system. Int. J. Electr. Power Energy Syst. 2022, 137, 107771. [Google Scholar] [CrossRef]
- Aryanezhad, M. A robust game-theoretic optimization model for battery energy storage in multi-microgrids by considering of renewable based DGs uncertainty. Electr. Power Syst. Res. 2022, 204, 107591. [Google Scholar] [CrossRef]
- Wen, K.; Li, W.; Zhao, Y.; Shen, J.K.; Li, Z.F.; Zhang, M.Z. Optimal operation framework of customer-premise battery storage for energy charge reduction and primary frequency regulation. J. Energy Storage 2021, 43, 103147. [Google Scholar] [CrossRef]
- Zhu, L.; Lian, G.; Hu, S. Research on a real-time control strategy of battery energy storage system based on filtering algorithm and battery state of charge. Sustain. Energy Technol. Assess. 2021, 47, 101524. [Google Scholar] [CrossRef]
- Li, W.; Wang, X.; Cen, P.Y.; Chen, Q.; De Cachinho Cordeiro, I.M.; Kong, L.; Lin, P.; Li, A. A Comparative Numerical Study of Lithium-Ion Batteries with Air-Cooling Systems towards Thermal Safety. Fire 2024, 7, 29. [Google Scholar] [CrossRef]
- Lind, J.; Möllerström, E.; Averfalk, H.; Ottermo, F. Energy flexibility using the thermal mass of residential buildings. Energy Build. 2023, 301, 113698. [Google Scholar] [CrossRef]
- Tian, H.; Ma, L.; Li, Q.; Li, D.; Jiang, W.; Zhang, X.; Hu, H.L.; Han, Y. Energy saving retrofit of rural house based on the joint utilization of solar collector and attached sunspace. Energy Build. 2023, 299, 113591. [Google Scholar] [CrossRef]
- Lin, J.; Zhong, X.; Wang, J.; Huang, Y.; Bai, X.T.; Wang, X.N.; Shah, N.; Xie, S.; Zhao, Y.R. Relative optimization potential: A novel perspective to address trade-off challenges in urban energy system planning. Appl. Energy 2021, 304, 117741. [Google Scholar] [CrossRef]
- Abdelshafy, A.M.; Jurasz, J.; Hassan, H.; Mohamed, A.M. Optimized energy management strategy for grid connected double storage (pumped storage-battery) system powered by renewable energy resources. Energy 2020, 192, 116615. [Google Scholar] [CrossRef]
- Ding, H.; Hu, Q.; Hou, K.; Dou, X.B.; Zhang, C. The coordinated operation of dual batteries energy storage system for cold areas. Energy Rep. 2021, 7, 84–91. [Google Scholar] [CrossRef]
- Englberger, S.; Chapman, A.C.; Tushar, W.; Almomani, T.; Snow, S.; Witzmann, R.; Jossen, A.; Hesse, H. Evaluating the interdependency between peer-to-peer networks and energy storages: A techno-economic proof for prosumers. Adv. Appl. Energy 2021, 3, 100059. [Google Scholar] [CrossRef]
- Henni, S.; Staudt, P.; Weinhardt, C. A sharing economy for residential communities with PV-coupled battery storage: Benefits, pricing and participant matching. Appl. Energy 2021, 301, 117351. [Google Scholar] [CrossRef]
- Tomin, N.; Shakirov, V.; Kozlov, A.; Sidorov, D.; Kurbatsky, V.; Rehtanz, C.; Lora, E.E.S. Design and optimal energy management of community microgrids with flexible renewable energy sources. Renew. Energy 2022, 183, 903–921. [Google Scholar] [CrossRef]
- Salameh, T.; Abdelkareem, M.A.; Olabi, A.G.; Sayed, E.T.; Al-Chaderchi, M.; Rezk, H. Integrated standalone hybrid solar PV, fuel cell and diesel generator power system for battery or supercapacitor storage systems in Khorfakkan, United Arab Emirates. Int. J. Hydrogen Energy 2020, 46, 6014–6027. [Google Scholar] [CrossRef]
- Seward, W.; Qadrdan, M.; Jenkins, N. Quantifying the value of distributed battery storage to the operation of a low carbon power system. Appl. Energy 2022, 305, 117684. [Google Scholar] [CrossRef]
- Liu, J.; Cao, S.; Chen, X.; Yang, H.X.; Peng, J.Q. Energy planning of renewable applications in high-rise residential buildings integrating battery and hydrogen vehicle storage. Met. Powder Rep. 2021, 281, 116038. [Google Scholar] [CrossRef]
- Jing, R.; Wang, J.; Shah, N.; Guo, M. Emerging supply chain of utilising electrical vehicle retired batteries in distributed energy systems. Adv. Appl. Energy 2020, 1, 100002. [Google Scholar] [CrossRef]
- Blonsky, M.; Maguire, J.; McKenna, K.; Cutler, D.; Balamurugan, S.P.; Jin, X. OCHRE: The Object-oriented, Controllable, High-resolution Residential Energy Model for Dynamic Integration Studies. Appl. Energy 2021, 290, 116732. [Google Scholar] [CrossRef]
- Thomas, D.; Deblecker, O.; Ioakimidis, C.S. Optimal operation of an energy management system for a grid-connected smart building considering photovoltaics’ uncertainty and stochastic electric vehicles’ driving schedule. Appl. Energy 2018, 210, 1188–1206. [Google Scholar] [CrossRef]
- Mulleriyawage, U.G.K.; Shen, W.X. Optimally sizing of battery energy storage capacity by operational optimization of residential PV-Battery systems: An Australian household case study. Renew. Energy 2020, 160, 109–125. [Google Scholar] [CrossRef]
- Zhou, Q.; Li, Y.; Zhao, D.; Li, J.; Williams, H.; Xu, H.M.; Yan, F.W.L. Transferable representation modelling for real-time energy management of the plug-in hybrid vehicle based on k-fold fuzzy learning and Gaussian process regression. Appl. Energy 2022, 305, 117853. [Google Scholar] [CrossRef]
- Robledo, C.B.; Oldenbroek, V.; Abbruzzese, F.; Wijk, A.J.M. Integrating a hydrogen fuel cell electric vehicle with vehicle-to-grid technology, photovoltaic power and a residential building. Appl. Energy 2018, 215, 615–629. [Google Scholar] [CrossRef]
- Saboori, H.; Jadid, S. Mobile and self-powered battery energy storage system in distribution networks–Modeling, operation optimization, and comparison with stationary counterpart. J. Energy Storage 2021, 42, 103068. [Google Scholar] [CrossRef]
- Woo, S.; Bae, S.; Moura, S.J. Pareto optimality in cost and service quality for an Electric Vehicle charging facility. Appl. Energy 2021, 290, 116779. [Google Scholar] [CrossRef]
- Gilleran, M.; Bonnema, E.; Woods, J.; Mishra, P.; Doebber, I.; Hunter, C.; Mitchell, M.; Mann, M. Impact of electric vehicle charging on the power demand of retail buildings. Adv. Appl. Energy 2021, 4, 100062. [Google Scholar] [CrossRef]
- Saini, P.; Gidwani, L. An investigation for battery energy storage system installation with renewable energy resources in distribution system by considering residential, commercial and industrial load models. J. Energy Storage 2022, 45, 103493. [Google Scholar] [CrossRef]
- Kotb, K.M.; Elmorshedy, M.F.; Salama, H.S.; Dán, A. Enriching the stability of solar/wind DC microgrids using battery and superconducting magnetic energy storage based fuzzy logic control. J. Energy Storage 2022, 45, 103751. [Google Scholar] [CrossRef]
- Mortaz, E.; Vinel, A.; Dvorkin, Y. An optimization model for siting and sizing of vehicle-to-grid facilities in a microgrid. Appl. Energy 2019, 242, 1649–1660. [Google Scholar] [CrossRef]
- Bayram, I.S.; Galloway, S.; Burt, G. A probabilistic capacity planning methodology for plug-in electric vehicle charging lots with on-site energy storage systems. J. Energy Storage 2020, 32, 101730. [Google Scholar] [CrossRef]
- Kucevic, D.; Englberger, S.; Sharma, A.; Trivedi, A.; Tepe, B.; Schachler, B.; Hesse, H.; Srinivasan, D.; Jossen, A. Reducing grid peak load through the coordinated control of battery energy storage systems located at electric vehicle charging parks. Appl. Energy 2021, 295, 116936. [Google Scholar] [CrossRef]
- Zheng, Y.; Shao, Z.; Jian, L. The peak load shaving assessment of developing a user-oriented vehicle-to-grid scheme with multiple operation modes: The case study of Shenzhen, China. Sustain. Cities Soc. 2021, 67, 102774. [Google Scholar] [CrossRef]
- Wang, Y.; Zhou, Z.; Botterud, A.; Zhang, K.F.; Ding, Q. Stochastic coordinated operation of wind and battery energy storage system considering battery degradation. J. Mod. Power Syst. Clean Energy 2016, 4, 581–592. [Google Scholar] [CrossRef]
- Cusenza, M.A.; Guarino, F.; Longo, S.; Mistretta, M.; Cellura, M. Reuse of electric vehicle batteries in buildings: An integrated load match analysis and life cycle assessment approach. Energy Build. 2019, 186, 339–354. [Google Scholar] [CrossRef]
- Ni, Y.; Xu, J.; Zhu, C.; Pei, L. Accurate residual capacity estimation of retired LiFePO4 batteries based on mechanism and data-driven model. Appl. Energy 2022, 305, 117922. [Google Scholar] [CrossRef]
- Gur, K.; Chatzikyriakou, D.; Baschet, C.; Salomon, M. The reuse of electrified vehicle batteries as a means of integrating renewable energy into the European electricity grid: A policy and market analysis. Energy Policy 2018, 113, 535–545. [Google Scholar] [CrossRef]
- Gao, Y.; Cai, Y.; Liu, C. Annual operating characteristics analysis of photovoltaic-energy storage microgrid based on retired lithium iron phosphate batteries. J. Energy Storage 2022, 45, 103769. [Google Scholar] [CrossRef]
- Luerssen, C.; Gandhi, O.; Reindl, T.; Sekhar, C.; Cheong, D. Life cycle cost analysis (LCCA) of PV-powered cooling systems with thermal energy and battery storage for off-grid applications. Appl. Energy 2020, 273, 115145. [Google Scholar] [CrossRef]
- Bertsch, V.; Geldermann, J.; Lühn, T. What drives the profitability of household PV investments, self-consumption and self-sufficiency? Applied Energy 2017, 204, 1–15. [Google Scholar] [CrossRef]
- Hackman, C.A.C. The Role of Federal Tax Credits in US Solar Industry Growth. Master’s Thesis, Georgetown University, Washington, DC, USA, 2018. [Google Scholar]
- Kirsten, S. Renewable Energy Sources Act and Trading of Emission Certificates: A national and a supranational tool direct energy turnover to renewable electricity-supply in Germany. Energy Policy 2014, 64, 302–312. [Google Scholar] [CrossRef]
- Aniello, G.; Shamon, H.; Kuckshinrichs, W. Micro-economic assessment of residential PV and battery systems: The underrated role of financial and fiscal aspects. Appl. Energy 2021, 281, 115667. [Google Scholar] [CrossRef]
- Zhu, Q.; Li, Q.; Zhang, B.; Wang, L.; Li, G.; Wang, R. Capacity Optimization for Electrical and Thermal Energy Storage in Multi-energy Building Energy System. Energy Procedia 2019, 158, 6425–6430. [Google Scholar] [CrossRef]
- Rayit, N.S.; Chowdhury, J.I.; Balta-Ozkan, N. Techno-economic optimisation of battery storage for grid-level energy services using curtailed energy from wind. J. Energy Storage 2021, 39, 102641. [Google Scholar] [CrossRef]
- Chen, X.; Huang, L.; Liu, J.; Song, D.R.; Yang, S. Peak shaving benefit assessment considering the joint operation of nuclear and battery energy storage power stations: Hainan case study. Energy 2022, 239, 121897. [Google Scholar] [CrossRef]
- Kazemi, M.; Ansari, M.R. An integrated transmission expansion planning and battery storage systems placement—A security and reliability perspective. Int. J. Electr. Power Energy Syst. 2022, 134, 107329. [Google Scholar] [CrossRef]
- Fioriti, D.; Pellegrino, L.; Lutzemberger, G.; Micolano, E.; Poli, D. Optimal sizing of residential battery systems with multi-year dynamics and a novel rainflow-based model of storage degradation: An extensive Italian case study. Electr. Power Syst. Res. 2022, 203, 107675. [Google Scholar] [CrossRef]
- You, C.; Kim, J. Optimal design and global sensitivity analysis of a 100% renewable energy sources based smart energy network for electrified and hydrogen cities. Energy Convers. Manag. 2020, 223, 113252. [Google Scholar] [CrossRef]
- Dougier, N.; Garambois, P.; Gomand, J.; Roucoules, L. Multi-objective non-weighted optimization to explore new efficient design of electrical microgrids. Applied Energy 2021, 304, 117758. [Google Scholar] [CrossRef]
- Al-Ghussain, L.; Abubaker, A.M.; Ahmad, A.D. Superposition of Renewable-Energy Supply from Multiple Sites Maximizes Demand-Matching: Towards 100% Renewable Grids in 2050. Appl. Energy 2021, 284, 116402. [Google Scholar] [CrossRef]
- Fonseca, J.D.; Commenge, J.M.; Camargo, M.; Falk, L.; Gil, I.D. Sustainability analysis for the design of distributed energy systems: A multi-objective optimization approach. Appl. Energy 2021, 290, 116746. [Google Scholar] [CrossRef]
- Lai, C.-M.; The, J. Network topology optimisation based on dynamic thermal rating and battery storage systems for improved wind penetration and reliability. Appl. Energy 2022, 305, 117837. [Google Scholar] [CrossRef]
- Belaid, S.; Rekioua, D.; Oubelaid, A.; Ziane, D.; Rekioua, T. A power management control and optimization of a wind turbine with battery storage system. J. Energy Storage 2022, 45, 103613. [Google Scholar] [CrossRef]
- Argyrou, M.C.; Marouchos, C.C.; Kalogirou, S.A.; Christodoulides, P. A novel power management algorithm for a residential grid-connected PV system with battery-supercapacitor storage for increased self-consumption and self-sufficiency. Energy Convers. Manag. 2021, 246, 114671. [Google Scholar] [CrossRef]
- Boogen, N.; Datta, S.; Filippini, M. Estimating residential electricity demand: New empirical evidence. Energy Policy 2021, 158, 112561. [Google Scholar] [CrossRef]
- Pichetjamroen, A.; Chindamanee, P.; Teerakawanich, N.; Somakettarin, N. Effect of flexible power control on batteries requirement and performance in PV power system. Energy Rep. 2022, 8, 338–344. [Google Scholar] [CrossRef]
- Rawat, T.; Niazi, K.R.; Gupta, N.; Sharma, S. Multi-objective techno-economic operation of smart distribution network integrated with reactive power support of battery storage systems. Sustain. Cities Soc. 2021, 75, 103359. [Google Scholar] [CrossRef]
- Liang, Z.; Chung, C.Y.; Zhang, W.; Wang, Q.; Lin, W.; Wang, C.Y. Enabling high-efficiency economic dispatch of hybrid AC/DC networked microgrids: Steady-state convex bi-directional converter models. In IEEE Transactions on Smart Grid; IEEE: New York, NY, USA, 2024. [Google Scholar]
- Watari, D.; Taniguchi, I.; Goverde, H.; Manganiello, P.; Shirazi, E.; Catthoor, F.; Onoye, T. Multi-time scale energy management framework for smart PV systems mixing fast and slow dynamics. Appl. Energy 2021, 289, 116671. [Google Scholar] [CrossRef]
- Chen, L.; Liu, N.; Li, C.; Wu, L.; Chen, Y.B. Multi-party stochastic energy scheduling for industrial integrated energy systems considering thermal delay and thermoelectric coupling. Appl. Energy 2021, 304, 117882. [Google Scholar] [CrossRef]
- Buttitta, G.; Jones, C.N.; Finn, D.P. Evaluation of advanced control strategies of electric thermal storage systems in residential building stock. Util. Policy 2021, 69, 101178. [Google Scholar] [CrossRef]
- Häring, T.; Rosin, A.; Biechl, H. Using common household thermal storages to support the PV- and battery system in nearly zero energy buildings in off-grid mode. Sustain. Energy Technol. Assess. 2019, 35, 12–24. [Google Scholar] [CrossRef]
- Luo, X.; Liu, Y.; Feng, P.; Gao, Y.; Guo, Z.X. Optimization of a solar-based integrated energy system considering interaction between generation, network, and demand side. Appl. Energy 2021, 294, 116931. [Google Scholar] [CrossRef]
- Wang, H.; Zhang, C.; Li, K.; Liu, S.; Li, S.Z.; Wang, Y. Distributed coordinative transaction of a community integrated energy system based on a tri-level game model. Appl. Energy 2021, 295, 116972. [Google Scholar] [CrossRef]
- Ogunmodede, O.; Anderson, K.; Cutler, D.; Newman, A. Optimizing design and dispatch of a renewable energy system. Appl. Energy 2021, 287, 116527. [Google Scholar] [CrossRef]
- Emrani-Rahaghi, P.; Hashemi-Dezaki, H.; Hosseini, S.A. Optimal operation and scheduling of residential energy hubs simultaneously considering optimal sizing of heat storage and battery storage systems. J. Energy Storage 2021, 44, 102038. [Google Scholar] [CrossRef]
- Zou, B.; Peng, J.; Li, S.; Li, Y.; Yan, J.Y.; Yang, H.X. Comparative study of the dynamic programming-based and rule-based operation strategies for grid-connected PV-battery systems of office buildings. Appl. Energy 2022, 305, 117875. [Google Scholar] [CrossRef]
- Esplin, R.; Nelson, T. Redirecting solar feed in tariffs to residential battery storage: Would it be worth it? Econ. Anal. Policy 2022, 73, 373–389. [Google Scholar] [CrossRef]
- Heitkoetter, W.; Schyska, B.U.; Schmidt, D.; Medjroubi, W.; Vogt, T.; Agert, C. Assessment of the regionalised demand response potential in Germany using an open source tool and dataset. Adv. Appl. Energy 2020, 1, 100001. [Google Scholar] [CrossRef]
- Ruggles, T.H.; Dowling, J.A.; Lewis, N.S.; Caldeira, K. Opportunities for flexible electricity loads such as hydrogen production from curtailed generation. Adv. Appl. Energy 2021, 3, 100051. [Google Scholar] [CrossRef]
- Dias, J.B.; da Graça, G.C. Using building thermal mass energy storage to offset temporary BIPV output reductions due to passing clouds in an office building. Build. Environ. 2022, 207, 108504. [Google Scholar] [CrossRef]
- Park, S.W.; Cho, K.S.; Hoefter, G.; Son, S.Y. Electric vehicle charging management using location-based incentives for reducing renewable energy curtailment considering the distribution system. Appl. Energy 2022, 305, 117680. [Google Scholar] [CrossRef]
- Chen, Y.; Zhang, D. Theory-guided deep-learning for electrical load forecasting (TgDLF) via ensemble long short-term memory. Adv. Appl. Energy 2021, 1, 100004. [Google Scholar] [CrossRef]
- Tong, X.; Wang, J.; Zhang, C.; Wu, T.; Wang, H.T.; Wang, Y. LS-LSTM-AE: Power load forecasting via Long-Short series features and LSTM-Autoencoder. Energy Rep. 2022, 8, 596–603. [Google Scholar] [CrossRef]
- Nitsch, F.; Deissenroth-Uhrig, M.; Schimeczek, C.; Bertsch, V. Economic evaluation of battery storage systems bidding on day-ahead and automatic frequency restoration reserves markets. Appl. Energy 2021, 298, 117267. [Google Scholar] [CrossRef]
- Polimeni, S.; Meraldi, L.; Moretti, L.; Leva, S.; Manzolini, G. Development and Experimental Validation of Hierarchical Energy Management System based on Stochastic Model Predictive Control for Off-grid Microgrids. Adv. Appl. Energy 2021, 2, 100028. [Google Scholar] [CrossRef]
- Tu, R.; Wang, L.; Liu, L. Performance and configuration optimization for a Grid-Connected PV power supply system with Demand-Supply matching in a data center’s centralized Water-Cooling system. Sol. Energy 2024, 276, 112667. [Google Scholar] [CrossRef]
- Liu, X.; Liu, X.; Jiang, Y.; Zhang, T.; Hao, B. Photovoltaics and energy storage integrated flexible direct current distribution systems of buildings: Definition, technology review, and application. CSEE J. Power Energy Syst. 2023, 9, 829–845. [Google Scholar]
- Xie, H.; Liu, H.; Wan, C.; Goh, H.H.; Rahman, S. Optimal Scheduling of Integrated Energy Systems with Multiple CCHPs for High Efficiency and Low Emissions. IEEE Internet Things J. 2023, 10, 22623–22635. [Google Scholar] [CrossRef]
- Zahraoui, Y.; Korõtko, T.; Rosin, A.; Ahmadiahangar, R. Stochastic Energy Management for Battery Storage System-Based Microgrid Considering Different Forecasting Models. In Proceedings of the 2023 IEEE 17th International Conference on Compatibility, Power Electronics and Power Engineering (CPE-POWERENG), Tallinn, Estonia, 14–16 June 2023; pp. 1–6. [Google Scholar]
- Subramanian, E.; Karthik, M.M.; Krishna, G.P.; Prasath, D.V.; Kumar, V.S. Solar Power Prediction Using Machine Learning. arXiv 2023, arXiv:2303.07875. [Google Scholar]
- Goswami, K.; Kandali, A.B. Machine learning algorithms for predicting electrical load demand: An evaluation and comparison. Sadhana-Acad. Proc. Eng. Sci. 2024, 49, 40. [Google Scholar] [CrossRef]






| Application | Characteristics | Advantages | Disadvantages |
|---|---|---|---|
| PV Combined with Windows |
|
|
|
| PV Combined with Walls |
|
|
|
| PV Combined with Roofs |
|
|
|
| Country | Number of PV Systems | Roof-Top PV Capacity | Upper Specific Yield Limit |
|---|---|---|---|
| The Netherlands | 978 | 10.70 MWp | 1500 kWh/kWp |
| Belgium | 4308 | 29.75 MWp | 1500 kWh/kWp |
| Luxembourg | 86 | 1.56 MWp | 1500 kWh/kWp |
| Germany | 24,204 | 325.73 MWp | 1500 kWh/kWp |
| France | 474 | 5.15 MWp | 1600 kWh/kWp |
| Italy | 2694 | 24.23 MWp | 1800 kWh/kWp |
| Total | 32,744 | 397.12 MWp |
| a | b | c | d | e | f | g | h |
| 0.0039 | 1.95 | 67.51 | 2070 | −0.011879 | −0.011879 | ||
| i | j | k | l | m | n | o | p |
| 4464 | −0.1382 | −1519 | −0.4305 | 5963 | −0.6531 | 321.4 | 0.03168 |
| Parameters | Numerical Value |
|---|---|
| Cost of investment: IC0 | 232 $/kW |
| Operation and maintenance: Comt | 0.005 $/kW |
| cost | |
| Rated power: Pout | 260 W |
| Conversion efficiency: ηOC | 0.97 |
| Rated temperature: Ta | 25 °C |
| Temperature coefficient: β | 0.47 |
| Life cycle: CL | 20 years |
| Indicator | Parameter | Description and Analysis |
|---|---|---|
| Economic Indicators | (Levelized Cost of Energy) |
|
(Net Present Value) |
| |
| IRR (Internal Rate of Return) |
| |
| Energy Optimization |
| |
| ||
| Investment Analysis | (Investment) |
|
(Operating Costs) |
| |
(Replacement Costs) |
| |
| ||
| Comprehensive Evaluation | (Life Cycle Cost) |
|
| Algorithm | Applicable Scenarios | Advantages | Limitations | Convergence Speed | Computational Cost |
|---|---|---|---|---|---|
| Genetic Algorithm (GA) | Suitable for complex, multi-objective, and constrained optimization problems, especially when the solution space is large | Strong adaptability, global search ability, can avoid local optima | May require large computational resources, prone to local optima | Moderate | High |
| NSGA-II | Suitable for multi-objective optimization problems, especially when there are conflicts between objectives | Efficient non-dominated sorting and crowding distance calculation, can effectively balance multiple objectives | Convergence may not be optimal, high computational cost in high-dimensional problems | Slow | Moderate |
| Random Walk-Latin Hypercube Sampling (RWLHS) | Used for high-dimensional complex problems, especially when the objective function is unknown or hard to represent | Can effectively generate random samples, suitable for optimization with unknown or nonlinear problems | Not suitable for highly complex optimization problems, high computational cost, slow convergence | Slow | High |
| Game Theory-Based Modeling Framework | Suitable for optimization problems involving multiple decision-makers and competitive or cooperative relationships | Can handle conflicts and collaboration between multiple participants | Model complexity, requires a deep understanding of participants’ strategies and goals, high computational cost | Moderate | High |
| Global Pareto Search Algorithm | Suitable for multi-objective optimization problems, especially when there are conflicts between objectives | Can effectively find the optimal solution between multiple objectives, suitable for multi-objective and multi-constrained scenarios | Requires large computational resources, slow convergence in complex problems | Slow | High |
| Newton Weighted Sum Frisch Method (NWSFA) | Suitable for nonlinear multi-objective optimization problems, especially with complex constraints | Good for handling nonlinear problems and offers high computational efficiency | Requires strong mathematical background, limited application scope, sensitive to initial conditions | Fast | Moderate |
| Stochastic Programming | Suitable for optimization problems involving uncertainty, especially decision problems with random variables | Can handle uncertainty, suitable for optimization under uncertain environments | Slow convergence, high computational cost in large-scale problems | Slow | High |
| Operation Strategy | Advantages | Disadvantages | Suitable Scenarios | Impact on Economic and Energy Efficiency |
|---|---|---|---|---|
| Time-of-Use Pricing (TOU) | Reduces energy costs by shifting usage to off-peak times | Requires accurate forecasting and user participation | Residential and commercial buildings with flexible loads | Improves economic efficiency, reduces peak demand |
| Demand Response (DR) | Enhances grid stability, reduces energy costs | Relies on user participation and technology integration | Buildings with smart devices and control systems | Optimizes energy usage, lowers operational costs |
| Accurate Forecasting Techniques | Improves energy management decisions | Requires advanced data analytics capabilities | Systems with variable load and generation patterns | Increases system reliability, optimizes battery usage |
| Flexible Power Point Tracking (FPPT) | Reduces battery capacity requirements, lowers costs | May capture less energy compared to MPPT | PV systems with limited storage capacity | Balances energy capture with storage limitations |
| Maximum Power Point Tracking (MPPT) | Maximizes energy capture from PV panels | Requires larger battery capacity, higher costs | Systems prioritizing maximum energy output | Enhances energy efficiency, higher initial investment |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tu, R.; Guo, Z.; Liu, L.; Wang, S.; Yang, X. Reviews of Photovoltaic and Energy Storage Systems in Buildings for Sustainable Power Generation and Utilization from Perspectives of System Integration and Optimization. Energies 2025, 18, 2683. https://doi.org/10.3390/en18112683
Tu R, Guo Z, Liu L, Wang S, Yang X. Reviews of Photovoltaic and Energy Storage Systems in Buildings for Sustainable Power Generation and Utilization from Perspectives of System Integration and Optimization. Energies. 2025; 18(11):2683. https://doi.org/10.3390/en18112683
Chicago/Turabian StyleTu, Rang, Zichen Guo, Lanbin Liu, Siqi Wang, and Xu Yang. 2025. "Reviews of Photovoltaic and Energy Storage Systems in Buildings for Sustainable Power Generation and Utilization from Perspectives of System Integration and Optimization" Energies 18, no. 11: 2683. https://doi.org/10.3390/en18112683
APA StyleTu, R., Guo, Z., Liu, L., Wang, S., & Yang, X. (2025). Reviews of Photovoltaic and Energy Storage Systems in Buildings for Sustainable Power Generation and Utilization from Perspectives of System Integration and Optimization. Energies, 18(11), 2683. https://doi.org/10.3390/en18112683








