Research on the Maximum Regenerative Energy Commutation Control Strategy of a Dual-Mode Synergistic Energy Recovery Pump-Controlled Grinder
Abstract
1. Introduction
2. Principle of Operation of Pump-Controlled Grinders
3. Modeling of Energy Recovery Systems for Pump-Controlled Grinders [31,32,33]
4. Direction Switching Strategy Based on Energy Peak Time Prediction
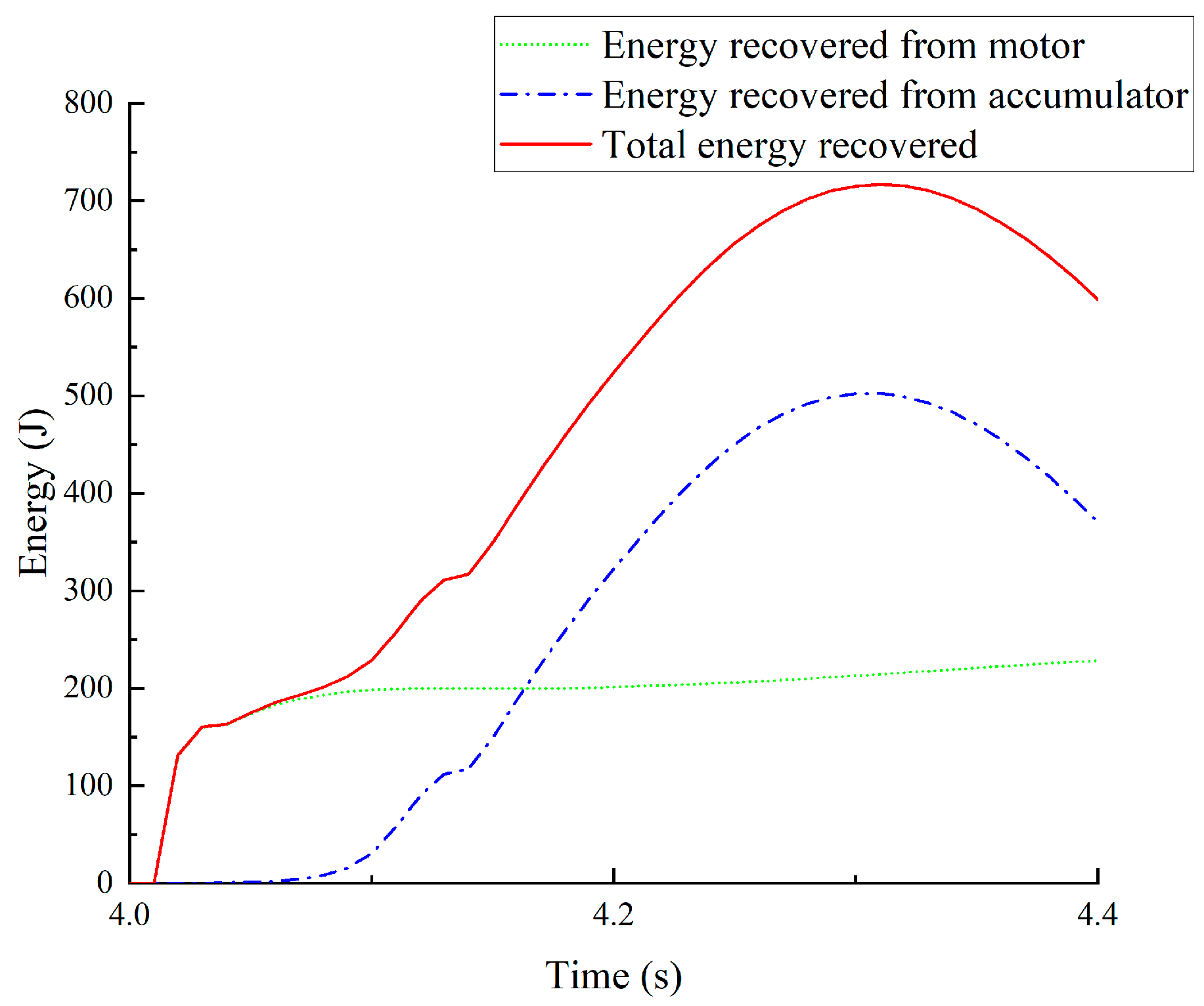
4.1. Prediction of Time to Peak Energy
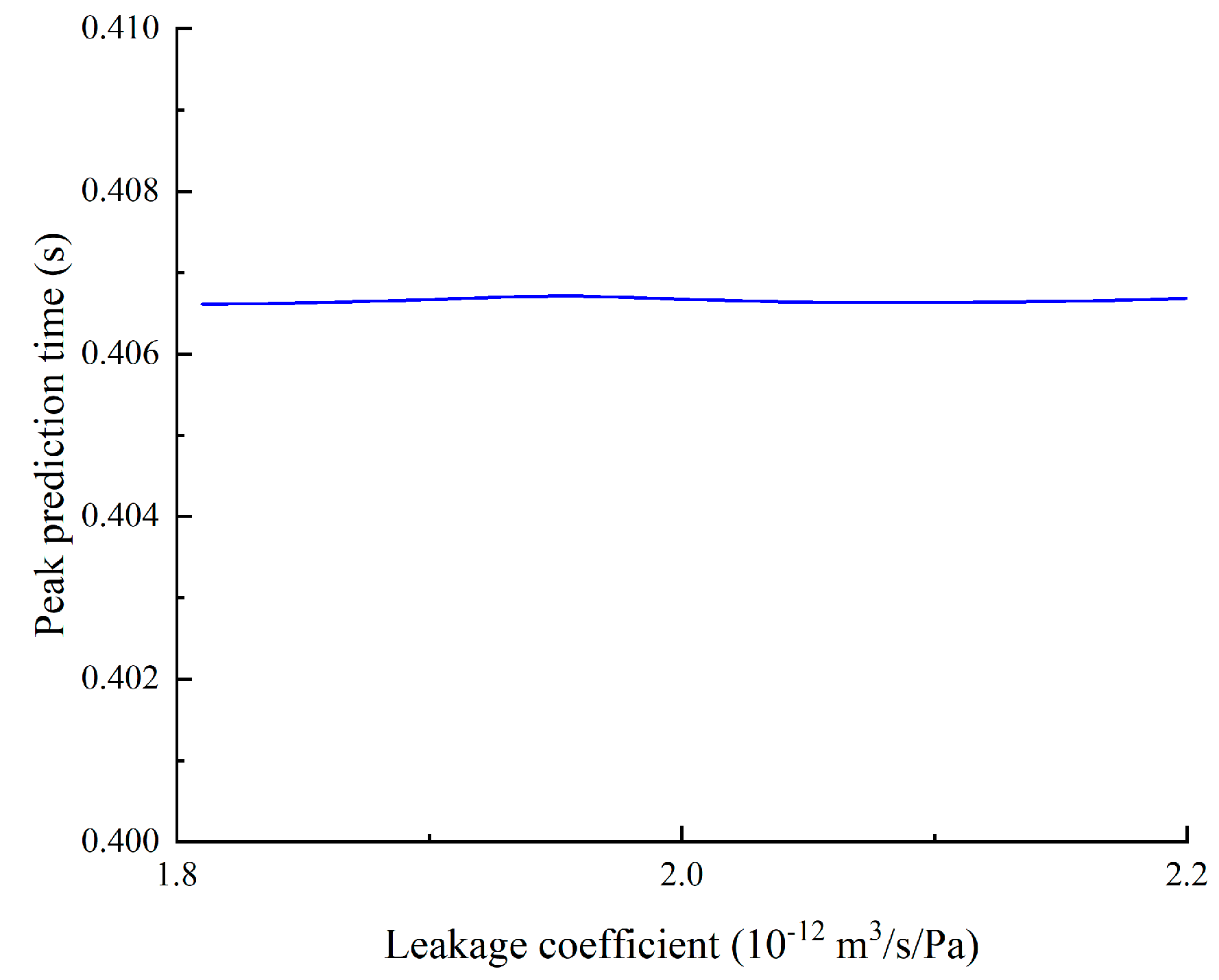
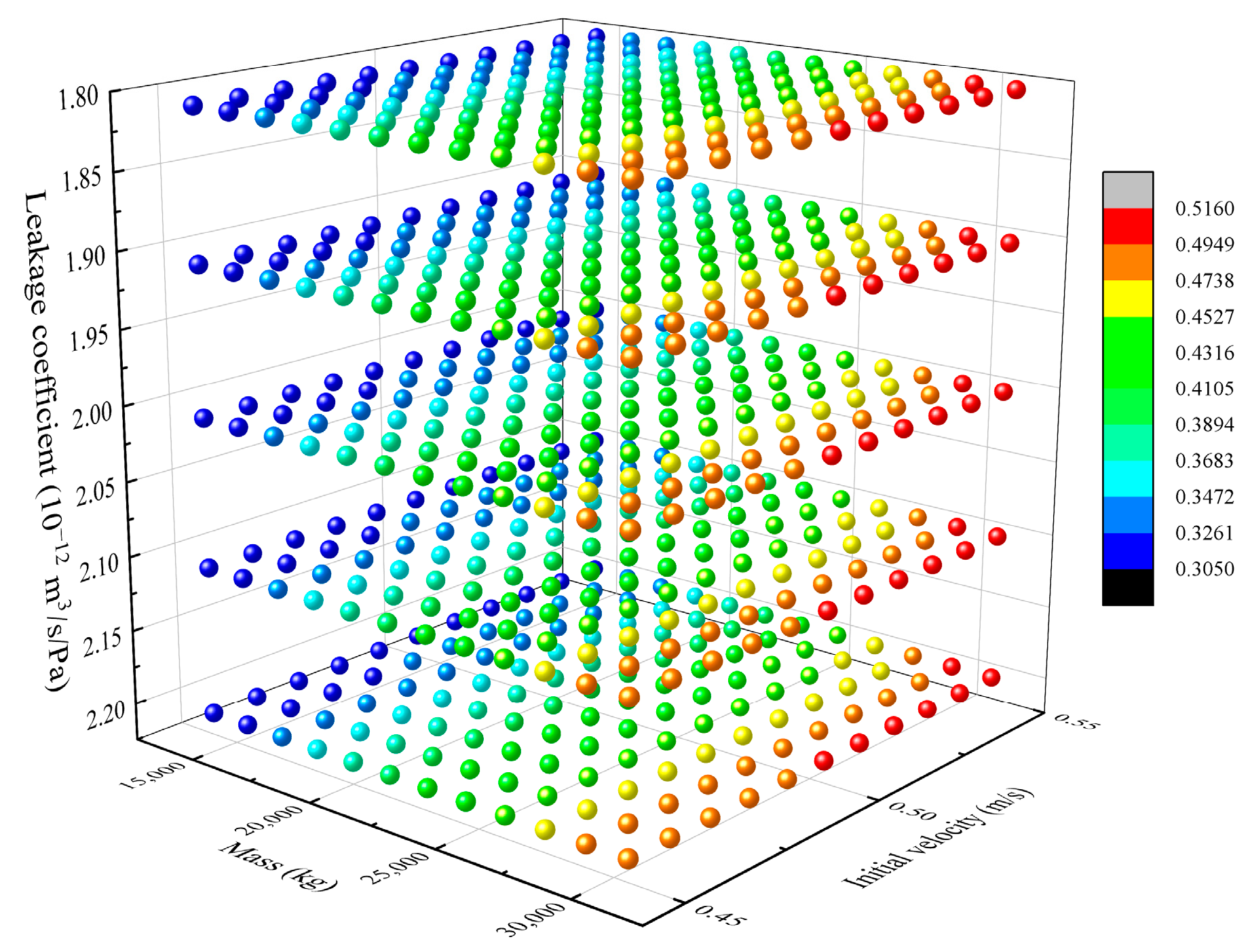
4.2. Parametric Sensitivity Analysis of the Peak Time of Recovered Energy
4.3. Switching Time Decision Strategy
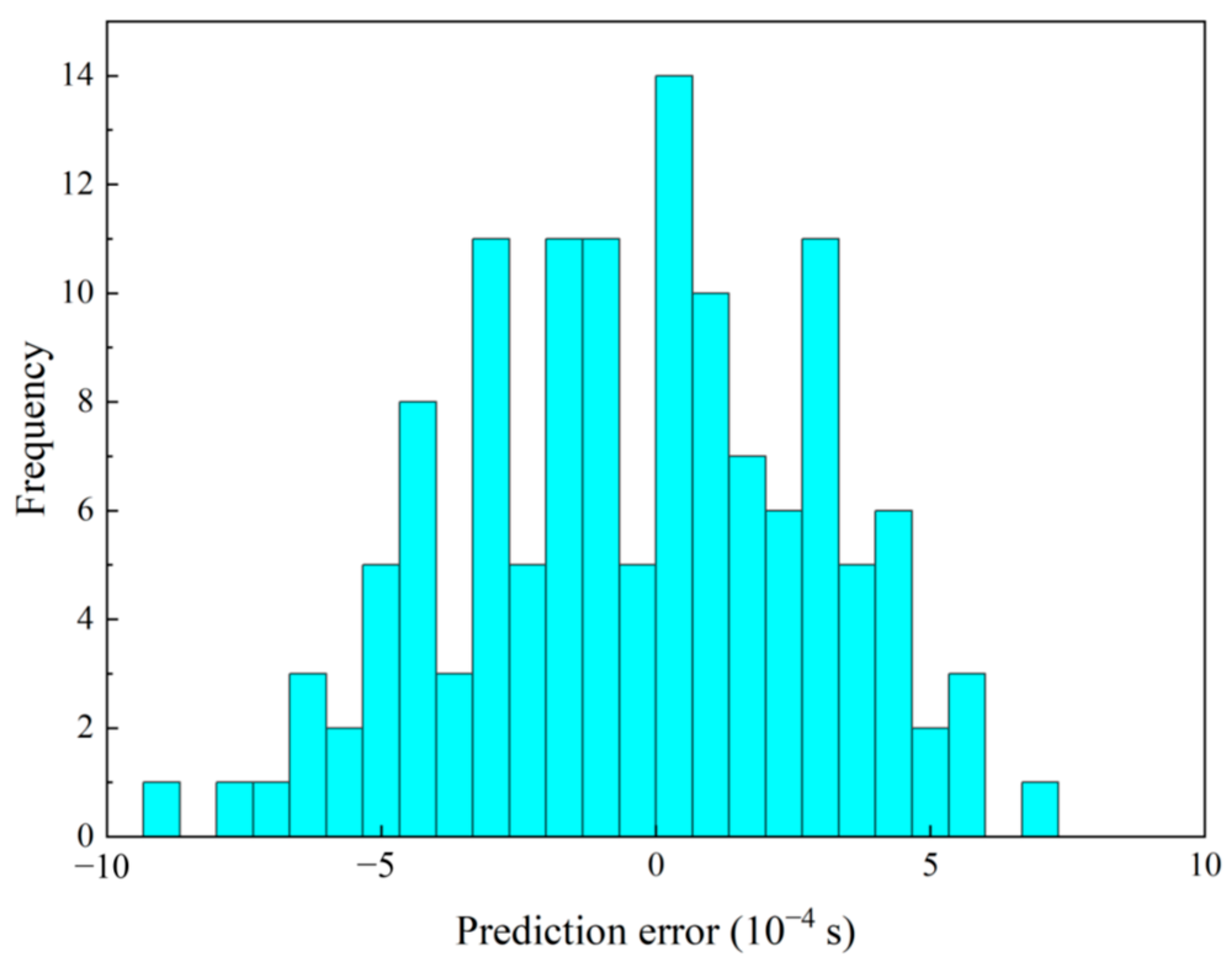
5. Simulation and Experimental Validation
5.1. Software Simulation Test
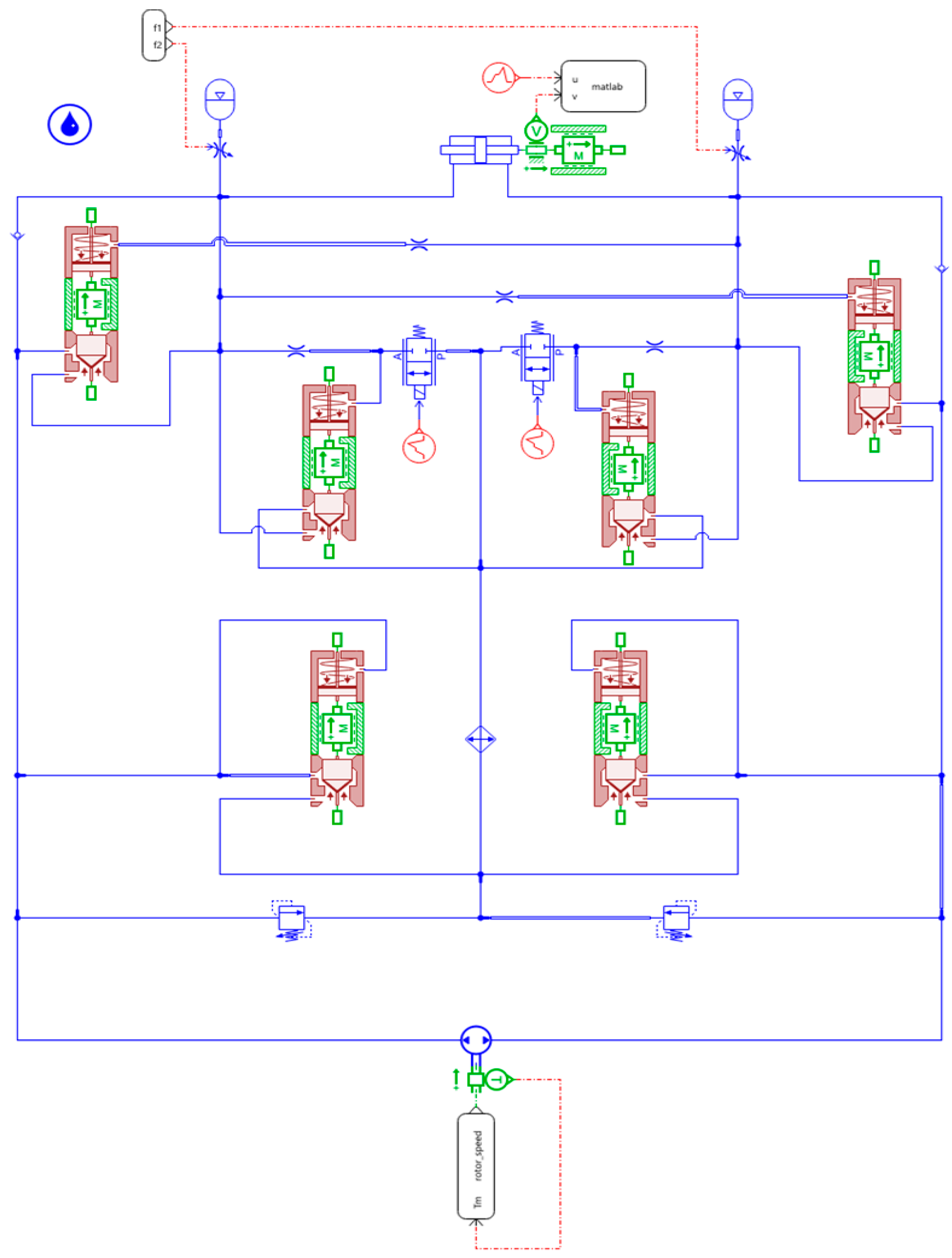
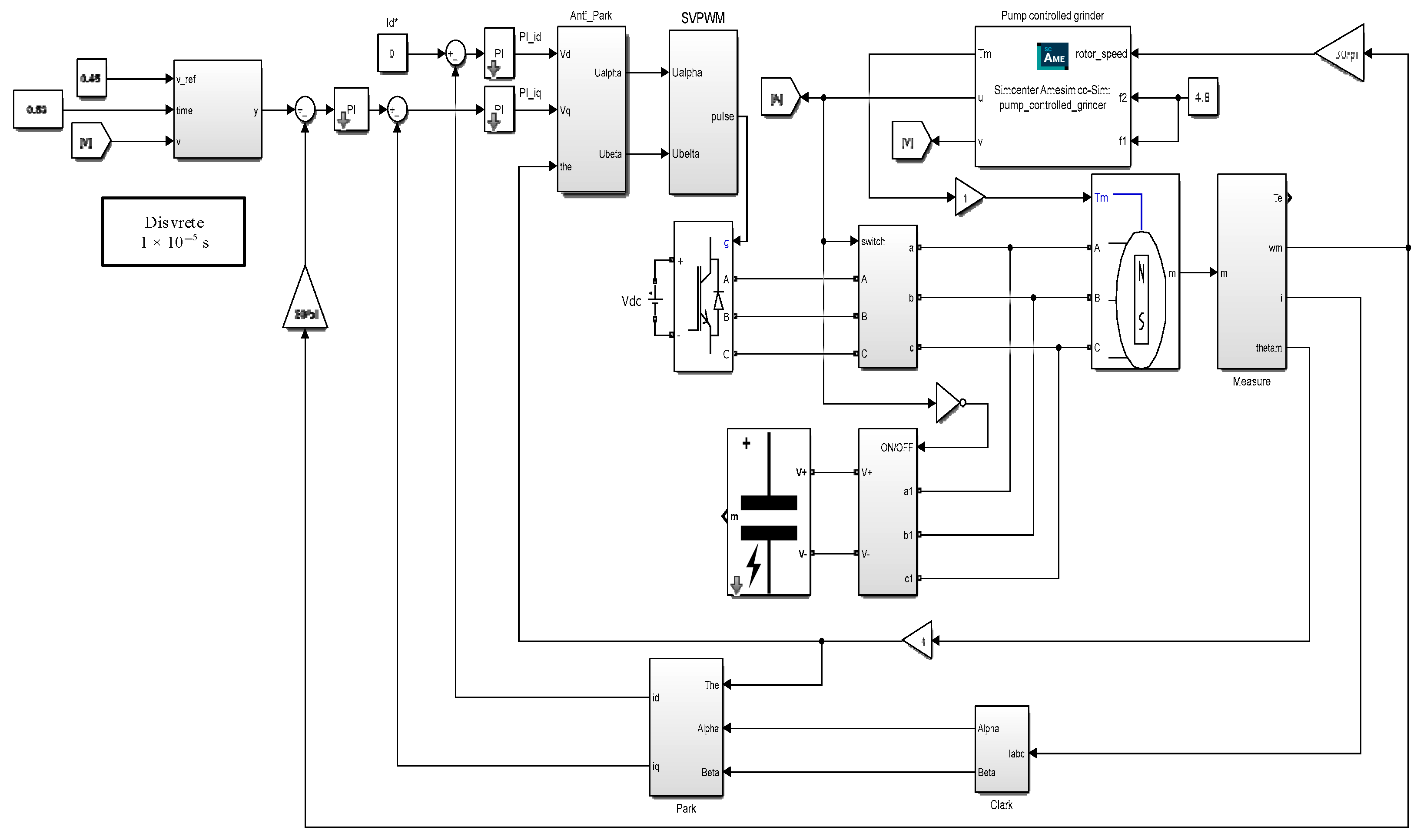
5.1.1. Simulink-Amesim Joint Simulation Platform
5.1.2. Simulation Test
5.2. Bench Test
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| GPR | Gaussian Process Regression |
| LR | Linear Regression |
| MAE | Mean Absolute Error |
| NN | Neural Network |
| RF | Random Forest |
| RMSE | Root Mean Square Error |
| SVM | Support Vector Machine |
References
- Liang, T.; Quan, L.; Ge, L.; Xia, L.P.; Wang, C.W. An Energy-Saving Scheme to Reduce Throttling Losses in Hydraulic Excavators Based on Electro-Hydraulic Energy Storage. IEEE Access 2024, 12, 125043–125056. [Google Scholar] [CrossRef]
- Xu, L.M.; Wang, K.Z.; Xie, C.L.; Shi, L. Improved spatial acceleration and jerk distributions for grinding force smoothness and energy-saving in reciprocating machining. J. Manuf. Process. 2023, 98, 186–195. [Google Scholar] [CrossRef]
- Lyu, L.T.; Chen, Z.; Yao, B. Energy Saving Motion Control of Independent Metering Valves and Pump Combined Hydraulic System. IEEE-ASME Trans. Mechatron. 2019, 24, 1909–1920. [Google Scholar] [CrossRef]
- Li, Z.S.; Su, L.; Lin, T.L. Overflow Energy Loss Recovery System Based on Hydraulic Motor-Electric Generator. Appl. Sci. 2021, 11, 941. [Google Scholar] [CrossRef]
- Ho, T.H.; Ahn, K.K. Design and control of a closed-loop hydraulic energy-regenerative system. Autom. Constr. 2012, 22, 444–458. [Google Scholar] [CrossRef]
- Xing, H.Y.; Zhao, J.Y.; Yin, X.; Ding, H.G.; Meng, X.Z.; Li, J.S.; Wang, G.Y. Simulated research on large-excavator boom based on hydraulic energy recovery. Proc. Inst. Mech. Eng. Part C-J. Eng. Mech. Eng. Sci. 2022, 236, 10690–10700. [Google Scholar] [CrossRef]
- Wang, J.L.; Tian, Y.B.; Hu, X.T.; Fan, Z.H.; Han, J.G.; Liu, Y.H. Development of grinding intelligent monitoring and big data-driven decision making expert system towards high efficiency and low energy consumption: Experimental approach. J. Intell. Manuf. 2024, 35, 1013–1035. [Google Scholar] [CrossRef]
- Wang, J.L.; Tian, Y.B.; Hu, X.T.; Li, Y.; Zhang, K.; Liu, Y.H. Predictive modelling and Pareto optimization for energy efficient grinding based on aANN-embedded NSGA II algorithm. J. Clean. Prod. 2021, 327, 14. [Google Scholar] [CrossRef]
- Guo, Y.S.; Duflou, J.R.; Lauwers, B. Energy-based optimization of the material stock allowance for turning-grinding process sequence. Int. J. Adv. Manuf. Technol. 2014, 75, 503–513. [Google Scholar] [CrossRef]
- Hu, L.K.; Zheng, P.; Liu, P.J.; Jia, S.; Cai, W.; Xu, K.K. Energy optimisation for the combination of turning and drilling features using differential evolution. Environ. Sci. Pollut. Res. 2023, 30, 125846–125865. [Google Scholar] [CrossRef]
- Wang, H.S.; Zhang, Y.B.; An, Z.S.; Liu, R.S. An Energy-Efficient Adaptive Speed-Regulating Method for Pump-Controlled Motor Hydrostatic Drive Powertrains. Processes 2024, 12, 25. [Google Scholar] [CrossRef]
- Wang, H.S.; Zhang, Y.B.; Li, G.Q.; Liu, R.S.; Zhou, X. Design and Control of an Energy-Efficient Speed Regulating Method for Pump-Controlled Motor System under Negative Loads. Machines 2023, 11, 437. [Google Scholar] [CrossRef]
- Wu, J.B.; Li, L.; Yan, Y.K.; Wang, P.J.; Wei, W. An Energy-Saving Position Control Strategy for Deep-Sea Valve-Controlled Hydraulic Cylinder Systems. J. Mar. Sci. Eng. 2022, 10, 567. [Google Scholar] [CrossRef]
- Hati, S.K.; Mandal, N.P.; Sanyal, D. Energy-saving design of variable-displacement bi-directional pump-controlled electrohydraulic system. Proc. Inst. Mech. Eng. Part I-J. Syst. Control Eng. 2021, 235, 1218–1236. [Google Scholar] [CrossRef]
- Li, W.C.; Vaziri, V.; Aphale, S.S.; Dong, S.M.; Wiercigroch, M. Energy saving by reducing motor rating of sucker-rod pump systems. Energy 2021, 228, 13. [Google Scholar] [CrossRef]
- Yue, D.L.; Gao, H.F.; Liu, Z.G.; Wei, L.J.; Liu, Y.S.; Zuo, X.K. Potential Energy Recovery and Direct Reuse System of Hydraulic Hybrid Excavators Based on the Digital Pump. Energies 2023, 16, 5229. [Google Scholar] [CrossRef]
- Li, J.S.; Han, Y.; Li, S.H. Flywheel-Based Boom Energy Recovery System for Hydraulic Excavators with Load Sensing System. Actuators 2021, 10, 126. [Google Scholar] [CrossRef]
- Zhao, P.Y.; Chen, Y.L.; Zhou, H. Simulation Analysis of Potential Energy Recovery System of Hydraulic Hybrid Excavator. Int. J. Precis. Eng. Manuf. 2017, 18, 1575–1589. [Google Scholar] [CrossRef]
- Cao, H.L. Kinetic energy recovery and reuse of traveling drive system of hybrid hydraulic electric loader. Adv. Mech. Eng. 2025, 17, 13. [Google Scholar] [CrossRef]
- Li, L.; Zhang, T.Z.; Wu, K.W.; Lu, L.Q.; Lin, L.H.; Xu, H.G. Design and Research on Electro-Hydraulic Drive and Energy Recovery System of the Electric Excavator Boom. Energies 2022, 15, 4757. [Google Scholar] [CrossRef]
- Ketelsen, S.; Schmidt, L.; Donkov, V.H.; Andersen, T.O. Energy Saving Potential in Knuckle Boom Cranes using a Novel Pump Controlled Cylinder Drive. Model. Identif. Control 2018, 39, 73–89. [Google Scholar] [CrossRef]
- Wu, J.J.; Liu, H.; Ren, X.L.; Nie, S.D.; Qin, Y.C.; Han, L.J. A multi-objective optimization approach for regenerative braking control in electric vehicles using MPE-SAC algorithm. Energy 2025, 318, 15. [Google Scholar] [CrossRef]
- Jiang, Y.X.; Tong, Z.M.; Tong, S.G.; Xu, Z.Y.; Li, Y.S. Hydraulic dual-module hybrid driving system with adjustable waste energy recovery for industrial vehicles. Energy 2024, 307, 18. [Google Scholar] [CrossRef]
- Gong, J.; Zhang, D.Q.; Guo, Y.; Tang, Z.Y.; Liu, C.S.; Hu, P.; Zhao, Y.M.; Quan, W.C.; Jin, Y.P. Potential energy recovery method based on alternate recovery and utilization of multiple hydraulic cylinders. Autom. Constr. 2020, 112, 14. [Google Scholar] [CrossRef]
- Li, J.S.; Zhao, J.Y.; Zhang, X.C. A Novel Energy Recovery System Integrating Flywheel and Flow Regeneration for a Hydraulic Excavator Boom System. Energies 2020, 13, 315. [Google Scholar] [CrossRef]
- Liu, J.J.; Xu, H.L.; Luo, T.Q.; Yao, Y.F.; Han, W.B. Model-based fault detection for an electrohydraulic braking system with cooperative regenerative braking management. Proc. Inst. Mech. Eng. Part D-J. Automob. Eng. 2025, 22, 09544070251323331. [Google Scholar] [CrossRef]
- Mitropoulos-Rundus, C.; Schwarz, C.; McGehee, D. Benefits estimation of regenerative braking versus service braking. Ergonomics 2021, 64, 1217–1227. [Google Scholar] [CrossRef]
- Jiang, B.; Zhang, X.W.; Wang, Y.X.; Hu, W.C. Regenerative Braking Control Strategy of Electric Vehicles Based on Braking Stability Requirements. Int. J. Automot. Technol. 2021, 22, 465–473. [Google Scholar] [CrossRef]
- Kumar, C.S.N.; Subramanian, S.C. Cooperative control of regenerative braking and friction braking for a hybrid electric vehicle. Proc. Inst. Mech. Eng. Part D-J. Automob. Eng. 2016, 230, 103–116. [Google Scholar] [CrossRef]
- Panchal, S.; Dincer, I.; Agelin-Chaab, M. Thermodynamic Analysis of Hydraulic Braking Energy Recovery Systems for a Vehicle. J. Energy Resour. Technol.-Trans. ASME 2016, 138, 9. [Google Scholar] [CrossRef]
- Yan, G.; Jin, Z.; Zhang, T.; Zhang, C.; Ai, C.; Chen, G. Exploring the Essence of Servo Pump Control. Processes 2022, 10, 786. [Google Scholar] [CrossRef]
- Han, D.; Xin-hui, L.; Xin, W.; Bo-yuan, Z.; Wei-quan, L.; Jia-yi, W. Impact of main parameters of accumulator on parallel hydraulic hybrid. J. Jilin Univ. 2015, 45, 420–428. [Google Scholar] [CrossRef]
- Munson, B.R.; Okiishi, T.H.; Huebsch, W.W.; Rothmayer, A.P. Fundamentals of Fluid Mechanics, 7th ed.; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2013. [Google Scholar]
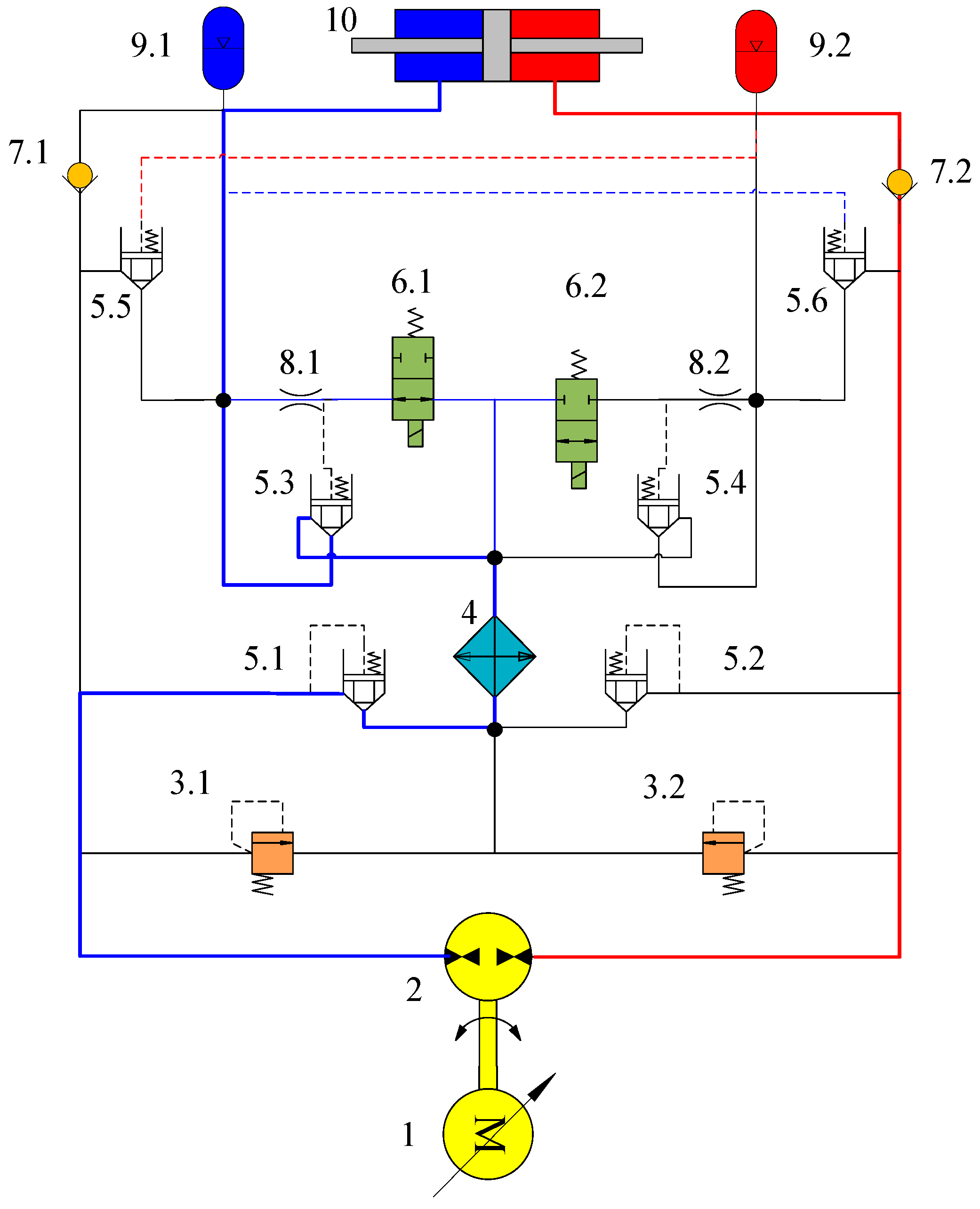
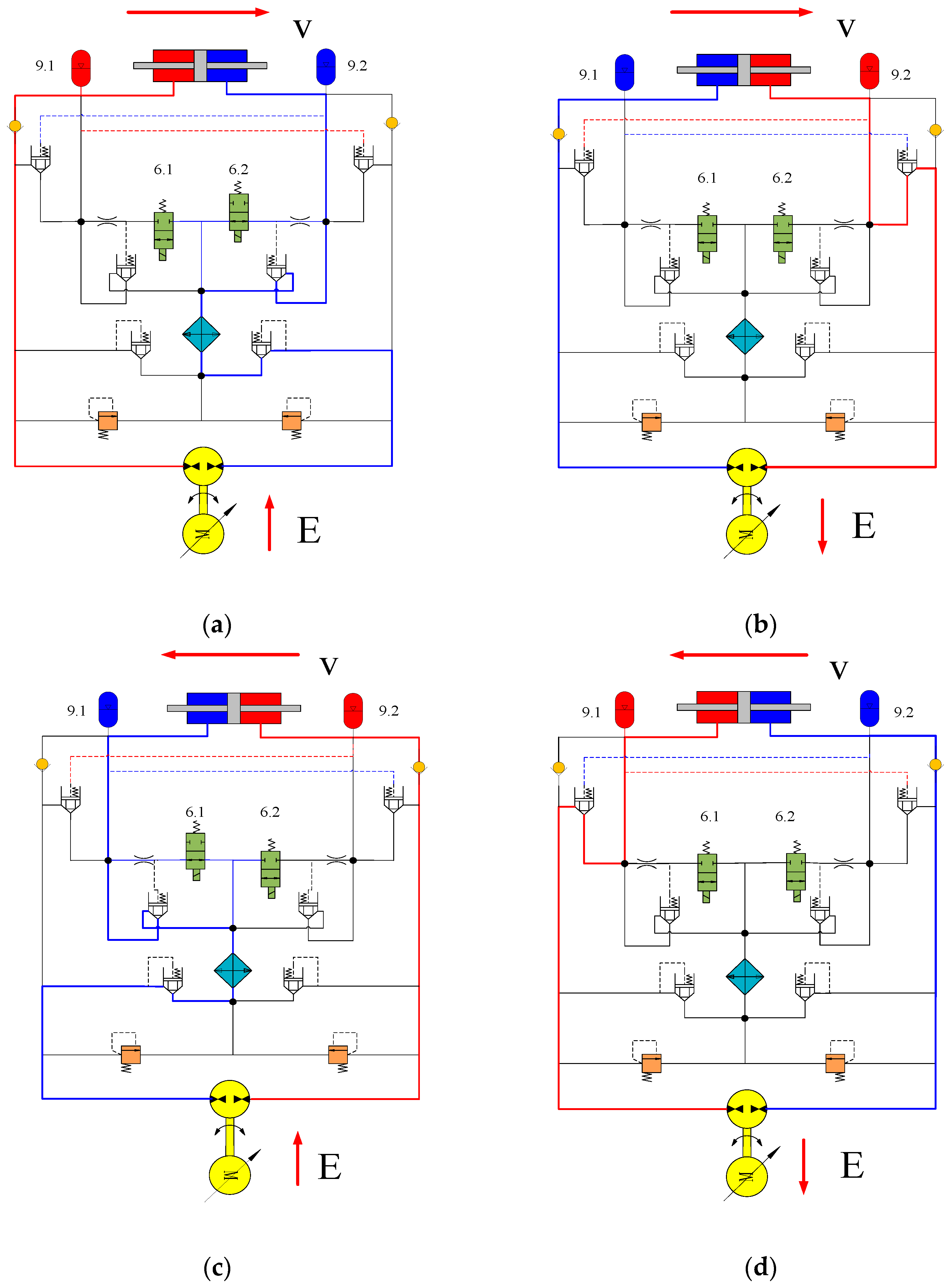

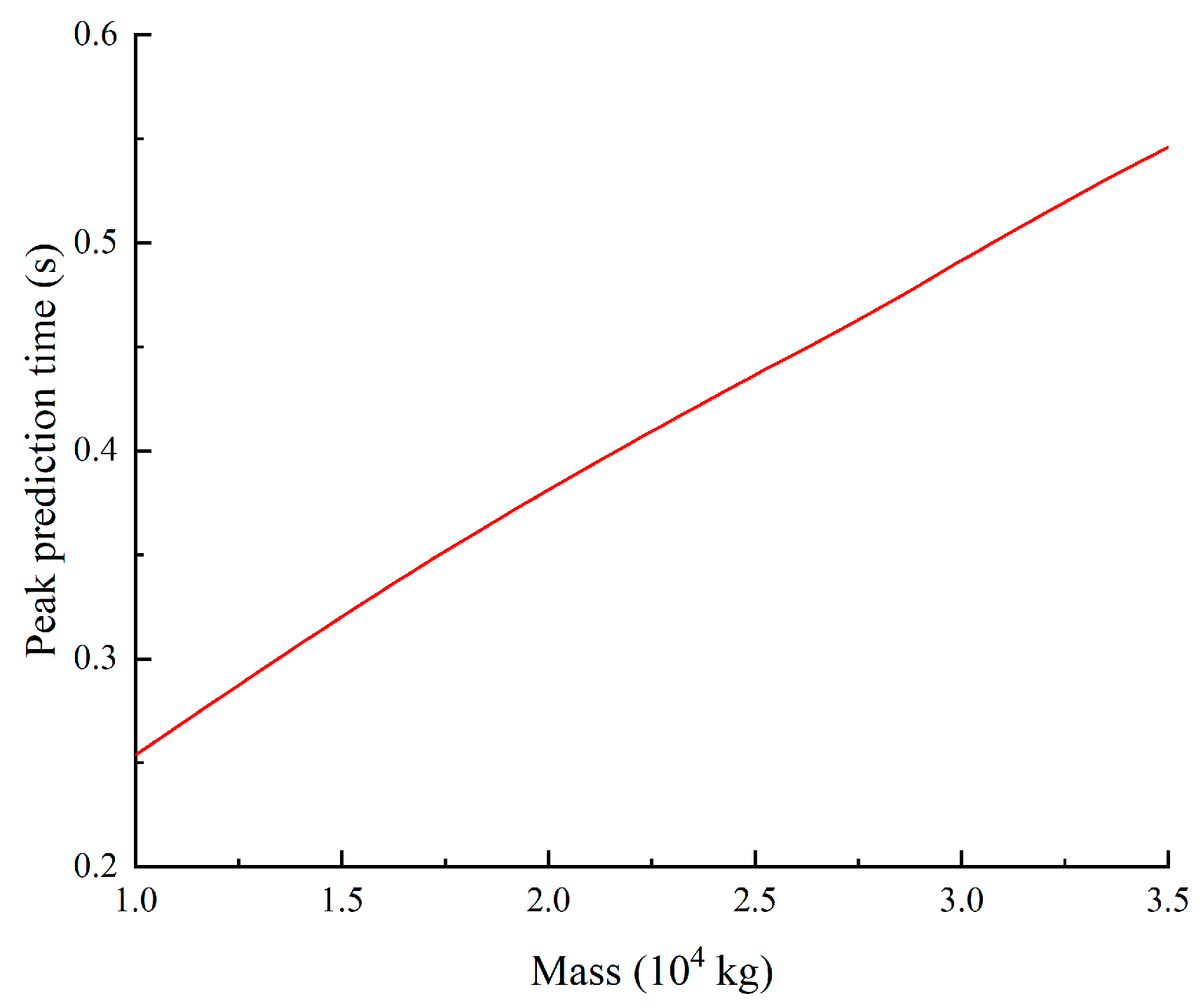


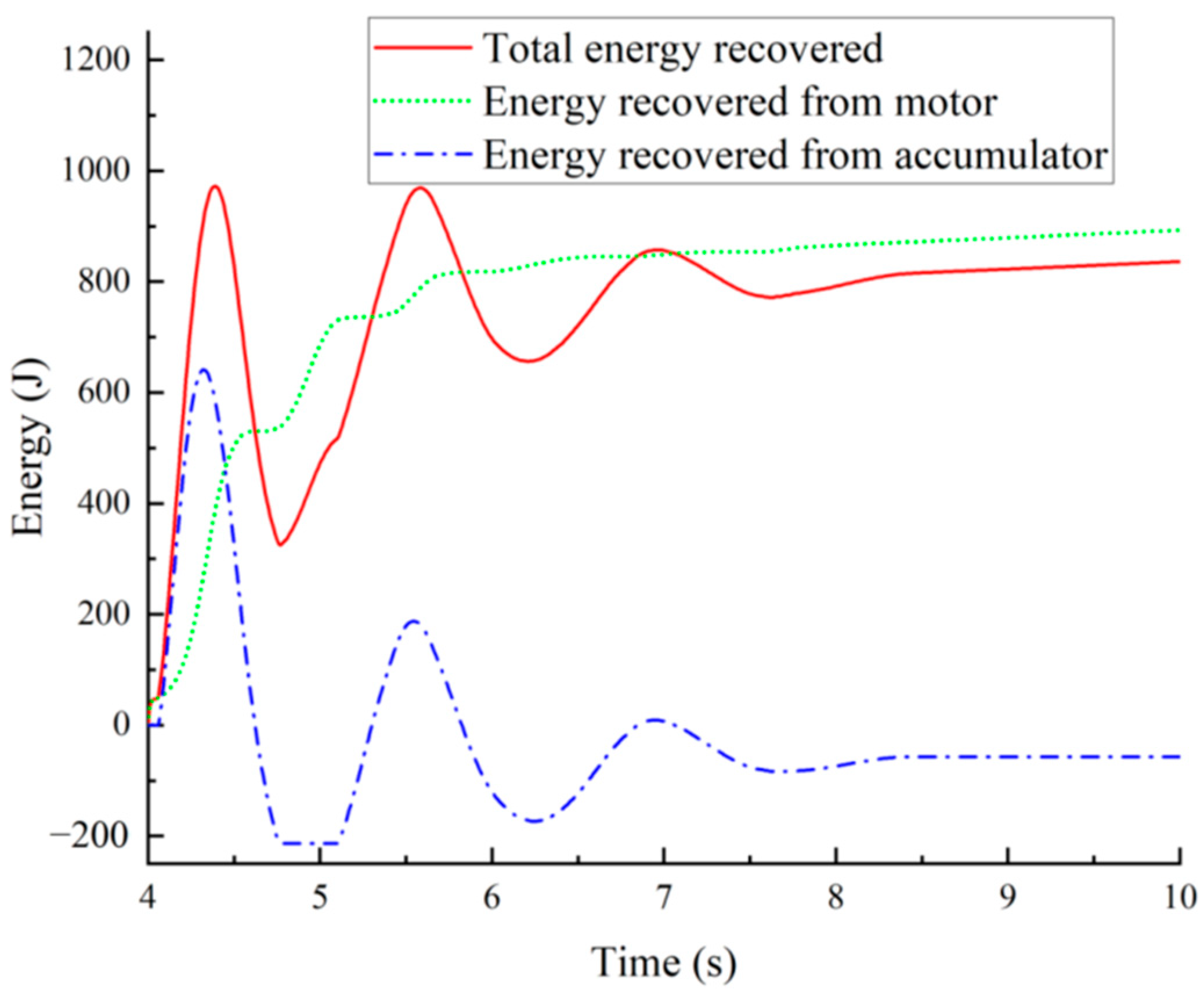
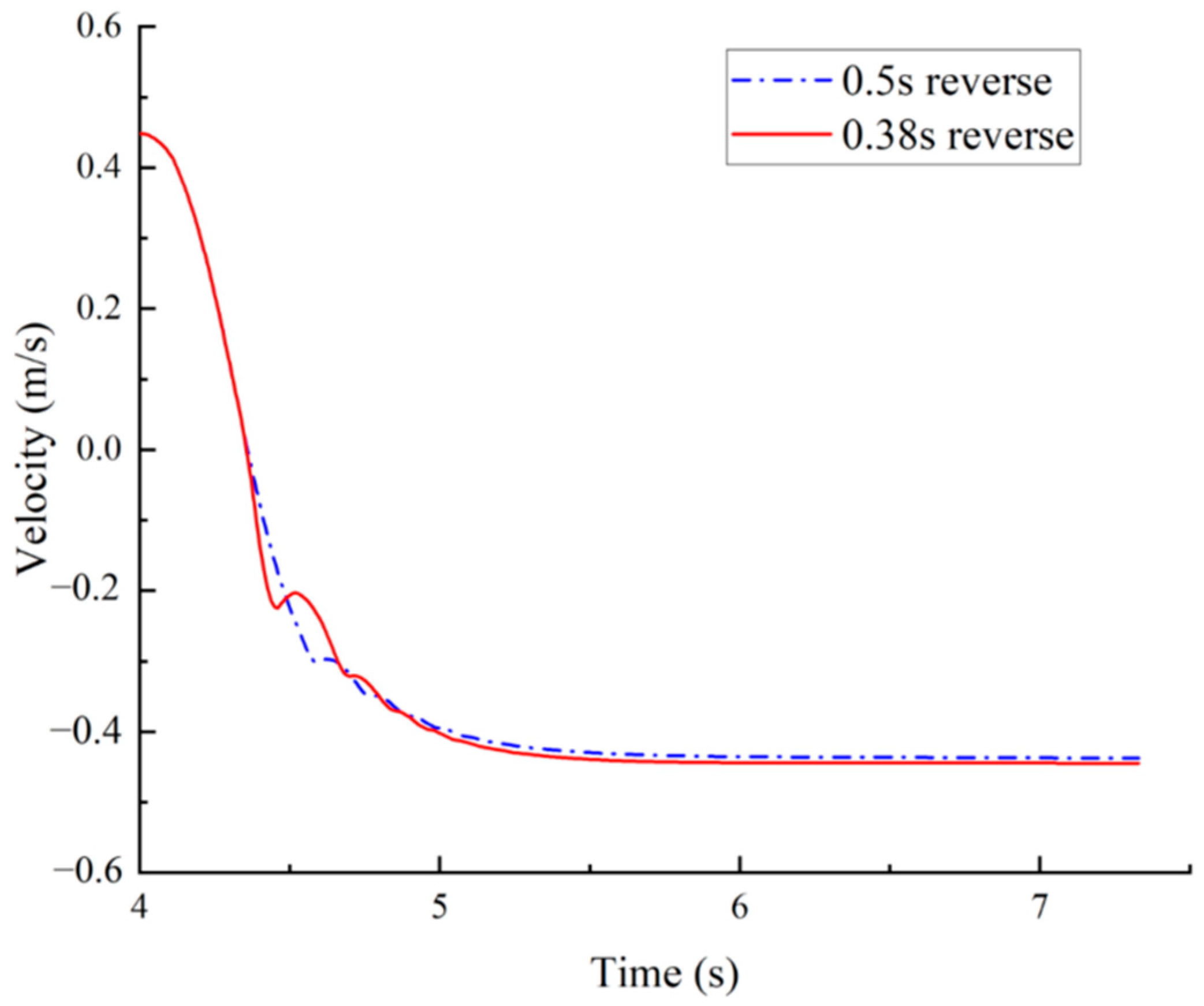
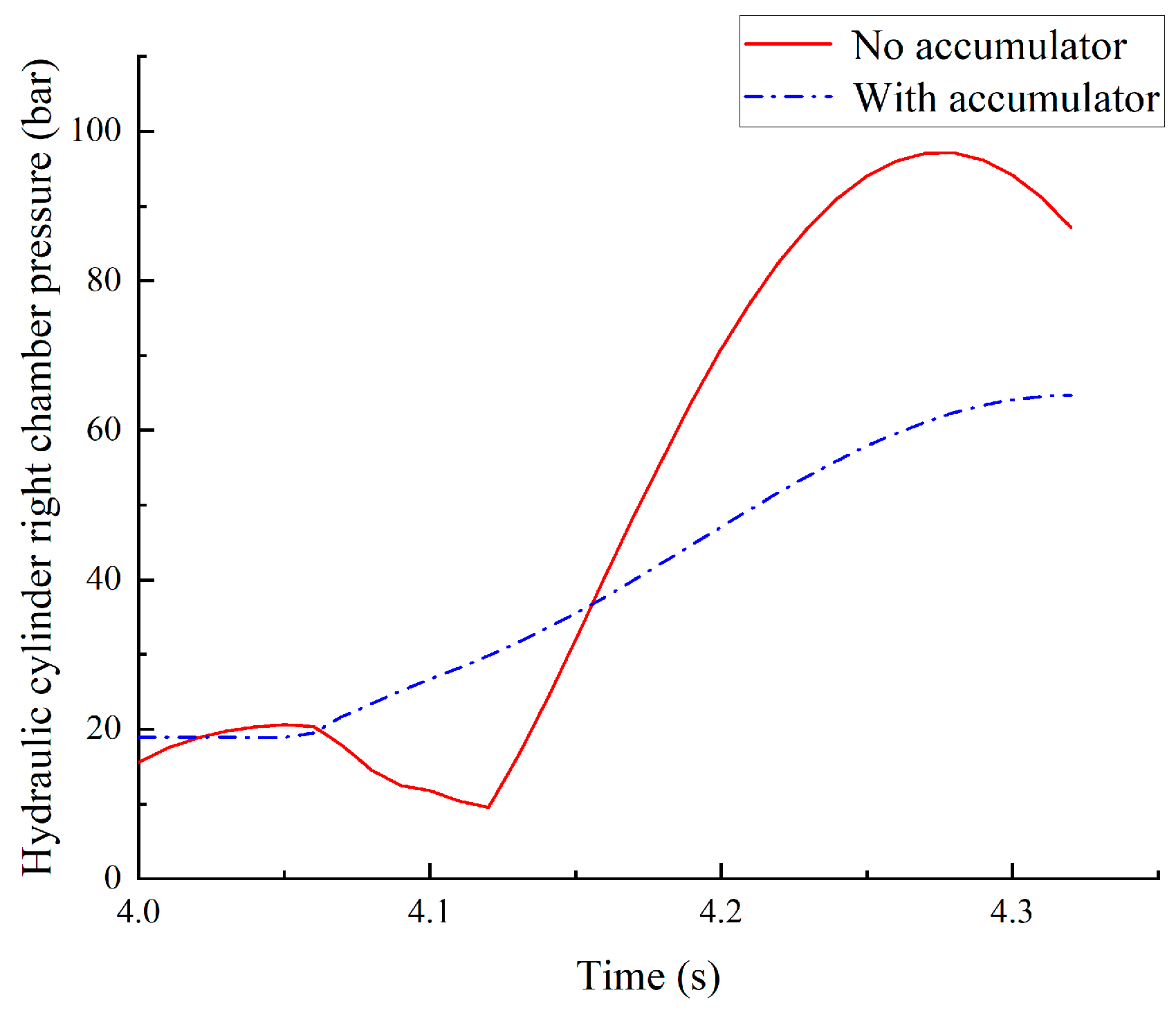
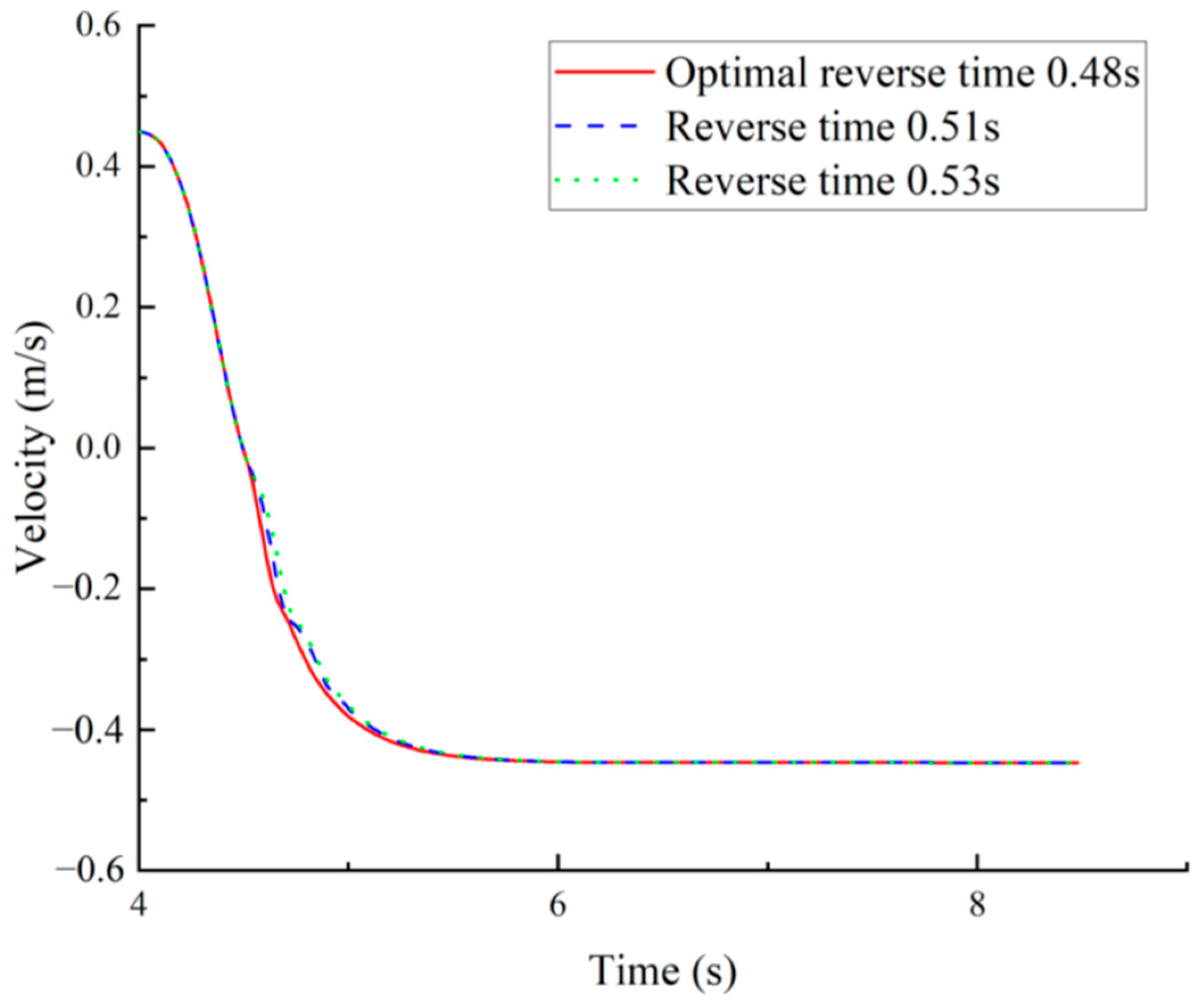


| Recovery Method | Main Control Features | Advantages | Disadvantages | Applicability to Pump-Controlled Grinding Machines |
|---|---|---|---|---|
| Motor | Four-quadrant operation to convert kinetic energy into electrical energy | Can store energy for long periods | Lower efficiency at low speeds | Suitable for conventional operations; difficult to meet the transient demands of high-frequency dynamic commutation |
| Accumulator | Direct hydraulic energy storage | No conversion needed, directly stores hydraulic energy | Limited by volume and pressure fluctuations; lacks long-term storage capability | Sensitive to pressure fluctuations; limited application in grinding machines with long work cycles |
| Flywheel | Converts hydraulic energy to rotational energy | Relatively efficient energy conversion | Requires additional mechanical transmission | Limited application in high-frequency commutation grinding due to space requirements and vibration issues |
| Motor + Flywheel | Flywheel handles peak loads; motor handles long-term storage | Enhanced dynamic response | System complexity increases | Mainly applied to engineering machinery rather than precision grinding machines |
| Motor + Accumulator | Integrated energy flow management | Optimized energy recovery under various working conditions | Requires precise timing to achieve optimal performance | Ideal for pump-controlled grinding machines with high-frequency commutation; reduces commutation time and improves productivity |
| Model | RMSE | R2 | MAE |
|---|---|---|---|
| LR | 0.0028611 | 0.99745 | 0.0022605 |
| SVM | 0.0014435 | 0.99935 | 0.0010713 |
| GPR | 0.0003302 | 0.99996 | 0.00026615 |
| RF | 0.015403 | 0.92604 | 0.011819 |
| NN | 0.0003256 | 0.99997 | 0.0002668 |
| Parameter Name | Unit | Value |
|---|---|---|
| Servo motor rated torque | Nm | 254 |
| Servo motor rated speed | r/min | 1800 |
| Servo motor power | kW | 48 |
| Hydraulic pump displacement | mL/r | 200 |
| Accumulator volume | L | 0.5 |
| Accumulator orifice diameter | mm | 4.8 |
| Load mass | t | 10 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yu, B.; Chen, G.; Liu, K.; Yan, G.; Zhang, Y.; Liu, Y. Research on the Maximum Regenerative Energy Commutation Control Strategy of a Dual-Mode Synergistic Energy Recovery Pump-Controlled Grinder. Energies 2025, 18, 2622. https://doi.org/10.3390/en18102622
Yu B, Chen G, Liu K, Yan G, Zhang Y, Liu Y. Research on the Maximum Regenerative Energy Commutation Control Strategy of a Dual-Mode Synergistic Energy Recovery Pump-Controlled Grinder. Energies. 2025; 18(10):2622. https://doi.org/10.3390/en18102622
Chicago/Turabian StyleYu, Bo, Gexin Chen, Keyi Liu, Guishan Yan, Yaou Zhang, and Yinping Liu. 2025. "Research on the Maximum Regenerative Energy Commutation Control Strategy of a Dual-Mode Synergistic Energy Recovery Pump-Controlled Grinder" Energies 18, no. 10: 2622. https://doi.org/10.3390/en18102622
APA StyleYu, B., Chen, G., Liu, K., Yan, G., Zhang, Y., & Liu, Y. (2025). Research on the Maximum Regenerative Energy Commutation Control Strategy of a Dual-Mode Synergistic Energy Recovery Pump-Controlled Grinder. Energies, 18(10), 2622. https://doi.org/10.3390/en18102622






