Control of Wind-Power Systems Operating at Variable Wind Speeds to Optimize Energy Capture

Abstract

This paper examines two contradictory aspects of wind turbine operation: the positive aspect of functioning at the maximum power point (MPP) and the negative aspect of power gaps that occur during significant fluctuations in wind speed. The analysis utilizes experimental data from a 2.5 MW wind turbine operating in the Dobrogea region, focusing on identifying the optimal energy zone. To maintain operation within this optimal zone, a control algorithm based on kinetic energies is developed. The control aims to adjust the load on the electric generator in relation to the wind speed value. The proposed approach ensures operation within the MPP through a control algorithm based on kinetic energies, which adjusts the load on the generator according to the wind speed values.

1. Introduction

According to the new strategies, the share of renewable energy in electricity is expected to reach 46% by 2030. Thus, in 2023, the global installed wind capacity was 1015 GW, with the construction of new wind capacities experiencing a 50% increase compared to 2022 [1]. In light of the growing number of wind farms [2], the use of variable generators in electricity production can aid in providing ancillary services, such as primary and secondary frequency regulation [3,4].

In both traditional wind systems and offshore installations, it is essential to monitor the maximum power point (MPP). For offshore systems, it is recommended to implement an integrated approach that includes an active rectifier and several passive rectifiers, in conjunction with a multi-port permanent magnet synchronous generator, to effectively manage the total output power [5].

This paper examines the operation of the wind turbine (WT) at the MPP, which corresponds to the optimal mechanical angular speed (MAS), ω_OPTIM.

To ensure maximum wind energy capture, it is necessary to correlate wind speed with mechanical angular speed. For this, it is necessary to determine the maximum power of the wind turbine at different wind speeds over time [6,7].

Most wind systems function under fluctuating wind velocities, necessitating continuous control of the output power [8]. Different strategies are used to measure or estimate wind speed, such as:

-

Use of a low-power, no-load turbine at the mechanical angular velocity [9];

-

Nonlinear mapping, which involves measuring rotor speed, tilt angle and aerodynamic torque as perceived by the disturbance observer [10];

-

The assessment of turbine torque and rotor speed is conducted utilizing sliding mode observers grounded in nonlinear control theory, with the aim of calculating the effective wind velocity by reversing the aerodynamic model of the turbine [11];

-

The original signal is decomposed into multiple sequences, utilizing deep learning prediction models and neural network optimization [12].

Various control strategies are employed for wind turbines operating at variable wind speeds. One proposed approach involves the use of an extended optimal torque controller, which is structured upon the accurate assessment of wind speed through nonlinear mapping. Simulations have demonstrated that this method enhances the precision of effective wind speed estimation by 2–7% and improves electricity production efficiency by 0.35% [10]. Another control strategy focuses on maximizing the amount of wind energy harvested by utilizing the optimal power curve and the power curve corresponding to different wind speeds [13]. Additionally, other studies suggest that optimize energy extraction from a wind turbine utilizing a doubly fed induction generator (DFIG), a combination of maximum power point (MPP) tracking using a high-gain observer, and a second order sliding mode control for the DFIG is recommended [14].

Control strategies must consider various operational scenarios of wind turbines. Consequently, during rapid load discharges, the turbine rotor will accelerate beyond its nominal speed, potentially leading to the breaking of blades or damage to a component of the wind energy system. To address this issue, it is essential to restrict the discharge to a maximum value [15]. This limitation can be implemented based on the response trajectory characteristics of the system [16]. Additionally, in the operation of wind systems, the power oscillation damping regulator can influence the structural system of the turbine, producing effects that are either comparable to or less significant than those caused by fluctuations in wind speed [17]. Other issues that may impact the operation of wind systems can arise from atmospheric discharges that affect the turbine blades and certain internal components [18,19], or from unbalanced loads [20].

In the specialized literature concerning the field addressed [5,9], valid solutions for wind turbines to operate at maximum power point under optimal mechanical angular velocity, amidst variable wind speeds over time, have not been identified. Furthermore, the operational wind systems have not been evaluated in terms of energy efficiency [13,21].

This article addresses precisely the issue of maximizing wind energy capture under varying wind speeds over time. When wind speeds fluctuate, the wind turbine operates continuously in a dynamic mode, with variable rotational speeds [4,16,22].

Given the dynamic nature of the process, the equation for kinetic momentum [10,23] is utilized in the following manner:

$$J\cdot {\displaystyle \frac{d\omega }{dt}}=M_{WT}-M_{EG}$$

(1)

where: ω—the mechanical angular speed, MAS, at the electric generators shaft, EG, J—the equivalent inertia moment, dω/dt—derivative of MAS in relation to time, M_WT—the moment, in relation to the EG axis, provided by the WT, M_EG—electromagnetic moment at EG’s shaft.

By multiplying the equation of angular momentum by ω, one derives the power equation [24,25]:

$$J\cdot {\displaystyle \frac{d\omega }{dt}}\cdot \omega =P_{WT}-P_{EG}$$

(2)

where: P_WT—useful power provided by the wind turbine, in relation to the axis of the electric generator, P_EG—the electromagnetic power of the electric generator at the shaft.

Optimal control is based on the value of inertial power:

$$P_{INERTIAL}=J\cdot {\displaystyle \frac{d\omega }{dt}}\cdot \omega$$

(3)

fundamental quantity in the dynamic process.

The inertial power, P_INERTIAL is imposed by the wind speed, V and its derivative, dV/dt.

In current systems, the electric generator’s load [9,11], P_EG, is adjusted according to the wind speed, based on the understanding of the relationship between optimal rotational speed and wind speed. For optimal wind energy capture at a designated wind speed, it is essential for the wind turbine to function at its optimal angular speed, ω_OPTIM, or optimal rotational speed, n_OPTIM [10,26].

The functioning of wind turbines at their maximum power point with the optimal mechanical angular speed, ω_OPTIM, presents a complex challenge under fluctuating wind speeds, attributable to the considerable mechanical inertia inherent in the wind energy system [15,27]. Achieving WT operation at the optimal mechanical angular speed at the MPP, relies on adjusting of the load on the electric generator according to the wind speed, V [11,17]. The power characteristic of the WT, PWT(ω), shows a peak in MPP, corresponding to the optimal mechanical angular speed, ω_OPTIM, which serves as a reference parameter within the control system.

The temporal fluctuations in wind result in a corresponding variation in the mechanical angular velocity ω. For the wind system to operate at optimal energy efficiency, the variations in wind speed must be synchronized with the changes in mechanical angular speed, ω. When the optimal mechanical angular speeds align with the temporal fluctuations of wind speed, the system is capable of maximizing wind energy capture.

The simulations in this paper are derived from the mathematical model of the wind turbine, (MM-WT), extracted from experimental data gathered from a of 2.5 MW, wind turbine operational in Galbiori—site on the Romanian Black Sea cost [28].

This paper develops a specific mathematical model for the analyzed turbine, grounded in experimental data and generic mathematical models. Utilizing the derived mathematical model, the power output is calculated, along with the optimal angular speed that yields maximum power. To optimize power output in relation to fluctuations in wind speed, it is crucial to modify the load of the electric generator in accordance with the wind speed. This involves examining the potential for modifying the power output of the generator based on the wind speed. Consequently, optimizing the wind system to reach its maximum power point is accomplished by specifying the optimal power of the generator, followed by maintaining the wind turbine at this maximum power point and ensuring the system operates at maximum power across various time intervals. The analysis continues with the presentation of the energy balance, highlighting the relationship between the wind energy captured and the electrical energy supplied by the generator, as well as the kinetic energy of the rotating masses. A similar analysis is conducted during intervals when wind speed decreases. The research concludes with discussion and conclusion sections that emphasize that the proposed control system relies on the variations in the kinetic energies of the rotating masses, which are dependent on the wind speed values.

The primary contribution of this work lies in maintaining optimal conditions through the calculation of kinetic energies, a method that has not been previously encountered in specialized literature.

2. Establishing the Mathematical Model for the Turbine

In the majority of studies [8,9,29], different representations of MM-WT are employed, yet the procedures for deriving these forms are not specified. Optimal wind energy capture can only be realized through an accurately established MM-WT [8,9,29].

As mechanical stresses, atmospheric conditions, and the geometry of the turbine evolve in time, the initially established MM-WT also undergoes modifications, necessitating a recalibration based on the most recent measured data. In numerous locations [2,14,20,30], the aging of turbines has led to calibration using mathematical models with outdated parameters, resulting in diminished energy efficiency.

The study is conducted under fluctuating wind over time and is based on the assessment of three essential parameters: power, P_EG, wind speed, V, and angular speed, ω, at EG. In the majority of the studies [16,27,31], existing wind systems are addressed based on inadequate MM-WT models and lack effective processing of experimental data.

The determination of the optimal mechanical angular velocity, ω_OPTIM (V), in relation to wind speed, V, is applicable to wind systems that operate under variable wind conditions over time and is grounded in the mathematical model of wind turbines (WT). The correlation between the ideal mechanical angular velocity and wind serves as a critical reference in Control Design, where precise knowledge of this relationship facilitates the maximization of wind energy capture. The assessment of MM-WT occurs while the wind system operates.

The mathematical model of the wind turbine (WT) employed in the analysis of wind system dynamics is, according to the authors, represented by the power characteristic of the WT, denoted as P_WT(ω,V) [5,10,14]. The specialized literature [4,9,20] presents various formulations of the power characteristic of the WT, referred to as the function P_WT(ω,V).

The usefulness scenario involves three parameters: a, b and c, structured as follows:

$$P_{WT}\left(\omega ,V\right)=a\left({\displaystyle \frac{V}{\omega }}-b\right)\cdot e^{-c\cdot {\displaystyle \frac{V}{\omega }}}\cdot V^3$$

(4)

The parameters a, b, and c are established through wind, power output, and rotational speed at the generator, n/ω, assessment. A precise understanding of the wind turbine’s mathematical model is crucial for the system control for ensuring the wind turbine to operate in MPP. The establishment of the mathematical model for the wind turbine (WT) is grounded in experimental data obtained from the 2.5 MW GEWE-B2.5-100 model [32], which is operational in the Dobrogea region, specifically at the Galbiori site [28].

The mechanical angular speed, ω, and the power at the shaft produced by a three-blade wind turbine (WT) can be determined using the following equation:

$$P_{WT}=\rho \cdot \pi \cdot R_p^2\cdot C_p\left(\lambda \right)\cdot V^3$$

(5)

where: ρ—air density of the location where the WT operats; R_B—radius of the blade; C_p(λ)—coefficient for power conversion; λ = ω·R_p/V; ω—mechanical angular speed, MAS; V—wind speed.

C_p(λ), the power conversion coefficient for wind turbines with three blades is calculated using the following relationship [11,13]:

$$C_p\left(\lambda \right)=c_1\cdot \left({\displaystyle \frac{c_2}{\Lambda }}-c_3\right)\cdot e^{-{\displaystyle \frac{c_4}{\Lambda }}}$$

(6)

where: c₁, c₂, c₃, c₄ are constructive constants, provided in the catalogue, and:

$${\displaystyle \frac{1}{\Lambda }}={\displaystyle \frac{1}{\lambda }}-0.035={\displaystyle \frac{V}{R_p\cdot \omega }}-0.035={\displaystyle \frac{V}{1.5\cdot \omega }}-0.035$$

(7)

$$C_p\left(\lambda \right)=c_1\cdot \left[c_2\left({\displaystyle \frac{V}{1.5\cdot \omega }}-0.035\right)-c_3\right]\cdot e^{-{\displaystyle \frac{c_4}{\Lambda }}}=\left[c_1\cdot c_2\left({\displaystyle \frac{V}{1.5\cdot \omega }}-0.035\right)-c_1\cdot c_3\right]\cdot e^{-{\displaystyle \frac{c_4}{\Lambda }}}$$

(8)

$$C_p\left(\lambda \right)=a\cdot \left({\displaystyle \frac{V}{\omega }}-b\right)\cdot e^{-c\cdot {\displaystyle \frac{V}{\omega }}}$$

(9)

resulting:

$${\displaystyle \frac{c_1\cdot c_2}{1.5}}=a; c_1\cdot c_2\cdot 0.035-c_1\cdot c_3=a\cdot b; {\displaystyle \frac{c_4}{1.5}}=c$$

(10)

Replacing Λ, the power conversion coefficient, C_p(λ), can be expressed as follows:

$$C_p\left(\lambda \right)=c_1\cdot \left(c_2\cdot {\displaystyle \frac{V}{1.5\cdot \omega }}-0.035\right)-c_3\cdot e^{-c_4\cdot \left({\displaystyle \frac{V}{1.5\cdot \omega }}-0.035\right)}=a\cdot \left({\displaystyle \frac{V}{\omega }}-b\right)\cdot e^{-c\cdot {\displaystyle \frac{V}{\omega }}}$$

(11)

And finally, the power provided by the wind turbine is determined using the following equation:

$$P_{WT}\left(\omega ,V\right)=a\cdot \left({\displaystyle \frac{V}{\omega }}-b\right)\cdot e^{-c\cdot {\displaystyle \frac{V}{\omega }}}\cdot V^3$$

(12)

where the values of a, b and c are established from the experimental data, in the sense of those given below:

• The maximum power value is achieved at ω_OPTIM by setting the derivative of power to zero:

$${\displaystyle \frac{d{P}_{WT}}{d\omega }}={\displaystyle \frac{d}{d\omega }}\cdot \left[a\cdot \left({\displaystyle \frac{V}{\omega }}-b\right)\cdot e^{-c\cdot {\displaystyle \frac{V}{\omega }}}\cdot V^3\right]=-V^4\cdot {\displaystyle \frac{a}{{\omega }^3}}\cdot e^{-V\cdot {\displaystyle \frac{c}{\omega }}}\left(\omega -V\cdot c+b\cdot c\cdot \omega \right)=0$$

(13)

or:

$$\omega -V\cdot c+b\cdot c\cdot \omega =0$$

(14)

or:

$${\omega }_{OPTIM}={\displaystyle \frac{c}{1+b\cdot c}}\cdot V=k\cdot V$$

(15)

From the experimental data, the following were obtained:

$${\displaystyle \frac{c}{1+b\cdot c}}=24.046$$

(16)

This represents the first system equation involving a, b, and c.

2.

The maximum power value of the WT corresponds to the optimal MAS, ω_OPTIM, and is:

$$P_{WT-MAX}\left(V\right)=a\cdot \left({\displaystyle \frac{V}{\omega }}-b\right)\cdot e^{-c\cdot {\displaystyle \frac{V}{\omega }}}\cdot V^3={\displaystyle \frac{a}{c}}\cdot e^{-1-c\cdot b}\cdot V^3=k_p\cdot V^3$$

(17)

Results:

$$k_p={\displaystyle \frac{a}{c}}\cdot e^{-1-c\cdot b}$$

(18)

According to the experimental data, similar to ω_OPTIM, the proportionality factor k_p is determined to be k_p = 2.7929. This leads to the systems second equation involving a, b, and c:

$${\displaystyle \frac{a}{c}}\cdot e^{-1-c\cdot b}=2.7929$$

(19)

These two equations are crucial for establishing the mathematical model of the WT and for identifying the coordinates of the maximum power point (MPP). To calculate the unknowns a, b, and c, a third equation is required. This equation can be derived from the ratio ω_OPTIM/ω_MAXIM.

3.

The ratio ω_OPTIM to ω_MAXIM yields Equation (3). This is due to the fact that the power WT is zero:

$$P_{WT}=a\cdot \left({\displaystyle \frac{V}{\omega }}-b\right)\cdot e^{-c\cdot {\displaystyle \frac{V}{\omega }}}\cdot V^3=0$$

(20)

at ω = ω_MAXIM, results ω_MAXIM = V/b.

By substituting the value of the ratio ω_OPTIM/ω_MAXIM, one obtains:

$${\displaystyle \frac{{\omega }_{OPTIM}}{{\omega }_{MAXIM}}}={\displaystyle \frac{\frac{c}{1+b\cdot c}}{\frac{1}{b}}}={\displaystyle \frac{b\cdot c}{1+b\cdot c}}$$

(21)

C_p(λ), the coefficient of power conversion, for a wind turbine with three rotor blades [8,11], indicates that the ratio of optimal angular velocity to maximum angular velocity is ω_OPTIM/ω_MAXIM = 0.42051.

Thus, we derive the system of equations in the unknowns a, b, and c:

$$\left\{\begin{array}{c}{\displaystyle \frac{c}{1+b\cdot c}}=24.046\\ {\displaystyle \frac{a}{c}}\cdot e^{-1-c\cdot b}=2.7929\\ {\displaystyle \frac{b\cdot c}{1+b\cdot c}}=0.42051\end{array}\right.$$

(22)

resulting in solutions: a = 650.86, b = 1.7488·10⁻², c = 41.495.

Using the data from the GEWE-B2.5-100 WT located in Galbiori, Romania, a mathematical model of the wind turbine was developed in the following form:

$$P_{WT-2}\left(\omega ,V\right)=650.86\cdot \left({\displaystyle \frac{V}{\omega }}-1.7488\cdot {10}^{-2}\right)\cdot e^{-41.495\cdot {\displaystyle \frac{V}{\omega }}}\cdot V^3 [\mathrm{kW}]$$

(23)

or:

$$P_{WT-2}\left(\omega ,V\right)=6.5086\cdot {10}^5\left({\displaystyle \frac{V}{\omega }}-1.7488\cdot {10}^{-2}\right)\cdot e^{-41.495\cdot {\displaystyle \frac{V}{\omega }}}\cdot V^3 [\mathrm{W}]$$

(24)

The wind turbine’s maximum power output is determined by the value of the wind speed:

$$P_{WT-MAX}\left(V\right)={\displaystyle \frac{a}{c}}\cdot e^{-1-c\cdot b}\cdot V^3={\displaystyle \frac{650.86}{41.495}}\cdot e^{-1-1.7488\cdot {10}^{-2}\cdot 41.495}\cdot V^3=2.7982\cdot V^3 [\mathrm{kW}]$$

(25)

With b and c established, the optimal mechanical angular speed, ω_OPTIM, can be obtained as a function of the wind:

$${\omega }_{OPTIM}={\displaystyle \frac{c}{1+b\cdot c}}\cdot V={\displaystyle \frac{41.495}{1+1.7488\cdot {10}^{-2}\cdot 41.495}}\cdot V=24.046\cdot V [\mathrm{rad}/\mathrm{s}]$$

(26)

The functioning of the turbine at peak power output is characterized by a one-to-one correspondence between the values of wind, V, and mechanical angular velocity, ω. This necessitates an adjustment of the load on the electric generator in accordance with the wind speed value, V [11,17,29].

3. Changing the Power of the Electric Generator in Relation to Measured Wind

The power adjustment in electric generators is typically achieved through the use of regulators, which often face intricate challenges in their calibration. Due to the rapid and unpredictable nature of dynamic processes influenced by wind speed variations, this issue becomes complex and often inadequately implemented, as observed in the case of the wind turbines under analysis.

• Case Study 1

The temporal fluctuations of both actual and optimal mechanical angular velocities at the Galbiori location [28] on 15 June 2022, are illustrated in Figure 1. The optimal MAS, ω_OPTIM, is intended to align with the wind, V, leading to the graphical representation of the function ω_OPTIM(t) in Figure 1. The function ω_OPTIM(t) is derived from the measured values of wind speed, while the function ω_REAL(t) relies on measured values of rotational speed.

In an ideal scenario, the two graphs representing the functions ω_OPTIM(t) and ω_REAL(t) would coincide; however, this is not evident from the analysis of the graphs depicted in Figure 1. Consequently, the wind turbine is not functioning at its MPP.

A wind turbine fails to function at its maximum power point because the actual rotational speed, ω_REAL, is not aligned with the wind’s velocity. Achieving the turbine’s maximum power point at ω_REAL = ω_OPTIM can only be accomplished by specifying the power value at the electric generator, P_EG-OPTIM, in direct relation with the actual variations in wind velocity.

By examining the actual variation in wind speed over the time periods A-B and B-C, as illustrated in Figure 2, the optimal power at the electric generator, P_EG-OPTIM, is determined to ensure that the wind turbine functions at its MPP.

The points A, B, and C represent the wind speed by the values shown in

Table 1. Wind speed at the points of analysis.

Point	Time [s]	V [m/s]
A	0	10.47
B	3.433	8.13
C	6.631	9.52

.

The linear wind speed variation from point A to B results in:

$$V\left(t\right)=10.47+{\displaystyle \frac{8.13-10.47}{3.433}}\cdot t=10.47-0.73171\cdot t$$

(27)

The power provided by the wind turbine is:

$$P_{WT-A-B}\left(\omega ,t\right)=650860\cdot {\displaystyle \frac{10.47-0.73171\cdot t}{\omega }}-1.7488\cdot {10}^{-2}\cdot e^{-41.495\cdot {\displaystyle \frac{10.47-0.73171\cdot t}{\omega }}}\cdot {\left(10.47-0.73171\cdot t\right)}^3$$

(28)

3.1. Achieving the Maximum Power Point of the Wind Turbine System

Achieving the maximum power point of the turbine necessitates an acceleration towards the optimal operating condition. This can be achieved in the shortest time possible through two methods:

• Disconnection of the generator from the network (a slower method).
• Converting the generator to operate in motor mode (a faster method).

The EG is viewed as to be decoupled from the grid and possesses the MAS value ω(0) = 122 [rad/s]. Based on the equation that describes powers of form:

$$J\cdot {\displaystyle \frac{d\omega }{dt}}\cdot \omega =P_{WT}\left(\omega ,t\right)$$

(29)

it is obtained:

$$\begin{array}{c}511.92\cdot {\displaystyle \frac{d\omega }{dt}}\cdot \omega =650860\cdot {\displaystyle \frac{10.47-0.73171\cdot t}{\omega }}-1.7488\cdot {10}^{-2}\cdot e^{-41.495\cdot {\displaystyle \frac{10.47-0.73171\cdot t}{\omega }}}\cdot {\left(10.47-0.73171\cdot t\right)}^3\\ \omega \left(0\right)=122\end{array}$$

(30)

By solving it, we obtain the time variation of the mechanical angular speed, ω.

At the time t*, according to Figure 3, the angular velocity MAS ω is measured at ω(3.3) = 197.6 [rad/s], which represents approximately equal to the optimal MAS:

$${\omega }_{OPTIM}\left(V\right)=24.046\cdot \left(10.47-0.73171\cdot t\right)=24.046\cdot \left(10.47-0.73171\cdot 3.3\right)=197.67 [\mathrm{rad}/\mathrm{s}]$$

(31)

At t = 3.3 s, the values of the optimal, ω_OPTIM, and real mechanical angular velocities, ω, are equal, the system functions at the turbine’s maximum power point, t*.

At the specific time t*, the speed of wind is measured at:

$$V\left(3.3\right)=+{\displaystyle \frac{8.13-10.47}{3.433}}\cdot 3.33=8.2207 [\mathrm{m}/\mathrm{s}]$$

(32)

Based on, P_WT(V,ω), the the power characteristic at ω(3.3):

$$\begin{array}{c}{P}_{WT}=650860\cdot {\displaystyle \frac{8.2207}{\omega }}-1.7488\cdot {10}^{-2}\cdot e^{-41.495\cdot {\displaystyle \frac{8.2207}{\omega }}}\cdot {\left(8.2207\right)}^3\\ \omega =197.67\end{array}$$

(33)

the power generated by the WT is obtained at a value of:

$$P_{WT}\left(8.2207\right)=1.5516\cdot {10}^6 [\mathrm{W}]$$

(34)

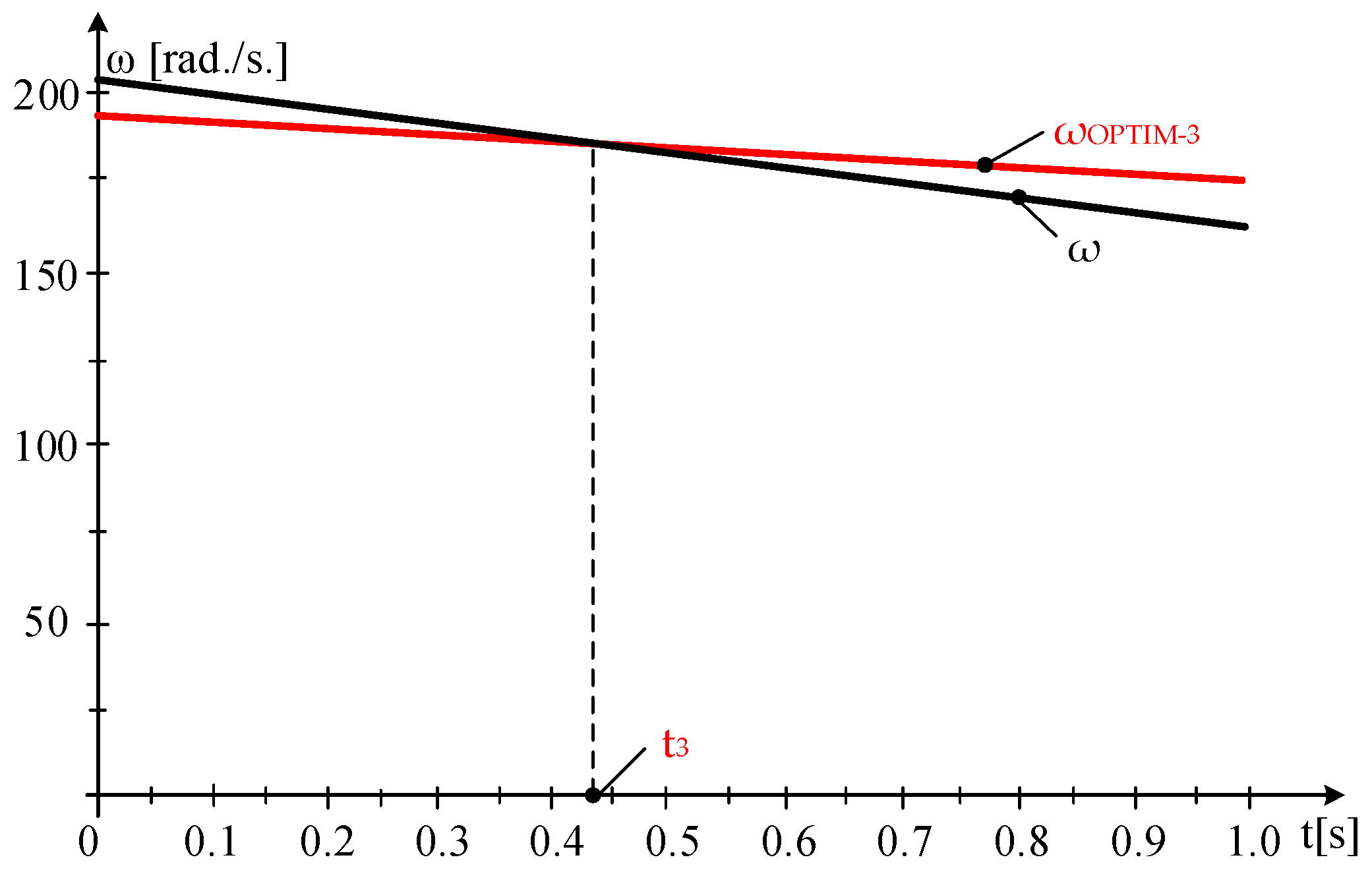
3.2. Sustaining the Wind System at the Turbine’s Maximum Power Point

From the power equation, when operating in MPP, the electromagnetic power, P_EG, is derived at the shaft of the EG:

$$J\cdot {\displaystyle \frac{d\omega }{dt}}\cdot \omega =P_{WT}-P_{EG}$$

(35)

In the energetically optimal zone, when operating at MPP, the optimal mechanical angular speed, ω_OPTIM, is determined by the wind speed, expressed as: ω_OPTIM = 24.046·V.

In the optimal range, the current MAS, ω, must equal the optimal mechanical angular velocity, ω_OPTIM, such that ω = ω_OPTIM. Consequently, the power equation is expressed as follows:

$$J\cdot {\displaystyle \frac{d{\omega }_{OPTIM}}{dt}}\cdot {\omega }_{OPTIM}=P_{WT-MAX}-P_{EG-OPTIM}$$

(36)

or:

$$24.046\cdot J\cdot {\displaystyle \frac{dV}{dt}}\cdot 24.046\cdot V=P_{WT-MAX}-P_{EG-OPTIM}$$

(37)

Therefore, by understanding how the optimal speed is influenced by wind speed, we can ascertain the optimal power output of the electric generator:

$$P_{EG-OPTIM}=P_{WT-MAX}-{24.046}^2\cdot J\cdot {\displaystyle \frac{dV}{dt}}\cdot V$$

(38)

The optimal electromagnetic power is achieved at an equivalent moment of inertia of J = 511.92 [kg·m²]:

$$P_{EG-OPTIM}=P_{WT-MAX}-{24.046}^2\cdot 511.92\cdot {\displaystyle \frac{dV}{dt}}\cdot V$$

(39)

Subsequently, at P_WT-MAX = 2792.8·V³, it follows that:

$$P_{EG-OPTIM}=2792.8\cdot V^3-2.96\cdot {10}^5\cdot {\displaystyle \frac{dV}{dt}}\cdot V$$

(40)

After the WT has been brought into the MPP at the time t*, the EG connects to the grid and charges at the power level:

$${P^{\ast }}_{EG}={P^{\ast }}_{WT}-J\cdot {\displaystyle \frac{d{\omega }_{OPTIM}}{dt}}\cdot {\omega }_{OPTIM}={P^{\ast }}_{WT}-2.96\cdot {10}^5\cdot {\displaystyle \frac{dV}{dt}}\cdot V$$

(41)

The power of WT, P*_WT can be determined by two methods:

• With MM-WT:

$${P^{\ast }}_{WT-MAX}=k_p\cdot V^3=2792.8\cdot V^3$$

(42)

• By integrating the kinetic momentum equation multiplied with ω, we derive the kinetic energies:

$$J\cdot {\displaystyle \frac{{\omega }_k^2-{\omega }_{k-1}^2}{2}}={\displaystyle \underset{t_{k-1}}{\overset{t_k}{\int }}{P}_{WT}}\cdot dt-{\displaystyle \underset{t_{k-1}}{\overset{t_k}{\int }}{P}_{EG}}\cdot dt$$

(43)

A temporal linear variation of the P_WT and P_EG powers, yields:

$$J\cdot {\displaystyle \frac{{\omega }_k^2-{\omega }_{k-1}^2}{2}}={\displaystyle \frac{P_{WT}\left(t_{k-1}\right)+P_{WT}\left(t_k\right)}{2}}\cdot \Delta t-{\displaystyle \frac{P_{EG}\left(t_{k-1}\right)+P_{EG}\left(t_k\right)}{2}}\cdot \Delta t$$

(44)

or:

$$J\cdot {\displaystyle \frac{{\omega }_k^2-{\omega }_{k-1}^2}{2\cdot \Delta t}}={\displaystyle \frac{P_{WT}\left(t_{k-1}\right)+P_{WT}\left(t_k\right)}{2}}-{\displaystyle \frac{P_{EG}\left(t_{k-1}\right)+P_{EG}\left(t_k\right)}{2}}$$

(45)

where: ω_k—MAS at t_k moment, ω_(k−1)—MAS at t_(k−1), Δt = t_k − t_(k−1), P_WT(t_k−1), P_EG(t_k−1)—powers at WT and EG at the time t_k−1, P_WT(t_k), P_EG(t_k)—powers at the moment t_k.

Consequently, the average power output from the WT is obtained over the specified period t_k−1 − t_k:

$$P_{WT-AVERAGE}\left(t_k^{\ast }\right)=J\cdot {\displaystyle \frac{{\omega }_k^2-{\omega }_{k-1}^2}{2\cdot \Delta t}}+P_{EG-AVERAGE}\left(t_k^{\ast }\right)$$

(46)

where:

$$t_k^{\ast }={\displaystyle \frac{t_k+t_{k-1}}{2}}$$

(47)

The duration of the time interval Δt is a value that must be correlated with the derivative of wind speed, dV/dt, and J, the equivalent inertia moment.

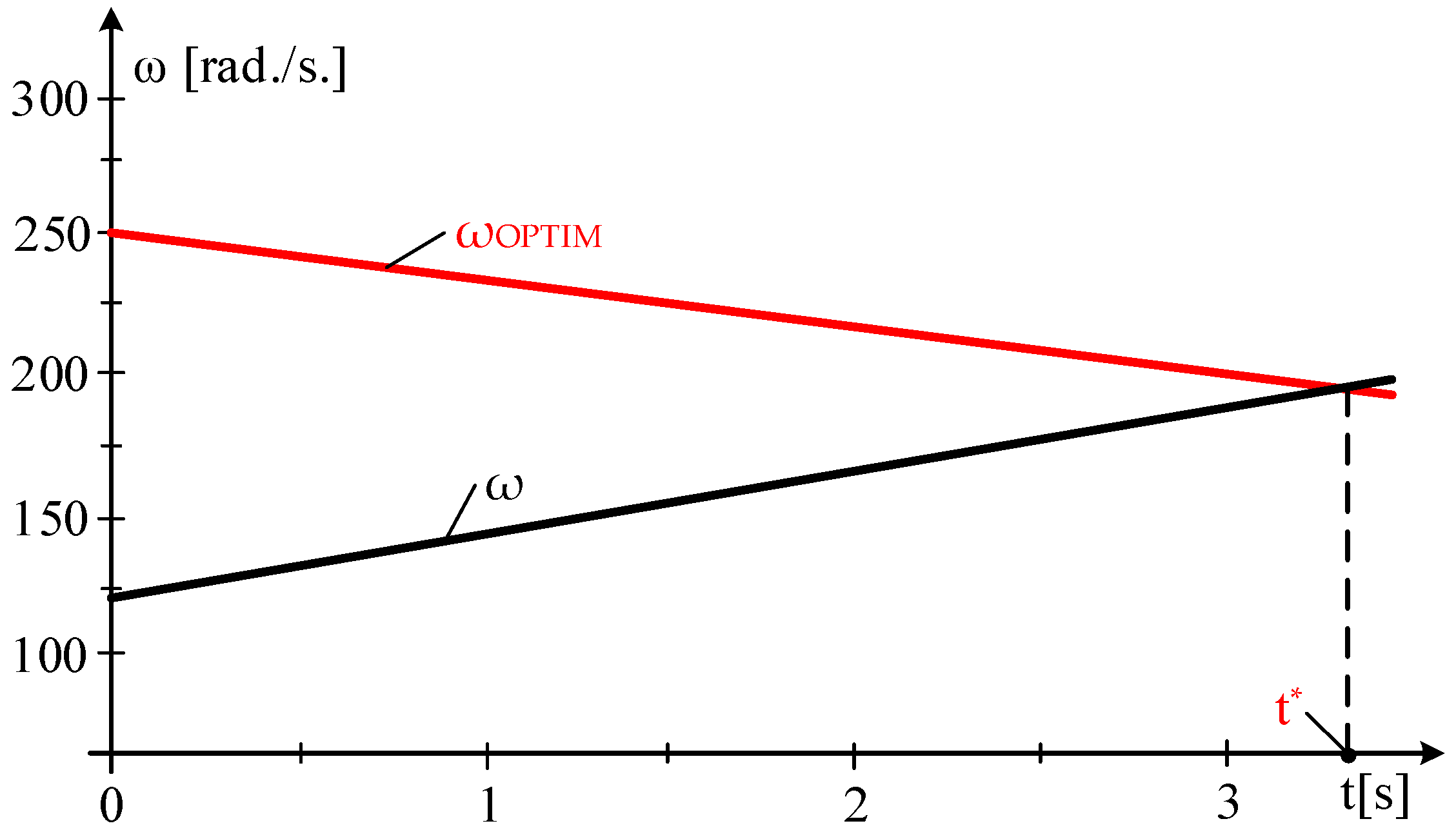
3.2.1. Sample Interval Value

The sampling interval value should be comparable to the value of the electromechanical time constant, H. In this particular case, it is as follows:

• J = 511.92 [kg·m²]—equivalent moment of inertia.
• P_N = 2.5 [MW] = 2,500,000 [W]—rated power.
• ω_N = 157.08 [rad/s]—nominal mechanical angular speed.
• H-value:

$$H={\displaystyle \frac{J\cdot {\omega }^2}{2\cdot P_N}}={\displaystyle \frac{511.92\cdot {157.08}^2}{5000000}}=2.5262 [\mathrm{s}]$$

(48)

Therefore, a sampling interval of Δt = 1 [s] is deemed valid, as Δt = 1 [s] exceeds H = 2.5262 [s].

In the examined location, the fluctuation of wind speed is particularly significant during the summer months. However, the duration of these wind speed variations falls within the magnitude of the sampling interval Δt and the time constant of the electromechanical system, H.

The power values at EG, P_EG(tk−1), and P_EG(tk) corresponding to MAS ω_k−1 and ω_k at the time points t_k−1 and t_k are achieved with minimal inaccuracies via direct measurements, thus ensuring their validity. These values are then used to calculate the average power from the wind turbine (WT) over the time interval Δt = t_k − t_k−1 = 1.

$$P_{WT-KINETIC}^{\ast }=J{\displaystyle \frac{{\omega }_k^2-{\omega }_{k-1}^2}{2\cdot \Delta t}}=511.92\cdot {\displaystyle \frac{{\omega }_k^2-{\omega }_{k-1}^2}{2}} [\mathrm{rad}/\mathrm{s}]$$

(49)

The maintenance of the WT in the MPP is carried out in accordance with the proposed adjustment algorithm outlined below.

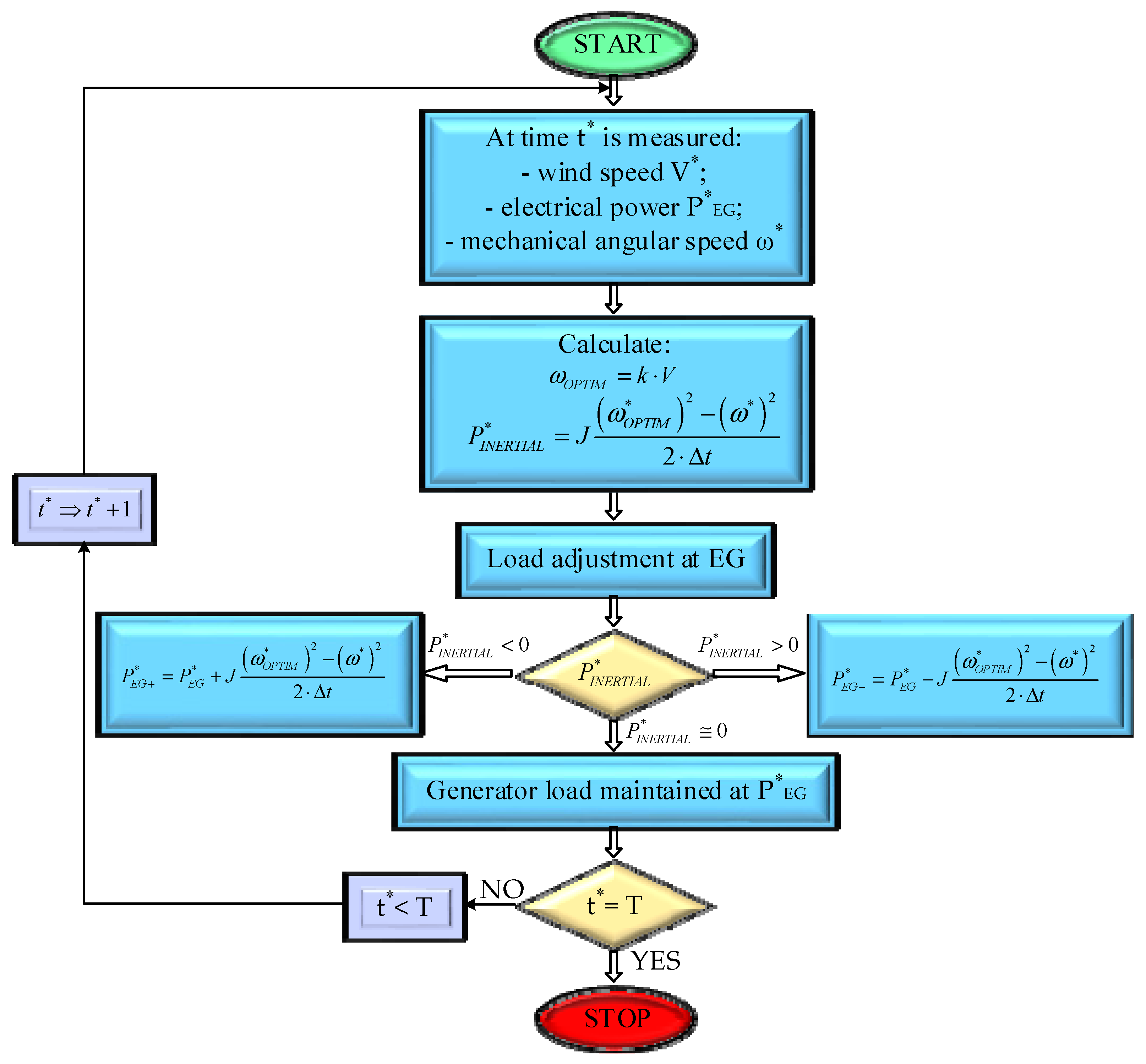
3.2.2. Control Algorithm

The algorithm consists of three operational steps (Figure 4):

• Step 1—the following are measured: wind speed, V*, generator power P*_EG and speed, ω*;
• Step 2—the optimal mechanical angular velocity, ω*_OPTIM, is calculated using the formula ω*_OPTIM = k_P⋅V*, along with the inertial power.

$$P_{INERTIAL}^{\ast }=J{\displaystyle \frac{{\left({\omega }_{OPTIM}^{\ast }\right)}^2-{\left({\omega }^{\ast }\right)}^2}{2\cdot \Delta t}}$$

(50)

• Step 3—The loading at EG is adjusted according to the sign of the inertial power value, P*_INERTIAL, as follows:

• P*_INERTIAL < 0, results in an increase in the EG load raised to the power of:

$$P_{EG+}^{\ast \ast }=P_{EG}^{\ast }+J{\displaystyle \frac{{\left({\omega }_{OPTIM}^{\ast }\right)}^2-{\left({\omega }^{\ast }\right)}^2}{2\cdot \Delta t}}$$

(51)

2.

P*_INERTIAL > 0, the load on EG decreases at the rate of:

$$P_{EG-}^{\ast \ast }=P_{EG}^{\ast }-J{\displaystyle \frac{{\left({\omega }_{OPTIM}^{\ast }\right)}^2-{\left({\omega }^{\ast }\right)}^2}{2\cdot \Delta t}}$$

(52)

3.

P*_INERTIAL > 0, the EG load is maintained at the P*_EG power level.

The system control is executed over a time interval T, with a sampling step that depends on dV/dt, the wind speed derivative and J, the equivalent inertia moment. At a sampling interval of 1 s, three operational steps are completed.

Simulation is utilized to verify the MPP and to determine the precise moments at which power imbalances take place.

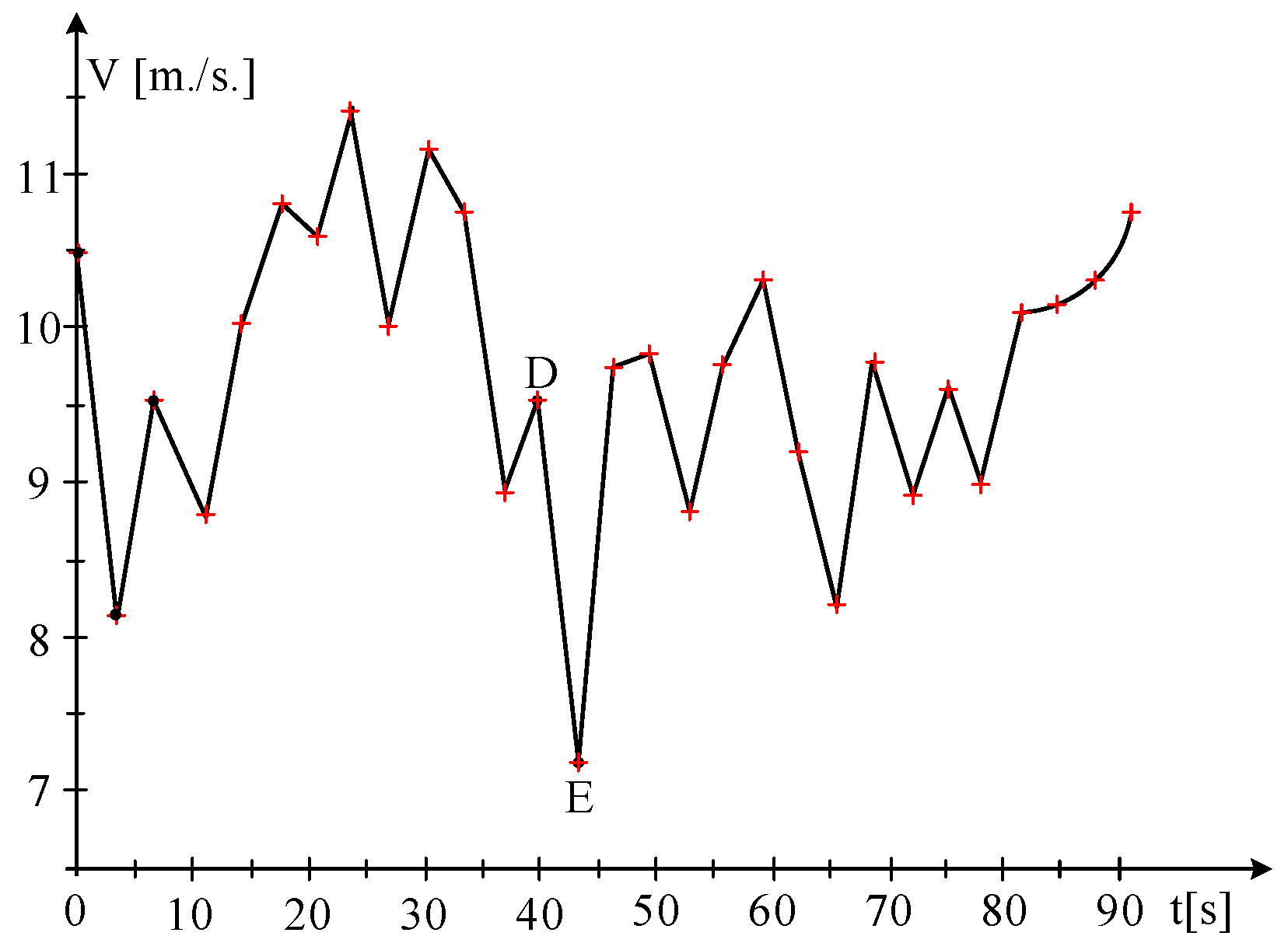
3.2.3. Time Intervals in Which Power Gaps Occur

From the analysis of the actual variation in wind speed, as in Figure 2, it is evident that there are intervals characterized by an increase in wind velocity and others when it decreases. When functioning inside the MPP region, the optimal power output of the electric generator, referred to as P_EG-OPTIM, will fluctuate in response to the wind, potentially leading to intervals where power deficits occur.

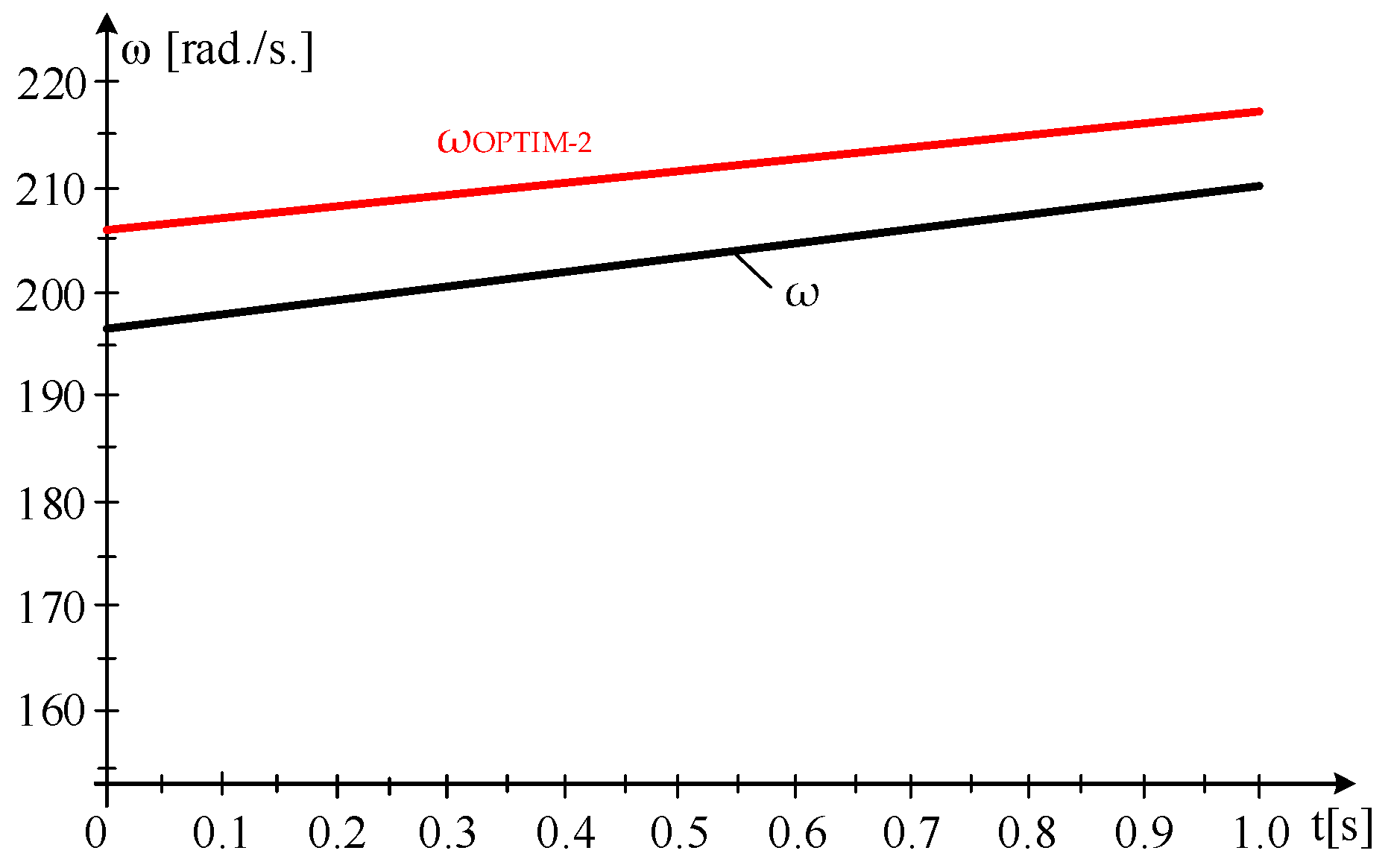
• Case Study 2—Verification in the MPP Area

The system’s performance is assessed after it attains the turbine’s maximum power point. At time t*, the wind turbine (WT) functions at the maximum power point, designated as point B, as in Figure 2 and reflected in

Table 2. Energies in the subintervals analyzed.

Subinterval	EWIND [J]	EWIND-MAX [J]	EELETRICAL [J]	EKINETIC [J]
1	1.6236·106	1.6254·106	1.5008·106	1.2247·105
2	1.8883·106	1.8927·106	5.4954·105	1.3384·106
3	2.1869·106	2.1877·106	0	2.1871·106

.

At t* = 0, the system functions in state B, at the maximum power point of the turbine, where the optimal mechanical angular velocity, ω_OPTIM, equals to the actual angular speed, ω:

$${\omega }_{OPTIM}=\omega =24.046\cdot 8.13=195.49 [\mathrm{rad}/\mathrm{s}]$$

(53)

The wind speed being V* = 8.13 [m/s], the load of EG is at P*_EG of value:

$$P_{EG}^{\ast }\left(0\right)=P_{WT-MAX}^{\ast }=k_P\cdot V^3=2792.8\cdot {8.13}^3=1.5008\cdot {10}^6 [\mathrm{W}]$$

(54)

On the interval B-C, considering the variation of wind speed to a linear progression, it follows:

$$V_{B-C}\left(t\right)=8.13+{\displaystyle \frac{9.52-8.13}{6.631-3.433}}\cdot t$$

(55)

The captured wind energy, E_WIND, can be determined by integrating the power of the WT:

$$E_{WIND}={\displaystyle \int P_{WT}}\cdot dt$$

(56)

or:

$${\displaystyle \frac{E_{WIND}}{dt}}=P_{WT}$$

(57)

The interval B-C is divided into four distinct subintervals:

• Subinterval 1:

Given that the sampling period is 1 s, at t* = 1 s, the obtained wind speed results:

$$V_1^{\ast }=8.13+{\displaystyle \frac{9.52-8.13}{6.631-3.433}}\cdot 1=8.5646 [\mathrm{m}/\mathrm{s}]$$

(58)

The variation of the wind speed is linear, between 8.13 [m/s] and 8.5646 [m/s].

$$V_{B-C-1}\left(t\right)=8.13+(8.5646-8.13)\cdot t=0.4346\cdot t+8.13$$

(59)

The optimal MAS, ω_OPTIM, is:

$${\omega }_{OPTIM-1}=24.046\cdot \left(0.4346\cdot t+8.13\right)$$

(60)

For these values, the energy and motion equations are derived in:

$$\left\{\begin{array}{c}\begin{array}{l}511.92\cdot {\displaystyle \frac{d\omega }{dt}}\cdot \omega =650860\left({\displaystyle \frac{0.4346\cdot t+8.13}{\omega }}-1.7488\cdot {10}^{-2}\right)\cdot e^{-41.495\cdot {\displaystyle \frac{0.4346\cdot t+8.13}{\omega }}}\cdot \\ {\left(0.4346\cdot t+8.13\right)}^3-1.5008\cdot {10}^6\end{array}\\ \begin{array}{l}{\displaystyle \frac{dE}{dt}}=650860\left({\displaystyle \frac{0.4346\cdot t+8.13}{\omega }}-1.7488\cdot {10}^{-2}\right)\cdot e^{-41.495\cdot {\displaystyle \frac{0.4346\cdot t+8.13}{\omega }}}\cdot \\ {\left(0.4346\cdot t+8.13\right)}^3\end{array}\\ \omega \left(0\right)=195.49\\ E\left(0\right)=0\end{array}\right.$$

(61)

In one second, significant wind energy is collected:

$$E_{WIND}\left(1\right)=E\left(1\right)=1.6236\cdot {10}^6 [\mathrm{J}]$$

(62)

At maximum power output, the captured wind energy during the same period is valued at:

$$E_{WIND-MAX}\left(1\right)={\displaystyle \underset{0}{\overset{1}{\int }}{P}_{WT-MAX}\cdot dt={\displaystyle \underset{0}{\overset{1}{\int }}\left[2792.8\cdot {\left(0.4346\cdot t+8.13\right)}^3\right]}}\cdot dt=1.6254\cdot {10}^6 [\mathrm{J}]$$

(63)

During the same period, the amount of electrical energy delivered is:

$$E_{ELECTRICAL}\left(1\right)={\displaystyle \underset{0}{\overset{1}{\int }}{P}_{EG}\cdot dt=}1.5008\cdot {10}^6 [\mathrm{J}]$$

(64)

At time t* = 1 s, as Figure 5 illustrates, the MAS ω is measured at ω(1) = 196.71 rad/s, in comparison with the optimal MAS.

$${\omega }_{OPTIM-1}=24.046\cdot 8.5646=205.94 [\mathrm{rad}/\mathrm{s}]$$

(65)

Due to the fact that ω_OPTIM-1 is greater than ω(1), ω_OPTIM-1 > ω(1), the turbines MPP was not attained at t* = 1 [s].

The value of inertial power being positive, P*_INERTIAL > 0:

$$P_{INERTIAL-1}^{\ast }=J{\displaystyle \frac{{\left({\omega }_{OPTIM}^{\ast }\right)}^2-{\left({\omega }^{\ast }\right)}^2}{2\cdot \Delta t}}=511.92{\displaystyle \frac{{\left(205.94\right)}^2-{\left(196.71\right)}^2}{2}}=9.5126\cdot {10}^5 [\mathrm{W}]$$

(66)

Within subinterval 2, the load of EG decreases at the rate of:

$$P_{EG-2}^{\ast \ast }=P_{EG}^{\ast }-J\cdot {\displaystyle \frac{{\left({\omega }_{OPTIM}^{\ast }\right)}^2-{\left({\omega }^{\ast }\right)}^2}{2\cdot \Delta t}}=1.5008\cdot {10}^6-9.5126\cdot {10}^5=5.4954\cdot {10}^5 [\mathrm{W}]$$

(67)

• Subinterval 2

At t = 2 [s], the value of the wind speed is:

$$V_2^{\ast }=8.13+{\displaystyle \frac{9.52-8.13}{6.631-3.433}}\cdot 2=8.9993 [\mathrm{W}]$$

(68)

Within the subinterval 2, the wind speed has a straight variation ranging between 8.5646 [m/s] and 8.9993 [m/s]:

$$V_{B-C-2}\left(t\right)=8.5646+(8.9993-8.5646)\cdot t=0.4347\cdot t+8.5646$$

(69)

MAS optim, ω_OPTIM, is:

$${\omega }_{OPTIM-2}=24.046\cdot \left(0.4347\cdot t+8.5646\right) [\mathrm{rad}/\mathrm{s}]$$

(70)

When comparing subinterval 2 to subinterval 1, there is a 1-s shift in the origin of time. This pattern continues to recur in each subsequent analyzed subinterval.

The energy and motion equations are expressed as follows:

$$\begin{array}{c}\begin{array}{l}511.92\cdot {\displaystyle \frac{d\omega }{dt}}\cdot \omega =650860\left({\displaystyle \frac{0.4347\cdot t+8.5646}{\omega }}-1.7488\cdot {10}^{-2}\right)\cdot e^{-41.495\cdot {\displaystyle \frac{0.4347\cdot t+8.5646}{\omega }}}\\ \cdot {\left(0.4347\cdot t+8.5646\right)}^3-5.4954\cdot {10}^5\end{array}\\ \begin{array}{l}{\displaystyle \frac{dE}{dt}}=650860\left({\displaystyle \frac{0.4346\cdot t+8.5646}{\omega }}-1.7488\cdot {10}^{-2}\right)\cdot e^{-41.495\cdot {\displaystyle \frac{0.4346\cdot t+8.5646}{\omega }}}\\ \cdot {\left(0.4346\cdot t+8.5646\right)}^3\end{array}\\ \omega \left(0\right)=196.71\\ E\left(0\right)=0\end{array}$$

(71)

The wind energy harnessed within a single second is valued at:

$$E_{WIND}\left(1\right)=E\left(1\right)=1.8883\cdot {10}^6 [\mathrm{J}]$$

(72)

When operating in MPP, the captured wind energy is:

$$E_{WIND-MAX}\left(1\right)={\displaystyle \underset{0}{\overset{1}{\int }}{P}_{WT-MAX}\cdot dt={\displaystyle \underset{0}{\overset{1}{\int }}\left[2792.8\cdot {\left(0.4346\cdot t+8.5646\right)}^3\right]}}\cdot dt=1.8927\cdot {10}^6 [\mathrm{J}]$$

(73)

The supplied electrical energy is:

$$E_{ELECTRICAL}\left(1\right)={\displaystyle \underset{0}{\overset{1}{\int }}{P}_{EG}\cdot dt=}5.4954\cdot {10}^5 [\mathrm{J}]$$

(74)

At t* = 1 [s], the mechanical angular speed ω is measured at ω(1) = 209.58 [rad/s]. In contrast, the optimal mechanical angular speed is calculated as ω_OPTIM-2 = 24.046⋅8.9993 = 216.4 [rad/s], as illustrated in Figure 6.

Once that ω_OPTIM-2 is greater than ω(1), the turbine did not achieve its maximum power point at t* = 1 [s]. Given that P*_INERTIAL > 0, the inertial power is positive,

$$P_{INERTIAL-1}^{\ast }=J{\displaystyle \frac{{\left({\omega }_{OPTIM}^{\ast }\right)}^2-{\left({\omega }^{\ast }\right)}^2}{2\cdot \Delta t}}=511.92{\displaystyle \frac{{\left(216.4\right)}^2-{\left(209.58\right)}^2}{2}}=7.4361\cdot {10}^5 [\mathrm{W}]$$

(75)

the loading of EG should diminish within subinterval 3, reaching the following:

$$P_{EG-3}^{\ast \ast }=P_{EG}^{\ast }-J\cdot {\displaystyle \frac{{\left({\omega }_{OPTIM}^{\ast }\right)}^2-{\left({\omega }^{\ast }\right)}^2}{2\cdot \Delta t}}=5.4954\cdot {10}^5-7.4361\cdot {10}^5=-1.9407\cdot {10}^5<0$$

(76)

The negative value of power at EG necessitates a transition to motor mode.

For the mechanical angular speed, ω, to attain its optimum, ω_OPTIM, within subinterval 3, it is essential for EG to be operated in motor mode, a condition that is challenging to achieve in practice.

• Subinterval 3

The EG power is less than zero within the interval 3, leading to its discharge, thus P**_EG-3 = 0. For t = 3 [s], the wind is:

$$V_3^{\ast }=8.13+{\displaystyle \frac{9.52-8.13}{6.631-3.433}}\cdot 3=9.4339 [\mathrm{W}]$$

(77)

Within the interval of 3, the wind velocity decreases linear, starting with 8.9993 [m/s] until 8.4339 [m/s].

$$V_{B-C-3}\left(t\right)=8.9993+(9.4339-8.9993)\cdot t=0.4346\cdot t+8.9993$$

(78)

ω_OPTIM, is:

$${\omega }_{OPTIM-3}=24.046\cdot \left(0.4346\cdot t+8.9993\right) [\mathrm{rad}/\mathrm{s}]$$

(79)

Consequently, the governing differential equations system related to energy and motion is expressed as follows:

$$\left\{\begin{array}{c}\begin{array}{l}511.92\cdot {\displaystyle \frac{d\omega }{dt}}\cdot \omega =650860\left({\displaystyle \frac{0.4346\cdot t+8.9993}{\omega }}-1.7488\cdot {10}^{-2}\right)\cdot e^{-41.495\cdot {\displaystyle \frac{0.4346\cdot t+8.9993}{\omega }}}\cdot \\ {\left(0.4346\cdot t+8.9993\right)}^3\end{array}\\ \begin{array}{l}{\displaystyle \frac{dE}{dt}}=650860\left({\displaystyle \frac{0.4346\cdot t+8.9993}{\omega }}-1.7488\cdot {10}^{-2}\right)\cdot e^{-41.495\cdot {\displaystyle \frac{0.4346\cdot t+8.9993}{\omega }}}\cdot \\ {\left(0.4346\cdot t+8.9993\right)}^3\end{array}\\ \omega \left(0\right)=209.58\\ E\left(0\right)=0\end{array}\right.$$

(80)

The value of wind energy captured in one second is:

$$E_{WIND}\left(1\right)=E\left(1\right)=2.1869\cdot {10}^6 [\mathrm{J}]$$

(81)

In the context of MPP operation, the value of the captured wind energy during the same period is:

$$E_{WIND-MAX}\left(1\right)={\displaystyle \underset{0}{\overset{1}{\int }}{P}_{WT-MAX}\cdot dt={\displaystyle \underset{0}{\overset{1}{\int }}\left[2792.8\cdot {\left(0.4346\cdot t+8.9993\right)}^3\right]}}\cdot dt=2.1877\cdot {10}^6 [\mathrm{J}]$$

(82)

The amount of electricity debited is zero:

$$E_{ELECTRICAL}\left(1\right)=0$$

(83)

At t* = 1 [s], ω, the MAS, is ω(1) = 229.06 [rad/s], which exceeds the optimal MAS:

$${\omega }_{OPTIM-3}=24.046\cdot 9.4339=226.85 [\mathrm{rad}/\mathrm{s}]$$

(84)

At t₃, as illustrated in Figure 7, the mechanical angular velocity ω attained its optimal value.

Thus, the accuracy of the proposed control algorithm has been confirmed. At this moment, the WT is operating at its MPP with the optimal MAS.

The value of harnessed wind energy is reflected in the electrical energy supplied to the power grid as well as in the kinetic energy associated with the masses in rotation. The kinetic energies of the subintervals—three in number, are:

$$\Delta E_{KINETIC-1}=J\cdot {\displaystyle \frac{{\left(\omega \left(1\right)\right)}^2-{\left(\omega \left(0\right)\right)}^2}{2}}=511.92\cdot {\displaystyle \frac{{\left(196.71\right)}^2-{\left(195.49\right)}^2}{2}}=1.2247\cdot {10}^5 [\mathrm{J}]$$

(85)

$$\Delta E_{KINETIC-2}=J\cdot {\displaystyle \frac{{\left(\omega \left(1\right)\right)}^2-{\left(\omega \left(0\right)\right)}^2}{2}}=511.92\cdot {\displaystyle \frac{{\left(209.58\right)}^2-{\left(196.71\right)}^2}{2}}=1.3384\cdot {10}^6 [\mathrm{J}]$$

(86)

$$\Delta E_{KINETIC-3}=J\cdot {\displaystyle \frac{{\left(\omega \left(1\right)\right)}^2-{\left(\omega \left(0\right)\right)}^2}{2}}=511.92\cdot {\displaystyle \frac{{\left(229.58\right)}^2-{\left(209.58\right)}^2}{2}}=2.1871\cdot {10}^6 [\mathrm{J}]$$

(87)

In conclusion, the energies across the three subintervals are displayed in Table 2, while the evolutions are illustrated in Figure 8.

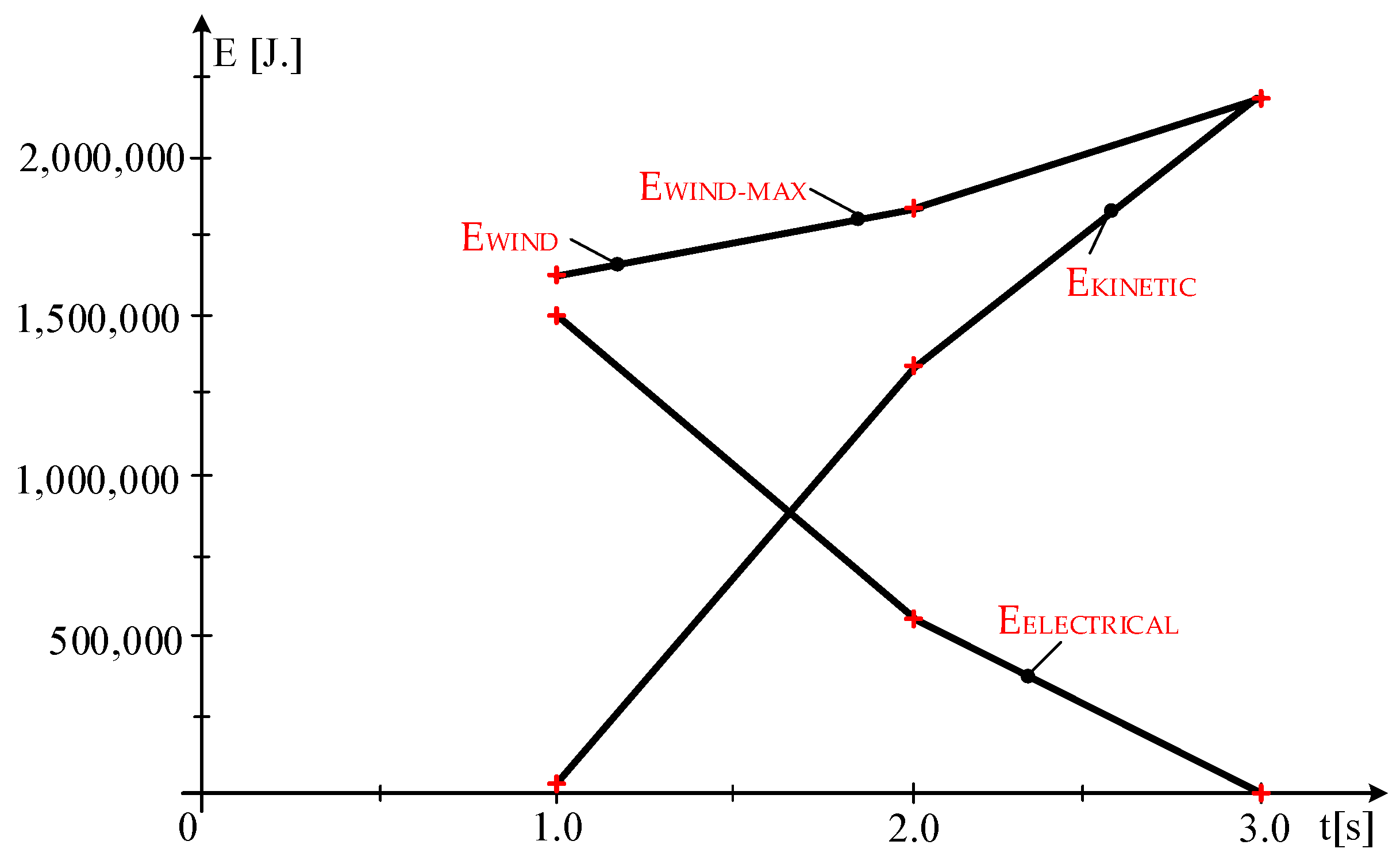
3.2.4. Energy Balance

The energy balance confirms that E_WIND, the wind energy captured, is present in the generated electrical energy, E_ELECTRICAL, and in the kinetic energy associated with rotating masses, ΔE_KINETIC.

The energy balance within subinterval 1, E_WIND = 1.6236·10⁶ [J], lie in:

$$E_{ELECTRICAL}+\Delta E_{KINETIC}=1.5008\cdot {10}^6+1.2247\cdot {10}^5=1.6233\cdot {10}^6 [\mathrm{J}]$$

(88)

The energy balance within subinterval 2, E_WIND = 1.8883·10⁶ [J] lie in:

$$E_{ELECTRICAL}+\Delta E_{KINETIC}=5.4954\cdot {10}^5+1.3384\cdot {10}^6=1.8879\cdot {10}^6 [\mathrm{J}]$$

(89)

The energy balance within subinterval 3, E_WIND = 2.1869·10⁶ [J] lie in:

$$E_{ELECTRICAL}+\Delta E_{KINETIC}=0+2.1871\cdot {10}^6=2.1871\cdot {10}^6 [\mathrm{J}]$$

(90)

At time t₃, maximum wind energy is collected, also while the energy generator is discharging (P**_EG-3 = 0). The turbine functions in MPP at the optimal MAS, energy that is not flowed into the system, (P**_EG-3 is zero), but can be located in the kinetic energy of the rotating masses. It appears that the turbine is not operating within the optimal energy efficiency range. There is a power gap at this point in time, it poses a disadvantage to the energy system stability.

From the variations in energies values (Figure 8), follows that:

• The values of the produced electrical energies, E_ELECTRICAL, decrease (the power to the generator diminishes).
• The variations of the kinetic energies, ΔE_KINETIC, increase and compensate for the reduction of grid-injected electrical energies.
• The harnessed wind energy increases in direct proportion to the increase in wind speed.

In conclusion, during periods where the wind speed grows, power gaps can occur if dV/dt, the wind speed derivative, and J, the equivalent inertia moment, surpass specific thresholds.

3.2.5. Periods Characterized by Diminished Wind Speed

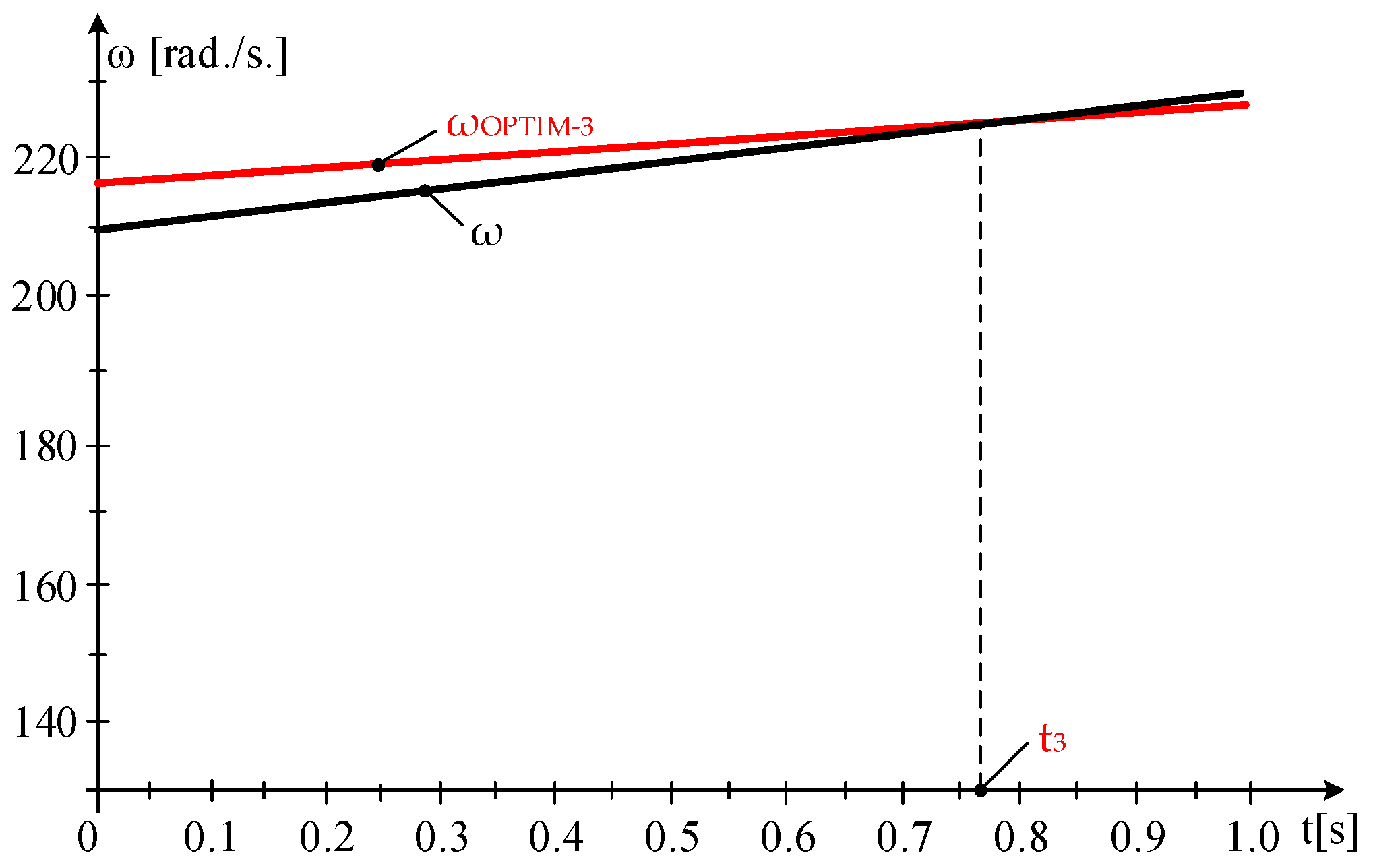
• Case Study 3—MPP Region Characterized by Diminishing Wind Velocity

In Figure 9, we select the time interval D-E. during which the wind speed diminishes. The corresponding time intervals and the related speeds are detailed in

Table 3. Wind speed at points A, D and E.

Point	Time [s]	V [m/s]
	1.198	10.47
D	39.858	9.52
E	43.073	7.142

.

At point D, Figure 9, WT is assumed to operate in MPP at the equality of the values of the optimal MAS, ω_OPTIM and the real angular velocities, ω:

$${\omega }_{OPTIM-D}={\omega }_D=24.046\cdot 9.52=228.92 [\mathrm{rad}/\mathrm{s}]$$

(91)

The velocity of the wind being VD = 9.52 [m/s], the EG load is at the P_EG-D power of value:

$$P_{EG-D}=P_{WT-MAX}^{\ast }=k_P\cdot V^3=2792.8\cdot {9.52}^3=2.4096\cdot {10}^6 [\mathrm{W}]$$

(92)

Taking into consideration the linear variation in wind speed over the D-E interval, it follows:

$$V_{D-E}\left(t\right)=9.52+{\displaystyle \frac{7.145-9.52}{43.073-39.858}}\cdot t=9.52-0.73872\cdot t$$

(93)

The interval D-E is divided into three subintervals.

• Subinterval 1:

Given that the sampling period is 1 s, at t* = 1 s, the calculated wind is:

$$V_1^{\ast }=9.52+{\displaystyle \frac{7.145-9.52}{43.073-39.858}}\cdot 1=8.7813 [\mathrm{m}/\mathrm{s}]$$

(94)

The wind speed exhibits a linear decrease ranging between 9.52 [m/s] and 8.7813 [m/s]:

$$V_{D-E-1}\left(t\right)=9.52+\left(8.7813-9.52\right)\cdot t=9.52-0.7387\cdot t$$

(95)

The optimal mechanical angular speed, ω_OPTIM, is:

$${\omega }_{OPTIM-1}=24.046\cdot \left(9.52-0.7387\right)\cdot t [\mathrm{rad}/\mathrm{s}]$$

(96)

Thus, the energy and motion equations are derived in the following:

$$\left\{\begin{array}{c}\begin{array}{l}511.92\cdot {\displaystyle \frac{d\omega }{dt}}\cdot \omega =650860\left({\displaystyle \frac{9.52-0.7387\cdot t}{\omega }}-1.7488\cdot {10}^{-2}\right)\cdot e^{-41.495\cdot {\displaystyle \frac{9.52-0.7387\cdot t}{\omega }}}\\ \cdot {\left(9.52-0.7387\cdot t\right)}^3-2.4096\cdot {10}^6\end{array}\\ \begin{array}{l}{\displaystyle \frac{dE}{dt}}=650860\cdot \left({\displaystyle \frac{9.52-0.7387\cdot t}{\omega }}-1.7488\cdot {10}^{-2}\right)\cdot e^{-41.495\cdot {\displaystyle \frac{9.52-0.7387\cdot t}{\omega }}}\\ \cdot {\left(9.52-0.7387\cdot t\right)}^3\end{array}\\ \omega \left(0\right)=228.92\\ E\left(0\right)=0\end{array}\right.$$

(97)

The amount of wind energy harnessed in a single second is E_WIND(1) = 2.1382·106 [J]. At maximum power operation, the harnessed wind energy within the same time frame is valued at:

$$E_{WIND-MAX}\left(1\right)={\displaystyle \underset{0}{\overset{1}{\int }}{P}_{WT-MAX}\cdot dt={\displaystyle \underset{0}{\overset{1}{\int }}\left[2792.8\cdot {\left(9.50+0.7387\cdot t\right)}^3\right]}}\cdot dt=2.1434\cdot {10}^6 [\mathrm{J}]$$

(98)

During the same time frame, the debited electricity is:

$$E_{ELECTRICAL}\left(1\right)={\displaystyle \underset{0}{\overset{1}{\int }}{P}_{EG}\cdot dt=}2.4096\cdot {10}^6 [\mathrm{J}]$$

(99)

At t* = 1 [s], as highlighted in Figure 10, ω, the MAS is ω(1) = 226.59 [rad/s] compared with the optimal MAS:

$${\omega }_{OPTIM-1}=24.046\cdot 8.7813=211.16 [\mathrm{rad}/\mathrm{s}]$$

(100)

Since ω_OPTIM-1 is less than ω(1), the value of the inertial power is negative, indicating that P*_INERTIAL is less than 0:

$$P_{INERTIAL-1}^{\ast }=J{\displaystyle \frac{{\left({\omega }_{OPTIM}^{\ast }\right)}^2-{\left({\omega }^{\ast }\right)}^2}{2\cdot \Delta t}}=511.92{\displaystyle \frac{{\left(211.16\right)}^2-{\left(226.59\right)}^2}{2}}=-1.7289\cdot {10}^6 [\mathrm{W}]$$

(101)

The loading of the EG increases within subinterval 2, at the power of:

$$P_{EG-2}^{\ast \ast }=P_{EG}^{\ast }-J\cdot {\displaystyle \frac{{\left({\omega }_{OPTIM}^{\ast }\right)}^2-{\left({\omega }^{\ast }\right)}^2}{2\cdot \Delta t}}=2.4096\cdot {10}^6+1.7289\cdot {10}^6=4.1385\cdot {10}^6$$

(102)

• Subinterval 2

At t = 2 [s], the wind speed is:

$$V_2^{\ast }=9.52+\left(8.7813-9.52\right)\cdot 2=8.0426 [\mathrm{m}/\mathrm{s}]$$

(103)

exhibiting a linear change, ranging between 8.7813 [m/s] and 8.0426 [m/s].

$$V_{D-E-2}\left(t\right)=8.7813+\left(8.0426-8.7813\right)\cdot t=8.7813-0.7387\cdot t$$

(104)

The optimal MAS, ω_OPTIM, is:

$${\omega }_{OPTIM-1}=24.046\cdot \left(8.7813-0.7387\cdot t\right) [\mathrm{rad}/\mathrm{s}]$$

(105)

The energy and motion equations result in:

$$\left\{\begin{array}{c}\begin{array}{l}511.92\cdot {\displaystyle \frac{d\omega }{dt}}\cdot \omega =650860\left({\displaystyle \frac{8.7813-1.7387\cdot t}{\omega }}-1.7488\cdot {10}^{-2}\right)\cdot e^{-41.495\cdot {\displaystyle \frac{8.7813-0.7387\cdot t}{\omega }}}\\ \cdot {\left(8.7813-0.7387\cdot t\right)}^3-4.1385\cdot {10}^6\end{array}\\ \begin{array}{l}{\displaystyle \frac{dE}{dt}}=650860\cdot \left({\displaystyle \frac{8.7813-0.7387\cdot t}{\omega }}-1.7488\cdot {10}^{-2}\right)\cdot e^{-41.495\cdot {\displaystyle \frac{8.7813-0.7387\cdot t}{\omega }}}\\ \cdot {\left(8.7813-0.7387\cdot t\right)}^3\end{array}\\ \omega \left(0\right)=226.59\\ E\left(0\right)=0\end{array}\right.$$

(106)

In a single second, the harnessed energy from the wind is valued at:

$$E_{WIND}\left(1\right)=E\left(1\right)=1.6549\cdot {10}^6 [\mathrm{J}]$$

(107)

At operation at the MPP, the captured wind energy during the same period, is:

$$E_{WIND-MAX}\left(1\right)={\displaystyle \underset{0}{\overset{1}{\int }}{P}_{WT-MAX}\cdot dt={\displaystyle \underset{0}{\overset{1}{\int }}\left[2792.8\cdot {\left(8.7813-0.7387\cdot t\right)}^3\right]}}\cdot dt=1.6656\cdot {10}^6 [\mathrm{J}]$$

(108)

For the same period, the generated electrical energy is:

$$E_{ELECTRICAL}\left(1\right)={\displaystyle \underset{0}{\overset{1}{\int }}{P}_{EG}\cdot dt=}4.1385\cdot {10}^6 [\mathrm{J}]$$

(109)

At t* = 1 [s], ω, the MAS is ω(1) = 204.06 [rad/s], compared to the optimal MAS:

$${\omega }_{OPTIM-2}=24.046\cdot 8.0426=193.39 [\mathrm{rad}/\mathrm{s}]$$

(110)

Since ω_OPTIM-1 is less than ω(1), the inertial power is negative, indicating that P*_INERTIAL < 0:

$$P_{INERTIAL-1}^{\ast }=J{\displaystyle \frac{{\left({\omega }_{OPTIM}^{\ast }\right)}^2-{\left({\omega }^{\ast }\right)}^2}{2\cdot \Delta t}}=511.92{\displaystyle \frac{{\left(193.39\right)}^2-{\left(204.06\right)}^2}{2}}=-1.0855\cdot {10}^6 [\mathrm{W}]$$

(111)

on subinterval 3, the load on EG is increased to the power of:

$$P_{EG-2}^{\ast \ast }=P_{EG}^{\ast }-J\cdot {\displaystyle \frac{{\left({\omega }_{OPTIM}^{\ast }\right)}^2-{\left({\omega }^{\ast }\right)}^2}{2\cdot \Delta t}}=4.1385\cdot {10}^6+1.0855\cdot {10}^6=5.224\cdot {10}^6 [\mathrm{W}]$$

(112)

• Subinterval 3

The wind speed is at t = 3 [s]:

$$V_3^{\ast }=9.52+\left(8.7813-9.52\right)\cdot 3=7.3039 [\mathrm{m}/\mathrm{s}]$$

(113)

Wind speed decreases from 8.0426 [m/s] to 7.3039 [m/s]:

$$V_{D-E-3}\left(t\right)=8.0426+\left(7.3039-8.0426\right)\cdot t=8.0426-0.7387\cdot t$$

(114)

ω_OPTIM, the optimal MAS, is:

$${\omega }_{OPTIM-3}=24.046\cdot \left(8.0426-0.7387\cdot t\right) [\mathrm{rad}/\mathrm{s}]$$

(115)

For the values provided, the energy and motion equations become:

$$\left\{\begin{array}{c}\begin{array}{l}511.92\cdot {\displaystyle \frac{d\omega }{dt}}\cdot \omega =650860\left({\displaystyle \frac{8.0426-0.7387\cdot t}{\omega }}-1.7488\cdot {10}^{-2}\right)\cdot e^{-41.495\cdot {\displaystyle \frac{8.0426-0.7387\cdot t}{\omega }}}\\ \cdot {\left(8.0426-0.7387\cdot t\right)}^3-5.224\cdot {10}^6\end{array}\\ \begin{array}{l}{\displaystyle \frac{dE}{dt}}=650860\cdot \left({\displaystyle \frac{8.0426-0.7387\cdot t}{\omega }}-1.7488\cdot {10}^{-2}\right)\cdot e^{-41.495\cdot {\displaystyle \frac{8.0426-0.7387\cdot t}{\omega }}}\\ \cdot {\left(8.0426-0.7387\cdot t\right)}^3\end{array}\\ \omega \left(0\right)=204.06\\ E\left(0\right)=0\end{array}\right.$$

(116)

In a duration of one second, the wind energy captured is E_WIND(1) = E(1) = 1.2619·10⁶ [J]. At maximum power point operation, the harnessed wind energy within the same period is:

$$E_{WIND-MAX}\left(1\right)={\displaystyle \underset{0}{\overset{1}{\int }}{P}_{WT-MAX}\cdot dt={\displaystyle \underset{0}{\overset{1}{\int }}\left[2792.8\cdot {\left(8.0426-0.7387\cdot t\right)}^3\right]}}\cdot dt=1.2647\cdot {10}^6 [\mathrm{J}]$$

(117)

The delivered electricity for the same period is:

$$E_{ELECTRICAL}\left(1\right)={\displaystyle \underset{0}{\overset{1}{\int }}{P}_{EG}\cdot dt=}5.224\cdot {10}^6 [\mathrm{J}]$$

(118)

At t* = 1 [s], ω, the MAS is measured as ω(1) = 161.74 [rad/s], compared to the optimal MAS:

$${\omega }_{OPTIM-3}=24.046\cdot 7.3039=175.63 [\mathrm{rad}/\mathrm{s}]$$

(119)

At time t₃, as Figure 11 highlights, the optimal MAS, ω_OPTIM-3, is equivalent to ω, the MAS, indicating that the MPP was attained. Consequently, the control algorithm has been validated.

Since ω_OPTIM-3 > ω(1), the value of the inertial power is positive, P*_INERTIAL > 0:

$$P_{INERTIAL-1}^{\ast }=J{\displaystyle \frac{{\left({\omega }_{OPTIM}^{\ast }\right)}^2-{\left({\omega }^{\ast }\right)}^2}{2\cdot \Delta t}}=511.92{\displaystyle \frac{{\left(175.63\right)}^2-{\left(161.74\right)}^2}{2}}=-1.1994\cdot {10}^6 [\mathrm{W}]$$

(120)

In the given context, during the subsequent time interval, the EG charge should decrease to the power:

$$P_{EG-2}^{\ast \ast }=P_{EG}^{\ast }-J\cdot {\displaystyle \frac{{\left({\omega }_{OPTIM}^{\ast }\right)}^2-{\left({\omega }^{\ast }\right)}^2}{2\cdot \Delta t}}=5.224\cdot {10}^6-1.1994\cdot {10}^6=4.0246\cdot {10}^6 [\mathrm{W}]$$

(121)

The harnessed wind energy is reflected in the electricity provided to the grid as well as in the kinetic energy associated with the rotating components. The fluctuations in kinetic energy across the three subintervals are as follows:

$$\Delta E_{KINETIC-1}=J\cdot {\displaystyle \frac{{\left(\omega \left(1\right)\right)}^2-{\left(\omega \left(0\right)\right)}^2}{2}}=511.92\cdot {\displaystyle \frac{{\left(226.59\right)}^2-{\left(228.92\right)}^2}{2}}=-2.7166\cdot {10}^5 [\mathrm{J}]$$

(122)

$$\Delta E_{KINETIC-2}=J\cdot {\displaystyle \frac{{\left(\omega \left(1\right)\right)}^2-{\left(\omega \left(0\right)\right)}^2}{2}}=511.92\cdot {\displaystyle \frac{{\left(204.06\right)}^2-{\left(226.59\right)}^2}{2}}=-2.4835\cdot {10}^6 [\mathrm{J}]$$

(123)

$$\Delta E_{KINETIC-3}=J\cdot {\displaystyle \frac{{\left(\omega \left(1\right)\right)}^2-{\left(\omega \left(0\right)\right)}^2}{2}}=511.92\cdot {\displaystyle \frac{{\left(161.74\right)}^2-\left(204.58\right){06}^2}{2}}=-3.9624\cdot {10}^6 [\mathrm{J}]$$

(124)

In conclusion, the values of the energy for the three subintervals are synthesized in

Table 4. Energies in the subintervals analyzed.

Subinterval	EWIND [J]	EWIND-MAX [J]	EELETRICAL [J]	EKINETIC [J]
1	2.1382·106	2.1434·106	2.4096·106	−2.7166·105
2	1.6549·106	1.6656·106	4.1385·106	−2.4835·106
3	1.2619·106	1.2647·106	5.224·106	−3.9624·106

.

Over a 3 s interval, where the wind speed decreases, 7.145 [m/s] < V(t) < 9.52 [m/s], Figure 12 represents the energy evolutions.

In this scenario, the energy balance is E_WIND = E_ELECTRICAL + ΔE_KINETIC. Across the three subintervals, it follows that: ω*_OPTIM = k·V*.

• Subinterval 1:

$$2.1382\cdot {10}^6=2.4096\cdot {10}^6-2.7166\cdot {10}^5=2.1379\cdot {10}^6 [\mathrm{J}]$$

(125)

• Subinterval 2:

$$1.6549\cdot {10}^6=4.1385\cdot {10}^6-2.4835\cdot {10}^6=1.655\cdot {10}^6 [\mathrm{J}]$$

(126)

• Subinterval 3:

$$1.2619\cdot {10}^6=5.224\cdot {10}^6-3.9624\cdot {10}^6=1.2616\cdot {10}^6 [\mathrm{J}]$$

(127)

On the periods during which the wind velocity diminishes, power gaps are absent, although the MAS velocity ω leans towards the value of the optimal MAS, ω_OPTIM. The turbine functions within MPP at the optimal MAS. The output power in the grid (P_EG) exceeds the WT provided power, excepting the kinetic energy of the rotating masses. This situation presents a benefit for the purpose of maintaining stability within the energy system.

From the energy variations illustrated in Figure 12, it can be concluded that:

• The values of electrical energy output, E_ELECTRICAL, increase even as wind speed decreases.
• The absolute differences in the values of the ΔE_KINETIC kinetic energies, grow and counterbalance the decline in the values of the captured wind energies.
• The values of the harnessed wind energies diminish in direct proportion to the reduction in wind speed.

In conclusion, during the periods when the wind velocity decreases, there are no power gaps, regardless of the values of the wind speed derivative, dV/dt, and J, the inertia equivalent moment.

4. Discussion

As a result of the presented study, the following findings were obtained:

• MM-WT was deduced, with experimental data.
• The actual wind speed variation in the Dobrogea region was analyzed, and the motion equation was employed to visualize its operation within the optimal area.
• A method has been proposed to bring and maintain the turbine in its MPP.
• A control algorithm has been validated, which is based on the sign of the inertial power value, derived from experimental data including wind speed and mechanical angular speed.
• The time intervals in which power gaps occur have been analyzed.
• The periods during which wind speed diminishes were analyzed.

Based on the obtained results, the following key points can be emphasized:

• The system is brought to the turbines MPP in the shortest possible time by either disconnecting the generator from the grid or by switching the engine to motor mode.
• By calculating the disparity between optimal MAS and present MAS, one can prescribe the power output of the generator.
• When the wind speed increases, gaps of power occur, leading to the disconnection of the generator from the grid, particularly when it is necessary to operate within the optimal energy efficiency range.
• As wind speeds diminish over time, power gaps do not occur; however, it is essential to function at MPP. The electrical power output in the system is higher than the power output of the turbine, with the excess power generated from the varying kinetic energies of the rotating masses.

The proposed method establishes a framework for control that considers wind and the angular mechanical speed. Based on the determination of the variations in kinetic energy of rotating masses, values acquired through measurements, the system is optimized to reach its MPP.

The proposed approach addresses genuine needs for wind farms located in areas where wind speed fluctuates significantly over time.

The practical advantages of the proposed approach enable the extraction of maxi-mum wind energy at considerably fluctuating wind velocities over time, where mechanical inertia and fluctuations in wind velocity play a crucial role.

5. Conclusions

This study examines the performance of a WT under fluctuating wind speeds over time and develops a control system based upon the fluctuations of kinetic energies of rotating masses, which are influenced by the wind speed values. In instances of significant changes in wind speed, the set value at the generator may become negative, leading to a power deficit within the electrical energy system.