Lattice Boltzmann Method Simulation of Bubble Dynamics for Enhanced Boiling Heat Transfer by Pulsed Electric Fields
Abstract
1. Introduction
2. Numerical Methods
2.1. Lattice Boltzmann Pseudopotential Model
2.2. Ideal Dielectric Model
2.3. Energy Equation Model
3. Computational Model and Validation
3.1. Computational Model
3.2. Model Validation
3.2.1. Validation of Young–Laplace Law
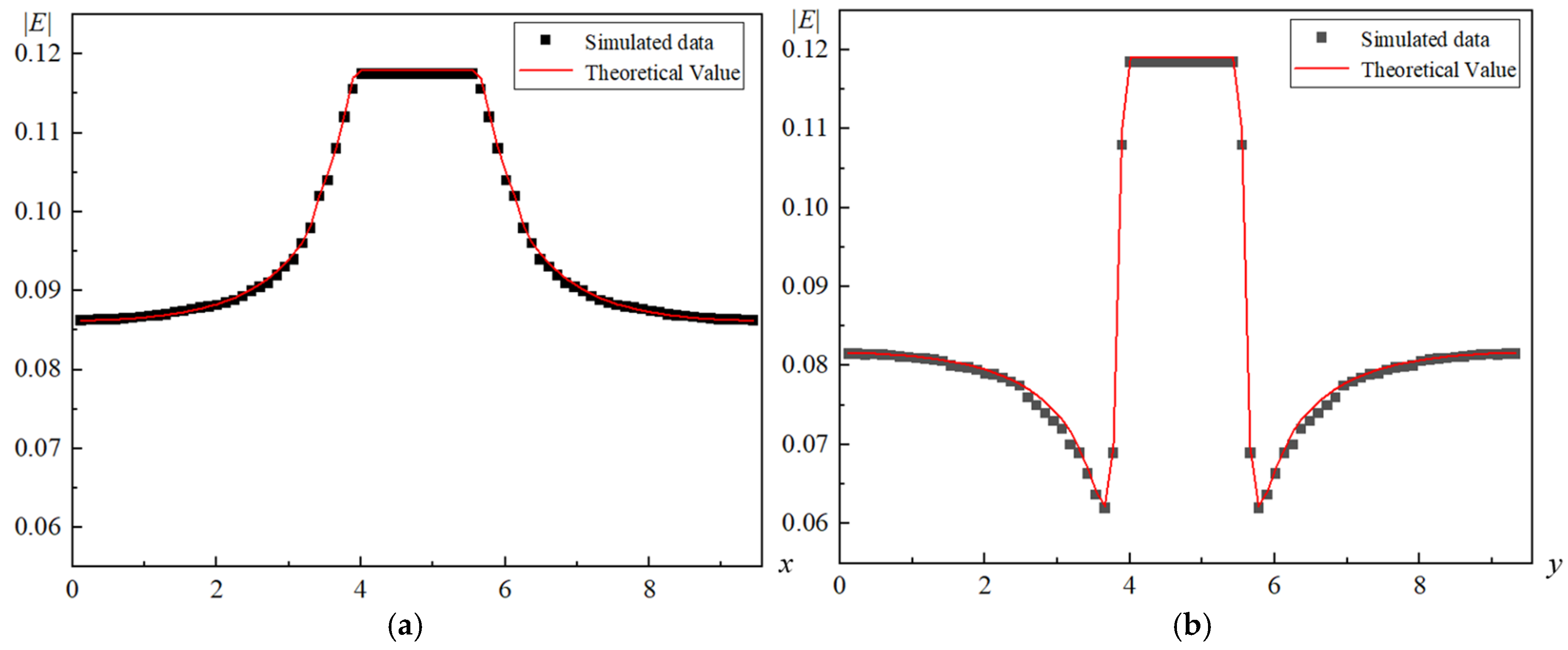
3.2.2. Validation of the Electric Field Model
4. Simulation Results and Discussion
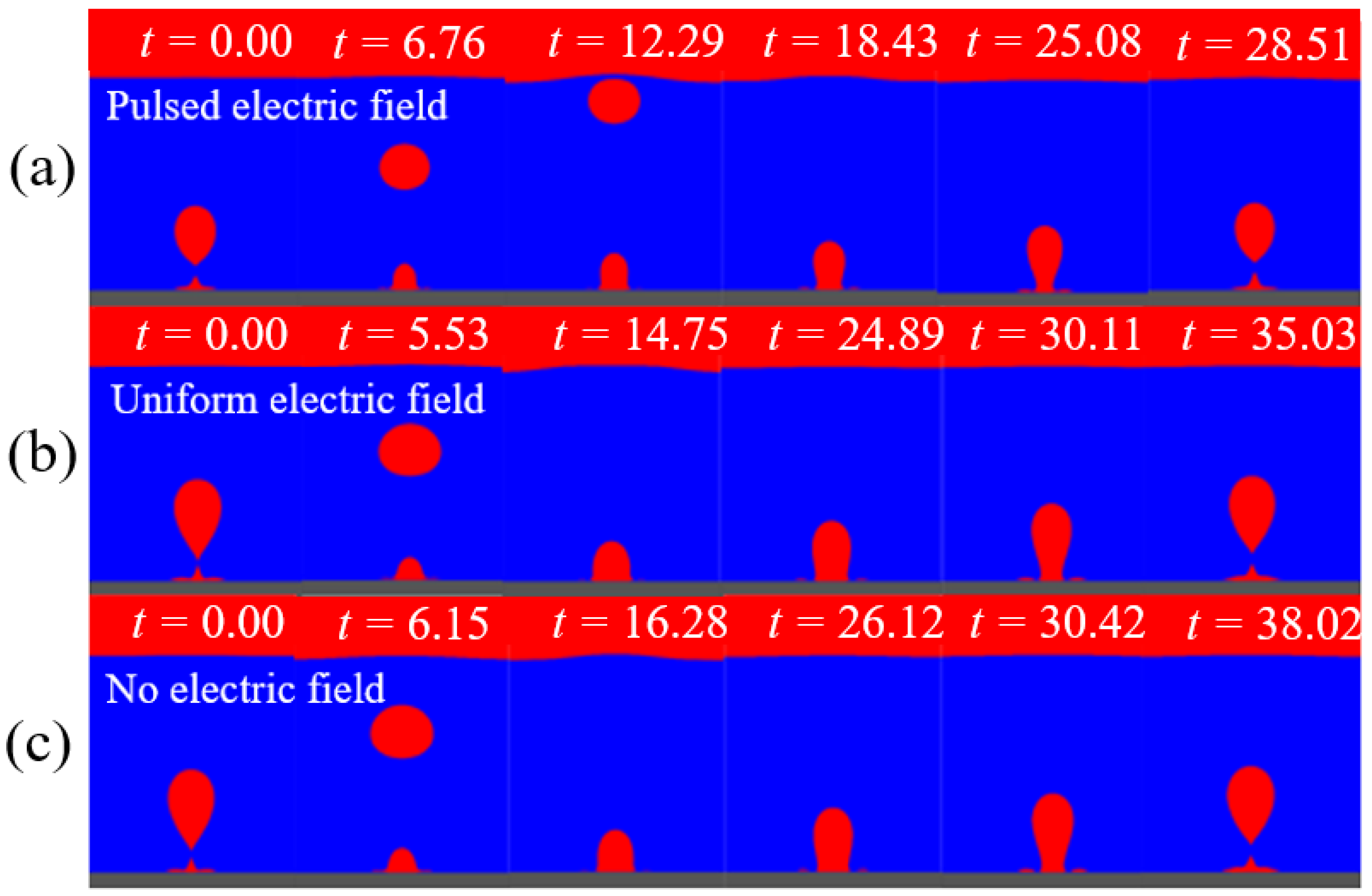
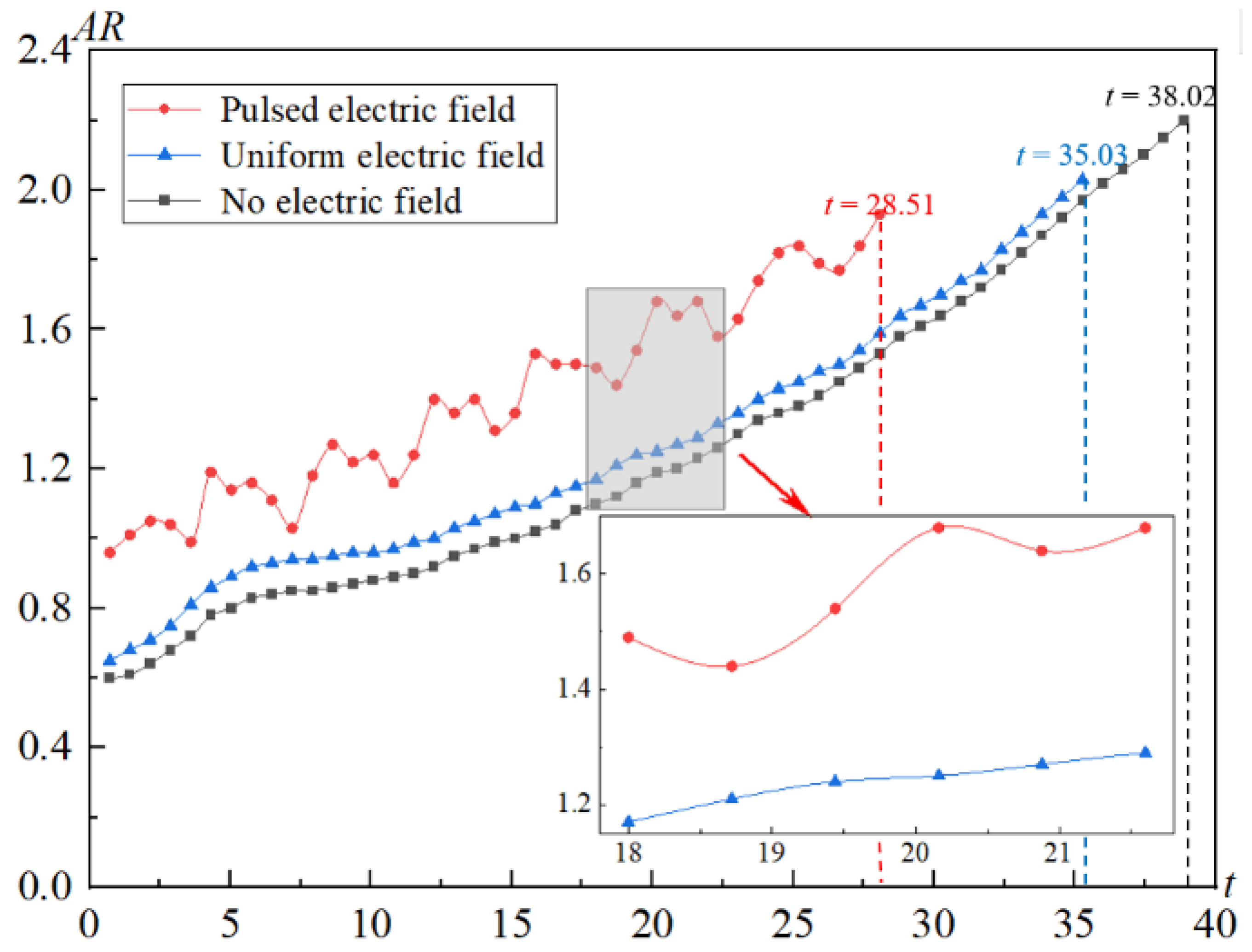
4.1. Influence of Different Types of Electric Field on Bubble Behavior
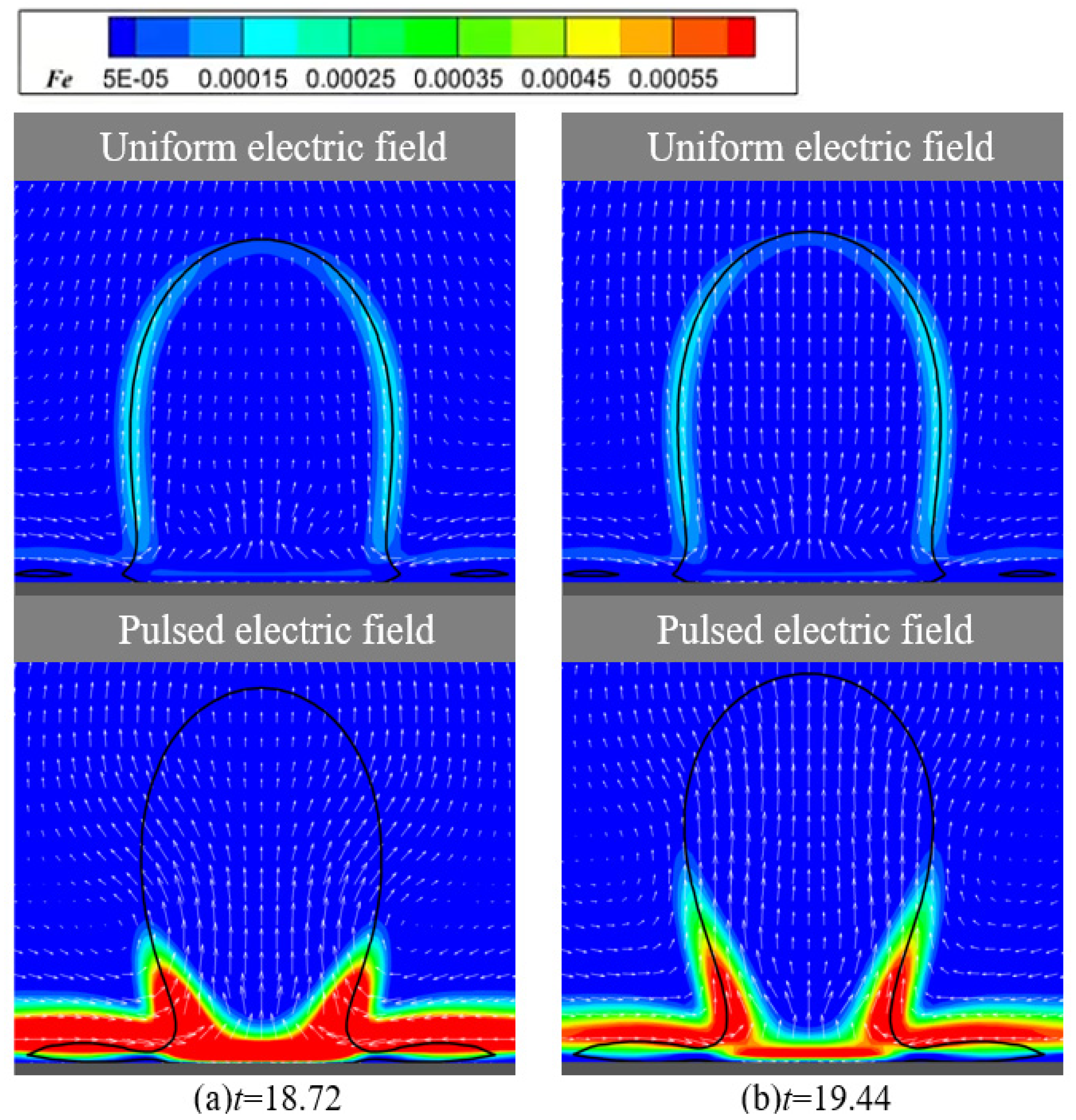
4.2. Influence of Electric Force on Bubble Behavior in Electric Field
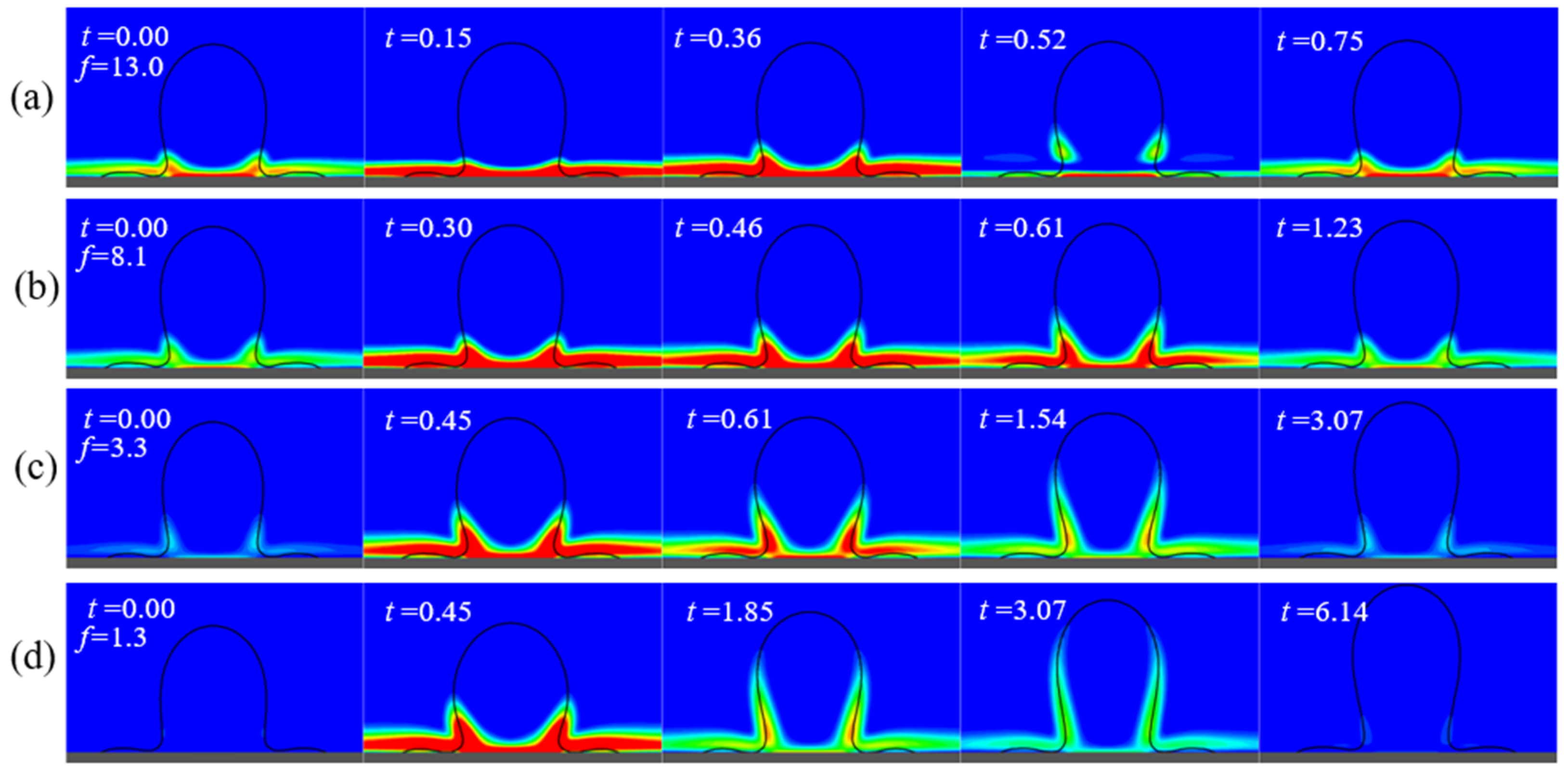
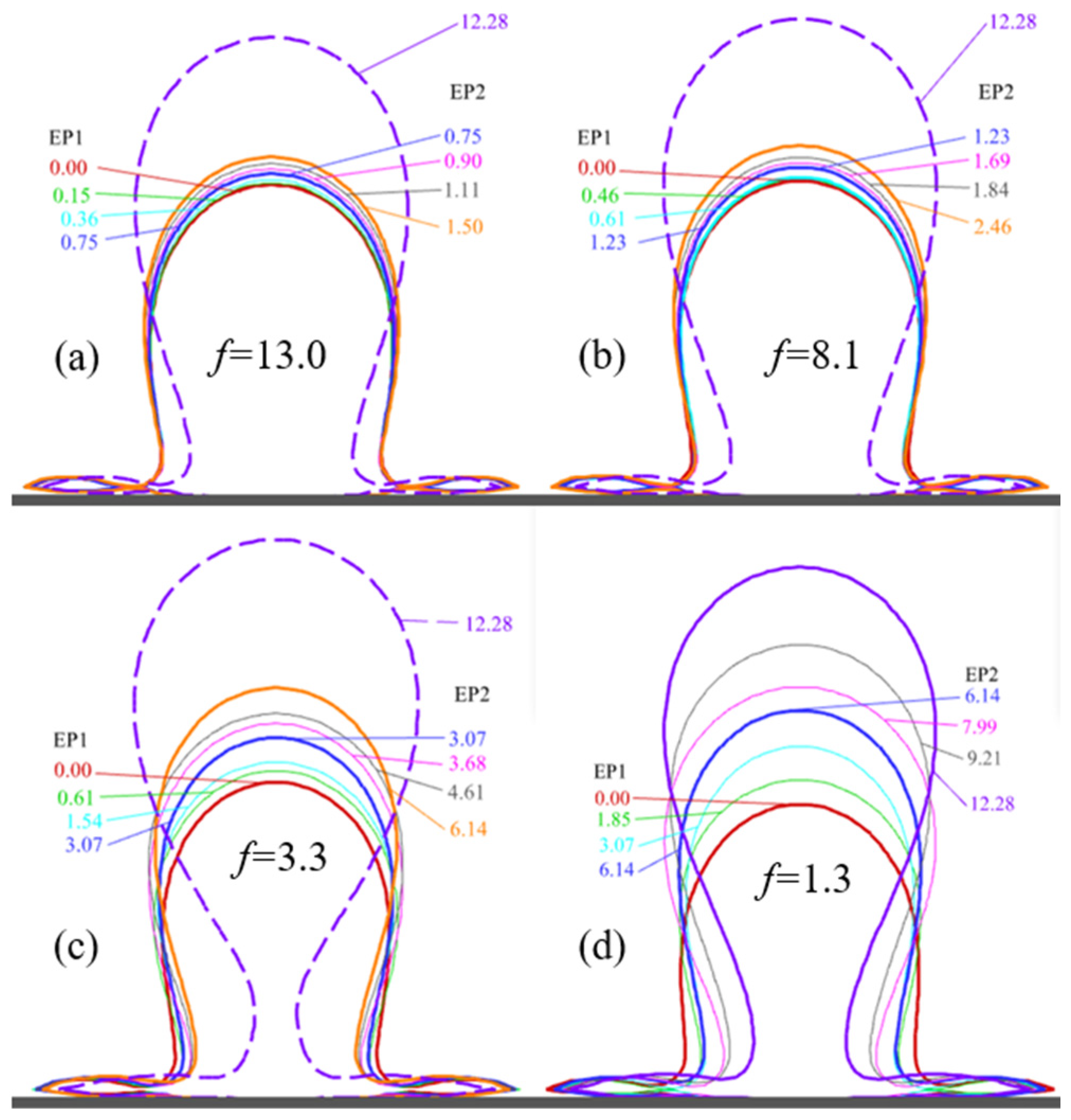
4.3. Effect of Electric Field Pulse Frequency on Bubble Behavior
5. Conclusions
- (1)
- Compared with uniform electric fields and the absence of an electric field, bubbles in pulsed electric field exhibit the most pronounced morphological changes, the fastest detachment speeds, and the highest local heat flux densities at the wall surface. The aspect ratio of bubbles in a pulsed electric field is also the largest and shows a trend of oscillating increase;
- (2)
- Pulsed electric fields generate abrupt changes in electric field force at the beginning and end of the peak segments of the pulse cycle. The phase boundary at the bubble base contracts subject to the electric field force, causing the internal gas to be compressed and accelerated upwards, resulting in an elongated bubble shape. In contrast, bubbles under a uniform electric field experience uniform and relatively small force changes, leading to slower internal gas flow speeds;
- (3)
- The detachment period and detachment diameter of bubbles first decrease and then increase as the pulse frequency increases. There exists an optimal frequency that minimizes the detachment period and detachment diameter of bubbles, resulting in the best wall heat transfer enhancement effect. The root of the bubble and the “V”-shaped region connected to the bottom of the bubble are effective areas for electric field-enhanced boiling heat transfer. The alternating action of electric field force in this region promotes early necking and detachment of the bubble, thereby enhancing boiling heat transfer.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Hong, S.; Jiang, S.; Hu, Y.; Dang, C.; Wang, S. Visualization investigation of the effects of nanocavity structure on pool boiling enhancement. Int. J. Heat Mass Transf. 2019, 136, 235–245. [Google Scholar] [CrossRef]
- Ma, X.; Cheng, P. Dry spot dynamics and wet area fractions in pool boiling on micro-pillar and micro-cavity hydrophilic heaters: A 3D lattice Boltzmann phase-change study. Int. J. Heat Mass Transf. 2019, 141, 407–418. [Google Scholar] [CrossRef]
- Baffigi, F.; Bartoli, C. Influence of the ultrasounds on the heat transfer in single phase free convection and in saturated pool boiling. Exp. Therm. Fluid Sci. 2012, 36, 12–21. [Google Scholar] [CrossRef]
- Tang, J.; Xie, G.; Bao, J.; Mo, Z.; Liu, H.; Du, M. Experimental study of sound emission in subcooled pool boiling on a small heating surface. Chem. Eng. Sci. 2018, 188, 179–191. [Google Scholar] [CrossRef]
- Luo, C.; Tagawa, T. Effect of heating wires with electric potential on pool-boiling heat transfer under an electric field. Appl. Therm. Eng. 2024, 240, 122327. [Google Scholar] [CrossRef]
- Feng, Y.; Li, H.; Guo, K.; Lei, X.; Zhao, J. Numerical study on saturated pool boiling heat transfer in presence of a uniform electric field using lattice Boltzmann method. Int. J. Heat Mass Transf. 2019, 135, 885–896. [Google Scholar] [CrossRef]
- Chen, Y.; Guo, J.; Liu, X.; He, D. Experiment and predicted model study of resuspended nanofluid pool boiling heat transfer under electric field. Int. Commun. Heat Mass Transf. 2022, 131, 105847. [Google Scholar] [CrossRef]
- Madadnia, J.; Koosha, H. Electrohydrodynamic effects on characteristic of isolated bubbles in the nucleate pool boiling regime. Exp. Therm. Fluid Sci. 2003, 27, 145–150. [Google Scholar] [CrossRef]
- Ahmad, S.; Karayiannis, T.; Kenning, D.; Luke, A. Compound effect of EHD and surface roughness in pool boiling and CHF with R-123. Appl. Therm. Eng. 2011, 31, 1994–2003. [Google Scholar] [CrossRef]
- Chang, H.; Liu, B.; Li, Q.; Yang, X.; Zhou, P. Effects of electric field on pool boiling heat transfer over composite microstructured surfaces with microcavities on micro-pin-fins. Int. J. Heat Mass Transf. 2023, 205, 123893. [Google Scholar] [CrossRef]
- Hristov, Y.; Zhao, D.; Kenning, D.B.R.; Sefiane, K.; Karayiannis, T.G. A study of nucleate boiling and critical heat flux with EHD enhancement. Heat Mass Transf. 2007, 45, 999–1017. [Google Scholar] [CrossRef]
- Chen, Y.; Guo, J.; Liu, X.; Li, J.; He, D. Experiment and prediction model study on pool boiling heat transfer of water in the electric field with periodically changing direction. Int. J. Multiph. Flow 2022, 150, 104027. [Google Scholar] [CrossRef]
- Li, X.; Chan, W.; Liang, S.; Chang, F.; Feng, Y.; Li, H. Numerical investigation on pool boiling heat transfer with trapezoidal/inverted trapezoidal micro-pillars using LBM. Int. J. Therm. Sci. 2024, 198, 108869. [Google Scholar] [CrossRef]
- Huang, Q.; Zhou, J.; Huai, X.; Zhou, F. Studying the effect of geometry of micro-cavity on pool boiling by LBM. J. Phys. Conf. Ser. 2023, 2441, 012016. [Google Scholar] [CrossRef]
- Shan, X.; Chen, H. Lattice Boltzmann model for simulating flows with multiple phases and components. Phys. Rev. E 1993, 47, 1815–1819. [Google Scholar] [CrossRef] [PubMed]
- Gong, S.; Cheng, P. Numerical investigation of droplet motion and coalescence by an improved lattice Boltzmann model for phase transitions and multiphase flows. Comput. Fluids 2012, 53, 93–104. [Google Scholar] [CrossRef]
- Cao, H.; An, Q.; Zuo, Q.; Liu, H.; Zhang, Z.; Zhao, X.; Wang, P. A New LB Model for Solid-liquid Conjugate Boiling Heat Transfer. J. Zhengzhou Univ. (Eng. Sci.) 2023, 44, 75–81. [Google Scholar]
- Zhang, S.; Lou, Q. A mesoscopic numerical method for enhanced pool boiling heat transfer on conical surfaces under action of electric field. J. Phys. 2024, 73, 226–238. [Google Scholar] [CrossRef]
- Li, W.; Li, Q.; Chang, H.; Yu, Y.; Tang, S. Electric field enhancement of pool boiling of dielectric fluids on pillar-structured surfaces: A lattice Boltzmann study. Phys. Fluids 2022, 34, 123327. [Google Scholar] [CrossRef]






| Symbol | Description | Value (Dimensionless) |
|---|---|---|
| Tc | Critical temperature | 0.0729 |
| Tl | Saturation temperature | 0.86 Tc |
| ρl | Liquid density | 7.098 |
| λl | Liquid thermal conductivity | 0.34182 |
| ρg | Saturated vapor density | 0.2156 |
| λg | Vapor thermal conductivity | 0.022788 |
| ρw | Solid density | 6 |
| λw | Solid thermal conductivity | 3.0 |
| cv | specific heat at constant volume | 5.0 |
| cpl | Liquid specific heat at constant pressure | 3.385 |
| cpv | Vapor specific heat at constant pressure | 1.034 |
| εl | Liquid dielectric constant | 0.2236 |
| εv | Vapor dielectric constant | 0.1 |
| ε0 | Vacuum dielectric constant | 1 |
| Th | Heat source temperature | 1.35 Tc |
| g | Gravitational acceleration | 3.0 × 10−5 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, X.; Guo, S.; Zhang, D.; Cao, H. Lattice Boltzmann Method Simulation of Bubble Dynamics for Enhanced Boiling Heat Transfer by Pulsed Electric Fields. Energies 2025, 18, 2540. https://doi.org/10.3390/en18102540
Zhao X, Guo S, Zhang D, Cao H. Lattice Boltzmann Method Simulation of Bubble Dynamics for Enhanced Boiling Heat Transfer by Pulsed Electric Fields. Energies. 2025; 18(10):2540. https://doi.org/10.3390/en18102540
Chicago/Turabian StyleZhao, Xiaoliang, Sai Guo, Dongwei Zhang, and Hailiang Cao. 2025. "Lattice Boltzmann Method Simulation of Bubble Dynamics for Enhanced Boiling Heat Transfer by Pulsed Electric Fields" Energies 18, no. 10: 2540. https://doi.org/10.3390/en18102540
APA StyleZhao, X., Guo, S., Zhang, D., & Cao, H. (2025). Lattice Boltzmann Method Simulation of Bubble Dynamics for Enhanced Boiling Heat Transfer by Pulsed Electric Fields. Energies, 18(10), 2540. https://doi.org/10.3390/en18102540





