Effects of Corrosion Depth on Wind-Induced Collapse Performance of an Angle Steel Transmission Tower
Abstract
1. Introduction
2. Corrosion Investigation of Transmission Towers
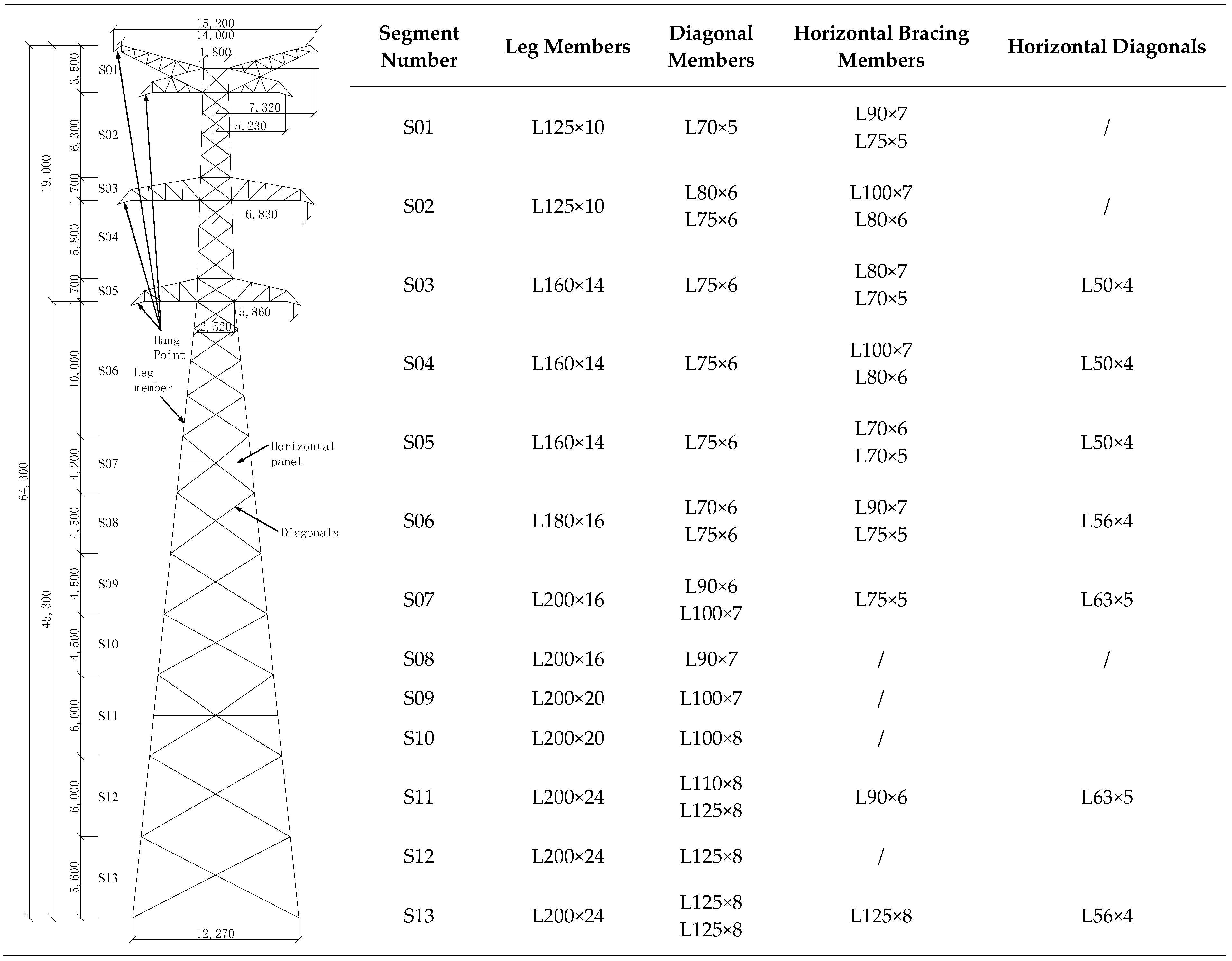
2.1. Investigation Tower Details
2.2. Investigation Procedures
 in Figure 1), were measured for their remaining thickness. Three measurement points were taken for each member: two at the ends and one in the center. The remaining thickness of each member was calculated as the average of the three measuring points. According to the analysis in Section 5.1, the depths of the members around the lower cross-arm can represent the average corrosion of the tower. Five typical members distributed around this segment of sixteen towers, numbered L01 to L16 (illustrated as
in Figure 1), were measured for their remaining thickness. Three measurement points were taken for each member: two at the ends and one in the center. The remaining thickness of each member was calculated as the average of the three measuring points. According to the analysis in Section 5.1, the depths of the members around the lower cross-arm can represent the average corrosion of the tower. Five typical members distributed around this segment of sixteen towers, numbered L01 to L16 (illustrated as  in Figure 1), were subsequently measured for their remaining thickness.
in Figure 1), were subsequently measured for their remaining thickness.3. Simulation of Progressive Collapse
3.1. FEM
3.2. Member Corrosion Model
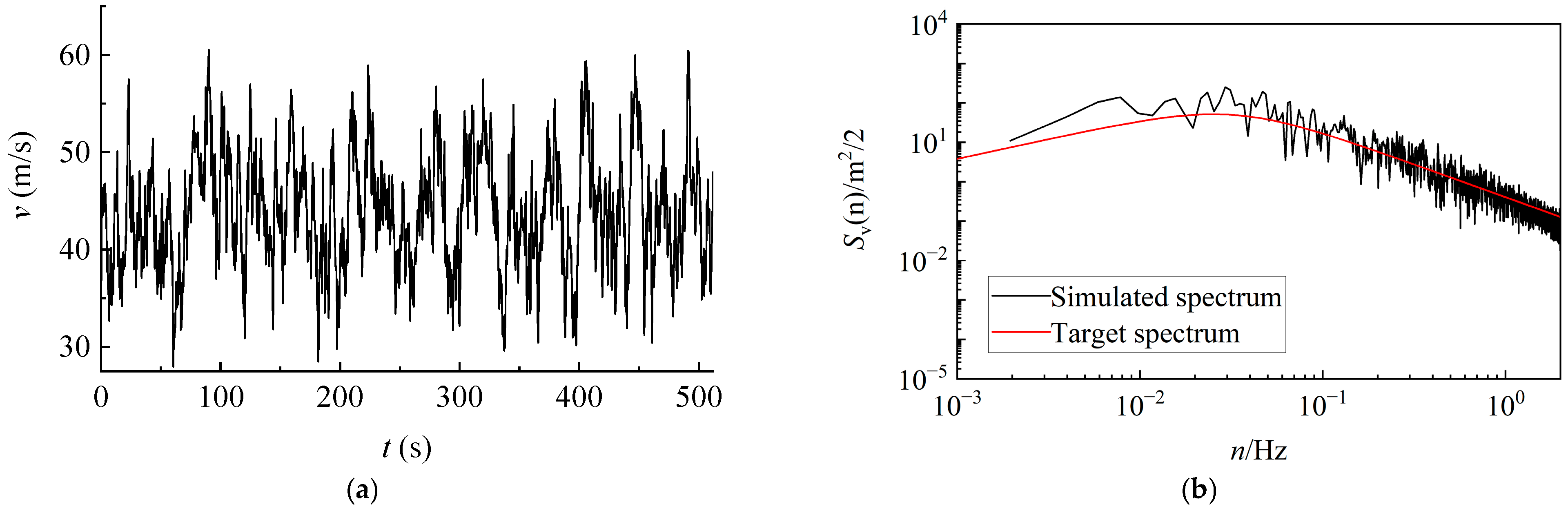
3.3. Wind Load Model
4. Methodologies for Progressive Collapse
5. Results and Discussion
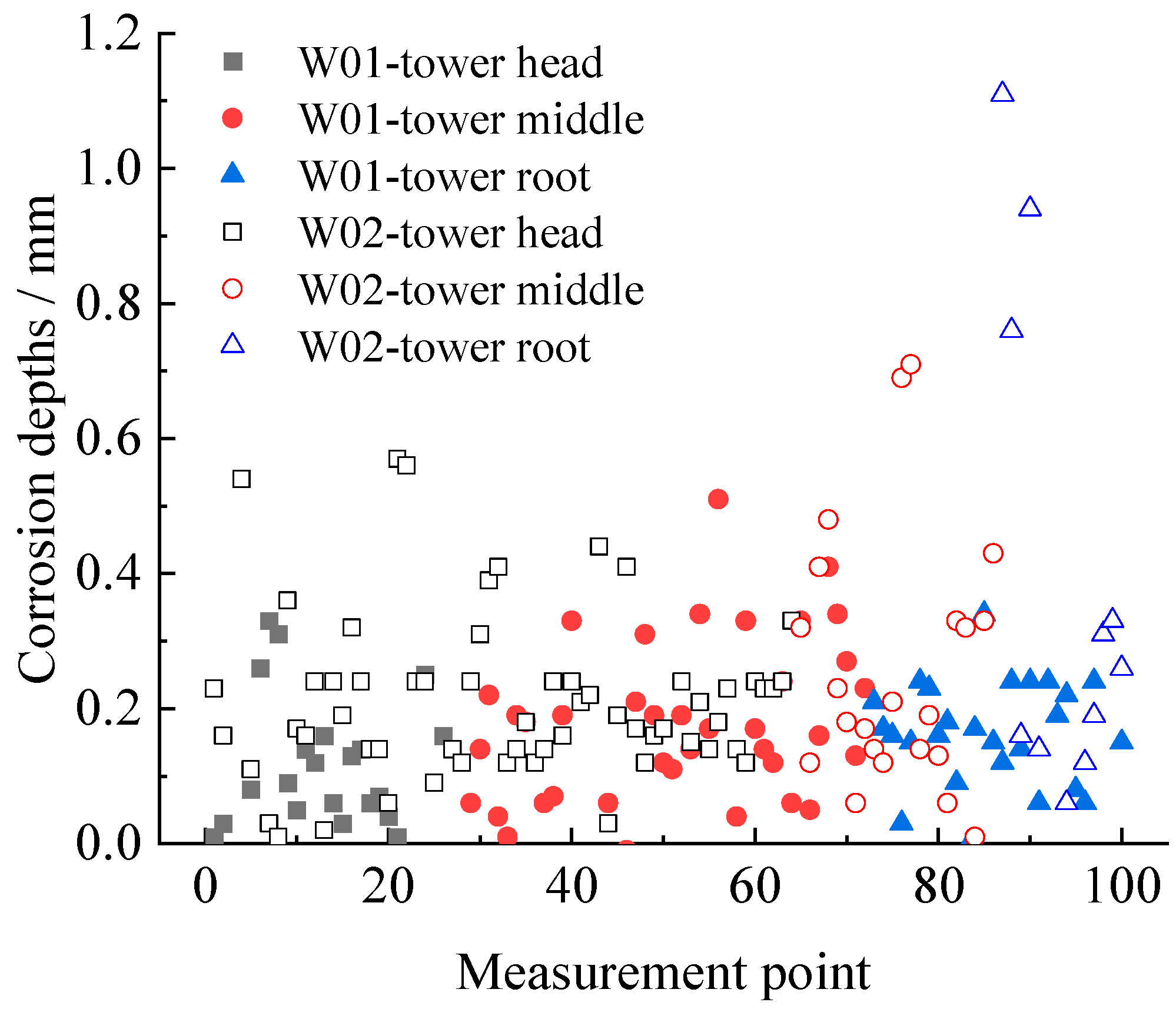
5.1. Corrosion Characteristics
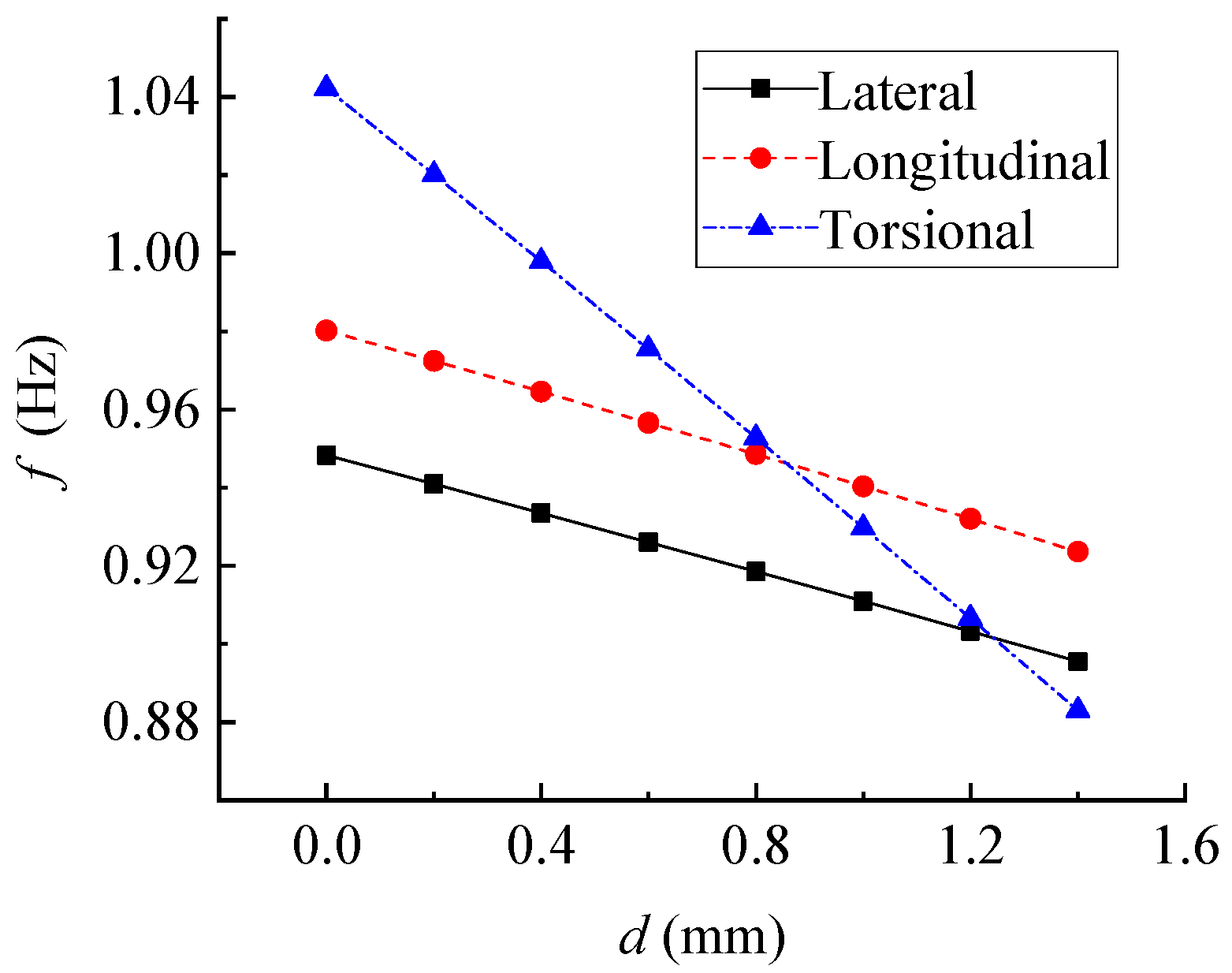
5.2. Vibration Features of Corroded Tower
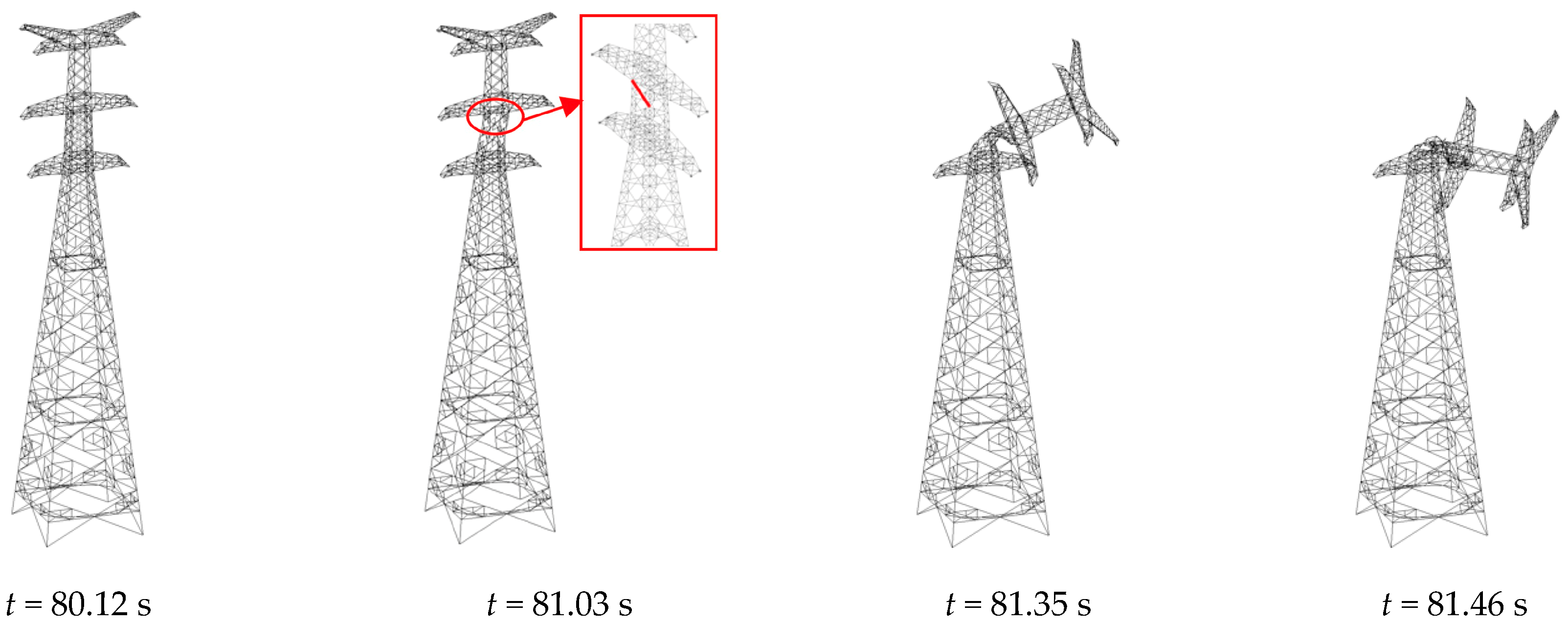
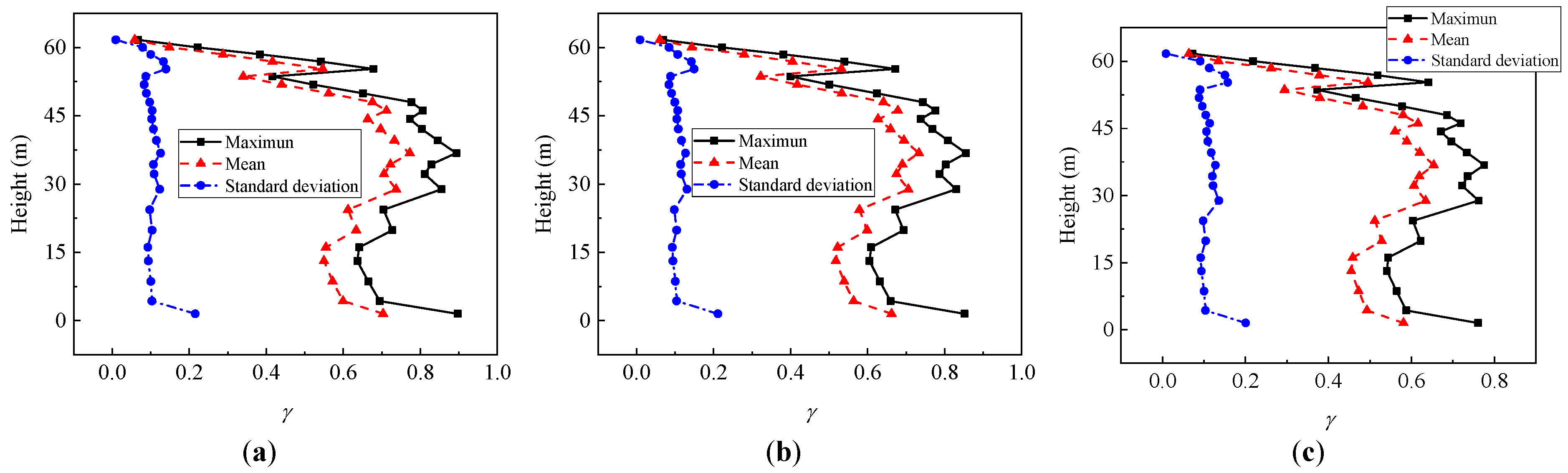
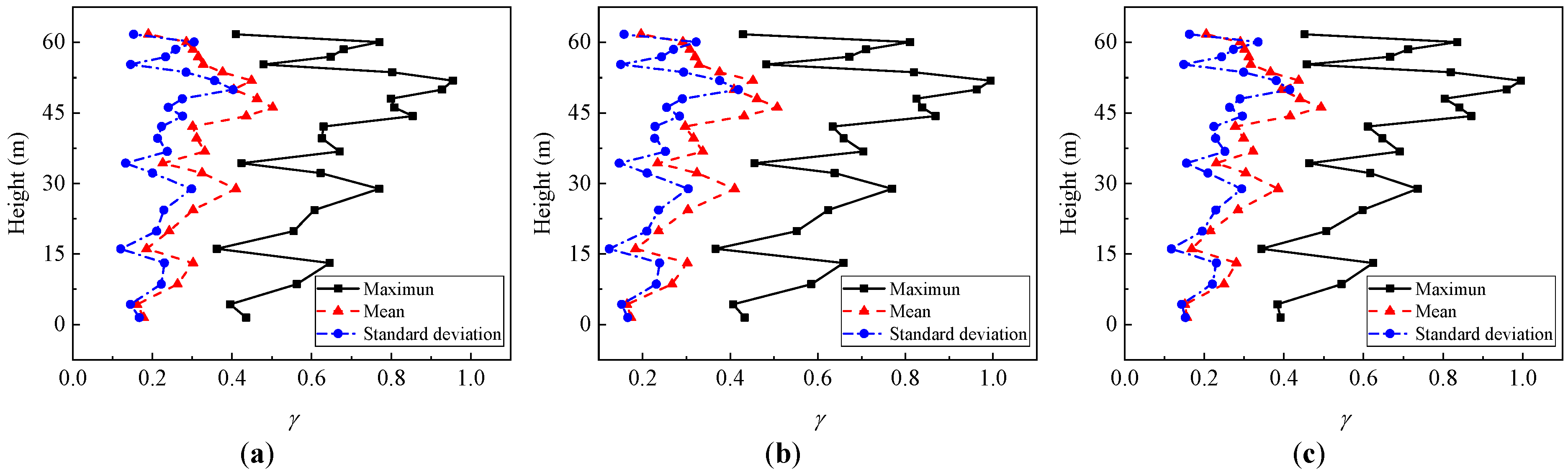
5.3. Progressive Collapse of Uncorroded Transmission Tower
5.4. Progressive Collapse of Corroded Transmission Tower
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Teng, Y.; Nie, Y.; Miao, C.; Chen, G.; Jin, S. Investigation on the corrosion of transmission towers in China. J. Anhui Electr. Eng. Prof. Tech. Coll. 2020, 25, 47–52. [Google Scholar]
- Shan, K.; Li, T.; Yan, C.; Hu, J.; Xia, J. Influence of tower feet corrosion on safety performance of power transmission tower. Corros. Prot. 2021, 24, 3. [Google Scholar]
- Zhou, J.; He, X.; Sun, K.; Huang, S.; Cai, W. Research of corrosion and monitoring protection of transmission lines in serious corrosion area. Corros. Prot. 2021, 42, 1–8. [Google Scholar]
- Liu, S.; Hu, X.; Gao, S.; Fan, Z. Causes and treatment scheme of tower foot corrosion of a 500 kV transmission tower. Corros. Prot. 2013, 34, 1026–1029. [Google Scholar]
- Huang, X. Study on the Natural Vibration Period of the Bucket Transmission Tower and the Overall Safety Performance While Corrosion. Master’s Thesis, South China University of Technology, Guangzhou, China, 2017. [Google Scholar]
- Meda, A.; Mostosi, S.; Rinaldi, Z.; Riva, P. Experimental evaluation of the corrosion influence on the cyclic behavior of RC columns. Eng. Struct. 2014, 76, 112–123. [Google Scholar] [CrossRef]
- Fernandez, I.; Bairán, J.M.; Marí, A.R. Corrosion effects on the mechanical properties of reinforcing steel bars. Fatigue and σ–ε behavior. Constr. Build. Mater. 2015, 101, 772–783. [Google Scholar] [CrossRef]
- Wang, Y.; Xu, S.; Wang, H.; Li, A. Predicting the residual strength and deformability of corroded steel plate based on the corrosion morphology. Constr. Build. Mater. 2017, 152, 777–793. [Google Scholar] [CrossRef]
- Shi, W.; Tong, L.; Chen, Y.; Li, Z.; Shen, K. Experimental study on influence of corrosion on behavior of steel material and steel beams. J. Build. Struct. 2012, 33, 53–60. [Google Scholar]
- Xu, S.; Zhang, H.; Bai, Y. Study on bending performance of corroded channel steel beams. J. Exp. Mech. 2019, 34, 1061–1067. [Google Scholar]
- Beaulieu, L.V.; Legeron, F.; Langlois, S. Compression strength of corroded steel angle members. J. Constr. Steel Res. 2019, 66, 1366–1373. [Google Scholar] [CrossRef]
- CSA S16-09; Design of Steel Structures. Canadian Standards Association, CSA Group: Singapore, 2009.
- AICS 2005; Steel Construction Manual (13th ed.). American Institute of Steel Construction: Chicago, IL, USA, 2005.
- ASCE 10-97; Design of Latticed Steel Transmission Structures. American Society of Civil Engineers: Reston, VA, USA, 1997.
- Zhang, C.; Fan, W.; Li, Z. Effects of corrosion on fatigue property of Q345 equal angles. Eng. Mech. 2013, 30, 211–218. [Google Scholar]
- Zhang, C.; Fan, W.; Li, Z. Quasi-static test of Q345 equal-angles in corrosion environment. Eng. Mech. 2014, 31, 53–62. [Google Scholar]
- GB 50017-2017; Standard for Design of Steel Structures. China Architecture & Building Press: Beijing, China, 2017.
- Chen, P.; Cao, B.; Luo, X.; Chen, R. Operation data and feature analysis of the main natural disasters of power network in China. Electr. Power 2014, 47, 57–61. [Google Scholar]
- Tu, Z.; Yao, J.; Xu, H.; Zhong, W.; Lou, W. Influence of refined wind load parameters and wind-loading mode on wind-induced responses of a long cross-arm angle-steel transmission tower. Int. J. Struct. Stab. Dyn. 2022, 22, 2250074. [Google Scholar] [CrossRef]
- Chen, Z.; Tang, K.; Zhou, Q.; Zhang, W.; Chen, J. Calculation models of ultimate bearing capacity and failure modes for transmission tower under wind load. J. Archit. Civ. Eng. 2018, 35, 47–55. [Google Scholar]
- Wei, W.; Zhou, X.; Deng, C.; Ji, B. Research on failure and collapse of transmission tower line system under downburst action based on energy method. J. Archit. Civ. Eng. 2020, 37, 73–80. [Google Scholar]
- Liu, S.; Huang, Z.; Yang, Y.; Zhang, C.; Gao, Q. Ultimate bearing capacity analysis of transmission tower-line system under equivalent static typhoon wind load. J. Disaster Prev. Mitig. Eng. 2020, 40, 757–763+778. [Google Scholar]
- Wang, W.; Li, H.; Tian, L. Progressive collapse analysis of transmission tower-line system under earthquake. Adv. Steel Constr. 2013, 9, 161–172. [Google Scholar]
- Edgar, T.; Sordo, E. Structural behaviour of lattice transmission towers subjected to wind load. Struct. Infrastruct. Eng. 2017, 13, 1462–1475. [Google Scholar] [CrossRef]
- Tian, L.; Pan, H.; Qiu, C.; Ma, R.; Yu, Q. Wind-induced collapse analysis of long-span transmission tower–line system considering the member buckling effect. Adv. Struct. Eng. 2019, 22, 30–41. [Google Scholar] [CrossRef]
- Li, Y.; Chen, Y.; Shen, G.; Lou, W.; Zhao, W.; Wang, H. Member capacity-based progressive collapse analysis of transmission towers under wind load. Wind. Struct. 2021, 33, 317–329. [Google Scholar]
- Fu, X.; Li, H. Uncertainty analysis of the strength capacity and failure path for a transmission tower under a wind load. J. Wind. Eng. Ind. Aerodyn. 2018, 173, 147–155. [Google Scholar] [CrossRef]
- Zhang, J.; Xie, Q. Failure analysis of transmission tower subjected to strong wind load. J. Constr. Steel Res. 2019, 160, 271–279. [Google Scholar] [CrossRef]
- Chen, Y. Life-Cycle Design and Time-Dependent Reliability in Corrosive Environment. Ph.D. Thesis, Southeast University, Nanjing, China, 2021. [Google Scholar]
- Wu, C. The Prediction of Corrosion Behavior of Coated Steel and Research on the Performance of Corroded Steel Members. Master’s Thesis, Southeast University, Nanjing, China, 2022. [Google Scholar]
- DL/T 5154-2012; Technical Code for the Design of Tower and Pole Structures of Overhead Transmission Line. China Planning Press: Beijing, China, 2012.
- Davenport, A.G. The spectrum of horizontal gustiness near the ground in high winds. Q. J. R. Meteorol. Soc. 1961, 87, 194–211. [Google Scholar] [CrossRef]
- Liang, S.; Zou, L.; Wang, D.; Cao, H. Investigation on wind tunnel tests of a full aeroelastic model of electrical transmission tower-line system. Eng. Struct. 2015, 85, 63–72. [Google Scholar] [CrossRef]
- Zhang, Z.; Li, H.; Li, G.; Wang, W.; Tian, L. The numerical analysis of transmission tower-line system wind-induced collapsed performance. Math. Probl. Eng. 2013, 2013, 413275. [Google Scholar] [CrossRef]
- GB/T 19292.1-2018; Corrosion of Metals and Alloys-Corrosivity of Atmospheres—Part 1: Classification, Determination and Estimation. Standard Press of China: Beijing, China, 2018.
- Panchenko, Y.; Marshakov, A. Long-term prediction of metal corrosion losses in atmosphere using a power-linear function. Corros. Sci. 2016, 109, 217–229. [Google Scholar] [CrossRef]
 represents the towers of which 100 members distributed from tower foot to tower head were investigated;
represents the towers of which 100 members distributed from tower foot to tower head were investigated;  represents the towers of which 5 typical members were investigated.
represents the towers of which 5 typical members were investigated.
 represents the towers of which 100 members distributed from tower foot to tower head were investigated;
represents the towers of which 100 members distributed from tower foot to tower head were investigated;  represents the towers of which 5 typical members were investigated.
represents the towers of which 5 typical members were investigated.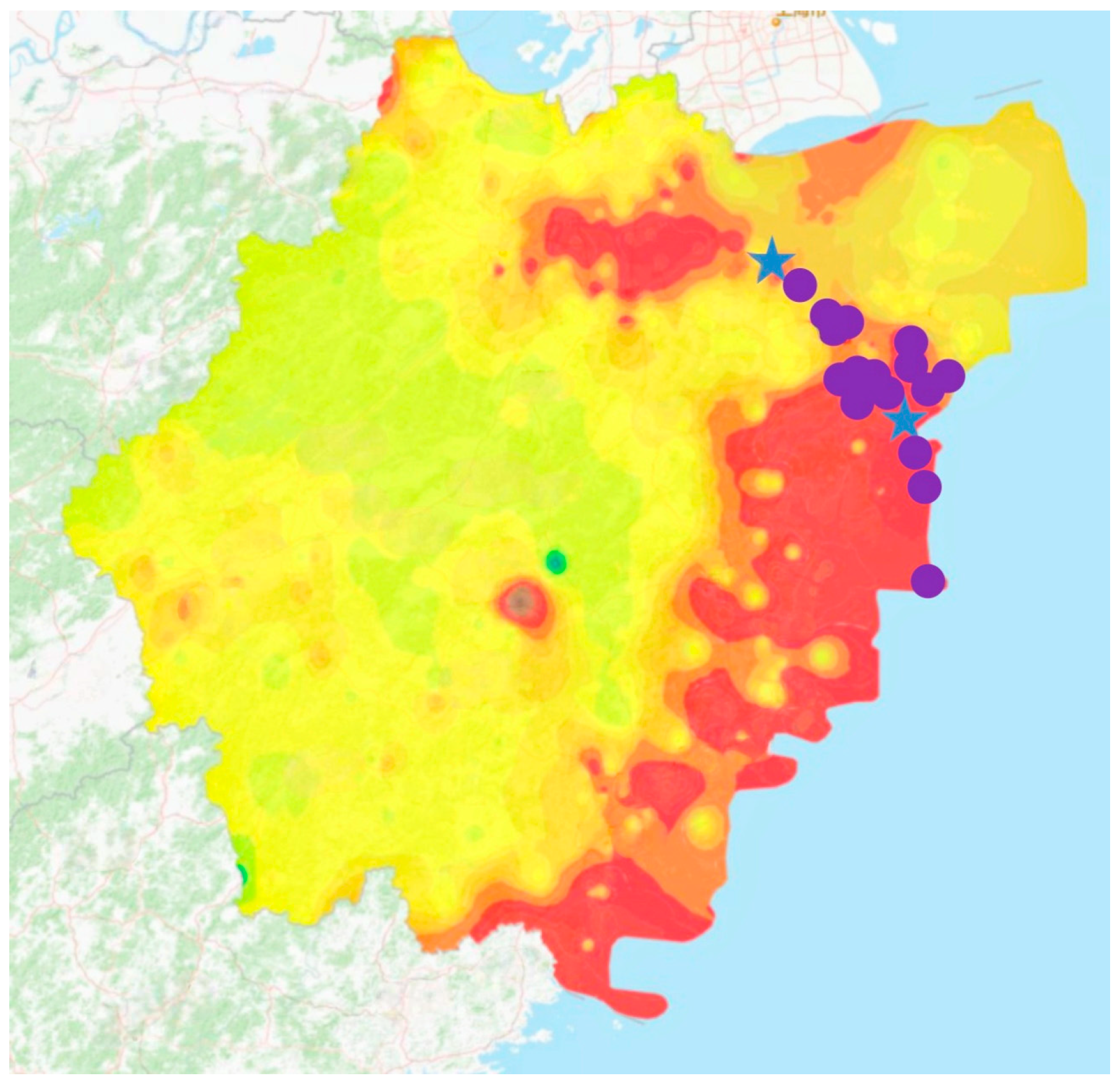




| Tower No. | Service Time (Years) | Distances to Manufacturing District (km) | Distances to Coastline (km) | Corrosion Grade |
|---|---|---|---|---|
| W-01 | 30 | >5.0 | 18.1 | C3 |
| W-02 | 30 | >5.0 | 8.9 | C4 |
| L-01 | 21 | >5.0 | 35.0 | C3 |
| L-02 | 16 | >5.0 | 32.0 | C3 |
| L-03 | 32 | >5.0 | 20.0 | C4 |
| L-04 | 25 | >5.0 | 6.0 | C4 |
| L-05 | 22 | >5.0 | 25.0 | C4 |
| L-06 | 18 | >5.0 | 26.0 | C4 |
| L-07 | 8 | 2.3 | 35.0 | C4 |
| L-08 | 3 | 2.7 | 18.0 | C4 |
| L-09 | 32 | >5.0 | 5.0 | C5 |
| L-10 | 26 | 1.2 | 4.8 | C5 |
| L-11 | 16 | 2.2 | 2.0 | C5 |
| L-12 | 15 | >5.0 | 0.4 | C5 |
| L-13 | 6 | 2.0 | 3.5 | C5 |
| L-14 | 35 | 0 | 0.8 | CX |
| L-15 | 30 | 0.3 | 2.8 | CX |
| L-16 | 6 | 1.2 | 5.0 | CX |
| Corrosion Depth | Interval | Corrosion Description |
|---|---|---|
| 0~1.4 mm | 0.2 mm | All members are assumed to have the same corrosion depth. |
| Members | Corrosion Depth (mm) | Segments S01~S02 | Segments S03~S05 | Segments S06~S08 | Segments S09~S10 | Segments S11~S13 |
|---|---|---|---|---|---|---|
| Leg | 0.2 | 1.9% | 1.4% | 1.2% | 1.0% | 0.8% |
| 0.4 | 3.8% | 2.7% | 2.4% | 1.9% | 1.6% | |
| 0.6 | 5.8% | 4.1% | 3.6% | 2.8% | 2.3% | |
| 0.8 | 7.7% | 5.5% | 4.8% | 3.8% | 3.1% | |
| 1.0 | 9.6% | 6.8% | 6.0% | 4.7% | 3.9% | |
| 1.2 | 11.5% | 8.2% | 7.2% | 5.7% | 4.7% | |
| 1.4 | 13.4% | 9.6% | 8.4% | 6.6% | 5.5% | |
| Diagonal | 0.2 | 3.9% | 3.2% | 3.9% | 2.8% | 2.4% |
| 0.4 | 7.7% | 6.4% | 7.7% | 5.5% | 4.8% | |
| 0.6 | 11.6% | 9.6% | 11.6% | 8.3% | 7.3% | |
| 0.8 | 15.4% | 12.8% | 15.5% | 11.0% | 9.7% | |
| 1.0 | 19.3% | 16.0% | 19.3% | 13.8% | 12.1% | |
| 1.2 | 23.1% | 19.2% | 23.2% | 16.5% | 14.5% | |
| 1.4 | 27.0% | 22.4% | 27.1% | 19.3% | 16.9% |
| Leg Members | Diagonal Members | All Members | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|
| Tower Foot | Tower Middle | Tower Head | Tower Foot | Tower Middle | Tower Head | Tower Foot | Tower Middle | Tower Head | Mean | |
| W-01 | 0.19 | 0.12 | 0.09 | 0.15 | 0.12 | 0.09 | 0.31 | 0.29 | 0.24 | 0.28 |
| W-02 | 0.94 | 0.61 | 0.08 | 0.23 | 0.19 | 0.11 | 0.46 | 0.40 | 0.39 | 0.40 |
| Tower No. | Corrosion Depth (mm) | Err1 (%) | Err2 (%) | ||
|---|---|---|---|---|---|
| Examined | Model 1 | Model 2 | |||
| W-01 | 0.28 | 0.24 | 0.31 | −14.29 | 10.71 |
| W-02 | 0.40 | 0.34 | 0.41 | −15.00 | 2.50 |
| L01 | 0.20 | 0.30 | 0.25 | 50.00 | 25.00 |
| L02 | 0.07 | 0.15 | 0.11 | 114.29 | 57.14 |
| L03 | 0.33 | 0.39 | 0.34 | 18.18 | 3.03 |
| L04 | 0.29 | 0.33 | 0.28 | 13.79 | −3.45 |
| L05 | 0.24 | 0.31 | 0.26 | 29.17 | 8.33 |
| L06 | 0.22 | 0.28 | 0.23 | 27.27 | 4.55 |
| L07 | 0.15 | 0.18 | 0.14 | 20.00 | −6.67 |
| L08 | 0.12 | 0.10 | 0.10 | −16.67 | −16.67 |
| L09 | 0.44 | 0.36 | 0.43 | −18.18 | −2.27 |
| L10 | 0.37 | 0.32 | 0.36 | −13.51 | −2.70 |
| L11 | 0.17 | 0.24 | 0.25 | 41.18 | 47.06 |
| L12 | 0.14 | 0.24 | 0.24 | 71.43 | 71.43 |
| L13 | 0.13 | 0.15 | 0.14 | 15.38 | 7.69 |
| L14 | 0.83 | 0.75 | 0.87 | −9.64 | 4.82 |
| L15 | 0.94 | 0.68 | 0.76 | −27.66 | −19.15 |
| L16 | 0.18 | 0.29 | 0.26 | 61.11 | 44.44 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tu, Z.; Yao, J.; Liu, Z.; Zhou, X.; Zhang, L. Effects of Corrosion Depth on Wind-Induced Collapse Performance of an Angle Steel Transmission Tower. Energies 2025, 18, 2518. https://doi.org/10.3390/en18102518
Tu Z, Yao J, Liu Z, Zhou X, Zhang L. Effects of Corrosion Depth on Wind-Induced Collapse Performance of an Angle Steel Transmission Tower. Energies. 2025; 18(10):2518. https://doi.org/10.3390/en18102518
Chicago/Turabian StyleTu, Zhibin, Jianfeng Yao, Zhitong Liu, Xing Zhou, and Ligang Zhang. 2025. "Effects of Corrosion Depth on Wind-Induced Collapse Performance of an Angle Steel Transmission Tower" Energies 18, no. 10: 2518. https://doi.org/10.3390/en18102518
APA StyleTu, Z., Yao, J., Liu, Z., Zhou, X., & Zhang, L. (2025). Effects of Corrosion Depth on Wind-Induced Collapse Performance of an Angle Steel Transmission Tower. Energies, 18(10), 2518. https://doi.org/10.3390/en18102518






