A Fast SOC Balancing Method for MMC-BESS Based on Nonlinear Model-Predictive Control
Abstract
1. Introduction
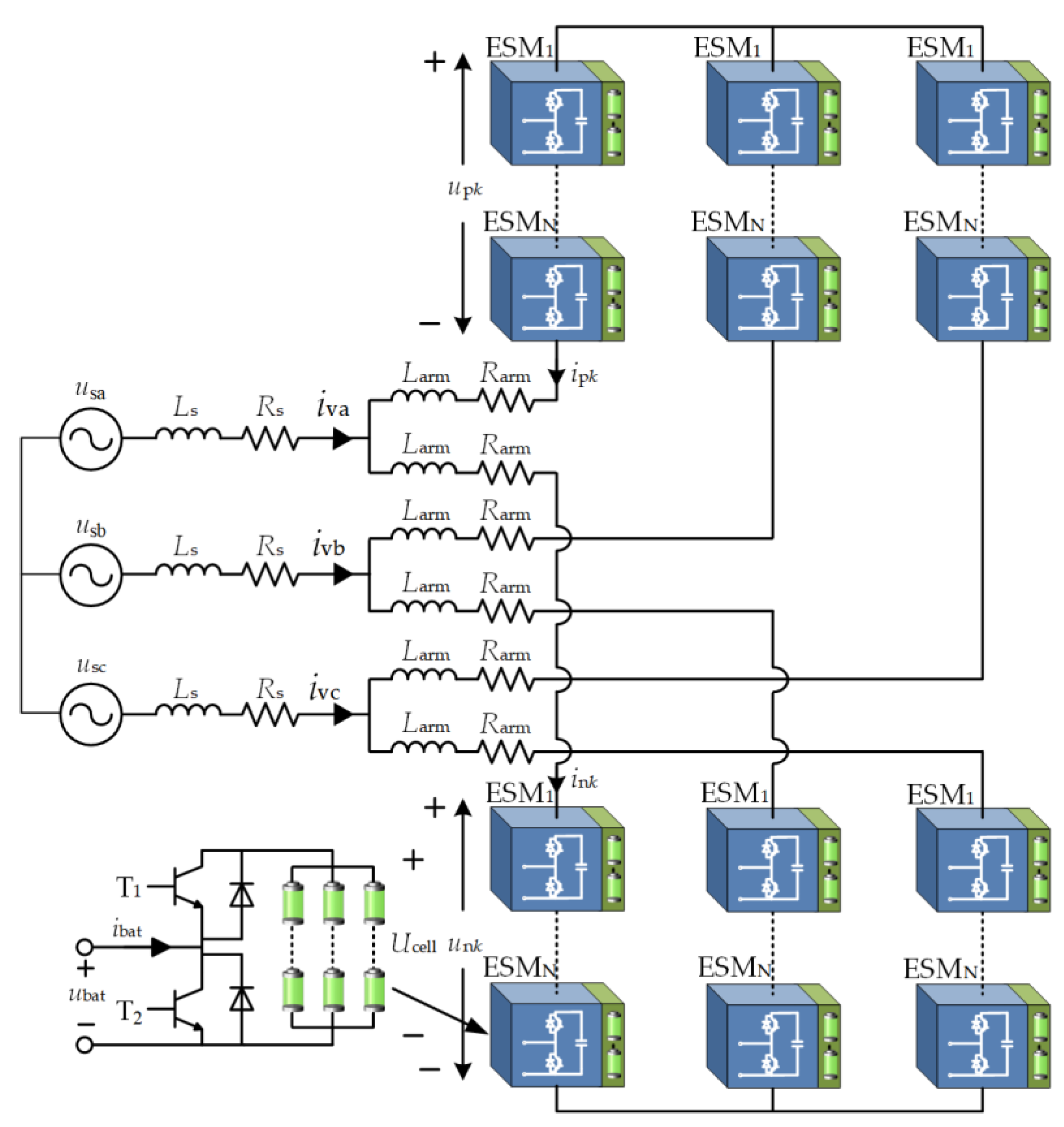
2. MMC-BESS Topology and Its Traditional Three-Level SOC-Balancing Control
2.1. Topological Structure
2.2. Model-Predictive Control of Output Current
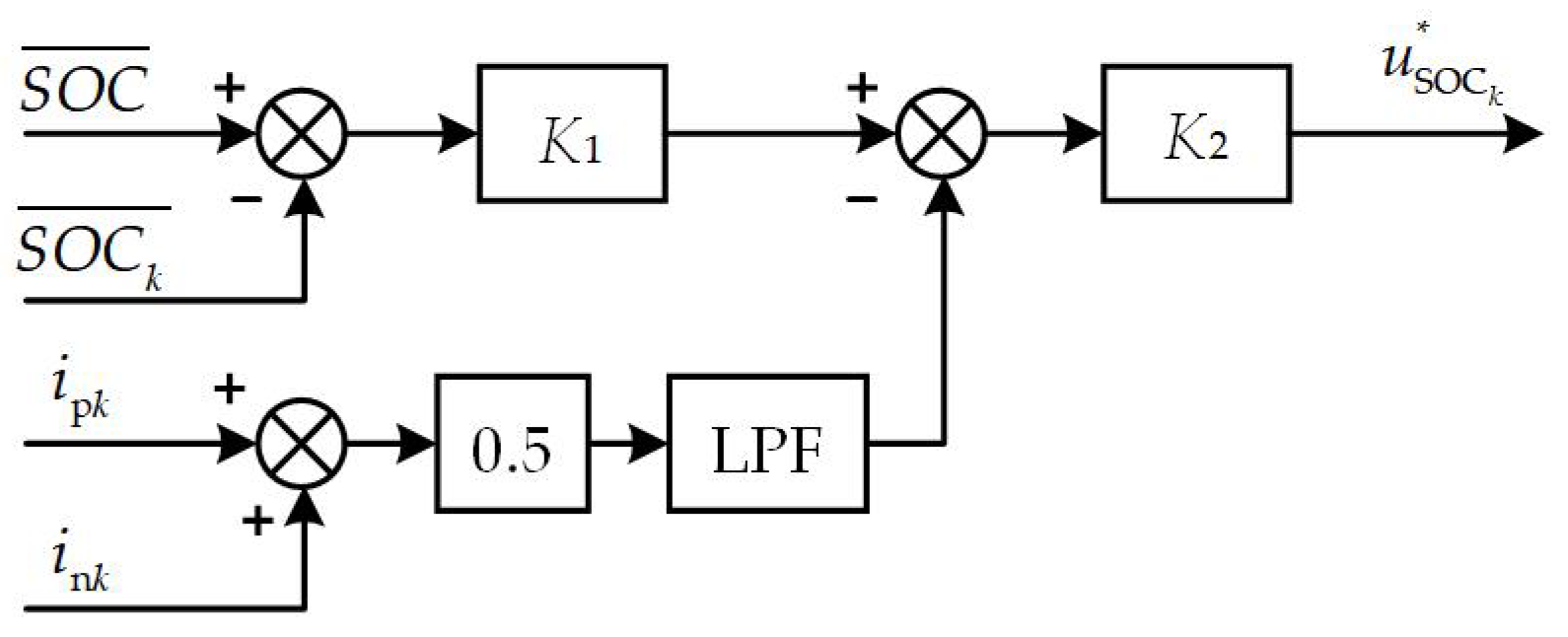
2.3. Traditional SOC-Balancing Control
- (1)
- Calculate the required number of submodules (n*) that need to be activated;
- (2)
- Sort all submodules within the arm according to their estimated SOC values;
- (3)
- Apply a current-direction-based selection algorithm: when the arm current causes the battery to discharge, the n submodules with the highest SOC values are activated; when it causes charging, those with the lowest SOC values are prioritized.
3. Nonlinear State-Space Model and Its Linearization
3.1. Nonlinear State-Space Model of MMC-BESS
3.2. Linearization Processing of State-Space Model
4. SOC-Balancing Control Strategy Based on Model-Predictive Control
4.1. MPC for Inter-Arm SOC Balancing
4.2. MPC for Inter-Phase SOC Balancing
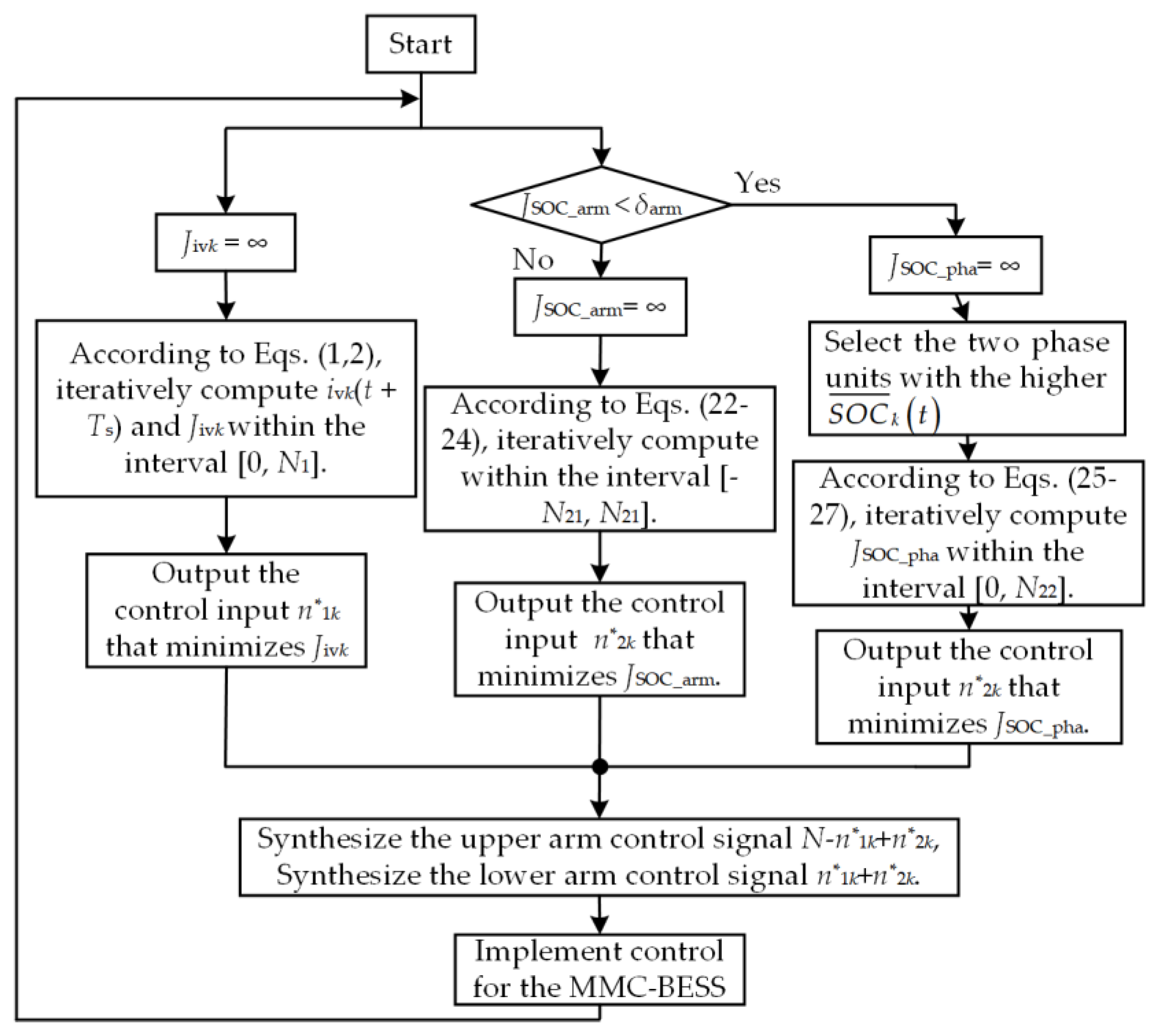
4.3. MPC Scheme Design Considering Inter-Arm and Inter-Phase SOC Balancing
- (1)
- Design Scheme One: Unified Control Approach
- (2)
- Design Scheme Two: Staged Control Approach
5. Simulation Verification
5.1. Simulation Parameters
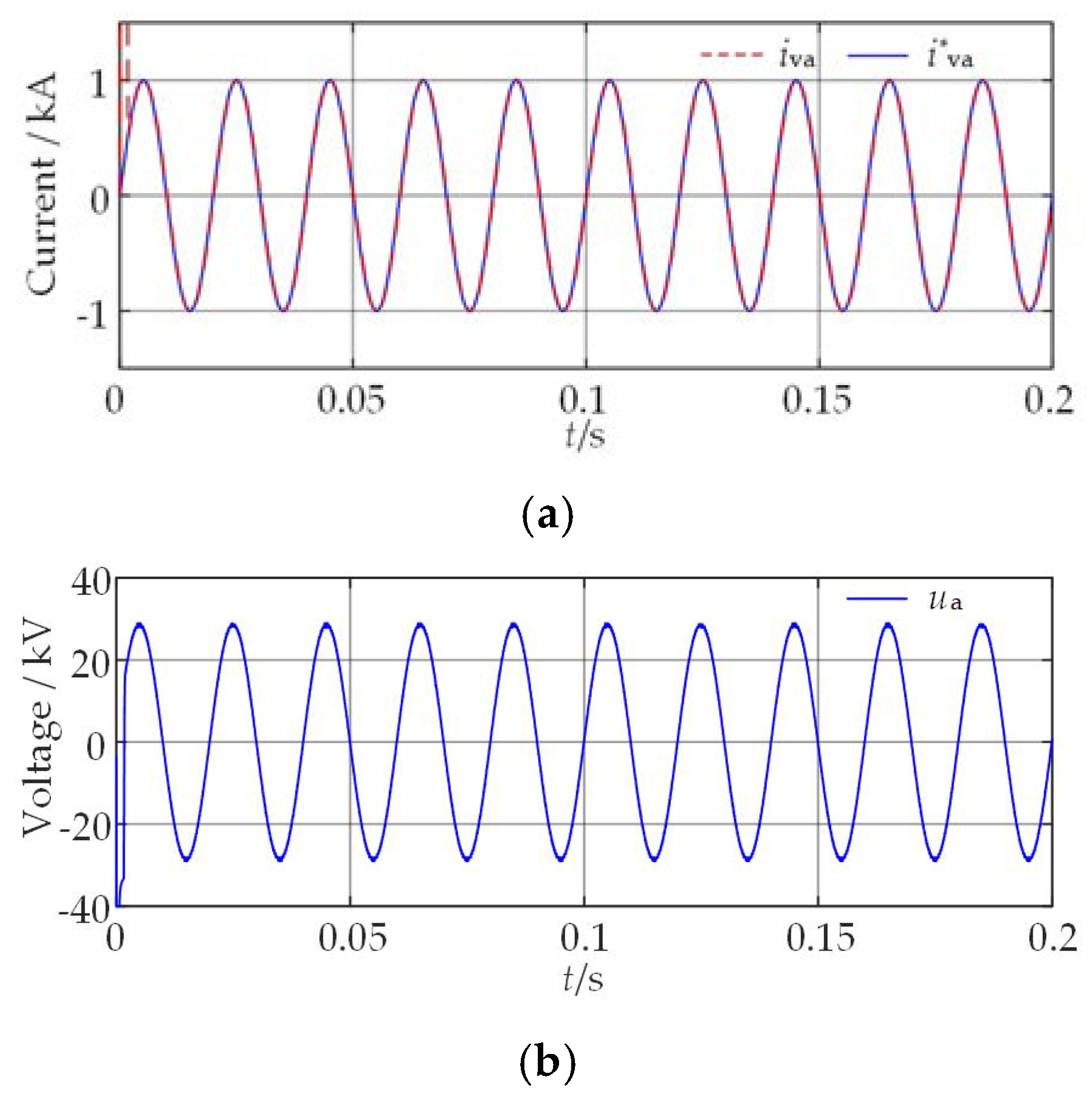
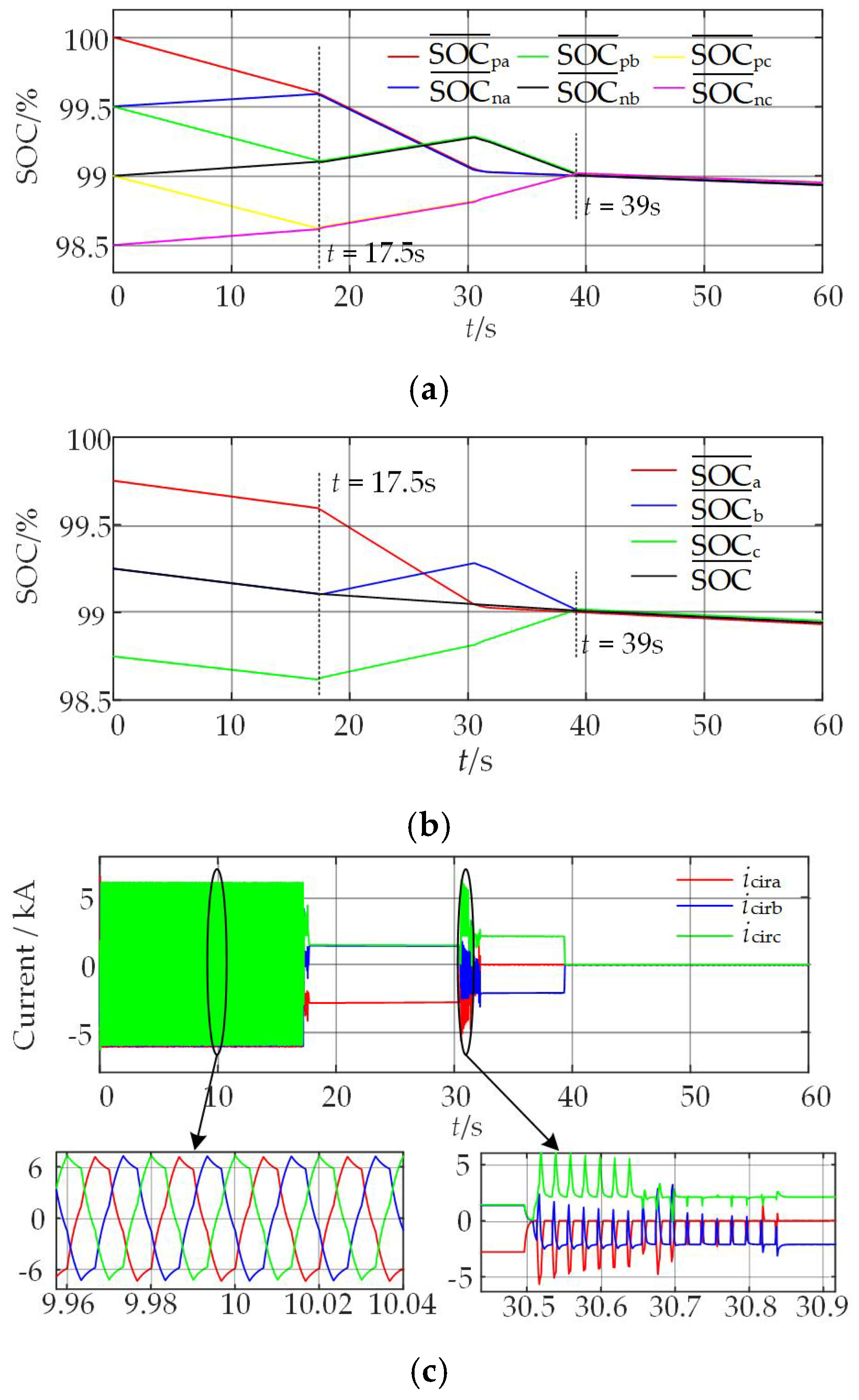
5.2. Simulation Results of the Proposed SOC-Balancing Control
5.3. Comparison with Traditional SOC-Balancing Control Method
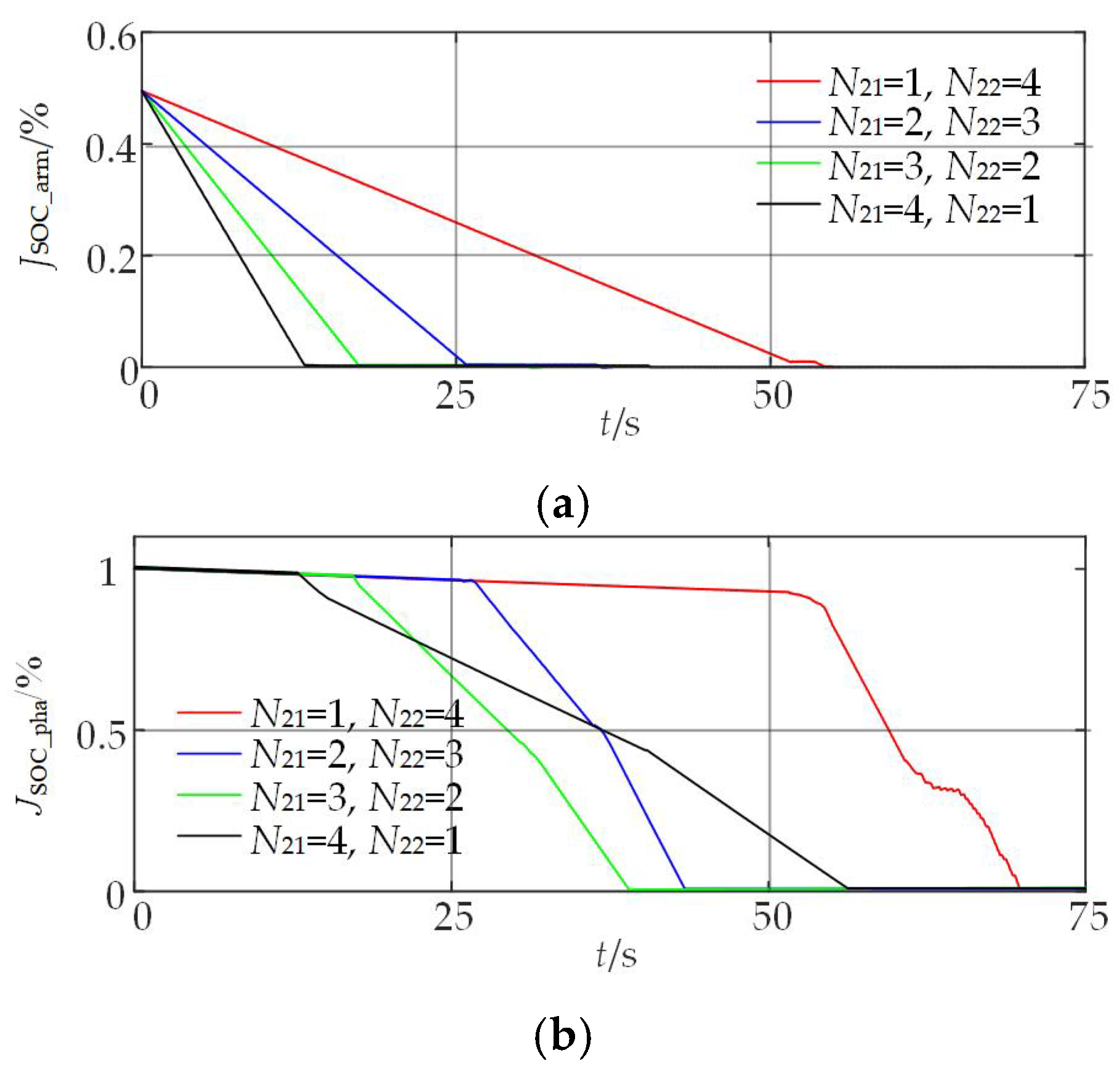
5.4. Comparison of SOC Balancing Rates with Different Submodule Number Proportions
5.5. Comparison of Computation Burden Between Unified and Staged-Control Approach
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zhang, X.; Feng, G. MMC-based PV grid-connected system with SMES-battery hybrid energy storage system. IEEE Trans. Appl. Supercond. 2024, 34, 1–4. [Google Scholar] [CrossRef]
- Babu, T.S.; Vasudevan, K.R.; Ramachandaramurthy, V.K.; Sani, S.B.; Chetmud, S.; Laljim, R.M. A comprehensive review of hybrid energy storage systems: Converter topologies, control strategies and future prospects. IEEE Access 2020, 8, 148702–148721. [Google Scholar] [CrossRef]
- Kasari, P.R.; Bhattacharjee, S. An HESS based on a modified MMCC-TSBC converter integrating energy storages. CSEE J. Power Energy Syst. 2023, 9, 1698–1709. [Google Scholar]
- Wang, H.; Yang, G.; Xiao, F.; Fan, X. Wide-range operation optimization strategy of bidirectional energy storage converter for 10 kV medium voltage DC integrated power system. IEEE Trans. Transp. Electrif. 2024, 10, 4604–4615. [Google Scholar] [CrossRef]
- Ma, Z.; Yu, F.; Zhao, X.; Gao, F. The multidimensional battery management strategy for MMC battery energy storage system. In Proceedings of the 2022 IEEE 7th Southern Power Electronics Conference (SPEC), Nadi, Fiji, 5–8 December 2022; IEEE: Piscataway, NJ, USA, 2022; pp. 1–5. [Google Scholar]
- He, R.; Tian, K.; Ling, Z. Offline equalization control of modular multilevel converter-based battery energy storage system. IEEE Trans. Ind. Electron. 2023, 71, 9003–9012. [Google Scholar] [CrossRef]
- Quraan, M.; Yeo, T.; Tricoli, P. Design and control of modular multilevel converters for battery electric vehicles. IEEE Trans. Power Electron. 2016, 31, 507–517. [Google Scholar] [CrossRef]
- Gao, F.; Zhang, L.; Zhou, Q.; Chen, M.; Xu, T.; Hu, S. State-of-charge balancing control strategy of battery energy storage system based on modular multilevel converter. In Proceedings of the 2014 IEEE Energy Conversion Congress and Exposition (ECCE), Pittsburgh, PA, USA, 14–18 September 2014; IEEE: Piscataway, NJ, USA, 2014; pp. 2567–2574. [Google Scholar]
- Maharjan, L.; Inoue, S.; Akagi, H.; Asakura, J. State-of-charge (SOC)-balancing control of a battery energy storage system based on a cascade PWM converter. IEEE Trans. Power Electron. 2009, 24, 1628–1636. [Google Scholar] [CrossRef]
- Luo, H.; Xu, C.; Dai, K.; Cheng, C.; Huang, Y.; Pan, F. Balance control of SOC for MMC-BESS with power fluctuation suppression, PCC voltage regulation, and harmonic mitigation in grid-connected wind farm. IEEE Access 2022, 10, 117732–117744. [Google Scholar] [CrossRef]
- Cheng, C.; Xu, C.; Dai, K.; Huang, Y.; Pan, F. Three-level equalization control strategy for state of charge of MMC-BESS. Power Syst. Prot. Control. 2021, 49, 100–108. [Google Scholar]
- Premchand, M.; Gudey, S.K. Analysis of PI, PR and SMC controllers for bidirectional converter used in electric vehicle. In International Conference on Automation, Signal Processing, Instrumentation and Control; Springer: Singapore, 2020; pp. 449–466. [Google Scholar]
- Xu, S.; Pei, T.; Wang, S. Model predictive control strategy of MMC based on energy decoupling. Power Electron. 2024, 58, 115–118. [Google Scholar]
- Cheng, Z.; Tian, F.; Yang, H.; Yang, T. Model predictive optimal control strategy for battery energy storage system of modular multilevel composite converter. Acta Energiae Solaris Sinica 2023, 44, 59–66. [Google Scholar]
- Wang, J.; Liu, X.; Xiao, Q.; Zhou, D.; Qiu, H.; Tang, Y. Modulated model predictive control for modular multilevel converters with easy implementation and enhanced steady-state performance. IEEE Trans. Power Electron. 2020, 35, 9107–9118. [Google Scholar] [CrossRef]
- Böcker, J.; Freudenberg, B.; The, A.; Dieckerhoff, S. Experimental comparison of model predictive control and cascaded control of the modular multilevel converter. IEEE Trans. Power Electron. 2014, 30, 422–430. [Google Scholar] [CrossRef]
- Qin, J.; Saeedifard, M. Predictive control of a modular multilevel converter for a back-to-back HVDC system. IEEE Trans. Power Deliv. 2012, 27, 1538–1547. [Google Scholar]
- Liu, Z.; Li, Q.; Fu, J.; Zhou, H.; Chen, J.; Xia, Z. An extended-level model predictive control method with reduced current THD for modular multilevel converter battery energy storage system. IEEE J. Emerg. Sel. Top. Power Electron. 2025. [Google Scholar] [CrossRef]
- Liu, Z.; Li, Q.; Zhou, H.; Fu, J.; Ren, D.; Zhang, K.; Qin, H. An improved SOC balancing strategy based on reduced computational burden voltage level model predictive control for modular multilevel converter-battery energy storage system. Electr. Eng. 2025. [Google Scholar] [CrossRef]
- Xu, J.; Wang, F.; Wang, J.; Li, G. SOC balancing control based on predictive power model amongst supercapacitor packs in MMC with embedded energy storage system. IEEE Trans. Power Deliv. 2023, 38, 2641–2649. [Google Scholar] [CrossRef]
- Zhao, G.; Shen, K.; Luo, G.; Zhao, D. A novel control strategy for modular multilevel converter with integrated supercapacitor energy storage system. In Proceedings of the IECON 2019-45th Annual Conference of the IEEE Industrial Electronics Society, Lisbon, Portugal, 14–17 October 2019; IEEE: Piscataway, NJ, USA, 2019; Volume 1, pp. 6037–6042. [Google Scholar]
- Sankar, S.G.; Dreke, V.D.R.; Lazar, M. Hierarchical Model Predictive Control for Modular Multilevel Converters: A Linear Parameter Varying Approach. IFAC-PapersOnLine 2024, 58, 126–131. [Google Scholar] [CrossRef]
- Cao, S.; Wang, Y.; Yu, X.; Yu, Y.; Yu, Z. SOC adaptive balance control strategy based on MMC-BESS. Power Supply 2024, 1–11. [Google Scholar]
- Tang, C.; Thiringer, T. A model predictive control method with adaptive weighting factors for enhancing performance of modular multilevel converters. IEEE J. Emerg. Sel. Top. Power Electron. 2024, 12, 3887–3899. [Google Scholar] [CrossRef]
- Akbari, E.; Shadlu, M.S. Integrated battery energy storage with modular multilevel converter for grid-connected photovoltaic system: Design and control. In Proceedings of the 2023 13th Smart Grid Conference (SGC), Tehran, Iran, 5–6 December 2023; pp. 1–6. [Google Scholar]
- Li, N.; Xie, Y.; Sha, Z.; Gao, F.; Wang, W. Hybrid predictive control method for battery integrated modular multilevel converter. In Proceedings of the 2016 IEEE 8th International Power Electronics and Motion Control Conference (IPEMC-ECCE Asia), Hefei, China, 22–26 May 2016; IEEE: Piscataway, NJ, USA, 2016; pp. 3777–3782. [Google Scholar]
- Li, N.; Gao, F. Hybrid model predictive control method for battery-energy-storage-based modular multilevel converter. Trans. China Electrotech. Soc. 2017, 32, 165–174. [Google Scholar]
- Wang, J.; Xu, J. Optimized control strategy for state-of-charge balancing of distributed energy-storage-based MMC batteries. Electr. Power Autom. Equip. 2023, 43, 44–50. [Google Scholar]
- Ma, W.; Sun, W.; Wang, Y.; Zhang, W.; Li, H.; Zhu, Y. MMC-based distributed energy storage system and its fast SOC balancing control strategy. Power Syst. Prot. Control. 2024, 52, 1–11. [Google Scholar]
- Chen, J.; Xiao, Y.; Zhou, G.; Li, X.; Luo, Y.; Zhang, W.; Wang, P.; Zhou, Y. A Hybrid Estimation Method for State-of-Charge (SOC) of Lithium-Ion Batteries. Chinese Patent CN201910460801.9; CN110133510A, 16 August 2019. [Google Scholar]
- Grüne, L.; Pannek, J.; Grüne, L.; Pannek, J. Nonlinear Model Predictive Control; Springer International Publishing: Berlin/Heidelberg, Germany, 2017. [Google Scholar]
- Vatani, M.; Bahrani, B.; Saeedifard, M.; Hovd, M. Indirect finite control set model predictive control of modular multilevel converters. IEEE Trans. Smart Grid 2015, 6, 1520–1529. [Google Scholar] [CrossRef]


| Control Method | Technical Features | Main Limitations. |
|---|---|---|
| Traditional three-level control [7] | Open-loop proportional control and sequencing strategy | Slow speed and sensitive parameters |
| PI/PR composite control [8,9,10,11,12] | Multi-stage closed-loop architecture | High complexity and poor dynamic response |
| Indirect MPC [25,26,27] | The SOC is indirectly balanced through the circulation cost function | The PI/PR controller is needed |
| Direct MPC [25,28] | Based on the SOC prediction model | Only applicable to the submodule with DC-DC converter |
| Hybrid MPC [15,29] | MPC with conventional controller cooperation | Still dependent on parameter tuning |
| Type | Items | Values |
|---|---|---|
| Circuit parameters | Grid voltage | 35 kV |
| Rated output power | 50 MW | |
| Equivalent inductance (Ls) | 2.2 mH | |
| Equivalent resistance (Rs) | 10 mΩ | |
| No. of ESMs within each arm (N) | 80 | |
| Arm inductance (Larm) | 0.6 mH | |
| Arm equivalent resistance (Rarm) | 200 mΩ | |
| Rated capacity of battery pack (Qmax) | 1000 Ah | |
| Rated battery pack voltage (Ucell) | 800 V | |
| Control parameters | Control step size | 100 μs |
| No. of ESMs for output current (N1) | 75 | |
| No. of ESMs for SOC balancing (N2) | 5 | |
| No. of ESMs for inter-arm SOC balancing (N21) | 3 | |
| No. of ESMs for inter-phase SOC balancing (N22) | 2 |
| Condition | Inter-Arm | Inter-Phase | Overall |
|---|---|---|---|
| (N21 = 1, N22 = 4) | 54.5 s | 15.5 s | 70.0 s |
| (N21 = 2, N22 = 3) | 26.0 s | 17.5 s | 43.5 s |
| (N21 = 3, N22 = 2) | 17.5 s | 21.5 s | 39.0 s |
| (N21 = 4, N22 = 1) | 13.0 s | 43.0 s | 56.0 s |
| Control Scheme | CPU Time |
|---|---|
| Unified Control | 45.682 s |
| Staged Control (N21 = 1, N22 = 4) | 4.882 s |
| Staged Control (N21 = 2, N22 = 3) | 4.837 s |
| Staged Control (N21 = 3, N22 = 2) | 4.808 s |
| Staged Control (N21 = 4, N22 = 1) | 4.796 s |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ji, X.; Xie, F.; Qi, Y.; Ji, Y.; Niu, D.; Yan, Q. A Fast SOC Balancing Method for MMC-BESS Based on Nonlinear Model-Predictive Control. Energies 2025, 18, 2502. https://doi.org/10.3390/en18102502
Ji X, Xie F, Qi Y, Ji Y, Niu D, Yan Q. A Fast SOC Balancing Method for MMC-BESS Based on Nonlinear Model-Predictive Control. Energies. 2025; 18(10):2502. https://doi.org/10.3390/en18102502
Chicago/Turabian StyleJi, Xiaofan, Fengxiang Xie, Yuantang Qi, Yongdong Ji, Decun Niu, and Qizhong Yan. 2025. "A Fast SOC Balancing Method for MMC-BESS Based on Nonlinear Model-Predictive Control" Energies 18, no. 10: 2502. https://doi.org/10.3390/en18102502
APA StyleJi, X., Xie, F., Qi, Y., Ji, Y., Niu, D., & Yan, Q. (2025). A Fast SOC Balancing Method for MMC-BESS Based on Nonlinear Model-Predictive Control. Energies, 18(10), 2502. https://doi.org/10.3390/en18102502






