Multi-Level Dynamic Weight Optimization Scheduling Strategy for Flexible Interconnected Distribution Substations Based on Three-Port SNOPs
Abstract
1. Introduction
2. SNOP-Based Flexible Interconnected Distribution Network
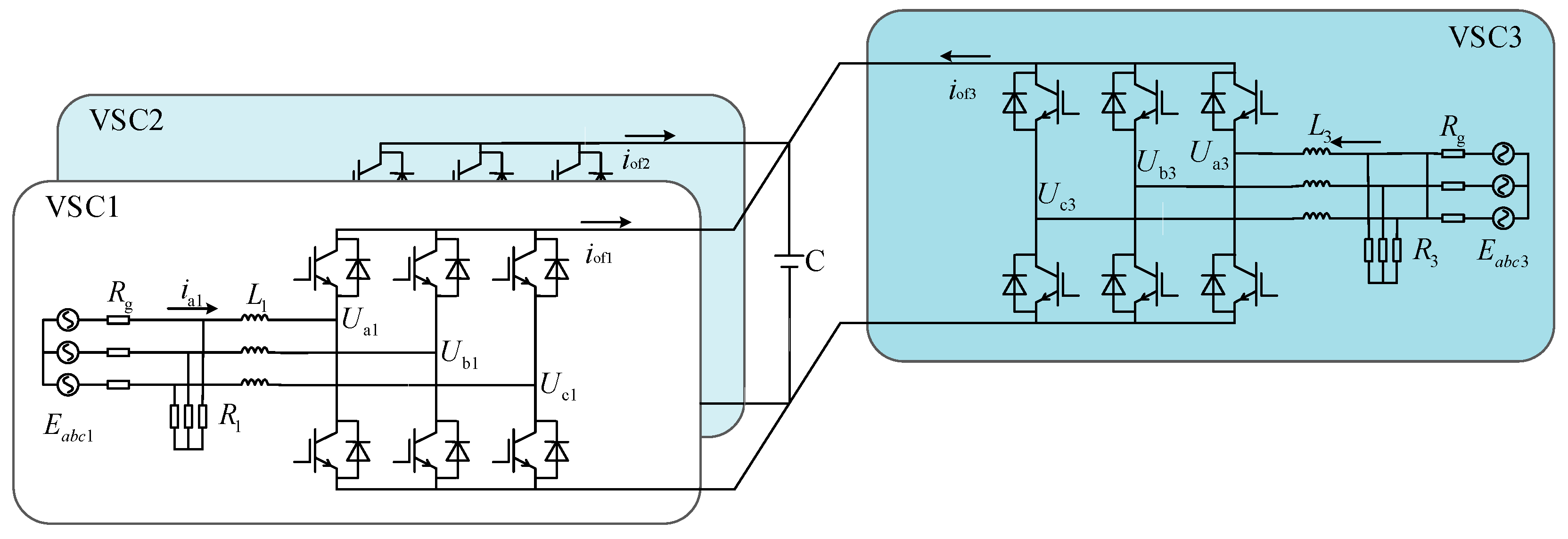
2.1. Form of FIDS
2.2. The SNOP Model
3. Multi-Level Optimal Dispatch Model of FIND
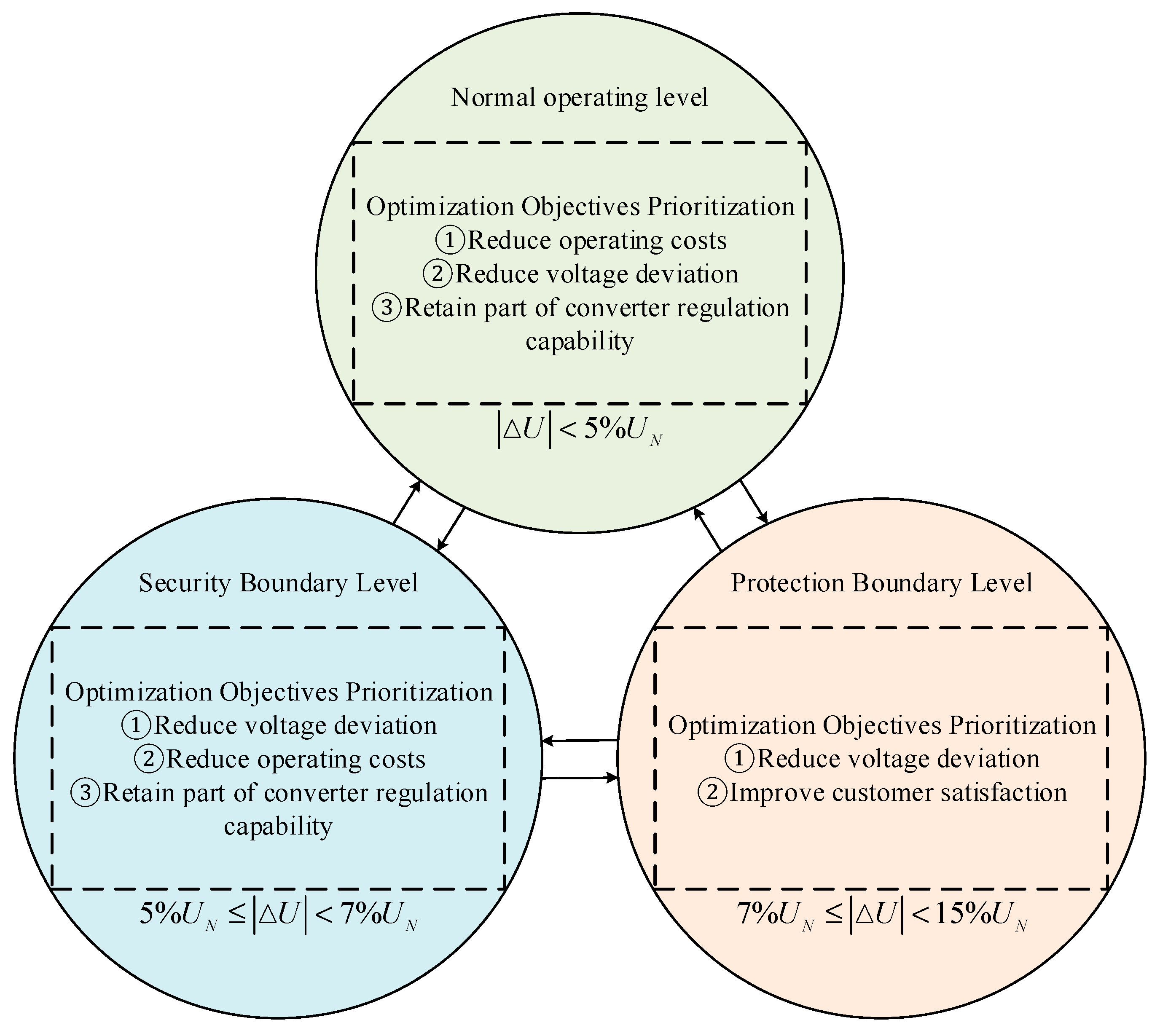
3.1. Classification of Voltage Overrun
3.2. FIND Multi-Level Optimal Scheduling Model Framework
3.3. Optimization Objectives
4. Principles for Determining Multi-Objective Dynamic Weighting Coefficients
5. Constraints and Conversion
5.1. Constraints
5.2. Model Second-Order Cone Processing
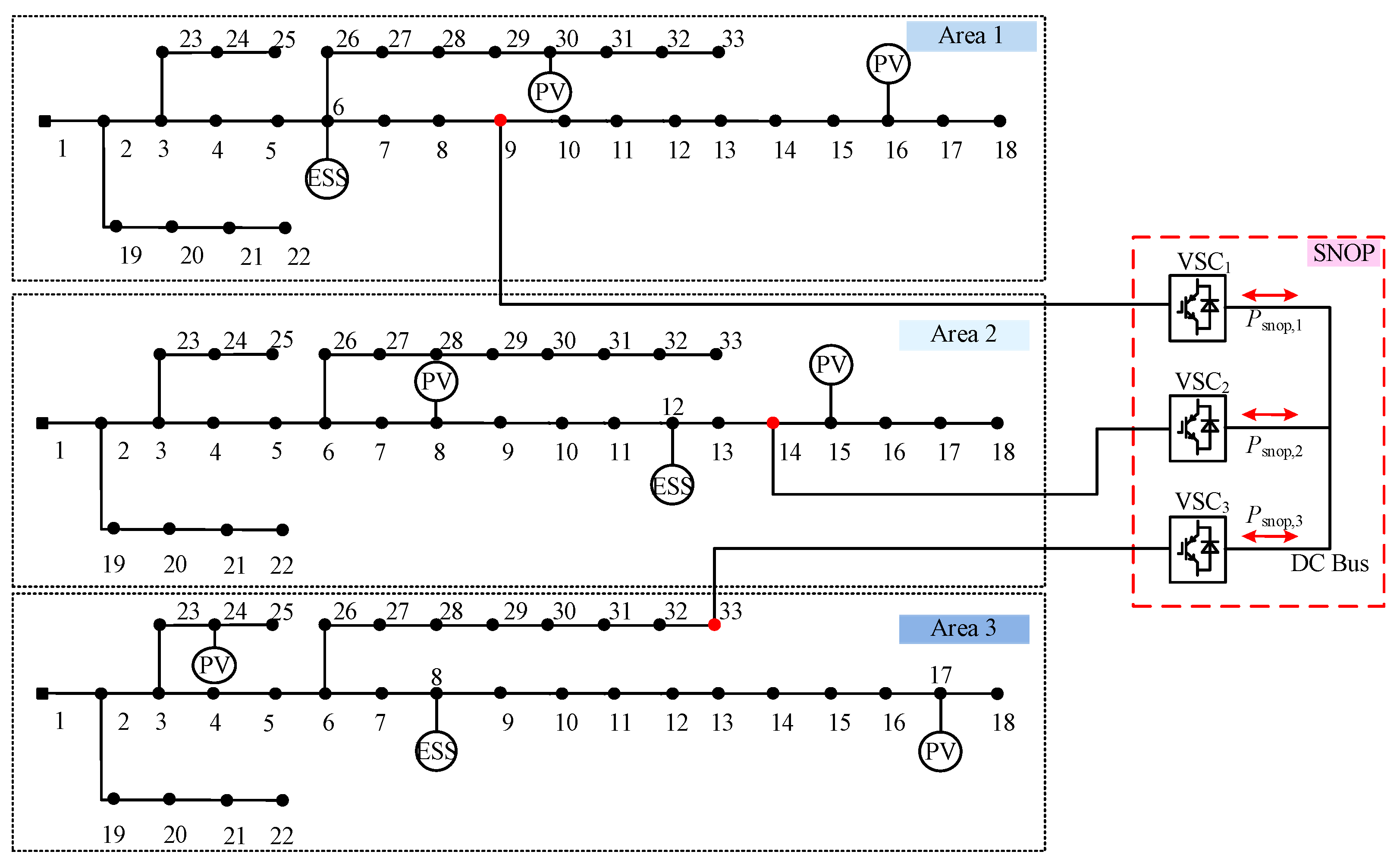
6. Example Analysis
6.1. Example Data
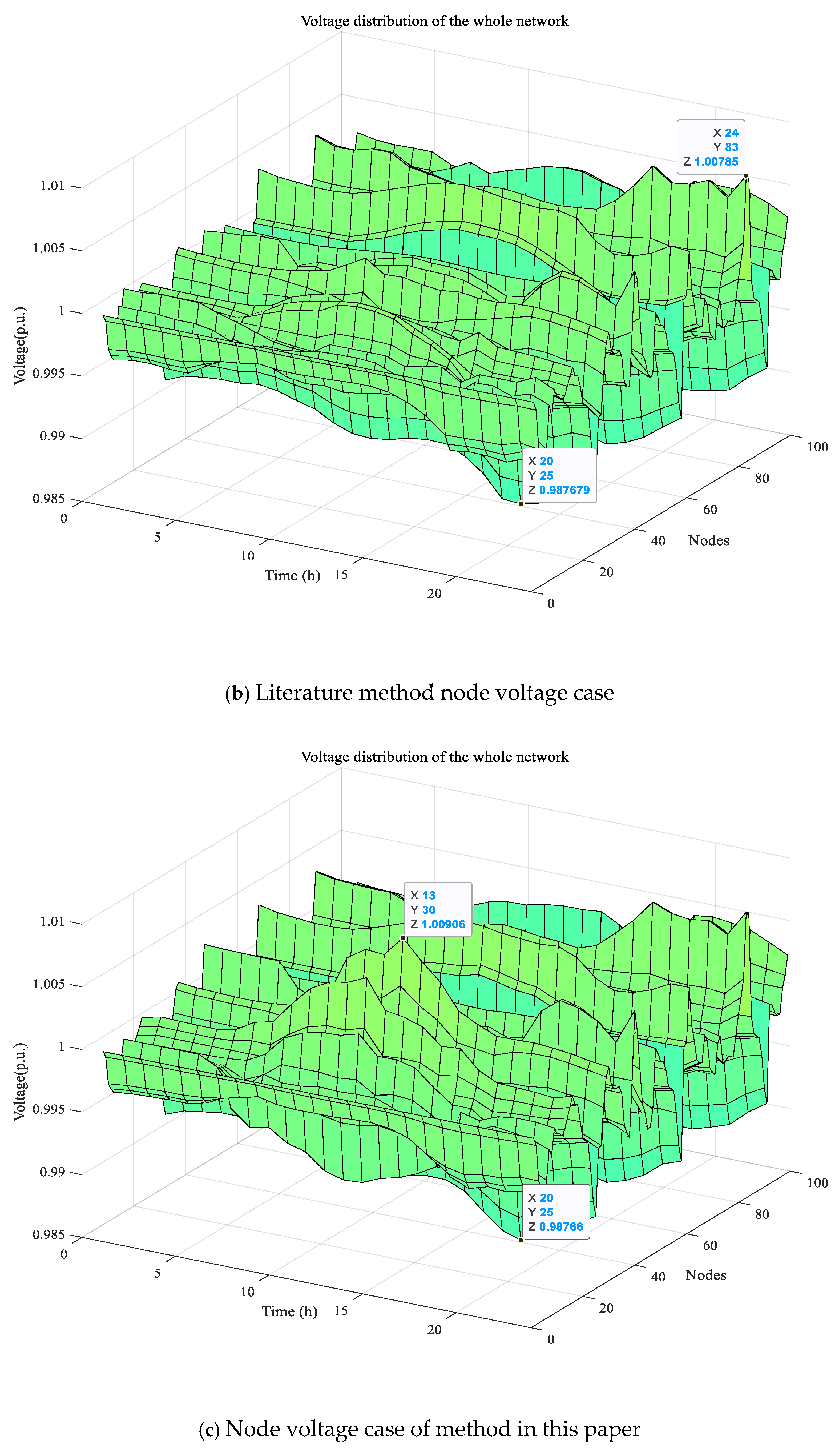
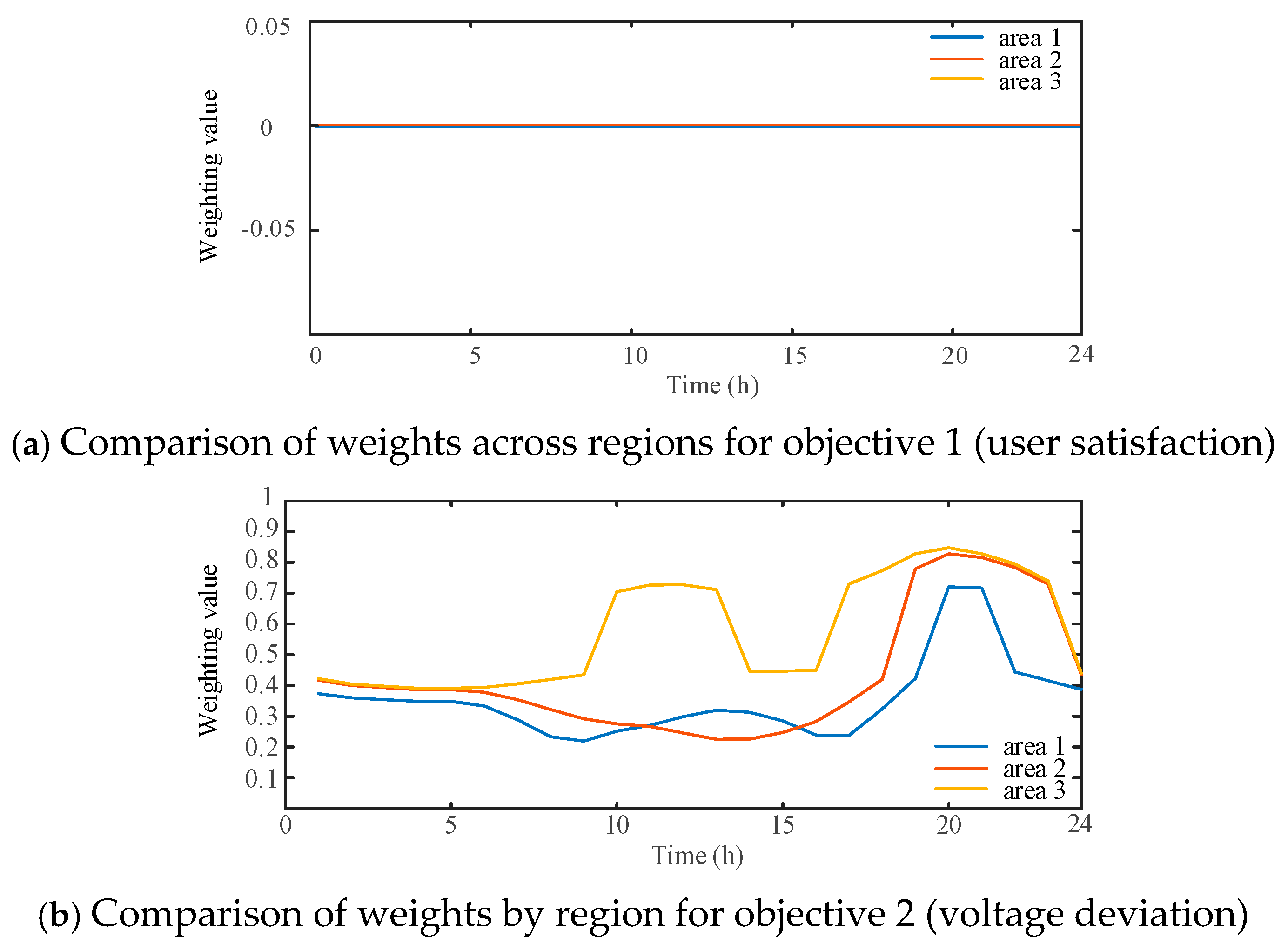
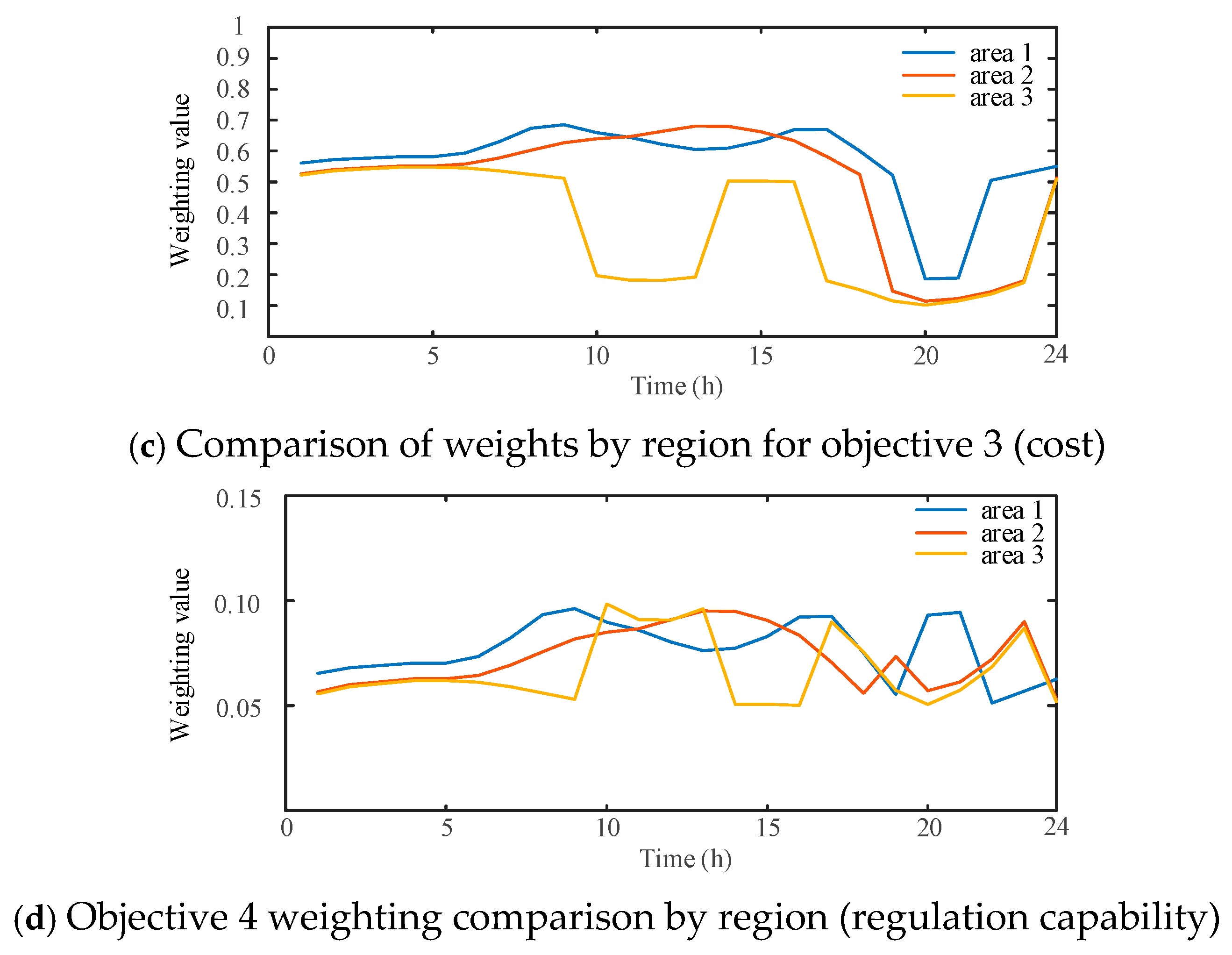
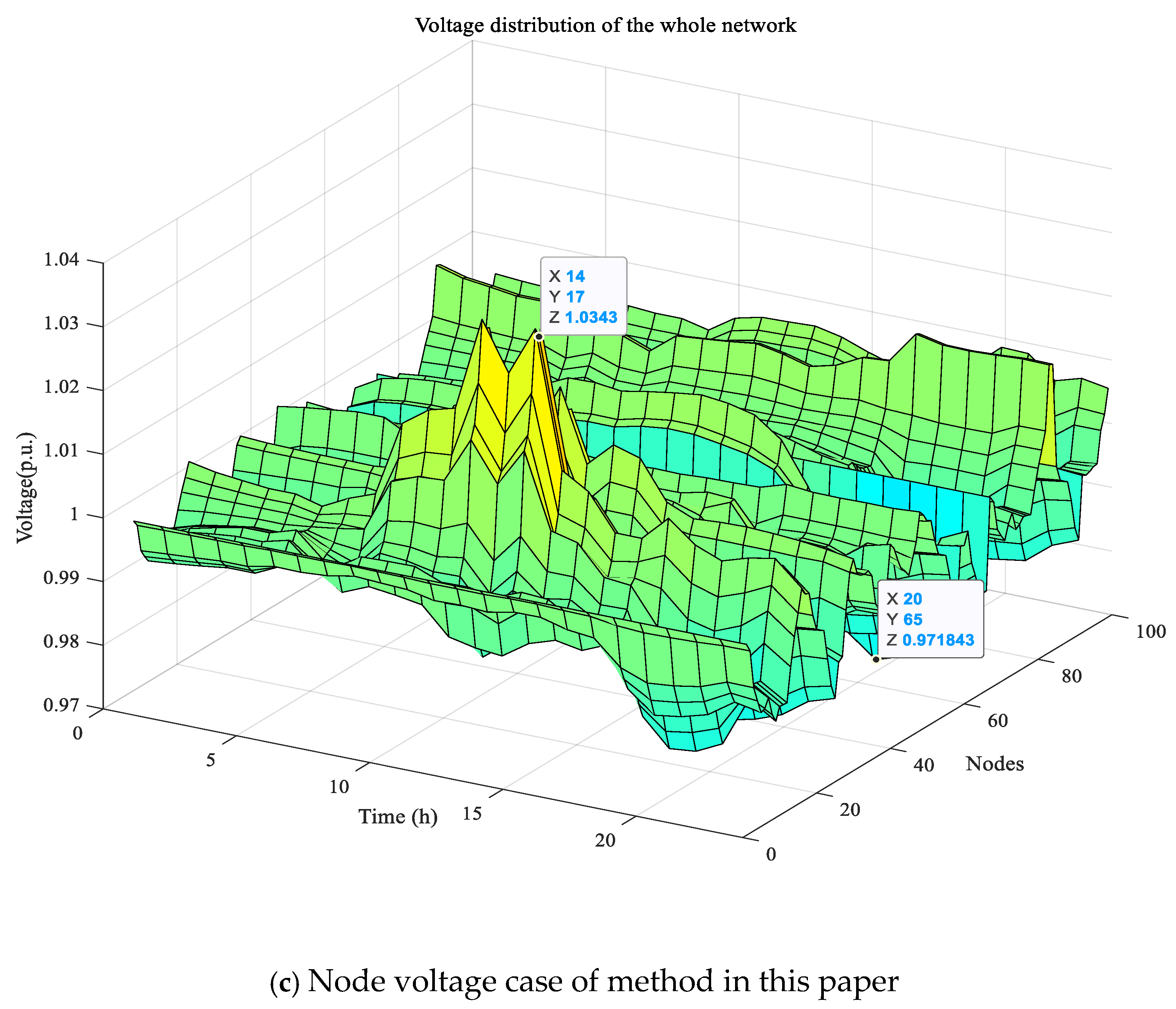
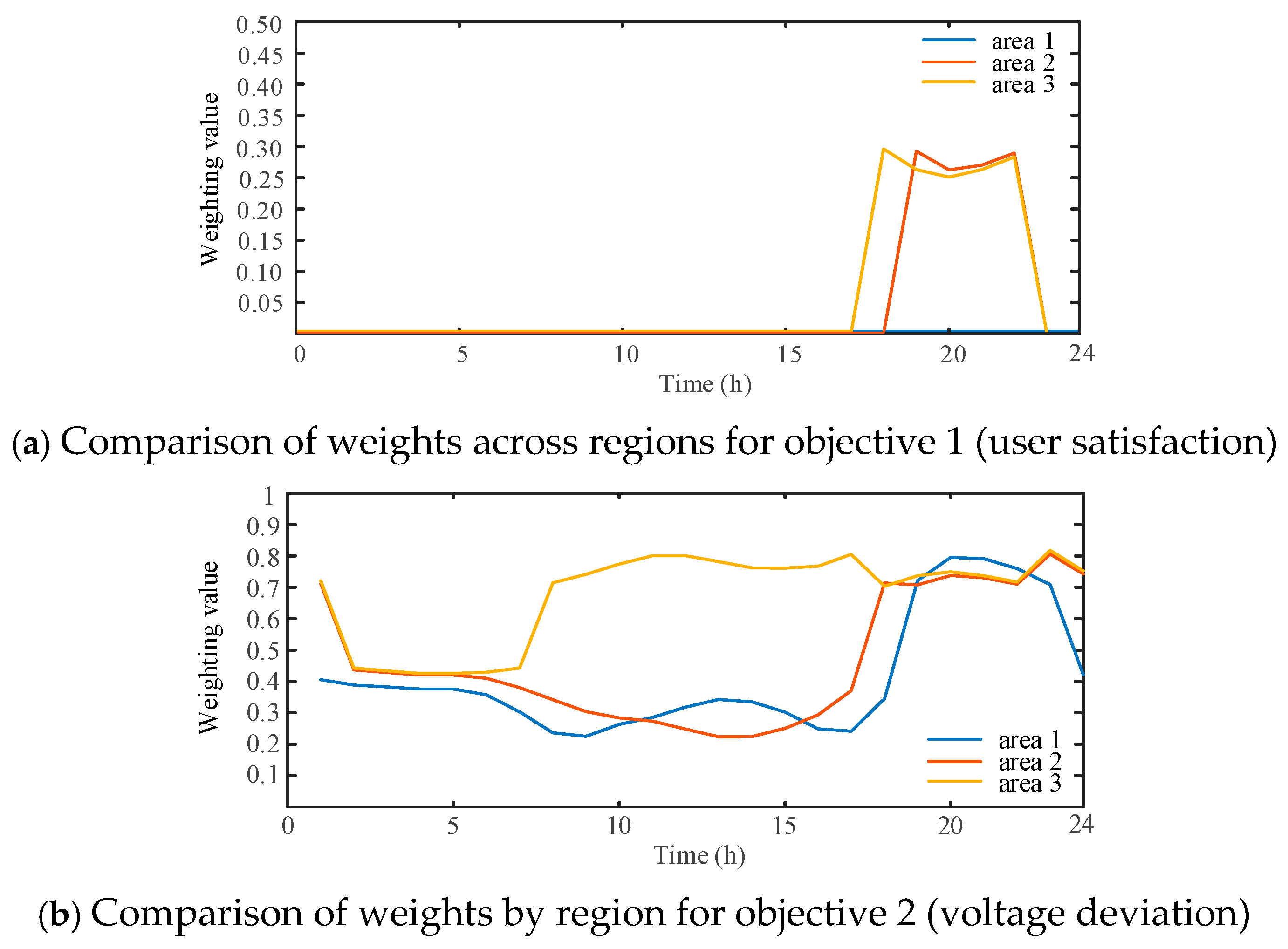
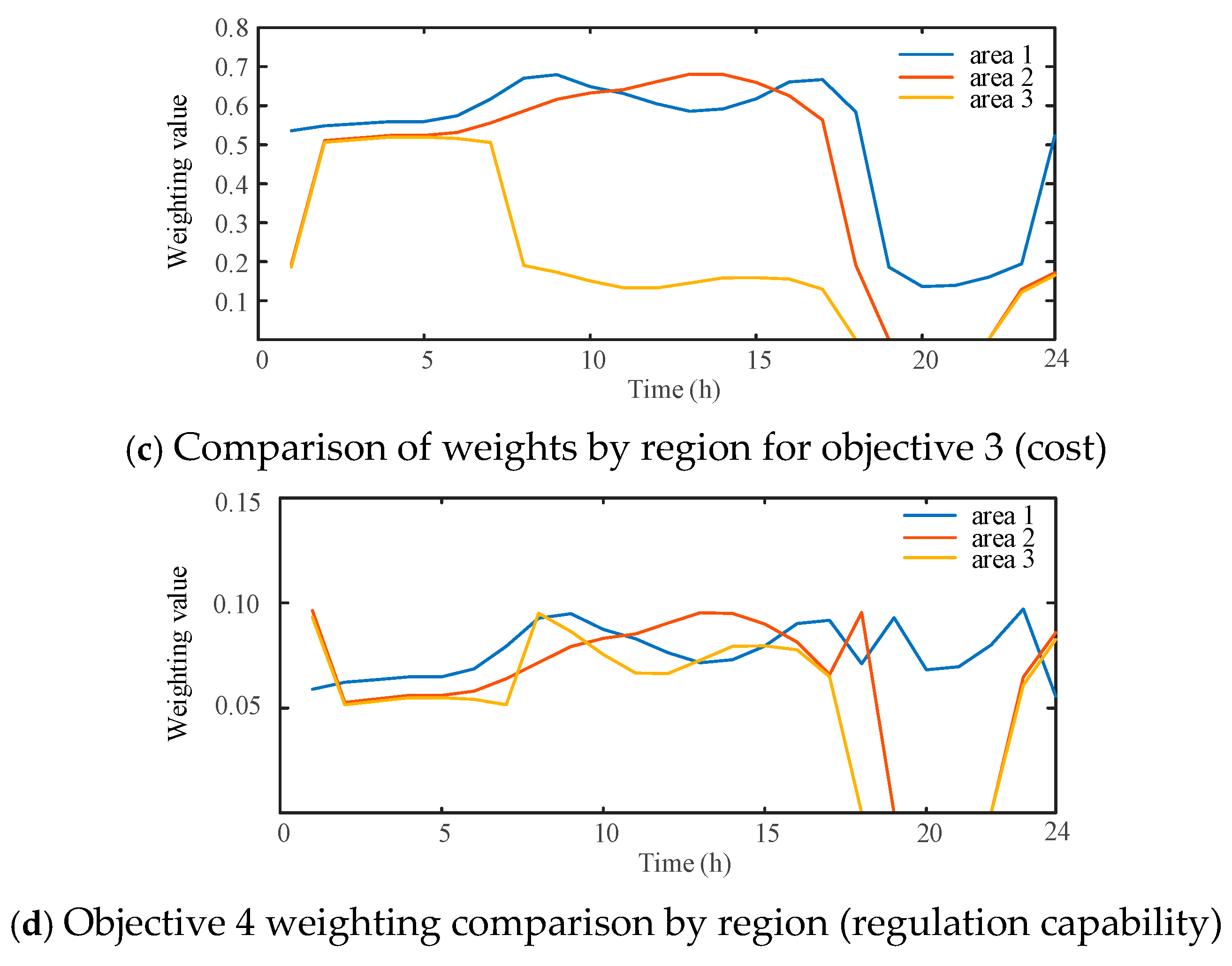
6.2. Comparison and Analysis of Example Results
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Yin, X.; Lai, J.; Yin, X.; Wang, Y.; Yin, Y.; Hu, J. Hybrid interlinking transformer and its fault blocking coordination control for microgrid. Electr. Power Autom. Equip. 2023, 43, 145–151+207. [Google Scholar]
- Li, J.; Wang, D.; Fan, H.; Yang, D.; Fang, R.; Sang, Z. Hierarchical optimal control method for active distribution network with mobile energy storage. Autom. Electr. Power Syst. 2022, 46, 189–198. [Google Scholar]
- Xue, J.; Wang, D.; Yu, Z.; Li, H.; Zhu, X.; Dou, C. Optimized dispatch of wind-diesel storage based on wind power adjustable uncertainty cost. J. Zhengzhou Univ. 2019, 40, 73–79. [Google Scholar]
- Liu, L.; Zhang, Y.; Xu, Q. An Interval Optimal Scheduling Method Considering the Influence of Power Uncertainty and the Flexibility of Distribution Network. J. Power Grid Technol. 2020, 44, 4654–4664. [Google Scholar]
- Rueda-Medina, A.C.; Padilh-Feltrin, A. Distributed generators as providers of reactive power support—A market approach. IEEE Trans. Power Syst. 2013, 28, 490–502. [Google Scholar] [CrossRef]
- Liang, X.; Saaklayen, A.; Igder, M.A.; Shawon, S.M.R.H.; Faried, S.O.; Janbakhsh, M. Planning and service restoration through microgrid formation and soft open points for distribution network modernization: A review. IEEE Trans. Ind. Appl. 2022, 58, 1843–1857. [Google Scholar] [CrossRef]
- Jiang, X.; Zhou, Y.; Ming, W.; Yang, P.; Wu, J. An overview of soft open points in electricity distribution networks. IEEE Trans. Smart Grid 2022, 13, 1899–1910. [Google Scholar] [CrossRef]
- Zheng, G.; Zhu, E.; Zhang, H.; Liu, Y.; Li, Z. Flexible interconnection planning for distribution station areas of high-ratio photovoltaic based on master-slave game. Electr. Power Constr. 2024, 45, 100–110. [Google Scholar]
- Hu, P.; Zhu, N.; Ji, D.; Ju, P.; Li, Y. Research Progress and Prospects of Key Technologies of Flexible Interconnected Smart Distribution Network. Autom. Electr. Power Syst. 2021, 45, 2–12. [Google Scholar]
- Zheng, S.; Liao, K.; Yang, J. Active-reactive Power Robust Collaborative Optimization Strategy for Active Distribution System with Multi-microgrids Based on Back-to-back Converter Interconnection. Power Syst. Technol. 2023, 47, 5005–5017. [Google Scholar]
- Sun, S.; Zhang, Y.; Qi, X. Optimized scheduling of low-voltage AC/DC distribution network considering the uncertainty of source and load. Distrib. Util. 2023, 40, 25–32. [Google Scholar]
- Zhang, S.; Yang, Y.; Pei, W. Research and comparative analysis of different port flexible multi-state switches for regulation and control of distribution network operation. High Volt. Eng. 2019, 45, 3120–3129. [Google Scholar]
- Gao, H.; Liu, J.; Wang, L.; Wei, Z. Decentralized energy management for networked microgrids in future distribution systems. IEEE Trans. Power Syst. 2018, 33, 3599–3610. [Google Scholar] [CrossRef]
- Zhao, J.; Zhang, M.; Zhang, S.; Yang, Q. Optimizationstrategy of multi-microgrid cooperative operation considering carbon trading and renewable energy uncertainties. Electr. Power 2023, 56, 62–71. [Google Scholar]
- Dong, Z.; Xu, T.; Li, Y. Multi-time Scale Optimal Scheduling of Active Distribution Network Considering Source Load Storage Coordination. J. Sci. Technol. Eng. 2024, 24, 10321–10329. [Google Scholar]
- Yang, Y.; Yang, P.; Zhao, Z.; Lai, L.L. A multi-timescale coordinated optimization framework for economic dispatch of micro-energy grid considering prediction error. IEEE Trans. Power Syst. 2024, 39, 3211–3226. [Google Scholar] [CrossRef]
- Liang, D.; Guo, Y.; Wang, X.; Liu, Q.; Wang, S. Two-Stage Robust Optimization for Flexible Interconnected Distribution Systems Considering Energy Storages and Dynamic Reconfiguration. J. Electr. Power Constr. 2022, 43, 94–103. [Google Scholar]
- Veisi, M.; Adabi, F.; Kavousi-Fard, A.; Karimi, M. A framework of electricity market based on two-layer stochastic power management for microgrids. IEEE Access 2022, 10, 41047–41063. [Google Scholar] [CrossRef]
- Zhu, X.; Jiang, Q.; Liu, M. Two-stage optimal scheduling of integrated energy system considering source-load uncertainty. Electr. Power Autom. Equip. 2023, 43, 9–16, 32. [Google Scholar]
- Ding, T.; Li, C.; Yang, Y.; Jiang, J.; Bie, Z.; Blaabjerg, F. A two-stage robust optimization for centralized-optimal dispatch of photovoltaic inverters in active distribution networks. IEEE Trans. Sustain. Energy 2017, 8, 744–754. [Google Scholar] [CrossRef]
- Wang, S.; Li, Q.; Zhao, Q.; Lin, Z.; Wang, K. Improved particle swarm algorithm for multi-objective optimization of AC/DC distribution network voltage taking into account source-load stochasticity. J. Power Syst. Autom. 2021, 33, 10–17. [Google Scholar]
- Xie, M.; Zhang, S.; Li, Y. Optimal dispatch of AC/DC hybrid low-voltage distribution network based on multi-mode flexible interconnection. Autom. Electr. Power Syst. 2023, 47, 79–89. [Google Scholar]
- Yan, Y.; Liao, Q.; Liu, D.; Hu, J. Power flow between ness based SNOP allocation and active distribution network optimization. South. Power Syst. Technol. 2015, 9, 92–98. [Google Scholar]
- Zhao, J.; Li, Y.; Li, P.; Ji, H.; Wang, C.; Wu, J. Sequential voltage regulation of soft normally open point in active distribution network based on second-order cone programming. High Volt. Eng. 2016, 42, 2134–2141. [Google Scholar]
- Zhu, G.; Zhang, Y.; Ge, L.; Wang, L. Multi time-scale voltage optimization of flexible interconnected distribution network with self-energy storage. Autom. Electr. Power Syst. 2021, 45, 71–79. [Google Scholar]
- Wang, Y.; Liu, S.; Wang, Y.; Lv, Z.; Liang, J. Adaptive optimal scheduling of flexible interconnected stations based on operation state classification. Power Autom. Equip. 2024, 44, 10–17. [Google Scholar]
- Wang, C.; Sun, C.; Li, P.; Wu, J.; Xing, F.; Yu, Y. SNOP-based operation optimization and analysis of distribution networks. Autom. Electr. Power Syst. 2015, 39, 82–87. (In Chinese) [Google Scholar]





| Voltage Overrun Level | |
|---|---|
| Normal operation | |
| Safe Boundary | |
| Protection Boundary |
| Optimized Scheduling Strategy | Fixed Weighting | Literature Method | Method of This Paper |
|---|---|---|---|
| Weighting factor Total system cost (¥) Total time spent (s) | 1:1:1:1 68,749.54 43.2543 | Adaptive weighting 65,802.34 44.8289 | Dynamic weighting 65,768.22 41.7904 |
| Iterations Convergence interval (%) | 21 0.000123 | 20 0.0000719 | 20 0.0000716 |
| Optimized Scheduling Strategy | Fixed Weighting | Literature Method | Method of This Paper |
|---|---|---|---|
| Weighting factor Total system cost (¥) Total time spent (s) | 1:1:1:1 104,051.95 44.1464 | Adaptive weighting 102,846.66 44.3285 | Dynamic weighting 98,660.59 43.0962 |
| Iterations Convergence interval (%) | 21 0.000083 | 21 0.0000834 | 21 0.0001118 |
| Optimized Scheduling Strategy | Fixed Weighting | Literature Method | Method of This Paper |
|---|---|---|---|
| Weighting factor Total system cost (¥) Total time spent (s) | 1:1:1:1 125,877.10 44.6357 | Adaptive weighting 122,202.83 45.0877 | Dynamic weighting 118,535.88 44.3198 |
| Iterations Convergence interval (%) | 20 0.000135 | 22 0.000058 | 23 0.0000667 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pang, D.; Wang, Z.; Shi, X.; Ge, J.; Wang, Z.; Yi, H.; Zhuang, Y.; Yin, Y.; Wang, W. Multi-Level Dynamic Weight Optimization Scheduling Strategy for Flexible Interconnected Distribution Substations Based on Three-Port SNOPs. Energies 2025, 18, 2421. https://doi.org/10.3390/en18102421
Pang D, Wang Z, Shi X, Ge J, Wang Z, Yi H, Zhuang Y, Yin Y, Wang W. Multi-Level Dynamic Weight Optimization Scheduling Strategy for Flexible Interconnected Distribution Substations Based on Three-Port SNOPs. Energies. 2025; 18(10):2421. https://doi.org/10.3390/en18102421
Chicago/Turabian StylePang, Dan, Zhipeng Wang, Xiaomeng Shi, Jinming Ge, Zhenhao Wang, Hongyin Yi, Yan Zhuang, Yu Yin, and Wei Wang. 2025. "Multi-Level Dynamic Weight Optimization Scheduling Strategy for Flexible Interconnected Distribution Substations Based on Three-Port SNOPs" Energies 18, no. 10: 2421. https://doi.org/10.3390/en18102421
APA StylePang, D., Wang, Z., Shi, X., Ge, J., Wang, Z., Yi, H., Zhuang, Y., Yin, Y., & Wang, W. (2025). Multi-Level Dynamic Weight Optimization Scheduling Strategy for Flexible Interconnected Distribution Substations Based on Three-Port SNOPs. Energies, 18(10), 2421. https://doi.org/10.3390/en18102421





