Experimental Testing of a Heat Exchanger with Composite Material for Deep Dehumidification
Abstract
1. Introduction
2. Materials
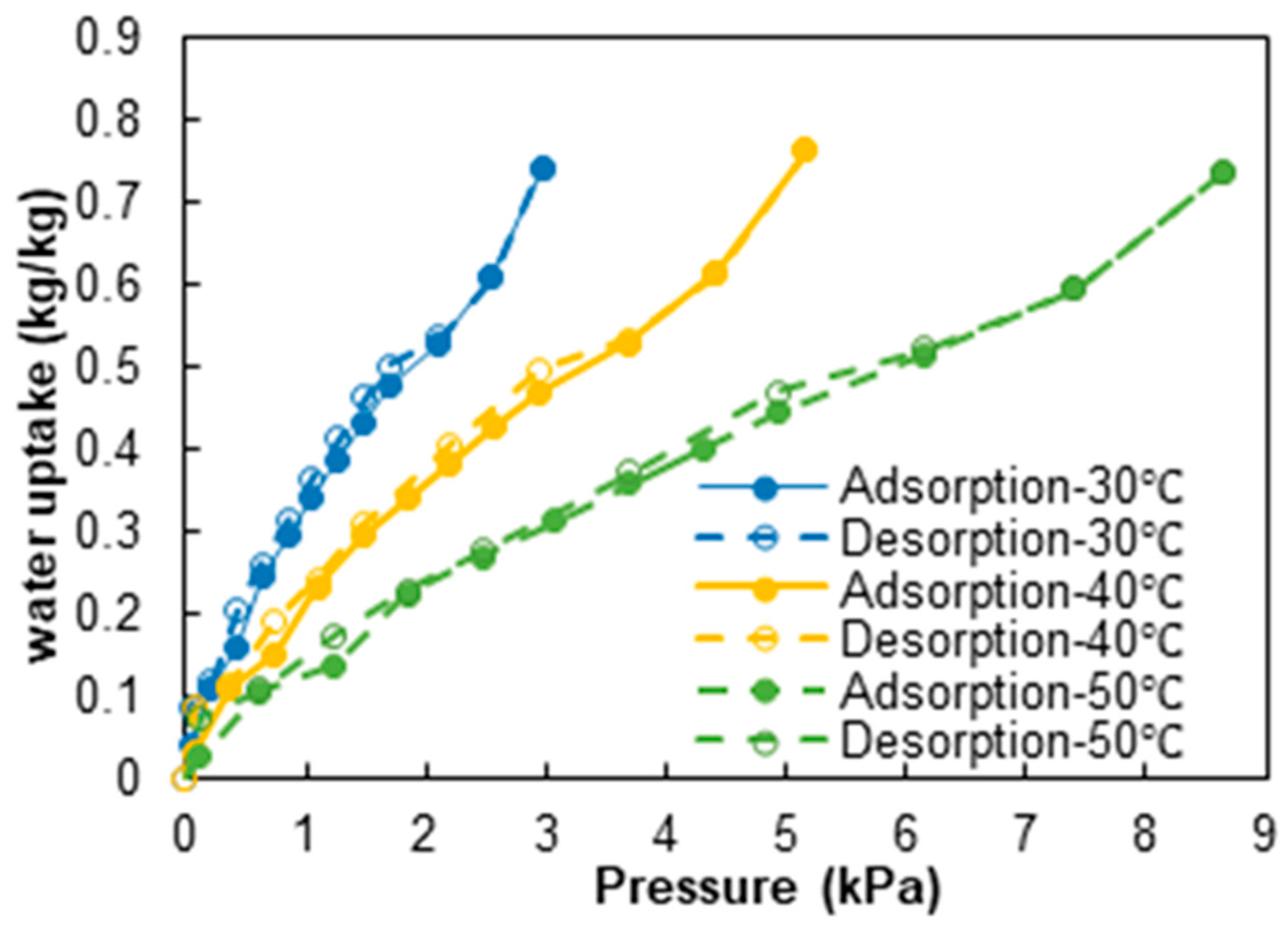
2.1. Preparation and Characterization of Composite Material
- The matrix and salt were dried in an oven at 150 °C for 8 h.
- The solution was prepared by combining distilled water with the salt. The required quantity of water was determined by considering the pore volume of the matrix and the desired total mass of the matrix. The mixing process took place in a plastic mixer, similar to the ones used for cement.
- The solution was added in small amounts onto the matrix while stirring gently to ensure even distribution.
- The composite was dried in an oven for 8 h.
2.2. Selection and Preparation of the Heat Exchanger
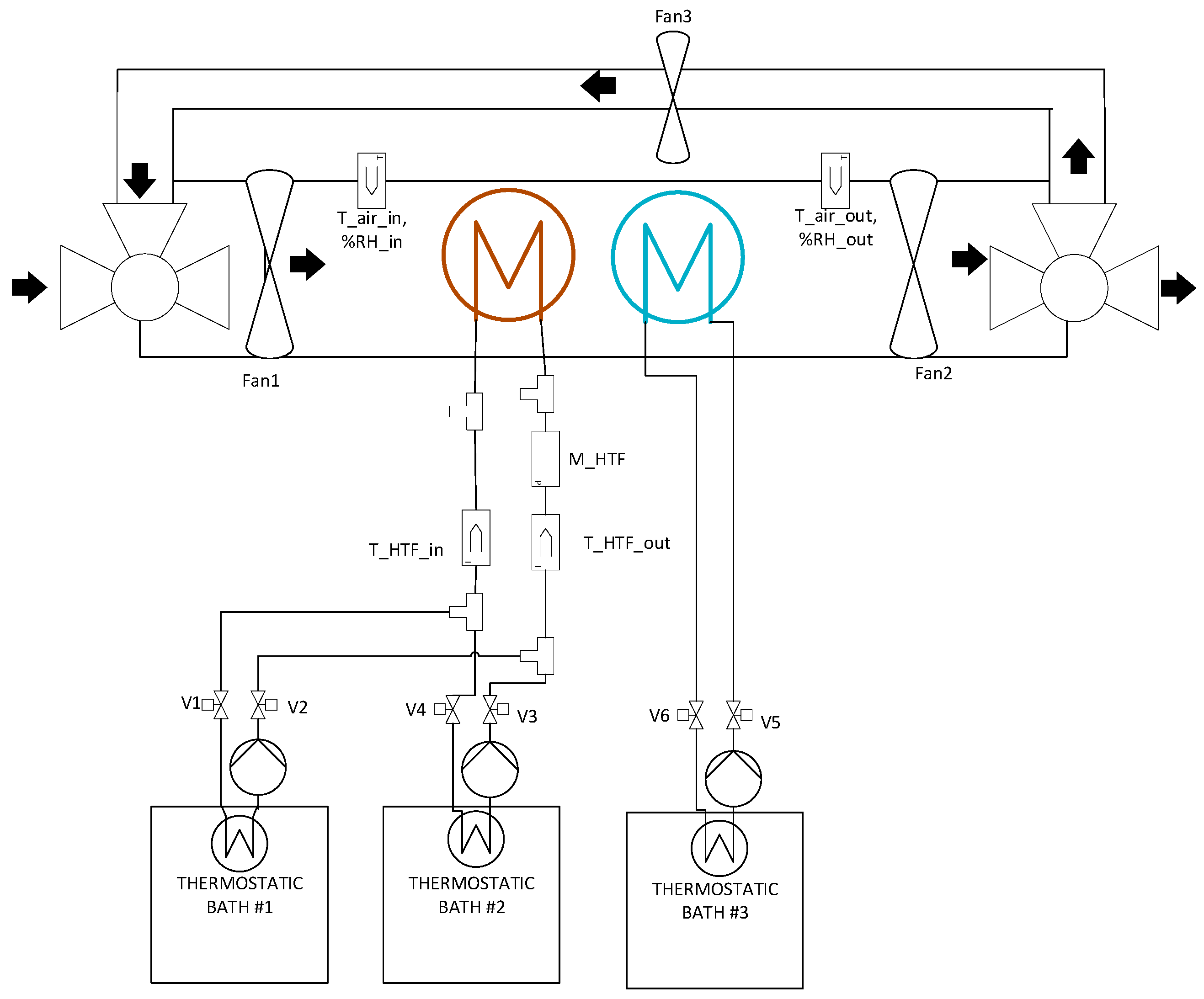
3. Experimental Facilities
4. Results
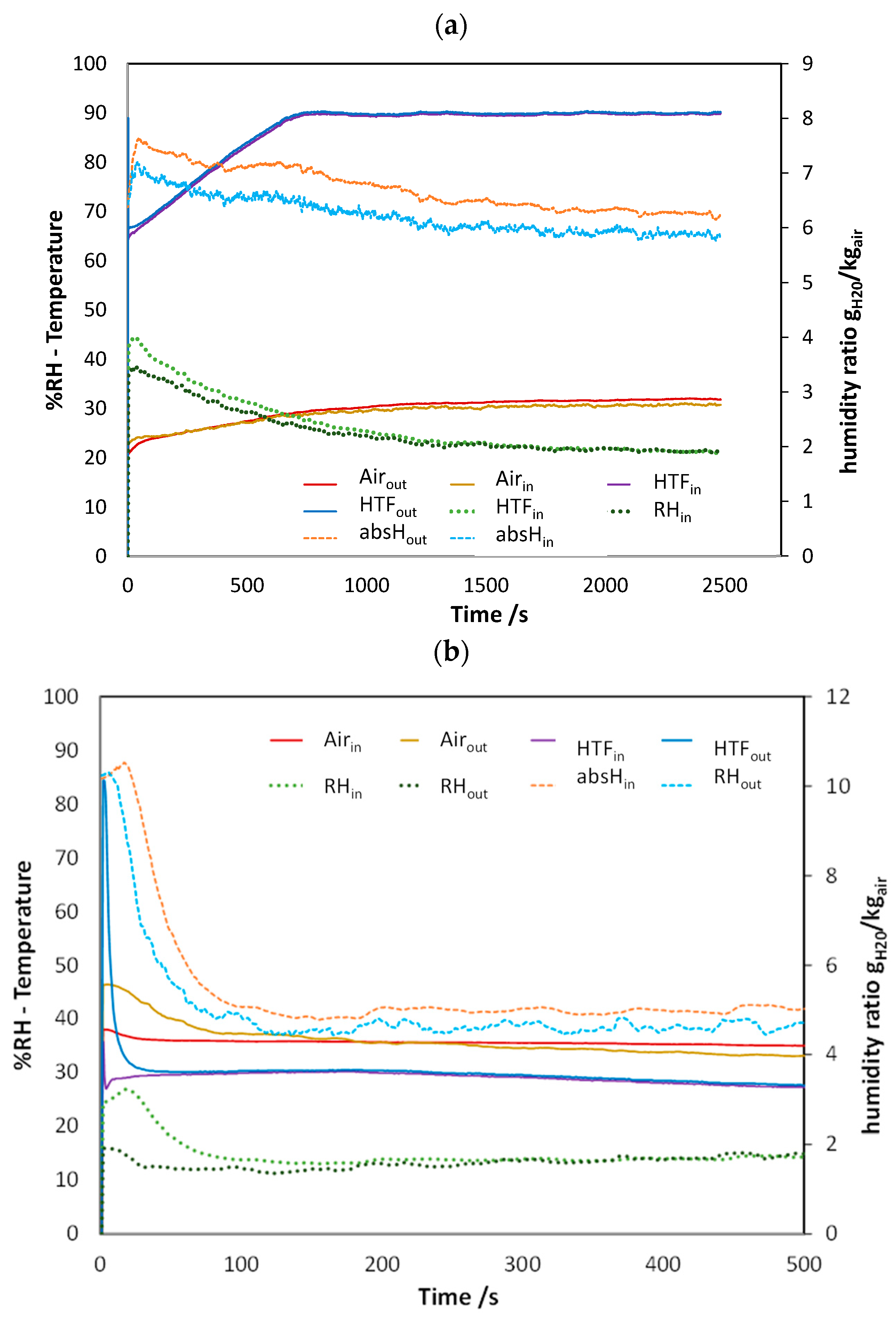
4.1. Typical Trends During Adsorption and Desorption
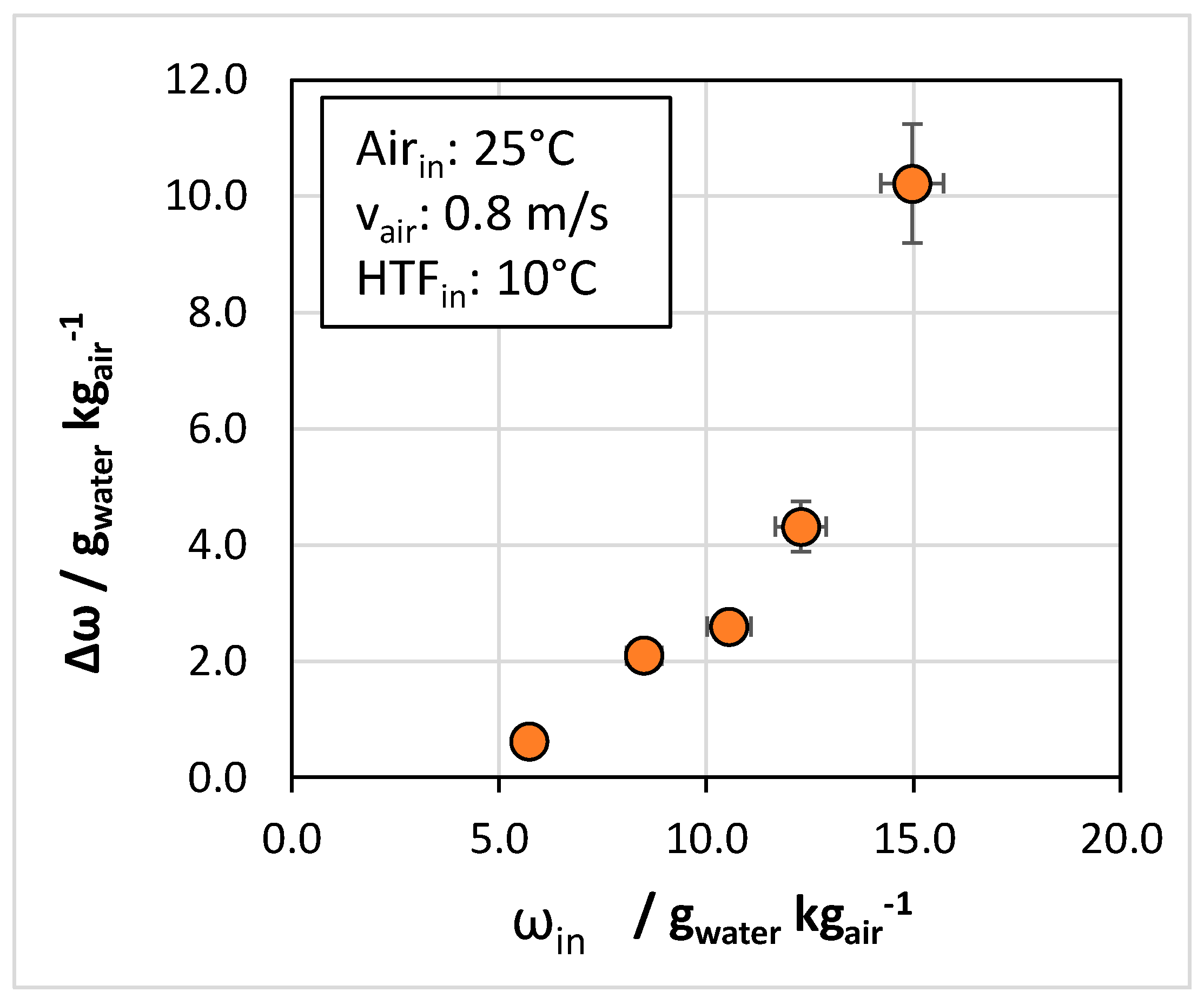
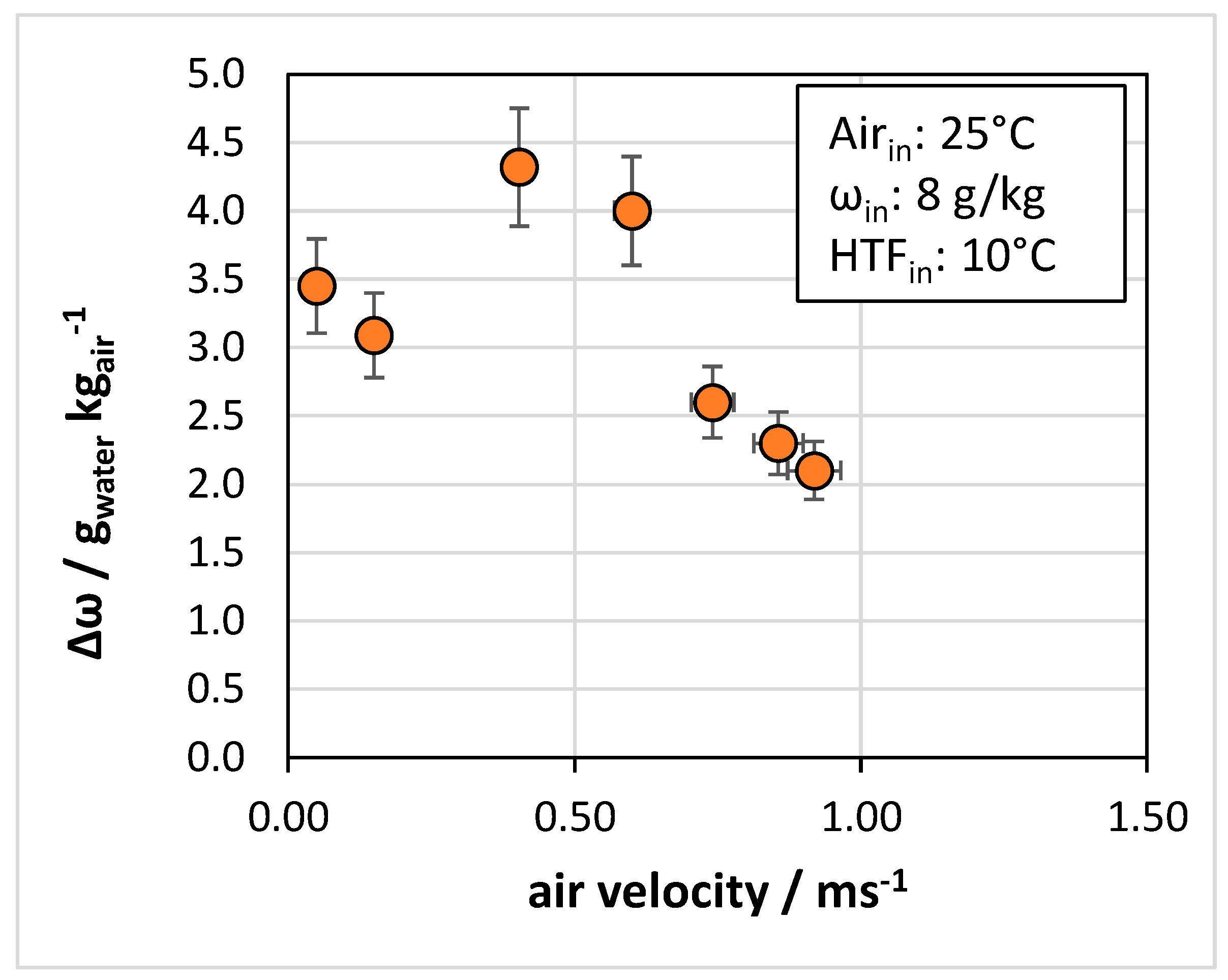
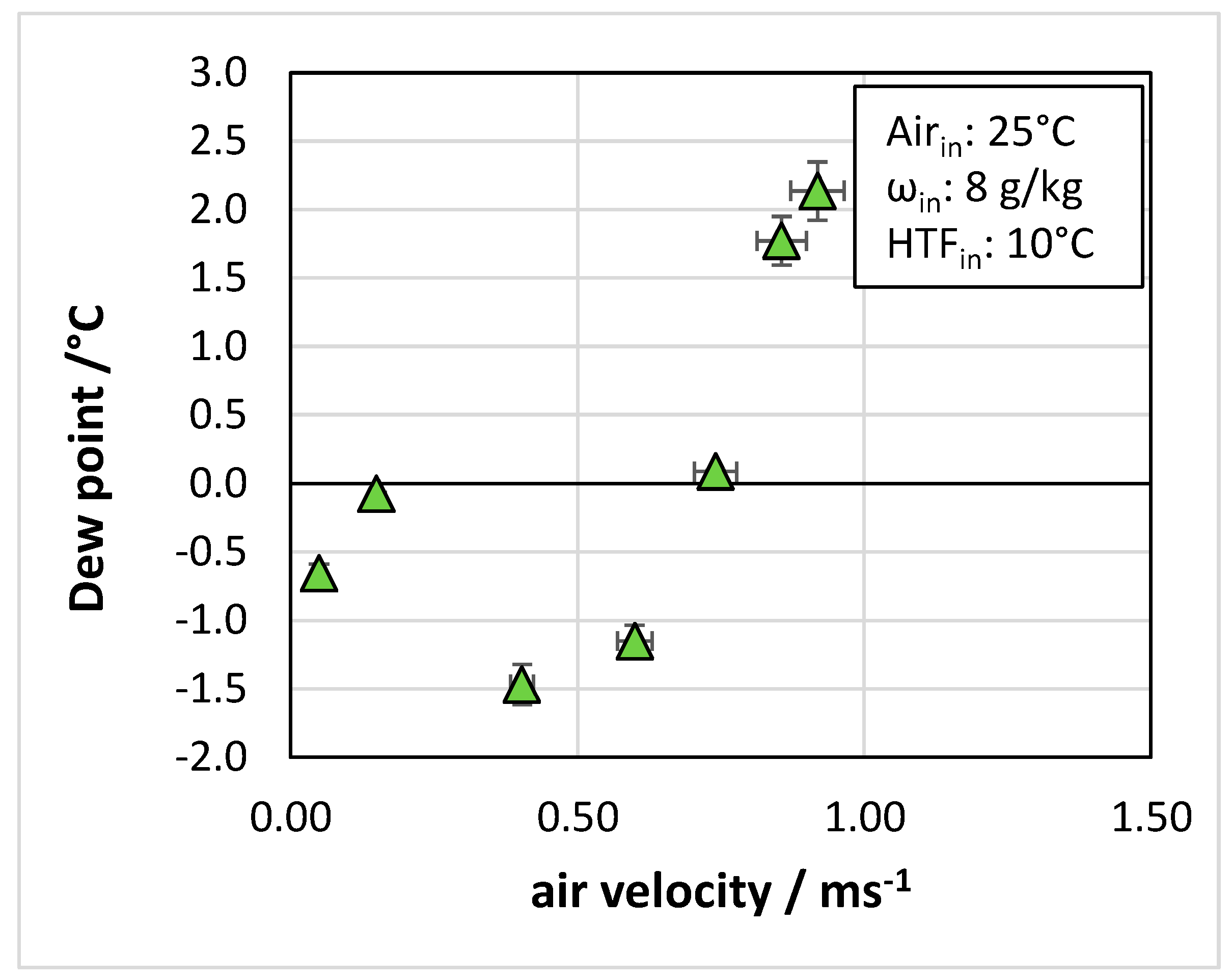
4.2. Effect of Ambient Conditions
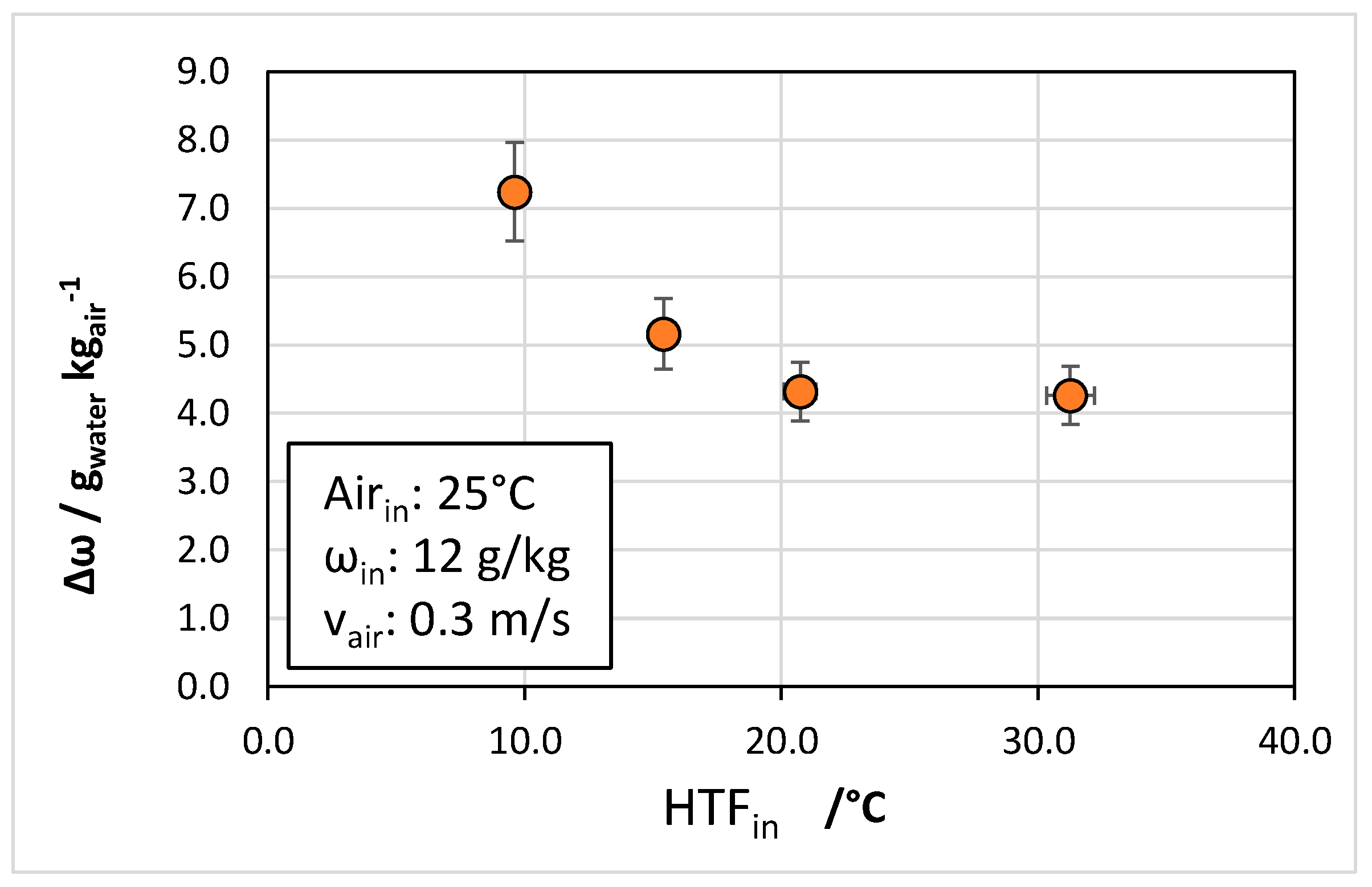
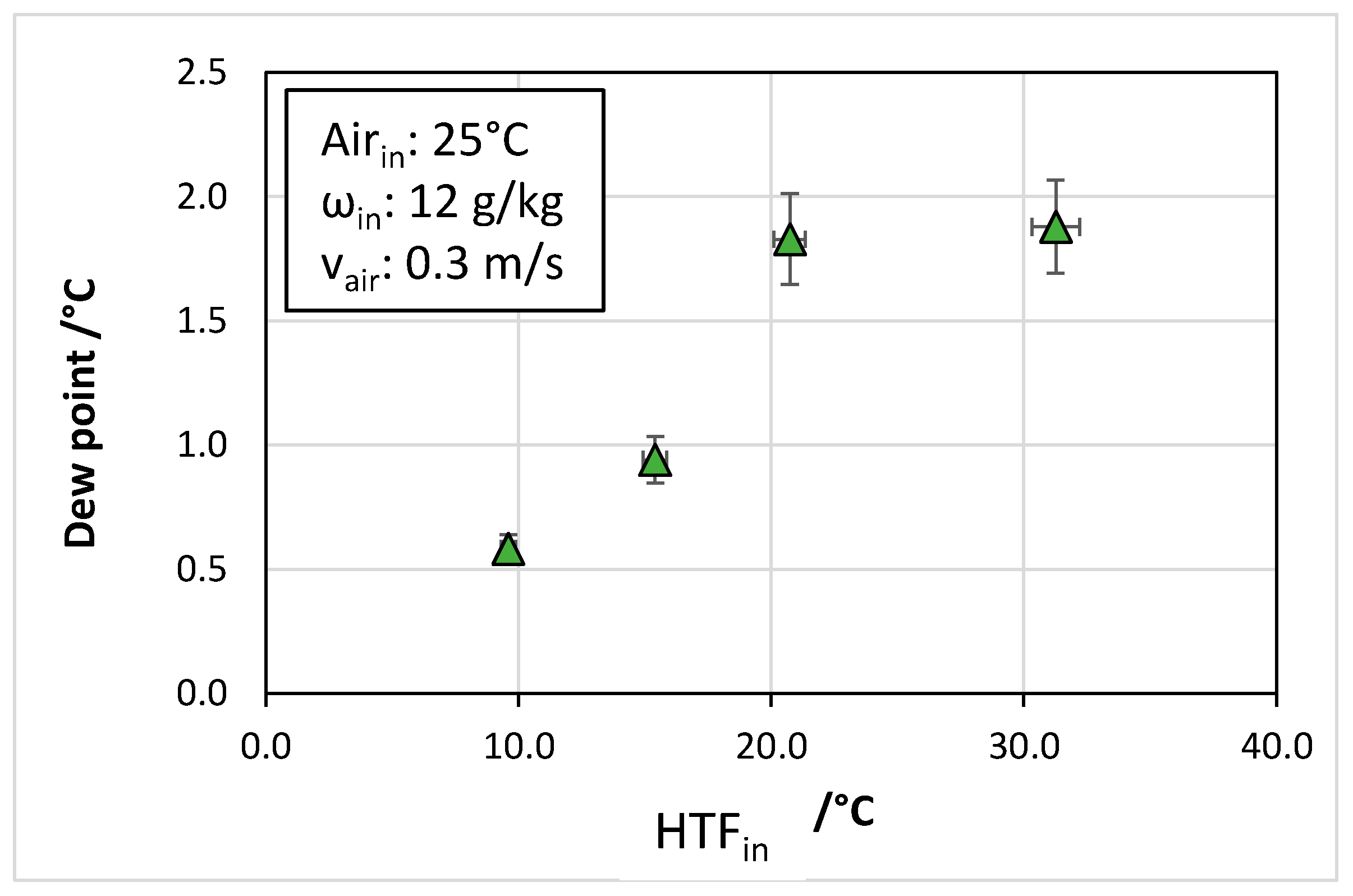
4.3. Effect of Operating Conditions
5. Discussion
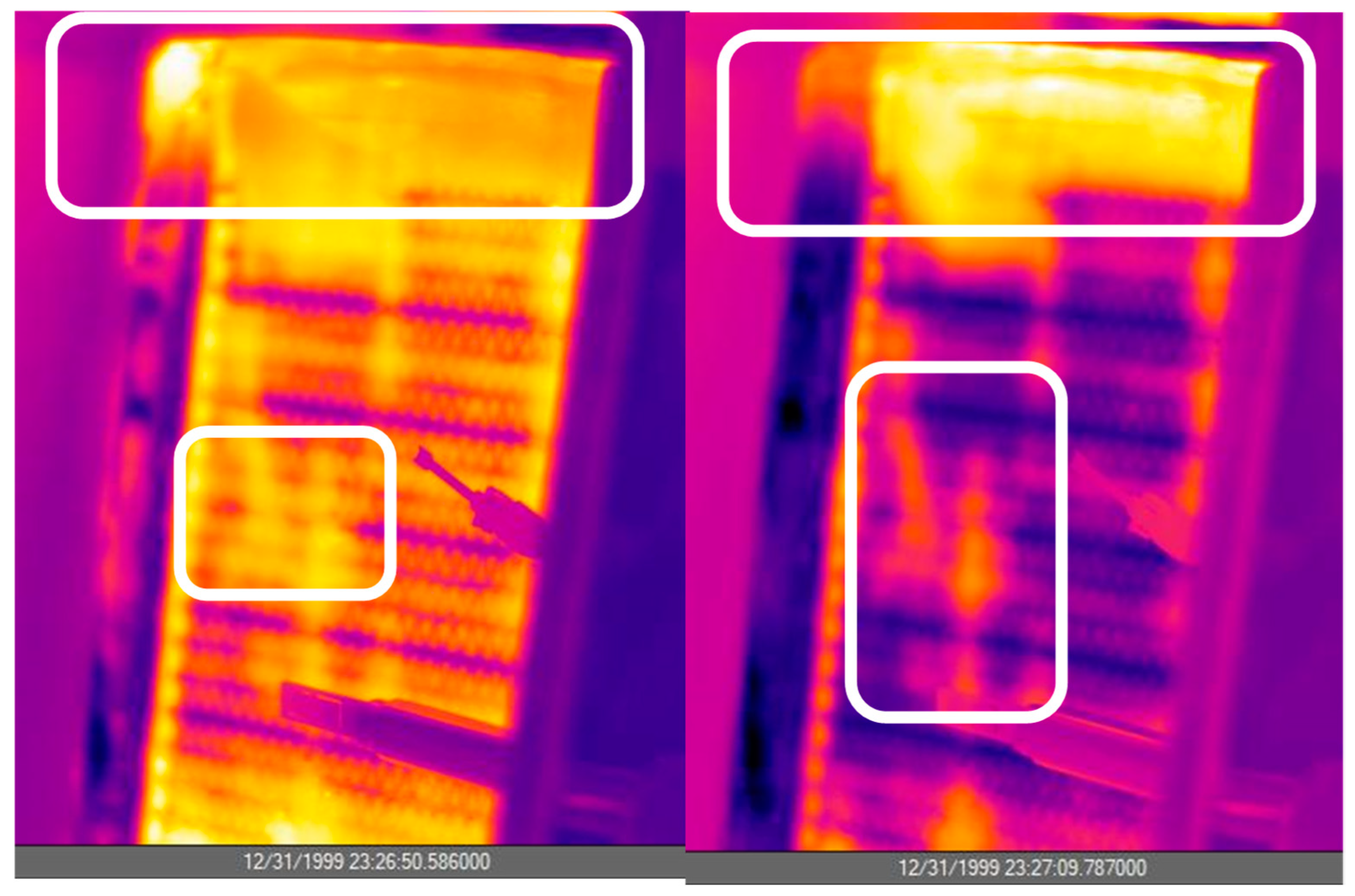
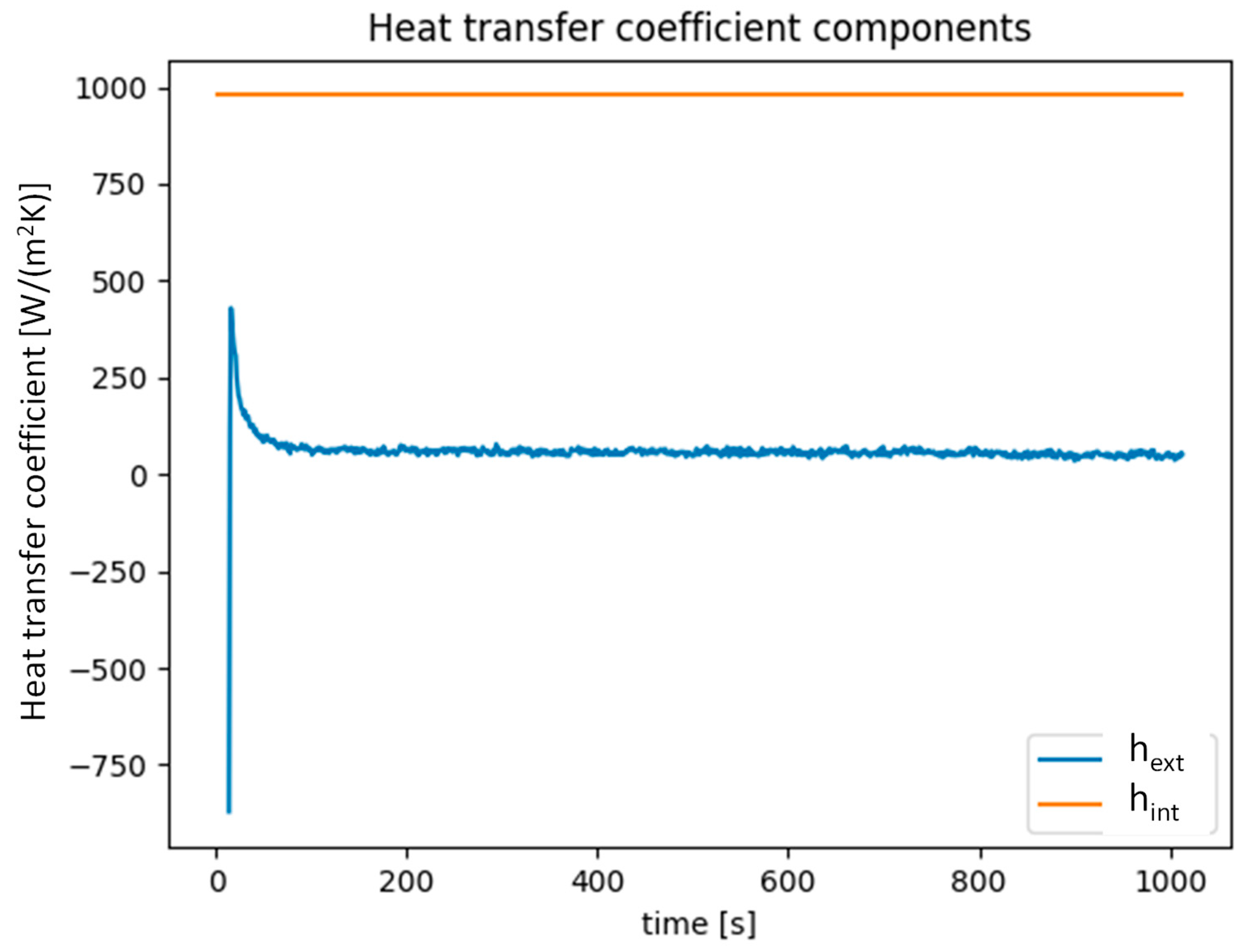
5.1. Verification of Heat Transfer in the HEX
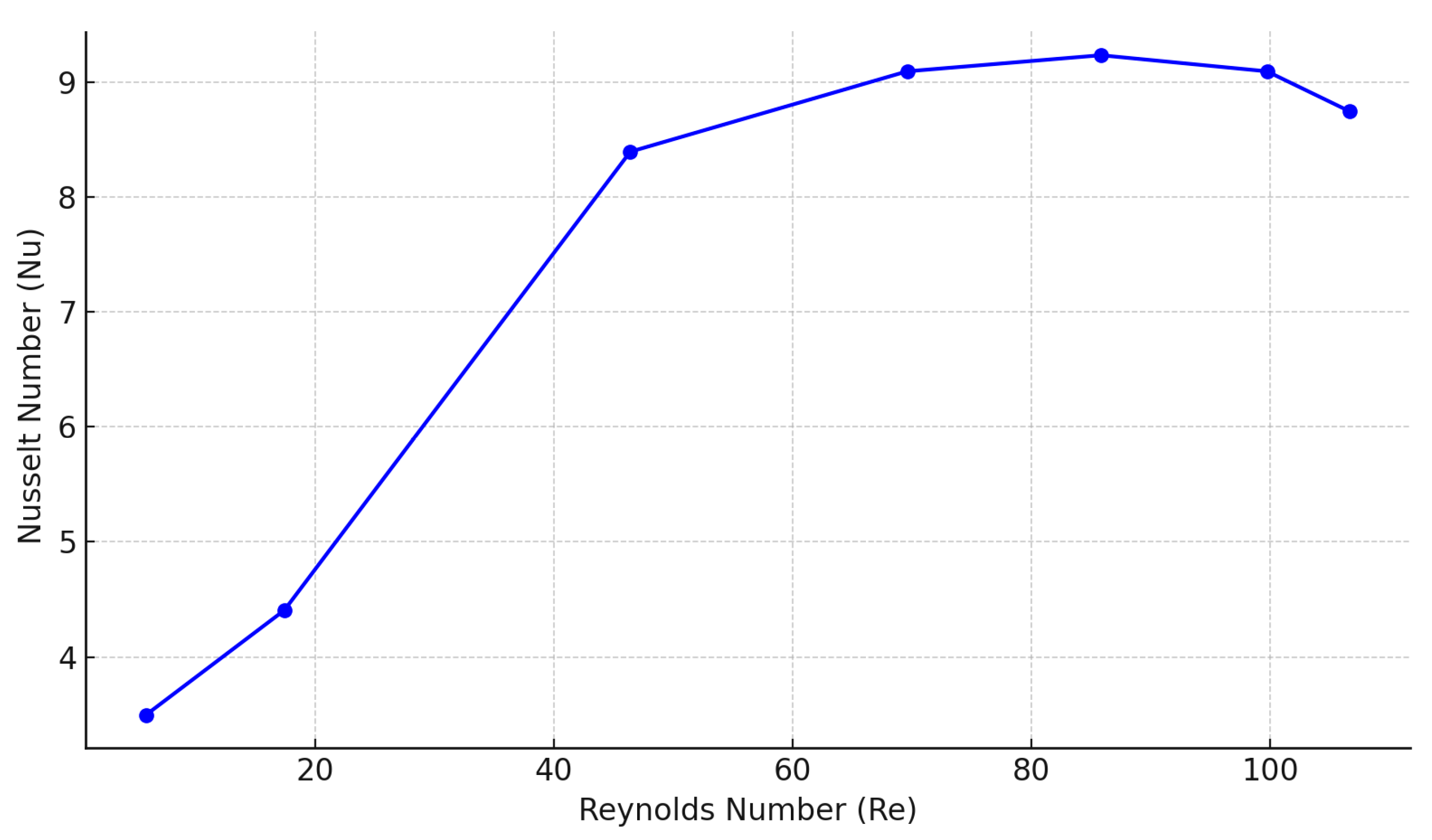
5.2. Heat Transfer Analysis
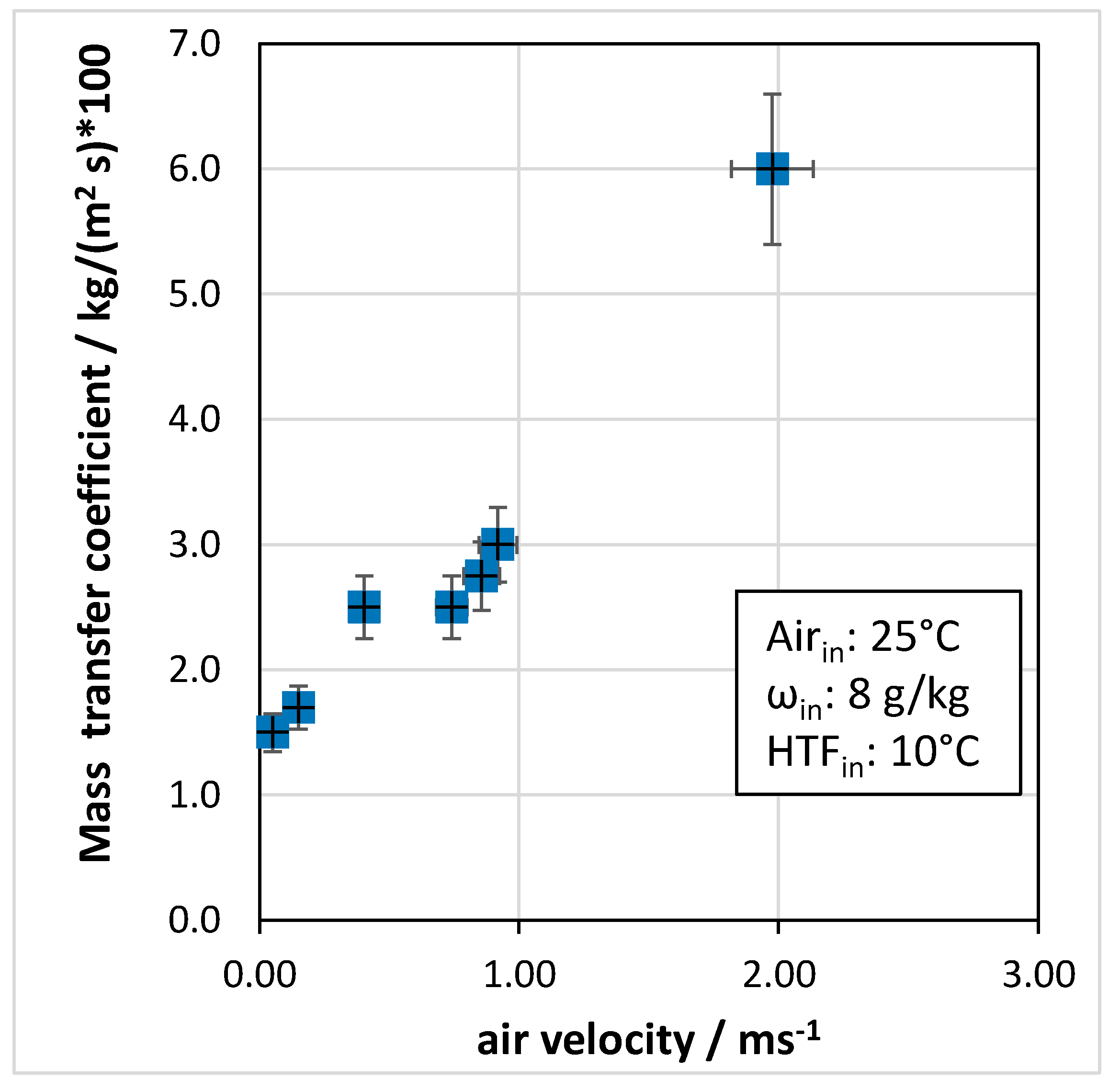
5.3. Mass Transfer Analysis
5.4. Comparison with Other Studies in the Literature
6. Conclusions
- Regarding ambient conditions, it was found that the lower the inlet relative humidity, the lower the reduction in the humidity ratio between the inlet and outlet.
- In terms of operating parameters, the most influential was the velocity of air passing through the heat exchanger: for the tested system, an optimal range of 0.4 to 0.6 m/s was identified.
- The temperature of the cooling fluid also played an important role, with the dew point of outlet air increasing from 0 °C to 2 °C when the heat transfer fluid temperature passed from 10 °C to 30 °C.
- A detailed heat and mass transfer analysis was carried out on the heat exchanger. The IR camera visualization technique revealed that within 10 s, the heat exchanger was cooled/heated to the heat transfer fluid temperature. On the air side, the most important parameter for heat transfer was air velocity.
- Heat transfer coefficients in the range of 80–140 W/(m2 K) were measured. In terms of mass transfer, with increasing air velocity, the mass transfer coefficient passed from 0.015 to 0.060 kg/(m2 s).
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| A | area, m2 |
| cp | specific heat, kJ/(kg K) |
| F | volumetric flow rate, m3/s |
| h | heat transfer coefficient for convection, W/(m2 K) |
| K | mass transfer coefficient, kg (m2 s) |
| mass flow rate, kg/s | |
| M | Molar mass, kg/mol |
| P | pressure, Pa |
| power, W | |
| T | temperature |
| U | heat transfer coefficient, W/(m2 K) |
| δ | fin thickness, mm |
| λ | thermal conductivity, W/(m K) |
| ω | humidity ratio, g/kg |
| Subscripts | |
| av | average |
| da | dry air |
| eq | equilibrium |
| ext | external |
| in | inlet |
| int | internal |
| out | outlet |
| v | vapor |
| Abbreviations | |
| HEX | heat exchanger |
| HTF | heat transfer fluid |
| LMTD | logarithmic mean temperature difference |
| RH | relative humidity |
| SG | silica gel |
References
- Xie, M.; Chen, E.; Huang, G.; Jia, T.; Dai, Y. Recent Advancements in Deep Dehumidification Technology: A Review. Renew. Sustain. Energy Rev. 2025, 211, 115321. [Google Scholar] [CrossRef]
- Lao, M.; Lin, J.; Mikšík, F.; Thu, K.; Miyazaki, T. Performance and Design Analyses of Various Configurations of Dew Point Evaporative Cooling-Based Desiccant Air-Conditioning (DAC) Systems for Hot and Humid Conditions. Int. J. Air-Cond. Refrig. 2022, 30, 12. [Google Scholar] [CrossRef]
- Venegas, T.; Qu, M.; Wang, L.; Liu, X.; Gluesenkamp, K.; Gao, Z. Review of Liquid Desiccant Air Dehumidification Systems Coupled with Heat Pump: System Configurations, Component Design, and Performance. Energy Build. 2023, 279, 112655. [Google Scholar] [CrossRef]
- Zhang, Q.; Tu, R.; Liu, M. Performance Analyses and Optimization Studies of Desiccant Wheel Assisted Atmospheric Water Harvesting System under Global Ambient Conditions. Energy 2023, 283, 128477. [Google Scholar] [CrossRef]
- Evron, Y.; Gommed, K.; Grossman, G. Efficient Deep Dehumidification Hybrid Air Conditioning System. Int. J. Refrig. 2019, 105, 50–58. [Google Scholar] [CrossRef]
- Fang, S.; Xu, Z.; Yao, Y.; Zhou, X.; Zhang, H.; Gan, H.; Zhi, X.; Qiu, L.; Wang, K. Compression Heat Self-Utilisation Systems with Cascade Deep Dehumidification for Industrial Compressor Energy Saving. J. Clean. Prod. 2024, 473, 143493. [Google Scholar] [CrossRef]
- Guan, B.; Liu, X.; Zhang, T.; Ma, Z.; Chen, L.; Chen, X. Experimental and Numerical Investigation of a Novel Hybrid Deep-Dehumidification System Using Liquid Desiccant. Energy Convers. Manag. 2019, 192, 396–411. [Google Scholar] [CrossRef]
- Guan, B.; Liu, X.; Zhang, T. On the Importance of Air-Solution Flow Rate Matching in Liquid-Desiccant Deep-Dehumidification System. Int. J. Heat Mass Transf. 2021, 164, 120614. [Google Scholar] [CrossRef]
- Fang, S.; Xu, Z.; Zhang, H.; Rong, Y.; Zhou, X.; Zhi, X.; Wang, K.; Markides, C.N.; Qiu, L. High-Performance Multi-Stage Internally-Cooled Liquid Desiccant Dehumidifier for High Gas–Liquid Flow Ratios. Energy Convers. Manag. 2021, 250, 114869. [Google Scholar] [CrossRef]
- Wen, T.; Lu, L.; Zhong, H.; Dong, C. Experimental and Numerical Study on the Regeneration Performance of LiCl Solution with Surfactant and Nanoparticles. Int. J. Heat Mass Transf. 2018, 127, 154–164. [Google Scholar] [CrossRef]
- Bai, H.; Zhu, J.; Chu, J.; Chen, X.; Cui, Y.; Yan, Y. Influences of the Mixed LiCl-CaCl2 Liquid Desiccant Solution on a Membrane-Based Dehumidification System: Parametric Analysis and Mixing Ratio Selection. Energy Build. 2019, 183, 592–606. [Google Scholar] [CrossRef]
- Su, X.; Geng, Y.; Huang, L.; Li, S.; Wang, Q.; Xu, Z.; Tian, S. Review on Dehumidification Technology in Low and Extremely Low Humidity Industrial Environments. Energy 2024, 302, 131793. [Google Scholar] [CrossRef]
- Bonaccorsi, L.; De Antonellis, S.; Tomaino, G.; Freni, A.; Malara, A.; Frontera, P.; Fotia, A. Electrospun Hybrid Microfibers for Desiccant Cooling/Air Dehumidification. Appl. Therm. Eng. 2025, 258, 124524. [Google Scholar] [CrossRef]
- Calabrese, L.; Mastronardo, E.; Piperopoulos, E.; Scionti, G.; De Antonellis, S.; Freni, A.; Milone, C. Effect of Alternating Humidity and Dryness on the Durability of Adsorbent Sheets Used in Open Cycle Adsorption Processes. Polym. Degrad. Stab. 2025, 234, 111201. [Google Scholar] [CrossRef]
- Mastronardo, E.; De Antonellis, S.; Freni, A.; Milone, C.; Calabrese, L. Stability of Adsorbent Sheets Under Accelerated-Aging Tests for Open-Cycle Adsorption Processes. Energies 2025, 18, 1023. [Google Scholar] [CrossRef]
- Zhang, Q.; Li, Y.; Zhang, Q.; Ma, F.; Lü, X. Application of Deep Dehumidification Technology in Low-Humidity Industry: A Review. Renew. Sustain. Energy Rev. 2024, 193, 114278. [Google Scholar] [CrossRef]
- Zeng, Y.; Woods, J.; Cui, S. The Energy Saving Potential of Thermo-Responsive Desiccants for Air Dehumidification. Energy Convers. Manag. 2021, 244, 114520. [Google Scholar] [CrossRef]
- Askalany, A.A.; Uddin, K.; Saha, B.B.; Sultan, M.; Santori, G. Water Desalination by Silica Supported Ionic Liquid: Adsorption Kinetics and System Modeling. Energy 2022, 239, 122069. [Google Scholar] [CrossRef]
- Guan, B.; Liu, X.; Zhang, T. Modification of Analytical Solutions of Coupled Heat and Mass Transfer Processes in Liquid Desiccant Dehumidifier for Deep Dehumidification. Int. J. Heat Mass Transf. 2021, 165, 120728. [Google Scholar] [CrossRef]
- Cheng, J.-H.; Wang, Z.-Y.; Cao, X.; Li, X.-Y.; Zhang, C.-L. Achieving Deep Dehumidification through a Heat Pump-Boosted Desiccant Wheel System. Energy Convers. Manag. 2024, 313, 118604. [Google Scholar] [CrossRef]
- Tu, R.; Hwang, Y. Efficient Configurations for Desiccant Wheel Cooling Systems Using Different Heat Sources for Regeneration. Int. J. Refrig. 2018, 86, 14–27. [Google Scholar] [CrossRef]
- Asadi, A.; Roshanzadeh, B. Improving Performance of Two-Stage Desiccant Cooling System by Analyzing Different Regeneration Configurations. J. Build. Eng. 2019, 25, 100807. [Google Scholar] [CrossRef]
- Li, Z.; Michiyuki, S.; Takeshi, F. Experimental Study on Heat and Mass Transfer Characteristics for a Desiccant-Coated Fin-Tube Heat Exchanger. Int. J. Heat Mass Transf. 2015, 89, 641–651. [Google Scholar] [CrossRef]
- Liu, L.; Huang, H.; Li, J.; Bai, Y.; He, Z.; Deng, L.; Gao, T.; Kubota, M.; Kobayashi, N. Deep Dehumidification Characteristics of a Silica Gel Coated Cross-Flow Heat Exchanger with a Circulating Blowing Loop. Energy Build. 2024, 325, 114991. [Google Scholar] [CrossRef]
- Liu, J.; Sun, C.; Chen, Q. Experimental Study of Desiccant-Coated Heat Exchangers for Deep Dehumidification. Energy Build. 2024, 319, 114554. [Google Scholar] [CrossRef]
- Brancato, V.; Gordeeva, L.G.; Sapienza, A.; Palomba, V.; Vasta, S.; Grekova, A.D.; Frazzica, A.; Aristov, Y.I. Experimental Characterization of the LiCl/Vermiculite Composite for Sorption Heat Storage Applications. Int. J. Refrig. 2019, 105, 92–100. [Google Scholar] [CrossRef]
- Sapienza, A.; Frazzica, A.; Freni, A.; Aristov, Y. Dynamics of Adsorptive Systems for Heat Transformation; Springer Briefs in Applied Sciences and Technology; Springer International Publishing: Cham, Switzerland, 2018. [Google Scholar]
- Grekova, A.D.; Tokarev, M.M.; Aristov, Y.I. On the Use of Finned Flat-Tube Heat Exchangers for Adsorptive Heat Storage and Transformation. J. Energy Storage 2024, 84, 110973. [Google Scholar] [CrossRef]
- Aristov, Y.I.; Gordeeva, L.G. Combining the Psychrometric Chart of Humid Air with Water Adsorption Isosters: Analysis of the Ventireg Process. Energy 2021, 239, 122278. [Google Scholar] [CrossRef]
- Massman, W.J. A Review of the Molecular Diffusivities of H2O, CO2, CH4, CO, O3, SO2, NH3, N2O, NO, and NO2 in Air, O2 and N2 near STP. Atmos. Environ. 1998, 32, 1111–1127. [Google Scholar] [CrossRef]
- Priyadarshi, G.; Kiran Naik, B. Experimental and Numerical Studies on Moisture Adsorption/Desorption Characteristics across the Circular Fin Tube Desiccant Coated Heat Exchanger. Therm. Sci. Eng. Prog. 2024, 53, 102755. [Google Scholar] [CrossRef]




| Operating Condition Tde (Tcond)/Tad (Teva) | 70 (20)/40 (20) [°C] | 90 (20)/40 (20) [°C] | 70 (20)/35 (15) [°C] | 90 (20)/35 (15) [°C] |
|---|---|---|---|---|
| Cycled water uptake [g/g] | 0.22688 | 0.29362 | 0.22983 | 0.2626 |
| Qad [kJ/kgsorbent] | 549.194 | 773.143 | 530.384 | 617.86 |
| ΔHad [kJ/kgwater] | 2420.64 | 2633.14 | 2307.723 | 2352.07 |
| Parameter | Unit | Value |
|---|---|---|
| Dimensions | mm | 170 × 257 × 27 |
| Metal mass | kg | 0.636 |
| Overall volume | dm3 | 1.1 |
| Typical adsorbent mass 1 | kg | 0.4 |
| Metal mass/adsorbent mass | kg/kg | 1.8 |
| Heat transfer surface | m2 | 1.66 |
| Ratio S/V | m2/dm3 | 1.5 |
| Ratio S/m | m2/kg | 4 |
| Tube pitch | mm | 10 |
| Fin pitch | mm | 1 |
| Fin thickness | mm | 0.7 |
| Measuring Point | Parameter | Sensor Type and Accuracy |
|---|---|---|
| Inlet/Outlet Air Stream | Air Temperature | Pt100 Class A, (Delta Strumenti (Gemonio, Italy) HD4817ETC2.5, ±0.3 °C) |
| Inlet/Outlet Air Stream | Relative Humidity | Thermoset polymer capacitive sensors (Delta Strumenti HD4817ETC2.5, ±1.5%) |
| Inlet Air Streams | Air Velocity | Hot wire anemometer for the air velocity (Schmidt (Georgen, Germany) SS 20.260, ±5% reading) |
| Hot/Cold Water Streams | Water Temperature | Class A type T thermocouples (TC Direct (Torino, Italy), ±0.2 °C) |
| Hot/Cold Water Streams (Return branch) | Water Flow | Electromagnetic water flow 0.5–60 L/min (Bronkhorst (Milano, Italy) MagFlow MVM-60 PA, ±2.5% FS) |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Palomba, V.; Fotia, A.; Costa, F.; La Rosa, D.; Brancato, V. Experimental Testing of a Heat Exchanger with Composite Material for Deep Dehumidification. Energies 2025, 18, 2418. https://doi.org/10.3390/en18102418
Palomba V, Fotia A, Costa F, La Rosa D, Brancato V. Experimental Testing of a Heat Exchanger with Composite Material for Deep Dehumidification. Energies. 2025; 18(10):2418. https://doi.org/10.3390/en18102418
Chicago/Turabian StylePalomba, Valeria, Antonio Fotia, Fabio Costa, Davide La Rosa, and Vincenza Brancato. 2025. "Experimental Testing of a Heat Exchanger with Composite Material for Deep Dehumidification" Energies 18, no. 10: 2418. https://doi.org/10.3390/en18102418
APA StylePalomba, V., Fotia, A., Costa, F., La Rosa, D., & Brancato, V. (2025). Experimental Testing of a Heat Exchanger with Composite Material for Deep Dehumidification. Energies, 18(10), 2418. https://doi.org/10.3390/en18102418









