A Simple Thermoelectrical Surface Approach for Numerically Studying Dry Band Formation on Polluted Insulators
Abstract
:1. Introduction
2. Empirical Equation of the Pollution Layer Surface Conductivity
2.1. Experimental Setup
- Using a spraying system, the pollution layer made with kaolin and salt solution was sprayed on the experimental model and allowed to dry at room temperature for at least 24 h.
- Each polluted model was then placed into a small climate chamber (1 m × 1 m × 1.2 m) set at the desired ambient temperature (at ±1 °C) for a minimum of 3 h.
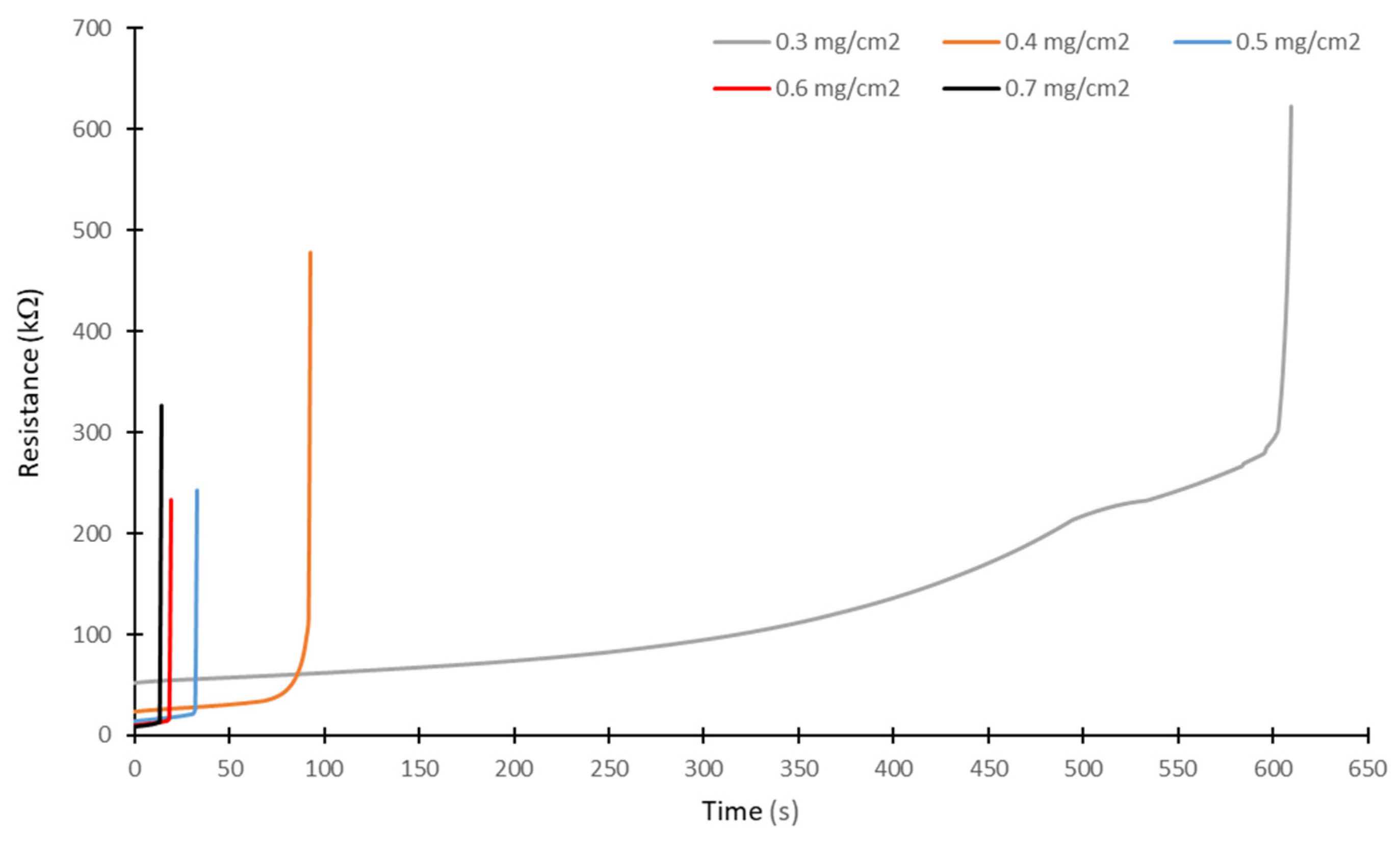
- The humidity of the chamber was set at 95 ± 5%, which was generated by steam for a duration of 810 s, the time previously demonstrated to be required to reach the maximum surface conductivity [19].
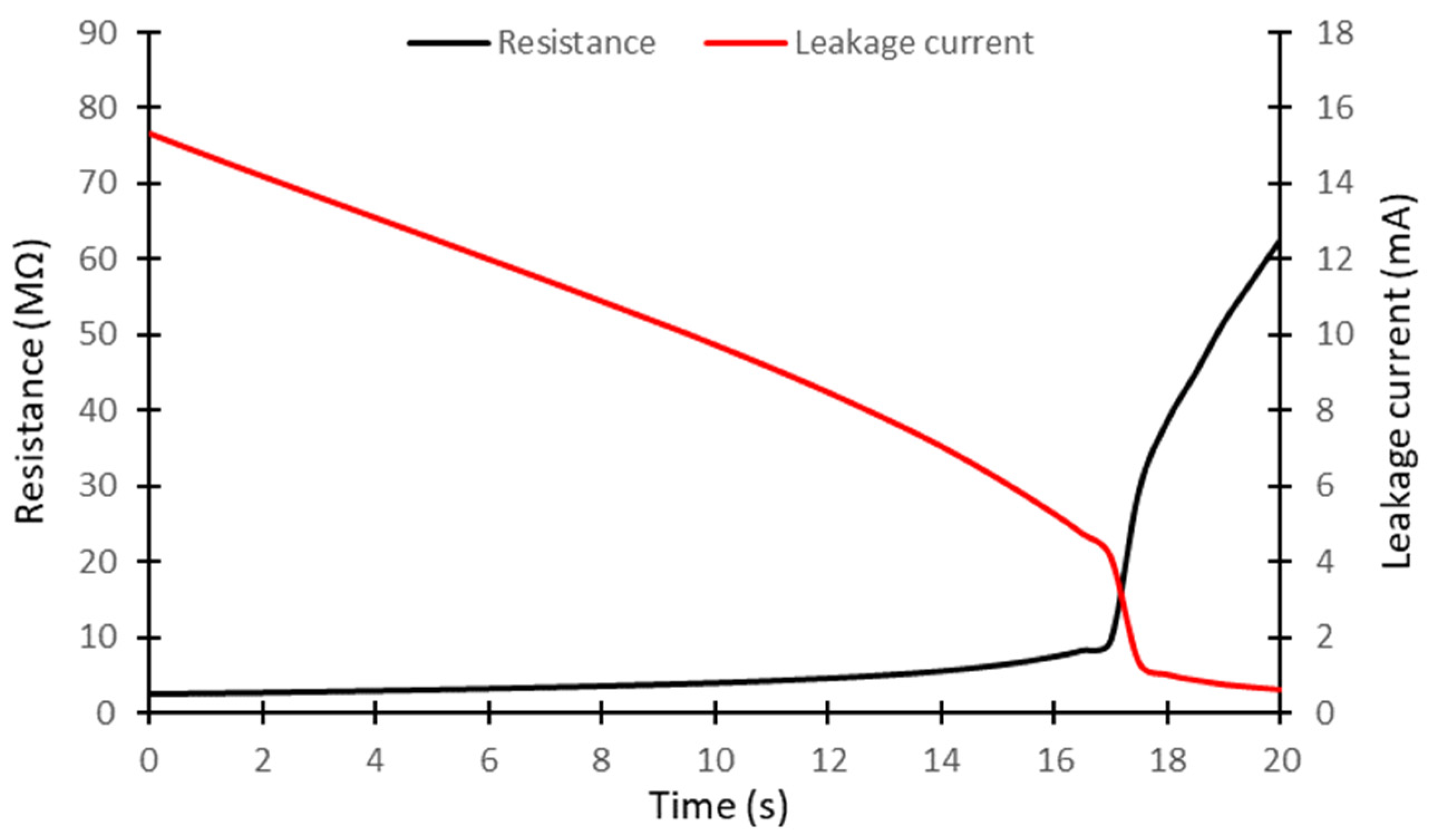
- The desired voltage was applied to the polluted model, and the leakage current was recorded, to automatically compute the pollution layer resistance until the dry band had completely formed. Simultaneously, the average temperature in the middle of the dry band was also recorded using an IR camera Optris PI400 from Optris Infrared Sensing, Portsmouth, NH, USA.
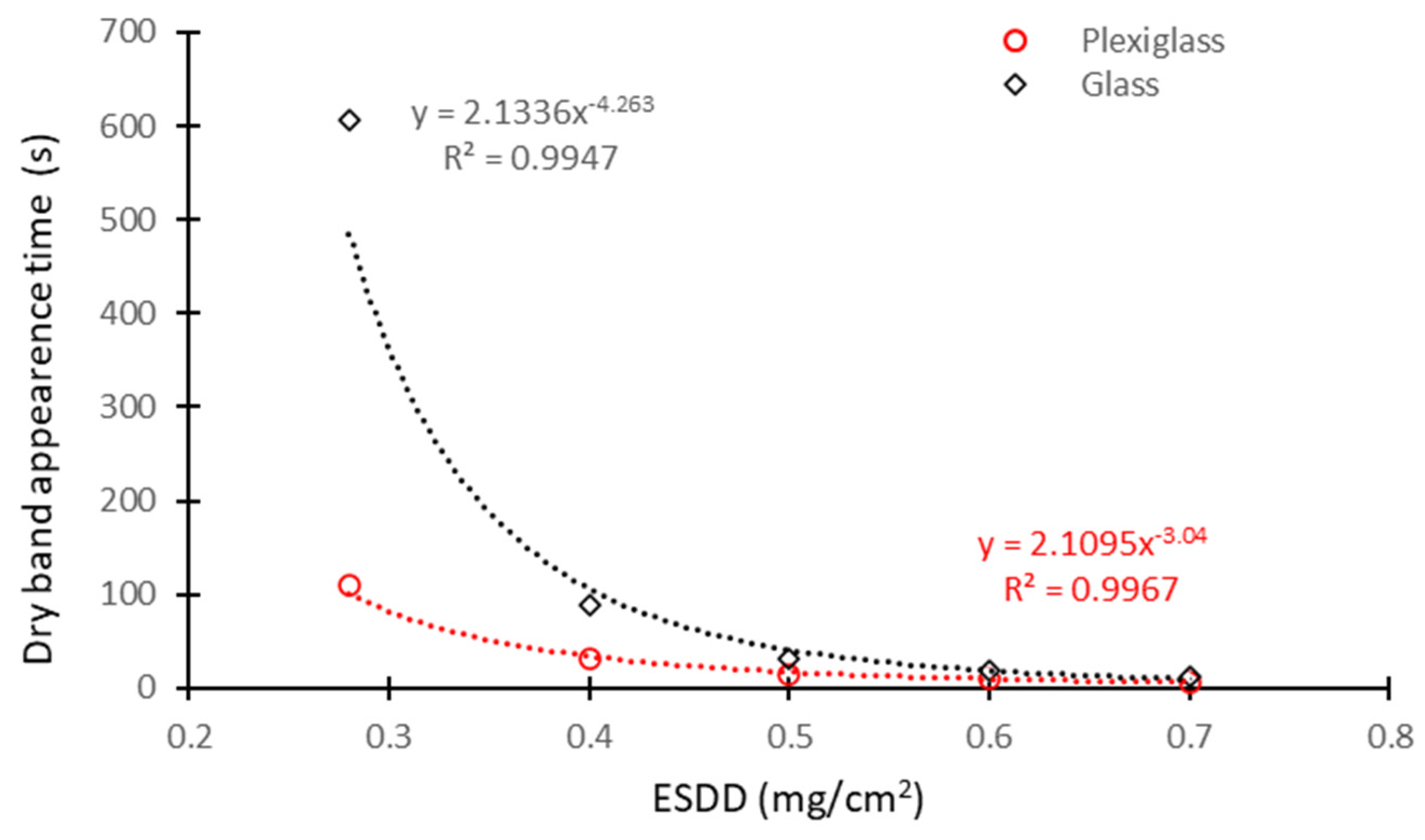
- Finally, the ESDD was measured and determined following the procedure described in [19].
2.2. Surface Conductivity of the Pollution Layer as a Function of the Temperature and ESDD
2.2.1. Procedure and Simplifying Assumptions
- ▪
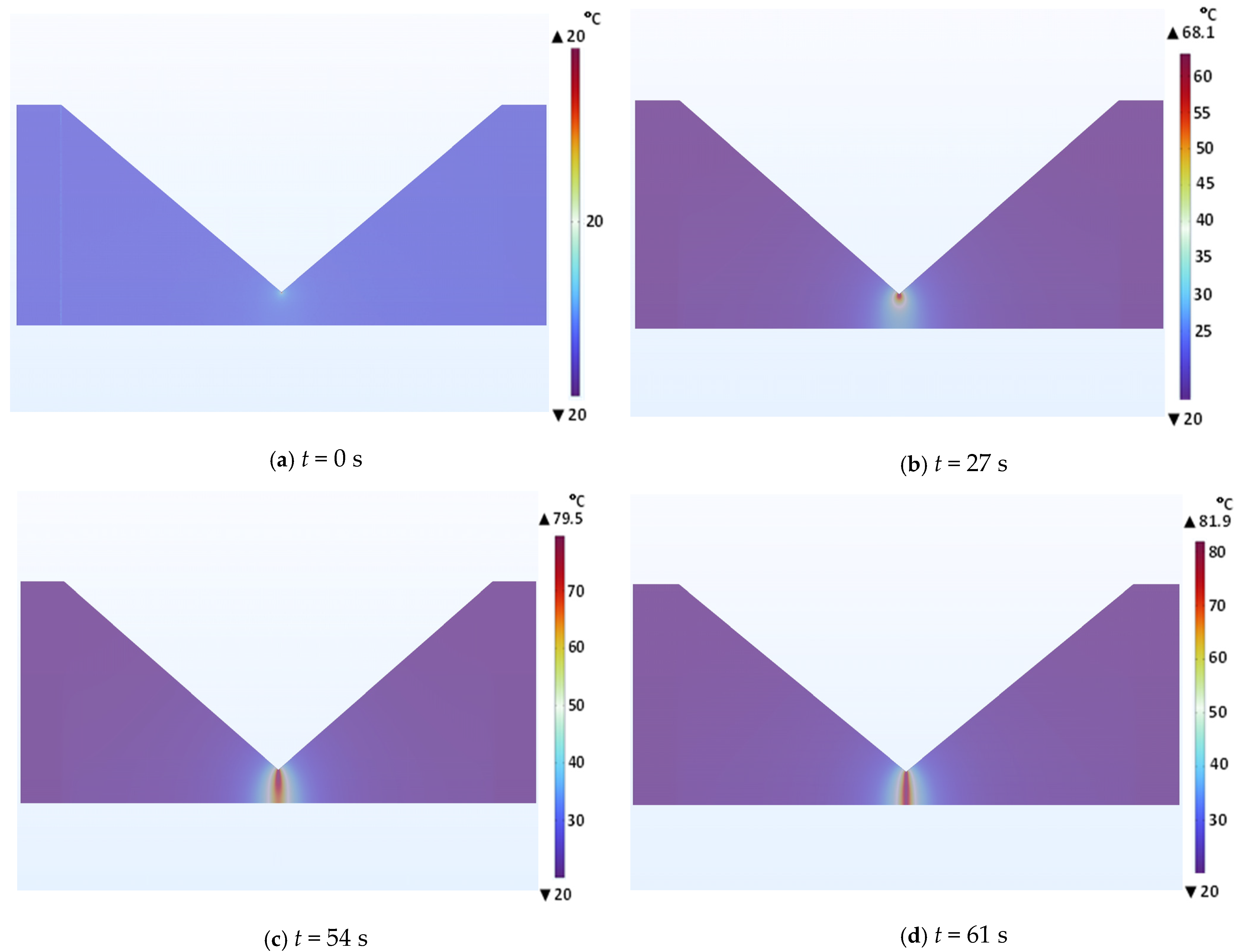
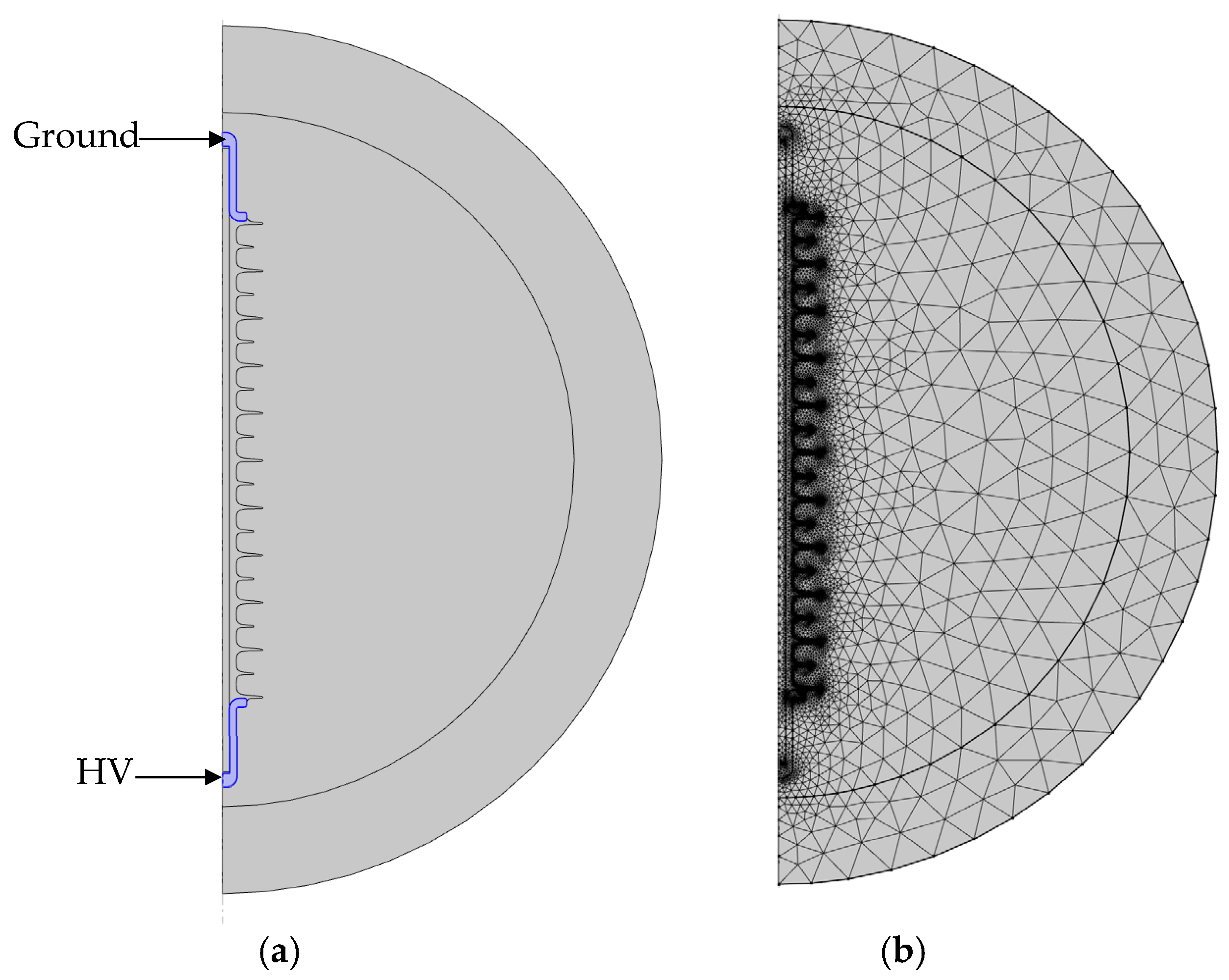
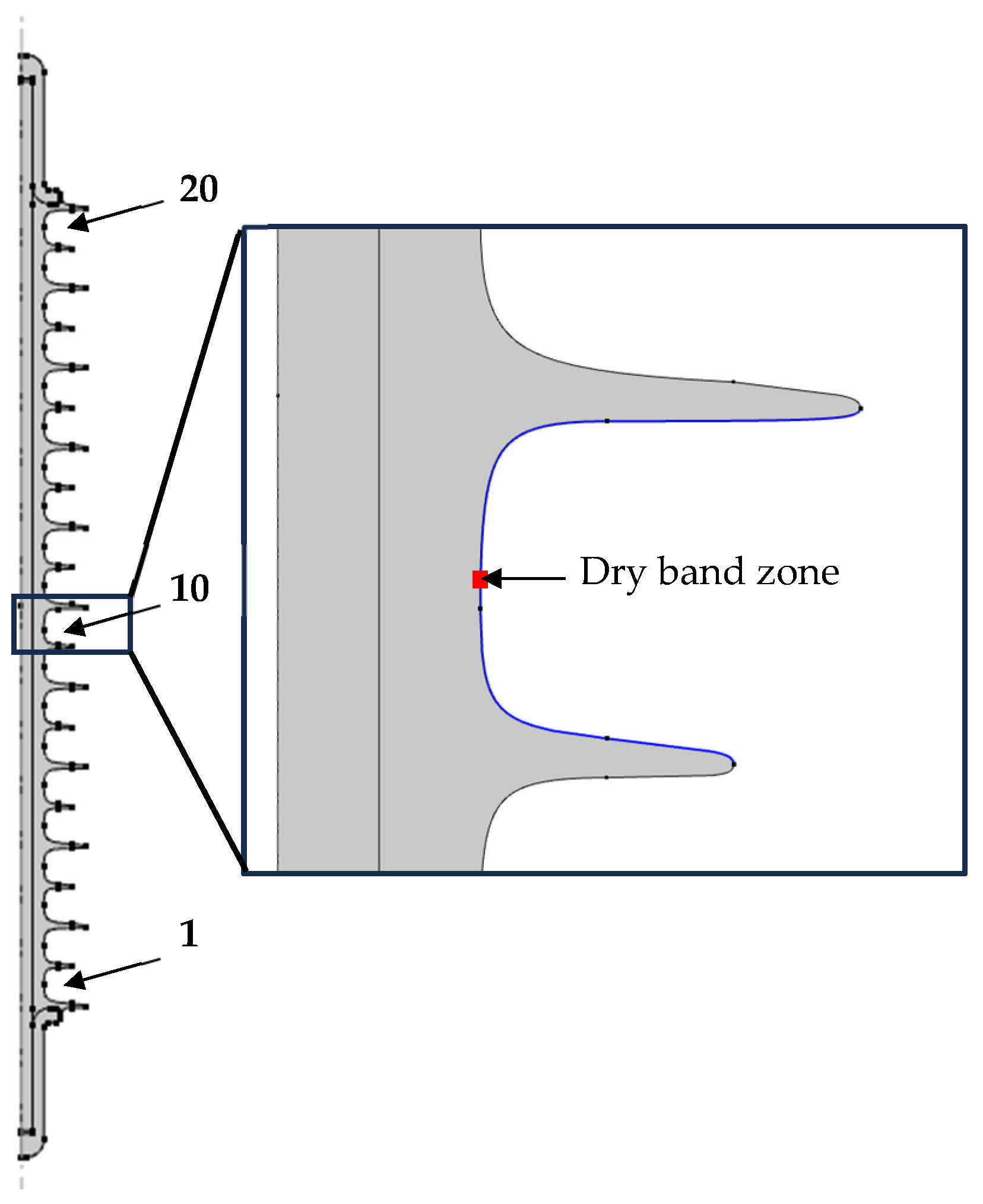
- The dry band is uniformly formed in the middle of the flat sample in the stress zone, as illustrated in Figure 1.
- ▪
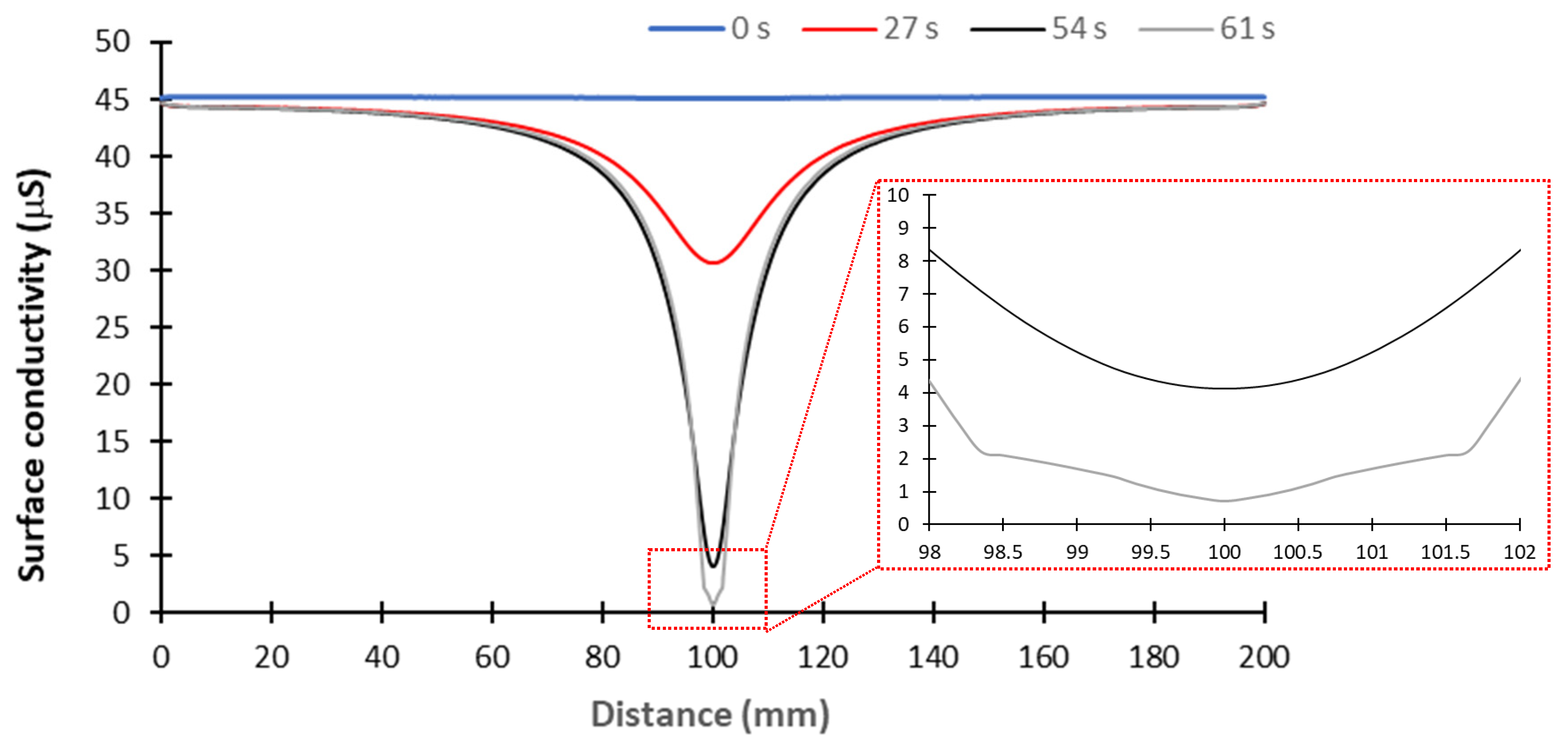
- The increase in the surface temperature along the flat insulator model occurs principally in the dry band zone, as observed experimentally [19]. This means that the temporal variation in the conductivity (or resistance) of the entire pollution layer is essentially governed by the evolution of the pollution layer conductivity in the dry band zone. In other words, all the electrical parameters such as the pollution layer resistance of leakage current (LC) are governed by the evolution of the dry band resistance.
2.2.2. Empirical Pollution Surface Conductivity Equation
3. Thermoelectric Numerical Model of Dry Band Formation
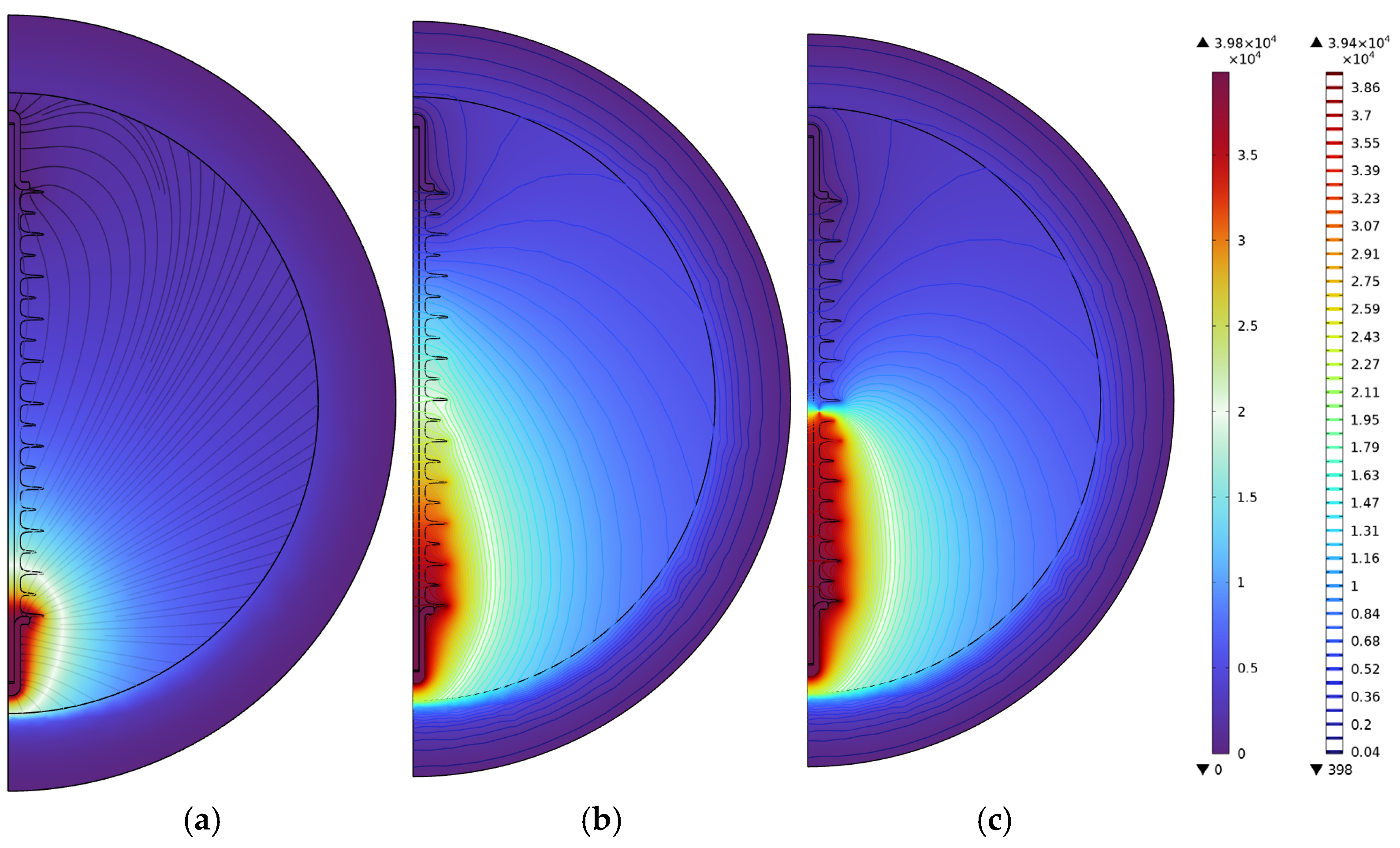
3.1. Presentation of the Model
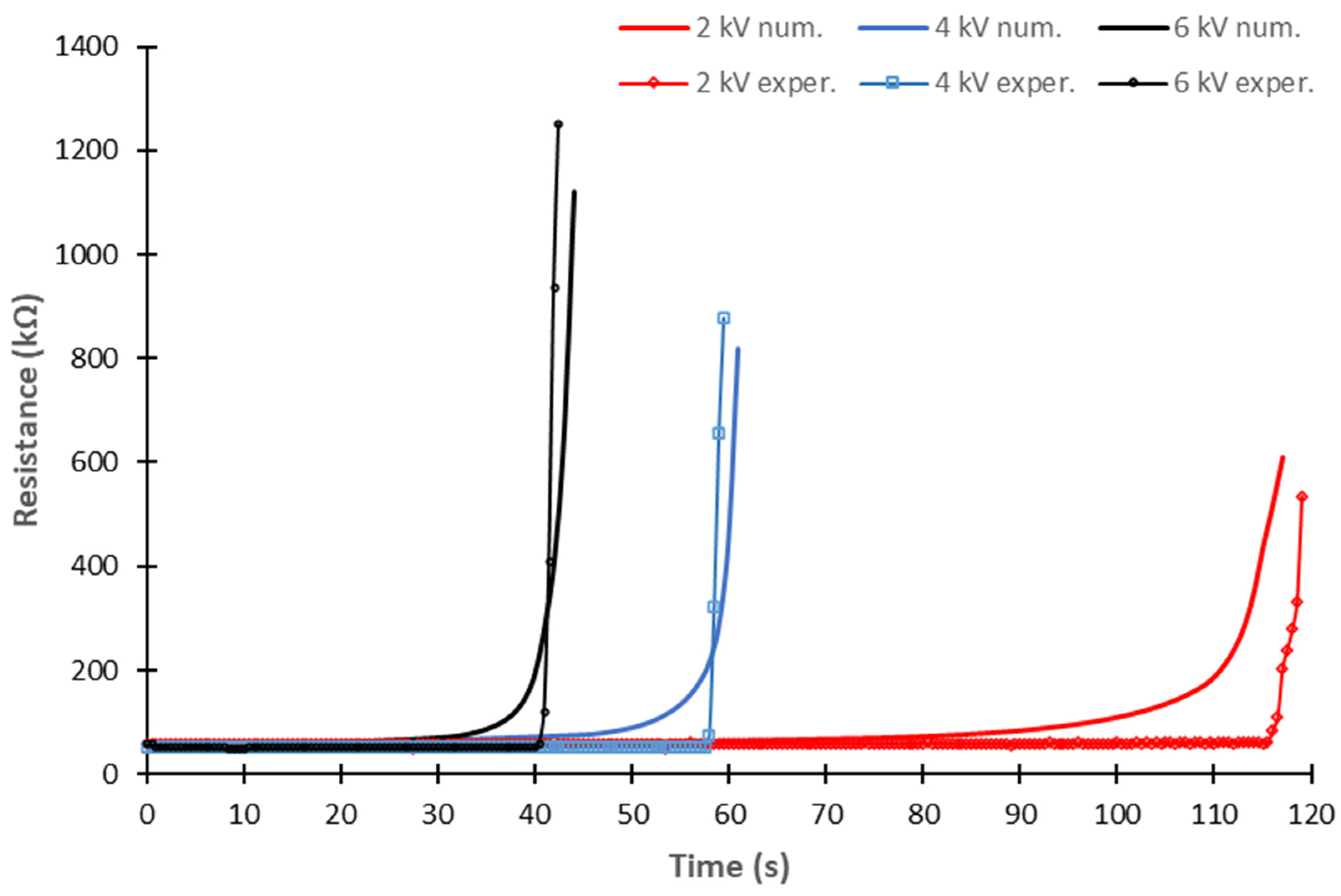
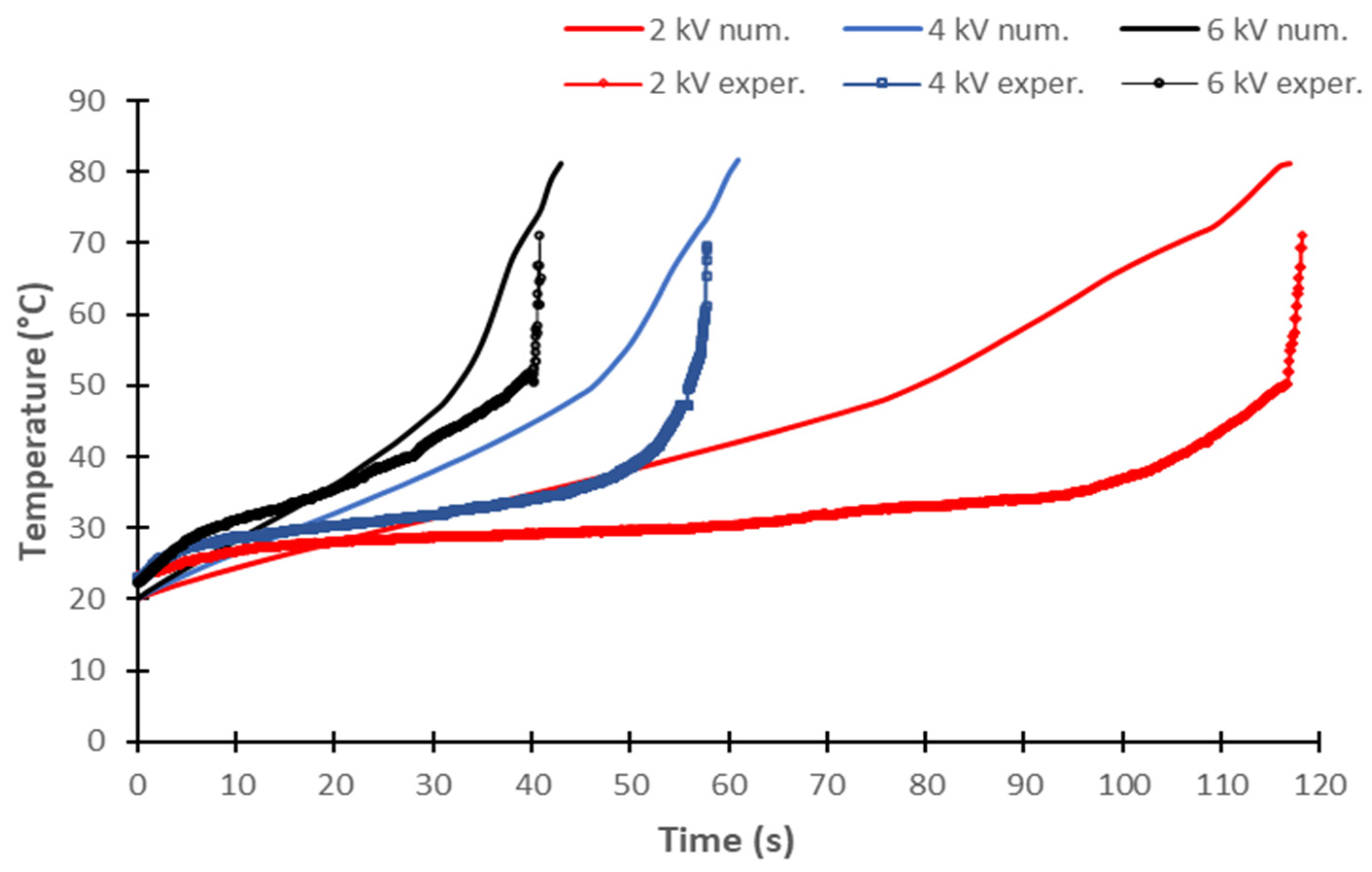
3.2. Validation of the Thermoelectrical Dry Band Formation Simple Model
4. Study of Parameters Influencing the Dry Band Formation
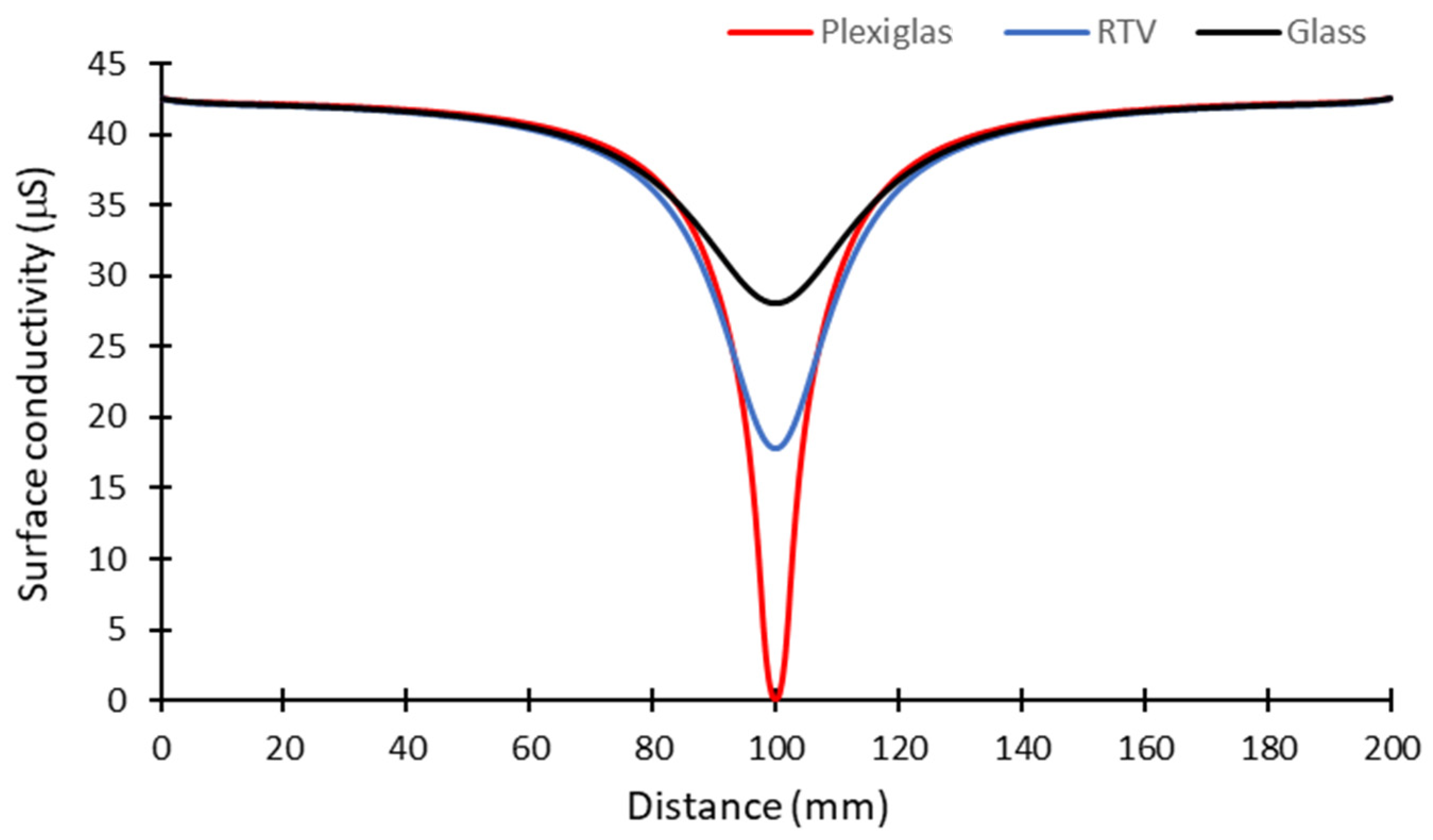
4.1. Influence of the Substrate Thermal Properties
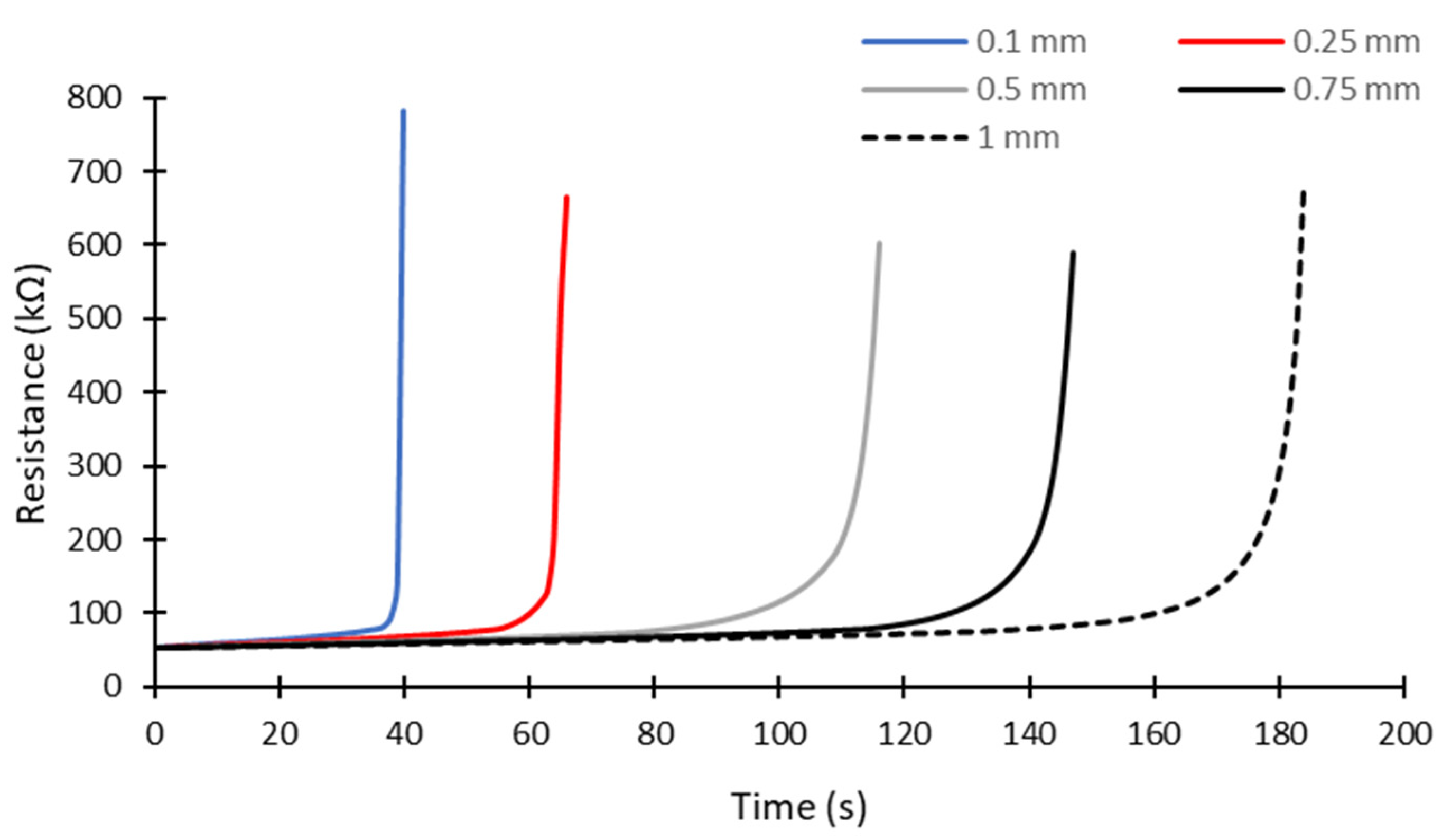
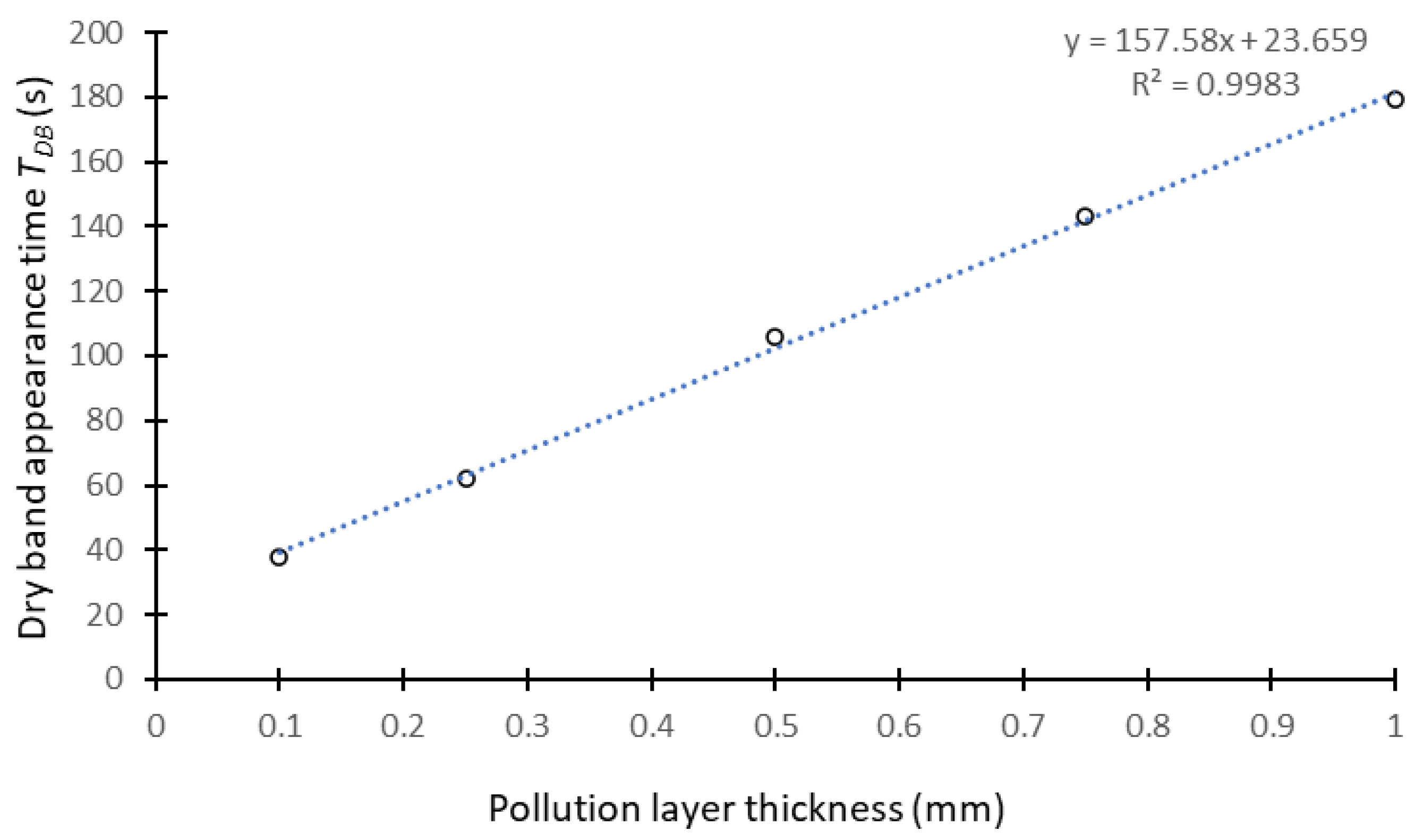
4.2. Influence of the Pollution Layer Thickness
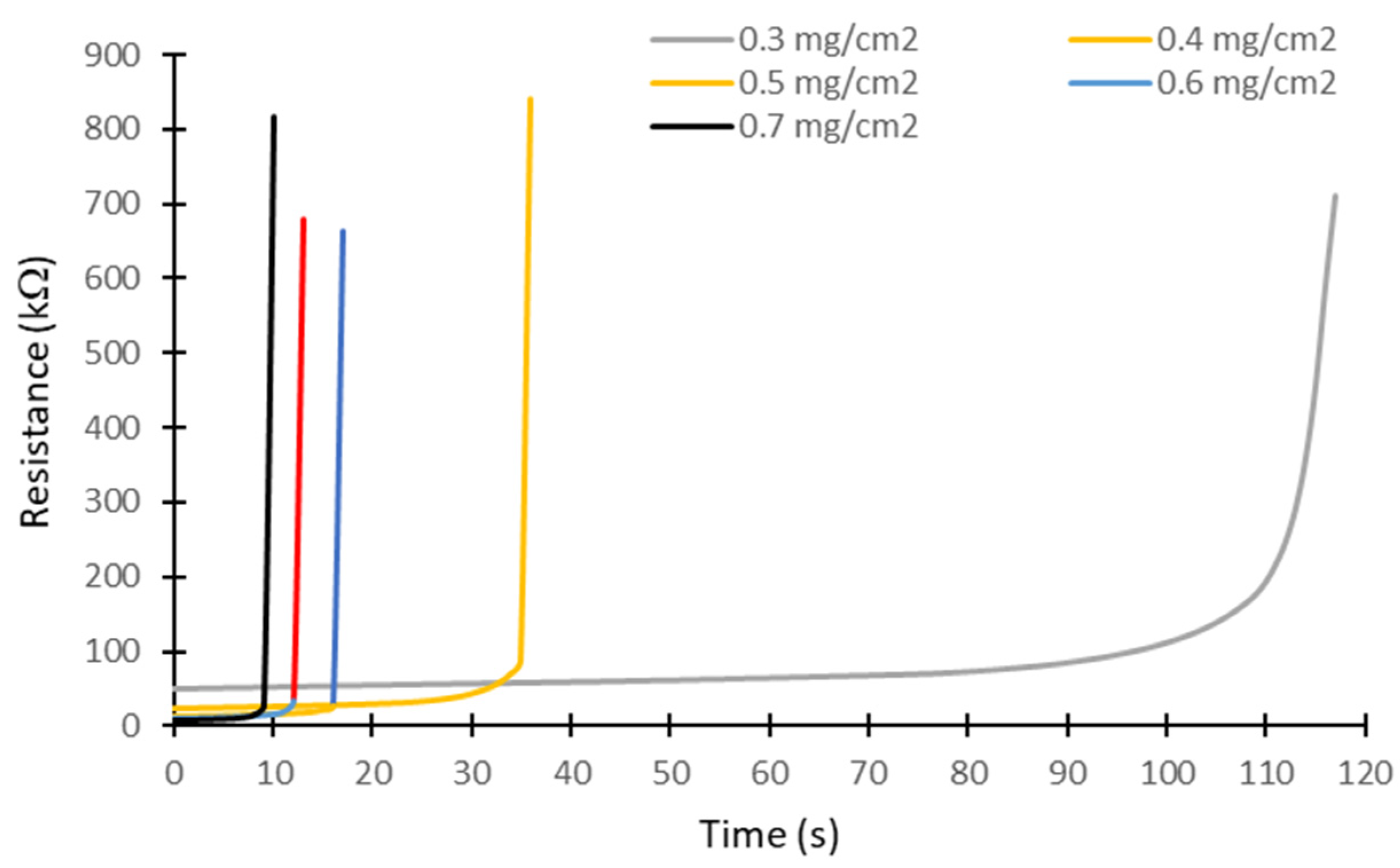
4.3. Influence of the Pollution Layer ESDD
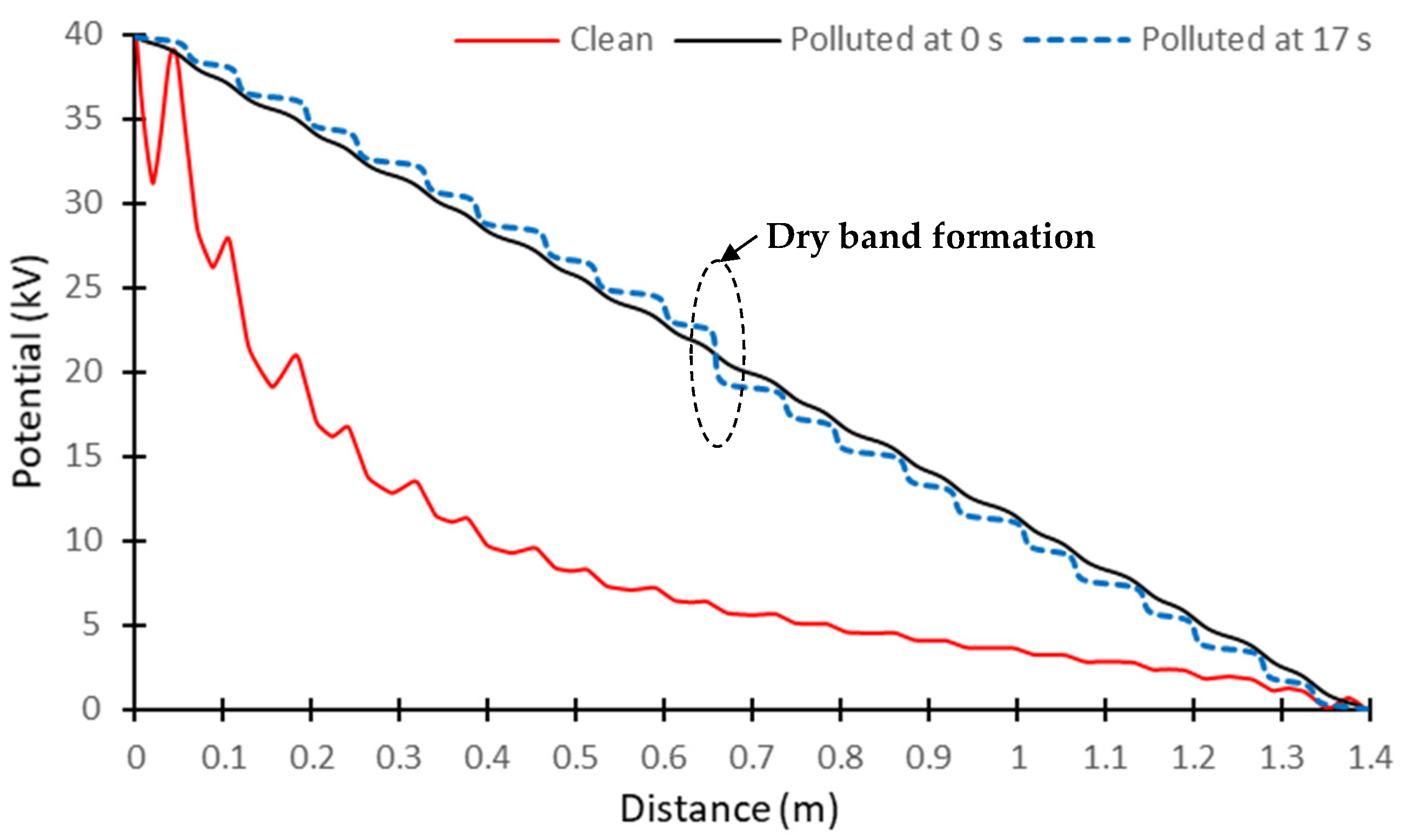
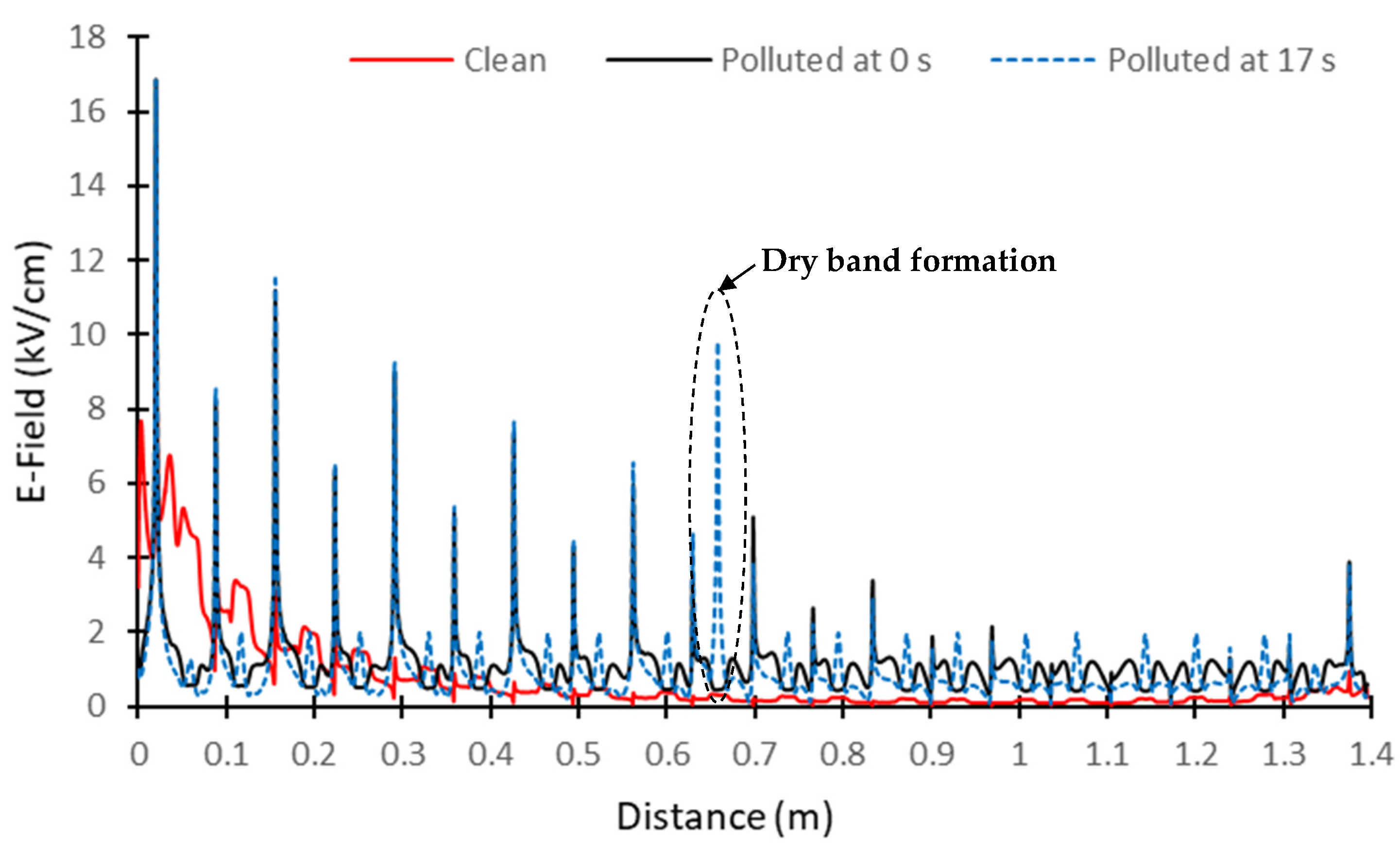
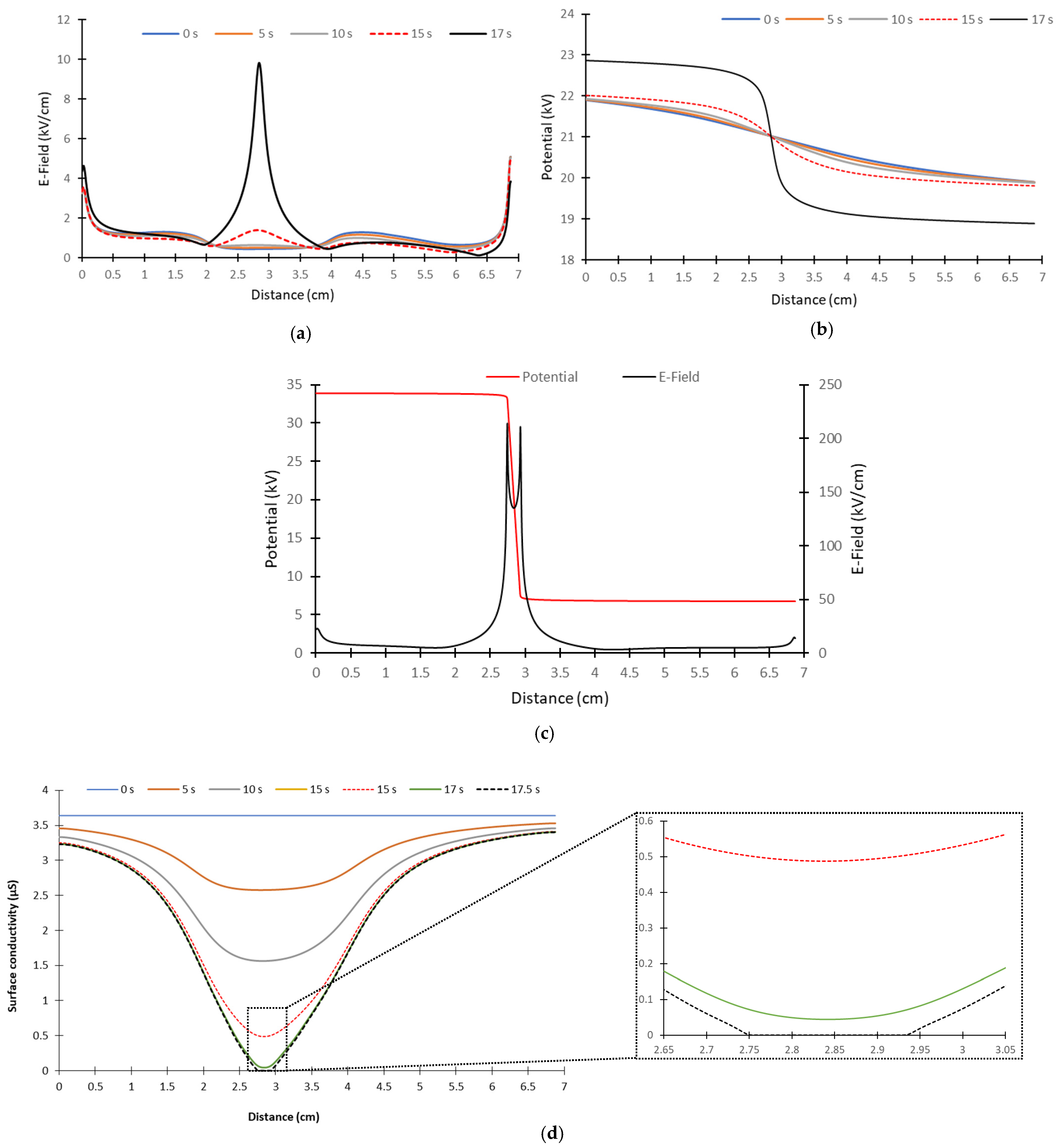
5. Application to a Polluted Composite Insulator
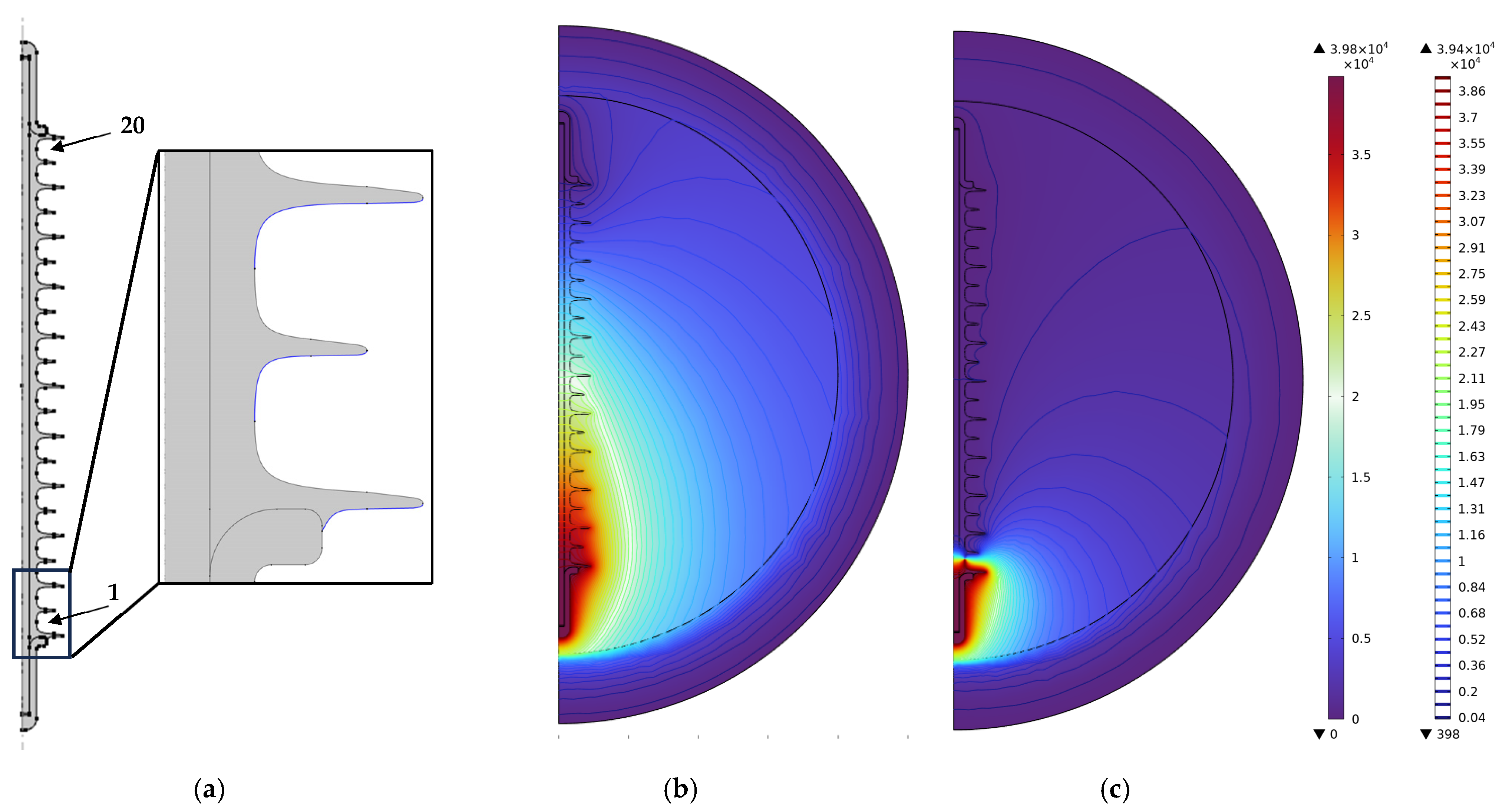
5.1. Polluted Composite Insulator Model
5.2. Numerical Results Relative to the Electrical Parameters
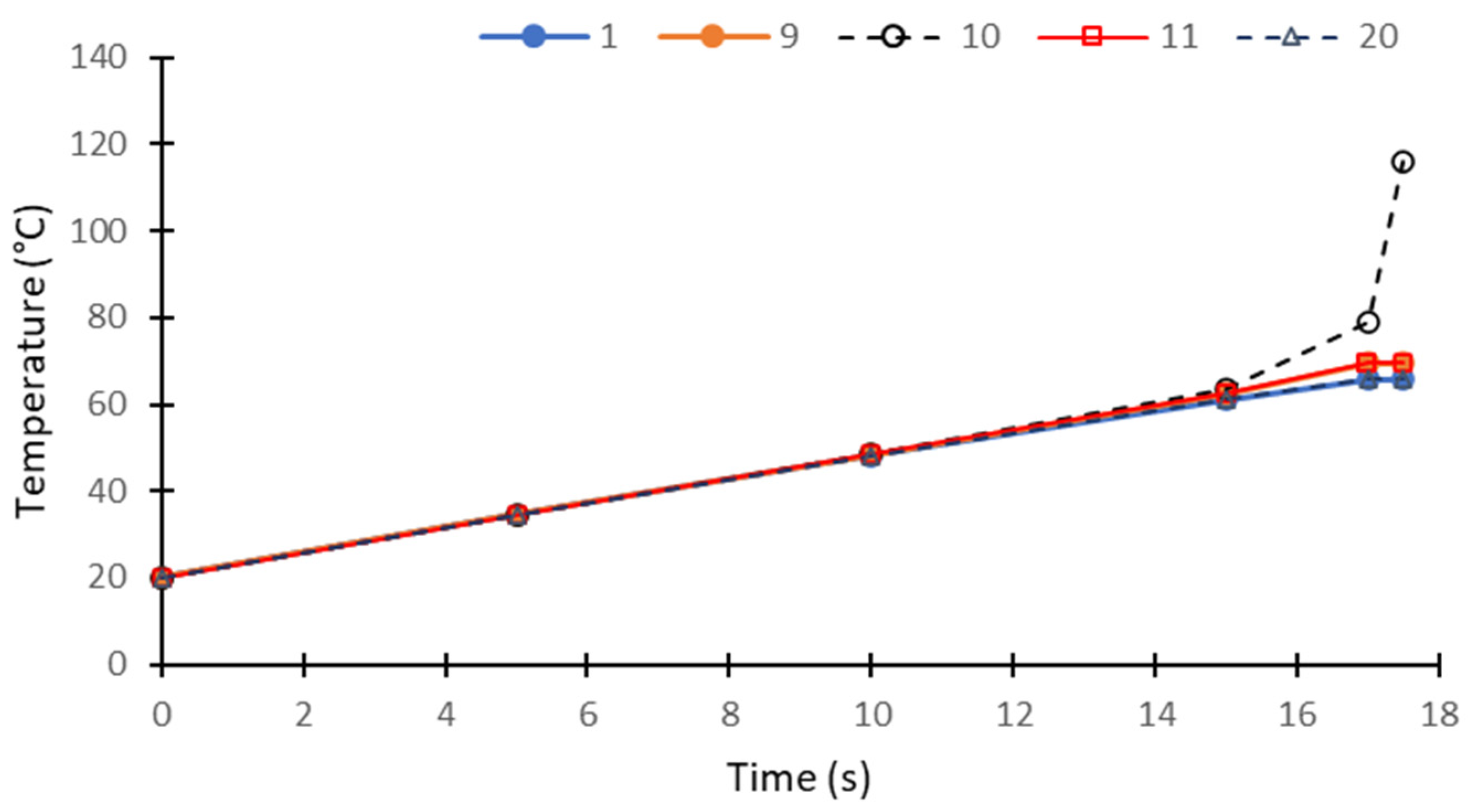
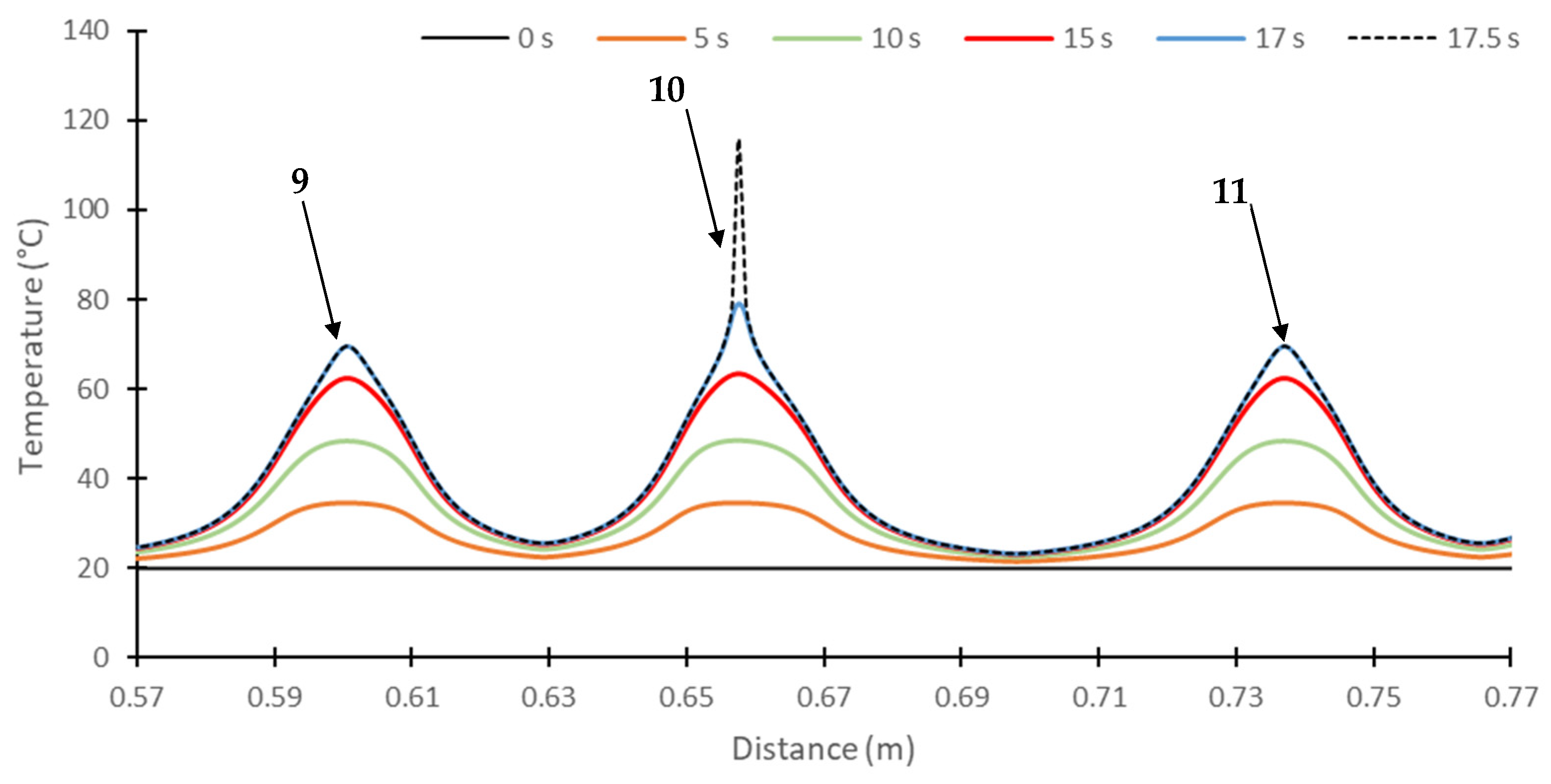
5.3. Numerical Results Relative to Thermal Parameters
5.4. Discussion of the Results Obtained
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Williams, D.L.; Haddad, A.; Rowlands, A.R.; Young, H.M.; Waters, R.T. Formation and characterization of dry bands in clean fog on polluted insulators. IEEE Trans. Dielectr. Electr. Insul. 1999, 6, 724–731. [Google Scholar] [CrossRef]
- Albano, M.; Haddad, A.M.; Bungay, N. Is the dry-band characteristic a function of pollution and insulator design? Energies 2019, 12, 3607. [Google Scholar] [CrossRef]
- Bo, L.; Gorur, R.S. Modeling flashover of AC outdoor insulators under contaminated conditions with dry band formation and arcing. IEEE Trans. Dielectr. Electr. Insul. 2012, 19, 1037–1043. [Google Scholar] [CrossRef]
- Gençoğlu, M.T.; Cebeci, M. The pollution flashover on high voltage insulators. Electr. Power Syst. Res. 2008, 78, 1914–1921. [Google Scholar] [CrossRef]
- Zhang, D.; Meng, F. Research on the interrelation between temperature distribution and dry band on wet contaminated insulators. Energies 2019, 12, 4289. [Google Scholar] [CrossRef]
- Albano, M.; Waters, R.T.; Charalampidis, P.; Griffiths, H.; Haddad, A. Infrared analysis of dry-band flashover of silicone rubber insulators. IEEE Trans. Dielectr. Electr. Insul. 2016, 23, 304–310. [Google Scholar] [CrossRef]
- Loberg, J.O.; Salthouse, E.C. Dry-Band Growth on Polluted Insulation. IEEE Trans. Electr. Insul. 1971, 6, 136–141. [Google Scholar] [CrossRef]
- Yang, H.; Cao, W.; Wen, R.; Wang, Y.; Shen, W.; Zhang, L. Study on surface conductivity distribution of pollution layer during the propagation of local arc on the wet polluted insulation surface. AIP Adv. 2022, 12, 015311. [Google Scholar] [CrossRef]
- He, J.; He, K.; Gao, B. Modeling of Dry Band Formation and Arcing Processes on the Polluted Composite Insulator Surface. Energies 2019, 12, 3905. [Google Scholar] [CrossRef]
- Bo, G.; Qingliang, W.; Jianbo, Z. Effect of dry band on electric field distribution of polluted insulator. High Volt. Eng. 2009, 35, 2421–2426. [Google Scholar]
- Arshad, N.A.; Mcmeekin, S.G.; Farzaneh, M. Numerical computation of electric field and potential along silicone rubber insulators under contaminated and dry band conditions. 3D Res. 2016, 7, 25. [Google Scholar] [CrossRef]
- Salem, A.A.; Lau, K.Y.; Abdul-Malek, Z.; Zhou, W.; Al-Ameri, S.; Al-Gailani, S.A.; Rahman, R.A. Investigation of high voltage polymeric insulators performance under wet pollution. Polymers 2022, 14, 1236. [Google Scholar] [CrossRef] [PubMed]
- Volat, C. Comparison between the use of surface and volume conductivity to compute potential distribution along an insulator in presence of a thin conductive layer. In Proceedings of the IEEE Electrical Insulation Conference (EIC), Ottawa, ON, Canada, 2–5 June 2013. [Google Scholar]
- Asenjo, S.E.; Morales, O.N.; Valdenegro, E.A. Solution of low frequency complex fields in polluted insulators by means of the finite element method. IEEE Trans. Dielectr. Electr. Insul. 1997, 4, 10–16. [Google Scholar] [CrossRef]
- Rasolonjanahary, J.; Krähenbühl, L.; Nicolas, A. Computation of electric fields and potential on polluted insulators using a boundary element method. IEEE Trans. Magn. 1992, 28, 1473–1476. [Google Scholar] [CrossRef]
- Arshad; Mughal, M.A.; Nekahi, A.; Khan, M.; Umer, F. Influence of Single and Multiple Dry Bands on Critical Flashover Voltage of Silicone Rubber Outdoor Insulators: Simulation and Experimental Study. Energies 2018, 11, 1335. [Google Scholar] [CrossRef]
- Dhahbi-Megriche, N.; Slama, M.E.-A.; Beroual, A. Influence of dry bands on polluted insulator performance. In Proceedings of the 2017 International Conference on Engineering & MIS (ICEMIS), Monastir, Tunisia, 8–10 May 2017. [Google Scholar]
- Wang, L.; Chong, J.; Dang, N.; Zhao, J.; Zhao, J. Research about the thermoelectric coupling of insulator surface dry band and COMSOL simulation. In Proceedings of the 16th IET International Conference on AC and DC Power Transmission (ACDC 2020), Online, 2–3 July 2020. [Google Scholar]
- Andoh, M.-A.; Gbah, K.; Volat, C. Development of a Simple Experimental Setup for the Study of the Formation of Dry Bands on Composite Insulators. Energies 2022, 15, 5108. [Google Scholar] [CrossRef]
- Andoh, M.-A.; Volat, C. Experimental investigation of parameters influencing the formation of dry bands and related electric field. Energies 2024, 17, 2373. [Google Scholar] [CrossRef]
- COMSOL Multiphysics User’s Manual, ed: Version 6.1. Available online: https://doc.comsol.com/6.1/doc/com.comsol.help.comsol/COMSOL_ReferenceManual.pdf (accessed on 10 January 2025).
- Luo, D.; Wu, Z.; Zhang, Z.; Chen, H.; Geng, L.; Ji, Z.; Zhang, P. Transient thermal analysis of a thermoelectric-based battery thermal management system at high temperatures. Energy 2025, 318, 134833. [Google Scholar] [CrossRef]
- Luo, D.; Yang, S.; Zhang, H.; Cao, J.; Yan, Y.; Chen, H. Performance improvement of an automotive thermoelectric generator by introducing a novel split fin structure. Appl. Energy 2025, 382, 125218. [Google Scholar] [CrossRef]
- Chen, Y.X.; Qin, W.; Mansoor, A.; Abbas, A.; Li, F.; Liang, G.X.; Zheng, Z.H. Realizing high thermoelectric performance via selective resonant doping in oxyselenide BiCuSeO. Nano Res. 2023, 16, 1679–1687. [Google Scholar] [CrossRef]
- Yu, H.; Hu, Z.; He, J.; Ran, Y.; Zhao, Y.; Yu, Z.; Tai, K. Flexible temperature-pressure dual sensor based on 3D spiral thermoelectric Bi2Te3 films. Nat. Commun. 2024, 15, 2521. [Google Scholar] [CrossRef] [PubMed]
- Kone, G.; Volat, C. Comparison of the volume and surface approaches to compute temperature and electric field along the stress-grading on stators bars. In Proceeding of the IEEE Conference on Electrical Insulation and Dielectric Phenomena (CEIDP), Cancun, Mexico, 21–24 October 2018. [Google Scholar]
- George, J.M.; Prat, S.; Lumb, C.; Virlogeux, F.; Gutman, I.; Lundengard, J.; Marzinotto, M. Field experience and laboratory investigation of glass insulators having a factory-applied silicone rubber coating. IEEE Trans. Dielectr. Electr. Insul. 2015, 21, 2594–2601. [Google Scholar] [CrossRef]
- Saison, J.Y. Étude du Phénomène d’Humidification de Dépôts Naturels et Artificiels de Pollution sur des Isolateurs Électriques. Ph.D. Thesis, Université Louis Pasteur, Strasbourg, France, 1994. [Google Scholar]
- Slama, M.E.A.; Albano, M.; Haddad, A.M.; Waters, R.T.; Cwikowski, O.; Iddrissu, I.; Scopes, O. Monitoring of dry bands and discharge activities at the surface of textured insulators with AC clean fog test conditions. Energies 2021, 14, 2914. [Google Scholar] [CrossRef]
- Savadkoohi, E.M.; Mirzaie, M.; Seyyedbarzegar, S.; Mohammadi, M.; Khodsuz, M.; Pashakolae, M.G.; Ghadikolaei, M.B. Experimental investigation on composite insulators AC flashover performance with fan-shaped non-uniform pollution under electro-thermal stress. Inter. Jour. Electri. Pow. Ener. Sys. 2020, 121, 106142. [Google Scholar] [CrossRef]
- Zhang, Z.; You, J.; Wei, D.; Jiang, X.; Zhang, D.; Bi, M. Investigations on AC pollution flashover performance of insulator string under different non-uniform pollution conditions. IET Gener. Transm. Distrib. 2016, 10, 437–443. [Google Scholar] [CrossRef]
- Zhang, Z.; Qiao, X.; Yang, S.; Jiang, X. Non-uniform distribution of contamination on composite insulators in HVDC transmission lines. Appl. Sci. 2018, 8, 1962. [Google Scholar] [CrossRef]










| Materials | Conductivity | k (W/m·K) | (J/kg·K) | |
|---|---|---|---|---|
| Air | 1 | 10−30 (S/m) | 0.030 | 1009 |
| Plexiglas | 2.27 | 1.67 × 10−18 (S/m) | 0.19 | 1450 |
| Pollution layer | 81 | (S) | 0.61 | 4190 |
| Glass | 4.1 | 10−15 (S/m) | 1.2 | 835 |
| RTV | 2.7 | 1.3 × 10−17 (S/m) | 0.29 | 1460 |
| Applied Voltage (kVrms) | Rav exp. (kΩ) | Rav num. (kΩ) | TDB exp. (s) | TDB num. (s) | Rav Discrepancy (%) | TDB Discrepancy (%) |
|---|---|---|---|---|---|---|
| 2 | 59.2 | 69.5 | 118 | 111 | 17.4 | 5.9 |
| 4 | 52.2 | 66.7 | 58 | 54 | 13.4 | 6.9 |
| 6 | 51.6 | 60.9 | 40 | 37 | 18.1 | 7.5 |
| Applied Voltage (kVrms) | Tav exp. (°C) | Tav num. (°C) | Tmax exp. (°C) | Tmax num. (°C) | Tav Discrepancy (%) | Tmax Discrepancy (%) |
|---|---|---|---|---|---|---|
| 2 | 36.5 | 42.6 | 71.2 | 80.9 | 16.7 | 13.6 |
| 4 | 33.2 | 37.5 | 69.5 | 81.9 | 13.0 | 17.8 |
| 6 | 31.9 | 36.5 | 71.8 | 81.3 | 14.4 | 13.2 |
| Voltage level, kV | 69 |  |
| Length X, mm | 866 | |
| ϕD1, mm | 92 | |
| ϕD2, mm | 72 | |
| Shed number | 21 | |
| Leakage distance, mm | 1395 |
| Materials | Electrical Conductivity (S/m) | Thermal Conductivity (W/m·k) | ||
|---|---|---|---|---|
| Rod | 7.2 | 2500 | 0.04 | |
| Envelop | 4.6 | 1200 | 0.29 | |
| Metal ends | 1 | 7850 | 44.5 | |
| Pollution layer | 81 | 2.6 | 0.6 | |
| Air | 1 | 1.225 | 0.024 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Andoh, M.-A.; Volat, C.; Koné, G. A Simple Thermoelectrical Surface Approach for Numerically Studying Dry Band Formation on Polluted Insulators. Energies 2025, 18, 2412. https://doi.org/10.3390/en18102412
Andoh M-A, Volat C, Koné G. A Simple Thermoelectrical Surface Approach for Numerically Studying Dry Band Formation on Polluted Insulators. Energies. 2025; 18(10):2412. https://doi.org/10.3390/en18102412
Chicago/Turabian StyleAndoh, Marc-Alain, Christophe Volat, and Gbah Koné. 2025. "A Simple Thermoelectrical Surface Approach for Numerically Studying Dry Band Formation on Polluted Insulators" Energies 18, no. 10: 2412. https://doi.org/10.3390/en18102412
APA StyleAndoh, M.-A., Volat, C., & Koné, G. (2025). A Simple Thermoelectrical Surface Approach for Numerically Studying Dry Band Formation on Polluted Insulators. Energies, 18(10), 2412. https://doi.org/10.3390/en18102412







