A Cable Defect Assessment Method Based on a Mixed-Domain Multi-Feature Set of Overall Harmonic Signals
Abstract
1. Introduction
2. Harmonic Current Test
2.1. Specimen Preparation
2.2. Current Collection
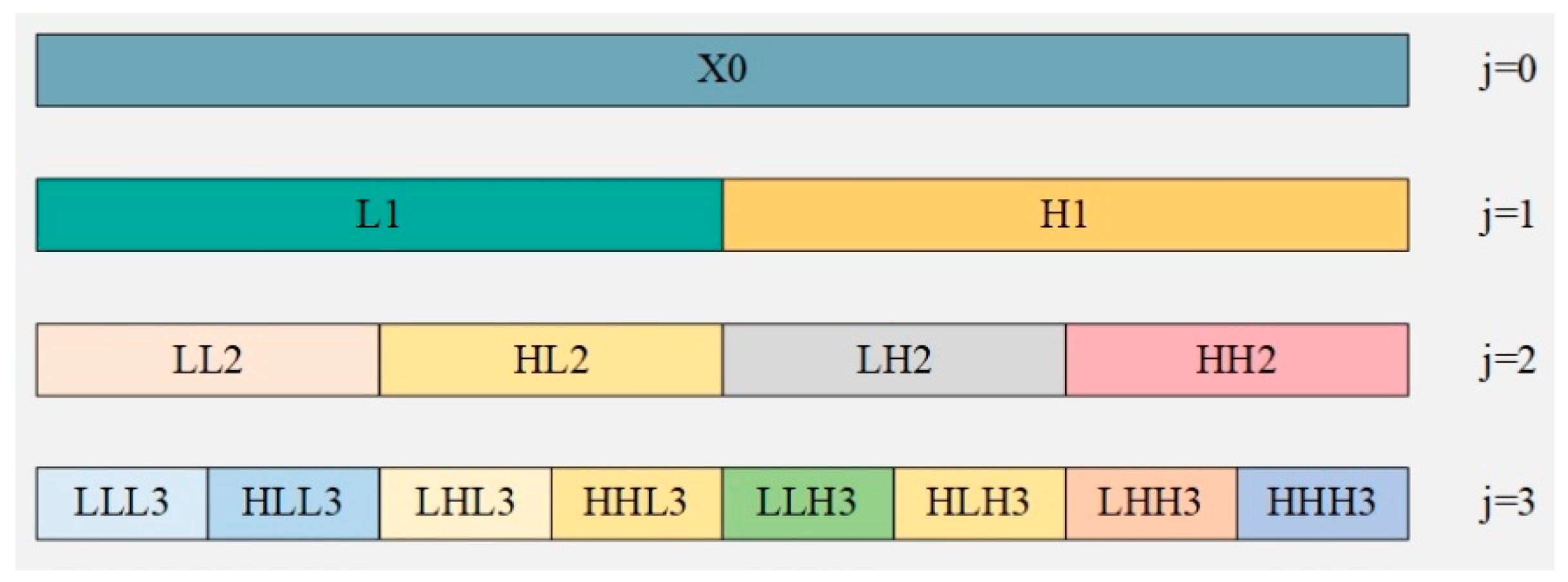
2.3. Harmonic Sequence Separation
3. Mixed-Domain Multi-Feature Set of Harmonic Sequence
3.1. Extraction Methods
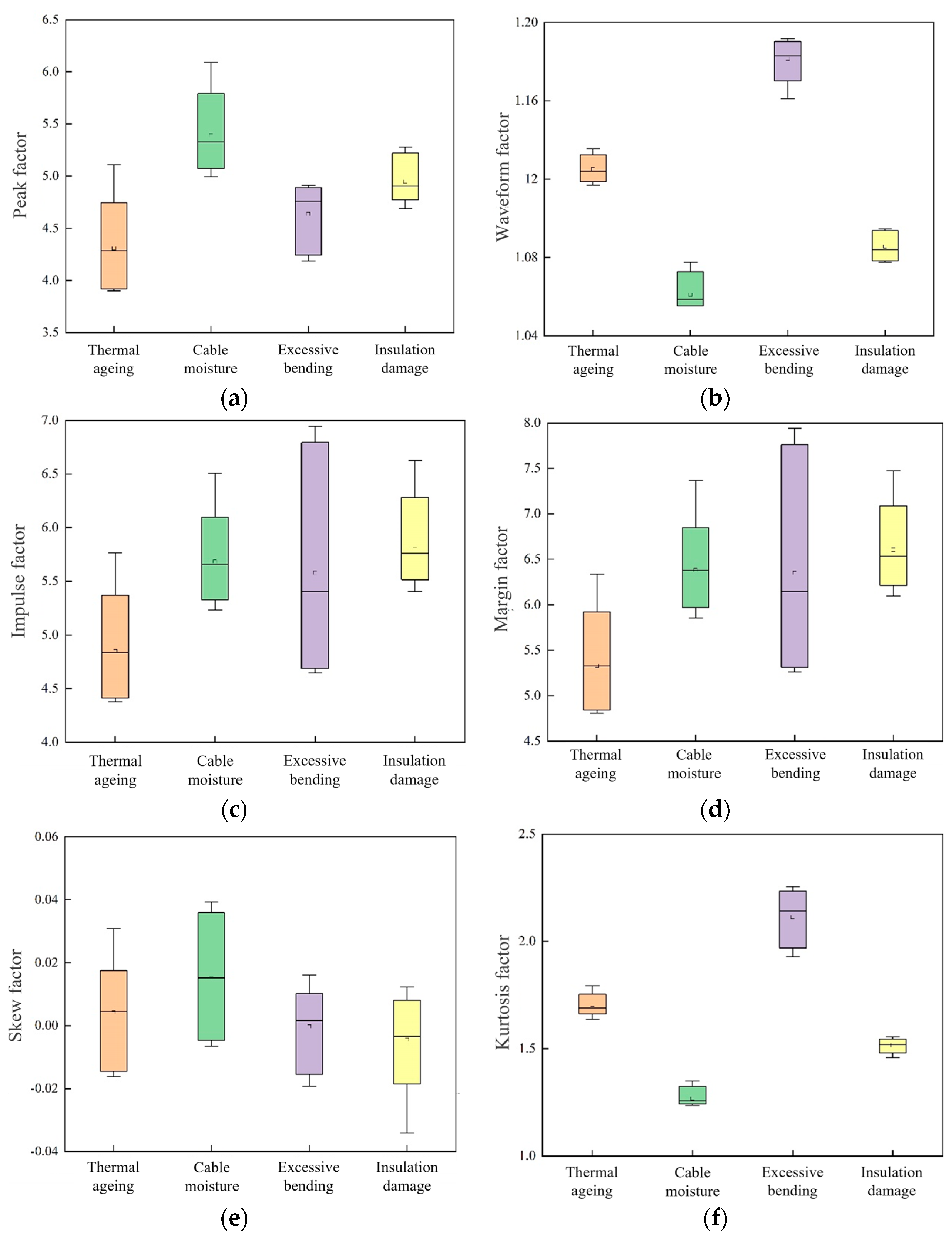
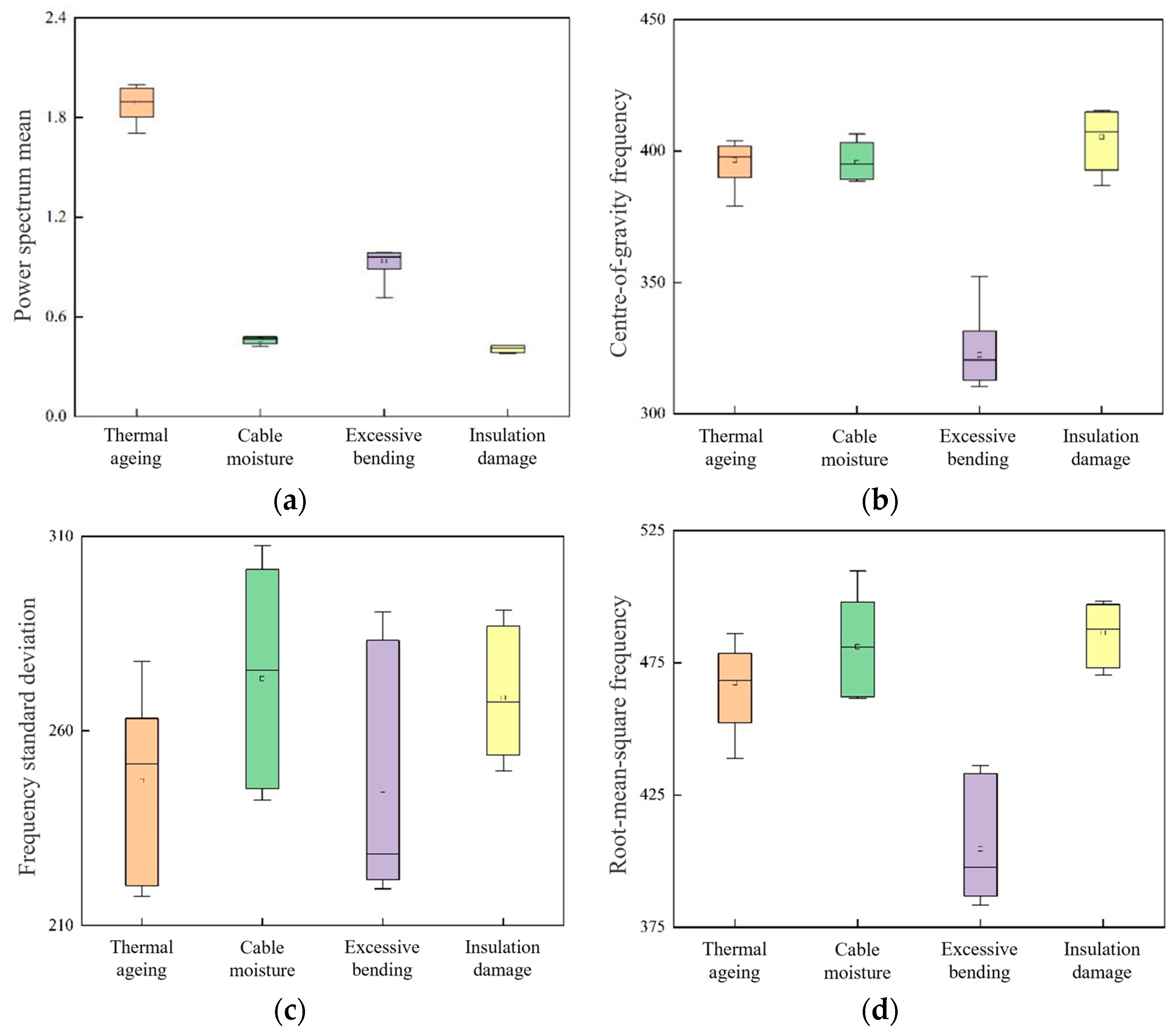
3.2. Feature Validity Analysis
4. Improved SVM Model for Cable Defect Recognition
4.1. Support Vector Machine (SVM)
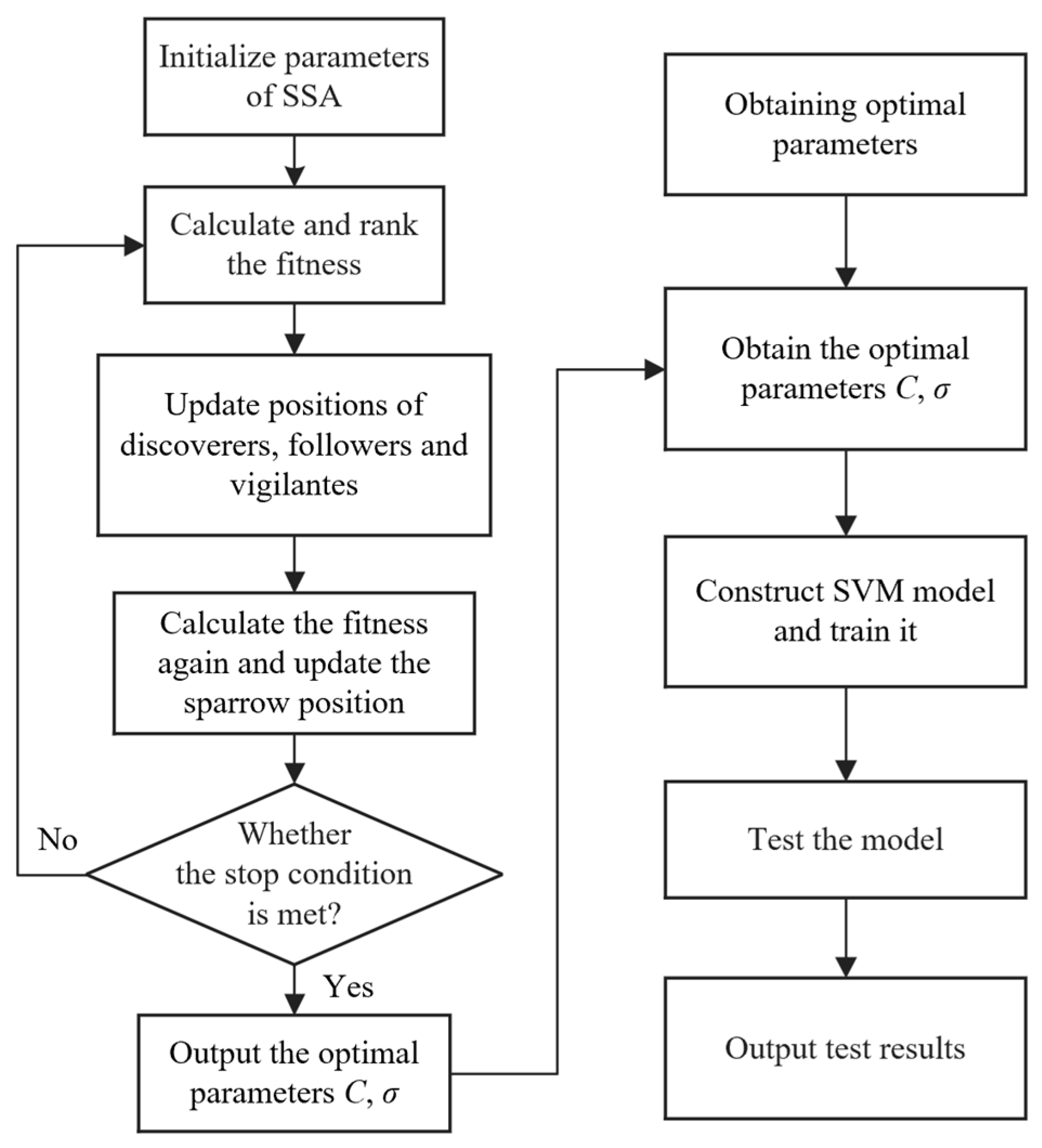
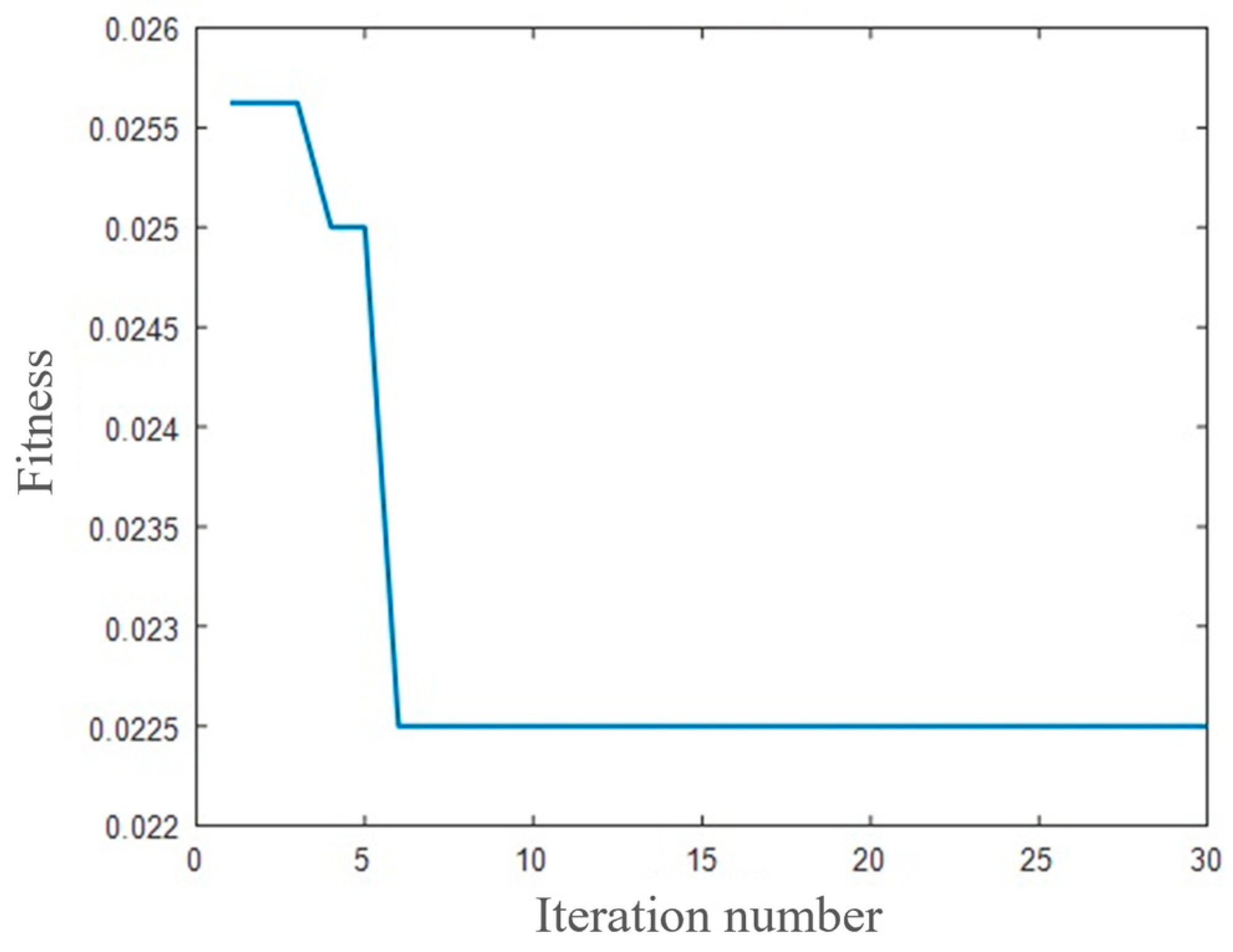
4.2. Model Improvement Through Sparrow Search Algorithm (SSA)
- (1)
- Initialize the SSA parameters, which include the number of sparrow groups, the maximum number of iterations, the ratios of discoverers and followers and vigilantes, and also the range of C and σ values;
- (2)
- Calculate and rank the fitness of each sparrow, and classify the group to which they belong;
- (3)
- Update the positions of the sparrows in the three groups according to the position update rule;
- (4)
- After the position update, calculate the fitness value of each sparrow again, compare the fitness values before and after the update, keep the optimal fitness, and continue the update;
- (5)
- Determine whether the termination condition of the algorithm is satisfied or whether the maximum number of iterations is reached, if so, output the optimal parameters C, σ, otherwise, return to step (2) to continue the iteration until the termination condition is satisfied.
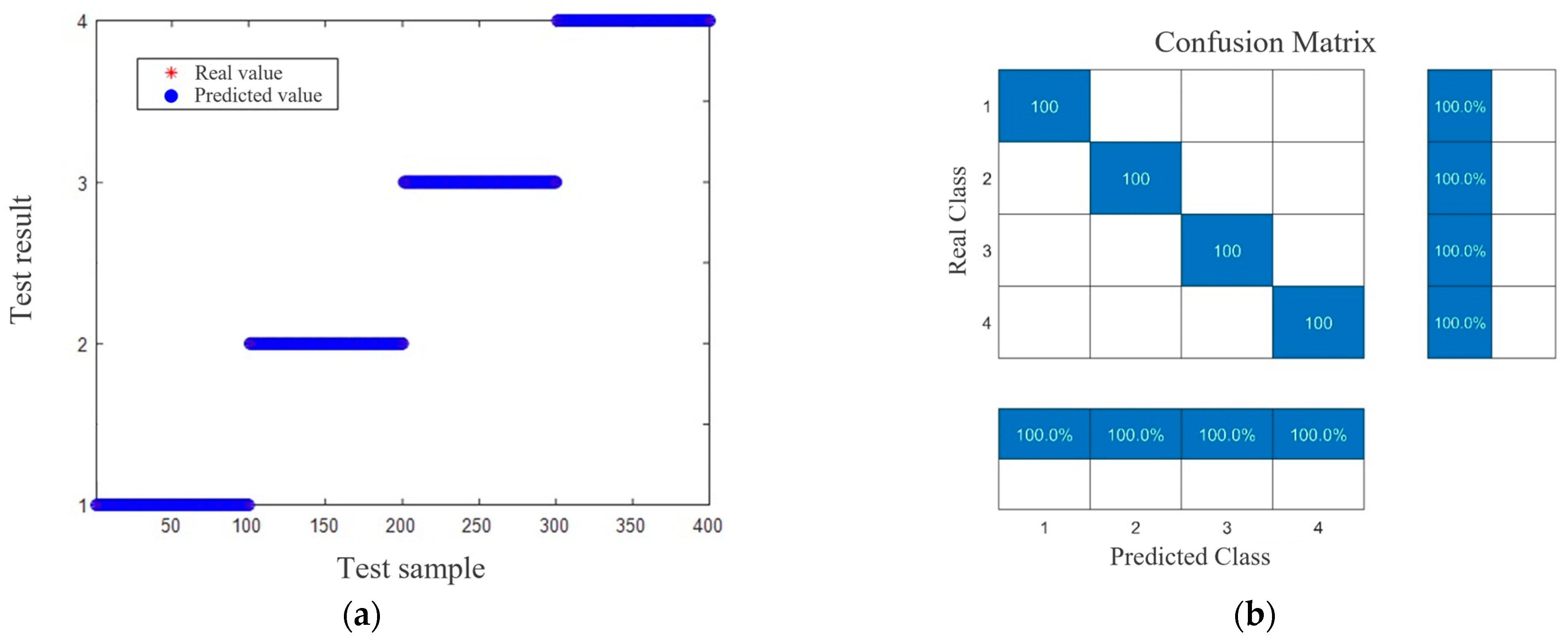
4.3. Testing Result and Comparison
5. Conclusions
- (1)
- The results of the grounding current test and VMD time series analysis show that different kinds of cable defects lead to significantly differentiated harmonic distortions in the grounding current waveforms, which can be used as a reliable basis for assessing defects in cables.
- (2)
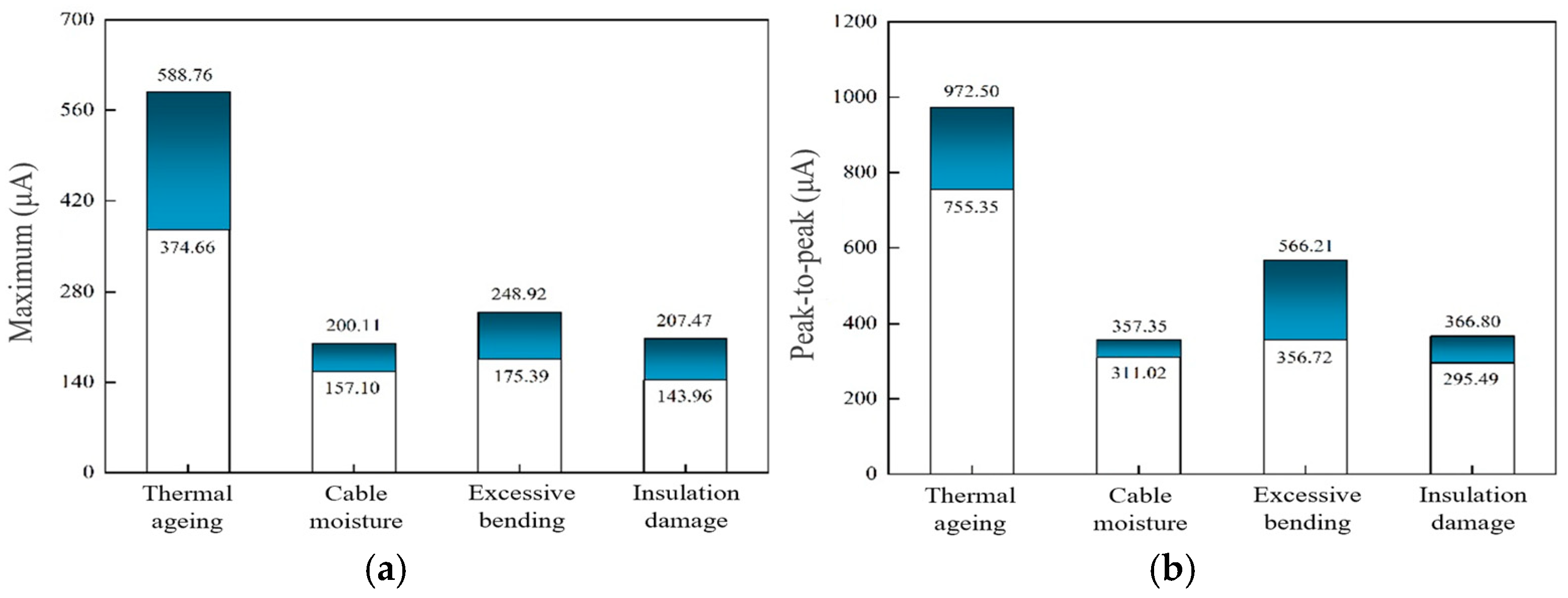
- The time-domain, frequency-domain, multi-scale relative energy, and sample entropy characteristic parameters of the overall harmonic sequences are extracted in this study. Through feature validity analysis, it is found that the maximum, peak-to-peak, absolute mean, standard deviation, root-mean-square, waveform factor, peak factor, kurtosis factor, power spectrum mean, centre-of-gravity frequency, root-mean-square frequency, LLL3 relative energy, HLL3 relative energy, and LHL3 relative energy, in total, 14 characteristic parameters have a good differentiation of cable defects, a total of 14 feature parameters have a good differentiation of cable defects.
- (3)
- For the cable defect recognition problem, the optimal values of C and σ in the SVM model are found to be 0.6121 and 16.4067, respectively, by SSA. The results show that the SSA-SVM model is effective in cable defect recognition, which is significantly better than the SVM model as well as the BPNN model, and the recognition rate reaches 100%.
- (4)
- Although the SSA-SVM model greatly improves the accuracy of cable defect assessment, the algorithm is very time-consuming. How to improve the computational efficiency of the model while ensuring a high recognition rate is the focus of subsequent research.
- (5)
- To better demonstrate the strength of the proposed method as well as its problems, a comparative analysis with other existing cable defect assessment methods will be further conducted. Sensitivity analysis on factors influencing method performance is also a focus of our future work.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Lu, H.; Zhang, W.H.; Wang, Y.; Xiao, X.Y. Cable Incipient Fault Identification Method Using Power Disturbance Waveform Feature Learning. IEEE Access 2022, 10, 86078–86091. [Google Scholar] [CrossRef]
- De Clippelaar, S.; Kruizinga, B.; van der Wielen, P.C.J.M.; Wouters, P.A.A.F. Wave-Velocity Based Real-Time Thermal Monitoring of Medium-Voltage Underground Power Cables. IEEE Trans. Power Deliv. 2024, 39, 983–991. [Google Scholar] [CrossRef]
- Liu, Y.; Xin, Y.; Huang, Y.; Du, B.; Huang, X.; Su, J. Optimal Design and Development of Magnetic Field Detection Sensor for AC Power Cable. Sensors 2024, 24, 2528. [Google Scholar] [CrossRef] [PubMed]
- Su, J.; Zhang, P.; Huang, X.; Pang, X.; Diao, X.; Li, Y. Current Measurement of Three-Core Cables via Magnetic Sensors. Energies 2024, 17, 4007. [Google Scholar] [CrossRef]
- Hu, S.; Wang, L.; Mao, J.; Gao, C.; Zhang, B.; Yang, S. Synchronous Online Diagnosis of Multiple Cable Intermittent Faults Based on Chaotic Spread Spectrum Sequence. IEEE Trans. Dielectr. Electr. Insul. 2019, 66, 3217–3226. [Google Scholar] [CrossRef]
- Chen, W.; Yang, Z.; Song, J.; Zhou, L.; Xiang, L.; Wang, X.; Hao, C.; Fan, X. A High-Resolution Defect Location Method for Medium-Voltage Cables Based on Gaussian Narrow-Band Envelope Signals and the S-Transform. Energies 2024, 17, 2218. [Google Scholar] [CrossRef]
- Abu-Rub, O.H.; Khan, Q.; Refaat, S.S.; Nounou, H. Cable Insulation Fault Identification Using Partial Discharge Patterns Analysis. IEEE Can. J. Electr. Comput. Eng. 2020, 45, 31–41. [Google Scholar] [CrossRef]
- Zhang, H. Cable Fault Detection and Diagnosis Method Based on Convolutional Neural Network. In Proceedings of the 2023 IEEE International Conference on Image Processing and Computer Applications (ICIPCA), Changchun, China, 11–13 August 2023; pp. 1463–1466. [Google Scholar]
- Liu, J.; Wang, S.; Yan, S.; Zhang, M.; Huang, L. Fast Detection Method on Water Tree Aging of MV Cable Based on Nonsinusoidal Response Measurement. IEEE Trans. Power Deliv. 2023, 38, 146–153. [Google Scholar] [CrossRef]
- Lu, X.; Hu, R.; Guo, K.; Lan, R.; Tian, J.; Wei, Y.; Li, G. Effect of Interface Defects on the Electric–Thermal–Stress Coupling Field Distribution of Cable Accessory Insulation. Energies 2024, 17, 4498. [Google Scholar] [CrossRef]
- Yuan, L.; Liu, W.; Zhao, Y. Multi-point sensing system for cable fault detection using fiber Bragg grating. Opt. Fiber Technol. 2024, 87, 103942. [Google Scholar] [CrossRef]
- Liu, K.; Yang, Z.; Wei, W.; Gao, B.; Xin, D.; Sun, C.; Gao, G.; Wu, G. Novel detection approach for thermal defects: Study on its feasibility and application to vehicle cables. High Volt. 2023, 8, 358–367. [Google Scholar] [CrossRef]
- Xie, J.; Sun, T.; Zhang, J.; Ye, L.; Fan, M.; Zhu, M. Research on Cable Defect Recognition Technology Based on Image Contour Detection. In Proceedings of the 2021 2nd International Conference on Big Data & Artificial Intelligence & Software Engineering (ICBASE), Zhuhai, China, 24–26 September 2021; pp. 387–391. [Google Scholar]
- IEC 60811-203-2012; Electric and Optical Fibre Cables—Test Methods for Non-Metallic Materials. IEC: Geneva, Switzerland, 2012.
- Dragomiretskiy, K.; Zosso, D. Variational mode decomposition. IEEE Trans. Signal Process. 2013, 62, 531–544. [Google Scholar] [CrossRef]
- Liu, Y.; Wang, H.; Zhang, H.; Du, B. Thermal Aging Evaluation of XLPE Power Cable by Using Multidimensional Characteristic Analysis of Leakage Current. Polymers 2022, 14, 3147. [Google Scholar] [CrossRef] [PubMed]
- He, K.; Li, X. Time–Frequency Feature Extraction of Acoustic Emission Signals in Aluminum Alloy MIG Welding Process Based on SST and PCA. IEEE Access 2019, 7, 113988–113998. [Google Scholar] [CrossRef]
- Xue, J. Research and Application of a Novel Swarm Intelligence Optimization Technique: Sparrow Search Algorithm. Master’s Thesis, Donghua University, Shanghai, China, 2020. [Google Scholar]

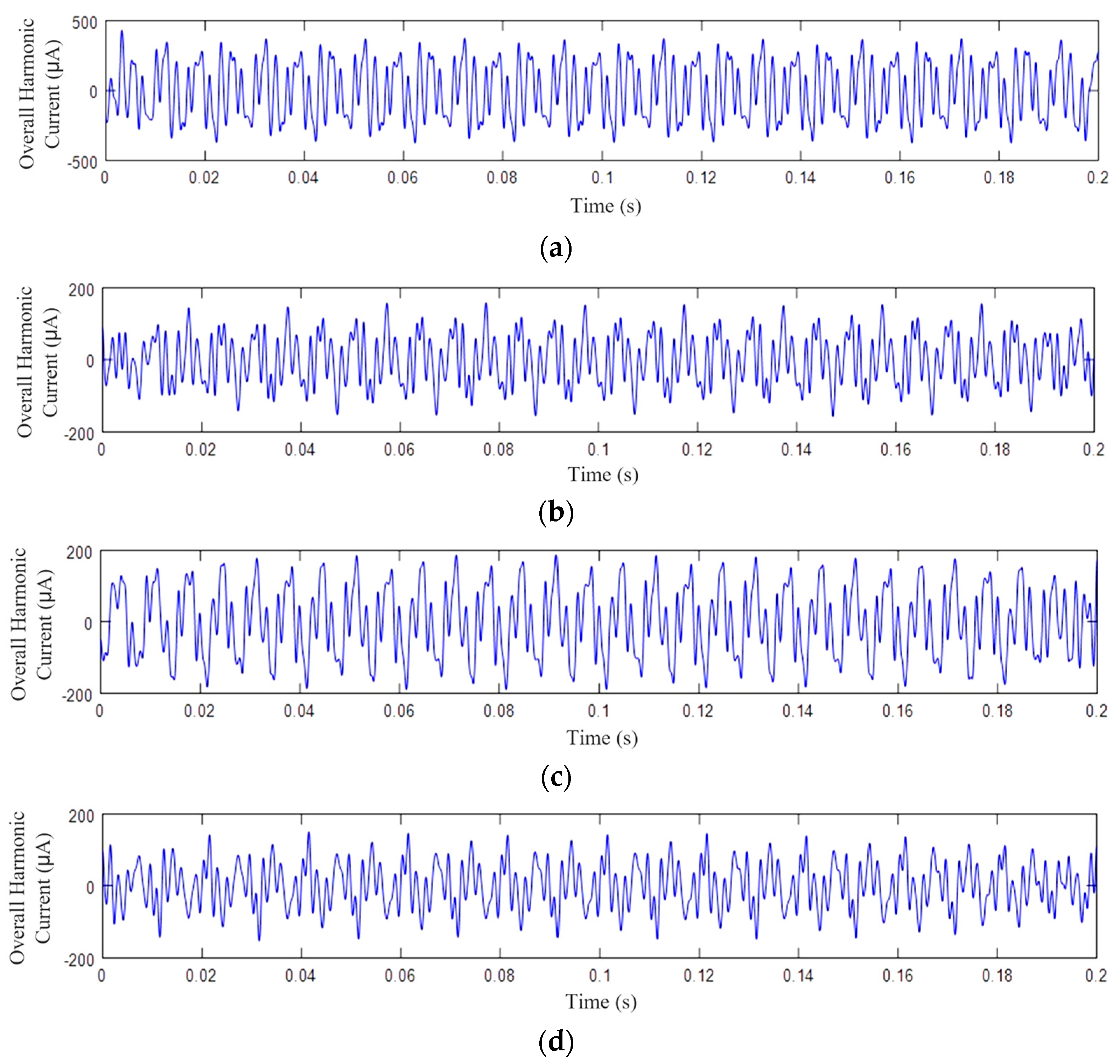

| Defect Type | Simulation Method |
|---|---|
| Thermal ageing | Use the HK-450A+ electrothermal constant temperature oven to accelerate thermal ageing. Put the specimen into the oven after the temperature reaches 120 °C. The sampling time is selected in an equal progression (12, 24, and 48 days) according to IEC 60811 [14]. |
| Cable moisture | Strip the outer sheath of the specimen, seal it with a heat-shrink sleeve filled with water, and test it at 5, 10, and 15 days. |
| Excessive bending | Fix the specimen to the wooden board using cable clamps and hexagonal screws according to the bending radius (R = 600 mm, R = 400 mm, R = 200 mm), corresponding to the specimen length of 2 m, 1.6 m, and 1.2 m. |
| Insulation damage | Peel off the outer sheath, metal shield, and insulating shield sequentially at the middle section of the specimen, with a length of 40 mm. Construct the scratch on the insulating layer to set three levels of damage, respectively, 40 mm × 2 mm × 1 mm, 40 mm × 4 mm × 1 mm, and 40 mm × 6 mm × 1 mm. |
| Equipment | Model/Parameter | Equipment | Model/Parameter |
|---|---|---|---|
| Regulator | TDGC2-3, CHNT, Wenzhou, China | High-frequency Acquisition Card | PCI-1712, 20 kHz |
| Test Transformer | TDM 11,000 kVA, Sanxin Huatai, Wuhan, China | Cable Specimen | YJLV8.7/15 kV-1 × 70 mm2 |
| Voltage Divider | RCF-50 kV, Sanxin Huatai, Wuhan, China | Protective Resistor | 1 MΩ |
| Oscilloscope | MSO5104, RIGOL, Suzhou, China | Sampling Resistor | 10 kΩ |
| Category | Calculation Formula | |||
|---|---|---|---|---|
| Time-domain features | Mean | Skewness | ||
| Variance | Kurtosis | |||
| Square root magnitude | Peak Factor | |||
| Absolute Mean Magnitude | Waveform Factor | |||
| Maximum | Impulse Factor | |||
| Minimum | Margin factor | |||
| Peak-to-peak | Skew factor | |||
| Root-Mean- Square | Kurtosis factor | |||
| Frequency-domain features | Power Spectrum Mean | |||
| Centre-of-gravity frequency | ||||
| Frequency Variance | ||||
| Frequency standard deviation | ||||
| Mean Square Frequency | ||||
| Root-mean-square Frequency | ||||
| Parameter | Setting |
|---|---|
| Number of sparrow groups | 10 |
| Maximum number of iterations | 30 |
| ST safety threshold | 0.7 |
| Proportion of discoverers | 40% |
| Proportion of vigilantes | 20% |
| Comparison Items | SVM | BPNN | SSA-SVM | |||
|---|---|---|---|---|---|---|
| Before PCA | After PCA | Before PCA | After PCA | Before PCA | After PCA | |
| Recognition rate/% | 93.75 | 95.25 | 92.5 | 98.5 | 97.75 | 100 |
| Time consumption/s | 0.8961 | 0.4233 | 3.6536 | 0.8614 | 53.8151 | 23.9943 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, R.; Pan, R. A Cable Defect Assessment Method Based on a Mixed-Domain Multi-Feature Set of Overall Harmonic Signals. Energies 2025, 18, 83. https://doi.org/10.3390/en18010083
Wang R, Pan R. A Cable Defect Assessment Method Based on a Mixed-Domain Multi-Feature Set of Overall Harmonic Signals. Energies. 2025; 18(1):83. https://doi.org/10.3390/en18010083
Chicago/Turabian StyleWang, Ruidong, and Ruzheng Pan. 2025. "A Cable Defect Assessment Method Based on a Mixed-Domain Multi-Feature Set of Overall Harmonic Signals" Energies 18, no. 1: 83. https://doi.org/10.3390/en18010083
APA StyleWang, R., & Pan, R. (2025). A Cable Defect Assessment Method Based on a Mixed-Domain Multi-Feature Set of Overall Harmonic Signals. Energies, 18(1), 83. https://doi.org/10.3390/en18010083





