Analysis, Design and Effectuation of a Tapped Inductor Current Converter with Fractional Output for Current Source Systems
Abstract
1. Introduction
1.1. Backgrounds
1.2. Basic Concept of the Duality
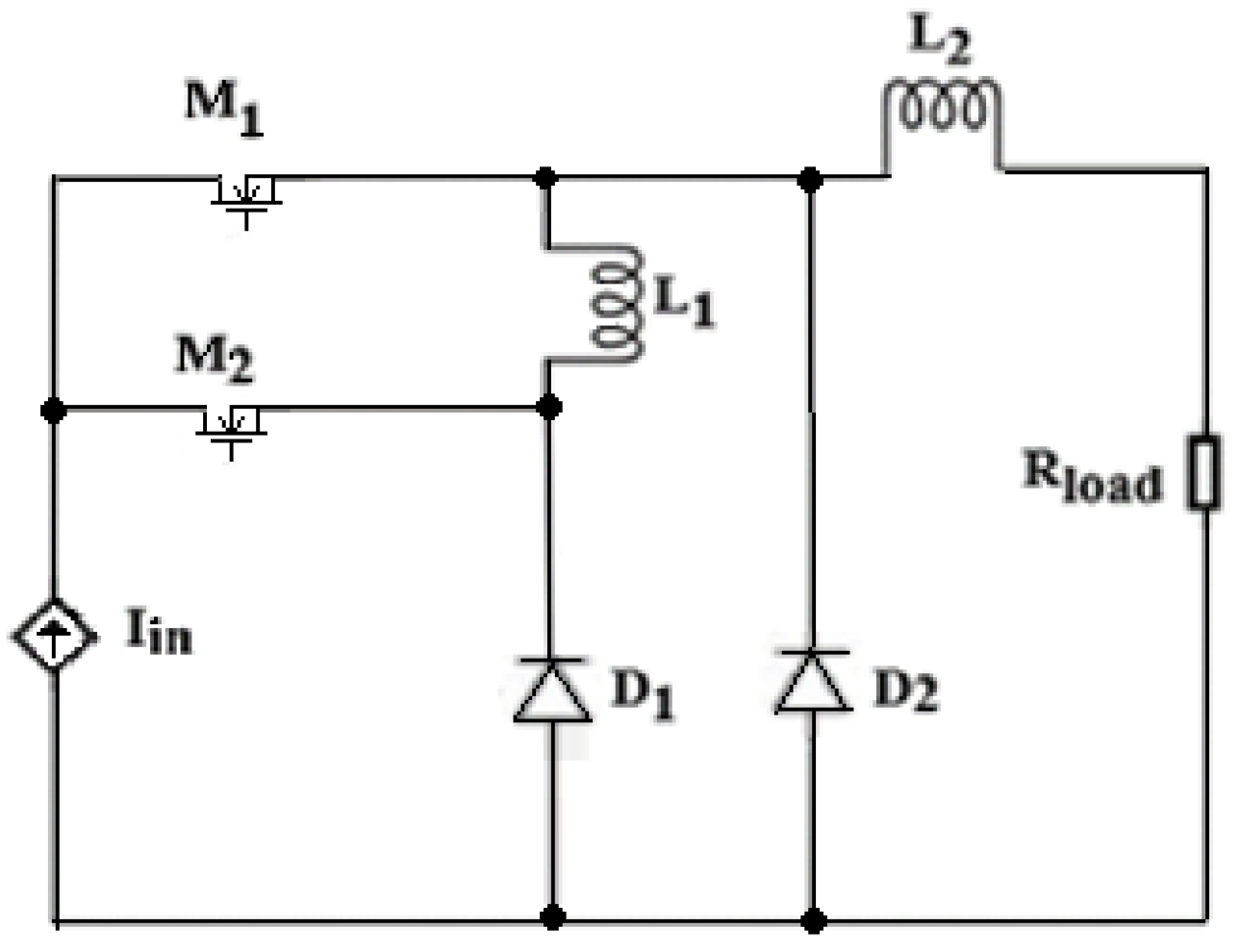
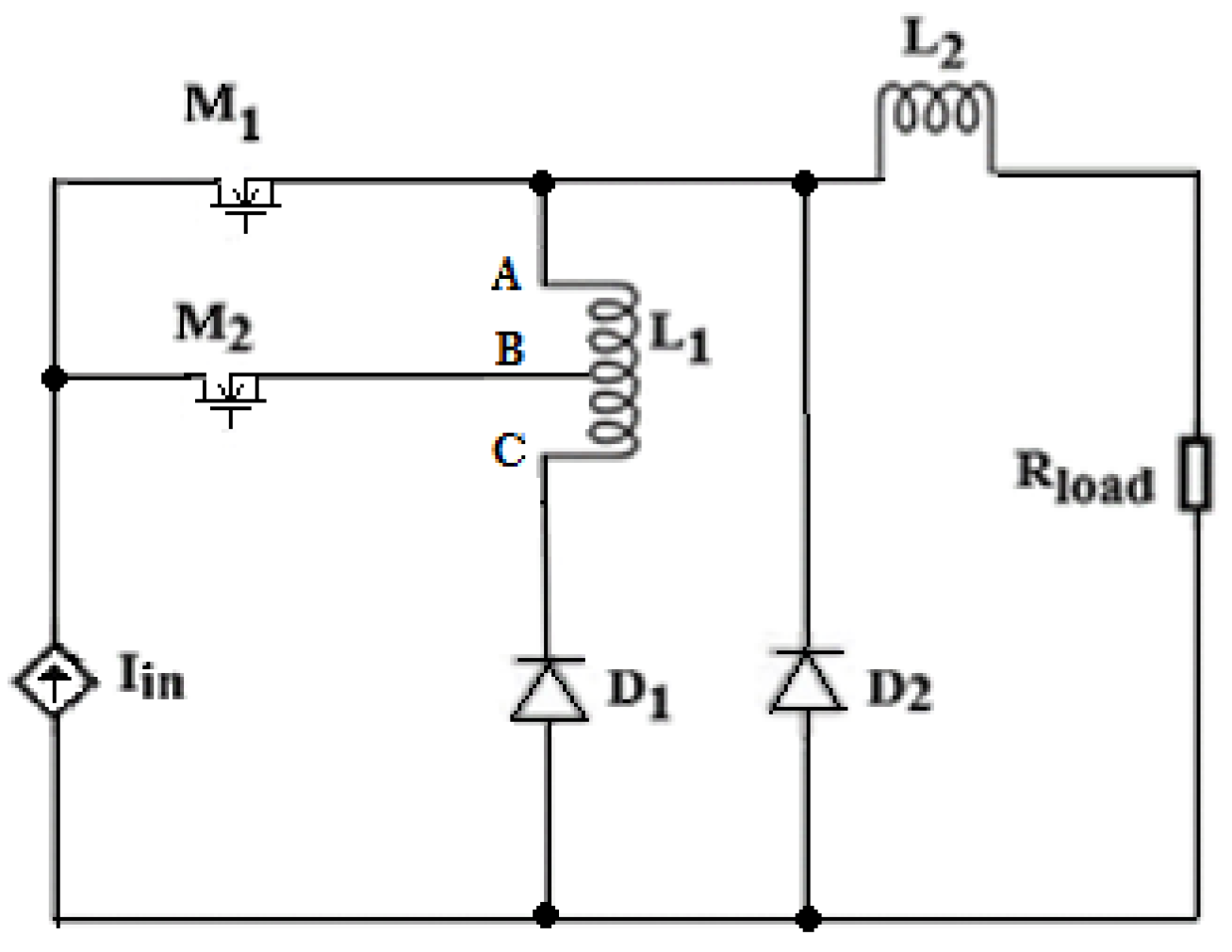
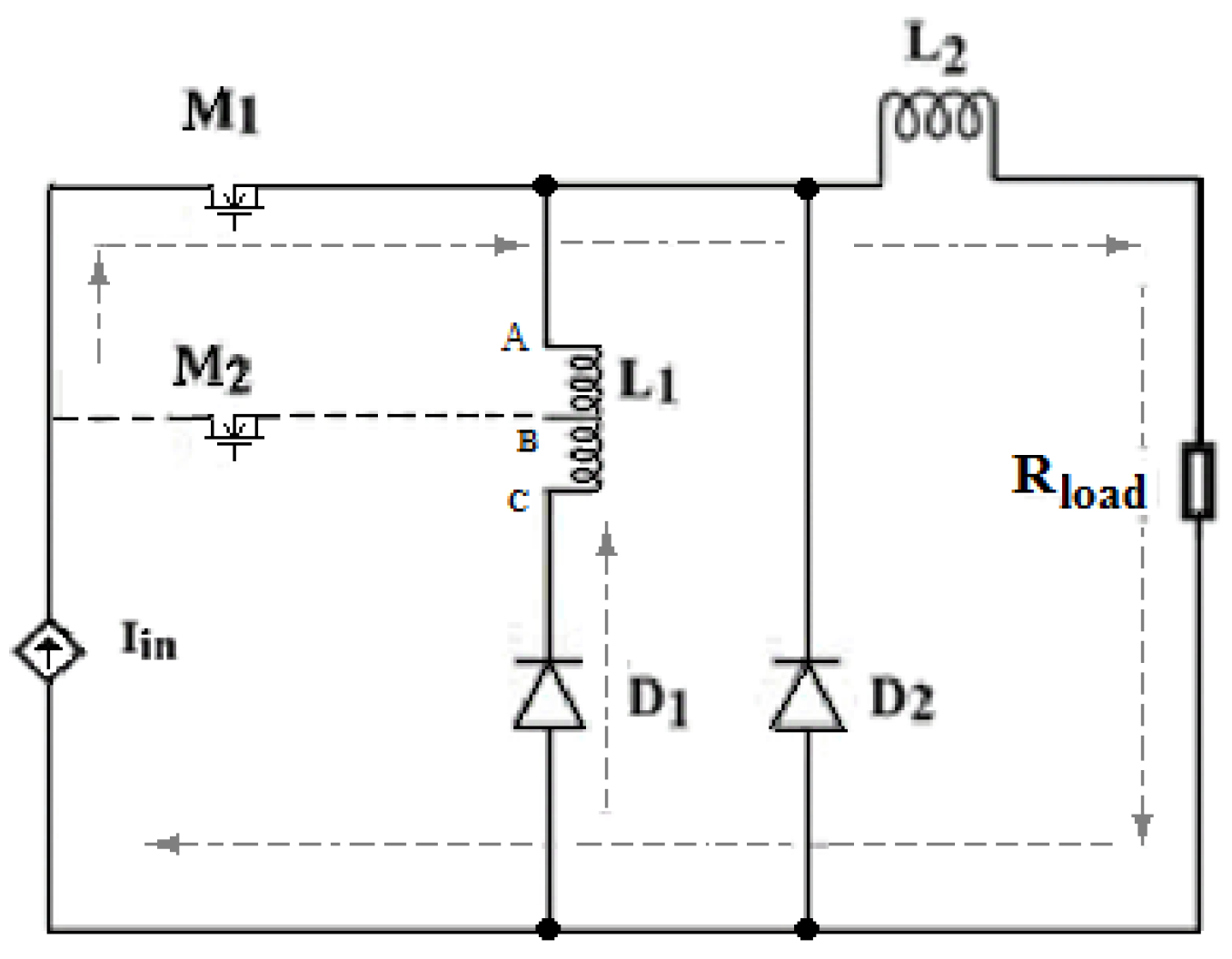
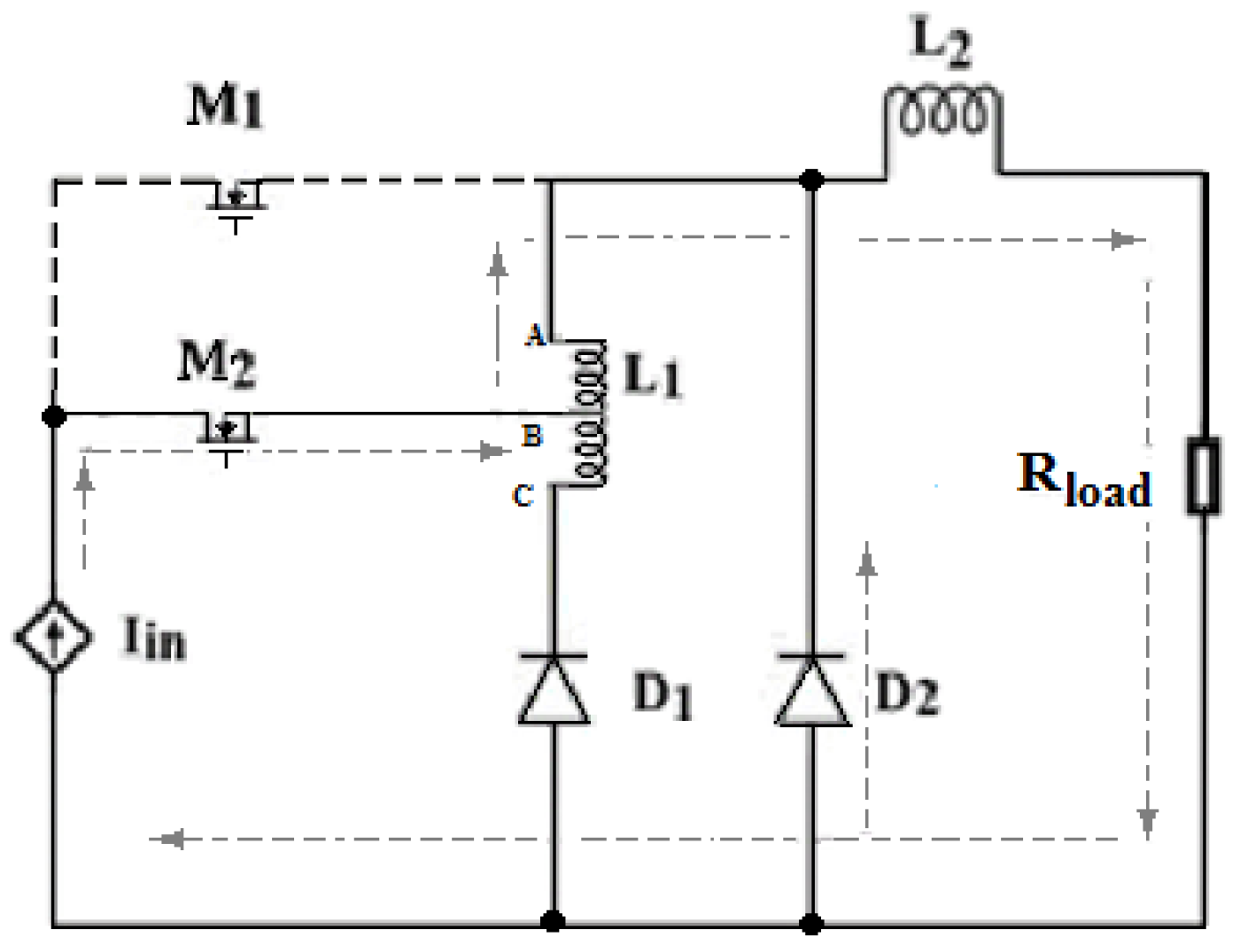
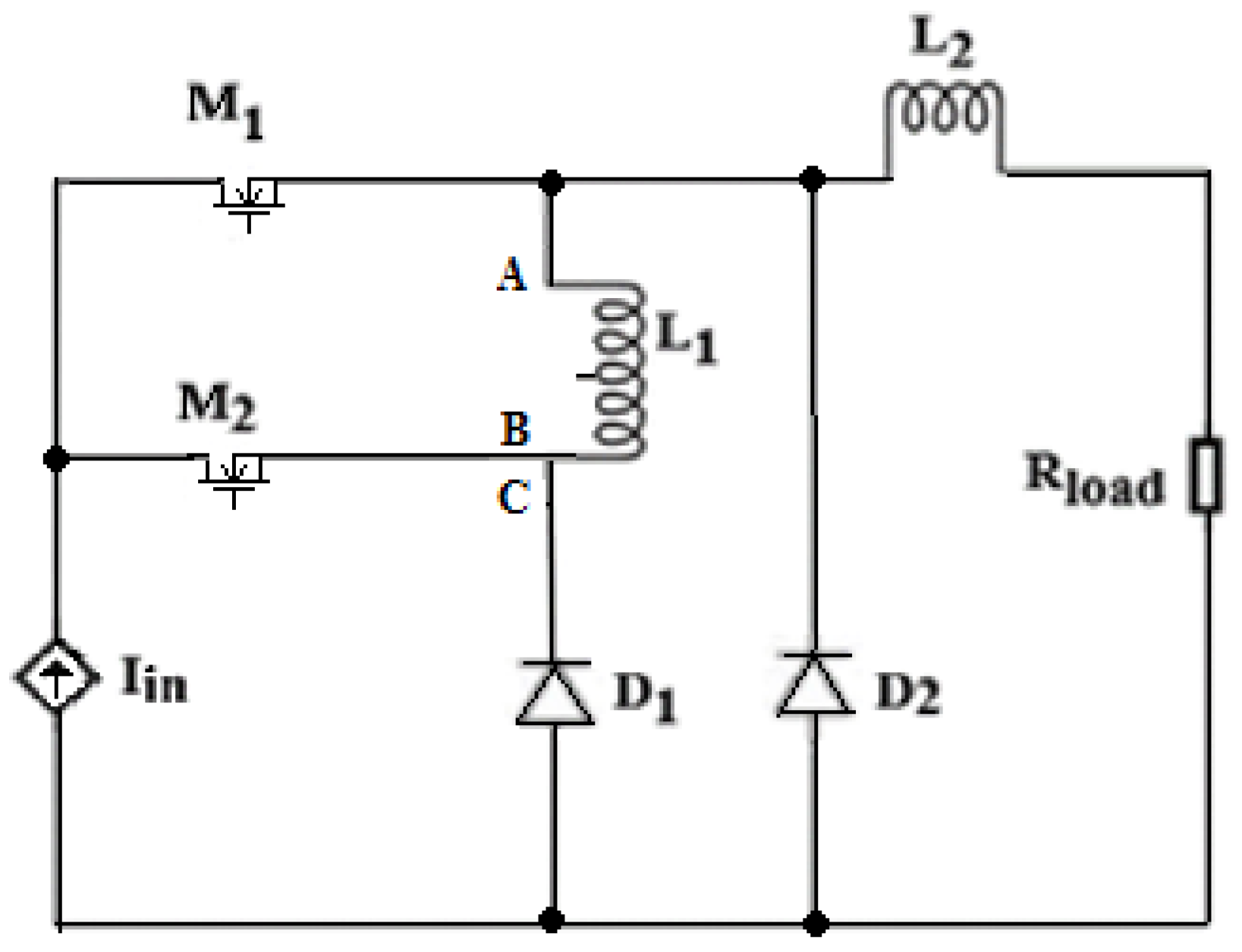
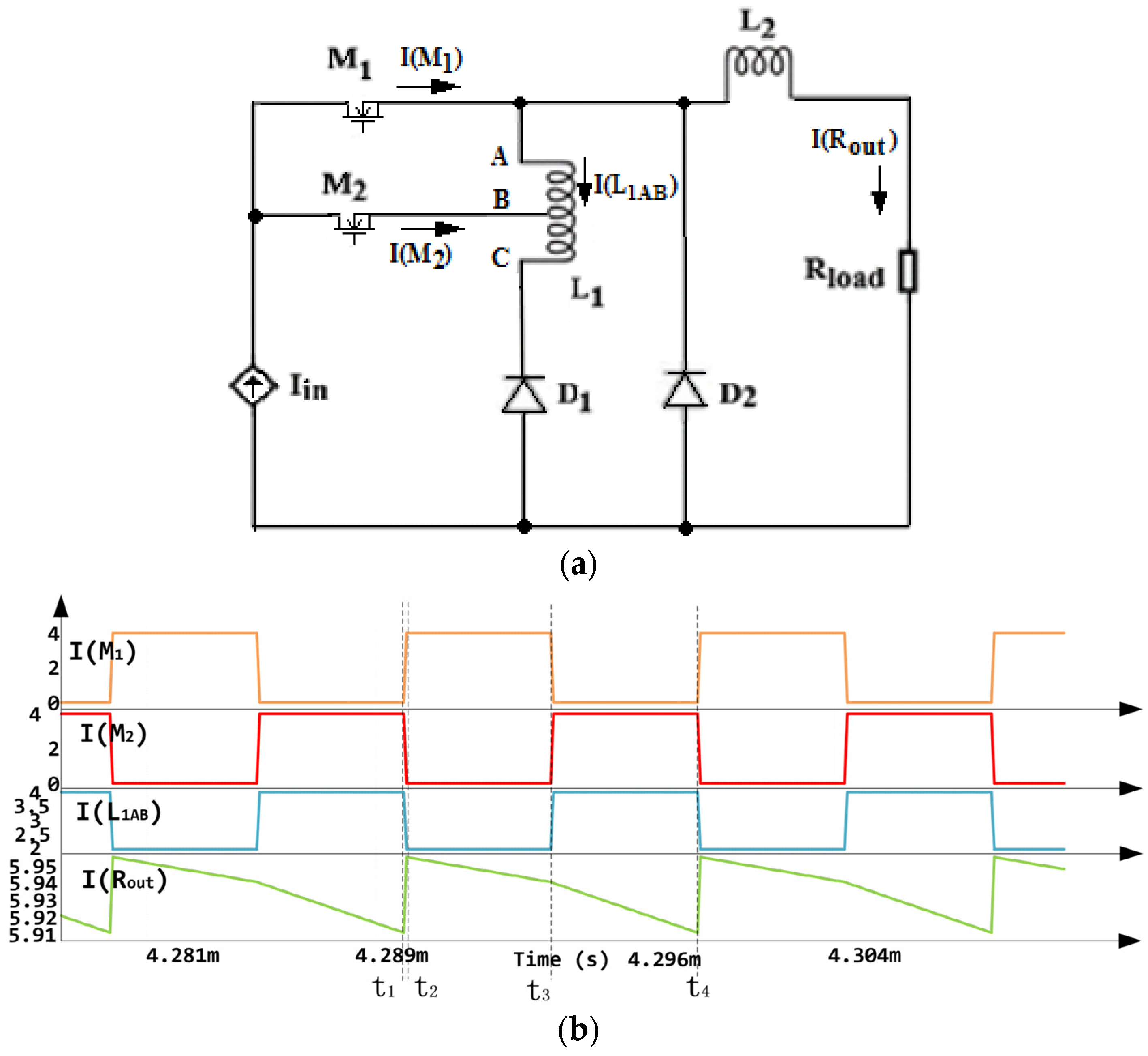
2. Tapped Inductor Converter Circuit Analysis
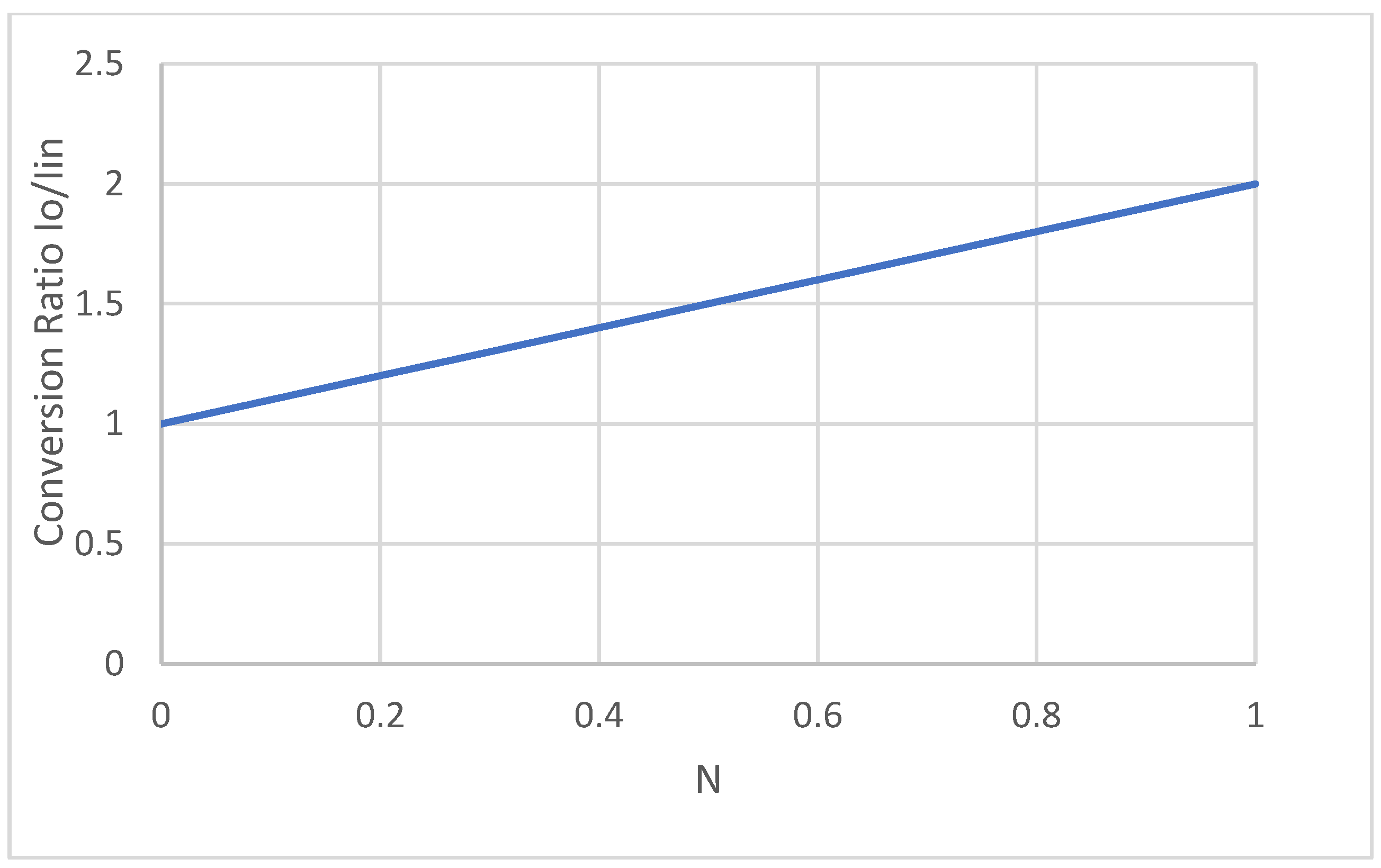
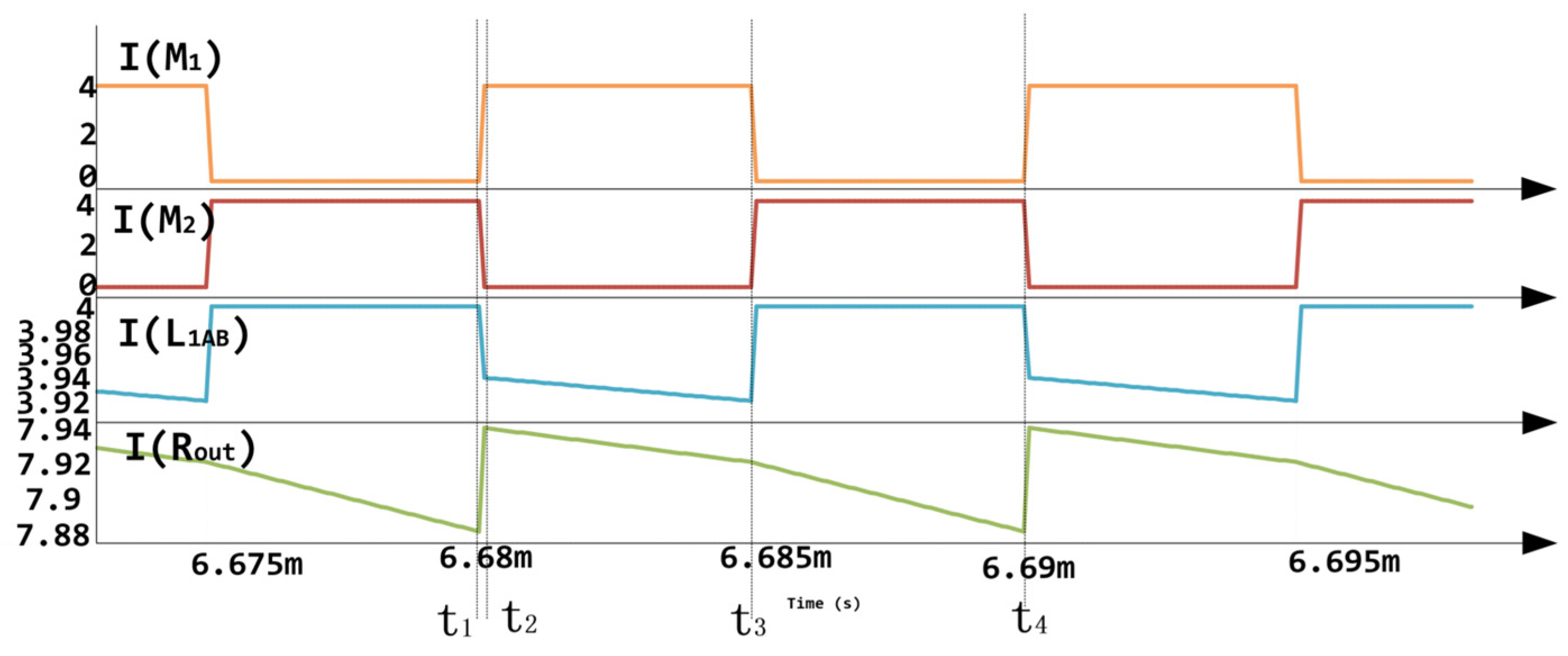
3. Tapped Inductor Converter Work on P-SIM Results
4. Higher Order
5. Prototype Experiments
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- de Freitas, C.A.F.; Bartholomeus, P.; Margueron, X.; Le Moigne, P. Series Architecture for the Reduction of the DC-DC Converter in a Hybrid Energy Storage System for Electric Vehicles. Energies 2023, 16, 7620. [Google Scholar] [CrossRef]
- Cheng, K.W.E.; Ye, Y.M. Duality approach to the study of switched-inductor power converters and its higher-order variations. IET Power Electron. 2015, 8, 489–496. [Google Scholar] [CrossRef]
- Tatar, K.; Chudzik, P.; Leśniewski, P. Sliding Mode Control of Buck DC–DC Converter with LC Input Filter. Energies 2023, 16, 6983. [Google Scholar] [CrossRef]
- Nguyen, M.-K. Power Converters in Power Electronics: Current Research Trends. Electronics 2020, 9, 654. [Google Scholar] [CrossRef]
- Xu, C.; Cheng, K.W.E. Topology and Formation of Current Source Step Down Resonant Switched Inductor Converters. Energies 2022, 15, 1697. [Google Scholar] [CrossRef]
- Zhao, B.; Abramovitz, A.; Liu, C.; Yang, Y.; Huangfu, Y. A Family of Single-Stage, Buck-Boost Inverters for Photovoltaic Applications. Energies 2020, 13, 1675. [Google Scholar] [CrossRef]
- Mishra, N.; Singh, B.; Cheng, K.W.E. Power Quality Assessment of CPUC Based Solar Photovoltaic System with NLMS for Grid-Tied Applications. IEEE Trans. Power Deliv. 2023, 38, 655–665. [Google Scholar] [CrossRef]
- Chen, W.; Cheng, K.W.E.; Shao, J. Circuit Topology Analysis for LED Lighting and its Formulation Development. Energies 2019, 12, 4203. [Google Scholar] [CrossRef]
- Lee, H.-S.; Yun, J.-J. Three-Port Converter for Integrating Energy Storage and Wireless Power Transfer Systems in Future Residential Applications. Energies 2020, 13, 272. [Google Scholar] [CrossRef]
- Wang, X.; Cheng, K.W.E.; Fong, Y.C. Zero Current Switching Switched-Capacitors Balancing Circuit for Energy Storage Cell Equalization and Its Associated Hybrid Circuit with Classical Buck-Boost. Energies 2019, 12, 2726. [Google Scholar] [CrossRef]
- Vishnuram, P.; P, S.; R, N.; K, V.; Nastasi, B. Wireless Chargers for Electric Vehicle: A Systematic Review on Converter Topologies, Environmental Assessment, and Review Policy. Energies 2023, 16, 1731. [Google Scholar] [CrossRef]
- Szczepaniak, M.; Otręba, P.; Otręba, P.; Sikora, T. Use of the Maximum Power Point Tracking Method in a Portable Lithium-Ion Solar Battery Charger. Energies 2021, 15, 26. [Google Scholar] [CrossRef]
- Shieh, Y.-T.; Wu, C.-C.; Jeng, S.-L.; Liu, C.-Y.; Hsieh, S.-Y.; Haung, C.-C.; Shieh, W.-Y.; Chieng, W.-H.; Chang, E.-Y. A Turn-Ratio-Changing Half-Bridge CLLC DC–DC Bidirectional Battery Charger Using a GaN HEMT. Energies 2023, 16, 5928. [Google Scholar] [CrossRef]
- Li, H.; Yang, Y.; Chen, J.; Xu, J.; Liu, M.; Wang, Y. A Hybrid Class-E Topology With Constant Current and Constant Voltage Output for Light EVs Wireless Charging Application. IEEE Trans. Transp. Electrif. 2021, 7, 2168–2180. [Google Scholar] [CrossRef]
- Pan, X.; Ghoshal, A.; Liu, Y.; Xu, Q.; Rathore, A.K. Hybrid-Modulation-Based Bidirectional Electrolytic Capacitor-Less Three-Phase Inverter for Fuel Cell Vehicles: Analysis, Design, and Experimental Results. IEEE Trans. Power Electron. 2018, 33, 4167–4180. [Google Scholar] [CrossRef]
- Shafiqurrahman, A.; Umesh, B.S.; Sayari, N.A.; Khadkikar, V. Electric Vehicle-to-Vehicle Energy Transfer Using On-Board Converters. IEEE Trans. Transp. Electrif. 2023, 9, 1263–1272. [Google Scholar] [CrossRef]
- Leung, C.P.; Cheng, K.W.E. Design, Analysis and Implementation of the Tapped-Inductor Boost Current Converter on Current Based System. Energies 2021, 14, 888. [Google Scholar] [CrossRef]
- Salo, M.; Tuusa, H. A Vector-Controlled PWM Current-Source-Inverter-Fed Induction Motor Drive With a New Stator Current Control Method. IEEE Trans. Ind. Electron. 2005, 52, 523–531. [Google Scholar] [CrossRef]
- Himmelstoss, F.A.; Votzi, H.L. A family of quadratic DC/DC converters with one low-side switch and a tapped inductor at the output side. In Proceedings of the 2019 International Aegean Conference on Electrical Machines and Power Electronics (ACEMP) & 2019 International Conference on Optimization of Electrical and Electronic Equipment (OPTIM), Istanbul, Turkey, 27–29 August 2019. [Google Scholar]
- de Carvalho, M.R.S.; Barbosa, E.A.O.; Bradaschia, F.; Limongi, L.R.; Cavalcanti, M.C. Soft-Switching High Step-Up DC–DC Converter Based on Switched-Capacitor and Autotransformer Voltage Multiplier Cell for PV Systems. IEEE Trans. Ind. Electron. 2022, 69, 12886–12897. [Google Scholar] [CrossRef]
- Imanlou, A.; Najmi, E.S.; Behkam, R.; Nazari-Heris, M.; Gharehpetian, G.B. A New High Voltage Gain Active Switched-Inductor Based High Step-Up DC–DC Converter With Coupled-Inductor. IEEE Access 2023, 11, 56749–56765. [Google Scholar] [CrossRef]
- Tang, Y.; Fu, D.; Wang, T.; Xu, Z. Hybrid Switched-Inductor Converters for High Step-Up Conversion. IEEE Trans. Ind. Electron. 2015, 62, 1480–1490. [Google Scholar] [CrossRef]
- Scirè, D.; Lullo, G.; Vitale, G. Non-Linear Inductor Models Comparison for Switched-Mode Power Supplies Applications. Electronics 2022, 11, 2472. [Google Scholar] [CrossRef]
- Scirè, D.; Vitale, G.; Ventimiglia, M.; Lullo, G. Non-Linear Inductors Characterization in Real Operating Conditions for Power Density Optimization in SMPS. Energies 2021, 14, 3924. [Google Scholar] [CrossRef]
- Roberto, S.F.; Scirè, D.; Lullo, G.; Vitale, G. Equivalent Circuit Modelling of Ferrite Inductors Losses. In Proceedings of the 2018 IEEE 4th International Forum on Research and Technology for Society and Industry (RTSI), Palermo, Italy, 10–13 September 2018. [Google Scholar]
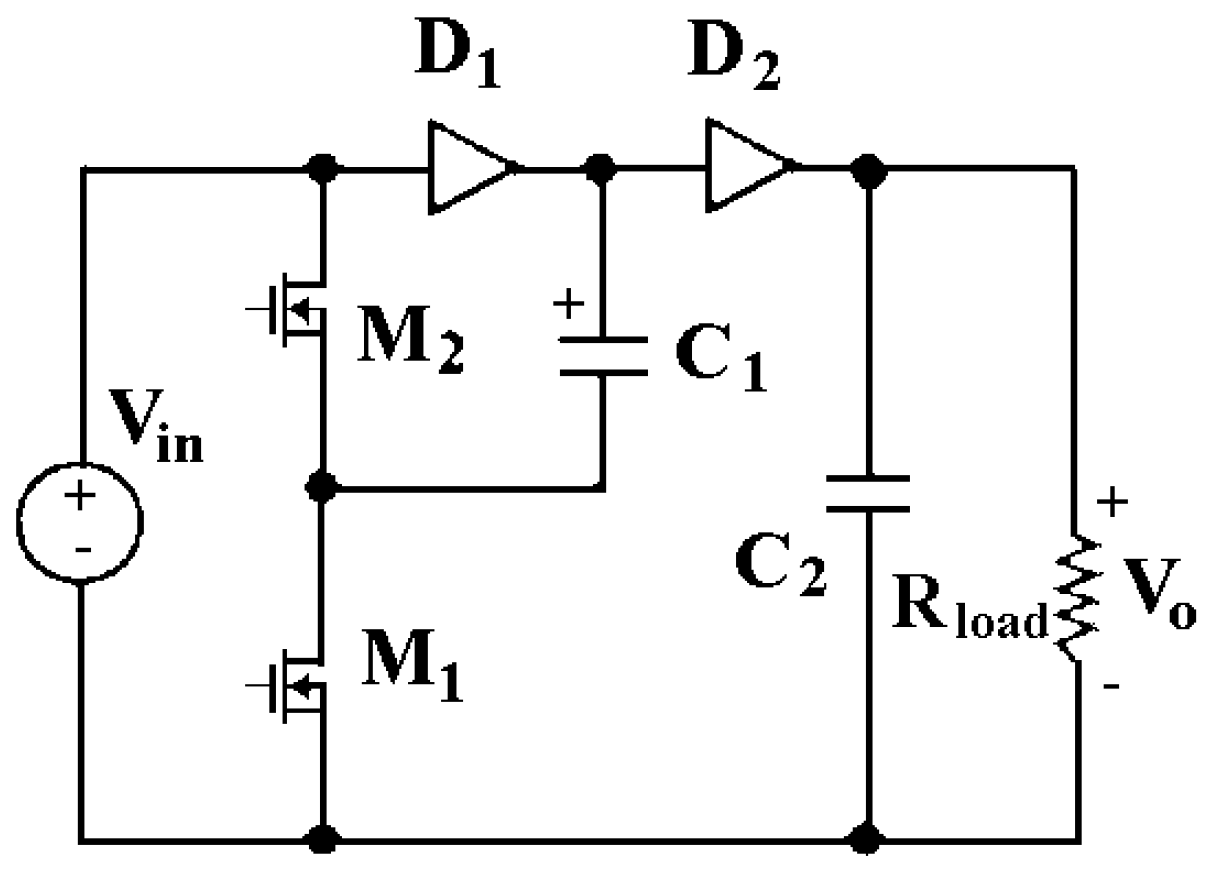
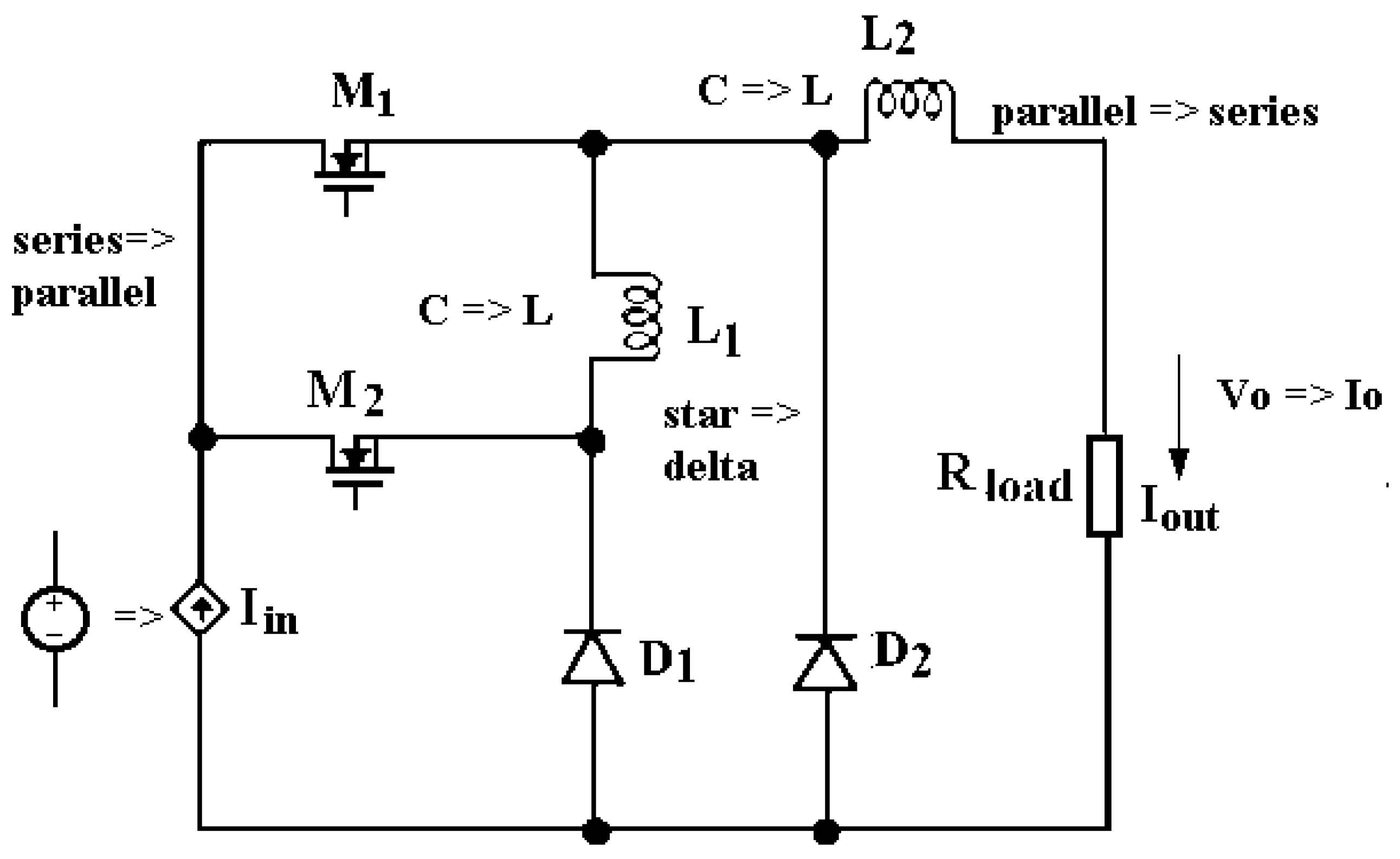








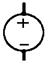
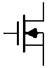
| Before Duality Translation | After Duality Translation |
|---|---|
 V V |  I I |
 M M |  M M |
 D D |  D D |
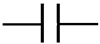 C C | 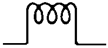 L L |
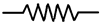 R R | 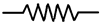 R R |
| Parallel | Series |
| Delta | Star |
| Name | Values | |
|---|---|---|
| Input current | 4 A | |
| M1 and M2 | IRF530N | |
| Switching frequency | 100 kHz | |
| D1 and D2 | IDH10G120C5 | |
| Output resistance | 4 Ω | |
| L1 | 1 mH | |
| L2 | 1 mH | |
| Controller | FPGA EP4CE6F17C8N | |
| Power supply | PWR1600H | |
| Load | E-load PLZ1004W |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mei, J.; Cheng, K.W.E.; Hua, T. Analysis, Design and Effectuation of a Tapped Inductor Current Converter with Fractional Output for Current Source Systems. Energies 2024, 17, 2204. https://doi.org/10.3390/en17092204
Mei J, Cheng KWE, Hua T. Analysis, Design and Effectuation of a Tapped Inductor Current Converter with Fractional Output for Current Source Systems. Energies. 2024; 17(9):2204. https://doi.org/10.3390/en17092204
Chicago/Turabian StyleMei, Jie, Ka Wai Eric Cheng, and Teke Hua. 2024. "Analysis, Design and Effectuation of a Tapped Inductor Current Converter with Fractional Output for Current Source Systems" Energies 17, no. 9: 2204. https://doi.org/10.3390/en17092204
APA StyleMei, J., Cheng, K. W. E., & Hua, T. (2024). Analysis, Design and Effectuation of a Tapped Inductor Current Converter with Fractional Output for Current Source Systems. Energies, 17(9), 2204. https://doi.org/10.3390/en17092204







