Abstract
The recent energy crisis has renewed interest in forecasting crude oil prices. This paper focuses on identifying the main drivers determining the evolution of crude oil prices and proposes a statistical learning forecasting algorithm based on regression analysis that can be used to generate future oil price scenarios. A combination of a generalized additive model with a linear transfer function with ARIMA noise is used to capture the existence of combinations of non-linear and linear relationships between selected input variables and the crude oil price. The results demonstrate that the physical market balance or fundamental is the most important metric in explaining the evolution of oil prices. The effect of the trading activity and volatility variables are significant under abnormal market conditions. We show that forecast accuracy under the proposed model supersedes benchmark specifications, including the futures prices and analysts’ forecasts. Four oil price scenarios are considered for expository purposes.
1. Introduction
Oil markets have exhibited multiple regime changes over the last two decades. This has created renewed interest in modeling and forecasting oil prices. Oil is a crucial factor in the global economy as it is not only a significant component of gross domestic product but also a key driver of inflation and interest rates. Therefore, the accurate forecast of oil prices is critical for central banks, financial analysts, energy corporations, utilities, investors, governments, and international organizations to implement policy responses to achieve an optimal allocation of resources.
The time series evolution of crude oil prices has been impacted by a wide range of variables, including global demand and supply disruptions, macroeconomic factors, geopolitical events, as well as regulation changes designed to foster the transition to a low-carbon economy. The interplay of different factors over the last two decades gave rise to four unanticipated steep oil price shocks, including the 2007–2008 Global Financial Crisis, the 2014 oil price collapse, the COVID pandemic, the June 2021–August 2022 energy crisis, and the war in Ukraine [1,2,3]. The persistence of underinvestment initiated during the 2014–2016 oil price shock [4] has been enhanced by the energy transition, which is expected to restrict long-term supply and add further shocks to the behavior of energy prices. Indeed, the global push to phase out fossil fuels is gaining new momentum as the COP28 celebrated, in November 2023, advocates for a historical transition from fossil fuels in energy systems to achieve net zero by 2050 (see “Ten key conclusions from COP28: a farewell to fossil fuels”, January 2023, the Oxford Institute for Energy Studies) and avoid a climate catastrophe. Such institutional developments suggest that there will be time-changing patterns on the demand side for oil in the medium term (see F.T. article “Peak in fossil fuel demand will happen this decade”, by Faith Birol, 12 September 2023).
A significant strand of the literature has developed statistical methods to establish the relationship between fundamentals and generate accurate energy price forecasts. Benchmark contributions include [5,6,7,8,9]. This literature concludes that an appropriate selection of fundamentals can lead to price forecasts that improve the random walk and no-change benchmarks. Vector autoregression (VAR) techniques have been extensively used in this literature, which has also applied the cointegration approach and the vector error correction model (VECM) as a forecasting algorithm for oil [10] and for agricultural commodities [11]. On a parallel dimension, the role of financial variables in predicting commodity prices gained significant momentum with the development of the financialization literature. Ref. [12] highlights the increased exposure to commodity futures of financial institutions and retail investors, empirically demonstrating the emergence of speculative investment flows impacting commodity futures prices [13,14,15]. Financial variables have also been used in the recent forecasting literature. Ref. [16] compiled a set of indicators to construct a new measure of global economic activity using a multidimensional approach that includes financial indicators.
One of the benchmark sources of crude oil price forecasts is the U.S. Energy Information Administration (EIA), which provides monthly, quarterly, and yearly forecasts for the crude oil price for horizons up to two years. Ref. [6] analyzes the EIA short forecasts, demonstrating that they do not outperform the naïve or no-change forecast. Ref. [17] analyzes the performance of Bloomberg analysts’ (1-year) forecast, demonstrating that these underperform the forecast of future prices at the aggregate level.
The work of [8] shows that while some fundamental-based econometric models have outperformed the EIA forecast for some horizons, no methodology is available in the literature performs well at all horizons for which the EIA generates predictions. This issue motivated them to use a combination of six different models considered in the literature, including the no-change forecast, oil futures prices, and VAR models of the global oil market. They concluded that forecast combinations help to improve accuracy and that all models are essential in contributing to forecast accuracy except for the no change. The naïve forecast is vital for comparing the forecast with different horizons as it controls for the maturity and volatility effect [17].
Statistical learning models are essential for accounting for non-linear interactions between input and output variables. This paper introduces the hybrid combination of a generalized additive model (GAM) combined with a linear transfer function time series approach as an oil price forecasting tool.
The existence of non-linear relations between price-driving factors and the price process implies that linear models cannot fully capture the underlying functional relationships. This singularity has motivated the use of machine learning approaches. Particularly noteworthy machine-learning applications in the crude oil forecasting literature include the LASSO regressions in [18]. The authors of that work show that the proposed regression LASSO method significantly improves the forecasting accuracy of prices compared to alternative benchmarks.
The proposed GAM model aims to explain the occurrence of remarkable price changes by capturing the different states and factor dynamics that determine the evolution of the price process. In doing this, it exploits the EIA expert forecast information in two dimensions. First, it uses IEA fundamental forecast data to feed the fundamental variable. Secondly, it uses the quarter Brent price forecast as a benchmark model for assessing predictive accuracy.
By allowing for non-linear relationships, the GAM model adds flexibility to the linear regression framework in analyzing data related to time-changing distributions by considering different price states assigned to the corresponding data of driving factors. GAM models are more interpretable than fully non-linear methods such as bagging, boosting support vector machines, and neural networks (deep learning). These methods are more flexible than the GAM algorithm because they can generate a more comprehensive range of possible shapes to estimate the explained variable. However, they are also less interpretable than linear regressions because predictors and responses are modeled using black-box non-linear functions. The crude oil forecasting literature has acknowledged the importance of considering possible non-linearities in model settings. Ref. [19] proposes a combination forecasting approach that accounts for structural breaks and then applies a time-varying transition probability Markov regime switching (TVIP-MRS) model, showing superior forecasting ability in four statistical tests.
The motivation for using the GAM approach to forecast oil prices is threefold. First, the literature has not identified a decisive outperforming framework for forecasting oil prices. Secondly, many financial time series, such as crude oil prices, contain non-linear characteristics that machine-learning methods can model. Third, within the statistical learning methods, the GAM specification provides the best trade-off between predictive accuracy and interpretability [20].
We aim to contribute in the following areas: First, we address the non-linearities documented in the crude oil price literature pertaining to the aftermath of the Global Financial Crisis. We use calculation and prediction methodologies that move away from the traditionally used linear models [21,22,23]. Second, we provide a price forecasting algorithm that incorporates the complex interplay of fundamental, financial, and economic factors that determine the evolution of oil prices, maintaining model interpretability. The error measures of simulated prices under the proposed algorithm supersede competing benchmarks, including futures prices. Outperformance with respect to the no-change and the futures price in terms of MAPE reductions is as high as 8% and 7%, respectively. Third, we develop a tool to provide oil price scenarios based on the selected input variables that can be used for the assessment of price risk and optimal decision making. This allows for exploring how much a given forecast would change relative to the baseline prediction under alternative hypotheses about future oil demand and supply conditions. Such a scenario analysis is crucial for end-users of oil price forecasts who are interested in evaluating the risk underlying a given prediction.
Our results have important implications for oil consumers, producers, and investors as accurate forecasts of oil prices lead to an improved allocation of resources. The reported findings are also relevant for regulators that use crude oil prices to set future inflation targets. As underlined by [24], central banks consider the price of oil as one of the instrumental variables in generating macroeconomic projections and determining macroeconomic risk. Accurate forecasting is also important for project investment decision making. Increases in oil price uncertainty complicate the appropriate discount rate for estimations of the net present value [1].
This paper is organized as follows: Section 2 describes the model methodology. Section 3 describes the data used in the forecasting exercise, including summary statistics, feature engineering, the GAM model approach, and preliminary statistical tests. The same also describes the factor selection process. Section 4 presents empirical results, including a sensibility analysis and forecasting results. The proposed forecasting algorithm is applied in Section 5 to generate future price scenarios. We conclude in Section 6.
2. Methodology: Combining the Generalized Additive Model with the Linear Transfer Function
Generalized additive models (GAMs) offer a general framework for extending a standard linear model by allowing non-linear functions of each variable while maintaining additivity. They offer a natural way to extend the multiple regression model to allow for non-linear relationships between each explanatory variable (feature) and the explained variable (response variable). The smooth functions are used as a replacement for the alternative detailed parametric relationship on the covariates. Moreover, this methodology is appropriate for the monthly data required in this study due to the low-frequency availability of oil fundamental data. The GAM methodology supersedes competing machine learning algorithms, such as neural networks, when large volumes of data are unavailable. It is also a preferred method because it allows a straightforward interpretation of results. This method calculates the sensibilities of the forecasted variable with respect to changes in input values, allowing a deeper understanding of underlying relationships than under competing machine learning models.
In essence, a generalized additive model (GAM) is a generalized linear model (GLM) in which the linear predictor is given by a sum of smooth non-linear functions of at least some (or possibly all) covariates [25]). The family of smooth functions is defined as the basis functions. The logarithmic function and a polynomial cubic spline are good examples of this specification class. Each basis function transforms the vector of explanatory variables x in terms of the type of basis considered.
The GAM can be formally expressed as follows:
where i = 1, …, n, and xi are the n independent input variables, fi is the unknown non-parametric smooth functions of xi, and εt is a i.i.d random error. This structure captures the non-linear relationships while providing a flexible framework for understanding the (linear or non-linear impact) of every variable considered.
We impose restrictions on the number of smooth functions allowed in the framework to prevent problems related to overfitting. For this reason, the specified models are usually fit by penalized likelihood maximization, and each penalty is multiplied by an associated smoothing parameter to control the balance between over- and underfitting. The MGCV implementation of GAM in R is applied. This module characterizes the smooth functions using penalized regression splines with smoothing parameters selected by the restricted maximum likelihood (REML).
In order to make the reported method robust to the existence of residual autocorrelation and dynamic causal effects, we consider a linear transfer function (LTF) with ARIMA noise [26] for the variables transformed by the GAM model.
We assume the series, yt and x1,t, …, xn,t are stationary variables. The classical multiple linear regression model given by
which assumes that the system’s noise εt is white noise and uncorrelated with the explanatory variables. In order to guarantee uncorrelated residuals and no cross-correlation between the residuals and the regressors, the LTF method with ARIMA noise, introduced by [27], is applied. The dependent variable is modeled as a function of its past values and lagged values of the explanatory variables. The following specification is used for this purpose:
where yt is the dependent output variable at time t, xi,t represents the i-th independent or explanatory input variables, νt is an autocorrelated ARIMA(p,d,q) noise, r, s, and b are constant integers, ω(L) and δ(L) are lagged polynomials, εt is white noise, and are the input variables transformed by the GAM model.
3. Data and Preliminary Results
The primary data used in this analysis have three main sources: The Energy Information Administration (EIA), the Commodity Futures Trading Commission (CFTC), and Bloomberg. We have a sample of monthly observations covering the period from January 1995 to December 2023. A detailed description of the initial variables considered is provided in Table A1. The EIA Short-Term Energy Outlook reports data series related to the fundamental balance in the crude oil market. It publishes monthly data on aggregate crude oil production, supply, and inventories. As shown below, these are used to construct the fundamental variable measure and provide input forecasts based on EIA data. Other fundamental variables that are initially considered but not selected as input variables include OPEC production, spare OPEC production, OECD consumption, OECD total inventory, China consumption, and the stocks–consumption ratio.
The CFTC releases weekly data on investor positions used to construct the financial variable. Data on long and short positions of non-commercial agents and open contracts are obtained for the entire sample period. Other position data that were initially considered but not selected as input data are specified in Table A1. Weekly data are transformed into monthly averages for analysis. Front-month Brent Intercontinental Exchange (ICE) crude oil daily data are downloaded from Bloomberg. This is used to calculate the monthly average price. The log of the monthly Brent price is the target variable within the model. However, model forecasts (provided in logs) are transformed into level Brent spot data to allow a comparison with benchmark forecasting models (the forecasting literature usually is designed to predict the nominal spot price of Brent or WTI prices. See [6]). The nominal Brent spot price returns are used to construct the historical (realized) volatility measure. We use daily quotations of the DXY dollar index to calculate a monthly measure of the dollar variable. We also download daily Brent ICE futures prices for the remaining available maturities (2–12 months) to construct the futures price benchmark as an alternative forecast measure.
3.1. Data Input Selection
The final input variables are selected based on the correlation coefficient between the logarithm of the Brent spot crude oil price and the input variables. Table A2 describes the four selected variables. A detailed correlation analysis of the raw data is provided in Table A3 in the Appendix A. In what follows, we briefly describe the variables selected for the model. The level of these variables is used in the forecasting algorithm.
Note that the variable selection is closely related to specifications similar to those in the crude oil forecasting literature. For example, ref. [19] uses fundamental (demand, supply, and stock), financial market (dollar index, exchange rate of the euro against the U.S. dollar, S&P500 index, speculative factor based on crude oil non-commercial long ratio), and technology indicators. These are the final variables built for the proposed model:
- (i)
- Balance in the physical market (FUN):
We consider the crude oil forecasting literature and define oil-related supply and demand metrics to define the fundamental variable. Ref. [8] include the percentage change in global oil production, the change in global crude oil inventories, and global economic activity, among other factors. Similar ratios as proxies of fundamentals are considered in [28] in their study of the bubble characteristics of non-ferrous metals. They define the consumption–supply ratio (CSR) as a measure of market fundamentals. This is measured as the ratio of metal consumption in the quarter in question to production in the same quarter plus the stock level at the end of the previous quarter. Specifically, we construct the ratio where the numerator is defined as the sum of aggregate OECD crude oil stocks to aggregate crude oil production over a 30-day period. The denominator includes the sum of world oil consumption over the same 30-day period. This fundamental variable (FUN) is specified under Equation (7) and measures the physical market balance. We can see from Table A4 in the Appendix A that it exhibits an inversely proportional relationship with Brent crude oil with a correlation equal to −0.887.
- (ii)
- Speculation in the crude oil market (FIN):
The variable used to capture the speculative activity and investors’ sentiment concerning oil prices is constructed with CFTC data. This requires the definition of the following input ratios. Open interest is the total amount of futures and/or option contracts that remain open overnight (and thus not offset by a transaction, delivery, or exercise). Note that all long open interest aggregates equal short open interest. Secondly, we use “commercial” or “non-commercial” CFTC classifications and define a “net non-commercial ratio” that considers net (long minus short) “non-commercial” positions in the numerator and total open interest in the denominator. The objective is to provide a metric gauging the direction of the market sentiment as “non-commercial” positions are defined as trades not designed for hedging purposes. The second measure is the sum of long and short “non-commercial” positions divided by the total open interest. This aims to provide the magnitude or impact of investors (or speculators) taking oil market positions. The proposed financial variable (denoted as FIN) is defined as the product of two ratios. Note that this metric is related to Working’s T-index, which has been used as a futures speculation proxy by [29] in the crude oil price case by [30] for multiple commodity markets and [31] for food commodities. See also [28,32] for the non-ferrous and agricultural market cases, respectively. While the FIN variable correlates with Working’s T index, it better fits the proposed forecasting model and is more closely related to the speculation-related measures used in the crude oil forecasting literature [19]. The underlying presumption is that a high (low) level of speculation will encourage higher (lower) prices, as shown by a correlation coefficient between the FIN variable and the crude oil Brent price, which is reported to be 0.51 in Table A4 in the Appendix A. The financial variable is therefore defined as follows:
- (iii)
- Realized Volatility (VOL):
We follow [33] and use a metric of uncertainty related to the crude oil market. Specifically, the realized volatility of Brent front-month futures prices is used. Volatility is often related to market risks and therefore has a negative impact on the price of oil. As reported in Table A4 in the Appendix A, the correlation coefficient of realized volatility with the oil price is equal to −0.21.
- (iv)
- U.S. Dollar (DXY):
The U.S. dollar is the numeraire in most oil contracts quoted in U.S. dollars. We use the DXY index to address the effect of the U.S. dollar on the oil price. As underlined by [34], changes in the exchange rate can be translated into changes in oil consumption for oil-importing countries and non-US-based investors. The dollar index (as well as the euro-dollar exchange rate) is considered by [19] in a recent oil forecasting exercise. Table A4 in the Appendix A shows that the correlation coefficient of the DXY index and the log of the Brent price is −0.52.
3.2. Descriptive Statistics
Table A2 in the Appendix A summarizes the series selected to construct the final variables, including data sources. Table A3 shows the correlations across the log of the Brent price and the main variables selected by the algorithm. The results show that the reported correlations between explanatory variables remain below 0.55, suggesting that the model will not suffer from multicollinearity problems.
Table 1 in the main text reports descriptive statistics of the selected input variables and the output or forecasted variable, which is the log of the Brent spot price labeled as log(Brent). Estimates are based on a sample of monthly data ranging from January 1995 to December 2023 (358 observations). We can see that the Brent spot price level exhibits the highest standard deviation and maximum level.

Table 1.
Summary statistics.
The normality and unit root test results are reported in Table 2. The results of the Jarque-B test and Ljung–Box show that the null hypothesis of normality and white noise errors is rejected for all variables considered. This table also reports results for the augmented Dicky–Fuller (ADF) [35], the Phillips–Peron (P.P.) [36], and Kwiatkowski–Phillips–Schmidt–Shin (KPSS) [37] unit root tests. The reported results show that the unit root hypothesis is accepted for all variables except the volatility variable (Vol). This motivates the use of the LTF model.

Table 2.
Normality and unit root test results.
The Bai and Perron test [38] for detecting multiple structural changes has also been performed for the logarithm of the Brent spot price as well as for the regression with the selected input and explained variables in differences. The results are reported in Table A5 and Table A6, respectively. They show that the log of Brent prices exhibits five breakpoints along our sample period (these correspond to September 1999, October 2004, August 2010, and November 2014. Such points are consistent with those detected in for crude oil in the bubble literature [4].). When we run the regression in differences (with log Brent as explained variable and the changes in the fundamental, financial dollar, and volatility as input variables), the reported results do not show evidence of structural breaks. The fact that structural breaks are no longer reported for the regression in differences shows that the input variables have been appropriately selected.
Figure 1 illustrates the complete process of the proposed methodology to forecast oil prices. The starting point is the data obtained from multiple sources, such as EIA or the Commodity Futures Exchange Commission (CFTC). The data are then used to build four variables (FUN, FIN, VOL, and DXY), which are transformed through a GAM model into the final input variables used by the linear transfer function model.
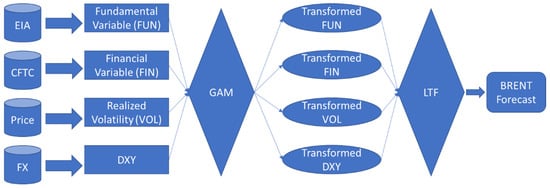
Figure 1.
Process of the proposed methodology: This figure exhibits the steps required for GAM method development. Step 1 involves raw data extractions; step 2 requires the creation of featured variables; step 3 performs the transformation through a GAM model into the final variables used by the linear transfer function model in step 4 to create the Brent forecast.
This analysis applies a feature engineering approach to crude oil price forecasting. Feature engineering is the process of using domain knowledge to obtain features (characteristics, properties, and attributes) of the analyzed variables. It involves the extraction and transformation of variables from raw data to a more effective set of inputs so that these can be used for training and prediction to improve the quality of results arising from a machine learning process. This increases model performance as it goes beyond supplying only the raw data to the machine learning process. This study combines a set of transformed variables (using basis functions) to create a parsimonious model specification. The proposed framework allows for an improved understanding of the oil price determinants through four representative variables that allow the development of a simple tool designed for scenario analysis. Feature engineering has been a successful method in machine learning models [39], and in the case of oil price forecasting, it could also be an advantage. The data pre-processing step (first applied under the statistical learning algorithm) adds different variables to create a combined metric representing some market features.
4. Model Identification and Empirical Results
This section describes the building process underlying the two-step method proposed to model the oil price. We first analyze each time series to determine the modeling methodology. The variable to be forecasted is the logarithmic monthly average Brent spot price.
The empirical application covers the January 1995 to June 2023 period and aims to forecast the monthly crude oil Brent price series as the current global crude oil price benchmark. The in-sample period runs up to December 2016. This selection makes the in-sample size comparable to the recent literature; ref. [8] uses an in-sample period ranging from 1997:12 to 2010:6. The model is tested for the 2017–2023 out-of-sample period. Note that this constitutes seven years of monthly data leading to 82 observations. While this out-of-sample window may be considered short compared to other benchmark analyses [8,40], recent research in the literature considering the existence of non-linearities [18] has used shorter out-of-sample periods. Specifically, it evaluates the out-of-sample forecast performance for the 2009:M5 to 2016:M11 period. We therefore follow the recent literature that addresses the sources of non-linearities and use shorter out-of-sample periods in our forecasting exercise. The sources of recent non-linearities include the collapse of the 2014–2016 crude oil price, the 2020 COVID-19 pandemic shock, the ongoing war in Ukraine, and a shift to green energy. Forecasting performance is measured in terms of MAPE values as well as the absolute ratios of MAPE with respect to the no change. The RMSE is also computed in the principal analysis as a means of robustness. The same out-of-sample period is considered for the sensitivity analysis. Possible scenarios are created for the four quarters of 2024.
4.1. Preliminary Analysis
Figure 2 illustrates the partial effects obtained with the GAM model of the transformed fundamental, financial, volatility, and dollar variables on the oil price. For instance, the top left-hand side (LHS) panel of Figure 2 illustrates the fundamental variable on the X-axis and the transformed variable on the Y-axis, indicating the effect of the fundamental on the oil price metric. The dotted lines illustrate 5% confidence intervals. The model results show non-linearities in every variable considered except for the fundamental metric. This is corroborated by “EDF” reported in column 2 of Table 3, representing the effective degrees of freedom, which measure the degree of non-linearities within a given curve. Note that when the reported EDFs are equal to one, as is the case for the fundamental variable, this implies that the curve is linear. The volatility variable depicted in the bottom right-hand side (RHS) panel exhibits the highest level of non-linearity, followed by the dollar in the bottom LHS panel and the financial metric in the top RHS panel.
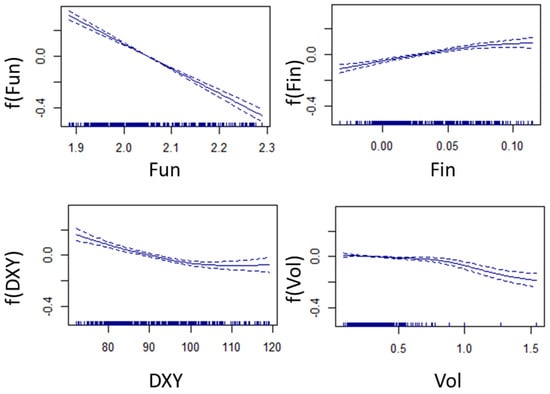
Figure 2.
Partial effects illustration under the GAM model: This figure illustrates the non-linear relationship between each of the variables considered and the oil price under the GAM estimation. The row input variables (represented by dots on the horizontal axis) are transformed using the basis functions (denoted by f()). The transformed variables are introduced in the LTF model at a later stage. The effects of the fundamental and financial variables are illustrated under the top left-hand side (LHS) and right-hand side (LHS) panels. The dollar and volatility variables are depicted under the bottom LHS and RHS panels. Moreover, 95% confidence intervals are depicted as dotted lines.

Table 3.
Summary of estimated coefficients under a GAM model specification.
In what follows, we interpret the plots in Figure 2, illustrating the partial effects for every explanatory variable. Note that the four signs of the function slopes are aligned with the correlation coefficient calculated with the oil prices, reported in Table A4. The top LHS panel in Figure 2 shows that the fundamental variable, which takes a low value under fundamental shortages, exhibits a well-fitted negative linear relationship with the oil Brent price, showing that excess supply market conditions lead to lower oil prices. While the effect of the financial variable on the oil price is almost linear, we can see that the financial variable presents some non-linear features. Specifically, we can see that the slope is slightly smoothed when the market sentiment becomes bullish so that positive investor bets outnumber the negative counterparts. The bottom LHS panel in Figure 2 shows a non-linear inverse relationship between the dollar index and oil benchmark that is significantly smoothed when the index exceeds 105. The negative influence of the dollar value on oil prices has been widely documented in the literature [18,41]. The relationship estimated implies that Brent prices increase under low dollar conditions. A lower dollar leads to higher demand and higher prices as producers try to protect the dollar-adjusted value of their revenues. Oil becomes relatively cheap for foreign investors, and this increases demand. However, the results illustrated in the LHS panel of Figure 2 suggest that the dollar’s impact on crude oil prices is lower when the dollar is under stronger conditions. The results depicted in the bottom RHS panel in Figure 2 show the effect of volatility, which is highly significant under high-volatility regimes and negatively affects prices. Episodes of extreme volatility (such as that seen during the 2014 oil price shock) are expected to decrease the oil price, while the volatility effect is reduced under normal market conditions. In fact, we can see that when the volatility is below 40%, it exhibits a reduced impact on oil prices. The existence of volatility-driven regime changes has been considered in the forecasting literature by the authors of [18], who document a “volatility upward regime” via the TVIP-MRS model and forecast the crude oil price.
The preliminary estimation results reported in Table 3 show that the adjusted R2 and the deviance explained demonstrate that the model fits the data correctly. The Box–Pierce test suggests that there is residual autocorrelation. The details can be found in Figure A1 in the Appendix A.
In order to correct this autocorrelation, we include a linear transfer function model with ARIMA noise in the second step. We estimate the LTF specification using an identification, estimation, and diagnosis procedure [42], following a similar approach to constructing the univariate Box–Jenkins ARIMA model [26]. The identification requires fitting a multiple regression model, adding as many lags of the regressors as required, and a low-order autoregressive model for the error term to capture most of the autocorrelation and be able to estimate the impulse response. If regression errors are not stationary, variables are differentiated. The next stage is identifying the transfer function and selecting the appropriate values for b, r, and s. We can identify the orders (b, r, and s) by visually comparing the estimated impulse response function with some standard theoretical functions. Then, the ARMA model for the regression errors must be determined to fit the complete model. Finally, several diagnostic tests are applied to determine the model selection model based on resulting cross-correlation and autocorrelation tests.
The explanatory variables are determined using the previously estimated GAM process. The final model identification suggests an ARIMA (1,1,0) for the residuals. The estimation results are reported in Table 4. We can see that the four independent variables are statistically significant, and the residuals do not exhibit s serial correlation, with Box–Pierce failing to reject that residuals are independently distributed. The partial autocorrelation function (PACF) and auto-correlation function (ACF) confirm the absence of a serial correlation (see Figure A2 in the Appendix A). Note that results reported for the regression in differences under the Bai and Perron test [39] (see Table A6) show that we failed to reject the null hypothesis of no structural breaks. This confirms that the LTF model can be applied to the residuals.

Table 4.
Summary of estimated coefficients under final specification.
The final equation of the complete model is as follows:
where ; ; ; and are the variables transformed by the GAM model (see Figure 2) and εt is the white noise.
Figure 3 depicts the one-month-ahead forecast of the Brent crude oil price under the proposed model versus the observed Brent price as well as the error defined as the difference between the estimated and observed values. A closer look at the figure shows that the goodness of fit is high but clearly deteriorates in times of increased uncertainty, such as during the 2008 crisis, the 2014 crude oil price collapse, or the 2020 COVID crisis.
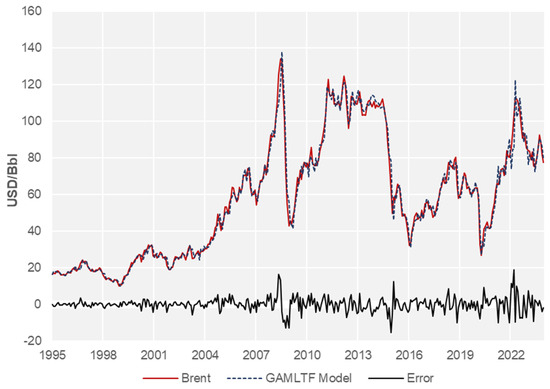
Figure 3.
Time series evolution of the Brent spot price level, the forecasted (one-step-ahead) Brent spot price level, and the model error: This figure illustrates the time series evolution of the observed price (Brent) price, the estimated Brent spot price (model), and the forecast error. The GAM model is estimated using the selected input values.
4.2. Sensitivity Analysis
The next step is to provide a sensitivity analysis, developed to show the future evolution of the crude oil price, given a one standard deviation shock to some of the explanatory variables over a six-month horizon, keeping the remaining variables constant. The results are reported in Figure 4.
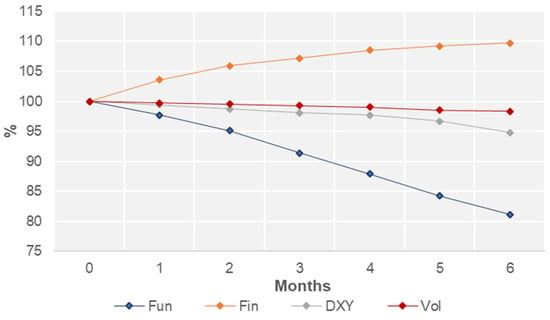
Figure 4.
Sensitivity analysis: This figure illustrates the effect of a one standard deviation shock in each explanatory variable on the Brent crude oil price over a 6-month horizon. The January 1995–December 2016 in-sample period is considered for this purpose. The sensitivity analysis is performed for the first two quarters of 2017.
We assume that variables were shocked in December 2016 and evaluated over the next six months.
They show that the variable with the most significant influence on crude oil is the fundamental variable, which decreases the crude oil price by 20% for a given one standard deviation shock. The second most important variable in terms of price impact is the financial variable, which has a positive 10% effect on Brent prices for a given one standard-deviation shock. The same shock applies to the dollar and volatility variables exert a negative impact of 5% and 2%, respectively. Our findings are consistent with the literature supporting supply and demand fundamentals as the main drivers of crude oil prices [7,8,29,43]. The market fundamental variable is the most important factor explaining the time series evolution of crude oil prices, with shocks remaining important after six months. Speculators are informed investors and enter the market to exploit fundamental-related trends [43]. Indeed, Table A4 in the Appendix A shows that the fundamental and financial variables exhibit a significant negative correlation of −0.56, implying that they share common characteristics. When fundamentals are tight, the market has a more significant inflow of speculative activity.
4.3. Forecasting Results
In what follows, we quantify the predictive performance of the proposed model specification. The analysis takes the 2017Q1 to 2023Q4 time frame for the out-of-sample test (21% of data). A forecast for different quarters within a window of 12 months (four quarters) is made at the beginning of every quarter. Data for the last seven years of the sample have been used to compare model performance with four forecasting methods. This implies that there are 25 quarterly forecasting periods. The average monthly forecast for each quarter is considered, and the mean absolute percentage error (MAPE) for each method considered is reported in Table 5. Note that this period represents the recovery from the 2014–2016 price slump and the COVID-induced crude oil price collapse. As discussed in the introduction, crude oil prices have experienced many different price swings over the forecasting period. Therefore, we believe it is essential to provide an appropriate testing framework to account for the observed non-linearities in the data.

Table 5.
MAPE error measures for different forecasting methods.
We benchmark the proposed model against the no-change or spot reference price. This uses the last available monthly spot price observation. The no-change forecast is set as the spot price under the previous month of the forecast during the whole forecast period. Next, we consider the forecasting performance of the Intercontinental Exchange (ICE) Brent futures prices. This price aggregates expectations for future price delivery across market participants. The benchmark built based on futures prices takes the average of the first-, second-, and third-month generic future contracts (Brent) for the first quarter forecast and the average of the fourth-, fifth-, and sixth-month contracts for the second quarter forecast. The same method is applied to forecast prices in the subsequent quarters. The benchmark is constructed the day before the forecast period begins, and as previously specified, the data source for the price of the futures prices is Bloomberg.
As an alternative analysts’ forecast benchmark, we first use the monthly forecast of the Department of Energy of the U.S. (EIA or DoE) released under the Short-Term Energy Outlook every month. This report calculates monthly Brent price forecasts for maturities ranging between 1 and 12 or up to 24 months. We construct quarterly forecasts by calculating three-month averages using the last report before the start of the forecast period.
The second benchmark source of analysts’ forecasts is the prediction provided by the Bloomberg survey with crude oil analyst forecasts (BBG). This offers industry experts’ price forecasts for different maturities. The median forecast for each quarter reported in this survey is taken as forecasts the day before the forecast period starts. See [15] for a detailed Bloomberg analysts’ forecast survey description.
We report forecasts for the GAMLTF with forecasted EIA fundamental inputs as well as from the actual input data. To measure the contribution of the GAM framework, we report a forecast for the LTF with no GAM. We select the mean absolute percentage error (MAPE) as a metric for evaluating the performance of the forecasting methods, which is defined as follows:
The choice of the MAPE metric is motivated by the high oil price variability during the sample period considered. Oil prices range between USD 30 and USD 140, implying that absolute differences in high-price states will be difficult to compare with absolute differences in low-price states. However, the RMSE metric is also included in the main forecasting analysis as a means of robustness.
The forecasting performance of a model with exogenous variables will depend on the forecast accuracy of the future values of the selected regressors. For that reason, we also test under two explanatory variables’ predictions. In the real data model, the observed values of the future selected explanatory variables are used for forecasting purposes. In the forecast data model, every explanatory variable is forecasted. In this sense, we use forecasts of the fundamental and U.S. dollar variables from the EIA, available in its Short-term Energy Outlook, providing information for world production, world demand, and OECD inventories. Therefore, we incorporate forward-looking information (based on EIA predictions) into our forecast framework. ARMA models are estimated for the financial and volatility variables.
The results reported in Table 5 show that the performance of each model varies over time. The average MAPE errors indicate that the best model is GAM-LTF with actual inputs followed by the GAM-LTF. However, a close look at the table shows that the no-change and the futures forecasts outperform in periods of high volatility, such as 2020Q3 and 2022Q2. Bloomberg analysts’ forecasts perform worse on average than futures prices, consistent with previous results reported in the literature [17]. However, it outperforms all the benchmarks considered during 2017Q3 and 2020Q1. Given that the best results at the average level are achieved when we know the variable data (GAMLTF actual inputs), we propose using the model for scenario analysis as the reported results suggest that it accurately captures the relationships between variables. This analysis is performed in Section 5.
Table A7 in the Appendix A provides the same forecasting results under the MRSE measure. The reported figures are qualitatively similar to those reported in Table 5, suggesting that the relative forecasting ability is not dependent on the forecast performance measure selected for the analysis.
In order to provide a deeper analysis of the results we report, Table 6 provides forecast accuracy in terms of the MAPE metrics for four maturities of the different models analyzed. The average forecast for each quarter is reported. For instance, if the forecast maturity is one quarter, in Q1 of 2016, the forecast for Q2 2016 is performed for each of the models considered and is used to calculate the average forecast for the Q2 forecast period. Similarly, in Q2 of 2016, the forecast for Q3 2016 is performed for each of the models considered for the reported average for the Q3 forecast. The same procedure is followed to calculate the forecast for longer horizons.

Table 6.
MAPE for different forecasting methods and horizons.
Our main findings can be summarized as follows: (i) In line with the previous literature [17], forecast accuracy decreases with maturity. (ii) The best forecasting performance for all horizons considered is reported for the proposed model with actual values of input variables. Furthermore, the second best performance is observed for the proposed model with forecasted input. This confirms that the proposed model can be used as an optimal tool for scenario analysis purposes (details will be provided in Section 5). (iii) The introduction of the GAM specification in the model, considering the non-linearities in the input/output relationships between the explanatory variables and the oil price, is important for improving forecasting results, as can be seen by comparing the last column with columns 5 and 6. The forecast provided by the LTF approach with no GAM is less accurate than that provided under the GAMLTF with actual and forecasted inputs. (iv) The model with forecasted variables (forecast data model) improves the forecasting performance when compared to other benchmarks for all quarters considered.
Table 7 reports the forecasting performance of the different models in terms of the MAPE metric in relation to the no-change forecast. The prediction horizon ranges from 1Q in the first panel to Q4 in the fourth. In this case, a moving window of six quarters is used to calculate the MAPE metric. The purpose is to quantify the evolution of predictive ability and robustness for the different models considered. Note that this requires changing the in-sample and out-of-sample period for every calculation. For instance, the forecast estimates corresponding to 2019Q4 include 2019Q4, 2020Q1, 2020Q2, 2020Q3, 2020Q4, and 2021Q1. Therefore, the in-sample period covers the January 1995 to December 2019Q3 range. However, the forecast estimate corresponding to 2020Q1 calculates the average prediction for 2020Q1, 2020Q2, 2020Q3, 2020Q4, 2021Q1, and 2021Q2 and uses the 1995Q1-2019Q4 as an in-sample period. As opposed to the results reported in Table 5, we provide forecasting results for every period of the out-of-sample window under each different quarter to analyze the persistence of the relative performance of the different methodologies considered. This is relevant given the high performance of regime-changing events seen during the 2017–2023 window, including the COVID crisis, the war in Ukraine, and the higher-than-expected recovery with high inflation and interest rate rises. Under this reporting format, the ratio takes a value of 1 if a given model performs equally as well as the naïve (no-change model). A close look at Table 5 shows that, as suggested in Figure 1, the forecasting performance of every model varies across time. The calculated results confirm the findings reported in Table 4. The proposed model with actual inputs performs best for almost all subsamples considered. The only exceptions are documented in 2018, a period dominated by the Fed tightening monetary policy. The results also demonstrate that the model with forecasted inputs is, on average, the second best when the horizon ranges from one quarter to two quarters. The model with forecasted inputs does not exhibit a clear outperformance for higher horizons. Since this specification is run based on predicted data, performance depends on the forecast accuracy of the different (EIA forecasted) inputs. We see that the longer the forecast horizon, the lower the forecast accuracy. The reported results confirm the view that the proposed model can be used to consider different (twelve-month maturity) scenarios underlying the selected explanatory variables.

Table 7.
Performance evolution versus no-change forecast (a six-quarter window ahead).
The forecasting ability of futures prices and the Bloomberg analyst survey can be compared with the results reported by [17], which demonstrate that futures prices outperform (at the aggregate level) analyst forecasts when considering forecasts performed on a yearly basis. The current analysis makes it unclear whether future prices will beat Bloomberg analysts’ forecasts. This may be explained by the different periods and prediction horizons considered in the forecasting exercise. While [17] considers the average forecast for a given year with Chicago Mercantile Exchange (CME) WTI futures prices for a sample ending in December 2019, the analysis in this paper uses ICE Brent futures prices and a six-quarter rolling window and includes forecasts ending the last quarter of 2023.
5. Oil Price Scenario Generation
We have seen in the previous section that the proposed model can explain and forecast very accurately when the observed (and not forecasted) values of the explanatory variables are used in the forecasting process. This tool can help understand the interaction of factors that determine the past oil price evolution and the future paths under different scenarios, quantifying the risk associated with a particular scenario compared to an alternative baseline forecast (selected as the EIA forecast). The proposed model identifies key variables driving upside and downside risks in the oil price forecast. For expository purposes, three scenarios involving hypothetical future oil market conditions are explored, starting in the first quarter of 2024. These main variables and estimated parameters correspond to world production, world demand, OECD stocks, non-commercial long and short positions, open interest, historical volatility, and the U.S. dollar. Figure 5 illustrates the twelve-month forecasts for the four variables in the three scenarios defined from 2024Q1. The illustrative scenarios are focused on the implications of shocks arising from the supply relative to the demand conditions.
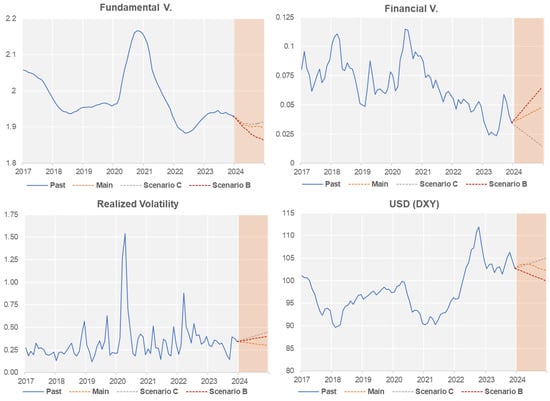
Figure 5.
Forecasts of input variables under different scenarios: This figure illustrates the evolution of the input variables used in the different scenarios. The main scenario: Scenario A uses EIA forecast input data. Scenario B analyzes the possibility of physical tightening. Scenario C addresses the case of low OPEC.
Scenario A: Main benchmark scenario with EIA forecast
The main scenario uses the U.S. Department of Energy forecast of the fundamental variable for the next 12 months, performed in December 2023. This includes the concern expressed by the DoE regarding the weakening global economic situation, which leads to lower expectations for global oil demand growth. An increase in demand of 1.3 mb/d is thus considered under this scenario. These views about the economy can potentially offset the upward pressure on prices stemming from lower short-term oil supply due to the OPEC’s and Russia’s supply cuts in crude oil production. Oil production cuts were first announced in October 2022 for a cut of 2 mb/d and were enhanced in April 2023 to 3.5 mb/d.
Furthermore, in June 2023, the OPEC and Russia decided to extend cuts to December 2024. In July, Saudi Arabia additionally announced voluntary cuts (details can be found at https://www.reuters.com/business/energy/saudi-arabia-expected-extend-voluntary-oil-cut-september-analysts-say-2023-07-28/ accessed on 15 August 2023). Full compliance (−3.5 mb/d from the level registered in August 2022) is not expected, but the agency forecasted, in December 2023, that production will increase by 0.6 mb/d, representing a slowdown when compared to growth levels reported of 1.6 mb/d in 2023. The fundamental variable is predicted to stay near last year’s lows. With the tightening of the physical market, investors will increase their positions. The U.S. dollar stabilizes around 102 as monetary policies are becoming more aligned in the U.S. and Europe. Crude oil price volatility returns to normal conditions, considering the Ukrainian crisis causes no other uncertainty-related spikes.
Scenario B: Physical Market tightening
This represents the case of full compliance with the OPEC’s quota supported by increased tensions in the Middle East (particularly in the Red Sea) and a robust economy that sustains oil consumption with a rebound in consumption driven by the airline sector, as forecasted by data from S&P Global. In this case, the fundamental variable will fall to the lowest value registered over our sample period. Under this scenario, investors will be attracted to exploit the upward price trend. The U.S. dollar will be weaker than in the main scenario, and volatility will rebound mildly because of increasing geopolitical pressures. Note that the OPEC plus group has announced an extension of 3 months to their voluntary cuts, making this scenario less likely. See the Financial Times article “Opec+ members extend production cuts to boost oil price”, 4 March 2024.
Scenario C: Low OPEC compliance and delay on the end of monetary tightening
OPEC compliance is less stringent than the main scenario, implying that production stands at 1 mb/d during 2023Q3–2024Q4. Oil demand growth moderates because of the delay in the monetary tightening. Under this scenario, investors will reduce their oil exposure in their portfolios, volatility will pick up, and the dollar will appreciate slightly.
Our model also allows us to do reverse engineering. This feature implies that we can calculate the values of the underlying variables implied by futures prices. In order to match quoted futures prices observed in December 2023, our framework shows that there should be low compliance with the announced the OPEC cuts in the first half of 2024. The prices are similar to Scenario C.
Forecasts under the different scenarios, including the main and EIA forecasts, are illustrated in Figure 6. First, our main benchmark scenario for the next 12 months is slightly more bullish than that reported by the EIA. Under the supply-stressed scenario (B), oil prices are expected to be higher than USD 100, given the context of deteriorated levels in the physical balance. The increase in geopolitical risk, partly driven by the recent moves by Saudi Arabia and Russia to extend their voluntary supply cuts, drives fears of future inflation and new periods of prolonged periods of low investment in new capacities. This fact is fundamental under the currently announced OPEC’s production cuts. While OPEC compliance has always been hesitant, the possibility of future supply cuts remains a primary concern for Western governments already struggling to contain inflation. We could see prices stabilizing around the USD 72/bbl level in the case of low OPEC compliance. The term structure of futures prices is in December 2023 in mild backwardation, with the December 2024 futures price trading at USD 75/bbl. This implies improved fundamentals compared to the term structure seen in November 2023.
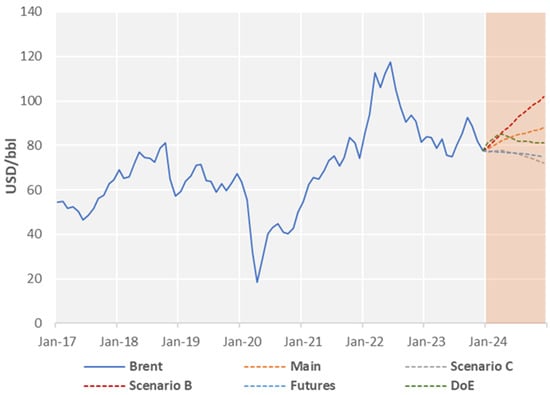
Figure 6.
Oil price forecast in different scenarios: The figure illustrates forecasting prices under the different scenarios considered, including the main (using EIA forecast), the EIA forecast (labeled DoE), the forecast implied by futures (labeled Futures), scenario B (tight fundamentals), and scenario C (low OPEC compliance).
Note that the set of scenarios envisaged for the explanatory variables allows the simulation of different geopolitical situations. Given that increased geopolitical tensions influence the price of oil, the proposed tool can be used to consider changes in the explanatory variables (and the corresponding crude oil price forecast) affected by increased geopolitical uncertainty. For instance, we expect that there will be supply disruptions under the surge of an armed conflict. These disruptions will reduce the value of the fundamental variable and therefore lead to a scenario similar to that described in scenario B.
6. Conclusions
Recent developments in energy markets have shown that the crude oil market is exposed to time-changing uncertainty. As a result, crude oil prices have been subject to significant fluctuations over the past two decades. This makes oil price prediction a very challenging task. While the forecasting frameworks developed in the literature are wide and varied, there is no consensus about the appropriate methodological framework to apply. This paper combines the classical regression model with machine learning approaches in a hybrid framework, selecting the GAM method across the feature engineering literature jointly with a transfer function with the ARIMA noise approach. Machine learning methods help to incorporate flexible non-linear capability in the modeling process.
Compared to competing machine learning approaches, the advantage of the proposed method is that it captures non-linearities under the analysis of partial effects. This allows input variable interpretation through estimated regression coefficients. The method identifies two main drivers explaining oil prices. The first and most important variable is the fundamental variable, which measures the physical market balance. The second is the financial variable quantifying and capturing crude oil investors’ speculative interest. The volatility and the dollar variables contribute to a lower impact on oil price movements. The results show that the non-linear effects are remarkably significant in the dollar and volatility variables. The impact of the dollar index is significant only under weak dollar conditions, while volatility is essential for forecasting purposes under high-volatility states.
We show that the algorithm may be applied using U.S. EIA forecasts of the fundamental and the input variables. The forecasting ability of the proposed framework outperforms benchmark techniques, including the futures prices and analysts’ crude oil price predictions provided by Bloomberg and the EIA.
A sensitivity analysis is performed in the second stage, confirming that the variable with the most significant influence on crude oil prices is the fundamental variable. One standard deviation increase in this variable results in an oil price reduction of 20%. The financial variable is the second most important, exerting an impact of 10% for a one standard deviation increase. The impact of the one standard deviation change in the dollar and volatility variables are 5% and 2% price change, respectively.
The proposed model is also highly suitable for scenario analysis. The algorithm demonstrates the ability to quantify the risk associated with a benchmark forecast based on an extensive analysis of how this forecast changes under alternative hypothetical scenarios about future oil demand and oil supply conditions. The main scenario (December 2023) predicts a rebound in oil prices towards USD 88/bbl, delivering higher prices than the EIA. Two additional situations are proposed for 2024, with the market balance variable acting as the main driving force. Under market tightening conditions arising from compliance with the OPEC’s and Russia’s production cuts, prices are pushed to new highs (above USD 100/bbl). Under a lower OPEC compliance scenario and lower consumption due to higher-than-expected interest rates, we could see a moderation in prices towards USD 72/bbl.
Our results show the relevance of supply and demand fundamentals in the price determination process and confirm that events that disrupt global oil supply are expected to increase oil prices, while events that suppress oil consumption growth will generally decrease oil spot prices (Baumeister and Kilian, 2015) [8]. The proposed hybrid model can be applied to risk management systems of energy corporations and institutions. It can also provide a quantitative assessment of the impact of a range of hypothetical events on the crude oil price. This is crucial in times of multiple sources of uncertainty arising from factors such as geopolitical tensions, interest rate risk, and energy transition-related shocks.
Author Contributions
Conceptualization, P.M., I.F.-F. and A.M.; methodology, P.M. and A.M.; software, P.M.; validation, A.M.; formal analysis, P.M., I.F.-F. and A.M.; investigation, P.M., I.F.-F. and A.M.; data curation, P.M.; writing—original draft preparation, P.M.; writing—review and editing, I.F.-F. and A.M.; supervision, I.F.-F. and A.M. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
Data is contained within the articles and sources cited.
Conflicts of Interest
The authors declare no conflict of interest.
Appendix A

Table A1.
Raw data description.
Table A1.
Raw data description.
| Raw Variable | Frequency | History | Source | Model Variable |
|---|---|---|---|---|
| Brent | Monthly (average daily data) | from January 1995 | Bloomberg | Fundamental Variable |
| Log(Brent) | ||||
| Total World Production | Monthly | from January 1995 | U.S. Energy Information Administration | Fundamental Variable |
| OPEC Production | ||||
| Spare OPEC Production | ||||
| Total World Consumption | ||||
| OECD Consumption | ||||
| China Consumption | ||||
| OECD Commercial Inventory | ||||
| OECD Total Inventory | ||||
| Stocks Consumption Ratio | ||||
| Long non-commercial Futures | Monthly (average weekly data) | from January 1995 | Commodity Futures Trading Commission | Financial Variable |
| Short non-commercial Futures | ||||
| Net non-commercial Futures | ||||
| Open Interest Futures | ||||
| Long non-commercial F&O | from March 1995 | |||
| Short non-commercial F&O | ||||
| Net non-commercial F&O | ||||
| Open Interest F&O | ||||
| DXY | Monthly (average daily data) | from January 1995 | Bloomberg | Dollar |
| USD/EUR | ||||
| Implied Volatility | Monthly (average daily data) | from January 1995 | Bloomberg | Volatility |
| Realized Volatility | Price |
Note: This table describes the data used in the initial stage of algorithm implementation. The second to fourth columns provide variable frequency, data history, and data source. The label “Model variable” in the last column describes the category of the given data series within the fundamental, financial, dollar, and volatility variables, according to dimensions for model input variables.

Table A2.
Description of selected input variables.
Table A2.
Description of selected input variables.
| Model Variable (Equation) | Raw Variable | Frequency | History | Source |
|---|---|---|---|---|
| Fundamental Variable (7) | Total Crude Oil Supply (World) | Monthly | From January 1995 | U.S. Energy Information Administration |
| Total Crude Oil Demand (World) | ||||
| Total Commercial OECD Stocks | ||||
| Financial Variable (8) | Non-Commercial Long Futures WTI | Monthly (average weekly data) | From January 1995 | Commodity Futures Trading Commission |
| Non-Commercial Short Futures WTI | ||||
| Open Interest Futures WTI | ||||
| Volatility Realized | Price First Brent Contract | Monthly (average daily data) | From January 1995 | Price |
| Dollar | DXY Index | Monthly (average daily data) | From January 1995 | Bloomberg |
Note: This table describes the selected input data used for GAM model implementation. The third to fifth columns provide variable frequency, data history, and data source. The label “Model variable” in the first column describes the category of the given data series within the fundamental, financial, dollar, and volatility variables according to dimensions for model input variables. The fundamental and financial variable definitions are linked to definitions specified in Equations (7) and (8), respectively.

Table A3.
Correlation matrix of primary variables used in the analysis.
Table A3.
Correlation matrix of primary variables used in the analysis.
| Brent | Log(Brent) | Total World Production | OPEC Production | Spare OPEC Production | Total World Consumption | OECD Consumption | China Consumption | OECD Commercial Inventory | OECD Total Inventory | Stocks Consumption Ratio | Fundamental Variable | Long Non-Commercial Futures | Short Non-Commercial Futures | Net Non-Commercial Futures | Open Interest Futures | Long Non-Commercial F&O | Short Non-Commercial F&O | Net Non-Commercial F&O | Open Interest F&O | Financial Variable Futures | Financial Variable F&O | DXY | USD/EUR | Implied Volatility | Realized Volatility | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Brent | 1.00 | 0.96 | 0.63 | 0.66 | −0.15 | 0.66 | −0.15 | 0.60 | 0.00 | 0.36 | −0.79 | −0.81 | 0.51 | 0.53 | 0.41 | 0.61 | 0.53 | 0.46 | 0.48 | 0.73 | 0.44 | 0.36 | −0.57 | 0.55 | −0.23 | −0.24 |
| Log(Brent) | 0.96 | 1.00 | 0.74 | 0.74 | −0.16 | 0.77 | −0.10 | 0.70 | 0.11 | 0.49 | −0.86 | −0.89 | 0.60 | 0.64 | 0.49 | 0.71 | 0.62 | 0.56 | 0.56 | 0.81 | 0.51 | 0.45 | −0.52 | 0.49 | −0.18 | −0.21 |
| Total World Production | 0.63 | 0.74 | 1.00 | 0.80 | −0.17 | 0.98 | −0.22 | 0.96 | 0.58 | 0.79 | −0.79 | −0.80 | 0.90 | 0.73 | 0.81 | 0.92 | 0.90 | 0.70 | 0.85 | 0.87 | 0.80 | 0.78 | −0.11 | 0.08 | 0.00 | 0.02 |
| OPEC Production | 0.66 | 0.74 | 0.80 | 1.00 | −0.56 | 0.78 | 0.03 | 0.65 | 0.35 | 0.63 | −0.71 | −0.72 | 0.64 | 0.76 | 0.49 | 0.70 | 0.66 | 0.73 | 0.56 | 0.77 | 0.53 | 0.48 | −0.38 | 0.35 | −0.08 | −0.06 |
| Spare OPEC Production | −0.15 | −0.16 | −0.17 | −0.56 | 1.00 | −0.12 | −0.41 | 0.05 | 0.20 | 0.07 | 0.26 | 0.29 | 0.05 | −0.13 | 0.11 | 0.02 | 0.04 | −0.16 | 0.09 | −0.01 | 0.08 | 0.09 | 0.18 | −0.16 | 0.08 | −0.01 |
| Total World Consumption | 0.66 | 0.77 | 0.98 | 0.78 | −0.12 | 1.00 | −0.13 | 0.95 | 0.55 | 0.77 | −0.84 | −0.80 | 0.89 | 0.74 | 0.79 | 0.92 | 0.89 | 0.70 | 0.84 | 0.87 | 0.78 | 0.77 | −0.14 | 0.10 | −0.06 | −0.06 |
| OECD Consumption | −0.15 | −0.10 | −0.22 | 0.03 | −0.41 | −0.13 | 1.00 | −0.38 | −0.45 | −0.36 | −0.16 | −0.01 | −0.43 | −0.14 | −0.47 | −0.36 | −0.42 | −0.18 | −0.45 | −0.29 | −0.50 | −0.46 | 0.06 | −0.07 | −0.06 | −0.13 |
| China Consumption | 0.60 | 0.70 | 0.96 | 0.65 | 0.05 | 0.95 | −0.38 | 1.00 | 0.64 | 0.80 | −0.72 | −0.71 | 0.93 | 0.68 | 0.87 | 0.95 | 0.93 | 0.65 | 0.91 | 0.86 | 0.85 | 0.85 | −0.09 | 0.07 | −0.01 | 0.00 |
| OECD Commercial Inventory | 0.00 | 0.11 | 0.58 | 0.35 | 0.20 | 0.55 | −0.45 | 0.64 | 1.00 | 0.88 | −0.02 | −0.05 | 0.71 | 0.57 | 0.65 | 0.65 | 0.70 | 0.61 | 0.64 | 0.54 | 0.65 | 0.66 | 0.16 | −0.17 | 0.15 | 0.14 |
| OECD Total Inventory | 0.36 | 0.49 | 0.79 | 0.63 | 0.07 | 0.77 | −0.36 | 0.80 | 0.88 | 1.00 | −0.38 | −0.41 | 0.85 | 0.81 | 0.73 | 0.85 | 0.85 | 0.81 | 0.76 | 0.81 | 0.75 | 0.74 | −0.16 | 0.13 | 0.07 | 0.05 |
| Stocks Consumption Ratio | −0.79 | −0.86 | −0.79 | −0.71 | 0.26 | −0.84 | −0.16 | −0.72 | −0.02 | −0.38 | 1.00 | 0.93 | −0.60 | −0.56 | −0.51 | −0.68 | −0.61 | −0.47 | −0.58 | −0.71 | −0.51 | −0.49 | 0.27 | −0.24 | 0.13 | 0.14 |
| Fundamental Variable | −0.81 | −0.89 | −0.80 | −0.72 | 0.29 | −0.80 | −0.01 | −0.71 | −0.05 | −0.41 | 0.93 | 1.00 | −0.59 | −0.56 | −0.50 | −0.67 | −0.60 | −0.48 | −0.56 | −0.73 | −0.50 | −0.46 | 0.28 | −0.26 | 0.02 | 0.04 |
| Long non-commercial Futures | 0.51 | 0.60 | 0.90 | 0.64 | 0.05 | 0.89 | −0.43 | 0.93 | 0.71 | 0.85 | −0.60 | −0.59 | 1.00 | 0.67 | 0.96 | 0.97 | 1.00 | 0.66 | 0.98 | 0.85 | 0.94 | 0.93 | −0.13 | 0.10 | −0.10 | −0.05 |
| Short non-commercial Futures | 0.53 | 0.64 | 0.73 | 0.76 | −0.13 | 0.74 | −0.14 | 0.68 | 0.57 | 0.81 | −0.56 | −0.56 | 0.67 | 1.00 | 0.44 | 0.73 | 0.68 | 0.96 | 0.52 | 0.83 | 0.49 | 0.47 | −0.35 | 0.32 | 0.14 | 0.10 |
| Net non-commercial Futures | 0.41 | 0.49 | 0.81 | 0.49 | 0.11 | 0.79 | −0.47 | 0.87 | 0.65 | 0.73 | −0.51 | −0.50 | 0.96 | 0.44 | 1.00 | 0.90 | 0.95 | 0.44 | 0.99 | 0.72 | 0.95 | 0.95 | −0.03 | 0.00 | −0.18 | −0.10 |
| Open Interest Futures | 0.61 | 0.71 | 0.92 | 0.70 | 0.02 | 0.92 | −0.36 | 0.95 | 0.65 | 0.85 | −0.68 | −0.67 | 0.97 | 0.73 | 0.90 | 1.00 | 0.97 | 0.70 | 0.94 | 0.93 | 0.86 | 0.84 | −0.21 | 0.19 | −0.09 | −0.05 |
| Long non-commercial F&O | 0.53 | 0.62 | 0.90 | 0.66 | 0.04 | 0.89 | −0.42 | 0.93 | 0.70 | 0.85 | −0.61 | −0.60 | 1.00 | 0.68 | 0.95 | 0.97 | 1.00 | 0.67 | 0.98 | 0.86 | 0.94 | 0.92 | −0.15 | 0.12 | −0.11 | −0.06 |
| Short non-commercial F&O | 0.46 | 0.56 | 0.70 | 0.73 | −0.16 | 0.70 | −0.18 | 0.65 | 0.61 | 0.81 | −0.47 | −0.48 | 0.66 | 0.96 | 0.44 | 0.70 | 0.67 | 1.00 | 0.49 | 0.77 | 0.51 | 0.47 | −0.30 | 0.27 | 0.10 | 0.09 |
| Net non-commercial F&O | 0.48 | 0.56 | 0.85 | 0.56 | 0.09 | 0.84 | −0.45 | 0.91 | 0.64 | 0.76 | −0.58 | −0.56 | 0.98 | 0.52 | 0.99 | 0.94 | 0.98 | 0.49 | 1.00 | 0.79 | 0.95 | 0.95 | −0.08 | 0.06 | −0.16 | −0.10 |
| Open Interest F&O | 0.73 | 0.81 | 0.87 | 0.77 | −0.01 | 0.87 | −0.29 | 0.86 | 0.54 | 0.81 | −0.71 | −0.73 | 0.85 | 0.83 | 0.72 | 0.93 | 0.86 | 0.77 | 0.79 | 1.00 | 0.70 | 0.65 | −0.40 | 0.38 | 0.03 | 0.03 |
| Financial Variable Futures | 0.44 | 0.51 | 0.80 | 0.53 | 0.08 | 0.78 | −0.50 | 0.85 | 0.65 | 0.75 | −0.51 | −0.50 | 0.94 | 0.49 | 0.95 | 0.86 | 0.94 | 0.51 | 0.95 | 0.70 | 1.00 | 0.97 | −0.10 | 0.06 | −0.18 | −0.11 |
| Financial Variable F&O | 0.36 | 0.45 | 0.78 | 0.48 | 0.09 | 0.77 | −0.46 | 0.85 | 0.66 | 0.74 | −0.49 | −0.46 | 0.93 | 0.47 | 0.95 | 0.84 | 0.92 | 0.47 | 0.95 | 0.65 | 0.97 | 1.00 | −0.03 | 0.00 | −0.18 | −0.12 |
| DXY | −0.57 | −0.52 | −0.11 | −0.38 | 0.18 | −0.14 | 0.06 | −0.09 | 0.16 | −0.16 | 0.27 | 0.28 | −0.13 | −0.35 | −0.03 | −0.21 | −0.15 | −0.30 | −0.08 | −0.40 | −0.10 | −0.03 | 1.00 | −0.98 | 0.26 | 0.26 |
| USD/EUR | 0.55 | 0.49 | 0.08 | 0.35 | −0.16 | 0.10 | −0.07 | 0.07 | −0.17 | 0.13 | −0.24 | −0.26 | 0.10 | 0.32 | 0.00 | 0.19 | 0.12 | 0.27 | 0.06 | 0.38 | 0.06 | 0.00 | −0.98 | 1.00 | −0.23 | −0.23 |
| Implied Volatility | −0.23 | −0.18 | 0.00 | −0.08 | 0.08 | −0.06 | −0.06 | −0.01 | 0.15 | 0.07 | 0.13 | 0.02 | −0.10 | 0.14 | −0.18 | −0.09 | −0.11 | 0.10 | −0.16 | 0.03 | −0.18 | −0.18 | 0.26 | −0.23 | 1.00 | 0.84 |
| Realized Volatility | −0.24 | −0.21 | 0.02 | −0.06 | −0.01 | −0.06 | −0.13 | 0.00 | 0.14 | 0.05 | 0.14 | 0.04 | −0.05 | 0.10 | −0.10 | −0.05 | −0.06 | 0.09 | −0.10 | 0.03 | −0.11 | −0.12 | 0.26 | −0.23 | 0.84 | 1.00 |
Note: This table shows the correlation matrix for every time series initially considered for building the final input (predictive) variables.

Table A4.
Correlation matrix of selected predictive variables and the target variable.
Table A4.
Correlation matrix of selected predictive variables and the target variable.
| Log(Brent) | Fundamental Variable | Financial Variable | Dollar | Realized Volatility | |
|---|---|---|---|---|---|
| Log(Brent) | - | −0.89 | 0.51 | −0.52 | −0.21 |
| Fundamental Variable | −0.89 | - | −0.50 | 0.28 | 0.04 |
| Financial Variable | 0.51 | −0.50 | - | −0.10 | −0.11 |
| Dollar | −0.52 | 0.28 | −0.10 | - | 0.26 |
| Realized Volatility | −0.21 | 0.04 | −0.11 | 0.26 | - |
Note: This table reports correlation coefficients across the variables that have been selected as final input variables. Correlations with the output variable defined as the log of the Brent spot price are also reported.

Table A5.
Bai and Perron structural breaks test results for log(Brent).
Table A5.
Bai and Perron structural breaks test results for log(Brent).
| Sequential F-Statistic Determined Breaks: 5 | |||||
|---|---|---|---|---|---|
| Break Test | F-Statistics | Scaled F-Statistic | Critical Value ** | Break Dates: | Dates: |
| 0 vs. 1 * | 1080.393 | 1080.393 | 8.58 | 1 | 09 September |
| 1 vs. 2 * | 75.975 | 75.975 | 10.13 | 2 | 04 October |
| 2 vs. 3 * | 55.274 | 55.274 | 11.14 | 3 | 10 August |
| 3 vs. 4 * | 112.946 | 112.946 | 11.83 | 4 | 14 November |
| 4 vs. 5 * | 23.992 | 23.992 | 12.25 | 5 | 19 April |
Note: This table provides the results for structural breaks test. The test report results for the null hypothesis H0 of no structural break. The alternative hypothesis H1 test for k structural breaks. There are five structural breaks. * Significant at the 0.05 level, ** Bai–Perron critical values [38] are used.

Table A6.
Bai and Perron structural breaks test for equation in differences.
Table A6.
Bai and Perron structural breaks test for equation in differences.
| Sequential F-Statistic Determined Breaks: 0 | |||
|---|---|---|---|
| Break Test | F-Statistics | Scaled F-Statistic | Critical Value ** |
| 0 vs. 1 | 2.321 | 11.605 | 18.23 |
Note: This table provides the results for structural breaks test for an equation that estimates changes in log of Brent as a function of the differences in the fundamental, financial, volatility, and dollar variables. The test report results for the null hypothesis H0 of no structural break. The alternative hypothesis H 1 tests for k structural breaks. There are no structural breaks. * Significant at the 0.05 level, ** Bai–Perron critical values [38] are used.

Table A7.
RMSE error measures for different forecasting methods.
Table A7.
RMSE error measures for different forecasting methods.
| 2017Q1 | 2017Q2 | 2017Q3 | 2017Q4 | 2018Q1 | 2018Q2 | 2018Q3 | 2018Q4 | 2019Q1 | |
|---|---|---|---|---|---|---|---|---|---|
| Constant | 4.144 | 8.880 | 18.581 | 15.593 | 8.447 | 6.380 | 8.179 | 13.759 | 6.934 |
| Futures | 5.636 | 7.773 | 15.878 | 15.226 | 8.143 | 5.323 | 8.619 | 15.330 | 9.668 |
| BBG Analysts Median | 3.579 | 5.715 | 9.903 | 15.761 | 14.872 | 7.939 | 3.620 | 8.961 | 6.447 |
| Department of Energy EIA | 4.122 | 7.213 | 16.305 | 17.359 | 12.688 | 9.786 | 3.722 | 11.440 | 5.120 |
| GAMLTF Forecasted Inputs | 5.233 | 7.560 | 14.174 | 12.368 | 10.994 | 6.288 | 6.422 | 14.046 | 4.808 |
| GAMLTF Actual Inputs | 9.409 | 4.215 | 6.703 | 3.854 | 4.197 | 8.550 | 3.273 | 7.585 | 5.452 |
| LTF Actual Inputs No GAM | 10.088 | 5.606 | 6.505 | 7.905 | 6.736 | 16.029 | 2.616 | 2.757 | 4.840 |
| 2019Q2 | 2019Q3 | 2019Q4 | 2020Q1 | 2020Q2 | 2020Q3 | 2020Q4 | 2021Q1 | 2021Q2 | |
| Constant | 7.253 | 16.155 | 16.047 | 22.900 | 16.258 | 17.497 | 23.071 | 22.156 | 16.696 |
| Futures | 7.938 | 15.825 | 13.880 | 20.262 | 12.529 | 15.967 | 20.520 | 21.594 | 21.916 |
| BBG Analysts Median | 11.110 | 19.716 | 16.965 | 17.981 | 6.908 | 16.904 | 19.816 | 24.502 | 21.498 |
| Department of Energy EIA | 6.009 | 18.994 | 15.179 | 18.653 | 15.237 | 12.696 | 18.851 | 20.654 | 20.239 |
| GAMLTF Forecasted Inputs | 7.748 | 17.138 | 20.165 | 17.989 | 16.629 | 14.133 | 8.360 | 6.372 | 11.279 |
| GAMLTF Actual Inputs | 4.120 | 5.043 | 7.977 | 5.408 | 12.576 | 11.860 | 9.243 | 4.998 | 5.232 |
| LTF Actual Inputs No GAM | 12.689 | 35.927 | 44.212 | 40.622 | 16.969 | 18.266 | 13.300 | 7.160 | 10.398 |
| 2021Q3 | 2021Q4 | 2022Q1 | 2022Q2 | 2022Q3 | 2022Q4 | 2023Q1 | TOTAL | ||
| Constant | 22.182 | 23.929 | 24.366 | 20.987 | 31.913 | 7.979 | 3.004 | 17.040 | |
| Futures | 25.044 | 24.891 | 24.864 | 7.277 | 11.495 | 5.855 | 3.954 | 15.323 | |
| BBG Analysts Median | 27.313 | 28.984 | 23.360 | 10.227 | 14.378 | 13.291 | 9.052 | 16.031 | |
| Department of Energy EIA | 26.232 | 25.283 | 24.485 | 10.465 | 11.659 | 10.816 | 3.961 | 15.400 | |
| GAMLTF Forecasted Inputs | 15.823 | 12.759 | 15.853 | 30.541 | 27.898 | 8.644 | 5.754 | 14.341 | |
| GAMLTF Actual Inputs | 16.721 | 17.960 | 22.357 | 25.347 | 18.111 | 8.847 | 3.981 | 11.123 | |
| LTF Actual Inputs No GAM | 10.190 | 9.670 | 11.454 | 40.561 | 37.043 | 9.519 | 6.019 | 20.065 |
Note: This table reports the forecasting performance in terms of the RMSE measure of the proposed framework for forecasted and actual input data as well as alternative benchmarks, including the LTF framework with no GAM. The in-sample period is 1995–2016, and the out-of-sample or forecasting period is 2017–2023. Forecasts are performed for the next four quarters. The following forecasting methods are considered: No-change: forecasts are the average price of the previous month for the whole forecast period. Futures: forecasts are the average of Brent first-, second-, and third-month contracts for the first quarter, fourth-, fifth-, and sixth-month contracts for the second quarter for the day before beginning the period of forecast. BBG: Bloomberg quarterly surveys are taken as forecasts the day before beginning the period of forecast. EIA: average monthly forecasts to create quarterly forecasts are taken from the last EIA report before beginning the period of forecast. GAMLFT with Forecasted Inputs: proposed new model fed by forecasted inputs. Highlighted in bold. GAMLFT with actual inputs: proposed new model fed by actual inputs. Highlighted in bold. LFT with actual inputs: linear function transfer model fed by forecasted inputs.
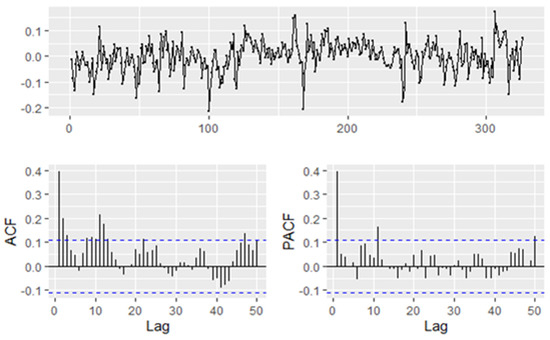
Figure A1.
PACF and ACF structure of the error term under a GAM model: This figure shows the PACF and ACF for the initial GAM model error. A clear autocorrelation can be observed in the regression errors since some lags exceed confidence limits.
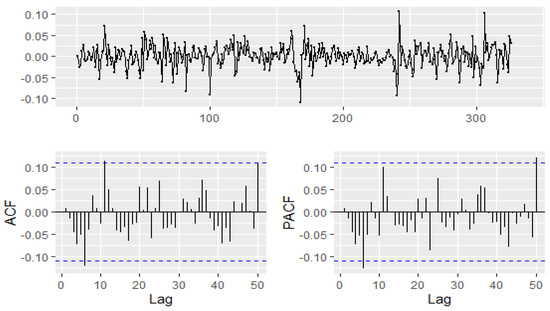
Figure A2.
PACF and ACF structures of the error term under GAM with LTF specification: This figure shows the PACF and ACF for the proposed model error. No problem of autocorrelation can be appreciated.
References
- Weijermars, R.; Sun, Z. Regression analysis of historic oil prices: A basis for future mean reversion prices scenarios. Glob. Financ. J. 2018, 35, 177–201. [Google Scholar] [CrossRef]
- Fabra, N. Reforming European electricity markets: Lessons from the energy crisis. Energy Econ. 2023, 126, 106963. [Google Scholar] [CrossRef]
- Chuliá, H.; Klein, T.; Mendoza, J.A.M.; Uribe, J.M. Vulnerability of European electricity markets: A quantile connectedness approach. Energy Policy 2024, 184, 113862. [Google Scholar] [CrossRef]
- Cervera, I.; Figuerola-Ferretti, I. Credit risk and bubble behavior of credit default swaps in the corporate energy sector. Int. Rev. Econ. Financ. 2023, 89 Pt A, 702–731. [Google Scholar] [CrossRef]
- Alquist, R.; Kilian, L. What Do We Learn from the Price of Crude Oil Futures? J. Appl. Econom. 2010, 25, 539–573. [Google Scholar] [CrossRef]
- Alquist, R.; Kilian, L.; Vigfusson, R.J. Forecasting the Price of Oil. In Handbook of Economic Forecasting; Elliott, G., Timmermann, A., Eds.; Elsevier: Amsterdam, The Netherlands, 2013; Volume 2A, pp. 427–507. [Google Scholar]
- Baumeister, C.; Kilian, L. Real-Time Analysis of Oil Price Risks using Forecast Scenarios. IMF Econ. Rev. 2014, 62, 119–145. [Google Scholar] [CrossRef]
- Baumeister, C.; Kilian, L. Forecasting the Real Price of Oil in a Changing World: A Forecast Combination Approach. J. Bus. Econ. Stat. 2015, 33, 338–351. [Google Scholar] [CrossRef]
- Ferrari, D.; Ravazzolo, F.; Vespignani, J. Forecasting Energy Commodity Prices: A Large Global Dataset Sparse Approach. CAMA Working Paper No. 90/2019. Energy Econ. 2021, 98, 105268. [Google Scholar] [CrossRef]
- Coppola, A. Forecasting oil price movements: Exploiting the information in the futures market. J. Futures Mark. 2008, 28, 34–56. [Google Scholar] [CrossRef]
- Aliu, F.; Kučera, J.; Hašková, S. Agricultural Commodities in the Context of the Russia-Ukraine War: Evidence from Corn, Wheat, Barley, and Sunflower Oil. Forecasting 2023, 5, 351–373. [Google Scholar] [CrossRef]
- Henderson, B.J.; Person, N.D.; Wang, L. New Evidence on the Financialization of Commodity Markets. Rev. Financ. Stud. 2015, 8, 1285–1311. [Google Scholar] [CrossRef]
- Singleton, K.J. Investor Flows and the 2008 Boom/Bust in Oil Prices. Manag. Sci. 2014, 60, 300–318. [Google Scholar] [CrossRef]
- Hamilton, J.D.; Wu, J.C. Risk premia in crude oil futures prices. J. Int. Money Financ. 2014, 42, 9–37. [Google Scholar] [CrossRef]
- Cheng, I.; Xiong, W. Financialization of Commodity Markets. Annu. Rev. Financ. Econ. 2014, 6, 419–441. [Google Scholar] [CrossRef]
- Baumeister, C.; Korobilis, D.; Lee, T.K. Energy markets and global economic conditions. Rev. Econ. Stat. 2022, 104, 828–844. [Google Scholar] [CrossRef]
- Figuerola-Ferretti, I.; Rodríguez, A.; Schwartz, E. Oil price analysts’ forecasts. J. Futures Mark. 2021, 41, 1351–1374. [Google Scholar] [CrossRef]
- Miao, H.; Ramchander, S.; Wang, T.; Yang, D. Influential factors in crude oil price forecasting. Energy Econ. 2017, 68, 77–88. [Google Scholar] [CrossRef]
- Chai, J.; Xing, L.M.; Zhou, X.Y.; Zhang, Z.G.; Li, J.X. Forecasting the WTI crude oil price by a hybrid-refined method. Energy Econ. 2018, 71, 114–127. [Google Scholar] [CrossRef]
- Gareth, J.; Daniela, W.; Trevor, H.; Robert, T. An Introduction to Statistical Learning: With Applications in R; Springer Texts in Statistics; Springer: Berlin/Heidelberg, Germany, 2013. [Google Scholar]
- Phillips, P.C.B.; Shi, S.-P.; Yu, J. (a) Testing for Multiple Bubbles: Limit Theory of Dating Algorithms. Int. Econ. Rev. 2015, 56, 1043–1098. [Google Scholar] [CrossRef]
- Phillips, P.C.B.; Shi, S.-P.; Yu, J. (b) Supplement to two papers on multiple bubbles. Int. Econ. Rev. 2015, 56, 1–99. [Google Scholar]
- Lammerding, M.; Stephan, P.; Trede, M.; Wilfling, B. Speculative bubbles in recent oil price dynamics: Evidence from a Bayesian Markov-switching state-space approach. Energy Econ. 2013, 36, 491–502. [Google Scholar] [CrossRef]
- Svensson, L. Oil prices and ECB monetary policy. In Briefing Paper for the Committee on Economic and Monetary Affairs of the European Parliament; European Parliament: Strasbourg, France, 2005; pp. 1–4. [Google Scholar]
- Wood, S.N.; Goude, Y.; Shaw, S. Generalized additive models for large datasets. J. R. Stat. Soc. 2015, 64, 139–155. [Google Scholar]
- Box, G.; Jenkins, G.; Reinsel, G. Time Series Analysis, Forecasting and Control, 3rd ed.; Prentice Hall: Englwood Cliffs, NJ, USA, 1994. [Google Scholar]
- Liu, L.; Hanssens, D.M. Identification of multiple-input transfer function models. Commun. Stat. Theory Methods 1982, 11, 297–314. [Google Scholar] [CrossRef]
- Figuerola-Ferretti, I.; McCrorie, J.R.; Paraskevopoulos, I. Mild explosivity in recent crude oil prices. Energy Econ. 2020, 87, 104387. [Google Scholar] [CrossRef]
- Figuerola-Ferretti, I.; Gilbert, C.L.; McCrorie, J.R. Testing for mild explosivity and bubbles in LME non-ferrous metals prices. J. Time Ser. Anal. 2015, 36, 763–782. [Google Scholar] [CrossRef]
- Haase, M.; Seiler, Y.; Zimmermann, H. Permanent and transitory price shocks in commodity futures markets and their relation to speculation. Empir. Econ. 2019, 56, 1359–1382. [Google Scholar] [CrossRef]
- Bruno, V.; Büyüksahin, B.; Robe, M.A. The Financialization of Food? Am. J. Agric. Econ. 2017, 99, 243–264. [Google Scholar] [CrossRef]
- Etienne, X.L.; Irwin, S.H.; Garcia, P. Price explosiveness, speculation, and grain futures prices. Am. J. Agric. Econ. 2015, 97, 65–87. [Google Scholar] [CrossRef]
- Calomiris, C.W.; Melek, N.Ç.; Mamaysky, H. Predicting the Oil Market NBER Working Papers 29379; National Bureau of Economic Research: Cambridge, MA, USA, 2021.
- Baumeister, C. Recent Developments in (Modeling) Energy Market Dynamics, Keynote at the Workshop on “Energy and Climate: Macroeconomic Implications”; B.I. Norwegian Business School: Oslo, Norway, 2022. [Google Scholar]
- Dickey, D.A.; Fuller, W.A. Likelihood ratio statistics for autoregressive time series with a unit root. Econometrica 1981, 49, 1057–1072. [Google Scholar] [CrossRef]
- Phillips, P.C.; Perron, P. Testing for a unit root in time series regression. Biometrika 1988, 75, 335–346. [Google Scholar] [CrossRef]
- Kwiatkowski, D.; Phillips, P.C.; Schmidt, P.; Shin, Y. Testing the null hypothesis of stationarity against the alternative of a unit root: How sure are we that economic time series have a unit root? J. Econ. 1992, 54, 159–178. [Google Scholar]
- Bai, J.; Perron, P. Computation and analysis of multiple structural change models. J. Appl. Econom. 2003, 18, 1–22. [Google Scholar] [CrossRef]
- Duboue, P. The Art of Feature Engineering: Essentials for Machine Learning; Cambridge University Press: Cambridge, UK, 2020. [Google Scholar]
- Garratt, A.; Vahey, S.P.; Zhang, Y. Real-Time Forecast Combinations for the Oil Price. J. Appl. Econom. 2019, 34, 1–22. [Google Scholar] [CrossRef]
- Beckmann, J.; Czudaj, R.; Arora, V. The Relationship between Oil Prices and Exchange Rates: Revisiting theory and evidence. Energy Econ. 2020, 88, 104772. [Google Scholar] [CrossRef]
- Pankratz, A. Forecasting with Dynamic Regression Models; Wiley-Interscience: Hoboken, NJ, USA, 1991. [Google Scholar]
- Kaufmann, R.K.; Ullman, B. Oil prices, speculation, and fundamentals: Interpreting causal relations among spot and futures prices. Energy Econ. 2009, 31, 550–558. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).