Abstract
A reasonable allocation of production schedules and savings in overall electricity costs are crucial for large manufacturing conglomerates. In this study, we develop an optimization model of off-site industrial production scheduling to address the problems of high electricity costs due to the irrational allocation of production schedules on the demand side of China’s power supply, and the difficulty in promoting industrial and commercial distributed photovoltaic (PV) projects in China. The model makes full use of the conditions of different PV resources and variations in electricity prices in different places to optimize the scheduling of industrial production in various locations. The model is embedded with two sub-models, i.e., an electricity price prediction model and a distributed photovoltaic power cost model to complete the model parameters, in which the electricity price prediction model utilizes a Long Short-Term Memory (LSTM) neural network. Then, the particle swarm optimization algorithm is used to solve the optimization model. Finally, the production data of two off-site pharmaceutical factories belonging to the same large group of enterprises are substituted into the model for example analysis, and it is concluded that the optimization model can significantly reduce the electricity consumption costs of the enterprises by about 7.9%. This verifies the effectiveness of the optimization model established in this paper in reducing the cost of electricity consumption on the demand side.
1. Introduction
Since September 2020, when China formally put forward its “dual-carbon” strategy, China’s National Development and Reform Commission (NDRC), National Energy Administration (NEA), and other Chinese ministries and commissions have continued to release favorable policies in respect of the distributed PV industry. This shows that distributed PV systems will play an important role in China’s realization of the “dual-carbon” strategy [1,2,3]. Among them, industrial and commercial distributed PV systems are developing extremely rapidly and have huge potential due to high market demand, minimal technical difficulties, etc. [4,5,6]. However, at present, China’s industrial and commercial distributed PV systems are encountering difficulties in respect of promotion [7,8]. Our research team found that, with the continuous construction and development of China’s power spot market, the market’s main body of transactions continues to expand, and industrial and commercial users are increasingly willing to participate in power spot market transactions. The power spot market trading price is often lower than that of distributed PV investment companies, and industrial and commercial users reach an agreement on the price of electricity [9,10]. In such a market environment, as well as at all levels of government across China, industrial and commercial distributed PV subsidies are frequently cancelled, and the difficulties associated with industrial and commercial distributed PV investment have greatly increased. Therefore, there is an urgent need for a new power supply model in the field of commercial and industrial distributed PV systems, which can minimize the off-site electricity costs of commercial and industrial users while guaranteeing the returns of distributed PV investors. This paper carries out research on the above issues.
A large amount of the literature has been reviewed before the beginning of the study. And it found that most scholars have conducted significant research on the traditional master–slave game relationship, with distributed PV investment companies as the leader and industrial and commercial users as the followers.
Paper [11] comprehensively investigated the state-of-the-art optimization methods for hybrid energy systems of photovoltaics, diesel turbine generators, and energy storage systems, and laid the foundation for solving the intricate and complex real-world problems related to the operation of distributed energy systems. Paper [12] proposed a joint optimization and operation mechanism of the distributed PV power generation market and the carbon market based on cross-chain trading technology from the perspective of the electric power market; Paper [13] put forward a novel trading energy-based operation framework, which helps to ensure the economic operation of aggregators and users in a distributed PV distribution system; Paper [14] comprehensively reviewed the development and impact of distributed PV in the electricity market, and discussed in detail the related market models and bidding strategies; Paper [15] proposed a novel distributed energy system integrating CHP, PV power generation, and ground-source heat pumps, and develops a new distributed energy system based on a hybrid of differential evolution and a particle swarm optimization algorithm and a hierarchical analysis method to develop a seasonal operation strategy; Paper [16] proposed a multi-stage and multi-period distributed energy optimization method based on deepening the market integration of distributed energy resources in the form of aggregation; Paper [17] established a bi-level planning model for distributed PV energy storage systems in distribution networks, taking into account the uncertainty of distributed PV power output and the demand response behavior of users in the context of the coordinated operation of China’s power market and carbon market; and Paper [18] conducted an analytical study of PV user demand response modeling and tariff mechanism from the perspective that the PV user demand response can improve the PV extinction rate.
In this study, we used the above literature as the research background to establish a new type of master–slave game relationship, with industrial and commercial users as leaders and distributed PV investment companies as followers. Under the circumstance of guaranteeing the investment interests of distributed PV companies, it is possible to minimize the cost of electricity for industrial and commercial users and improve the success rate of distributed PV contracting as much as possible. Since commercial power consumption cannot be deployed off-site, this paper only discusses the optimization of off-site industrial power consumption. For large manufacturing group enterprises using assembly line operation, electricity consumption is proportional to the production plan, i.e., the production plan deployment can be reflected in the respective electricity consumption of off-site factories. Due to the light resources, natural conditions, and market mechanism, the cost of photovoltaic power generation is not the same everywhere. The production deployment of heterogeneous industrial parks can make good use of the different costs of photovoltaic power generation in different places to optimize the production deployment, and thus save the cost of electricity. In the case of logistics, deployment costs are not taken into account, since low electricity cost areas produce more products and high electricity cost areas as far as possible reduce production. However, from a practical point of view, because of the volatility of electricity prices, distributed photovoltaic power generation is unstable and other factors, belonging to the same enterprise’s off-site factories, are difficult to make effective optimal deployment decisions. This study addresses this issue.
In this paper, a mathematical model applicable to the optimization of the enterprise’s off-site industrial production scheduling is first established. Secondly, because of the missing parameters of the model in practical application, an electricity price prediction model and a distributed PV levelized kWh cost model are established, in which the electricity price prediction model employs an LSTM neural network. Finally, the particle swarm optimization algorithm is used to solve the model.
To verify the relevance and effectiveness of the model in solving the problem of off-site production scheduling on the demand side of electricity, two off-site pharmaceutical factories were researched. These are located in Kunming, Yunnan Province, China, and Binzhou, Shandong Province, China, and belong to the same large-scale pharmaceutical enterprise. The research was conducted via field visits and telephone interviews, through which we obtained the relevant research data. Finally, the research data’s results, based on the model solution, show that the enterprise off-site industrial production scheduling optimization model can effectively reduce an enterprise’s electricity costs.
This research makes two main contributions: (1) the construction of a new master–slave game relationship, with industrial and commercial users as leaders and distributed PV investment companies as followers; and (2) the construction of an optimal scheduling model that can reduce the cost of off-site electricity consumption of enterprises. The above two points will provide ideas for the future promotion of industrial and commercial distributed PV construction in China.
The next part of this paper will describe the research in detail. Section 2 introduces the industrial production optimization scheduling model, Section 3 introduces the electricity price prediction model, and Section 4 introduces the distributed photovoltaic kWh cost model. Section 5 presents the actual operation simulation of the setup example system to verify the validity of the proposed model in this paper.
2. Industrial Production Optimization Scheduling Model
Aiming at the problem of the high cost of electricity consumption of off-site factories belonging to the same enterprise, this study proposes an optimization model of off-site industrial production scheduling for the enterprise. The model can make good use of different PV resources, different electricity prices, and other conditions to reduce the total cost of electricity for enterprises’ off-site factories, and increase the contracting rate of distributed PV investment.
2.1. Tripartite Electricity Trading Model
A three-party power trading model is first developed for a single-site factory; this is proposed on the basis of the traditional distributed PV contract energy management model (EMC). This distributed PV operation model consists of a factory providing a roof for free and a third party investing in the construction of a PV power plant; the third party is the asset owner but also needs to share the revenue with the factory. The third party, i.e., the distributed PV investor, signs an agreement with the factory that, under the premise of guaranteeing a return on the distributed PV investment, the factory purchases the agreed power from the distributed PV investor at an agreed tariff on a daily basis as the basic time unit. Essentially, the factory is the leader and the distributed PV investor is the follower, and the two constitute a master–slave game relationship [19].
The advantage of this operation model is that usually the customer-side tariff is significantly higher than the residual feed-in tariff, the distributed PV investor can sell electricity to the factory for higher profit, and the factory can save electricity costs by using the investor’s PV power generation. This mode of operation increases the willingness of factories to provide distributed PV installation sites compared to the traditional EMC mode, as the factories will be more flexible in the way they use electricity under this mode of operation.
As shown in Figure 1, the plant can purchase agreed power from the distributed photovoltaic company at an agreed tariff and can purchase power from the power day-ahead trading market, and the distributed photovoltaic company’s remaining power is fed into the grid at the coal-fired benchmark price.
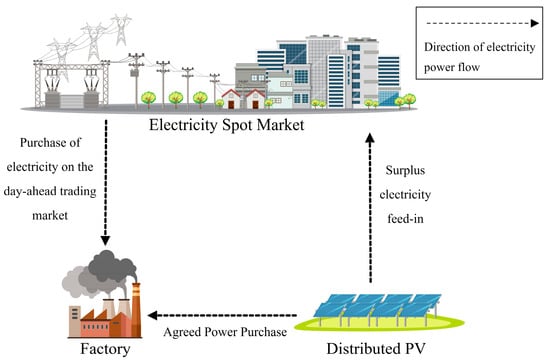
Figure 1.
Tripartite electricity trading model.
2.2. Enterprise Off-Site Industrial Production Optimization Scheduling Model
For the case of joint production of multiple factories in different places, the above model is no longer applicable, so this study proposes an enterprise off-site industrial production optimization scheduling model (see Figure 2). The daily production schedules of the off-site factories distributed in each province of China are decided by the enterprise headquarters, i.e., the enterprise headquarters run the off-site industrial production optimization scheduling model to derive the daily electricity consumption and the agreed amount of electricity of the factories in each place. Finally, the factories in each province purchase the difference between the daily power consumption and the agreed power, i.e., the daily power purchased from the grid, from the provincial power trading center.
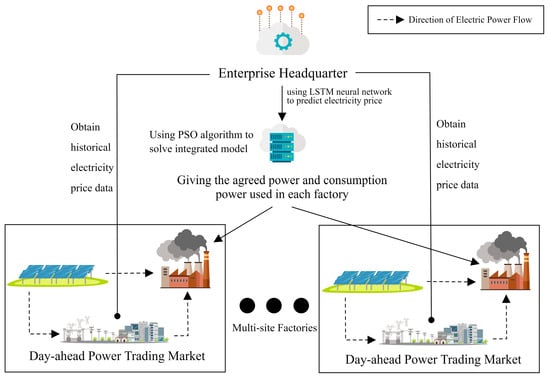
Figure 2.
Enterprise off-site industrial production optimization scheduling model.
A mathematical model is developed with respect to the model structure in Figure 2, where the objective of optimal scheduling is to minimize the total cost of electricity (i.e., the cost of electricity to the enterprise) for all factories in the off-site location while producing the same number of products, and the objective function of the model is thus listed. (See Appendix A for a description of the relevant symbols.)
The daily power consumption of each plant can be expressed by the following equation. The daily source of electrical energy for the plant consists of two parts: the first part is grid power and the second part is distributed PV power. Therefore, Equation (2) can be written as follows
The constraints of the model are discussed next. The first is that the total number of goods produced by all factories needs to satisfy the total number of goods in the production plan. Second, due to the limited capacity of each factory, there is an upper limit on the number of commodities it can produce per day. Finally, the deployment of commodity production directly affects the agreed electricity quantity, which in turn affects the revenue of the distributed PV company. Therefore, the production deployment needs to ensure the return on investment of the distributed PV company.
It is assumed that the industrial assembly line of each factory is almost the same, so in the case of producing the same kind of commodities, the electricity required per unit quantity of commodities can be regarded as being the same. Therefore, the production deployment of the commodity can be expressed indirectly using the power consumption of the factory.
In summary, the following constraints can be listed
2.3. Particle Swarm Optimization Algorithm Solution
In summary, the optimization model to be solved is a quadratic programming model, and this study uses a particle swarm modern optimization algorithm for solving. The structure of the particle swarm optimization algorithm is shown in Figure 3.
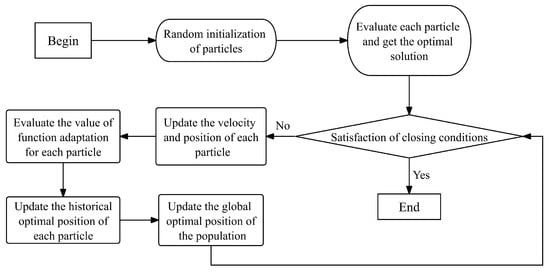
Figure 3.
Particle swarm optimization algorithm structure.
The algorithm simulates the collaboration and information sharing between individuals in a population by continuously adjusting the direction of movement of the individuals in the expectation of finding an optimal solution to the problem. At the beginning of the algorithm, particles are randomly distributed in the search space according to some initialization strategy. Then, each particle updates its velocity and position based on its current position and velocity as well as the information of other particles in the neighborhood. This updating process includes two important parts: individual experience and social experience. Individual experience is the ability of a particle to adjust its velocity and position based on the optimal solutions it has found in its history. Social experience is the particle’s ability to adjust its speed and position by observing the optimal solutions of other particles in its neighborhood. These two types of experience allow particles to retain both individual optimal solutions in the search space and to search globally through group collaboration. In each iteration, the particle evaluates the current solution based on the updated velocity and position and compares it to the optimal solutions found historically. If a better solution is found, the historical optimal solution is updated. The algorithm proceeds iteratively until a stopping condition is met, such as reaching the maximum number of iterations or finding a solution that satisfies the accuracy requirement.
The particle swarm optimization algorithm has better global search ability and convergence speed, and has been proved by the related literature [20,21,22,23,24,25,26] to be suitable for solving various types of optimization problems such as continuous, discrete, and multimodal problems.
In the actual production operation, the enterprise headquarters in the implementation of the production plan the day before the comprehensive consideration of the constraints (plant capacity, distributed PV power generation, production plan, etc.), the particle swarm optimization algorithm is run to solve the optimization model and the results will be fed back to the factories around the factories, factories around the respective provinces of the power trading centers, and distributed PV investors reported to purchase power. As most of the provinces in China’s power market adopt the day-ahead trading method, this trading method requires the power generator to report the power and tariff the day before the power consumption, while the power purchaser only reports the power, i.e., the purchaser is unable to determine the day-ahead trading tariff. Therefore, it is difficult for the enterprise headquarters to determine the next day’s electricity trading price and distributed PV levelized cost of electricity, resulting in a lack of parameters for this optimization model to be solved efficiently. The electricity price prediction model and distributed PV levelized cost of electricity model will be discussed in Section 3 and Section 4. The electricity price prediction model is used to calculate the , and the distributed PV levelized cost of electricity model is used to calculate the based on the equations in Section 2.2.
3. Electricity Price Prediction Model Based on an LSTM Neural Network
At present, China’s electricity market is far less free for market transactions than the electricity markets in the United States, the United Kingdom, and other Western countries due to the constraints of the planned economy. Only a few provinces under the jurisdiction of the State Grid Corporation (SGC) and the Southern Power Grid Corporation (SPGC) have piloted the spot market, and most provinces have adopted the medium- and long-term trading system, supplemented by the day-ahead trading market [27,28,29,30]. Compared with the spot market, the trading price in the day-ahead trading market is more stable, which is more in line with the power trading mode required by the optimal scheduling model of industrial production described in this paper. Therefore, the model established in this paper is an electricity price prediction model in the context of the day-ahead trading mode of the electricity market.
Second, in such a trading context, two factories located in different provinces need to report their grid power purchases one day before the transaction. According to the formula in Section 2.2, since the plant’s daily electricity consumption is a fixed value, the amount of power purchased from the grid is determined by the agreed amount of power. The trading price in the electricity market on the day of the transaction will directly affect the agreed amount of electricity reported by the plant to the distributed PV company. Therefore, an accurate prediction of the trading price in the power market is crucial for off-site industrial production scheduling.
The forecasting of trading prices in electricity markets is essentially a one-dimensional time series forecasting problem [31,32,33]. There are many methods used to solve the time series forecasting problem, including the traditional Autoregressive Integrated Moving Average (ARIMA) model and the Seasonal and Trend Decomposition (STL) model, but these traditional time series forecasting models are only suitable for smooth seasonal and linear forecasting tasks. For more stochastic and volatile power market price forecasting tasks, the traditional time forecasting models are not able to perform well, and the use of neural networks in machine learning is required. Currently, the neural networks applicable to time series prediction problems are Recurrent Neural Network (RNN), Long Short-Term Memory Network (LSTM), Gated Recurrent Unit (GRU), and Transformer and Convolutional Neural Network (CNN) [34,35]. However, the relevant literature [36] illustrates that Transformer and CNN perform poorly in solving time series prediction problems with a small sample size. Further, since the current electricity day-ahead trading market in most provinces of China has been established for too short a period of time, mostly within three years, the sample size of data in respect of the electricity price is too small. Such a data situation will cause the Transformer model and CNN, which need large-scale data support, to perform poorly in the time series prediction problem described in this paper, so this study adopts an improved LSTM neural network structure based on RNN [37,38,39].
The LSTM neural network’s structure is shown in Figure 4; it is different from the traditional LSTM neural network in that the neural network employs the ReLU function. This helps to alleviate the problem of gradient vanishing during information transfer for long sequences, and reduces the redundancy of parameters, improves the generalization ability of the model, and helps the neural network to learn more complex feature representations. In the actual model training, a sequence input layer with a dimension of 40 was set up, followed by an LSTM layer with 20 hidden units, and finally a fully connected layer and a regression output layer.
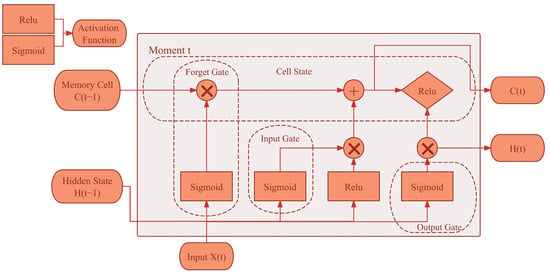
Figure 4.
LSTM neural network structure.
4. Distributed Photovoltaic kWh Cost Model
To evaluate and predict the economic operation of distributed photovoltaic (PV) power generation projects, we used the Net Present Value (NPV) method to calculate the average unit cost of power generation over the entire project cycle [40]. The formula is as follows (See Appendix B for a description of the relevant symbols.)
4.1. Total Cost of the Distributed PV Project
Specifically, the following formula was used to calculate the discounted cost of distributed PV projects
The relevant parameter settings for the formula are shown in Appendix C.
4.2. Total Power Generation over the Project Cycle
Meteorological conditions are critical to distributed PV power generation. Factors such as light duration and temperature will directly affect the power generation efficiency of PV panels. In this study, we utilized the built-in metenorm meteorological database in the PVsyst 7.4.0 software to set up the meteorological sites of the pharmaceutical factory as a reference for meteorological data.
The module mounting type has an important impact on the annual power generation of a PV, and in this paper we will use the module mounting type with seasonally adjustable orientation, and a preset tilt angle of 20 degrees in summer and 50 degrees in winter. The PV array characteristics include, PV modules, inverter selection, operating conditions (temperature), module area, and other major factors that determine the efficiency of the PV array in the array construction planning stage, which has been taken into account in the initial investment costs. This paper will be common in the market 300 Wp photovoltaic modules, and a 30 kWac inverter was used as a preset condition.
In this paper, in respect of predicting the total life cycle power generation, the losses are discussed in several parts such as heat loss, line loss, module quality LID mismatch loss, fouling loss, and IAM loss with aging. Heat loss concerns the field heat loss coefficient, the preset stand type is open, and annual heat loss reaches 3.00%. Line losses for DC loop arrays are defaulted to 1.5%. Total module power loss is preset to 2.8%. LID deterioration due to light irradiation is preset to 2%, and voltage mismatch loss is 0.15%. The annual fouling loss factor is preset to 3%. Among them, the total annual attenuation coefficient of individual PV modules is 3.8%, and the efficiency decrement is carried out year by year through Monte Carlo calculations. The above data are set according to the recognized simulation values of distributed PV industry given by PVsyst software.
The was obtained by summing the annual total power generation forecasts of 25 years output year by year through PVsyst software, respectively.
5. Case Analysis
To validate the off-site industrial production optimization scheduling model established in this study, as well as the corresponding sub-models and algorithms, we conducted fieldwork and research on two factories located in Kunming, Yunnan Province, China, and Binzhou, Shandong Province, China, and obtained relevant data. The Kunming factory in Yunnan Province and the Binzhou factory in Shandong Province mainly produce I.V. preparations, which are produced via automated assembly lines operating 24 h a day. The two factories belong to the same group of companies, whose parent company is a leading pharmaceutical company in China. The electricity consumption of the two pharmaceutical factories is not affected by seasons, climate, and other objective factors, and the electricity consumption is determined only by the production plan. From the perspective of policies of the two provinces, the power trading policies and distributed PV policies of the two provinces are basically the same. From the perspective of PV resources, the two provinces have excellent light conditions and are currently popular provinces for PV investment in China. Combining the above conditions, the computational example is an ideal arithmetical example for the model in this paper.
5.1. Description of the Case System
To reflect the optimal scheduling characteristics of this paper’s model for heterogeneous industrial production, we retrieved the electricity consumption data of the pharmaceutical factories in the two locations for the whole year of 2023 (see Figure 5). The electricity consumption of the pharmaceutical factories in the two locations was summed up to obtain the total electricity consumption data. The optimal scheduling model for heterogeneous industrial production reallocated the total electricity consumption in 2023, which laterally reflected the allocation of the production plan. Therefore, the time horizon of this algorithmic system was 365 days in 2023, and the geographic scope was Kunming, Yunnan, China, and Binzhou, Shandong, China. The related geographic information is shown in Table 1.
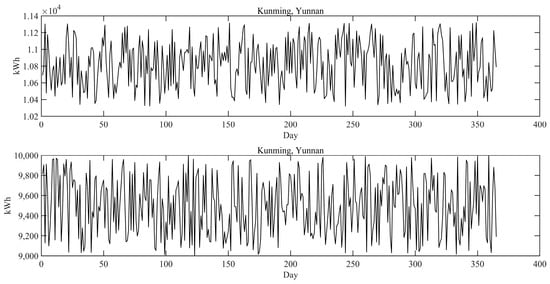
Figure 5.
Electricity consumption of two factories for the whole of 2023.

Table 1.
Related geographic information.
This study researched the energy and electricity tariff policies of Yunnan and Shandong provinces and obtained information on the parameters of the relevant examples. Among them, the distributed PV residual power feed-in price is set according to the local province’s coal-fired benchmark price according to the relevant policy; the industrial electricity price consists of the feed-in tariff, feed-in link line-loss cost, transmission and distribution tariff, system operation cost, governmental funds and surcharges, etc., according to the relevant policy; the agreed tariff is determined according to the average of the local industrial electricity price; and the daily power generation of distributed PV is simulated by the PVsyst software for the first year that electricity generation is derived. The overall parameter settings are shown in Table 2.

Table 2.
Overall parameter settings.
5.2. Description of the Results of the Sub-Model Operations
5.2.1. Distributed Photovoltaic Power Generation
PVsyst software was used to simulate the distributed PV projects. The distributed PV projects in the two locations use roof-mounted, fixed arrays and seasonal tilting systems, which are installed on the largest scale under the premise of ensuring that the PV modules are not shaded. The roof area of Kunming, Yunnan Province, is 20,868 square meters, with an installed PV capacity of 3848 kW, while the roof area of Binzhou, Shandong Province, is 21,520 square meters, with an installed PV capacity of 3967 kW. The total project cycle is 25 years, and the annual power generation is shown in Figure 6. The first year’s electricity generation is shown in Figure 7.
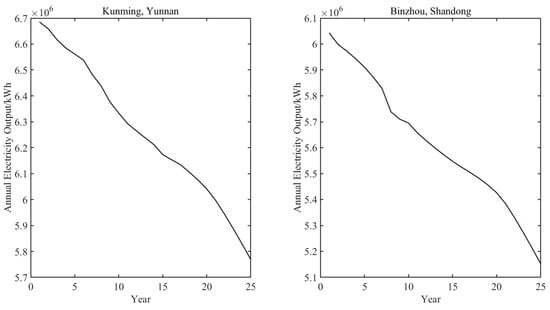
Figure 6.
Annual power generation.
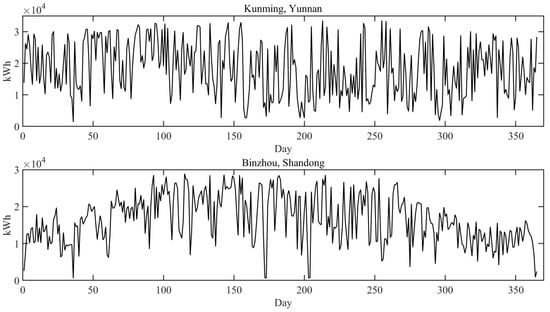
Figure 7.
First year’s electricity generation.
5.2.2. Distributed Photovoltaic Power Generation Costs
According to Equation (7) in Section 4.1, the total cost of distributed PV power generation in the two locations was obtained by substituting the research data, as shown in Table 3.

Table 3.
Total cost of distributed PV power generation.
Combined with the total power generation of the 25-year project cycle simulated using PVsyst software in Section 5.2.1, the unit power generation cost was obtained by dividing the cost of the 25th year in Table 3 by the total power generation. The final calculation results were 0.1741 RMB/kWh for Kunming in Yunnan Province and 0.1996 RMB/kWh for Binzhou in Shandong Province.
5.2.3. Results of Tariff Forecasts
Electricity price data for the two provinces in 2023 were used separately to train neural networks applicable to electricity trading in the provinces. A total of 70% of the data was selected as the training set, and the remaining 30% of the data was used as the test set. The model training was undertaken using CPU (AMD Ryzen 7-5800H 4.4 GHz), GPU (NVIDIA GeForce RTX 3060 6 GB), RAM memory (16 GB), Windows Operating System, and the MATLAB R2023b software environment. The maximum number of training iterations was set to 4800, and the total number of learnable parameters reached 4900. It took 51 s to complete the model training for Yunnan Province, and 36 s to complete the model training for Shandong Province. The final standardized root-mean-squared error for Yunnan Province was about 0.06. The final standardized root-mean-squared error for Yunnan Province was about 0.05.
The training and test set prediction results for Yunnan Province are shown in Figure 8, and the training and test set prediction results for Shandong Province are shown in Figure 9.
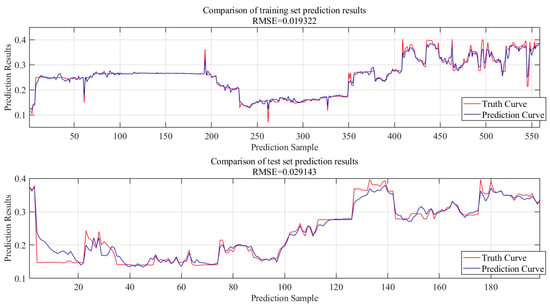
Figure 8.
Training and test set prediction results for Yunnan Province.
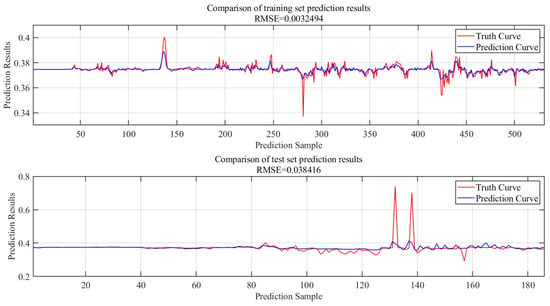
Figure 9.
Training and test set prediction results for Shandong Province.
In order to better show the prediction ability of the LSTM neural network, we iteratively predicted the electricity prices of Yunnan and Shandong provinces in the next 40 days. The prediction results are shown in Figure 10.
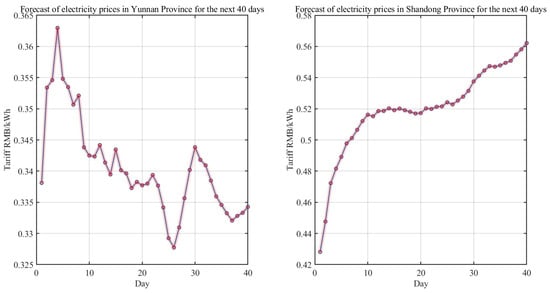
Figure 10.
Forecast of electricity prices in two provinces for the next 40 days.
5.3. Results
Combining the research data in Section 5.1 and the sub-model solution data in Section 5.2, the optimized electricity cost for the two pharmaceutical factories in 2023 was calculated using the integrated optimization model. In particular, to better test the effectiveness of the LSTM algorithm in predicting the electricity price, the predicted electricity price for the last 40 days in Section 4.2 was substituted for the day-ahead market traded electricity price for the last 40 days in 2023(see Figure 11). The solution was then performed. The software runtime environment for the solution was MATLAB and the solver used was the particle swarm optimization algorithm toolbox. The optimized electricity consumption and agreed electricity of the pharmaceutical factory in Yunnan Province are shown in Figure 12, and the optimized electricity consumption and agreed electricity of the pharmaceutical factory in Shandong Province are shown in Figure 13. Figure 12 and Figure 13 represent the allocation of the electricity consumption plan for pharmaceutical plants in 2023 after optimization by the scheduling model in this paper. Since the electricity price in Yunnan Province is generally lower than that in Shandong Province, the optimized model may allocate more production tasks to the pharmaceutical factory in Yunnan Province. From the theoretical analysis, the optimized simulation structure meets the theoretical expectation.
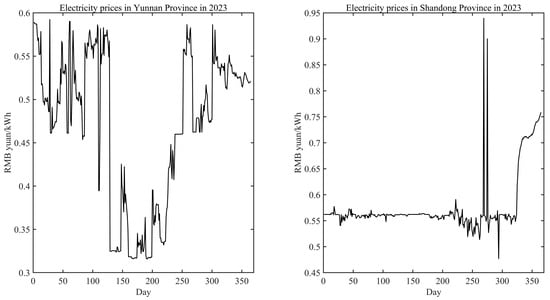
Figure 11.
Replacement 2023 tariff.
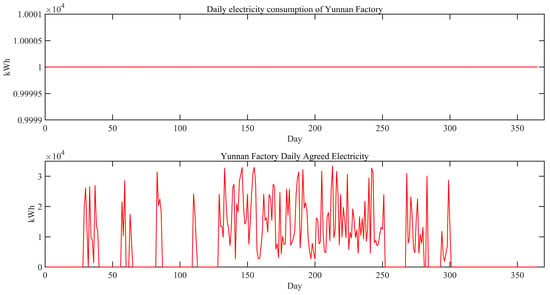
Figure 12.
The optimized electricity consumption and agreed electricity in Yunnan Province.
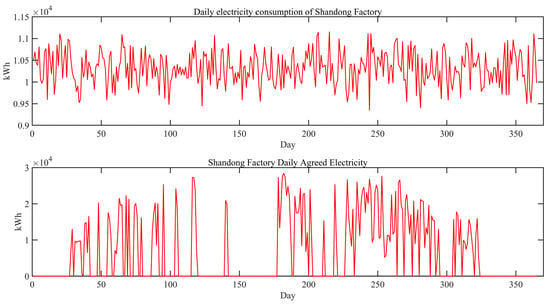
Figure 13.
Optimized electricity consumption and agreed electricity in Shandong Province.
The electricity cost before and after optimization for the whole year in the two provinces is shown in Figure 14. The electricity tariff before optimization was calculated according to the full use of distributed PV power generation by the pharmaceutical plant, and the pharmaceutical plant will only purchase power from the grid when the distributed PV power generation is not enough to meet the power consumption of the pharmaceutical plant. It is easy to see from Figure 14 that there is a significant decrease in the total electricity cost after optimization compared with the pre-optimization period. The total electricity cost before optimization is RMB 3,874,600, and the total electricity cost after optimization is RMB 3,590,800, which represents a decrease of about 7.9%.
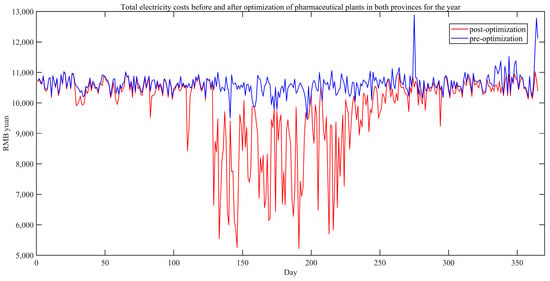
Figure 14.
Total electricity costs before and after optimization in 2023.
6. Conclusions
In summary, the off-site industrial production scheduling optimization model for enterprises established in this paper can reduce the total electricity cost of enterprises in the example data by 7.9%. This indicates that this model can significantly reduce the cost of off-site electricity consumption on the demand side of electricity.
This study has resulted in the following innovations:
(1) A new master–slave game relationship was proposed, with industrial and commercial users as leaders and distributed PV companies as followers. (2) An enterprise off-site industrial production optimization scheduling model was established, which can significantly reduce the cost of electricity for enterprises. (3) The particle swarm optimization algorithm and LSTM neural network were integrated into the large model with excellent results.
Of course, the optimization model also has certain limitations:
(1) It simplifies the actual industrial production process and does not consider the logistics scheduling cost between different locations. (2) The feed-in tariff for distributed PV residual power is calculated according to the coal-fired benchmark price, and does not take into account the pilot transaction of China’s green power market. (3) The environmental protection benefits are not considered, and the carbon emission right trading benefits are not calculated.
This model will provide theoretical support for the construction of integrated energy systems in off-site industrial parks in the future, empowering the development of the industry at the demand-side level of electricity.
Author Contributions
Conceptualization, P.W. and S.X.; methodology, S.X.; software, S.X. and Y.L.; validation, P.W., S.X. and Y.L.; formal analysis, S.X. and Y.L.; investigation, S.X.; data curation, S.X.; writing—original draft preparation, S.X.; writing—review and editing, P.W., S.X. and Y.L. All authors have read and agreed to the published version of the manuscript.
Funding
This work was partially supported by the Innovation and Entrepreneurship Training Program for College Students of North China Electric Power University (202301019) and Chengdu Silicoms Technology Co., LTD.
Data Availability Statement
The data set can be obtained by contacting the corresponding author. The data are not publicly available due to the fact that experimental data are confidential. The geographic coordinates mentioned in this paper are not accurate due to confidentiality requirements. The data in the tariff section come from the Kunming Power Exchange Center (https://www.kmpex.com accessed on 1 January 2023) and the Shandong Power Exchange Center (https://pmos.sd.sgcc.com.cn accessed on 1 January 2023).
Conflicts of Interest
All authors declare that the research was conducted in the absence of any commercial or financial relationships that could be construed as a potential conflict of interest.
Appendix A
Appendix A shows the notation for the equations in Section 2.2.
| Notation | Explanation |
| Daily electricity consumption of the th plant | |
| Daily agreed electricity of the th plant | |
| Daily grid purchase of electricity for the th plant | |
| Daily surplus electricity feed-in for the th plant | |
| Distributed photovoltaic power generation per day | |
| Agreed tariffs | |
| Feed-in tariff for surplus electricity | |
| Price of electricity for industrial use in the th plant | |
| Daily cost of electricity consumed by the th plant | |
| Distributed PV daily revenue | |
| Minimum daily income from distributed PV with guaranteed ROI | |
| Minimum daily revenue per for distributed PV with guaranteed ROI | |
| Maximum daily electricity consumption of the th plant (maximum capacity) |
Appendix B
Appendix B shows the notation for the equations in Section 4.
| Notation | Explanation |
| Distributed PV kWh cost | |
| Total cost of the distributed PV project | |
| Total power generation over the project cycle | |
| Initial investment cost of the PV system | |
| Annual operation and maintenance cost rate | |
| Insurance premium rate (assumed to be a fixed percentage to simplify the evaluation process) | |
| Representative of the annual interest expense due to the loan | |
| Discount rate | |
| Period of the investment |
Appendix C
Appendix C shows the source of the data setting for this article.
is the discount rate, which is taken to be 8.5% according to the provision of the “Financial Benchmark Returns of Construction Projects” of the National Development and Reform Commission of China.
Initial investment cost () is the total cost to be paid at the beginning of the project, the initial full investment in China’s commercial and industrial distributed PV systems mainly consists of the purchase of PV modules, installation of electrical equipment, etc. This cost is a one-time payment, which is not affected by time during the entire project cycle, and therefore does not need to be discounted. The full investment cost of China’s commercial and industrial distributed PV systems in 2022 is 3.74 RMB/W. The operation and maintenance expense () is taken to be 1% of the initial investment cost (), the distributed PV long-term loan interest rate () is 6.5%, the insurance premium rate () is taken to be 0.1% of the initial investment cost (), and the initial investment cost () is taken to be the base model of 20% of own funds and 80% of the bank loan. All of the above data sources can be found at this website: https://www.in-en.com/.
The relevant data in Table 2 are from the National Development and Reform Commission of China.
References
- Pan, W.J.; Zhang, Y.; Jin, W.W.; Liang, Z.D.; Wang, M.N.; Li, Q.Q. Photovoltaic-Based Residential Direct-Current Microgrid and Its Comprehensive Performance Evaluation. Appl. Sci. 2023, 13, 12890. [Google Scholar] [CrossRef]
- Tong, L.; Geng, Y.; Zhang, Y.Y.; Zhang, Y.; Wang, H. Testing the effectiveness of deploying distributed photovoltaic power systems in residential buildings: Evidence from rural China. Environ. Impact Assess. Rev. 2024, 104, 107300. [Google Scholar] [CrossRef]
- Zhang, L.F.; Yu, J.Y.; Shi, Q.Y.; Kong, Q. An evaluation of the economic benefits of rooftop distributed photovoltaic projects in the whole county in China. J. Cleaner Prod. 2023, 432, 139744. [Google Scholar] [CrossRef]
- Hong, J.H.; Zhang, L.Y.; Hu, Z.D.; Lin, W.W.; Zou, Y.C. A robust system model for the photovoltaic in industrial parks considering photovoltaic uncertainties and low-carbon demand response. Front. Energy Res. 2024, 12, 1343309. [Google Scholar] [CrossRef]
- Timilsina, G.R. The economics of deploying distributed solar photovoltaics in developing countries: Some insights from an analysis for Bangladesh. Energy Sustain. Dev. 2022, 70, 247–258. [Google Scholar] [CrossRef]
- Xue, L.Y.; Liu, J.L.; Lin, X.J.; Li, M.Y.; Kobashi, T. Assessing urban rooftop PV economics for regional deployment by integrating local socioeconomic, technological, and policy conditions. Appl. Energy 2024, 353, 122058. [Google Scholar] [CrossRef]
- Cai, T.T.; Dong, M.Y.; Chen, K.; Gong, T.R. Methods of participating power spot market bidding and settlement for renewable energy systems. Energy Rep. 2022, 8, 7764–7772. [Google Scholar] [CrossRef]
- Lu, T.; Zhang, W.G.; Ding, X.W. Operation Strategy of Electricity Retailers Based on Energy Storage System to Improve Comprehensive Profitability in China’s Electricity Spot Market. Energies 2021, 14, 6424. [Google Scholar] [CrossRef]
- Qi, L.L.; Lin, X.Y.; Shi, X.L.; Zhang, Y.Q.; Pan, H.R.; Sharp, B. Feed-in tariffs and the carbon emission trading scheme under China’s peak emission target: A dynamic CGE analysis for the development of renewable electricity. J. Environ. Manag. 2023, 335, 117535. [Google Scholar] [CrossRef]
- Zhang, X.P.; Feng, S.D.; Zhang, H.N.; Yuan, J.H. Developing Distributed PV in Beijing: Deployment Potential and Economics. Front. Energy Res. 2020, 7, 155. [Google Scholar] [CrossRef]
- Alzahrani, A.M.; Zohdy, M.; Yan, B. An Overview of Optimization Approaches for Operation of Hybrid Distributed Energy Systems with Photovoltaic and Diesel Turbine Generator. Electr. Power Syst. Res. 2021, 191, 106877. [Google Scholar] [CrossRef]
- He, H.Y.; Luo, Z.; Wang, Q.; Chen, M.X.; He, H.Q.; Gao, L.J.; Zhang, H.X. Joint Operation Mechanism of Distributed Photovoltaic Power Generation Market and Carbon Market Based on Cross-Chain Trading Technology. IEEE Access 2020, 8, 66116–66130. [Google Scholar] [CrossRef]
- Hou, P.; Yang, G.Y.; Hu, J.J.; Douglass, P.J.; Xue, Y.S. A Distributed Transactive Energy Mechanism for Integrating PV and Storage Prosumers in Market Operation. Engineering 2022, 12, 171–182. [Google Scholar] [CrossRef]
- Jiang, S.F.; Wan, C.; Chen, C.; Cao, E.B.; Song, Y.H. Distributed Photovoltaic Generation in the Electricity Market: Status, Mode and Strategy. IEEE J. Power Energy Syst. 2018, 4, 263–272. [Google Scholar] [CrossRef]
- Ma, W.W.; Fang, S.; Liu, G. Hybrid optimization method and seasonal operation strategy for distributed energy system integrating CCHP, photovoltaic and ground source heat pump. Energy 2017, 141, 1439–1455. [Google Scholar] [CrossRef]
- Schwidtal, J.M.; Agostini, M.; Coppo, M.; Bignucolo, F.; Lorenzoni, A. Optimized operation of distributed energy resources: The opportunities of value stacking for Power-to-Gas aggregated with PV. Appl. Energy 2023, 334, 120646. [Google Scholar] [CrossRef]
- Yang, S.X.; Wang, X.F.; Yang, Y.G.; Li, J.L. Bi-level planning model of distributed PV-energy storage system connected to distribution network under the coordinated operation of electricity-carbon market. Sustain. Cities Soc. 2023, 89, 104347. [Google Scholar] [CrossRef]
- Yu, J.C.; Wu, L.; Yao, C.; Chen, J.; Li, S.Y.; Ma, X.F. A Review of Distributed PV Operation Analysis and Demand Response Research. In Proceedings of the 3rd Asia Conference on Power and Electrical Engineering (ACPEE), Kitakyushu, Japan, 22–24 March 2018. [Google Scholar]
- Zhang, Q.; Chen, L.; Li, X.; Mei, S. Optimization decision of purchasing and selling power between industrial park operators and distributed optical storage users based on Stackelberg game. Acta Energ. Sol. Sin. 2024, 45, 450–456. [Google Scholar]
- Gad, A.G. Particle Swarm Optimization Algorithm and Its Applications: A Systematic Review. Arch. Comput. Methods Eng. 2022, 29, 2531–2561. [Google Scholar] [CrossRef]
- Liu, Y.Y.; Dai, J.J.; Zhao, S.S.; Zhang, J.H.; Shang, W.D.; Li, T.; Zheng, Y.C.; Lan, T.; Wang, Z.Y. Optimization of five-parameter BRDF model based on hybrid GA-PSO algorithm. Optik 2020, 219, 164978. [Google Scholar] [CrossRef]
- Pan, J.H.; Wang, H.; Yang, X.G. A Random Particle Swarm Optimization Algorithm with Application. In Proceedings of the 2nd International Conference on Chemical, Material and Metallurgical Engineering (ICCMME 2012), Kunming, China, 15–16 December 2012. [Google Scholar]
- Qu, L.P.; Meng, Y.; Li, D.H.; Xue, H.B.; Soc, I.C. A Quantum Particle Swarm Optimization Algorithm with Available Transfer Capability. In Proceedings of the 19th International Symposium on Distributed Computing and Applications for Business Engineering and Science (DCABES), Xuzhou, China, 16–19 October 2020. [Google Scholar]
- Shami, T.M.; El-Saleh, A.A.; Alswaitti, M.; Al-Tashi, Q.; Summakieh, M.A.; Mirjalili, S. Particle Swarm Optimization: A Comprehensive Survey. IEEE Access 2022, 10, 10031–10061. [Google Scholar] [CrossRef]
- Thirunavukkarasu, M.; Sawle, Y.; Lala, H. A comprehensive review on optimization of hybrid renewable energy systems using various optimization techniques. Renew. Sustain. Energy Rev. 2023, 176, 113192. [Google Scholar] [CrossRef]
- Yang, X.J.; Jiao, Q.J.; Liu, X.K. Center Particle Swarm Optimization Algorithm. In Proceedings of the IEEE 3rd Information Technology, Networking, Electronic and Automation Control Conference (ITNEC), Chengdu, China, 15–17 March 2019. [Google Scholar]
- Hao, Z.; Hai, L.; Enbo, L.; Yanting, H.; Zhi, W.; Chong, T.; Wenmeng, Z.; Guo, X. Research on power trade potential and power balance between Lancang-Mekong countries and southern China under long-term operation simulation. Front. Energy Res. 2023, 11, 1109254. [Google Scholar] [CrossRef]
- Hu, B.; Zhou, P. Can the renewable power consumption guarantee mechanism help activate China’s power trading market? Energy 2022, 253, 124182. [Google Scholar] [CrossRef]
- Wu, Q.L.; Zhang, S.S.; Zhou, B.Z. Research and application of power market trading index system for power generation enterprises. Energy Rep. 2022, 8, 270–274. [Google Scholar] [CrossRef]
- Yang, S.; Chen, K.N.; Li, M.; Qu, Y.Y.; Wu, Z.C.; Zhang, X.X. Typical Cohesion Modes of Foreign Long-Term Power Market with Spot Market and Implications for China. In Proceedings of the 5th International Conference on Advances in Energy Resources and Environment Engineering (ICAESEE), Chongqing, China, 6–8 December 2019. [Google Scholar]
- Jiang, H.Y.; Fu, Y.Y.; Ge, Q.B. Overview of Bidding Strategies Based on Electricity Price Forecast for Generation Side under New Electricity Reform. In Proceedings of the 35th Youth Academic Annual Conference of Chinese-Association-of-Automation (YAC), Zhanjiang, China, 16–18 October 2020. [Google Scholar]
- Lyu, Z.; Wang, Y.S.; Wang, J.Y.; Zhang, L.; Shen, J.; Wang, X. Short-term electricity price forecasting G-LSTM model and economic dispatch for distribution system. In Proceedings of the 4th International Conference on Energy Engineering and Environmental Protection (EEEP), Xiamen, China, 19–21 November 2019. [Google Scholar]
- Matsumoto, T.; Endo, M. Electricity price forecast based on weekly weather forecast and its application to arbitrage in the forward market. In Proceedings of the 11th International Conference on Power, Energy and Electrical Engineering (CPEEE), Electr Network, Shiga, Japan, 26–28 February 2021. [Google Scholar]
- Bouktif, S.; Fiaz, A.; Ouni, A.; Serhani, M.A. Optimal Deep Learning LSTM Model for Electric Load Forecasting using Feature Selection and Genetic Algorithm: Comparison with Machine Learning Approaches. Energies 2018, 11, 1636. [Google Scholar] [CrossRef]
- Torres, J.F.; Hadjout, D.; Sebaa, A.; Martínez-alvarez, F.; Troncoso, A. Deep Learning for Time Series Forecasting: A Survey. Big Data 2021, 9, 3–21. [Google Scholar] [CrossRef] [PubMed]
- Khan, A.; Raufu, Z.; Sohail, A.; Khan, A.R.; Asif, H.; Asif, A.; Farooq, U. A survey of the vision transformers and their CNN-transformer based variants. Artif. Intell. Rev. 2023, 56 (Suppl. 3), S2917–S2970. [Google Scholar] [CrossRef]
- Ewees, A.A.; Al-qaness, M.A.A.; Abualigah, L.; Abd Elaziz, M. HBO-LSTM: Optimized long short term memory with heap-based optimizer for wind power forecasting. Energy Convers. Manag. 2022, 268, 116022. [Google Scholar] [CrossRef]
- Huang, X.Q.; Li, Q.; Tai, Y.H.; Chen, Z.Q.; Liu, J.; Shi, J.S.; Liu, W.M. Time series forecasting for hourly photovoltaic power using conditional generative adversarial network and Bi-LSTM. Energy 2022, 246, 123403. [Google Scholar] [CrossRef]
- Peng, L.; Liu, S.; Liu, R.; Wang, L. Effective long short-term memory with differential evolution algorithm for electricity price prediction. Energy 2018, 162, 1301–1314. [Google Scholar] [CrossRef]
- Wang, Y.; He, J.J.; Chen, W.Y. Distributed solar photovoltaic development potential and a roadmap at the city level in China. Renew. Sust. Energ. Rev. 2021, 141, 110772. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).