Numerical Investigation on the Solar Absorption Performance of Plasmonic Nanoparticles in the Focused Electric Field
Abstract
1. Introduction
2. Materials and Methods
3. Results and Discussion
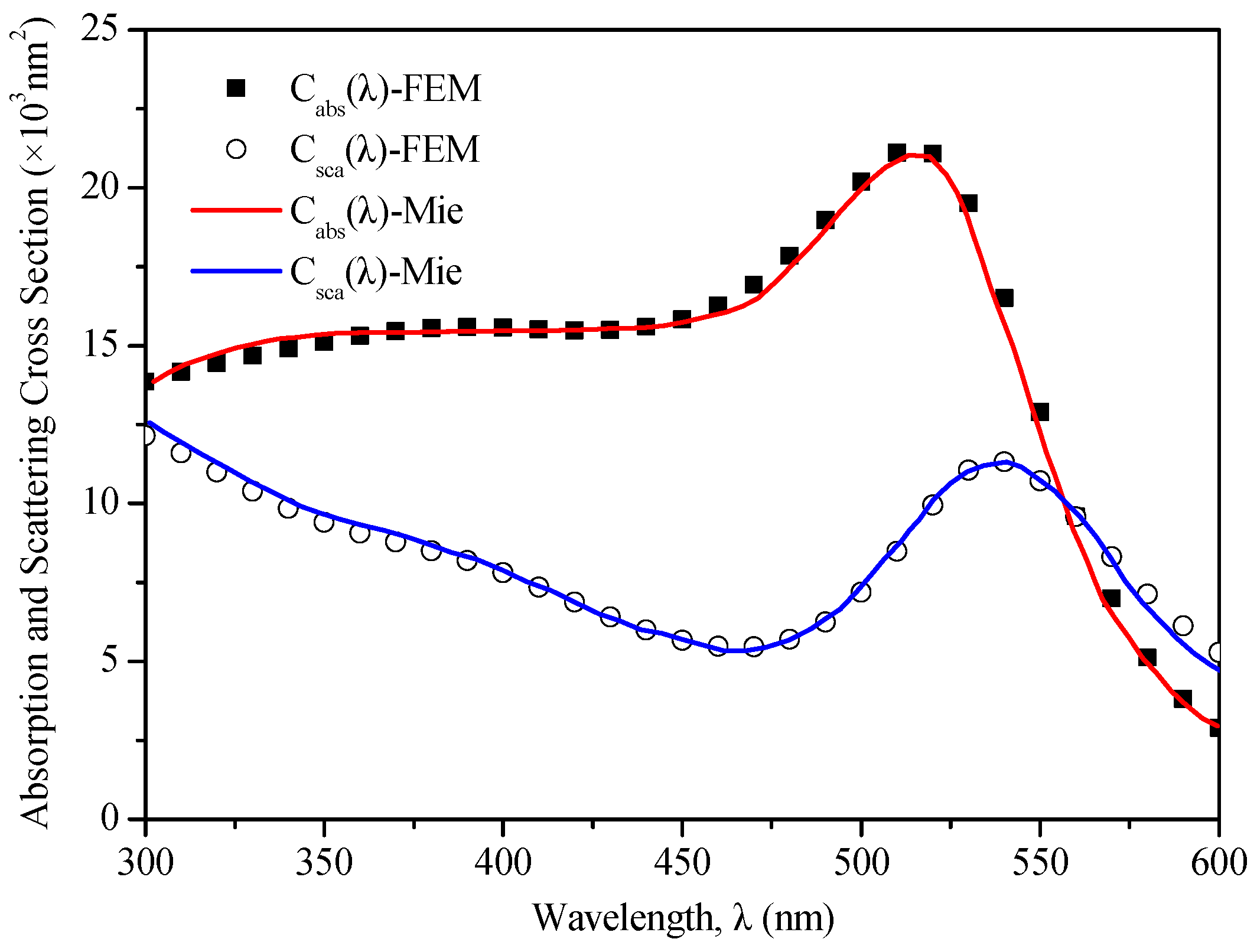
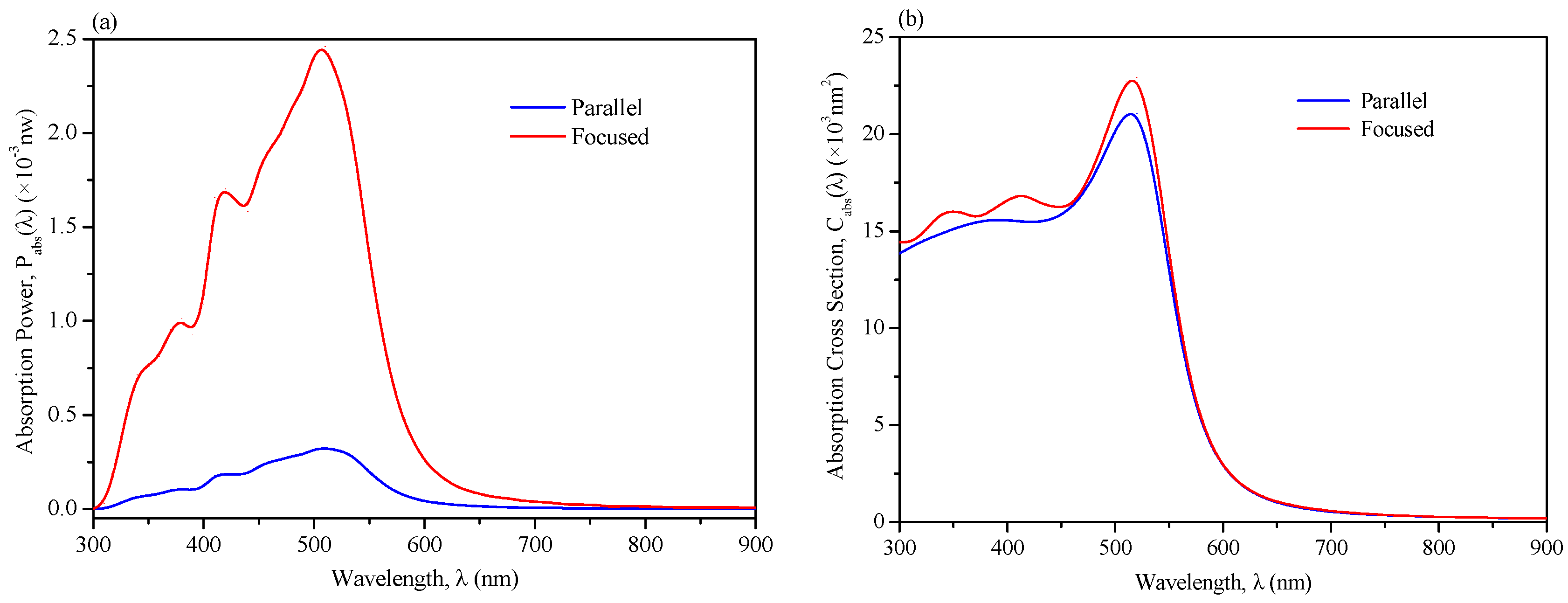
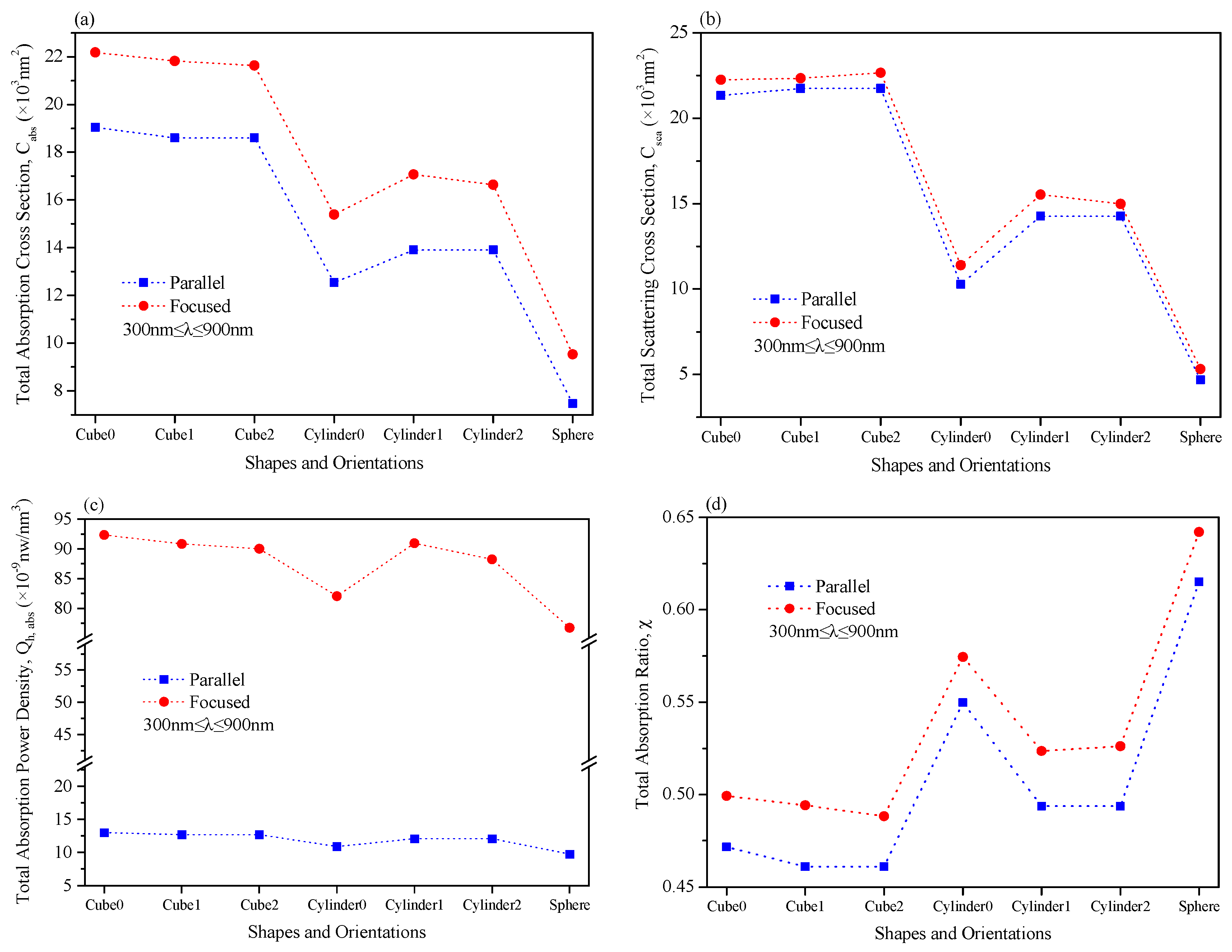
3.1. Optical Properties of a Single Plasmonic Nanoparticle in the Parallel and Focused Electric Fields
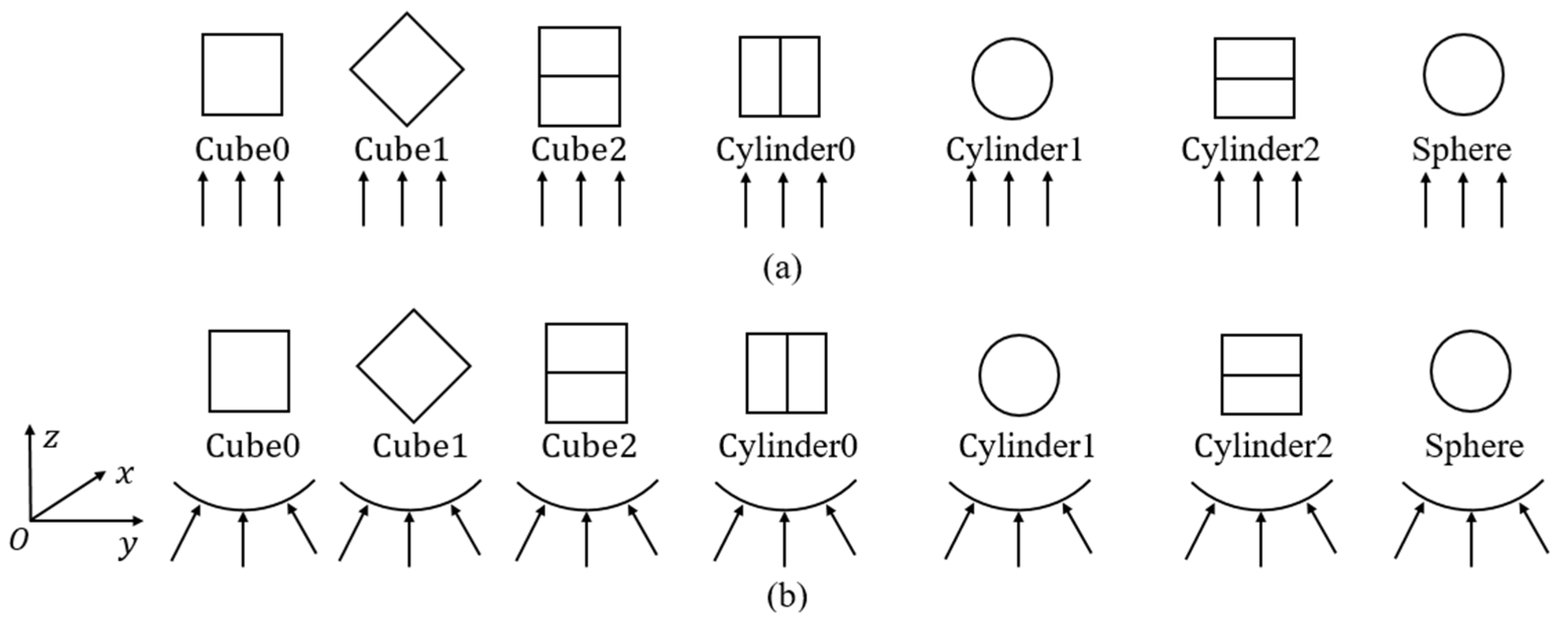
| Shapes | Feature Length | Label | (W/m2) | Orientations |
|---|---|---|---|---|
| Cube | The length of the side is 100 nm. | Cube 0 | 683.65 | As seen in Figure 4 |
| Cube 1 | ||||
| Cube 2 | ||||
| Cylinder | Both the diameter and height are 100 nm. | Cylinder 0 | ||
| Cylinder 1 | ||||
| Cylinder 2 | ||||
| Sphere | The diameter is 100 nm. | Sphere |
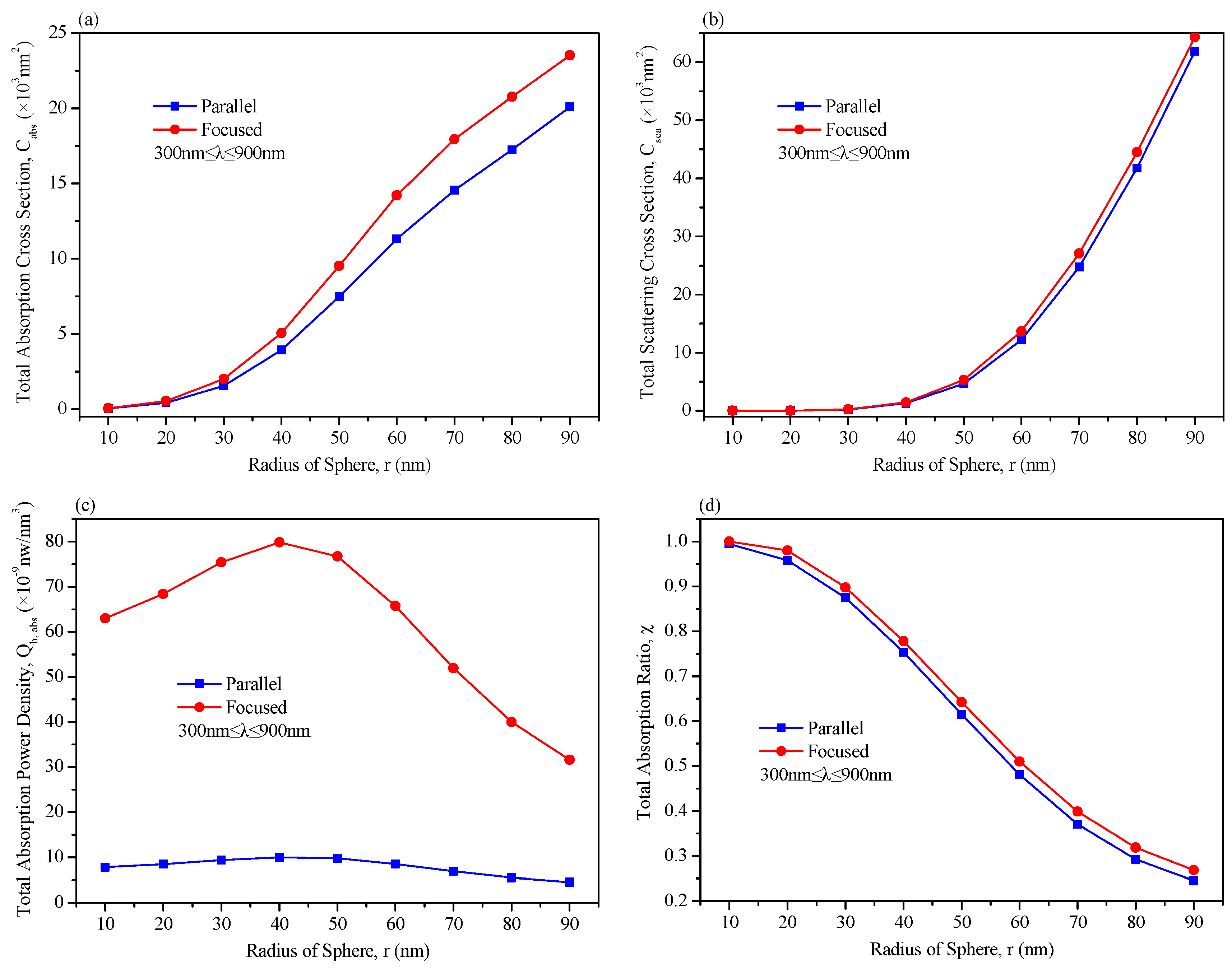
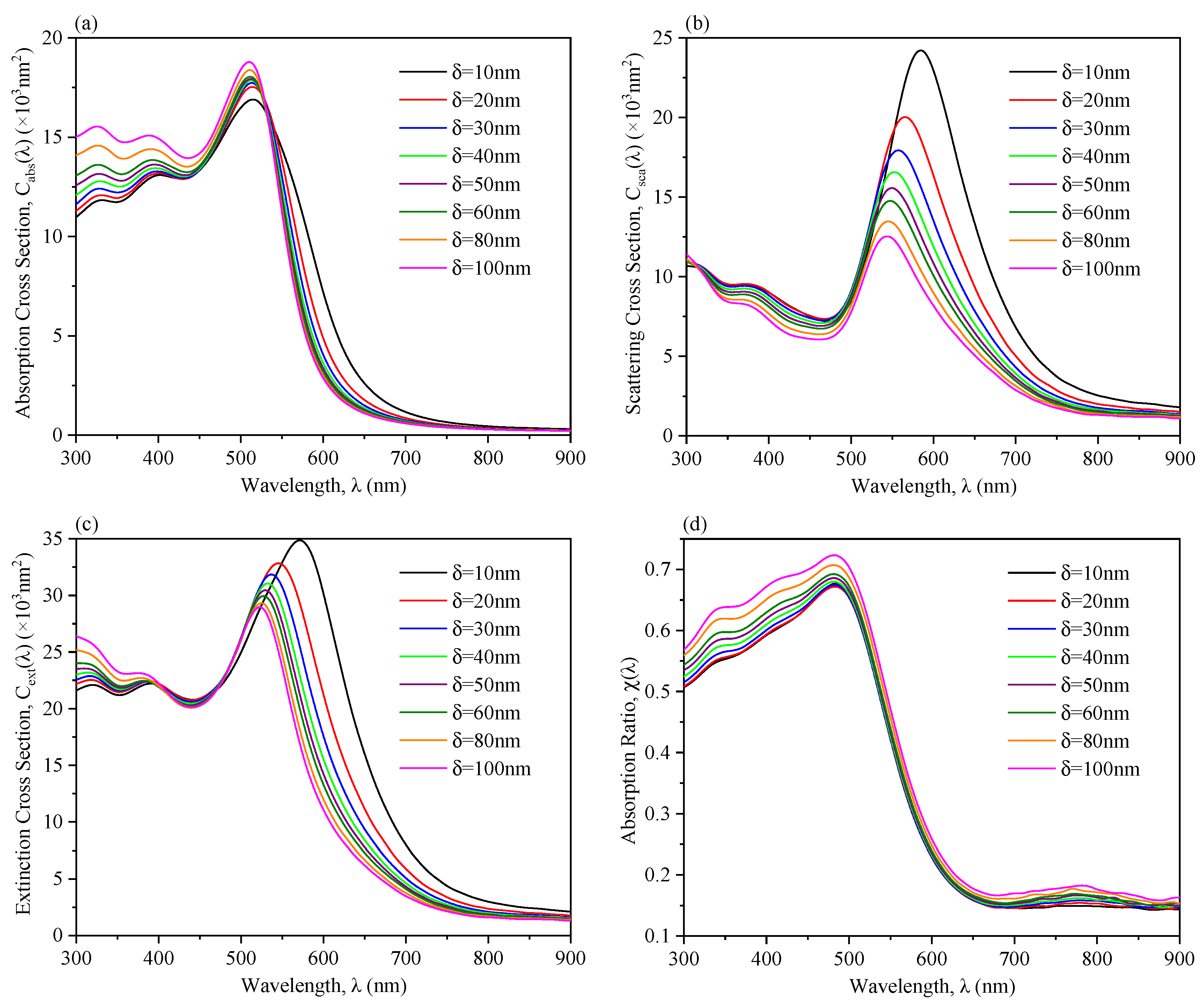
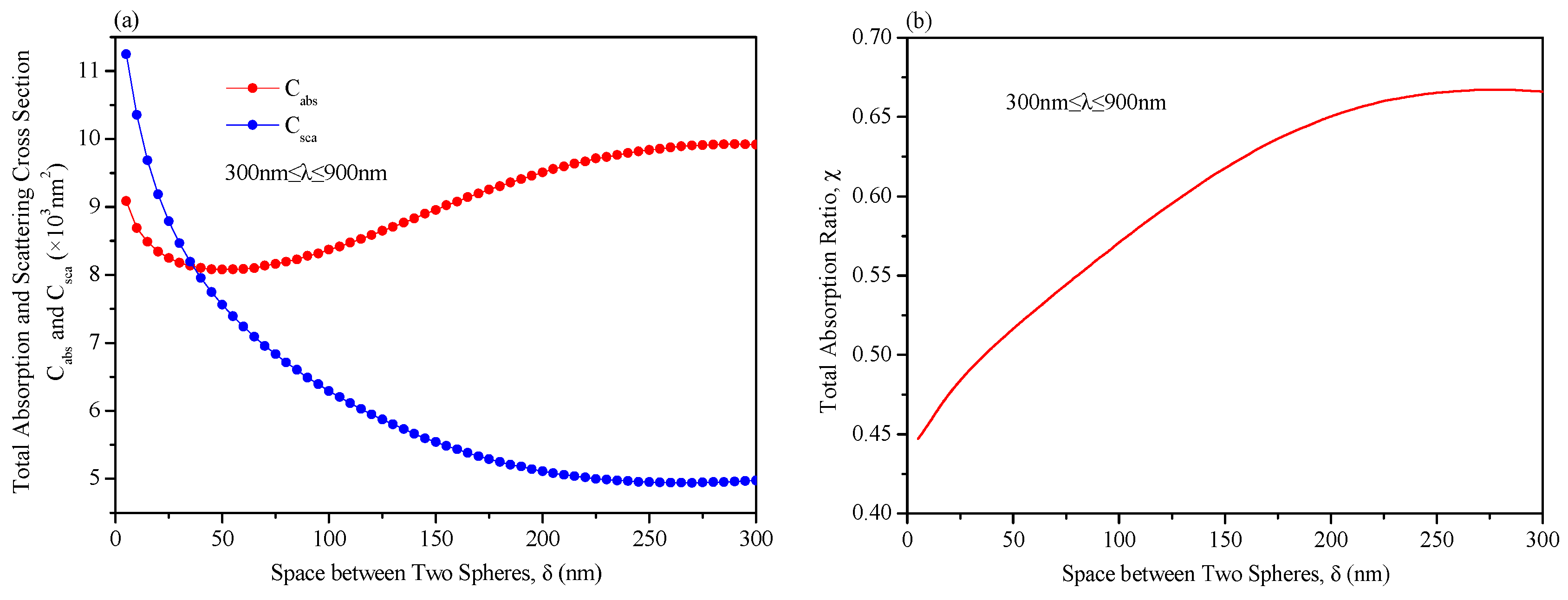
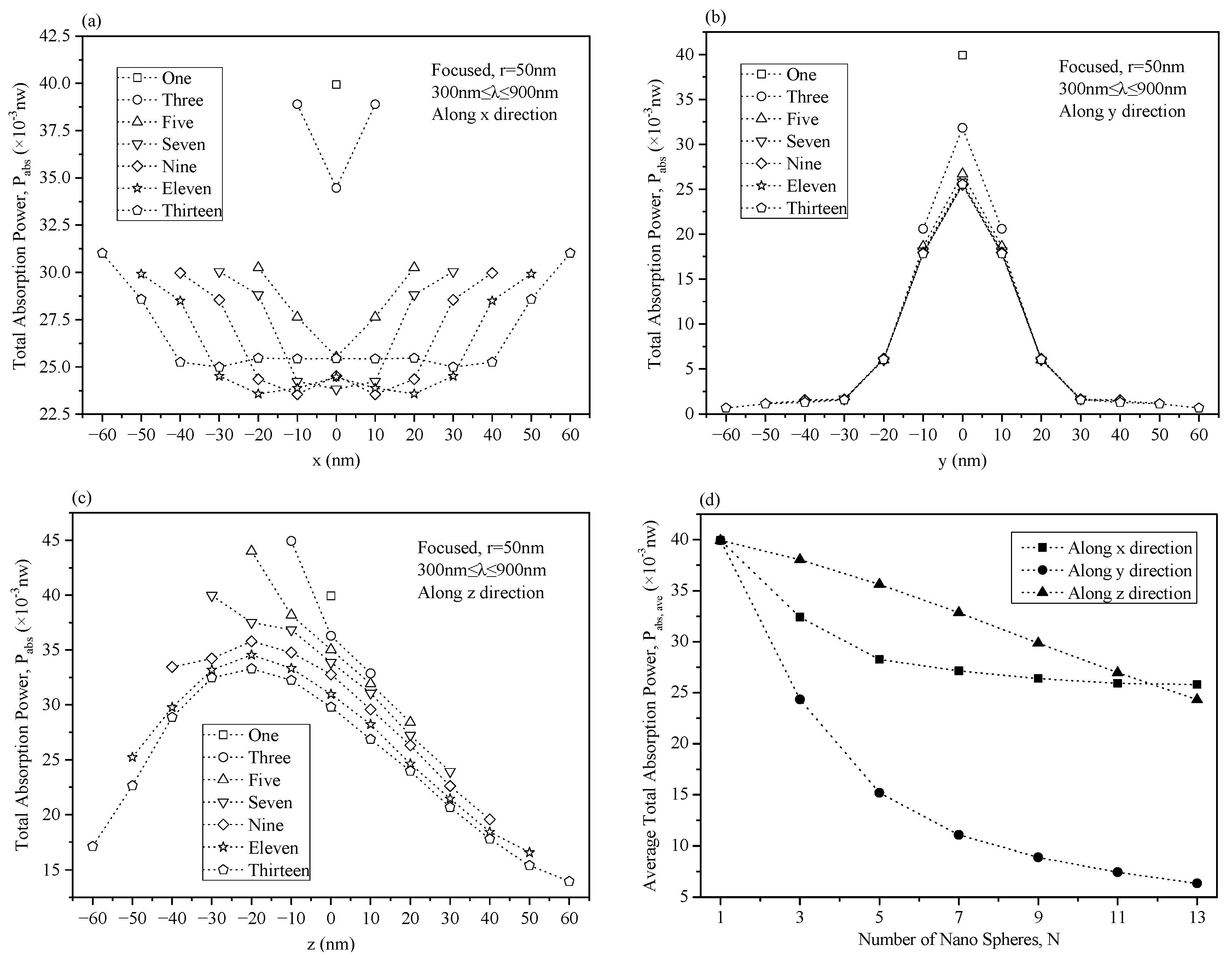
3.2. Optical Properties of Multi-Plasmonic Nanoparticles in the Focused Electric Field
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Song, J.; Wang, W.; Niu, Y.; Wang, J.; Yu, H. A note of optical error diagnosis of parabolic trough concentrator based on flux image. Sol. Energy 2020, 197, 359–362. [Google Scholar] [CrossRef]
- Fend, T.; Wenzel, K. Optical flux measurements in the focal area of a parabolic trough concentrator. J. Phys. IV 1999, 9, 605–609. [Google Scholar] [CrossRef]
- Gharat, P.V.; Bhalekar, S.S.; Dalvi, V.H.; Panse, S.V.; Deshmukh, S.P.; Joshi, J.B. Chronological development of innovations in reflector systems of parabolic trough solar collector (PTC)—A review, Renew. Sustain. Energy Rev. 2021, 145, 111002. [Google Scholar] [CrossRef]
- Sallaberry, F.; Pujol-Nadal, R.; Perers, B. Optical losses due to tracking Misalignment on linear concentrating solar thermal collectors. In Proceedings of the Euro Sun 2016, Palma de Mallorca, Spain, 11–14 October 2016; International Solar Energy Society: Freiburg, Germany, 2016; pp. 1–12. [Google Scholar]
- Sallaberry, F.; Pujol-Nadal, R.; Larcher, M.; Rittmann-Frank, M.H. Direct tracking error characterization on a single-axis solar tracker. Energy Convers. Manag. 2015, 105, 1281–1290. [Google Scholar] [CrossRef]
- Stanek, B.; Wecel, D.; Bartela, L.; Rulik, S. Solar tracker error impact on linear absorbers efficiency in parabolic trough collector-Optical and thermodynamic study. Renew. Energy 2022, 196, 598–609. [Google Scholar] [CrossRef]
- Unger, B.L.; Schmidt, G.R.; Moore, D.T. Dimpled Planar Lightguide Solar Concentrators. In Proceedings of the International Optical Design Conference (IODC) and Optical Fabrication and Testing (OF&T), Jackson Hole, WY, USA, 13–17 June 2010; Optical Society of America: Washington, DC, USA, 2010; p. ITuE5P. [Google Scholar]
- Karp, J.H.; Tremblay, E.J.; Hallas, J.M.; Ford, J.E. Orthogonal and secondary concentration in planar micro-optic solar collectors. Opt. Express 2011, 19, A673–A685. [Google Scholar] [CrossRef]
- Svanbaev, E.; Mukhametkali, B.; Komesh, T.; Bekbolatov, Y.; Omirgali, A. Planar multicollector solar concentrator. In Proceedings of the International Conference on Natural Resource Management: Mechanics, Energy, Environment, Al-Ain, Abu-Dhabi, United Arab Emirates, 24–27 February 2013; pp. 215–219. [Google Scholar]
- Rudnitsky, A.; Zaban, A.; Zalevsky, Z. Passive high ratio sunlight concentration configurations. J. Europ. Opt. Soc. Rap. Public. 2013, 8, 13033. [Google Scholar] [CrossRef]
- Pan, J.W.; Su, Y.C.; Lee, S.Y. Optimized planar micro-optic concentrator design. J. Opt. 2016, 18, 065901. [Google Scholar] [CrossRef]
- Pesala, B. Planar Solar Concentrators using Subwavelength Gratings. In Proceedings of the Frontiers in Optics (FiO) 2011 and Laser Science (LS) XXVII Technical Digest, Optical Society of America and American Physical Society, San Jose, CA, USA, 16–20 October 2011; p. FWZ3. [Google Scholar]
- Komar, P.; Gębski, M.; Czyszanowski, T.; Dems, M.; Wasiak, M. Planar focusing reflectors based on monolithic high contrast gratings: Design procedure and comparison with parabolic mirrors. Opt. Express 2020, 28, 38745–38761. [Google Scholar] [CrossRef]
- Zhang, C.; Zhan, Y.; Qiu, Y.; Xu, L.; Guan, J. Planar metasurface-based concentrators for solar energy harvest from theory to engineering. PhotoniX 2022, 3, 28. [Google Scholar] [CrossRef]
- Hsu, L.; Dupré, M.; Ndao, A.; Kanté, B. From parabolic-trough to metasurface-concentrator assessing focusing in the wave-optics limit. Opt. Lett. 2017, 42, 1520–1523. [Google Scholar] [CrossRef] [PubMed]
- Ding, Q.; Jacobs, K.; Choubal, A.; Mensing, G.; Zhang, Z.; Tirawat, R.; Zhu, G.; Wendelin, T.; Guo, L.J.; Ferreira, P.; et al. A Simple Planar Focusing Collector for Concentrated Solar Power Applications. In Proceedings of the Optics for Solar Energy: Light, Energy and the Environment (E2, P.V., SOLAR, SSL), Boulder, CO, USA, 6–9 November 2017; Optical Society of America: Washington, DC, USA, 2017; p. RM2C.3. [Google Scholar]
- Qing, D.; Aakash, C.; Kimani, T. Design of a Nanopatterned Long Focal-Length Planar Focusing collector for concentrated solar power. In Proceedings of the Society of Photo-Optical Instrumentation Engineers (SPIE) Conference Series: Photonic and Phononic Properties of Engineered Nanostructures VII, San Francisco, CA, USA, 20 February 2017; p. 10112. [Google Scholar]
- Ding, Q.; Barna, S.; Jacobs, K.; Choubal, A.; Mensing, G.; Zhang, Z.; Yamada, K.; Tirawat, R.; Kincaid, N.; Zhu, G.; et al. A Metasurface-inspired Focusing Collector for Concentrated Solar Power Applications. In Proceedings of the OSA Frontiers in Optics/Laser Science, Washington, DC, USA, 20 September 2018; p. JTu3A.14. [Google Scholar]
- Ding, Q.; Barna, S.F.; Jacobs, K.; Choubal, A.; Mensing, G.; Zhang, Z.; Yamada, K.; Kincaid, N.; Zhu, G.; Tirawat, R.; et al. Feasibility Analysis of Nanostructured Planar Focusing Collectors for Concentrating Solar Power Applications. ACS Appl. Energy Mater. 2018, 1, 6927–6935. [Google Scholar] [CrossRef]
- Kalogirou, S.A. Solar thermal collectors and applications. Prog. Energy Combust. Sci. 2004, 30, 231–295. [Google Scholar] [CrossRef]
- Raj, P.; Subudhi, S. A review of studies using nanofluids in flat-plate and direct absorption solar collectors, Renew. Sustain. Energy Rev. 2018, 84, 54–74. [Google Scholar] [CrossRef]
- Minardi, J.E.; Chuang, H.N. Performance of a ‘‘black’’ liquid flat-plate solar collector. Sol. Energy 1975, 17, 179–183. [Google Scholar] [CrossRef]
- Chen, M.; He, Y.; Ye, Q. Solar thermal conversion and thermal energy storage of CuO/Paraffin phase change composites. Int. J. Heat Mass Tran. 2019, 130, 1133–1140. [Google Scholar] [CrossRef]
- Qin, C.; Kang, K.; Lee, I. Optimization of a direct absorption solar collector with blended plasmonic nanofluids. Sol. Energy 2017, 150, 512–520. [Google Scholar] [CrossRef]
- Wang, X.; He, Y.; Chen, M. ZnO-Au composite hierarchical particles dispersed oil-based nanofluids for direct absorption solar collectors. Sol. Energy Mater. Sol. Cells 2018, 179, 185–193. [Google Scholar] [CrossRef]
- Sezer, N.; Atieh, M.A.; Koc, M. A comprehensive review on synthesis, stability, thermophysical properties, and characterization of nanofluids. Powder Technol. 2019, 344, 404–431. [Google Scholar] [CrossRef]
- Rasamani, K.D. Composite Nanostructures as Effective Catalysts for Visible-Light-Driven Chemical Transformations. Ph.D. Thesis, Temple University, Philadelphia, PA, USA, 2020. [Google Scholar]
- Nakul, S.; Arunachala, U.C. Status, trends and significance of parabolic trough technology in the changing heat transportation scenario. Sol. Energy 2019, 187, 57–81. [Google Scholar] [CrossRef]
- Liu, Y.; Yu, S.; Feng, R.; Bernard, A.; Liu, Y.; Zhang, Y.; Duan, H.; Shang, W.; Tao, P.; Song, C.; et al. A Bioinspired, Reusable, Paper-Based System for High-Performance Large-Scale Evaporation. Adv. Mater. 2015, 27, 2768–2774. [Google Scholar] [CrossRef] [PubMed]
- Zhou, L.; Tan, Y.; Wang, J.; Xu, W.; Yuan, Y.; Cai, W.; Zhu, S.; Zhu, J. 3D self-assembly of aluminium nanoparticles for plasmon-enhanced solar desalination. Nat. Photonics 2016, 10, 393–399. [Google Scholar] [CrossRef]
- Zhou, L.; Zhuang, S.; He, C.; Tan, Y.; Wang, Z.; Zhu, J. Self-assembled spectrum selective plasmonic absorbers with tunable bandwidth for solar energy conversion. Nano Energy 2017, 32, 195–200. [Google Scholar] [CrossRef]
- Zhu, M.; Li, Y.; Chen, F.; Zhu, X.; Dai, J.; Li, Y.; Yang, Z.; Yan, X.; Song, J.; Wang, Y.; et al. Plasmonic Wood for High-Efficiency Solar Steam Generation. Adv. Energy Mater. 2018, 8, 1701028. [Google Scholar] [CrossRef]
- Zhao, J.; Pinchuk, A.O.; Mcmahon, J.M.; Li, S.; Ausman, L.K.; Atkinson, A.L.; Schatz, G.C. Methods for Describing the Electric Properties of Silver and Gold Nanoparticles. Chem. Soc. Rev. 2008, 41, 1710–1720. [Google Scholar]
- Johnson, P.; Christy, R. Optical constants of transition metals: Ti, V, Cr, Mn, Fe Co, Ni, and Pd. Phys. Rev. B. 1974, 9, 5056–5070. [Google Scholar] [CrossRef]
- Loudon, R. The propagation of electric energy through an absorbing dielectric. J. Phys. A Proc. Phys. Soc. Gen. 1970, 3, 233–245. [Google Scholar] [CrossRef]
- Liao, J.; Zhang, Y.; Yu, W. Linear aggregation of gold nanoparticles in ethanol. Colloids Surf. A Physicochem. Eng. Asp. 2003, 223, 177–183. [Google Scholar] [CrossRef]
- Moerloose, J.; Zutter, D. Poynting’s theorem for the finite difference time domain method. Microw Opt. Technol. Lett. 1995, 8, 257–260. [Google Scholar] [CrossRef]
- ASTM G173-03(2012); Standard Tables for Reference Solar Spectral Irradiances: Direct Normal and Hemispherical on 37° Tilted Surface. ASTM: West Conshohocken, PA, USA, 2012.



Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, X.; Bai, F.; Zhang, X.; Wang, T.; Wang, Z. Numerical Investigation on the Solar Absorption Performance of Plasmonic Nanoparticles in the Focused Electric Field. Energies 2024, 17, 2138. https://doi.org/10.3390/en17092138
Zhang X, Bai F, Zhang X, Wang T, Wang Z. Numerical Investigation on the Solar Absorption Performance of Plasmonic Nanoparticles in the Focused Electric Field. Energies. 2024; 17(9):2138. https://doi.org/10.3390/en17092138
Chicago/Turabian StyleZhang, Xueqing, Fengwu Bai, Xuesong Zhang, Tengyue Wang, and Zhifeng Wang. 2024. "Numerical Investigation on the Solar Absorption Performance of Plasmonic Nanoparticles in the Focused Electric Field" Energies 17, no. 9: 2138. https://doi.org/10.3390/en17092138
APA StyleZhang, X., Bai, F., Zhang, X., Wang, T., & Wang, Z. (2024). Numerical Investigation on the Solar Absorption Performance of Plasmonic Nanoparticles in the Focused Electric Field. Energies, 17(9), 2138. https://doi.org/10.3390/en17092138






