Improved Error-Based Ensemble Learning Model for Compressor Performance Parameter Prediction
Abstract
1. Introduction
2. Methods
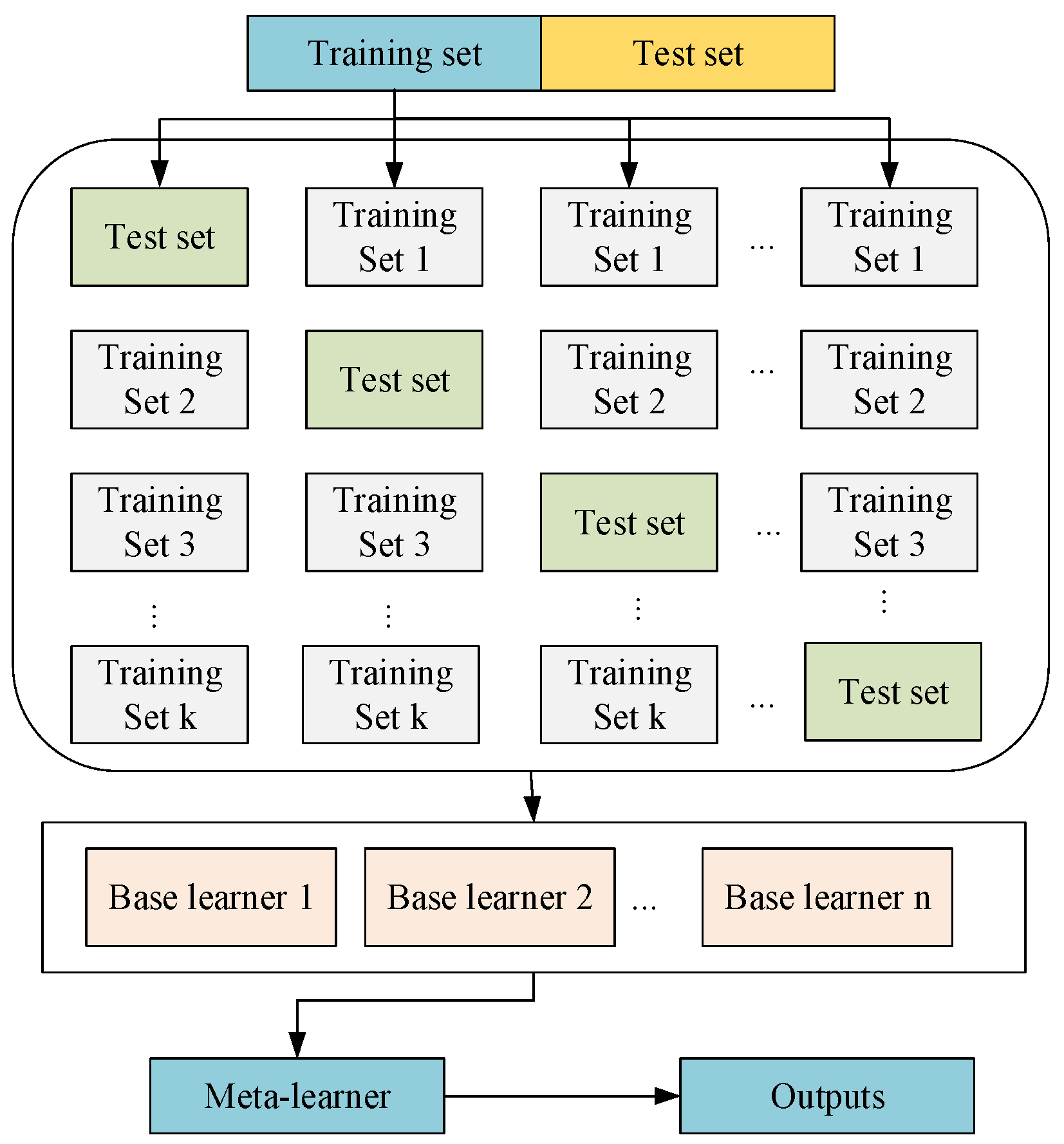
2.1. Stacking Integration Algorithm
- (1)
- Divide the original dataset into training and testing sets. Then, divide the training set equally into k subsets, select the union of k-1 subsets as the training set, and select the remaining 1 subset as the validation set.
- (2)
- Train and validate the learner using this k set of training and validation sets for each base model. Combine the predicted results with the true labels to form a new training set, which is then used to train the second-layer meta-learner.
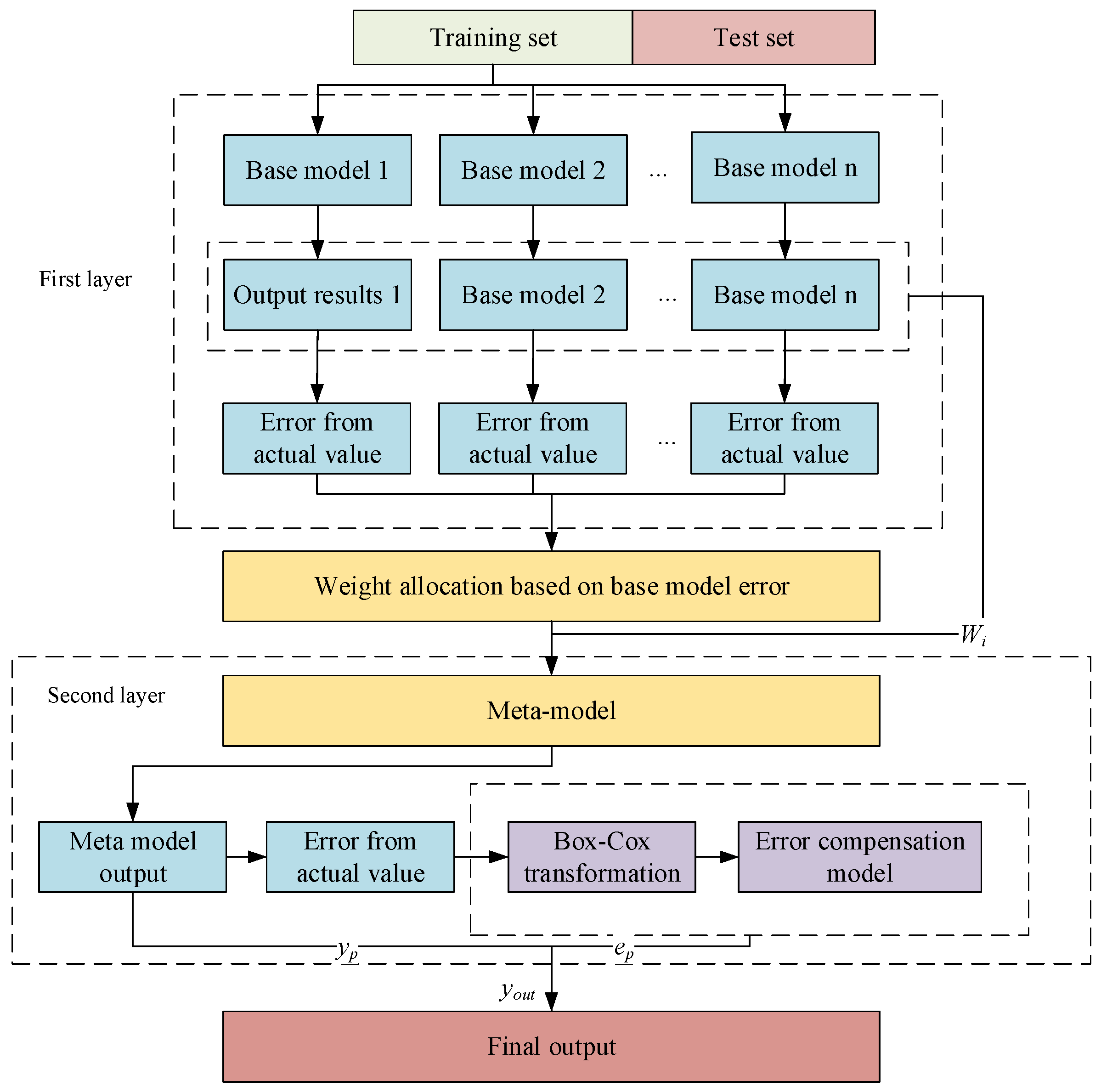
2.2. Improved Stacking Model
2.2.1. Error-Based Weight Allocation Method
2.2.2. Error Correction Method Based on Box–Cox Transformation
2.3. Base Model of the Stacking Model
2.3.1. Encoder–Decoder Model for Hierarchical Input
2.3.2. RBF Neural Network Model
2.4. Establishment of Compressor Performance Parameter Prediction Model
- (1)
- The raw compressor data obtained are processed to eliminate outliers, and the cleaned data are used for feature correlation analysis. The input and output parameters of the predictive model are determined based on the results of the analyses. The cleaned data are divided into training and testing sets according to a specific ratio.
- (2)
- Based on the selected feature parameters, a base model for compressor performance parameter prediction is established in the first layer. Parameter optimisation is performed for each model to ensure prediction accuracy.
- (3)
- The selected base learners are trained via cross-validation. The training error of each base learner is calculated and the weight of the base learner is determined.
- (4)
- The second-layer meta-learner is trained using the prediction dataset as input features. Error compensation based on Box–Cox transformation is performed on the output results of the meta-learner to obtain the final prediction results.
3. Results and Discussion
3.1. Experimental Data
3.2. Base Learner Experimental Results
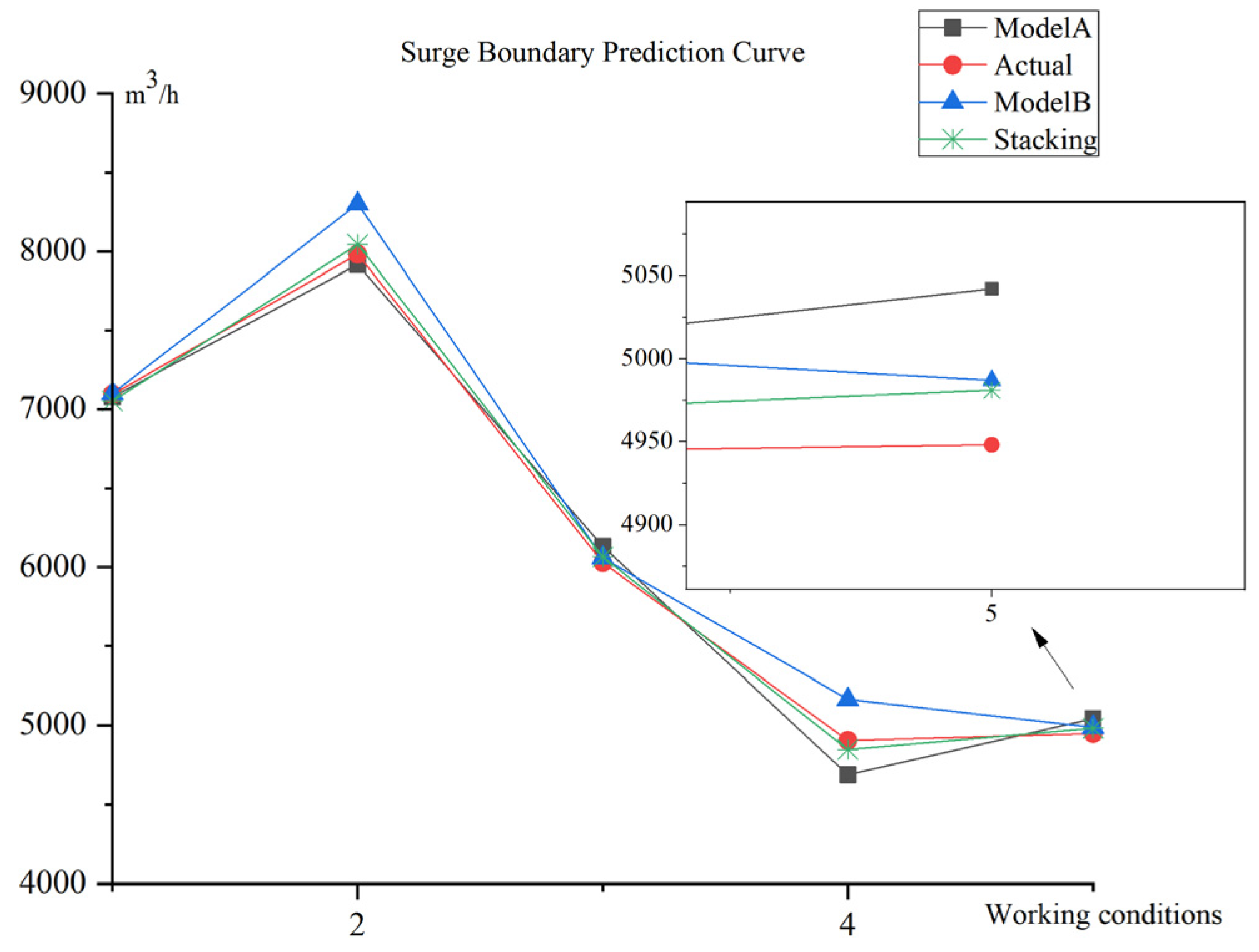
3.3. Stacking Model Analysis
3.3.1. Analysis of Traditional Stacking Ensemble Learning Model
3.3.2. Analysis of Improved Stacking Integrated Learning Model
- Model 1: Classic Stacking model;
- Model 2: Weight allocation for the traditional Stacking model;
- Model 3: Error correction is performed on the prediction results of the traditional Stacking model;
- Model 4: The model described in this article.
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Ye, Z. Study on the natural gas consumption and its change prediction. J. Phys. Conf. Ser. 2020, 1549, 042103. [Google Scholar] [CrossRef]
- Zhou, D.; Huang, D.; Jia, X.; Li, T.; Wang, C.; Wang, D.; Ren, Y. Study on the maintenance scheduling model for compressor units of long-distance natural gas networks considering actual maintenance demands. J. Nat. Gas Sci. Eng. 2021, 94, 104065. [Google Scholar] [CrossRef]
- Arya, A.K. A critical review on optimization parameters and techniques for gas pipeline operation profitability. J. Pet. Explor. Prod. Technol. 2022, 12, 3033–3057. [Google Scholar] [CrossRef]
- Galvas, M.R. Computer Program for Predicting Off-Design Performance of Centrifugal Compressors. 1974, No. LEW-12186. Available online: https://api.semanticscholar.org/CorpusID:60741619 (accessed on 24 April 2024).
- Wang, Z.H.; Xi, G. The effects of gas models on the predicted performance and flow of a centrifugal refrigeration compressor stage. Technol. Sci. 2008, 51, 1160–1168. [Google Scholar] [CrossRef]
- Cutrina Vilalta, P.; Wan, H.; Patnaik, S.S. Centrifugal compressor performance prediction using gaussian process regression and artificial neural networks. Am. Soc. Mech. Eng. 2019, 59452, V008T09A045. [Google Scholar]
- Chu, F.; Wang, F.L.; Wang, X.G.; Zhang, S. A model for parameter estimation of multistage centrifugal compressor and compressor performance analysis using genetic algorithm. Sci. China (Technol. Sci.) 2012, 55, 3163–3175. [Google Scholar] [CrossRef]
- Shi, J.Q.; Zhang, J.H. Load forecasting based on multi-model by Stacking ensemble learning. Proc. CSEE 2019, 39, 4032–4042. [Google Scholar]
- Ribeiro, M.H.D.M.; dos Santos Coelho, L. Ensemble approach based on bagging, boosting and stacking for short-term prediction in agribusiness time series. Appl. Soft Comput. 2020, 86, 105837. [Google Scholar] [CrossRef]
- Ganaie, M.A.; Hu, M.; Malik, A.K.; Tanveer, M.; Suganthan, P.N. Ensemble deep learning: A review. Eng. Appl. Artif. Intell. 2022, 115, 105151. [Google Scholar] [CrossRef]
- Cui, S.; Yin, Y.; Wang, D.; Li, Z.; Wang, Y. A stacking-based ensemble learning method for earthquake casualty prediction. Appl. Soft Comput. 2021, 101, 107038. [Google Scholar] [CrossRef]
- Khan, I.; Zhang, X.; Rehman, M.; Ali, R. A literature survey and empirical study of meta-learning for classifier selection. IEEE Access 2020, 8, 10262–10281. [Google Scholar] [CrossRef]
- Wang, R.; Lu, S.; Feng, W. A novel improved model for building energy consumption prediction based on model integration. Appl. Energy 2020, 262, 114561. [Google Scholar] [CrossRef]
- Li, M.; Yan, C.; Liu, W. The network loan risk prediction model based on Convolutional neural network and Stacking fusion model. Appl. Soft Comput. 2021, 113, 107961. [Google Scholar] [CrossRef]
- Baradaran, R.; Amirkhani, H. Ensemble learning-based approach for improving generalization capability of machine reading comprehension systems. Neurocomputing 2021, 466, 229–242. [Google Scholar] [CrossRef]
- Peng, J.; Zheng, Z.; Zhang, X.; Deng, K.; Gao, K.; Li, H.; Chen, B.; Yang, Y.; Huang, Z. A data-driven method with feature enhancement and adaptive optimization for lithium-ion battery remaining useful life prediction. Energies 2020, 13, 752. [Google Scholar] [CrossRef]
- Pek, J.; Wong, O.; Wong, A.C. How to address non-normality: A taxonomy of approaches, reviewed, and illustrated. Front. Psychol. 2018, 9, 2104. [Google Scholar] [CrossRef]
- Ali, A.A.; Ali, H.T.M. Box-Cox Transformation for Exponential Smoothing with Application. Acad. J. Nawroz Univ. 2023, 12, 311–316. [Google Scholar]
- Chang, Z.; Hao, L.; Yan, Q.; Ye, T. Research on manipulator tracking control algorithm based on RBF neural network. J. Phys. Conf. Ser. 2021, 1802, 032072. [Google Scholar] [CrossRef]
- Zhang, L.; Chen, C.; Xia, Y.; Song, Q.; Cao, J. Prediction of Blade Tip Timing Sensor Waveforms Based on Radial Basis Function Neural Network. Appl. Sci. 2023, 13, 9838. [Google Scholar] [CrossRef]
- Singh, D.; Singh, B. Investigating the impact of data normalization on classification performance. Appl. Soft Comput. 2020, 97, 105524. [Google Scholar] [CrossRef]
- Zhang, W.; Wu, C.; Li, Y.; Wang, L.; Samui, P. Assessment of pile drivability using random forest regression and multivariate adaptive regression splines. Georisk Assess. Manag. Risk Eng. Syst. Geohazards 2021, 15, 27–40. [Google Scholar] [CrossRef]
- Nguyen, Q.H.; Ly, H.B.; Ho, L.S.; Al-Ansari, N.; Van Le, H.; Tran, V.Q.; Prakash, I.; Pham, B.T. Influence of data splitting on performance of machine learning models in prediction of shear strength of soil. Math. Probl. Eng. 2021, 2021, 4832864. [Google Scholar] [CrossRef]
- Borhani, T.N.; García-Muñoz, S.; Luciani, C.V.; Galindo, A.; Adjiman, C.S. Hybrid QSPR models for the prediction of the free energy of solvation of organic solute/solvent pairs. Phys. Chem. Chem. Phys. 2019, 21, 13706–13720. [Google Scholar] [CrossRef]
- Chen, C.; Liu, H. Medium-term wind power forecasting based on multi-resolution multi-learner ensemble and adaptive model selection. Energy Convers. Manag. 2020, 206, 112492. [Google Scholar] [CrossRef]
- Kong, L.; Nian, H. Fault detection and location method for mesh-type DC microgrid using Pearson correlation coefficient. IEEE Trans. Power Deliv. 2020, 36, 1428–1439. [Google Scholar] [CrossRef]



| Output Variables | Input Variables |
|---|---|
| Power | Speed, inlet flow, 100% speed, inlet pressure, outlet pressure, inlet temperature, outlet pressure |
| Blocking Boundary | Speed, inlet temperature, 100% speed, inlet pressure, outlet temperature, outlet pressure |
| Surge Boundary | Speed, 100% speed, inlet temperature, inlet pressure, outlet temperature, outlet pressure |
| Parameters | R2 | RMSE |
|---|---|---|
| Power | 0.97519 | 638 |
| Surge Boundary | 0.92213 | 896 |
| Blocking Boundary | 0.93762 | 884 |
| Parameters | R2 | RMSE |
|---|---|---|
| Power | 0.96372 | 749 |
| Surge Boundary | 0.93213 | 732 |
| Blocking Boundary | 0.93762 | 877 |
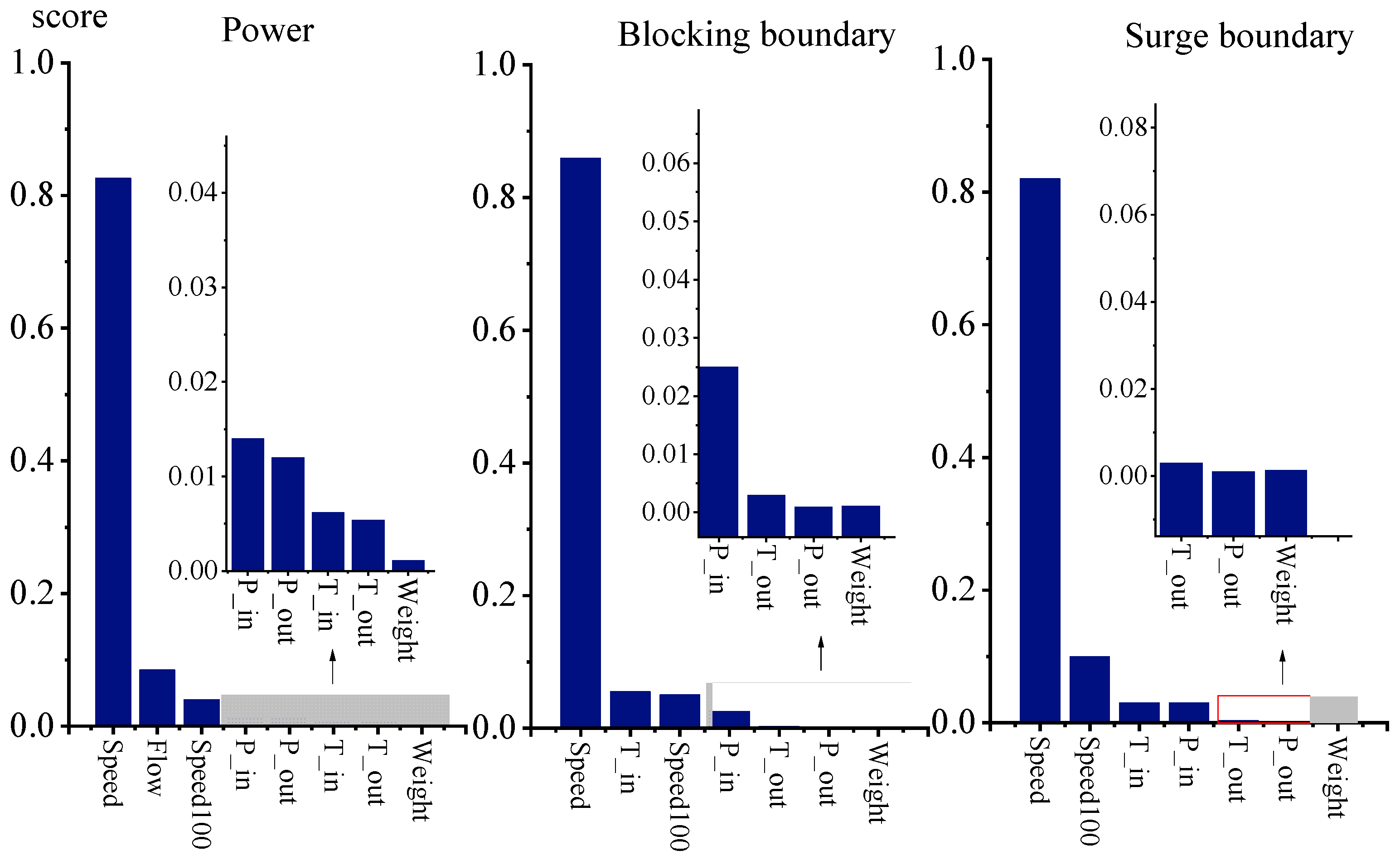
| Prediction Parameters | Correlation |
|---|---|
| Power | 0.31 |
| Surge boundary | 0.35 |
| Blocking boundary | 0.29 |
| Parameters | Model | R2 | RMSE |
|---|---|---|---|
| Power | Model A | 0.97519 | 638 |
| Model B | 0.96372 | 749 | |
| Stacking model | 0.98076 | 511 | |
| Surge Boundary | Model A | 0.92213 | 896 |
| Model B | 0.93213 | 732 | |
| Stacking model | 0.95145 | 684 | |
| Blocking Boundary | Model A | 0.93762 | 884 |
| Model B | 0.93762 | 877 | |
| Stacking model | 0.94974 | 779 |
| Parameters | Model | R2 | RMSE |
|---|---|---|---|
| Power | Model 1 | 0.98076 | 511 |
| Model 2 | 0.98546 | 433 | |
| Model 3 | 0.98655 | 463 | |
| Model 4 | 0.99265 | 387 | |
| Surge Boundary | Model 1 | 0.95145 | 684 |
| Model 2 | 0.96451 | 614 | |
| Model 3 | 0.96486 | 597 | |
| Model 4 | 0.97465 | 543 | |
| Blocking Boundary | Model 1 | 0.94974 | 779 |
| Model 2 | 0.95781 | 688 | |
| Model 3 | 0.96895 | 623 | |
| Model 4 | 0.97894 | 597 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Miao, X.; Liu, L.; Wang, Z.; Chen, X. Improved Error-Based Ensemble Learning Model for Compressor Performance Parameter Prediction. Energies 2024, 17, 2113. https://doi.org/10.3390/en17092113
Miao X, Liu L, Wang Z, Chen X. Improved Error-Based Ensemble Learning Model for Compressor Performance Parameter Prediction. Energies. 2024; 17(9):2113. https://doi.org/10.3390/en17092113
Chicago/Turabian StyleMiao, Xinguo, Lei Liu, Zhiyong Wang, and Xiaoming Chen. 2024. "Improved Error-Based Ensemble Learning Model for Compressor Performance Parameter Prediction" Energies 17, no. 9: 2113. https://doi.org/10.3390/en17092113
APA StyleMiao, X., Liu, L., Wang, Z., & Chen, X. (2024). Improved Error-Based Ensemble Learning Model for Compressor Performance Parameter Prediction. Energies, 17(9), 2113. https://doi.org/10.3390/en17092113






