Research on Optimal Operation of Power Generation and Consumption for Enterprises with Captive Power Plants Participating in Power Grid Supply–Demand Regulation
Abstract
1. Introduction
- (1)
- Based on different demand response scenarios, the analysis of ECPPs’ regulatory strategies and the establishment of a mathematical model for their adjustment potential aids in evaluating and quantifying the demand response capabilities of ECPPs.
- (2)
- An optimization model for power generation and consumption of ECPPs considering load regulation is established. This model can reduce the pressure on system peak shaving and renewable energy integration while promoting the low-carbon development of ECPPs, all while ensuring their economic benefits.
- (3)
- The day-ahead and intra-day two-stage dispatching model described in this paper can better alleviate the supply–demand imbalance within the system and fully utilize the regulatory flexibility of ECPPs, and a segmented/sequential feedback solution strategy for optimization is proposed.
- (4)
- Considering price uncertainty strengthens the risk resistance capability of ECPPs and provides a basis for the grid system, which become aware of the changes in ECPP’s willingness to participate in supply–demand regulation during price fluctuations.
2. Mechanism Analysis of ECPPs Participating in Power Grid Supply–Demand Regulation
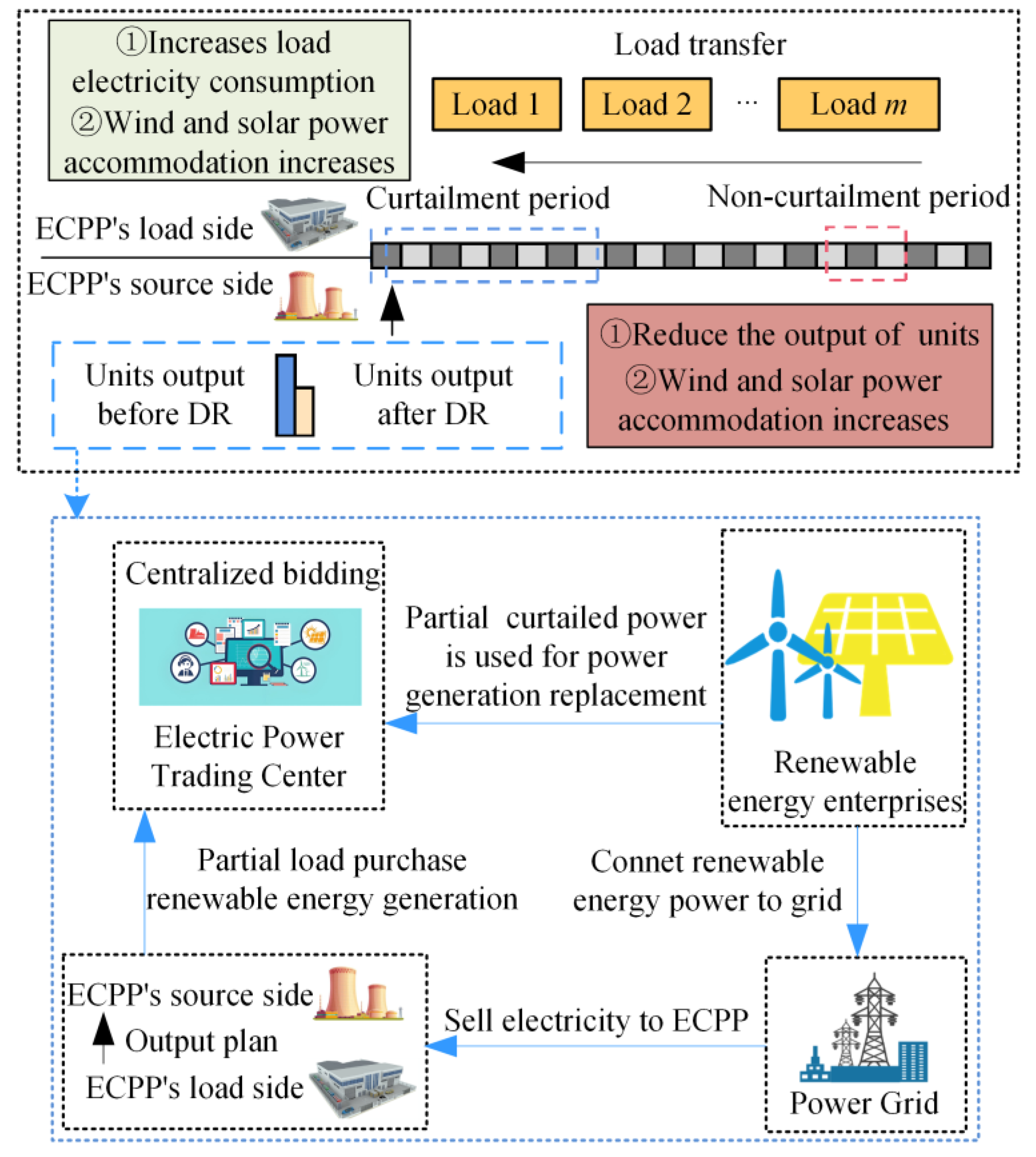
2.1. Regulation Mechanism of ECPPs in the Power Surplus Scenario
2.2. Regulation Mechanism of ECPPs in the Power Shortage Scenario
3. Power Generation and Consumption Optimization Model of ECPPs
3.1. Load Regulation Model and Cost Analysis of ECPPs
3.1.1. Load Shifting Model of ECPPs
3.1.2. Load Reduction Model of ECPPs
3.2. Source-Load Power Generation and Consumption Optimization Model of ECPPs
3.2.1. Objective Function
- (1)
- The operating cost of the CPP
- (2)
- The interaction cost with the power grid
- (3)
- Carbon emission cost
- (4)
- Load regulation cost
- (5)
- The cost of the CPP participating in power generation rights trading
3.2.2. Restrictions
- (1)
- Unit output and ramp rate constraints
- (2)
- Unit startup and shutdown time constraints
- (3)
- Power balance constraint of ECPPs
- (4)
- Interacting power constraints with the power grid
- (5)
- Load shifting constraints
- (6)
- The constraint of the CPP participating in power generation rights trading
3.2.3. Day-Ahead and Intra-Day Two-Stage Dispatching Model of ECPPs
- (1)
- If the supply and demand of the power system have already reached a balance, there is no need to activate the demand response mechanism, and the aforementioned day-ahead plan will be issued as the official plan to each power entities.
- (2)
- If there is a power shortage in the system after the output of the public power plant has been increased to its maximum capacity, the ECPPs will activate the demand response mechanism according to the regulation strategy outlined in Section 2.2 and based on power system requirements. The regulation methods include load shifting, load reduction, and peak shaving by transmitting power. The ECPP will carry out optimization dispatching of power generation and consumption and report the results to the EPDC. Subsequently, the EPDC will generate a day-ahead dispatching plan and issue the information to all power entities.
- (3)
- If there is a power surplus in the system after the output of the public power plant has been reduced to its minimum, the ECPP will activate the demand response mechanism according to the regulation strategy outlined in Section 2.1 and based on system requirements. The regulation methods will include load shifting and participating in power generation rights trading. Renewable energy enterprises first declare the trading information to the Electric Power Trading Center (EPTC), followed by ECPPs. After centralized bidding in the EPTC, the trading electricity quantity and price are determined, and the pre-clearing results are sent to the EPDC for power security verification. The specific trading process of the power generation right is shown in Appendix C. ECPPs perform internal optimal dispatching based on the system requirements and the regulation strategy in Section 2.1, report to the EPDC, and the EPDC generates and issues the day-ahead dispatching plan to complete the formal clearing of the power generation rights trading.
- (1)
- In the power shortages scenario, a huge power gap emerges due to the sudden decrease in wind and solar power output. Based on the new demand response model, ECPPs can perform emergency peak shaving according to their own source-load characteristics, thus reducing the peak shaving pressure on public power plants and avoiding power rationing or blackouts.
- (2)
- In the power surplus scenario, the new demand response model enhances the matching degree of power generation rights trading capacity. The existing power generation rights trading is mostly monthly and annual based, which cannot solve the intra-day supply–demand imbalance contradiction caused by source-load forecast errors of the system. The power generation rights trading under the two-stage mechanism of ECPPs described in this paper belongs to a short-term trading mode, which can alleviate the contradiction between the medium and long-term trading mode and actual intra-day dispatching, as well as stimulate more of the supply–demand regulation flexibility of ECPPs.
- (1)
- In terms of ECPPs, the optimization model proposed in this paper has universal significance and can be applied to other industries as well as high-energy-consuming enterprises with other forms of self-supplied power.
- (2)
- At the level of grid dispatch, Figure 4 can include more distributed energy resources (DERs), facilitating the expansion of the power system.
- (3)
- In terms of the similarity of the electricity market, the application scenarios for the models and frameworks proposed in this article can be categorized under the concept of TESs. In TESs, prosumers can become sellers or buyers based on their own energy usage, representing a peer-to-peer (P2P) attribute of the electricity market. The models described in the article require a community-based P2P electricity market, where participants cannot engage in direct transactions. Instead, a community manager serves as an intermediary, responsible for energy management and energy transactions. From the perspective of transaction models, this article involves both wholesale and bidding modes, which align with the transactional characteristics of TESs.
3.2.4. Solution Strategy and the Superiority
- (1)
- The optimization of internal generation and consumption of ECPPs
- (2)
- Optimization outside of ECPPs (Grid’s perspective)
3.3. IGDT Robust Dispatching Model Considering Price Uncertainty
4. Results and Discussions
4.1. Basic Data
4.2. Deterministic Dispatching Results
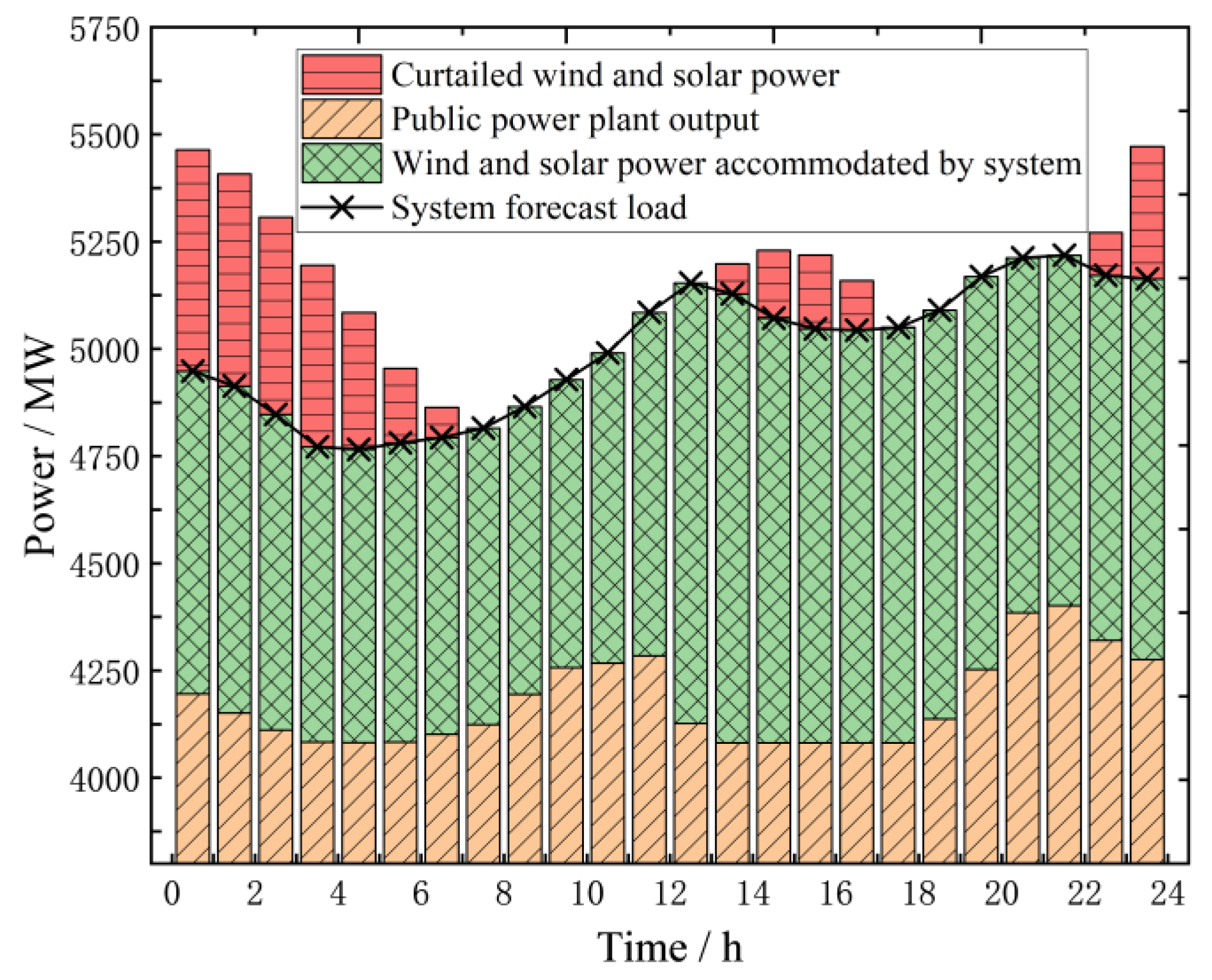
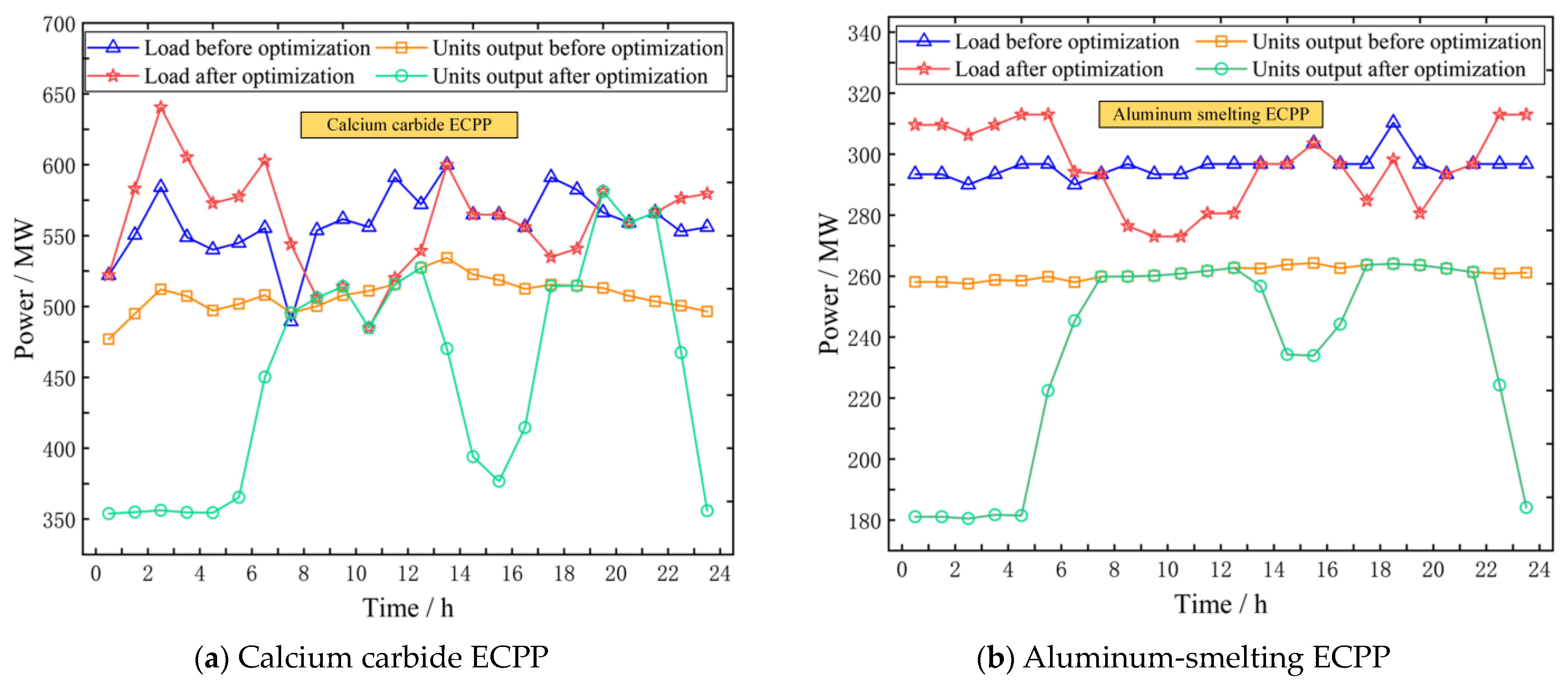
4.2.1. Day-Ahead Optimization Dispatching Results
4.2.2. Intra-Day Optimization Dispatching Results
4.2.3. Comparative Analysis of Different Scenarios
- (a)
- ECPPs will only have the willingness to participate in power generation rights trading when the sum of new energy accommodation cost, units operating cost, and carbon emission costs after participating in the power generation rights trading is less than the sum of units operating costs and carbon emission costs before the transaction. In this process, the power generation rights trading price and coal price are uncertain key influencing factors.
- (b)
- ECPPs will only have the willingness to participate in on-grid power supply when the sum of unit operating cost, power grid interaction cost, and carbon emission costs after participating in on-grid power supply is less than the sum of the above costs before the participation. In this process, the coal price and carbon price are uncertain key influencing factors.
4.3. Influence of Price Uncertainty on Dispatching Results
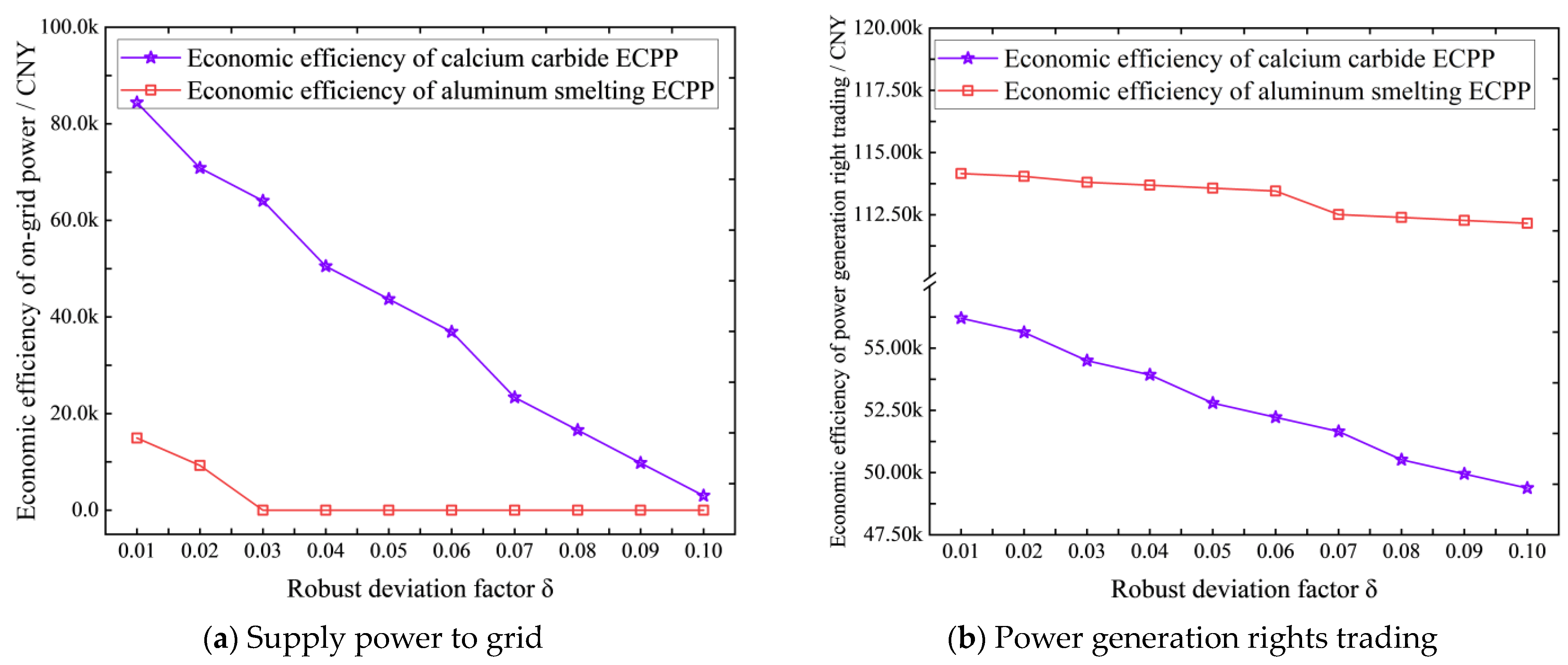
4.3.1. The Effect of the Robust Deviation Factor on Dispatching Results of the IGDT Model
4.3.2. The Effect of Weight Coefficients on the Dispatching Results of the IGDT Model
5. Conclusions
- (1)
- Under the two-stage dispatching model, ECPPs can better alleviate the supply and demand contradiction in the power system. At the same time, power generation rights trading and load regulation can be conducive to ECPPs’ source-load decoupling to a certain extent and release more regulation potential. A segmented/sequential feedback solution strategy is beneficial for solving this.
- (2)
- For high-energy-consumption enterprises with different industry categories, installed capacity and process characteristics, the power generation and consumption optimization model described in this paper can ensure their economic viability and promote their low-carbon development, as well as the safe and stable operation of the power grid system.
- (3)
- Taking price uncertainty into account, ECPPs can maintain their own profitability during price fluctuations, and this could clarify the willingness of ECPPs to participate in regulation, which helps the power system grasp their regulatory potential. Meanwhile, IGDT contributes to ECPPs maintaining profitability in generation rights trading quotations.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A
| Parameter Name | Industry Category | Specific Data |
|---|---|---|
| Installed capacity/MW | Calcium carbide | 2 × 300 |
| Aluminum smelting | 2 × 150 | |
| Maximum and minimum technical output/MW | Calcium carbide | 300, 175 |
| Aluminum smelting | 150, 90 | |
| Ramp-up and ramp-down rates/(MW/min) | Calcium carbide | 3, 3 |
| Aluminum smelting | 2, 2 | |
| Unit consumption characteristic parameters a/(t/MW2) b/(t/MW) c/t | Calcium carbide | 0.00013 |
| 0.27601 | ||
| 16.00726 | ||
| Aluminum smelting | 0.0004 | |
| 0.2285 | ||
| 27.6206 | ||
| Generation right shifting trading prices/(CNY/kWh) | Calcium carbide | 0.1 |
| Aluminum smelting | 0.13 |
| Type of New Energy Power Plant | Install Capacity/MW |
|---|---|
| Wing power plant | 1383 |
| Photovoltaic power station | 650 |
| Period Type | Time | Electricity Price/(CNY/kWh) |
|---|---|---|
| Peak time period | 8:00–11:00 | 0.700085 |
| 19:00–24:00 | ||
| Normal time period | 0:00–2:00 | 0.488259 |
| 11:00–14:00 | ||
| 16:00–19:00 | ||
| Valley time period | 2:00–8:00 | 0.176433 |
| 14:00–16:00 |
| Parameter Name | Specific Data |
|---|---|
| Benchmark on-grid price of thermal power /(CNY/kWh) | 0.22 |
| Coal price /(CNY/t) | 350 |
| Carbon price /(CNY/t) | 56 |
| Transmission–distribution price /(CNY/kWh) | 0.0738 |
| Government funds and surcharges /(CNY/kWh) | 0.0041 |
| Self-generated electricity emission factor | 0.9 |
| Purchased electricity emission factor | 0.2 |
| Compensation price of load reduction (day-ahead) /(CNY/kWh) | 0.15 |
| Compensation price of load reduction (intra-day) /(CNY/kWh) | 0.3 |
| Task Number | Reduction Level | ||
|---|---|---|---|
| 1 | 4.14 | 3 | 0, 8 |
| 5 | 0.8 | 2 | 0, 6 |
| Parameter Name | Specific Data |
|---|---|
| Water volume to electricity conversion coefficient /(m3/MWh) | 561.75, 748.5 |
| /MW | 0, 300 0, 300 |
| /(104m3) | 71.46, 190 |
Appendix B
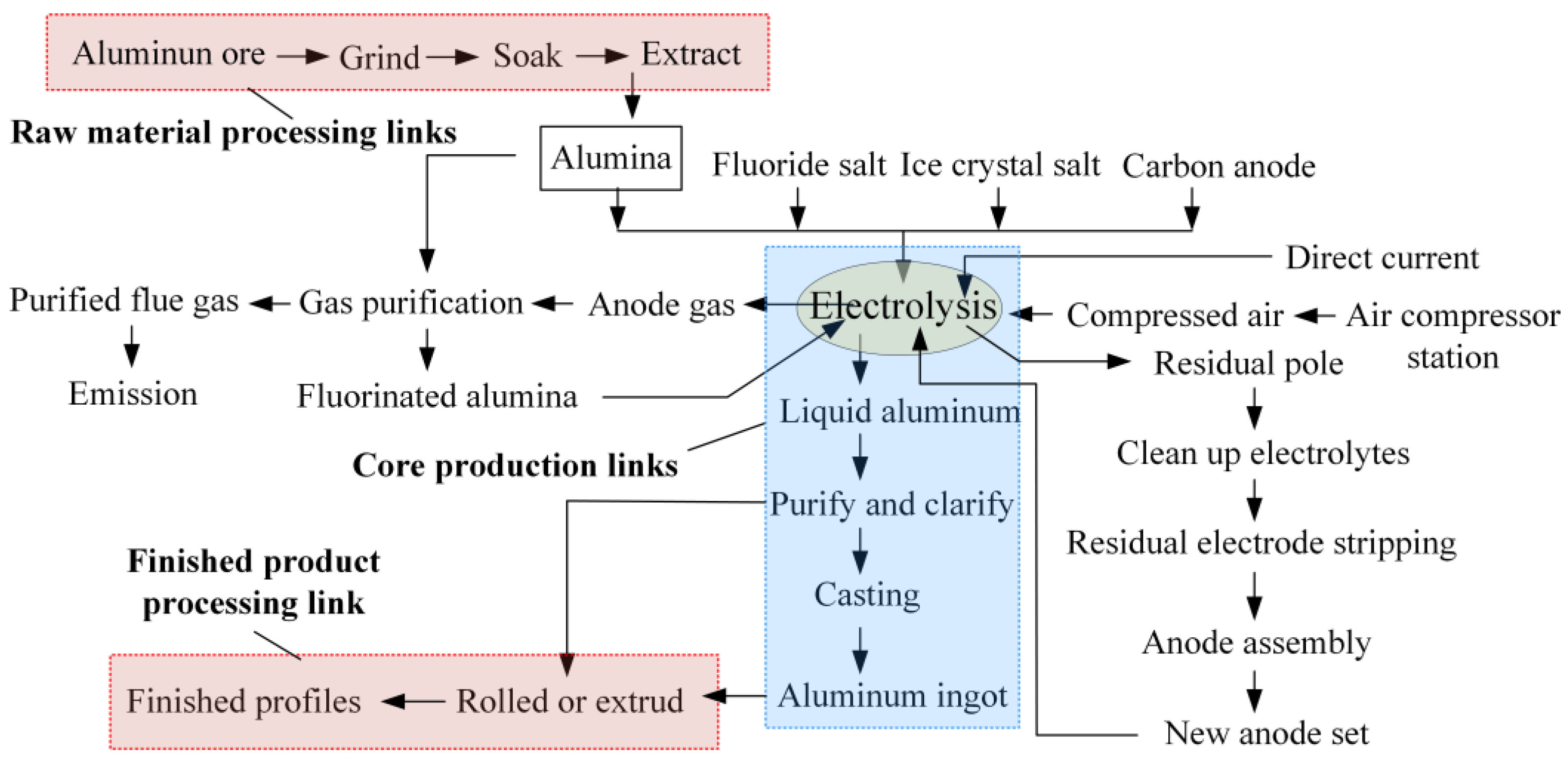

Appendix C
| … | ||||
| … | ||||
| … | ||||
| … | … | … | … | … |
Appendix D
References
- Baležentis, T.; Štreimikiene, D. Sustainability in the electricity sector through advanced technologies: Energy mix transition and smart grid technology in China. Energies 2019, 12, 1142. [Google Scholar] [CrossRef]
- He, S.J.; Liu, Y.J. Optimal Allocation Stochastic Model of Distributed Generation Considering Demand Response. Energies 2024, 17, 795. [Google Scholar] [CrossRef]
- Williams, B.; Bishop, D.; Gallardo, P.; Chase, J.G. Demand Side Management in Industrial, Commercial, and Residential Sectors: A Review of Constraints and Considerations. Energies 2023, 16, 5155. [Google Scholar] [CrossRef]
- Golmohamadi, H. Demand-side management in industrial sector: A review of heavy industries. Renew. Sust. Energ. Rev. 2022, 156, 111963. [Google Scholar] [CrossRef]
- Abdul-Majeed, M.A.; Al-Hadhrami, L.M.; Al-Soufi, K.Y.; Ahmad, F.; Rehman, S. Captive power generation in saudi arabia-overview and recommendations on policies. Energy. Policy 2013, 62, 379–385. [Google Scholar] [CrossRef]
- Naqvi, S.R.; Naqvi, M.; Taqvi, S.A.A.; Iqbal, F.; Inayat, A.; Khoja, A.H.; Mehran, M.T.; Ayoub, M.; Shahbaz, M.; Amin, N.A.S. Agro-industrial residue gasification feasibility in captive power plants: A South-Asian case study. Energy 2021, 214, 118952. [Google Scholar] [CrossRef]
- Goswami, U.; Sadju, P.K.; Chakraborty, S. Enhancement of controllability to improve the transient performance for captive power plant in islanding condition: A case of study. Int. J. Electr. Power Energy Syst. 2016, 83, 188–202. [Google Scholar] [CrossRef]
- Liu, J.; Huang, X.X.; Liu, X.L.; Han, Z.L. Research on Energy Management Strategy of Captive Power Plant Based on Hybrid. Method Sens. 2019, 31, 2155–2165. [Google Scholar]
- Ramin, D.; Spinelli, S.; Brusaferri, A. Demand-side management via optimal production scheduling in power-intensive industries: The case of metal casting process. Adv. Technol. Electr. Eng. Energy 2018, 225, 622–636. [Google Scholar] [CrossRef]
- Adesanya, A.A.; Pearce, J.M. Econnmic viability of captive off-grid solar photovoltaic and diesel hybrid energy systems for the Nigerian private sector. Renew. Sustain. Energy Rev. 2019, 114, 109348. [Google Scholar] [CrossRef]
- Bagdadee, A.H.; Zhang, L. Power Quality Impact on the Industrial Sector: A Case Study of Bangladesh. J. Electr. Eng. Technol. 2019, 14, 1841–1857. [Google Scholar] [CrossRef]
- Afandi, A.N.; Gumilar, L.; Fadlika, I. Local Power Grid Assessment of the Power System Expansion Considering Captive Power Plants. In Proceedings of the 4th International Conference on Industrial, Mechanical, Electrical, and Chemical Engineering, Surakarta, Indonesia, 9–11 October 2018; p. 030072. [Google Scholar]
- Peng, B.Y.; Zhao, H.F.; Bai, J.M.; Wang, W.Z. Study on Solution of Renewable Energy Accommodation Based on Quantitative Analysis Model. In Proceedings of the 3th International Conference on Smart Power and Internet Energy Systems (SPIES), Shanghai, China, 25–28 September 2021; pp. 414–420. [Google Scholar]
- Ali, A.; Innocent, K. Energy management in microgrids using transactive energy control concept under high penetration of Renewables; A survey and case study. Renew. Sustain. Energy Rev. 2023, 176, 113161. [Google Scholar]
- Qi, H.; Waqas, A.; Khalid, U.; Hoay, B.G.; Foo, Y.S.E.; Muhammad, A.; Mahnoor, S.; Abdullah, A.K.; Syed, A.A. A review of transactive energy systems: Concept and implementation. Energy Rep. 2021, 7, 7804–7824. [Google Scholar]
- Lucas, S.M.; Fernando, L.T.; Diego, I.; Marcos, E.P.M.; Giovanni, C.B.; Raimundo, F.S.; Ruth, P.S.L. Co-simulation platform for the assessment of transactive energy systems. Electr. Power. Syst. Res. 2023, 233, 109693. [Google Scholar]
- PAULUS, M.; BORGGREFE, F. The potential of demand-side management in energy-intensive industries for electricity market in Germany. Appl. Energy 2011, 88, 432–441. [Google Scholar] [CrossRef]
- Wang, Z.J.; Gao, F.; Zhai, Q.Z.; Guan, X.H.; Wu, J.; Liu, K. Electrical Load Tracking Analysis for Demand Response in Energy Intensive Enterprise. IEEE Trans. Smart Grid. 2013, 4, 1917–1927. [Google Scholar] [CrossRef]
- Reddy, B.K.; Singh, A.K. Optimal Operation of a Photovoltaic Integrated Captive Cogeneration Plant with a Utility Grid Using Optimization and Machine Learning Prediction Methods. Energies 2021, 14, 4935. [Google Scholar] [CrossRef]
- Mohanta, D.K.; Sadhu, P.K.; Chakrabarti, R. Deterministic and stochastic approach for safety and reliability optimization of captive power plant maintenance scheduling using GA/SA-based hybrid techniques: A comparison of results. Reliab. Eng Syst. Saf. 2007, 92, 187–199. [Google Scholar] [CrossRef]
- Kunche, A.; Mielczarek, B. Application of System Dynamic Modelling for Evaluation of CO2 Emissions and Expenditure for Captive Power Generation Scenarios in the Cement Industry. Energies 2021, 14, 3115. [Google Scholar] [CrossRef]
- Zhang, S.R.; Zhang, J.; Cheng, L.; Wang, Z.B.; Li, W.; Liu, C. A bi-level framework for interactive competition and CPPs-based demand response. J. Renew. Sustain. Energy 2023, 15, 035502. [Google Scholar] [CrossRef]
- Mahmood, A. Gazing Lean through the lens of System of Systems Dynamics: A case of weaving mill. J. Eng. Fibers Fabr. 2019, 14, 155892501987070. [Google Scholar] [CrossRef]
- Xu, J.H.; Du, Y.L.; Cui, H.J.; Yin, Z.; Zhang, Z.; Ma, F.; Tan, C.; Lou, T.Y. Research on alternative electricity calculation method of alternative transaction between new energy and captive power plant. J. Phys. Conf. Ser. 2018, 1087, 022029. [Google Scholar] [CrossRef]
- Li, S.T.; Zhang, S.F.; Andrews-Speed, P. Using diverse market-based approaches to integrate renewable energy: Experiences from China. Energy Policy 2019, 125, 330–337. [Google Scholar] [CrossRef]
- He, Y.X.; Pang, Y.X.; Guan, J. A TOU Pricing Mechanism to Promote Renewable Energy Consumption: The Case of the Western Inner Mongolia Grid in China. Math. Probl. Eng. 2017, 2017, 9454358. [Google Scholar] [CrossRef]
- Liu, H.H.; You, D.N.; Cai, Y.B.; Zhang, G.Q.; Wang, H.; Zhang, L. Peak shaving market mechanism of captive power plants considering energy consumption characteristics of enterprises. In Proceedings of the 2021 International Conference on Power System Technology: Carbon Neutrality and New Type of Power System, Haikou, China, 8–9 December 2021; pp. 720–724. [Google Scholar]
- Liu, Z.D.; Nazari-Heris, M. Optimal bidding strategy of multi-carrier systems in electricity markets using information gap decision theory. Energy 2023, 280, 128043. [Google Scholar] [CrossRef]
- Naghdehforoushha, M.; Fooladi, M.D.T.; Rezvani, M.H.; Sadeghi, M.M.G. A robust model for spot virtual machine bidding in the cloud market using information gap decision theory (IGDT). Turk. J. Electr. Eng. Comput. Sci. 2023, 31, 193–215. [Google Scholar] [CrossRef]
- Hosseini, S.E.; Najafi, M.; Akhavein, A.; Shahparasti, M. Day-Ahead Scheduling for Economic Dispatch of Combined Heat and Power With Uncertain Demand Response. IEEE Access 2022, 10, 42441–42458. [Google Scholar] [CrossRef]







| Task Number | Pm,k/MW | Tm,t/h | Working Interval | |
|---|---|---|---|---|
| 1 | 4.17 | 10 | 100 | 6:00–20:00 |
| 2 | 12.2 | 14 | 10 | 0:00–24:00 |
| 3 | 14.8 | 9 | 10 | 6:00–20:00 |
| 4 | 32.7 | 11 | 5 | 0:00–24:00 |
| 5 | 23.6 | 10 | 10 | 0:00–24:00 |
| Scenario Number | Industry Category | New Energy Accommodation/MW | On-Grid Power Supply/MW | Reduce Carbon Emission/t |
|---|---|---|---|---|
| 1 | Calcium carbide | - | - | - |
| Aluminum smelting | - | - | - | |
| 2 | Calcium carbide | 1075.97 | 428.51 | 766.85 |
| Aluminum smelting | 499.32 | 102.67 | 236.57 | |
| 3 | Calcium carbide | 1354.94 | 445.38 | 766.85 |
| Aluminum smelting | 577.36 | 119.39 | 606.7 | |
| 4 | Calcium carbide | 1354.94 | 322.01 | 766.85 |
| Aluminum smelting | 557.36 | 90.23 | 606.7 |
| Scenario Number | Industry Category | CG/CNY | CB/CNY | CC/CNY | CS/CNY | CN/CNY | Csum/CNY |
|---|---|---|---|---|---|---|---|
| 1 | Calcium carbide | 1,588,083 | 635,494 | 185,988 | - | - | 2,409,565 |
| Aluminum smelting | 1,179,440 | 408,958 | 97,823 | - | - | 1,686,211 | |
| 2 | Calcium carbide | 1,446,162 | 359,501 | 172,326 | 68,354 | 135,516 | 2,181,859 |
| Aluminum smelting | 1,039,266 | 337,847 | 95,673 | 35,802 | 60,572 | 1,569,160 | |
| 3 | Calcium carbide | 1,404,830 | 260,901 | 161,444 | 41,703 | 151,594 | 2,020,472 |
| Aluminum smelting | 1,008,738 | 229,182 | 87,190 | 20,694 | 72,456 | 1,418,260 | |
| 4 | Calcium carbide | 1,413,805 | 279,072 | 170,669 | 41,736 | 155,323 | 2,060,605 |
| Aluminum smelting | 1,021,936 | 243,245 | 84,740 | 20,648 | 75,354 | 1,445,923 |
| Csum/CNY | |||||||
|---|---|---|---|---|---|---|---|
| 5 | 1 | 5 | 0.0062 | 0.0554 | 0.0238 | 0.23 | 2,060,581 |
| 5 | 1 | 10 | 0.0062 | 0.0561 | 0.0241 | 0.31 | 2,060,594 |
| 10 | 1 | 10 | 0.0063 | 0.0571 | 0.0246 | 0.38 | 2,060,605 |
| 10 | 1 | 15 | 0.0064 | 0.0589 | 0.0252 | 0.42 | 2,060,611 |
| 20 | 1 | 10 | 0.0064 | 0.0591 | 0.0253 | 0.4831 | 2,060,620 |
| Csum/CNY | |||||||
|---|---|---|---|---|---|---|---|
| 5 | 1 | 5 | 0.013 | 0.0357 | 0.0384 | 0.3053 | 1,445,417 |
| 5 | 1 | 10 | 0.013 | 0.0357 | 0.0384 | 0.4759 | 1,445,417 |
| 10 | 1 | 10 | 0.0131 | 0.036 | 0.04 | 0.5669 | 1,445,923 |
| 10 | 1 | 15 | 0.0131 | 0.0361 | 0.0431 | 0.8137 | 1,446,285 |
| 20 | 1 | 10 | 0.0132 | 0.0363 | 0.0431 | 1.03 | 1,446,456 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, H.; Zhao, H.; Yang, J.; Peng, D. Research on Optimal Operation of Power Generation and Consumption for Enterprises with Captive Power Plants Participating in Power Grid Supply–Demand Regulation. Energies 2024, 17, 2106. https://doi.org/10.3390/en17092106
Liu H, Zhao H, Yang J, Peng D. Research on Optimal Operation of Power Generation and Consumption for Enterprises with Captive Power Plants Participating in Power Grid Supply–Demand Regulation. Energies. 2024; 17(9):2106. https://doi.org/10.3390/en17092106
Chicago/Turabian StyleLiu, Hangming, Huirong Zhao, Jincheng Yang, and Daogang Peng. 2024. "Research on Optimal Operation of Power Generation and Consumption for Enterprises with Captive Power Plants Participating in Power Grid Supply–Demand Regulation" Energies 17, no. 9: 2106. https://doi.org/10.3390/en17092106
APA StyleLiu, H., Zhao, H., Yang, J., & Peng, D. (2024). Research on Optimal Operation of Power Generation and Consumption for Enterprises with Captive Power Plants Participating in Power Grid Supply–Demand Regulation. Energies, 17(9), 2106. https://doi.org/10.3390/en17092106





