Air Purification Performance Analysis of Magnetic Fluid Filter with AC Non-Thermal Plasma Discharge
Abstract
1. Introduction
2. Physical Transport Phenomena and the Principle of PM Collection in a Magnetic Fluid Filter with NTP Discharge
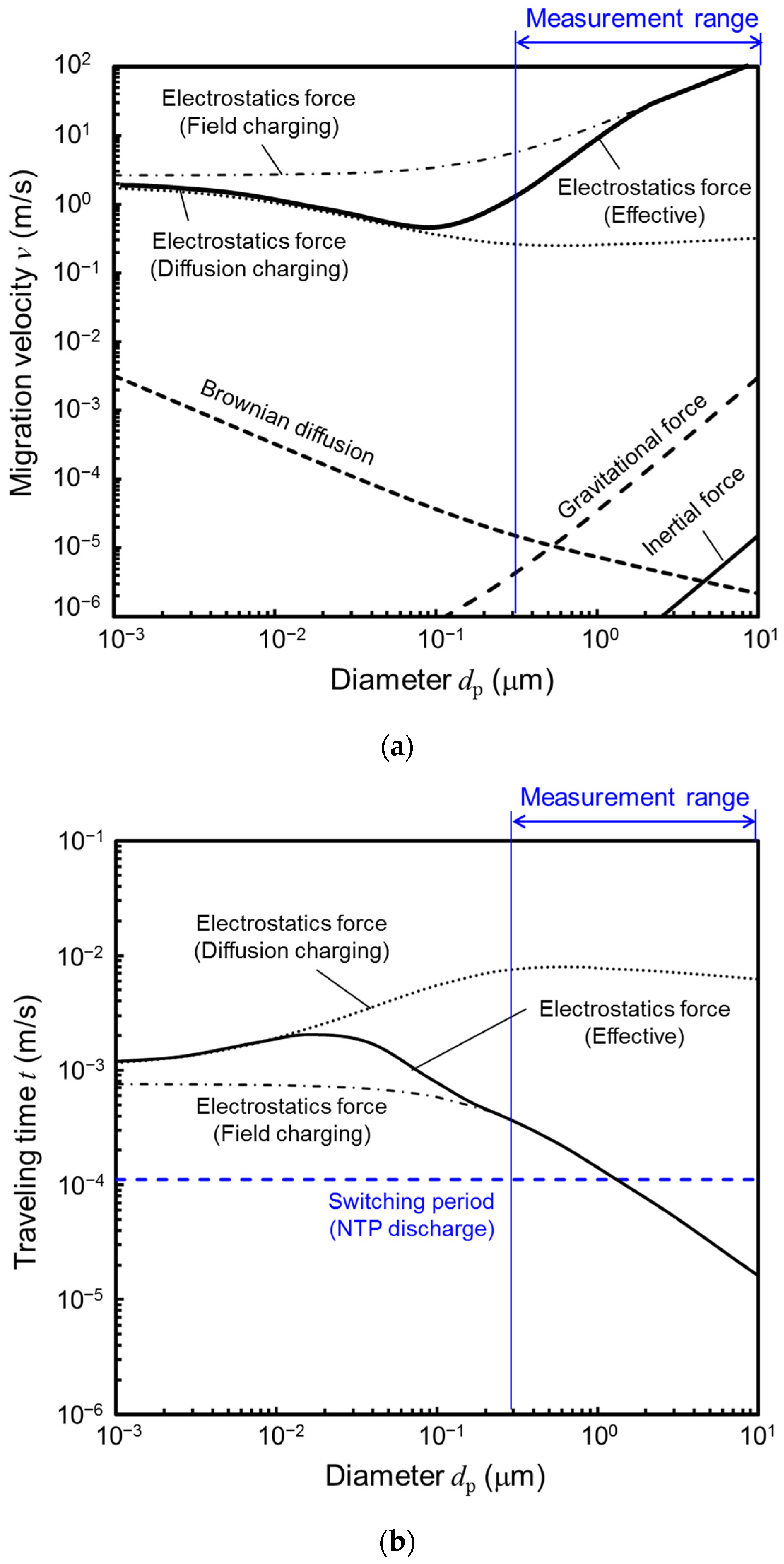
2.1. Physical Transport Phenomena Contribution to PM Collection
- (1)
- Migration velocity vg due to gravitational force (terminal settling velocity)
- (2)
- Migration velocity vc due to centrifugal force
- (3)
- Migration velocity vi due to inertial force
- (4)
- Migration velocity vB due to Brownian diffusion
- (5)
- Migration velocity ve due to electrostatic force
2.2. Principle of PM Collection in a Magnetic Fluid Filter with NTP Discharge
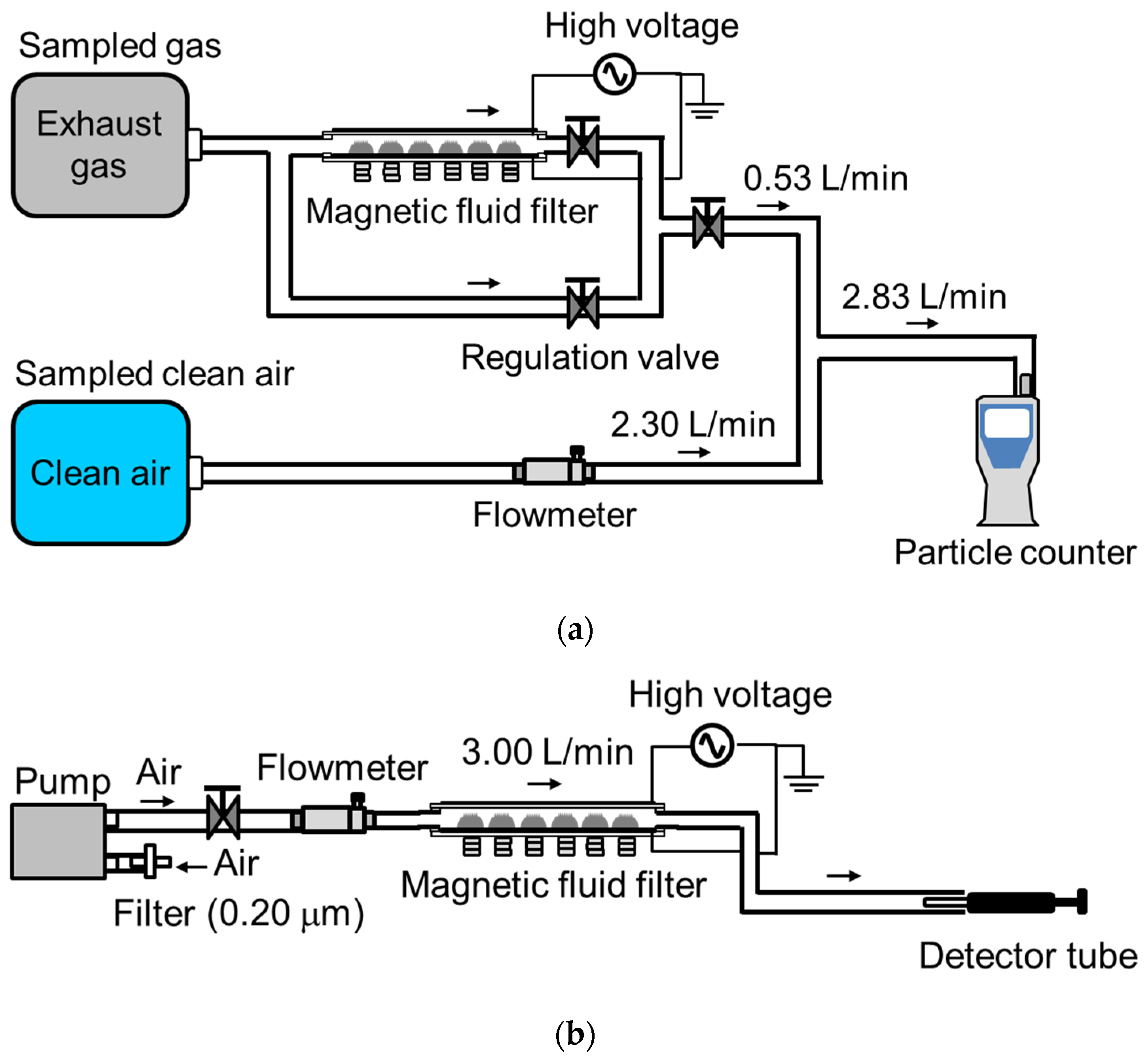
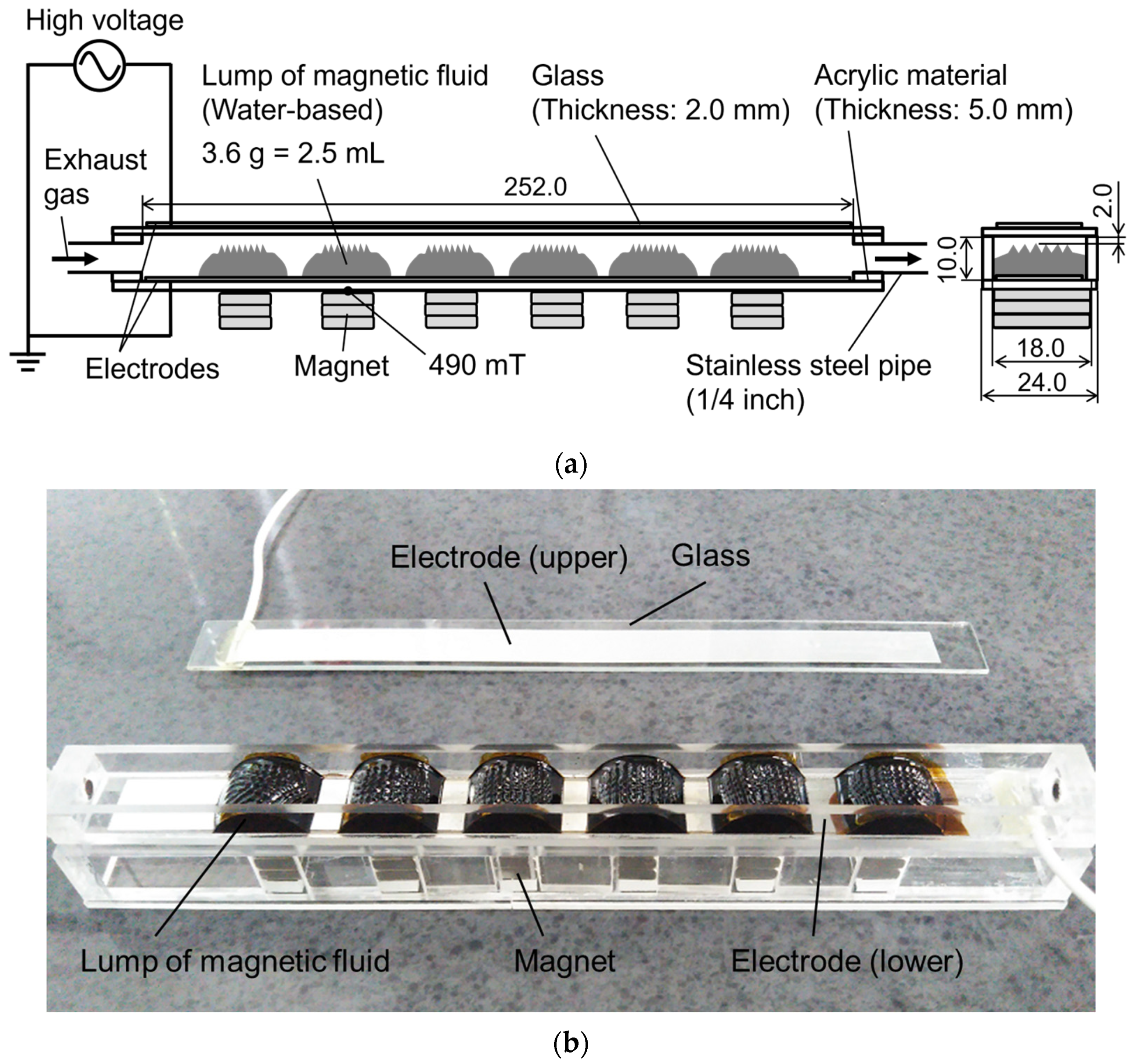
3. Experimental Setup and Method
4. Results and Discussion
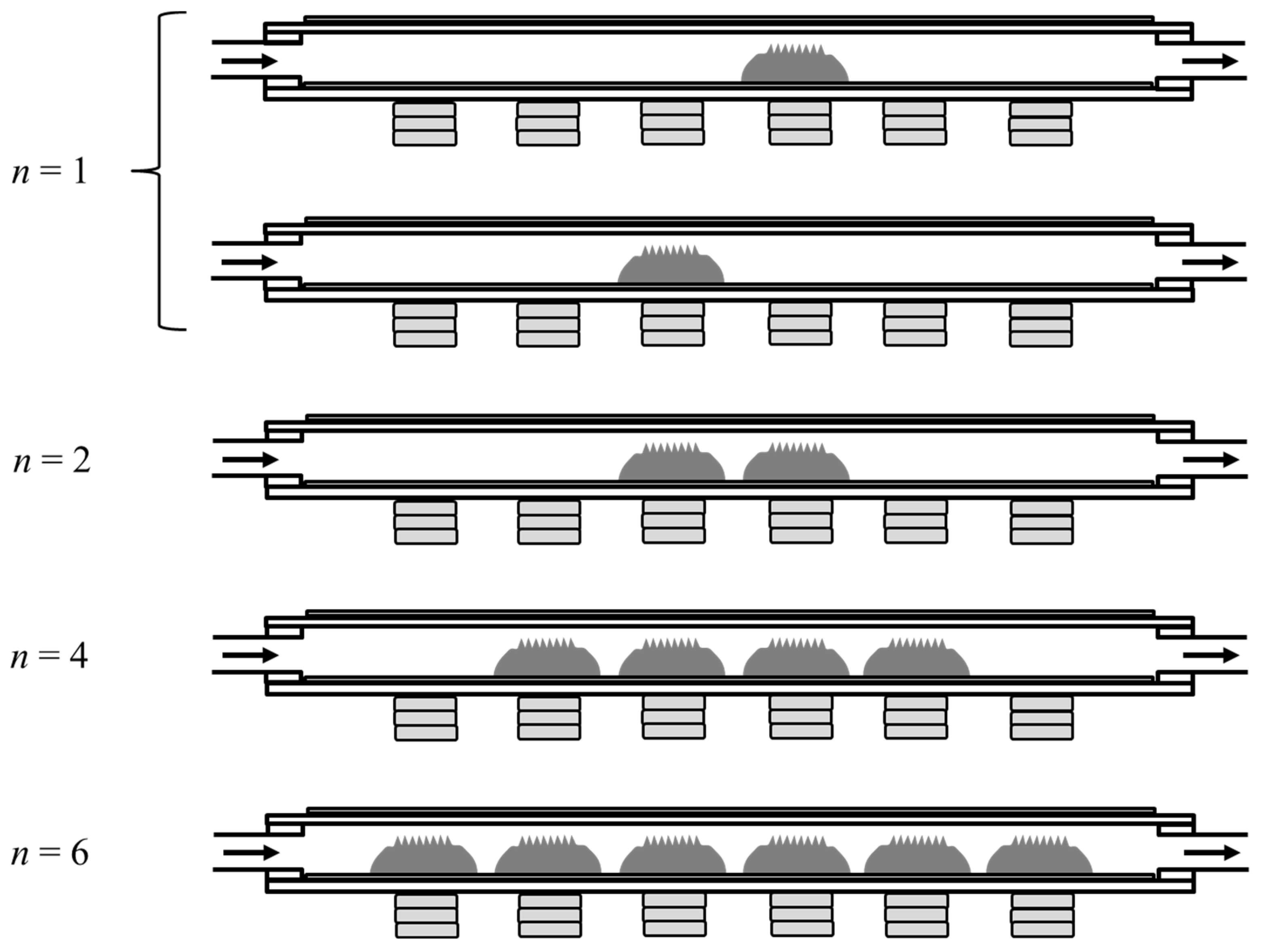
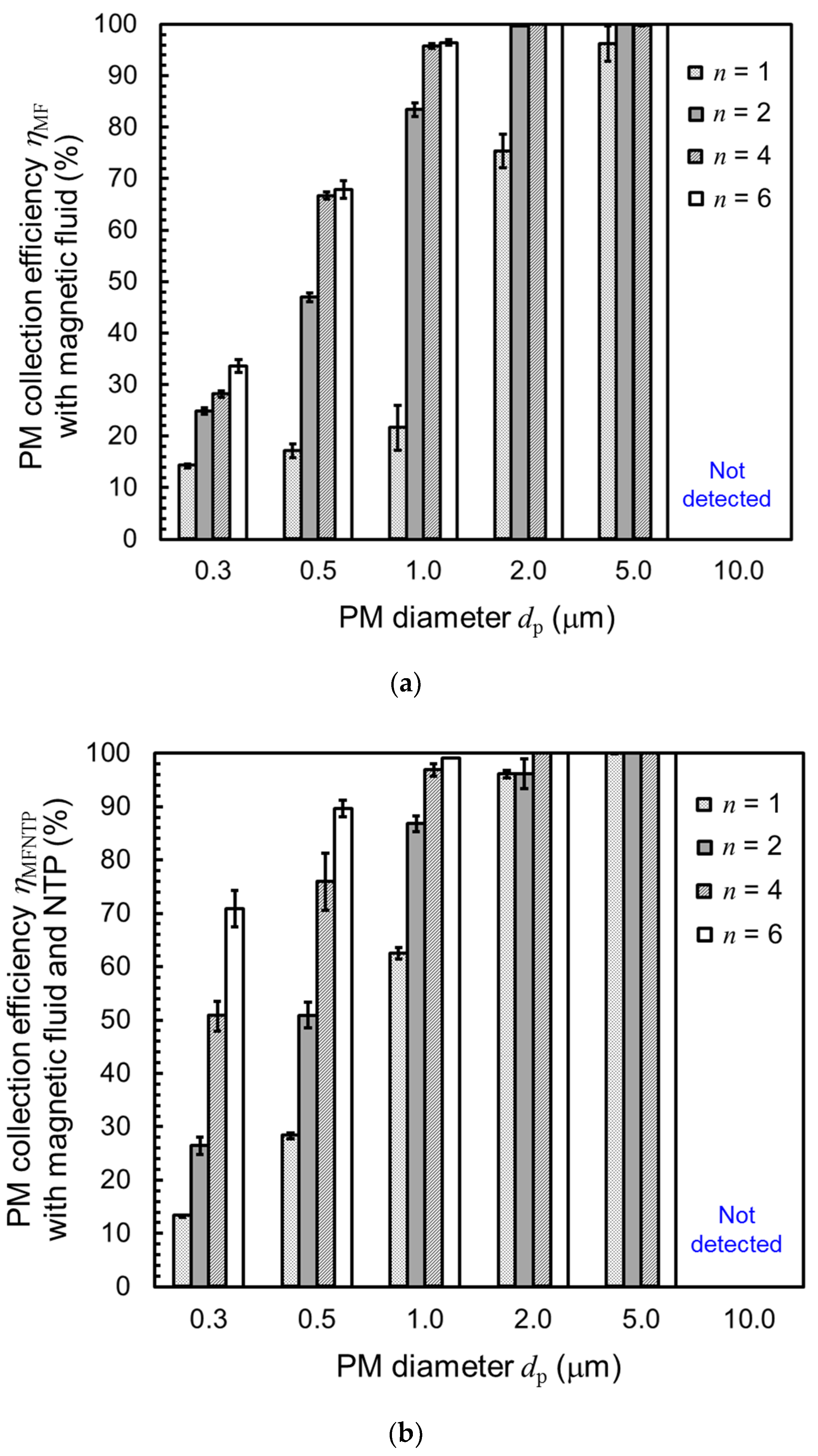
4.1. PM Collection in a Magnetic Fluid Filter
4.2. Power Consumption of NTP Discharge in a Magnetic Fluid Filter
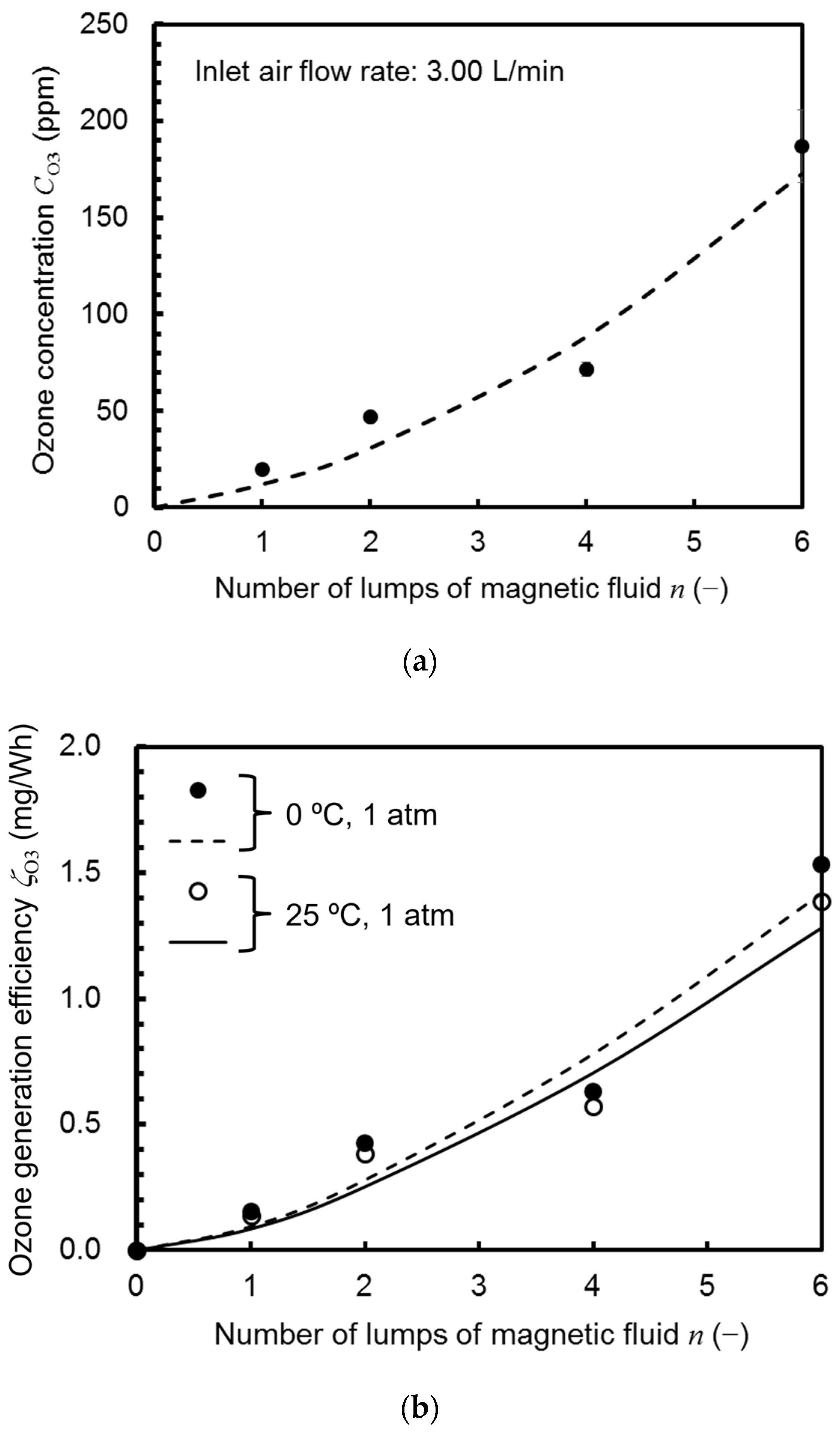
4.3. O3 Generation of a Magnetic Fluid Filter
5. Conclusions
- (1)
- The relationship between the minimum diameter of PM in the measurement range dp and the PM collection efficiency with NTP ηMFNTP for different numbers of lumps of magnetic fluid n are investigated. Under n = 6, ηMFNTP = 71, 90, 99, 100, and 100% for dp ≥ 0.3, 0.5, 1.0, 2.0, and 5.0 μm, respectively. These collection rates are sufficiently high for air purification. As dp increases, ηMFNTP also increases at all values of n. As n increases, ηMFNTP increases. The PM collection mechanism is a function of the particle migration velocity.
- (2)
- The power consumption of the magnetic fluid filter with NTP P and the generated O3 concentration CO3 are investigated for different numbers of lumps of the magnetic fluid n and the O3 generation efficiency ζO3 is calculated from these data. The results show that ζO3 increases proportionally with n. For 25 °C and 1 atm, the ζO3 values are 0.14, 0.39, 0.57, and 1.39 mg/Wh at n = 1, 2, 4, and 6, respectively.
- (3)
- Performance efficiency is improved in both PM collection and O3 generation with an increase in the number of lumps of magnetic fluid or with an increase in the number of spikes of the magnetic fluid with discharge. Namely, the hypothesis that an increase in spikes leads to improved collection efficiencies with energy conservation has been validated.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Xu, S.C.; Zhou, Y.F.; Feng, C.; Zhang, J.N. The factors of regional PM2.5 emissions inequality in China. Process. Saf. Environ. Prot. 2021, 150, 79–92. [Google Scholar] [CrossRef]
- Karagulian, F.; Belis, C.A.; Dora, C.F.C.; Prüss-Ustün, A.M.; Bonjour, S.; Adair-Rohani, H.; Amann, M. Contributions to cities’ ambient particulate matter (PM): A systematic review of local source contributions at global level. Atmos. Environ. 2015, 120, 475–483. [Google Scholar] [CrossRef]
- Tian, E.; Xia, F.; Wu, J.; Zhang, Y.; Li, J.; Wang, H.; Mo, J. Electrostatic air filtration by multifunctional dielectric heterocaking filters with ultralow pressure drop. ACS Appl. Mater. Interfaces 2020, 12, 29383–29392. [Google Scholar] [CrossRef]
- Kim, H.J.; Han, B.; Kim, Y.J.; Yao, S.J. Characteristics of an electrostatic precipitator for submicron particles using non-metallic electrodes and collection plates. J. Aerosol Sci. 2010, 41, 987–997. [Google Scholar] [CrossRef]
- Mo, J.; Tian, E.; Pan, J. New electrostatic precipitator with dielectric coatings to efficiently and safely remove sub-micro particles in the building environment. Sustain. Cities Soc. 2020, 55, 102063. [Google Scholar] [CrossRef]
- Dong, H.; Zhang, Y.; Du, Q.; Gao, J.; Shang, Q.; Feng, D.; Huang, Y. Generation and emission characteristics of fine particles generated by power plant circulating fluidized bed boiler. Energies 2022, 15, 6892. [Google Scholar] [CrossRef]
- Popa, G.N.; Dinis, C.M.; Iagăr, A. Investigations on three-section plate-type electrostatic precipitators used in thermoelectric power plants. Energies 2023, 16, 1186. [Google Scholar] [CrossRef]
- Suhonen, H.; Laitinen, A.; Kortelainen, M.; Yli-Pirilä, P.; Koponen, H.; Tiitta, P.; Ihalainen, M.; Jokiniemi, J.; Suvanto, M.; Tissari, M.; et al. High temperature electrical charger to reduce particulate emissions from small biomass-fired boilers. Energies 2020, 14, 109. [Google Scholar] [CrossRef]
- Drga, J.; Holubčík, M.; Čajová Kantová, N.; Červenka, B. Design of a low-cost electrostatic precipitator to reduce particulate matter emissions from small heat sources. Energies 2022, 15, 4148. [Google Scholar] [CrossRef]
- Jidenko, N.; Borra, J.P. Self-cleaning, maintenance-free aerosol filter by non-thermal plasma at atmospheric pressure. J. Hazard. Mater. 2012, 235–236, 237–245. [Google Scholar] [CrossRef]
- Zhu, Y.; Tao, S.; Chen, C.; Liu, J.; Chen, M.; Shangguan, W. The experimental and simulation investigation of the dynamic characteristic of submicron-scale aerosol in high-voltage electric field by a visualization method. J. Hazard. Mater. 2021, 416, 126227. [Google Scholar] [CrossRef] [PubMed]
- Zhang, J.; Wang, J.; Jiang, Z.; Xu, D. Trapping PM2.5 particles from electrostatic precipitator equipped with magnetic field under different gas velocities. Process. Saf. Environ. Prot. 2022, 158, 115–122. [Google Scholar] [CrossRef]
- Yamamoto, T.; Mimura, T.; Otsuka, N.; Ito, Y.; Ehara, Y.; Zukeran, A. Diesel PM collection for marine and automobile emissions using EHD electrostatic precipitators. IEEE Trans. Ind. Appl. 2010, 46, 1606–1612. [Google Scholar] [CrossRef]
- Kuwahara, T. Fundamental characteristics of low-resistive particulate matter removal using a magnetic fluid and non-thermal plasma. J. Magn. Magn. Mater. 2020, 498, 166161. [Google Scholar] [CrossRef]
- Cheon, T.W.; Lee, J.Y.; Bae, J.Y.; Yook, S.J. Enhancement of collection efficiency of an inertial impactor using an additional punched impaction plate. Aerosol Air Qual. Res. 2017, 17, 2349–2357. [Google Scholar] [CrossRef]
- Cottrell, F.G. Art of Separating Suspended Particles from Gaseous Bodies. U.S. Patent 895729, 11 August 1908. [Google Scholar]
- Penney, G.W. A new electrostatic precipitator. Electr. Eng. 1937, 56, 159–163. [Google Scholar] [CrossRef]
- Davies, C.N. Definitive equations for the fluid resistance of spheres. Proc. Phys. Soc. 1945, 57, 259–270. [Google Scholar] [CrossRef]
- Allen, M.D.; Raabe, O.G. Slip correction measurements of spherical solid aerosol particles in an improved Millikan apparatus. Aerosol Sci. Technol. 1985, 4, 269–286. [Google Scholar] [CrossRef]
- Kim, J.H.; Mulholland, G.W.; Kukuck, S.R.; Pui, D.Y.H. Slip correction measurements of certified PSL nanoparticles using a nanometer differential mobility analyzer (Nano-DMA) for Knudsen number from 0.5 to 83. J. Res. Natl. Inst. Stand. Technol. 2005, 110, 31–54. [Google Scholar] [CrossRef]
- Einstein, A. Über die von der molekularkinetischen Theorie der Wärme geforderte Bewegung von in ruhenden Flüssigkeiten suspendierten Teilchen. Ann. Physik. 1905, 322, 549–560. [Google Scholar] [CrossRef]
- White, H.J. Particle charging in electrostatic precipitation. Trans. Am. Inst. Electr. Eng. 1951, 70, 1186–1191. [Google Scholar] [CrossRef]
- Intra, P.; Tippayawong, N. An overview of unipolar charger developments for nanoparticle charging. Aerosol Air Qual. Res. 2011, 11, 187–209. [Google Scholar] [CrossRef]
- Cowley, M.D.; Rosensweig, R.E. The interfacial stability of a ferromagnetic fluid. J. Fluid Mech. 1967, 30, 671–688. [Google Scholar] [CrossRef]
- Fukuda, Y.; Douhara, N. Study on interfacial phenomena of magnetic fluids. JSME Int. J. Ser. B 2005, 48, 735–742. [Google Scholar] [CrossRef]
- Uehara, S.; Itoga, T.; Nishiyama, H. Discharge and flow characteristics using magnetic fluid spikes for air pollution control. J. Phys. D Appl. Phys. 2015, 48, 282001. [Google Scholar] [CrossRef]
- Kuwahara, T. Reduction in energy consumption using fuel cells in non-thermal plasma-based water sterilization by bubbling ozone. IEEE Trans. Ind. Appl. 2018, 54, 6414–6421. [Google Scholar] [CrossRef]
- Tomiyasu, H.; Fukutomi, H.; Gordon, G. Kinetics and mechanism of ozone decomposition in basic aqueous solution. Inorg. Chem. 1985, 24, 2962–2966. [Google Scholar] [CrossRef]
- Buehler, R.E.; Staehelin, J.; Hoigné, J. Ozone decomposition in water studied by pulse radiolysis. 1. Perhydroxyl (HO2)/hyperoxide (O2−) and HO3/O3− as intermediates. J. Phys. Chem. 1984, 88, 2560–2564. [Google Scholar] [CrossRef]
- Kuwahara, T.; Nishii, S.; Kuroki, T.; Okubo, M. Complete regeneration characteristics of diesel particulate filter using ozone injection. Appl. Energy. 2013, 111, 652–656. [Google Scholar] [CrossRef]
- Shi, Y.; He, Y.; Cai, Y.; Li, Z.; Wang, W.; Zhou, Y.; Lu, Y.; Yang, Y. Effect of nonthermal plasma with different ozone concentrations on the oxidation and removal of different components in particulate matter. J. Energy Inst. 2022, 102, 268–277. [Google Scholar] [CrossRef]
- de Castro, B.J.C.; Sartim, R.; Guerra, V.G.; Aguiar, M.L. Hybrid air filters: A review of the main equipment configurations and results. Process Saf. Environ. Prot. 2020, 144, 193–207. [Google Scholar] [CrossRef]
- Flagan, R.C.; Seinfeld, J.H. Fundamentals of Air Pollution Engineering; Prentice Hall: Upper Saddle River, NJ, USA, 1988; pp. 420–425. ISBN 0-13-332537-7. [Google Scholar]
- Choi, D.Y.; An, E.J.; Jung, S.H.; Song, D.K.; Oh, Y.S.; Lee, H.W.; Lee, H.M. Al-coated conductive fiber filters for high-efficiency electrostatic filtration: Effects of electrical and fiber structural properties. Sci. Rep. 2018, 8, 5747. [Google Scholar] [CrossRef] [PubMed]

Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kuwahara, T.; Asaka, Y. Air Purification Performance Analysis of Magnetic Fluid Filter with AC Non-Thermal Plasma Discharge. Energies 2024, 17, 1865. https://doi.org/10.3390/en17081865
Kuwahara T, Asaka Y. Air Purification Performance Analysis of Magnetic Fluid Filter with AC Non-Thermal Plasma Discharge. Energies. 2024; 17(8):1865. https://doi.org/10.3390/en17081865
Chicago/Turabian StyleKuwahara, Takuya, and Yusuke Asaka. 2024. "Air Purification Performance Analysis of Magnetic Fluid Filter with AC Non-Thermal Plasma Discharge" Energies 17, no. 8: 1865. https://doi.org/10.3390/en17081865
APA StyleKuwahara, T., & Asaka, Y. (2024). Air Purification Performance Analysis of Magnetic Fluid Filter with AC Non-Thermal Plasma Discharge. Energies, 17(8), 1865. https://doi.org/10.3390/en17081865





