Detonation Cell Size Prediction Using Artificial Neural Networks (ANNs) for Hydrogen/Hydrocarbon/Ammonia/Nitrous Oxide Mixtures

Abstract

In this work, a previously developed three-feature Artificial Neural Network (ANN) model with dimensional inputs is directly applied to predict the cell size of hydrocarbon/ammonia/nitrous oxide mixtures and compare these to experimental data. This model uses as inputs three ZND parameters (M_CJ, Δ_I, and ${\dot{\sigma }}_{\mathit{max}}$), which are mainly calculated using Konnov’s and Mével’s mechanisms. A similar prediction is obtained with the two mechanisms for the biogas–O₂, H₂–O₂, H₂–N₂O, and NH₃–O₂ mixtures, indicating that the model is not only limited to Konnov’s chemical kinetic mechanism which was used for its training. The overall good agreement between the ANN predictions and the actual experimental values for the aforementioned mixtures, which are not used in the original training of the ANN model, is promising and shows its potential for application and extension to other mixtures and initial conditions, provided that the chemical kinetic parameters describing the ideal reaction zone structure could be computed. The model is then used to compare experimental cell size data from two detonation tube facilities, and also different chemical kinetic mechanisms for NH₃-N₂O mixtures. In the end, the original ANN model is expanded with the inclusion of additional cell size data, showing a slightly lower mean error for the predicted cell sizes if the data for the mixtures considered in this study are taken into account for the training of the new ANN model.

1. Introduction

A detonation is a self-sustained, supersonic, combustion-driven compression wave across which a significant pressure and temperature change occurs [1]. Detonation research is generally focused on the safety of engineering applications and industrial processes in the chemical and energy sectors [2,3], and also on the development of hypersonic propulsion systems [4,5,6]. In recent years, there has been a strong focus, especially in the transportation and aerospace industry, to explore greener aviation fuels, that are either carbon-neutral, like biogas [7,8,9], or carbon-free, like hydrogen (H₂) [10] and ammonia (NH₃) or its blend [11,12,13,14,15], which can also be used as a carrier of green hydrogen. While hydrogen/nitrogen/ammonia/air mixtures have been shown to have similar combustion characteristics as gasoline, they are also susceptible to auto-ignition or detonation phenomena. Likewise, nitrous oxide (N₂O) has been used in a variety of industrial applications and is considered as a relatively safer oxidizer to store and carry on board in a rocket motor engine. Like with oxygen, N₂O mixed with other gaseous fuels can result in an explosion risk potential and the occurrence of detonation [16]. Compared to other combustible mixtures, characteristic detonation cell size values for fuel–N₂O mixtures are relatively scarce. Most of them focused on H₂/CH₄/NH₃/N₂O-derived mixtures [17,18,19].

To quantify the sensitivity of a detonation or to scale different dynamic parameters, the cell size λ is commonly used as a characteristic length [20]. This is obtained by tracking the triple point trajectory of a detonation, which can be experimentally achieved by placing an aluminum foil covered with soot under a propagating detonation. Sample soot foils can be seen in Figure 1.

The cell size λ is commonly related to the chemical induction length scale Δ_I of the steady 1D ZND detonation model. Although this model is simplified and does not account for the multidimensional and unsteady nature of detonations, it can still describe the coupling between gas dynamics and chemical reactions. Considering that this structure can be calculated and obtained easily, it seems logical to relate the cell size to a parameter of this model, and specifically the induction length Δ_I, typically with a constant proportionality factor (λ = A · Δ_I) [21], or a variable factor that is a function of the stability parameter (λ $=A\left(\chi \right)·{\Delta }_{\mathrm{I}}=\sum _{\mathrm{k}=0}^{\mathrm{N}}\left({\mathrm{a}}_{\mathrm{k}}{\chi }^{-\mathrm{k}}+{\mathrm{b}}_{\mathrm{k}}{\chi }^{\mathrm{k}}\right)·{\Delta }_{\mathrm{I}})$ [22]. These correlations, however, are not ideal, as the first is limited only to the specific mixtures used to create it, while the second, although improved, is still an empirical correlation.

An alternative approach to obtain these correlations is to use machine learning techniques and neural networks. In recent years, these have been successfully used in combustion [23] and, in particular, different detonation studies, such as to reconstruct the detonation front [24,25] or identify the wave modes in a Rotating Detonation Engine (RDE) [26]. Indeed, a better predictive model [27] has been developed based on machine learning, and more specifically by creating Artificial Neural Networks (ANNs), suitable for a wide range of combustible mixtures and initial conditions. Developing ANN models to predict detonation cell sizes has also been used in other studies [28,29], but in both cases, it was limited only to the few mixtures that were used to create these models. In contrast, our recently developed model [27] was trained on a wide range of mixtures and conditions, using chemical kinetic parameters as input features, meaning that it could technically be used for any mixture and initial condition, as long as the reaction zone structure described by the required chemical kinetic parameters could be computed. This study will try to explore this argument by looking at reactive mixtures and conditions beyond those that were used for its training. To this end, the three-feature Artificial Neural Network (ANN) model using Konnov’s chemical kinetic mechanism with dimensional inputs reported in [27] is first applied as a “black box” tool to predict cell sizes for the present mixtures, which were not considered in its original development, with required inputs determined using other mechanisms. In the end, we re-train the ANN model, following the same procedure outlined in [27], with the additional data used in this work.

The structure of this study is as follows: In Section 2, for completeness, we briefly present the general structure and training process of the ANN model developed in [27], as well as the experimental setup information and the chemical kinetics used to obtain the chemical kinetic parameters that are used as inputs by the model. In Section 3, we first compare the cell size predictions of the three-feature ANN model to the actual experimental results for different reactive mixtures. We then use the model to evaluate chemical kinetics and detonation tube facilities. We close Section 3 by re-training our model using as additional data most of the experimental data that are presented in this work. Finally, we conclude this paper with a discussion in Section 4.

2. Materials and Methods

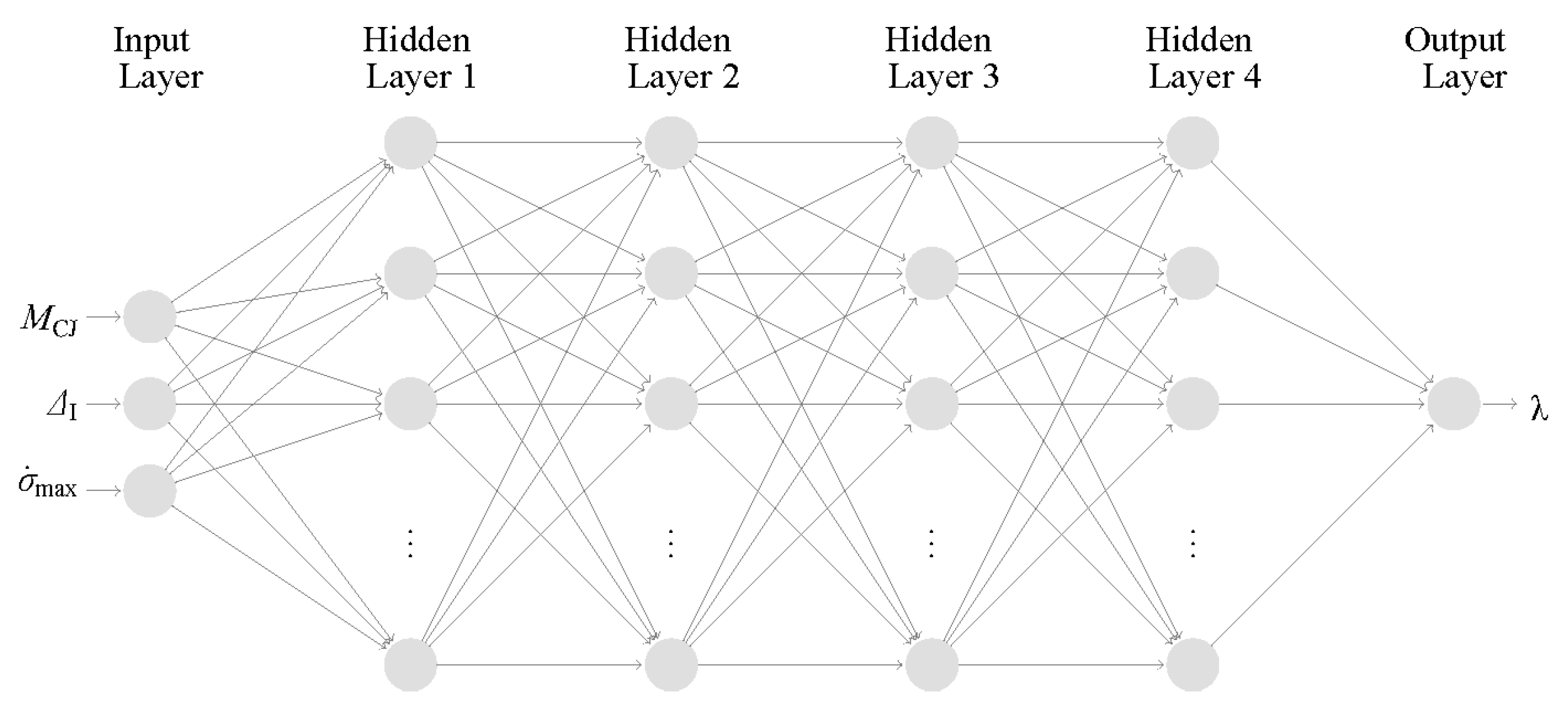
The previously developed [27] 3-feature optimal Artificial Neural Network (ANN) was used to predict the detonation cell sizes of gaseous detonations. For complete details about this ANN model formulation and validation, please see [27]. For a brief illustration, Figure 2 shows the structure of this model, which uses 3 input features to calculate the detonation cell size. These input features were determined from a parametric study to be ZND induction length (Δ_I), the detonation Mach number (M_CJ), and the maximum thermicity (${\dot{\sigma }}_{\mathit{max}}$). These are parameters relevant to describing the detonation reaction zone structure and are indirectly related to the stability parameter χ [30]. Obtaining these parameters requires thermodynamic equilibrium and chemical kinetic computations, which were performed using either the CHEMKIN II package [31] or the Detonation Toolkit [32]. For these calculations, Konnov’s v0.4 mechanism [33] and Mével’s mechanism [34] were mainly used. Konnov’s mechanism was used in our previous work [27] to develop the ANN that is used here. For NH₃-N₂O mixtures, additional mechanisms were deemed necessary, more specifically the mechanisms by Zhang et al. [35], Miller and Bowman [36], Otomo et al. [37], and Han et al. [38], all calibrated for the combustion of NH₃-N₂O mixtures.

The ANN model was used to predict the cell sizes for different mixtures, and compare them with the corresponding experimental cell sizes. These experimental cell sizes were mainly sourced from studies in the literature [7,17,18,34,39,40]. In addition to those, detonation cell sizes from two series of experiments for a stoichiometric C₂H₂-N₂O mixture at different pressures were obtained as part of this study, and subsequently compared against the ANN predictions. These were obtained for the same conditions from two independent detonation tube facilities, one located at Concordia University and the other at Shanghai Jiao Tong University (courtesy of B. Zhang). The first is a 26.4 mm-diameter circular detonation tube with a length of 0.59 m, while the second is a tube with a square cross-section of 38.1 mm by 63.5 mm and a length of 2.5 m. Sample results of these experiments can be seen in Figure 1.

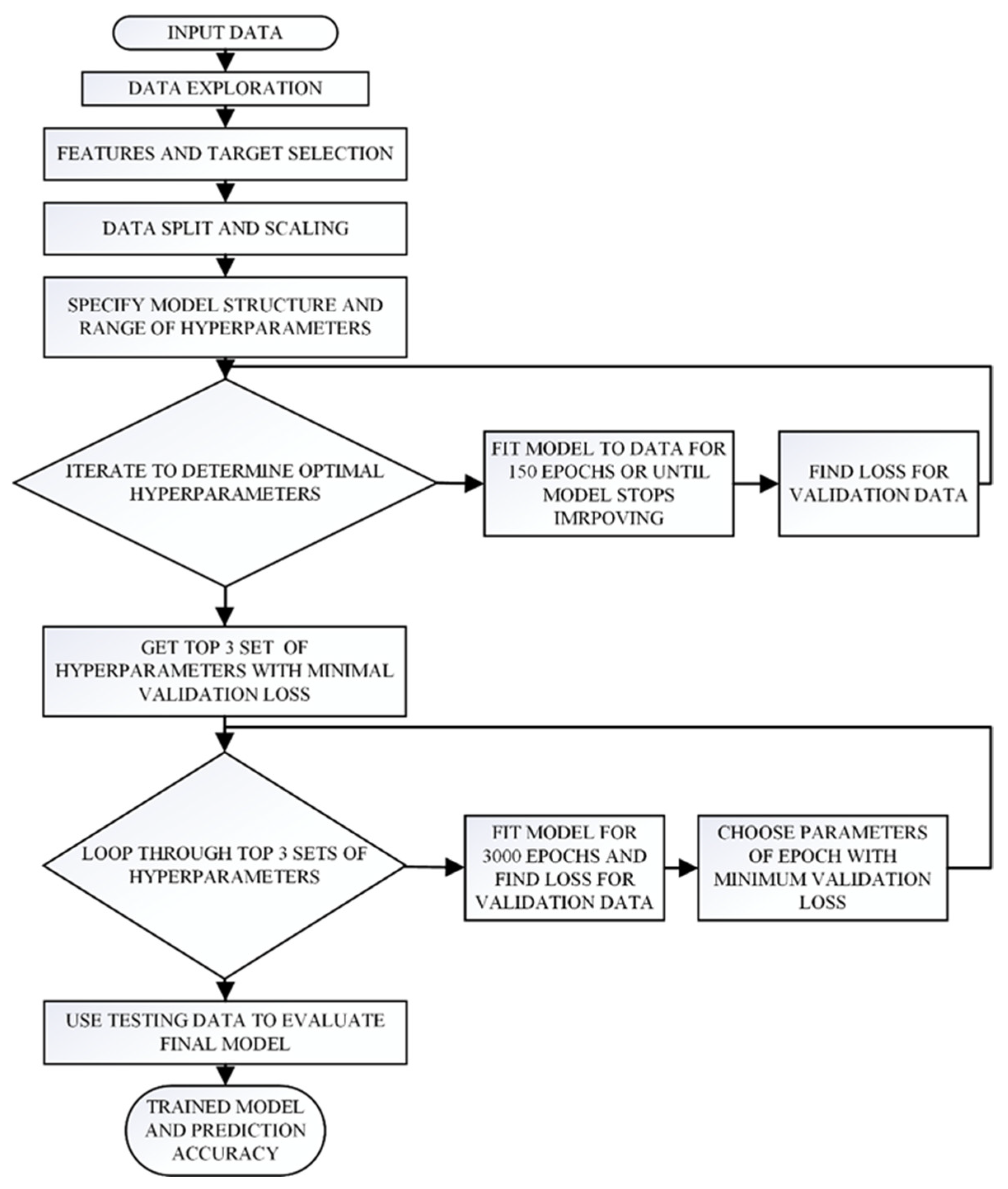
Finally, the model was updated and further expanded by including most of the experimental cell size data that were considered in this study. These were added to the previously used dataset from the Caltech detonation database [41] of a wide range of mixtures and initial conditions. The same process that was developed previously and is shown in Figure 3 was used to retrain and test the model with the updated dataset [27]. In brief, this process required first the division of the overall available dataset into three subsets, the training (60%), validation (20%), and testing (20%) datasets. The model was created and trained using the training dataset, with the intent of minimizing the loss function for the training dataset, while constantly monitoring the loss for the validation data to avoid overfitting. The loss function, which compares the predicted to the actual detonation cell sizes, is given as:

$$\mathrm{Loss}=\frac{1}{\mathrm{N}}\sum _1^{\mathrm{N}}{\left(\frac{\left({\lambda }_{\mathrm{pred}}-{\lambda }_{\mathrm{act}}\right)}{{\lambda }_{\mathrm{act}}}·100\%\right)}^2$$

(1)

Once this process was complete, meaning that the structure and parameters of the ANN model were determined, the model was evaluated using the testing data, which were kept separate from the model creation process.

3. Results

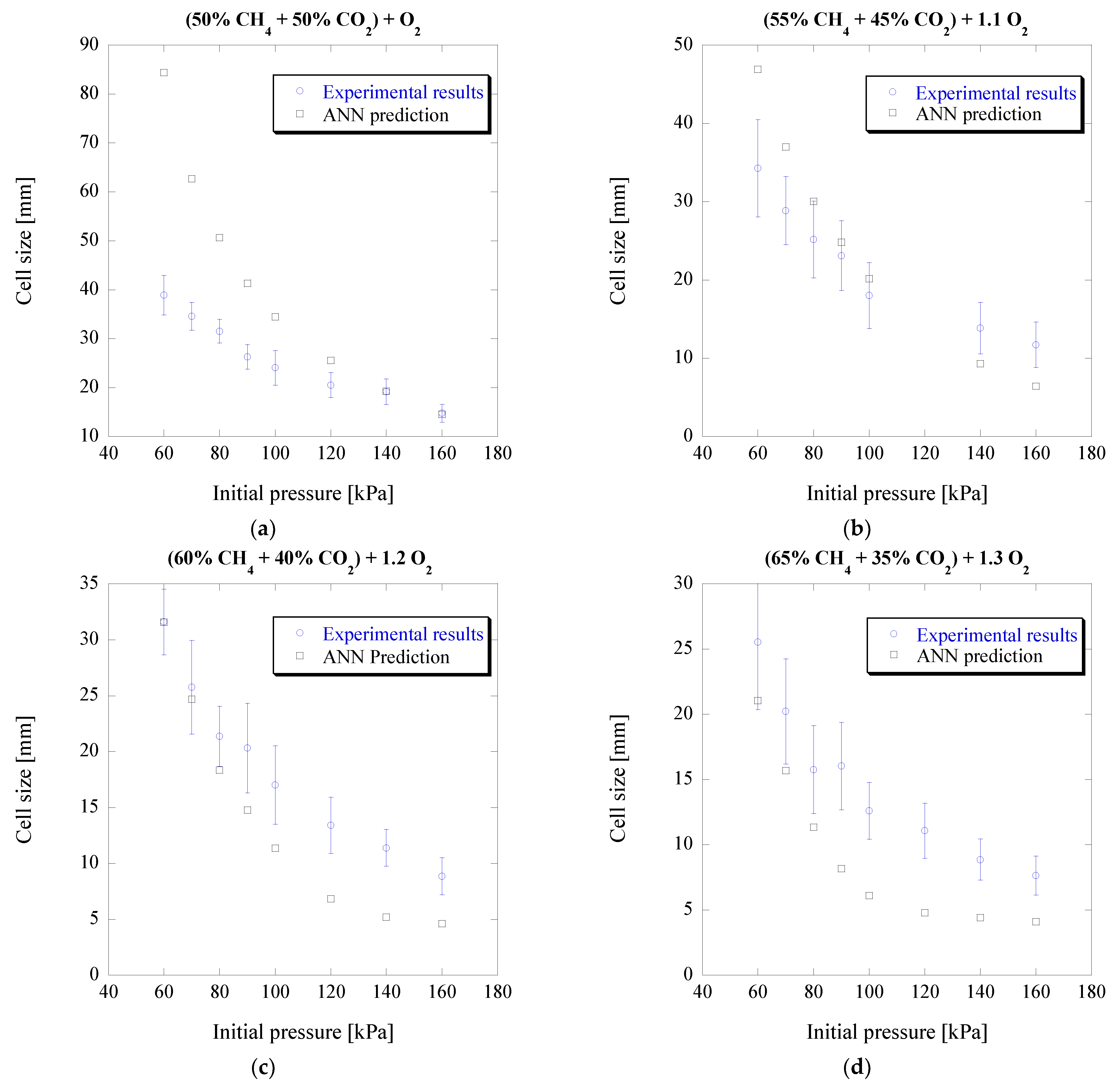
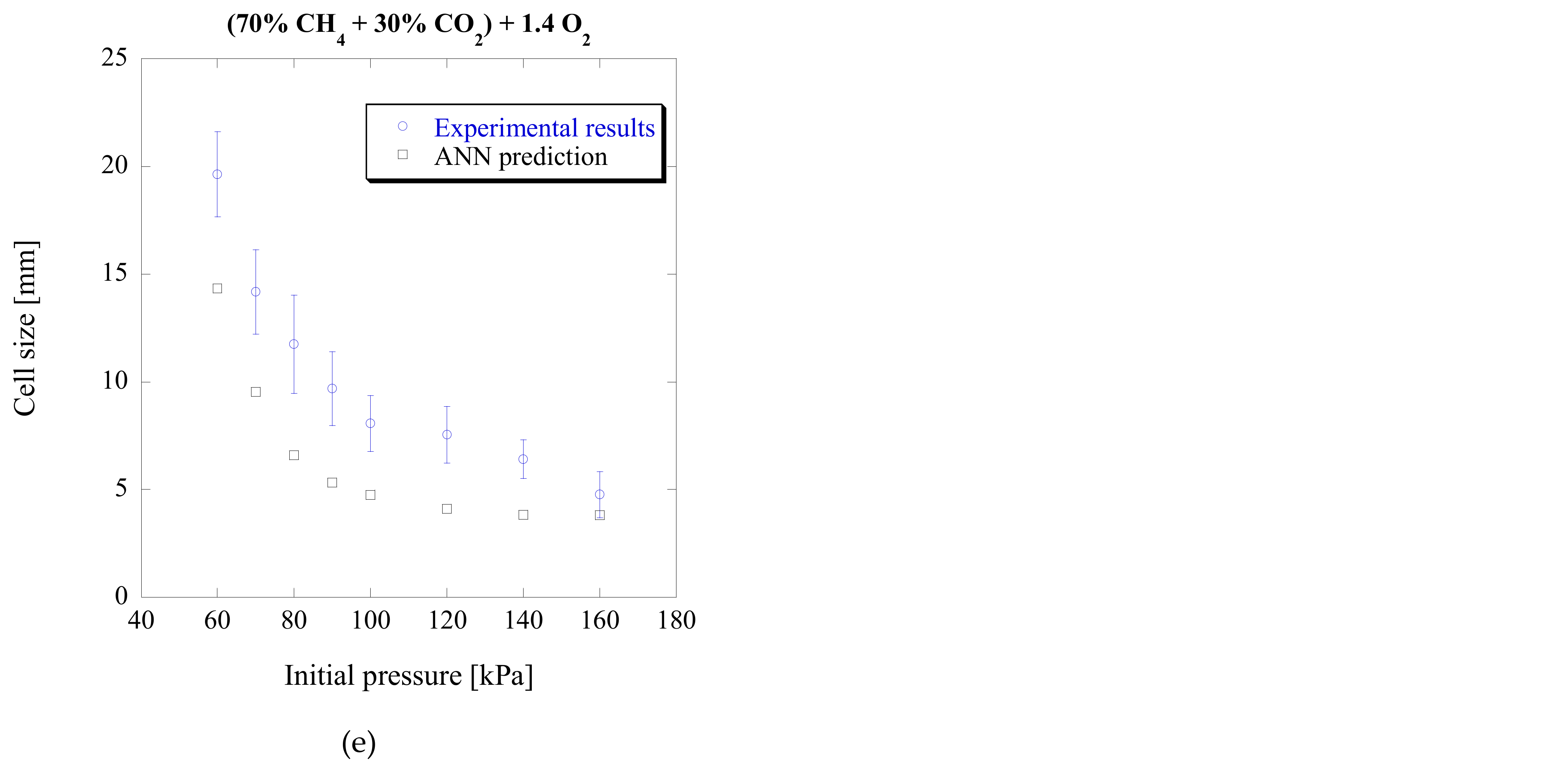
3.1. Biogas-Oxygen Mixtures (CH₄-CO₂-O₂)

In this study, the prediction limits and capabilities of the original ANN model [27] were further tested. This was accomplished using different combinations of reactive mixtures and initial conditions and different chemical kinetics, beyond those used during the training process of the ANN.

As a first step of this process, the experimental cell sizes of biogas–oxygen mixtures [7] were chosen to be compared with the ANN predictions. This fuel–oxidizer combination (CH₄-O₂) had been used in the ANN’s training process, but was now highly diluted with CO₂ at different initial conditions. For these mixtures, the chemical kinetic parameters were obtained using the Konnov’s-v.0.4 chemical kinetic mechanism, the same that had been used to create the original ANN model. The predicted and experimental cell sizes for these mixtures at different CO₂ concentrations and different initial pressures are portrayed in Figure 4.

As can be seen, good prediction accuracy can be achieved for most mixtures and initial pressures, with the exception of lower initial pressures of the first mixture (a) which has a high concentration of CO₂. The maximum difference among all the results shown in Figure 4 is 117%, close to about a factor of two. It is worth noting that for lower initial pressure conditions, the experimental data independence to measurement and the unstable cellular detonation behavior become significant. For lower pressure or off-stoichiometric conditions, the cellular detonation structure is irregular with a broad cell size distribution. It can easily be seen from [41] that the experimental measurement can be subjective and can often vary by a factor of two from one study to another, for instance, for nitrogen-diluted mixtures [42]. Taking into account the limited number of experimental data available only from one particular study for these mixtures, the irregularity of cellular patterns and the subjectivity of the cell size measurement from smoked foil, the present ANN model still provides a reasonably good prediction over a wide range of conditions for blended biogas-based mixtures.

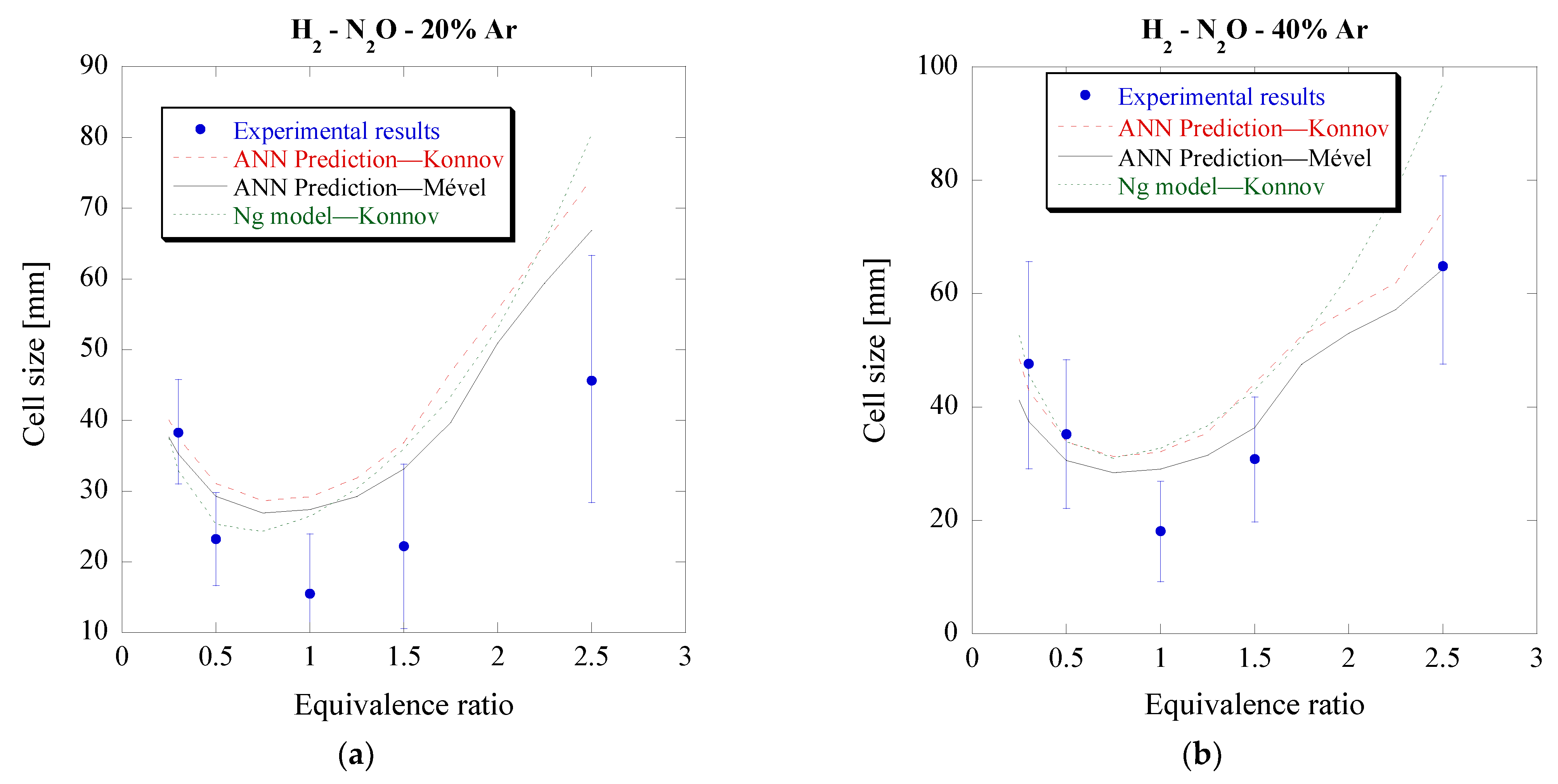
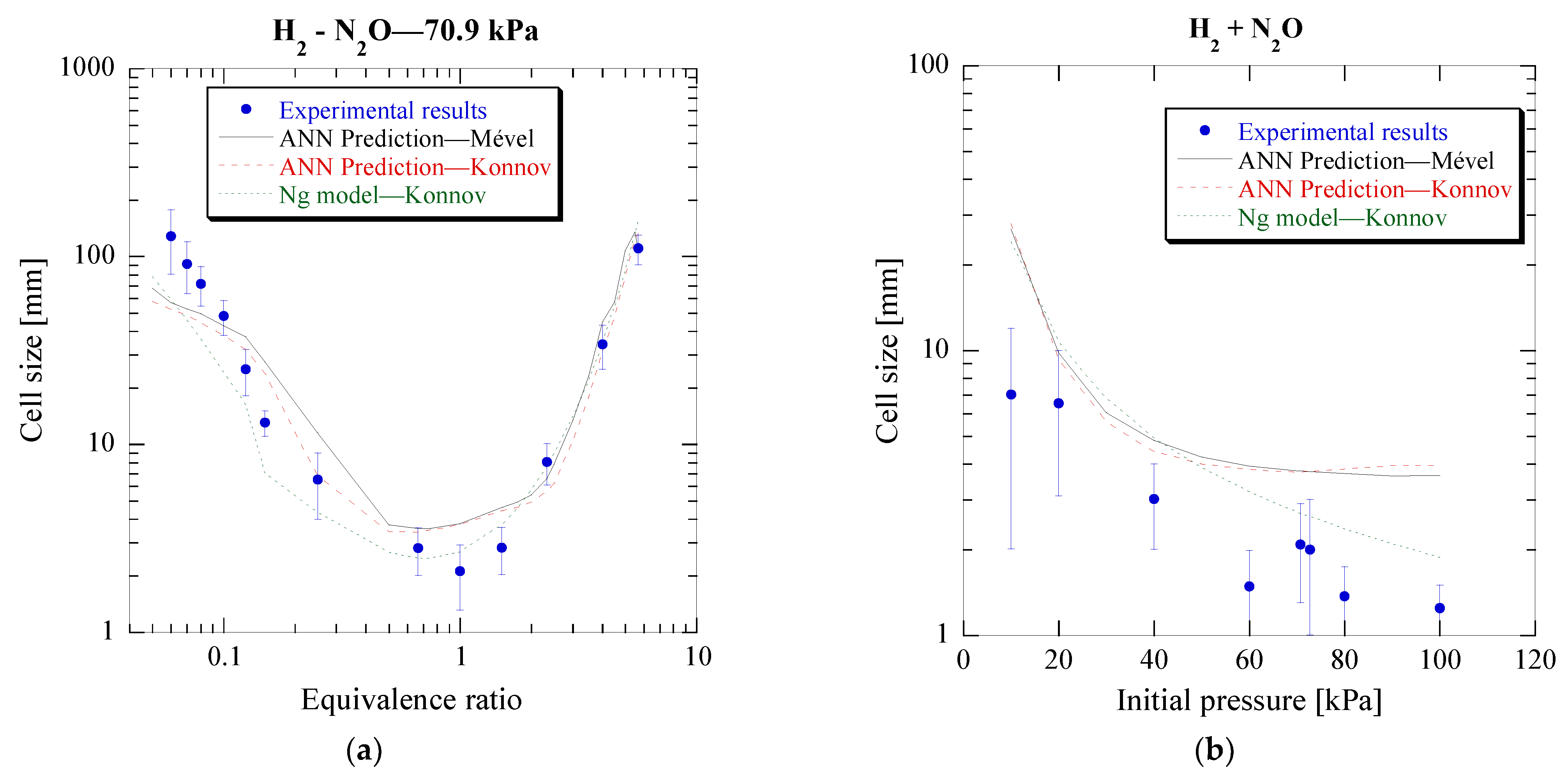
3.2. Hydrogen–Nitrous Oxide Mixtures (H₂-N₂O)

The next step of the validation process is dual. Firstly, it aims to test whether the model can accurately predict the cell size of fuels used in its training process but with a different oxidizer. Secondly, it seeks to determine whether the model is limited only to Konnov’s-v0.4 mechanism, which was used during its training process, or if any mechanism can be used to calculate the ZND parameters, provided that the mechanism is suitable for the specific mixtures and conditions that are studied. For this purpose, H₂-N₂O mixtures were chosen to be studied, with and without argon dilution, at different pressures and equivalent ratios, and compared to the experimentally obtained cell sizes [17,18,34]. The mechanisms used to obtain the chemical kinetic parameters were Konnov’s-v.04 and Mével’s mechanism. The predicted cell sizes for both mechanisms, along with the experimental values can be seen in Figure 5 and Figure 6. For reference, the predictions obtained using the simplified approach of Ng [22] are also included.

Overall, the ANN model can predict well the cell size of the argon-diluted H₂-N₂O mixtures, with a better prediction outcome for the 40% Ar diluted mixture. The predictions for undiluted H₂-N₂O mixtures are mixed, with good prediction error for certain initial pressures (P₀ = 20, 40 and 70.9 kPa) and worse but still acceptable for the rest. These results thus further support the hypothesis that the ANN model could be used to predict the cell size of mixtures outside those used during training. Similar predictions are obtained when using these two mechanisms, with a slightly larger difference for the argon-diluted mixtures. This outcome indicates that any mechanism could be used to compute the input features of the ANN model, provided that the mechanism is suitable for the specific mixture and initial conditions.

3.3. Ammonia–Oxygen Mixtures (NH₃-O₂)

The final step of testing and validating the ANN requires using a mixture not related to the ANN creation process. As a result, the detonation cell sizes of stoichiometric ammonia (NH₃)–O₂ and NH₃-O₂-N₂ mixtures were predicted using the ANN model and compared to the experimental values [17,18,40]. It is worth noting that NH₃ is less reactive than other commonly studied hydrocarbon fuels, and the detonability of NH₃-based mixtures is limited with respect to the mixture’s equivalence ratio. In the study by Jing et al. [43], no self-sustained detonation could be observed above ϕ = 2.2.

Once again, two mechanisms were used (Konnov’s and Mével’s) to compute the required chemical kinetic parameters. Figure 7 shows the calculated ZND induction lengths for both mechanisms for undiluted NH₃-O₂ reactive mixtures and Figure 8 shows the comparison between the predicted and experimentally measured cell sizes for these mixtures. The predictions for the NH₃-O₂ mixtures with N₂ dilution follow in Figure 9. The predictions obtained using the simplified approach of Ng’s [22] are also shown in both figures for reference.

Once again, the ANN model is proven to give a good prediction accuracy overall, for both mechanisms. This outcome, along with the previous results, strongly supports our hypothesis that the ANN can predict with a high level of confidence the cell size of gaseous detonations for mixtures and conditions beyond those used during its creation process. This is a particularly significant outcome, as experimental cell size measurements are generally limited in number, and in certain cases are very difficult to obtain. It should be noted that although the model has been proven so far accurate for a wide range of mixtures and conditions, the underlying limitations are still to be explored.

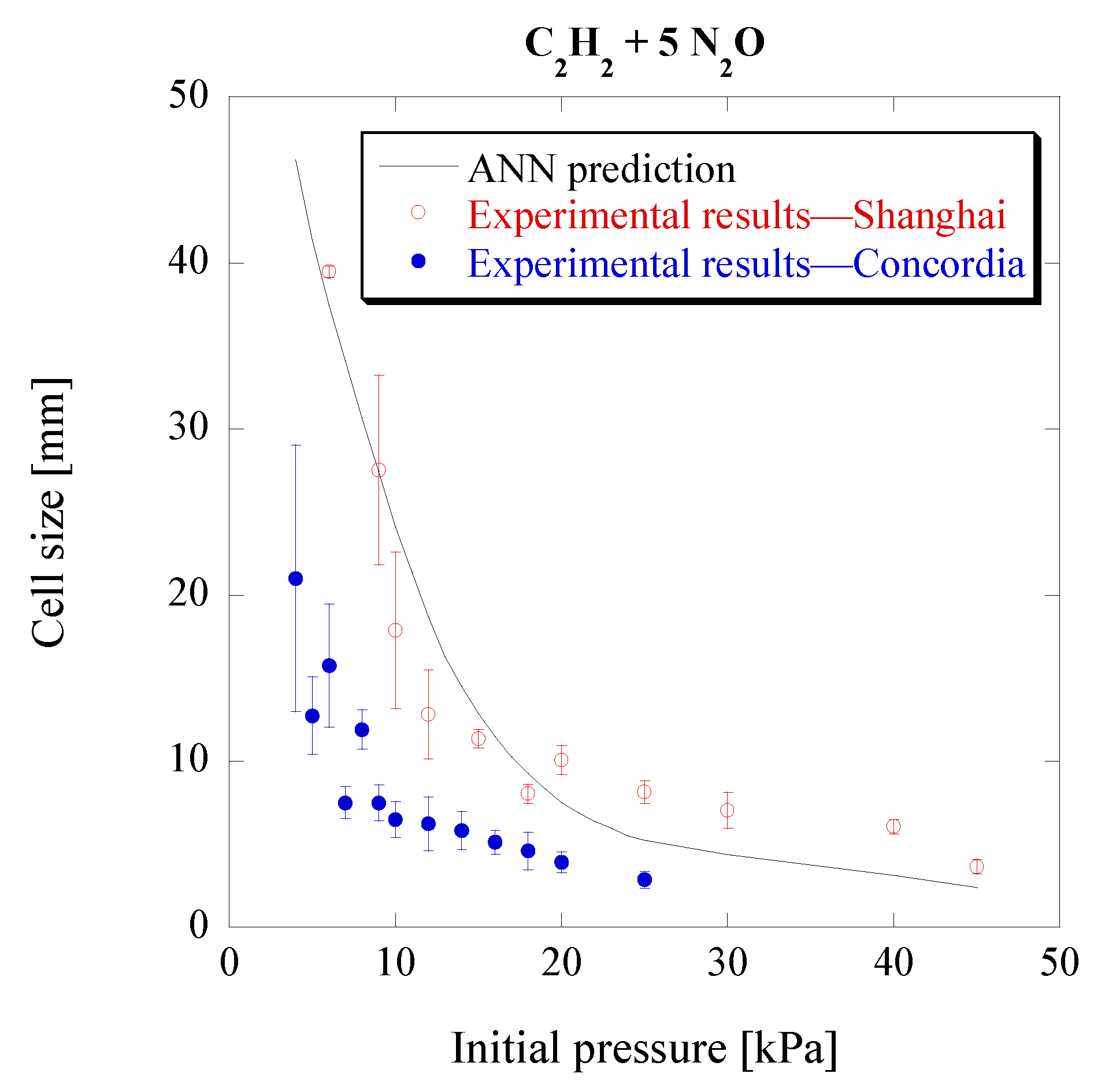
3.4. Acetylene-Nitrous Oxide Mixtures (C₂H–N₂O)

As seen previously, the model has been further validated for mixtures outside those used in its training process. Therefore, it could now be used as a tool to predict detonation cell sizes for specific mixtures and conditions in order to evaluate the actual experimental values. This could help identify errors in experimental setups or at least prompt further investigation when the measured values differ significantly from the expected ones, obtained from the ANN model. Given the limited amount of experimental cell size data, this could be particularly useful in newly studied mixtures. To that end, the model is used to predict the cell sizes for stoichiometric C₂H₂-N₂O mixtures at different initial pressures. These predictions are compared to experimental cell sizes from two different setups, one located at Concordia University and the second at Shanghai Jiao Tong University. The results can be seen in Figure 10.

The results show a close agreement of the ANN model with the experimental results from Shanghai Jiao Tong University, while for Concordia University it deviates, although still capturing the overall trend. Again, the cell size ratio of approximately two between the two facilities, although significant, is not uncommon in detonation studies, as can be observed from the experimental cell sizes found in the detonation database. The lower measured cell sizes of Concordia’s setup could possibly be attributed to the smaller size of the detonation tube, and thus a bigger influence of the boundary to the detonation propagation, and the large cell size variability at low pressures. Another factor could be the different geometries of the tubes, which have been shown to be impactful to the cell size [44]. Finally, the difference can also be due to the purity of the fuel from commercial cylinders, where acetylene gas is typically dissolved in acetone which may have an influence on the acetylene combustion characteristics [45].

Nevertheless, it is therefore shown that the ANN could indeed be a valuable tool in evaluating experimental cell sizes when similar measurements are not available for comparison in the literature.

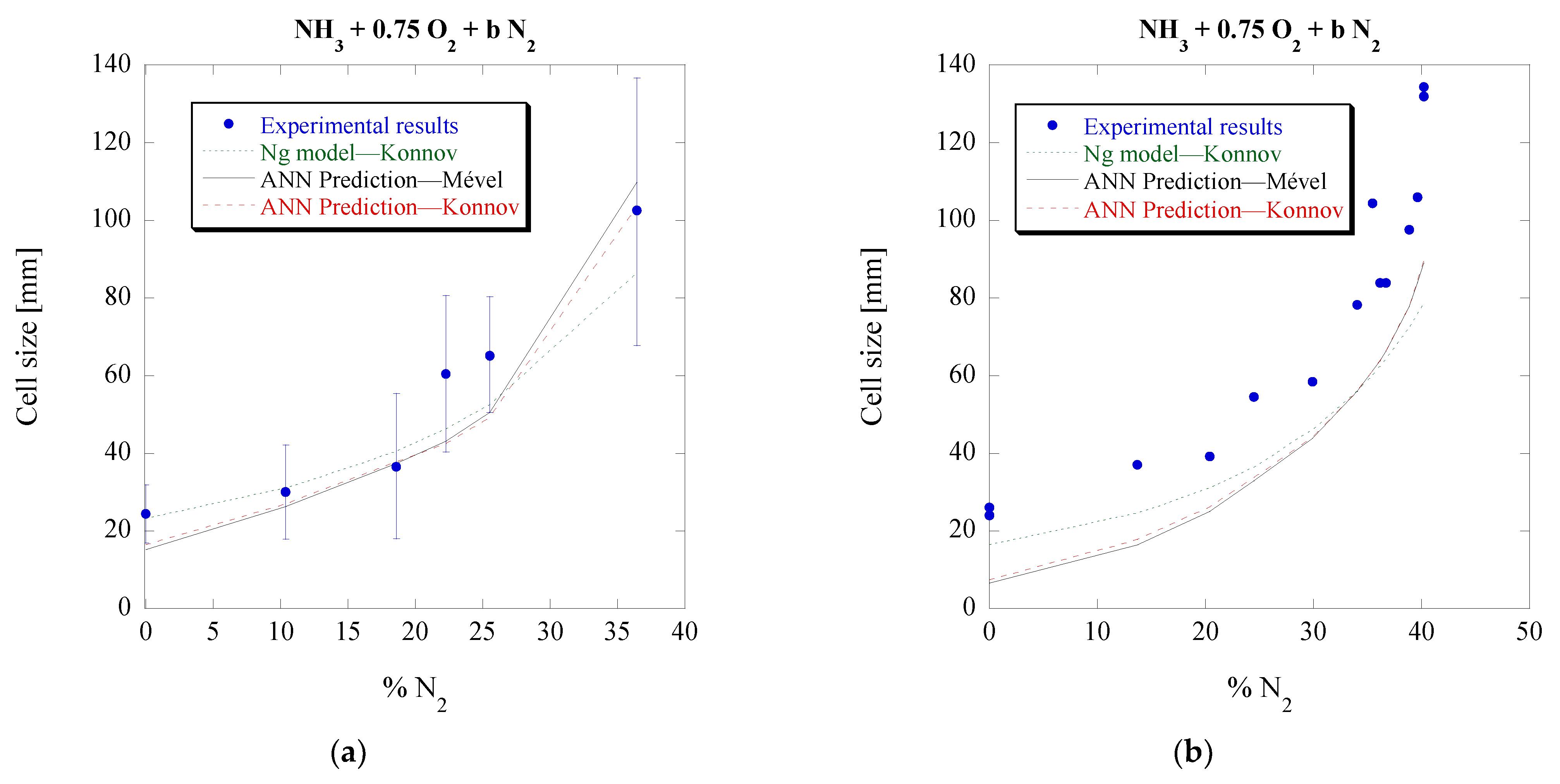
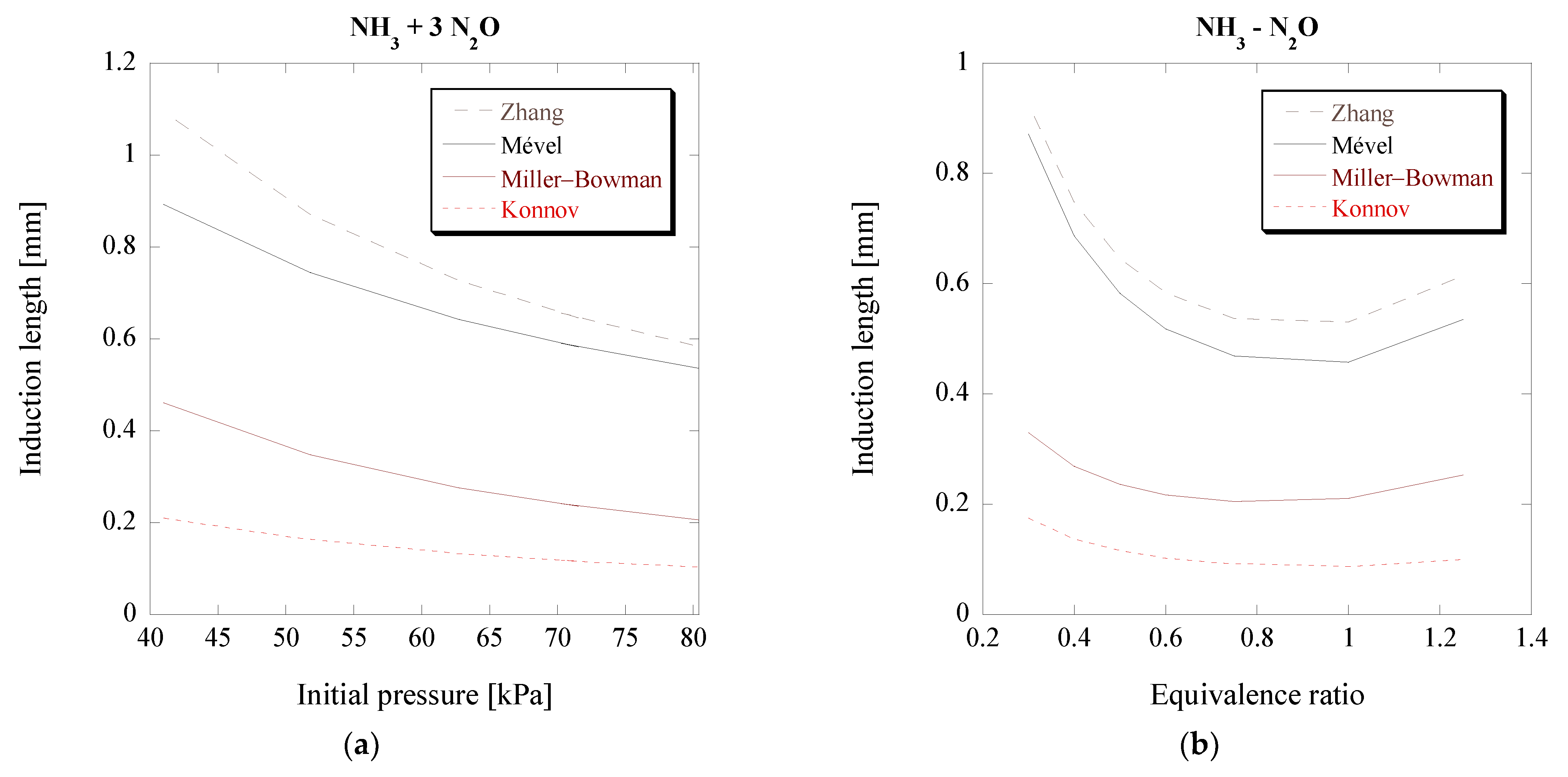
3.5. Ammonia-Nitrous Oxide Mixtures (NH₃-N₂O)

Finally, the cell sizes of NH₃-N₂O mixtures are chosen to be predicted by the ANN model. Unlike the previous mixtures, the NH₃-N₂O mixtures are challenging and require a careful approach in order to predict their cell size. The reason is that their detonation characteristics and calculated ZND parameters (M_CJ, Δ_I, ${\dot{\sigma }}_{\mathit{max}}$) of such mixtures can vary significantly based on the chosen chemical kinetics. This can be demonstrated from the difference in the calculated induction length between Konnov’s and Mével’s mechanisms for the same initial conditions, seen in Figure 11, along with two additional mechanisms, suitable for these reactive mixtures.

Contrary to the NH₃-O₂ mixtures, there are significant differences between the Konnov and Mével mechanisms, with the ZND induction length of Mével being almost four times the Δ_I calculated using Konnov’s mechanism. Considering that Δ_I is one of the three input features of the ANN, it is apparent that this significant variation will lead to very different cell size predictions for the two mechanisms, thus necessitating the use of additional mechanisms that are specifically calibrated for these mixtures. These significant differences between the two mechanisms also bring a unique opportunity for the ANN: to determine which chemical kinetic mechanisms that are tuned for NH₃-N₂O combustion are suitable to be used for detonation studies of these specific mixtures at these initial conditions. Hence, two additional mechanisms are considered. The first was developed by Miller and Bowman and was shown to be the most suitable one for such mixtures in a previous study by Kaneshige et al. [18], while the second mechanism was recently developed by Zhang et al. [35]. The induction lengths for both can be seen in Figure 11. Additional mechanisms, calibrated for NH₃-N₂O mixtures, were considered, specifically those by Han et al. [38] and by Otomo et al. [37]. Using these last two mechanisms, a much higher induction length, and thus predicted cell size, was obtained, and therefore they are not portrayed in the figures. 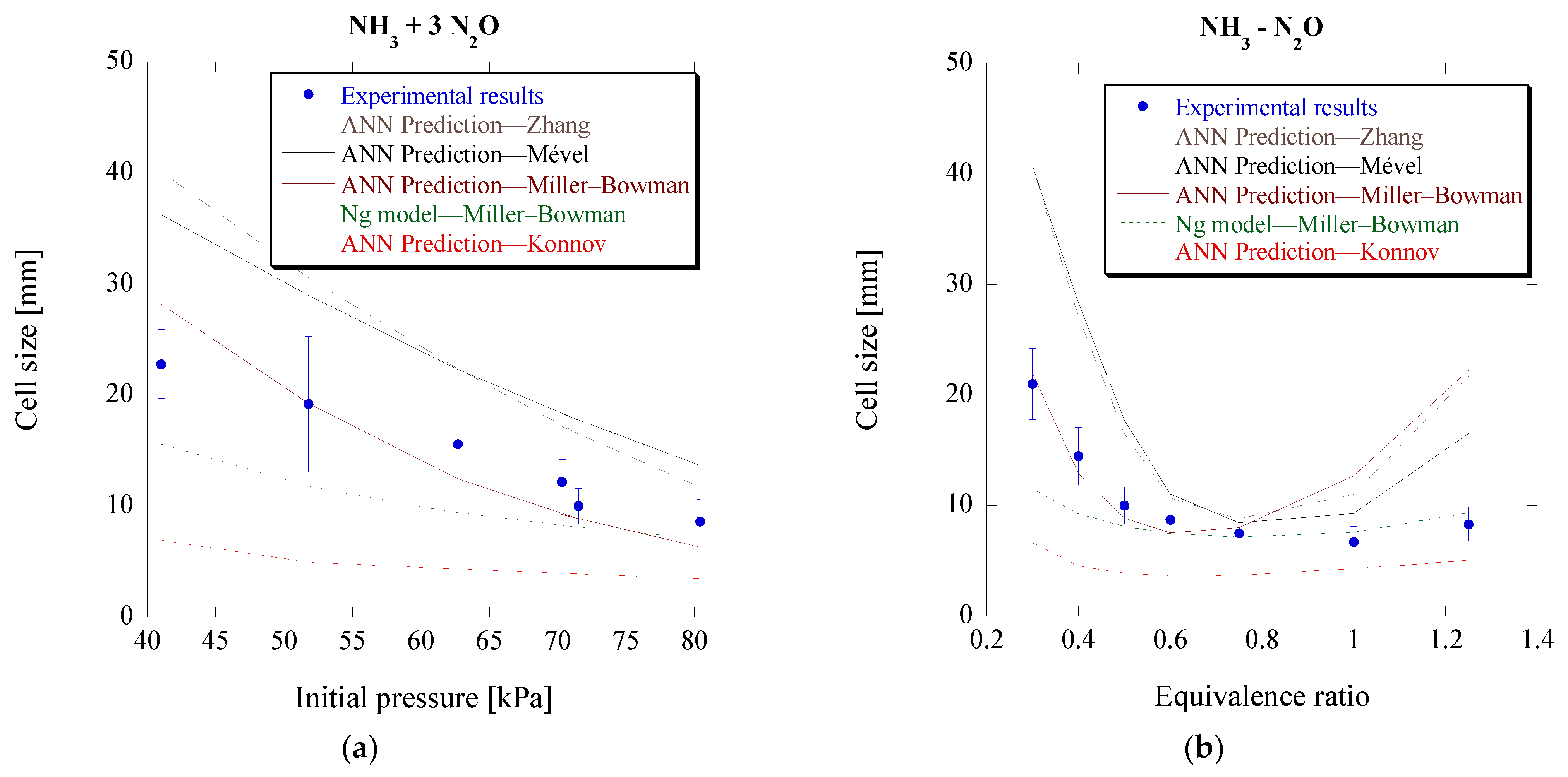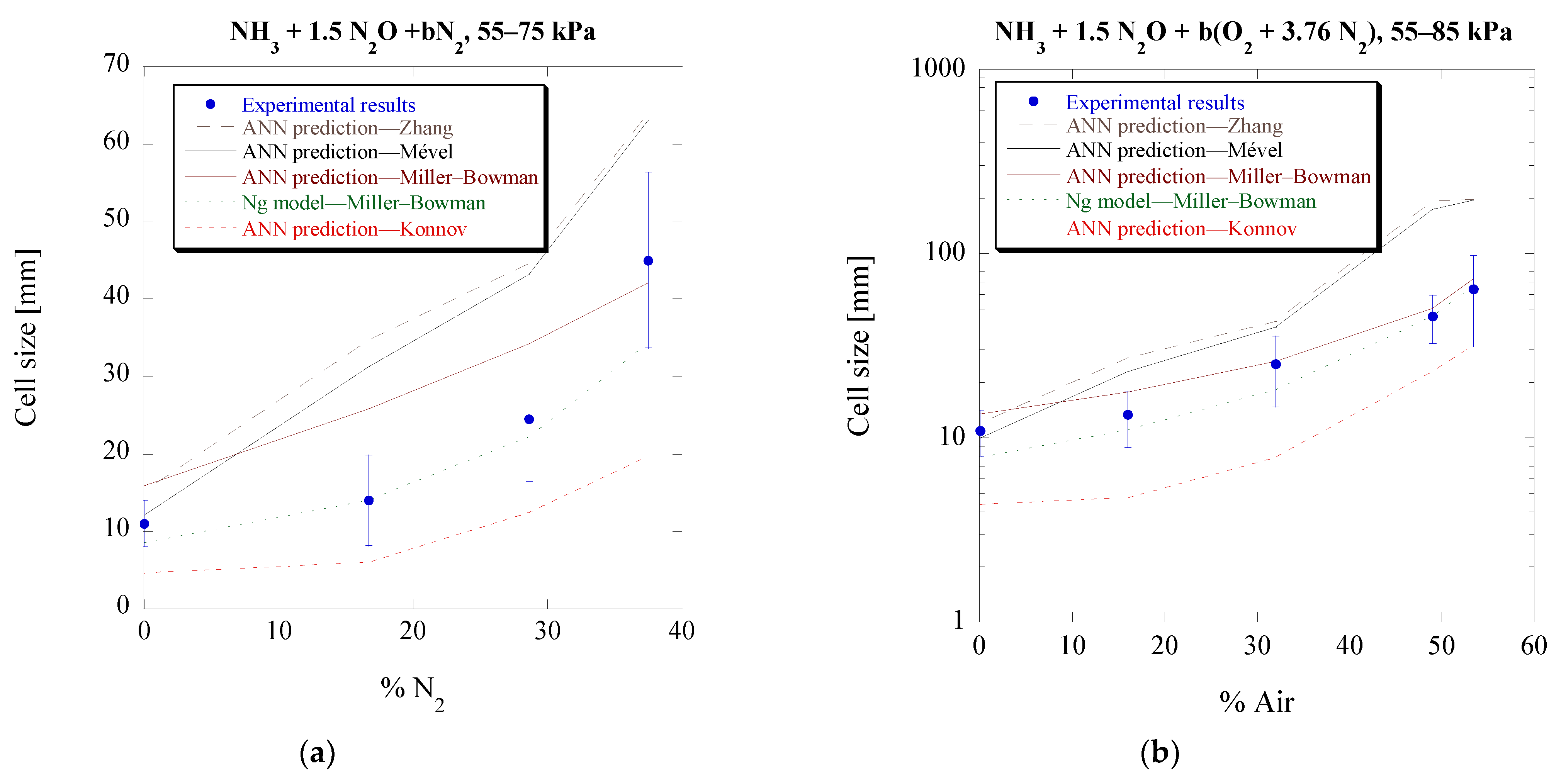The predictions for the four mechanisms that were used along with the actual experimental results can be seen in Figure 12 and Figure 13. In addition, for reference, the predictions using Ng’s model coupled with the mechanism by Miller and Bowman [22] are also included in these plots.

Overall, all mechanisms seem to give an acceptable prediction for the mixtures and conditions that are considered here. Konnov’s mechanism seems to be the only one leading to an under-prediction of the cell size, while the rest lead to an over-prediction. As expected, based on the difference in induction length, there are significant cell size differences between Konnov’s and Mével’s mechanisms. Out of all mechanisms, the Miller–Bowman one has the lowest prediction error, at an average of about 30%. The ANN therefore recognizes that this is the best mechanism to be used for numerical studies of NH₃-N₂O detonations at these conditions. It should be noted though that the Miller–Bowman mechanism was found to be only suitable for NH₃-N₂O mixtures, as it was unable to correctly predict the cell sizes for the NH₃-O₂ mixtures. These findings could also explain why the previously created model by Ng [46], which relies on Δ_I to predict cell size, is over-predicting the cell sizes in the study of Weng et al. [40]. As shown in Figure 11, Zhang’s mechanism has a higher induction length compared to the mechanism by Miller and Bowman.

Another observation is that the discrepancies between the experimental data and predictions for off-stoichiometric conditions are more significant, but still within a factor of two. As mentioned before, NH₃-based mixtures are more unstable and have narrower detonability limits. The experimental data are obtained from one study [40] with a tube diameter of 78 mm. As discussed before, such discrepancies can stem from the uncertainty due to the unstable nature of the cellular detonation and the challenge of determining the unique cell size at near-limit conditions. For those cases, more experiments from different facilities, as shown in Figure 10, would be desirable to further validate the predictions.

In general, considering all the data used for the model development, Ng’s model gives a mean error of 46.3% as reported in [22], which is higher than that of the ANN model (i.e., 22.3%, as shown in [27]). For the results of Figure 12 and Figure 13, Ng’s model still provides a good prediction with an average error of 20.7%, while the ANN model gives a relatively good value of 30.4%. It is worth noting that if the two outliers from the 23 data points are neglected, the average error for the ANN model would significantly improve to 20.6%.

3.6. ANN Model Expansion and Improvement

The ANN model, as mentioned previously, was developed using 388 cell size values, with the assumption that it could be further expanded and potentially improved by including more cell size data as they become available, preferably from mixtures that were not previously considered. To test that assumption, 102 additional data rows were included, with the mixture specifics shown in

Table 1. Mixture compositions and initial conditions for all additional cell size data considered in the new model.

Mixture	Initial Condition	Variation	Reference
50% CH4–50% CO2/O2 55% CH4–45% CO2/O2 60% CH4–40% CO2/O2 65% CH4–35% CO2/O2 70% CH4–30% CO2/O2	T0 = 293 K; ϕ = 1	P0 = 60 kPa–160 kPa	Siatkowski et al. [7]
NH3/O2	T0 = 295 K; ϕ = 1	P0 = 42.6 kPa–100.1 kPa	Weng et al. [40]
NH3/O2	T0 = 295 K; P = 71.5 kPa	ϕ = 0.6–1.5	Weng et al. [40]
NH3/O2/N2	T0 = 293 K; ϕ = 1	P0 = 66.9–81.1 kPa	Akbar et al. [17]
NH3/O2/N2	T0 = 295 K; P = 101 kPa	0–40% N2	Kaneshige et al. [18]
H2/N2O/Ar	T0 = 295 K; P = 10 kPa	ϕ = 0.3–2.5	Mével [34]
H2/N2O	T0 = 295 K; P = 70.9 kPa	ϕ = 0.05–6	Akbar et al. [17]
H2/N2O	T0 = 295 K; ϕ = 1	P0 = 10–100 kPa	Kaneshige et al. [18]

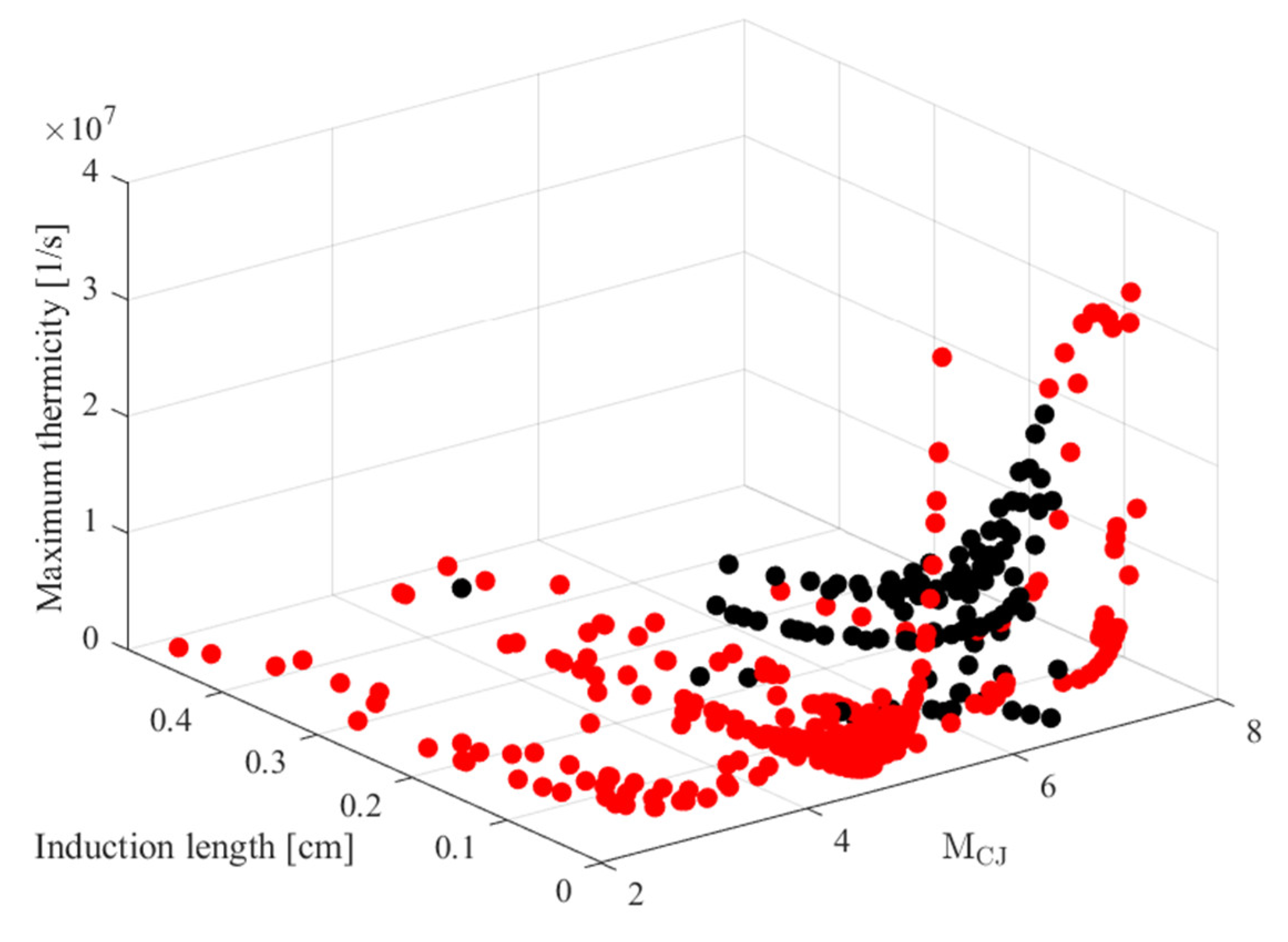
. These correspond to the majority of the experimental cell sizes that were presented previously in this section. Figure 14 also shows in red the range of the original data used in [27] and in black the new additional data considered in the previous sections. Specifically, the original model used inputs from a range of [2.29, 7.60], [8.96 × 10⁻⁵, 1.875 × 10¹] (cm), and [3.25 × 10⁴, 5.19 × 10⁸] (1/s) for the detonation Mach number (M_CJ), the ZND induction length (Δ_I), and the maximum thermicity (${\dot{\sigma }}_{\mathit{max}}$), respectively, and the additional data are within [4.79, 6.61], [4.93 × 10⁻³, 4.50 × 10⁻¹] (cm), and [2.90 × 10⁵, 2.81 × 10⁷] (1/s). This highlights, for the comparison presented before, that the input conditions are within the training set which already covers a wide range in the original ANN construction.

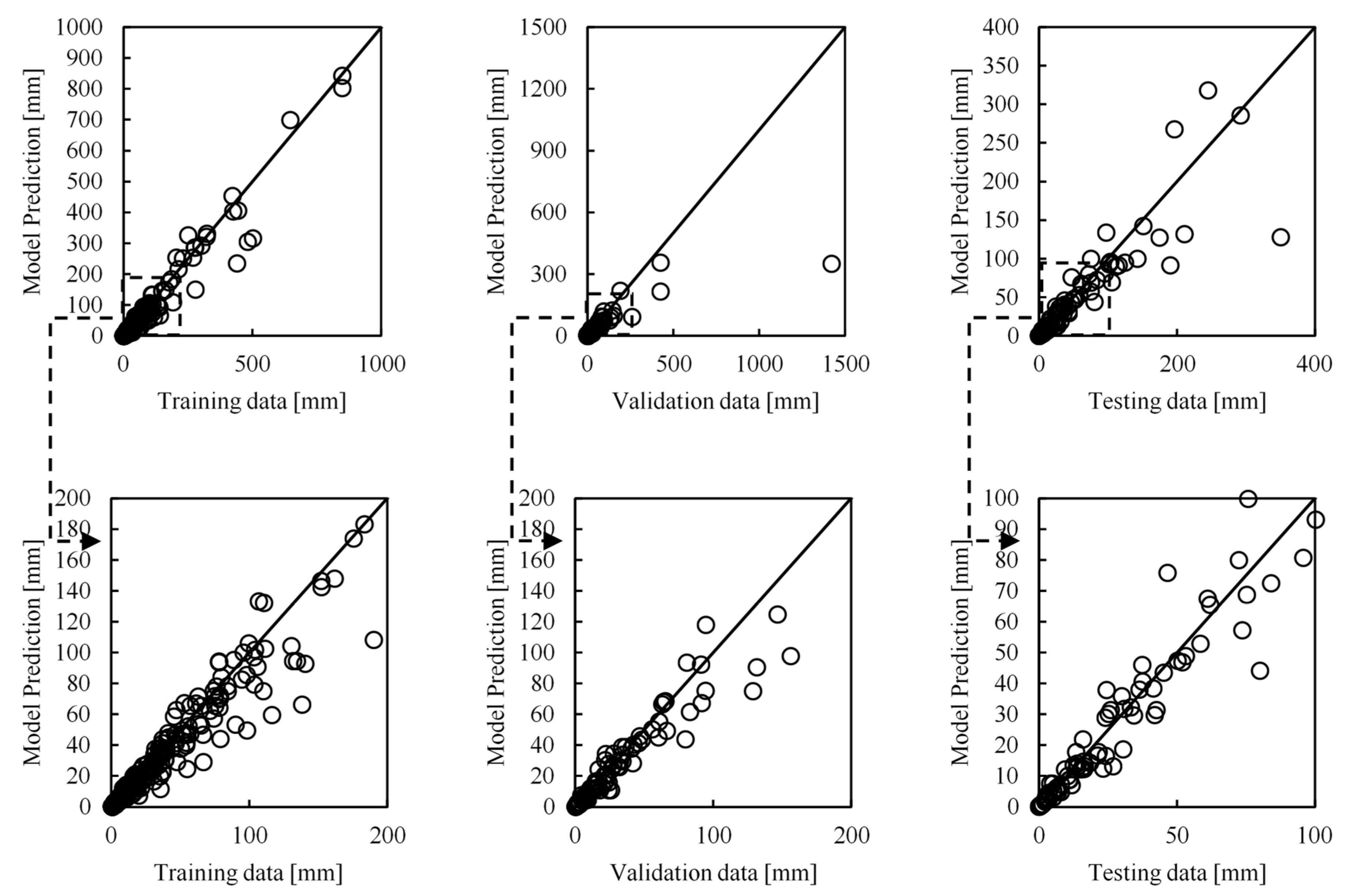
Using these additional data points, we updated the neural network, following the same training, validation, and testing process that had been used for our initial model [27] and is illustrated in Figure 3. The updated model, trained on the new dataset, had again four hidden layers, but now with 480, 248, 80 and 34 neurons on each layer, and approximately 144 thousand trainable parameters. The prediction analysis of this model for each one of the training, validation, and testing datasets can be seen in

Table 2. Error analysis of updated model using the training, validation, and testing data.

	Training Data	Validation Data	Testing Data
Count	294	98	98
Mean error %	14.5	22.4	20.7
Std	13.3	22.1	16.4
Minimum	0.042	0.068	0.349
25%	5.17	5.92	7.62
50%	10.3	15.5	18.9
75%	20.3	32.3	30.3
Maximum	67.3	120	88.5

and Figure 15.

As can be seen, this updated model shows an improved performance compared to the initial model, as the mean error % for the testing data, which determines the performance of the network, has dropped by 1.5% to 20.7%. The standard deviation has also decreased by 1.5%, while 75% of the data still has an error lower than 30.3%. Similar improvement can be seen for the training data, while there is an error increase of 1% for the validation data. Therefore, the ANN model has clearly improved by introducing more experimental raw data from different mixtures to the training process of the model. This clearly supports our hypothesis that the model can be further improved by using more data to retrain it. An additional comparison is performed for the two models using the initial and final datasets, with the results seen in

Table 3. Mean error % comparison of the initial and updated models for the two datasets.

	Initial Model	Updated Model
Initial dataset	0.193	0.176
Final dataset	0.242	0.173

.

As expected, there is a clear improvement in the mean error % with the second model. Regarding the first model, the error difference between the two datasets again supports using the ANN to predict cell sizes of mixtures and conditions outside those used during their training process. As for the updated model, it is shown to maintain an almost identical mean error % for both datasets.

The mean standard deviations and the mean errors shown in Table 2 and Table 3 express the variability of predictions by the ANN model and provide an indication of the uncertainty in the estimate of the mean. To further illustrate the errors or uncertainties in the model estimates in a different range of conditions, Figure 16 shows the Bland–Altman plots [47], where the illustrations are a combination of the predicted cell sizes from the ANN model and the actual (experimental) cell sizes. In the X-axis, the average of the two is given, and in the Y-axis is the difference (i.e., prediction–actual).

From these plots, a higher prediction accuracy is shown in the cell size region of 0–200 mm for all three datasets (almost all within the confidence level of the average difference). A larger scattering is indeed expected at the larger cell size range as these are usually related to conditions near limits (e.g., low initial pressure, off-stoichiometric conditions, or as a result of physical boundary effects), where measurement data are scarce and cell patterns are highly irregular, from which the characteristic dominant cell size is difficult to measure.

4. Concluding Remarks

In this study, a previously developed ANN model was used to predict the cell size of gaseous detonations for a wide range of reactive mixtures at different initial conditions. The reactive mixtures comprised biogas, acetylene, hydrogen, and ammonia fuels oxidized with air, O₂, and N₂O. The predicted cell sizes were compared to the corresponding experimental cell size measurements, showing for most mixtures and conditions a good agreement between experiments and ANN predictions. This outcome is promising, as these are mixtures and conditions beyond those used for the model’s training reported in [27]. These results thus support the potential use and extension of this three-feature ANN model for other reactive mixtures, provided that the chemical kinetic parameters could be accurately computed. This tool is particularly useful as there are certain reactive mixtures or specific conditions that make experimental measurements challenging, thus leading to very limited or even non-existent experimental cell size data in the literature. Naturally, the accuracy of the model is highly linked to the input parameters, which are functions of the thermo-chemical data and chemical kinetic mechanism. A larger error in the prediction is also expected for mixtures in which the detonation structure is highly unstable with irregular cellular patterns. The ANN may require further training and validation with more experimental data for those mixtures to pinpoint the underlying limitations of the model, and also revisiting the ANN formulation with more advanced concepts, e.g., [48,49], to address the model uncertainty and sensitivity.

Aside from the model’s validation, this study had two further useful outcomes. The first was recognizing the potential use of the model to evaluate experimental setups and identify those that produce cell sizes that deviate from the expected values, so that they can be rectified, or at least explain these deviations, as is the case with different tube geometries. For stoichiometric C₂H₂-N₂O, which has limited experimental data in the literature, it was found that one of the two setups had lower experimental values compared to the ANN model predictions, with possible explanations involving the experimental uncertainty, impurities in the C₂H₂, the smaller tube dimensions, and the difference in the geometry of the cross-section. The other outcome is that the model could be used to identify which chemical kinetic mechanisms should be considered for detonation studies of reactive mixtures that still present challenges, such as the NH₃-N₂O mixture. For that mixture, different mechanisms predicted different ZND characteristics. According to the ANN model, the Miller–Bowman mechanism was found to be the best option for these mixtures. Nonetheless, the large discrepancies between different chemical kinetic mechanisms suggest that further studies are needed to revisit the reaction pathway for this specific NH₃-N₂O mixture even at detonation conditions.

Finally, it was shown that the ANN model can be updated and improved when additional experimental data are used to retrain the model. In addition, although the ANN model indirectly considers the unstable nature of the detonation structure by having the three input features that affect the detonation instability, it still remains a type of correlation for the cell size output. In future works, physics-inspired or phenomenological models such as [50], which include physical mechanisms for detonation cell generations could be considered and coupled with a similar ANN framework for the required input prediction (e.g., kernel size) for model closure. Methods such as those used in assessing chemical kinetic mechanisms could help in evaluating prediction uncertainty and model limitations [51,52].