Effect of Rotational Angle of Discrete Inclined Ribs on Horizontal Flow and Heat Transfer of Supercritical R134a
Abstract
1. Introduction
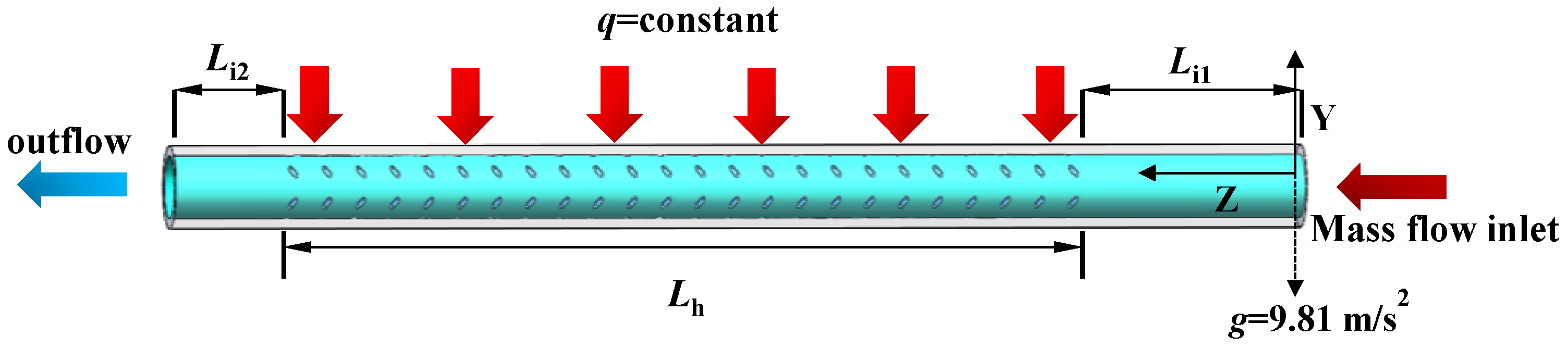
2. Numerical Modeling
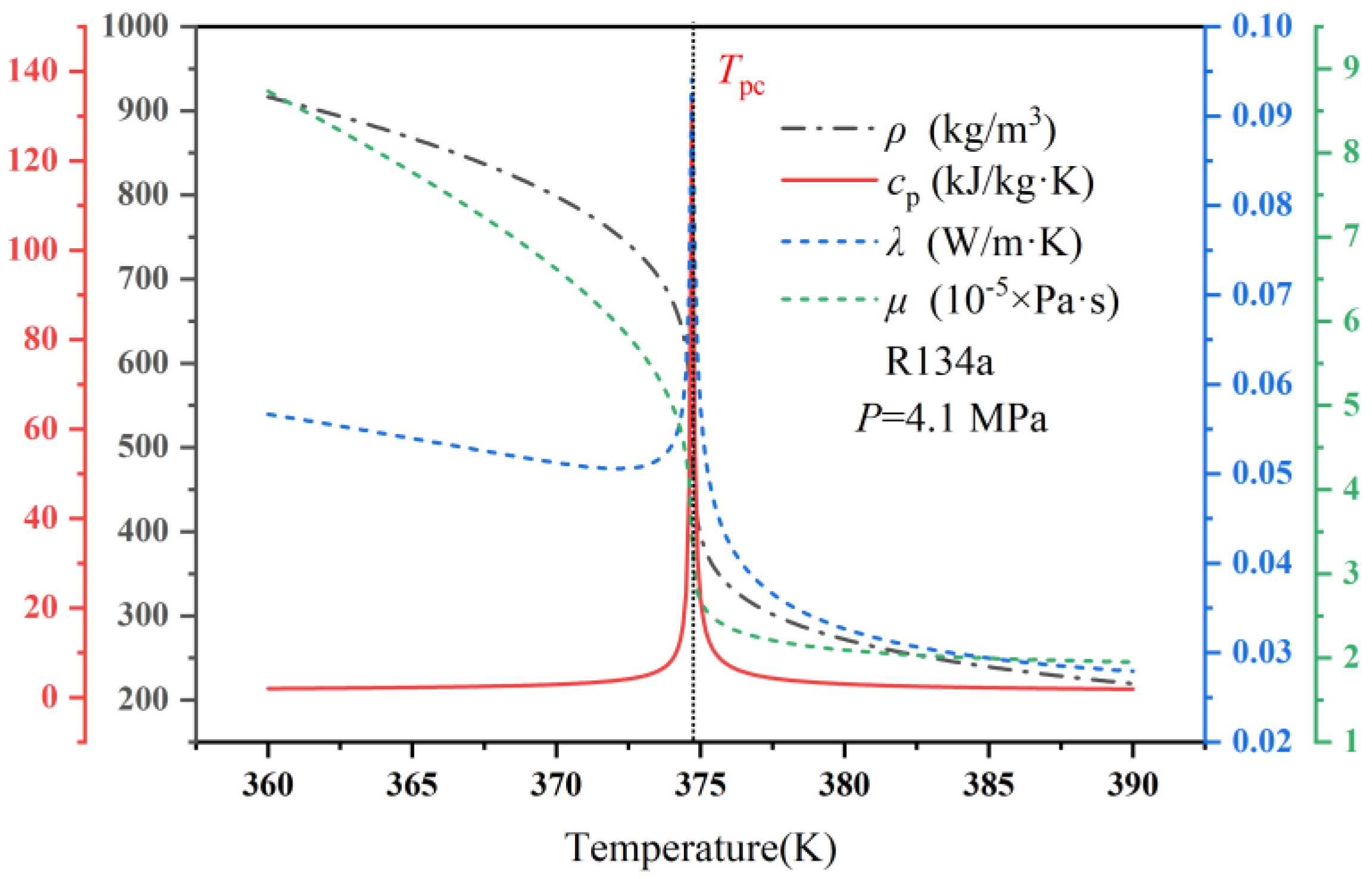
2.1. Control Equations
2.2. Turbulence Models
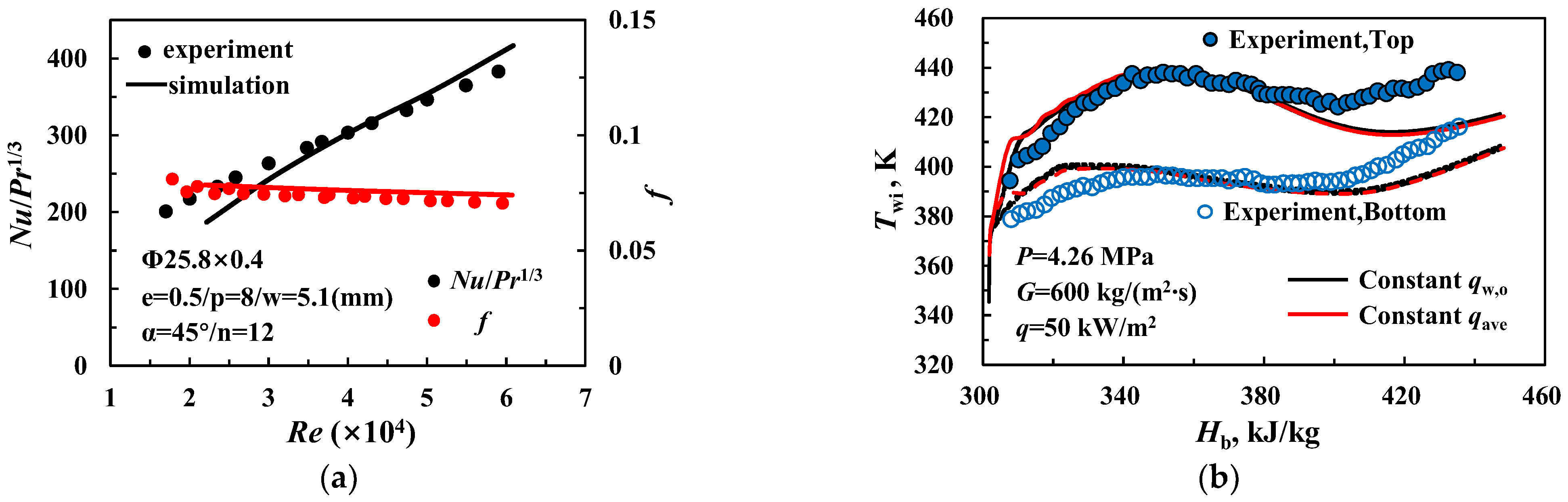
2.3. Model Validaton
2.4. Grid Independence Validation
3. Results and Discussion
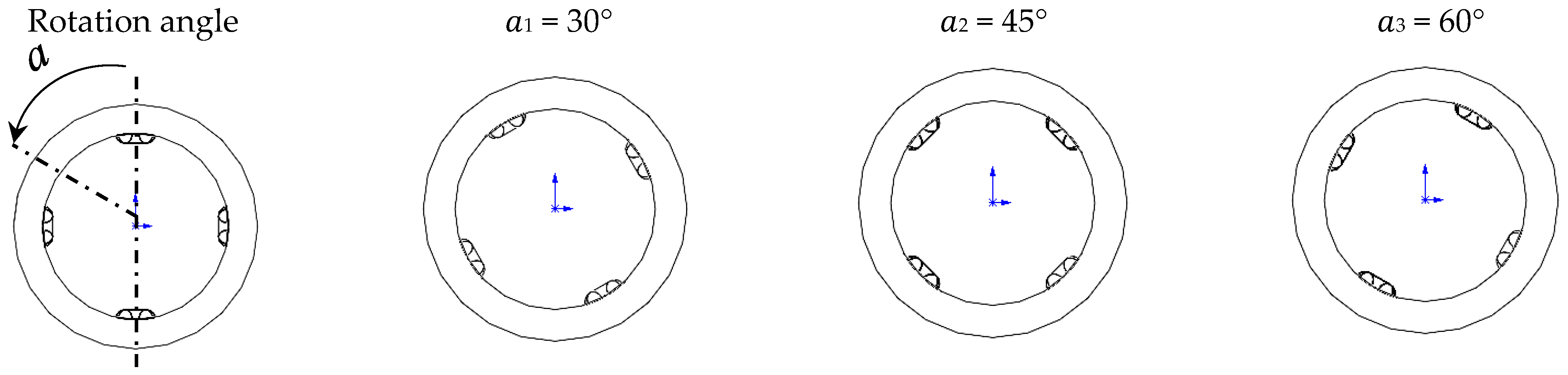
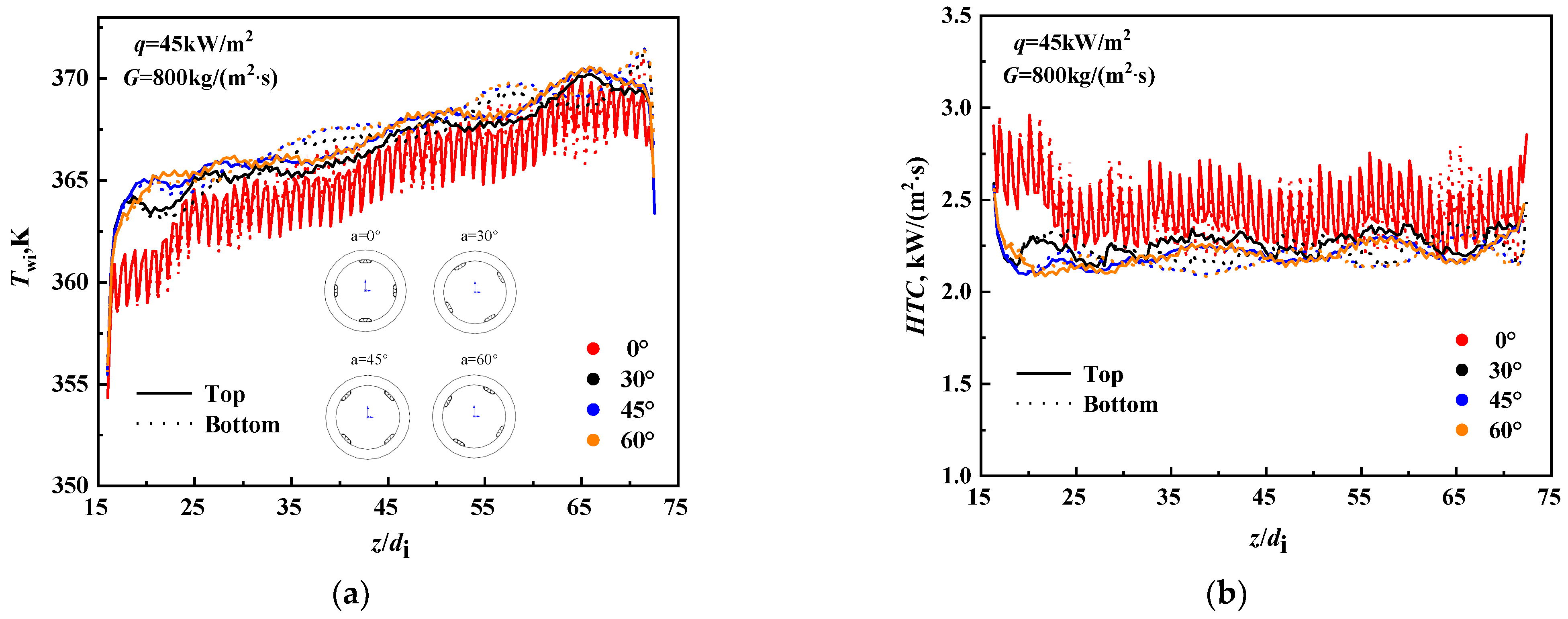
3.1. Influence on Axial Heat Transfer Characteristics
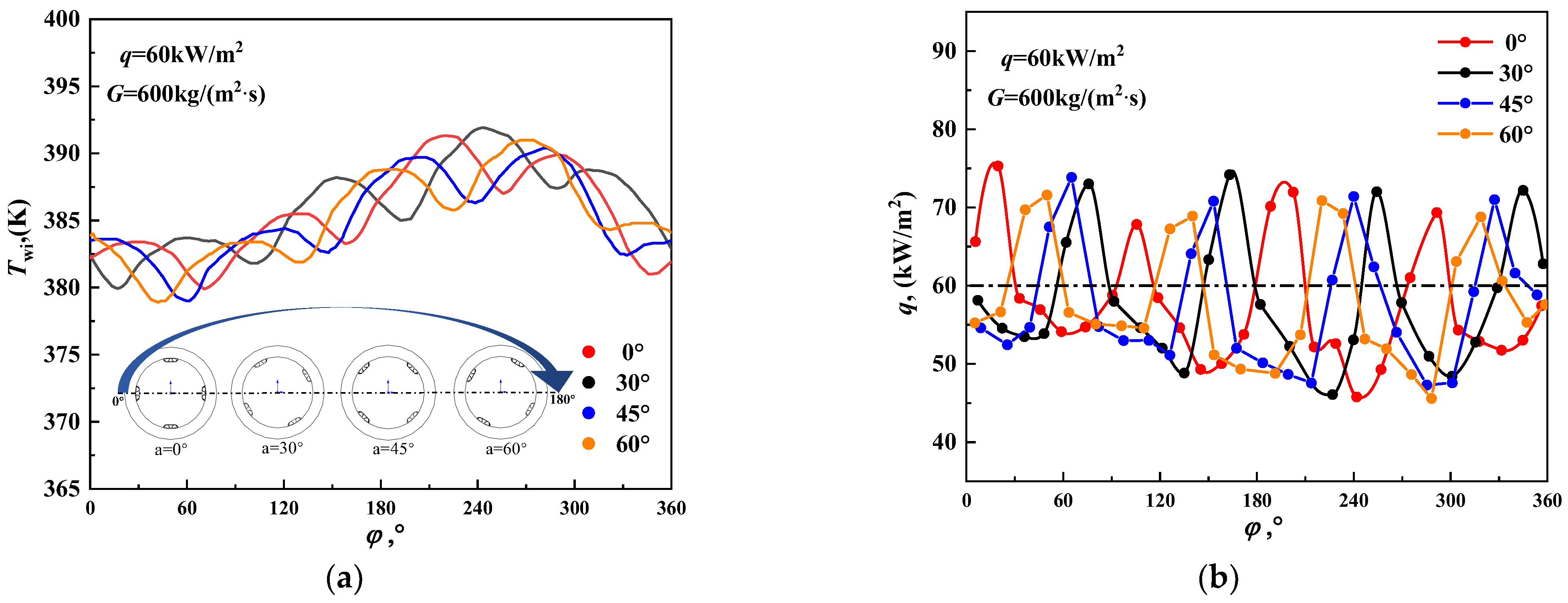
3.2. Influence on Circumferential Heat Transfer Characteristics
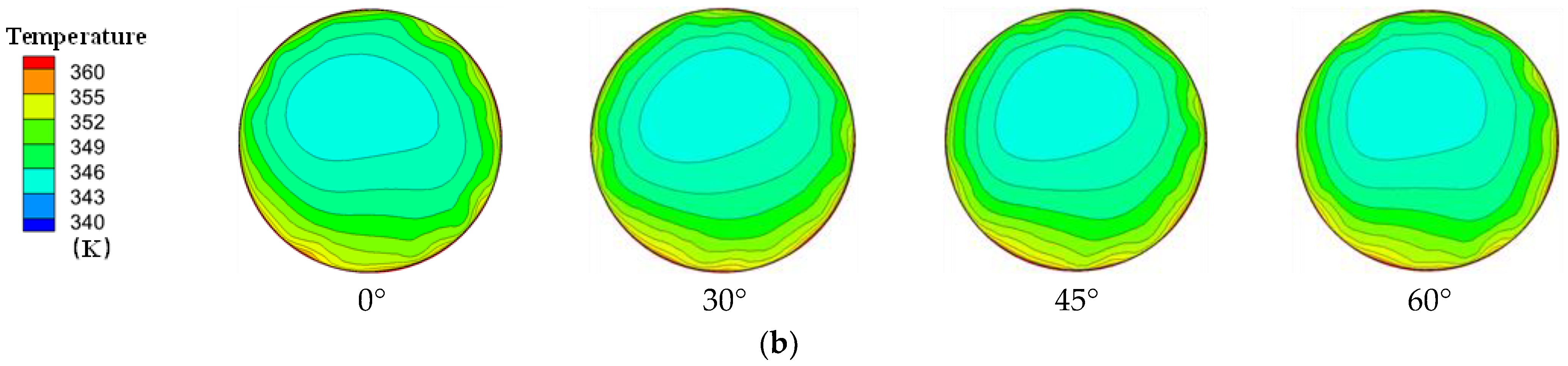
3.3. Analysis of Impact Mechanism
4. Conclusions
- Under the influence of strong buoyancy, a noticeable circumferential thermal unevenness persists in the DDIR horizontal tube. However, the temperature distribution of the top and bottom inner walls exhibits alternating periodic fluctuations, differing from the traditional supercritical horizontal flow. As the buoyancy weakens, the temperature fluctuation amplitude of the top and bottom inner walls in the DDIR horizontal tube decreases.
- The number of rib groups in the circumferential direction of the DDIR horizontal tube determines the fluctuation period of the circumferential inner wall temperature and inner wall heat flux. However, the change in the rotation angle of the inclined discrete ribs along the axial direction does not have a significant impact on the axial heat transfer or the distribution of circumferential wall temperature and inner wall heat flux in the DDIR horizontal tube.
- The change in the rotation angle of the inclined discrete ribs does not significantly affect the supercritical R134a flow field in the DDIR horizontal tube. Its impact is mainly observed in the position of the circumferential inner wall temperature and the inner wall heat flux peak. The relative positions between the peaks depend on the differences in rotation angles.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| insulation section I | |||
| insulation section II | |||
| in | |||
| Acronyms | |||
| UDF | user-defined functions | ||
| Greek symbols | |||
| Subscripts | |||
References
- Liu, P.; Shu, G.; Tian, H.; Feng, W.; Shi, L.; Wang, X. Experimental study on transcritical Rankine cycle (TRC) using CO2/R134a mixtures with various composition ratios for waste heat recovery from diesel engines. Energy Convers. Manag. 2020, 208, 112574. [Google Scholar] [CrossRef]
- Buonomano, A.; Calise, F.; Palombo, A.; Vicidomini, M. Energy and economic analysis of geothermal–solar trigeneration systems: A case study for a hotel building in Ischia. Appl. Energy 2015, 138, 224–241. [Google Scholar] [CrossRef]
- Walraven, D.; Laenen, B.; D’Haeseleer, W. Economic system optimization of air-cooled organic Rankine cycles powered by low-temperature geothermal heat sources. Energy 2015, 80, 104–113. [Google Scholar] [CrossRef]
- Yu, G.; Shu, G.; Tian, H.; Wei, H.; Liang, X. Multi-approach evaluations of a cascade-Organic Rankine Cycle (C-ORC) system driven by diesel engine waste heat: Part B-techno-economic evaluations. Energy Convers. Manag. 2016, 108, 596–608. [Google Scholar] [CrossRef]
- Wang, D.; Dai, X.; Tian, R.; Shi, L. Experimental investigation of the heat transfer of supercritical R134a in a horizontal micro-fin tube. Int. J. Therm. Sci. 2019, 138, 536–549. [Google Scholar] [CrossRef]
- Akbar, S.; Vaimann, T.; Asad, B.; Kallaste, A.; Sardar, M.U.; Kudelina, K. State-of-the-Art Techniques for Fault Diagnosis in Electrical Machines: Advancements and Future Directions. Energies 2023, 16, 6345. [Google Scholar] [CrossRef]
- Irriyanto, M.Z.; Lim, H.-S.; Choi, B.-S.; Myint, A.A.; Kim, J. Thermal stability and decomposition behavior of HFO-1234ze(E) as a working fluid in the supercritical organic Rankine cycle. J. Supercrit. Fluids 2019, 154, 104602. [Google Scholar] [CrossRef]
- Gunawan, R.; Irriyanto, M.Z.; Cahyadi, H.S.; Irshad, M.; Lim, H.-S.; Choi, B.-S.; Kwak, S.-K.; Myint, A.A.; Kim, J.-H. Mechanism of thermal decomposition of HFO-1234ze(E) under supercritical fluid conditions. J. Supercrit. Fluids 2020, 160, 104792. [Google Scholar] [CrossRef]
- Yildiz, S.; Groeneveld, D.C. Diameter effect on supercritical heat transfer. Int. Commun. Heat Mass Transf. 2014, 54, 27–32. [Google Scholar] [CrossRef]
- Yu, S.; Li, H.; Lei, X.; Feng, Y.; Zhang, Y.; He, H.; Wang, T. Influence of buoyancy on heat transfer to water flowing in horizontal tubes under supercritical pressure. Appl. Therm. Eng. 2013, 59, 380–388. [Google Scholar] [CrossRef]
- You, T.; Pan, Y.; Zhai, Y.; Wang, H.; Li, Z. Heat transfer in a U-bend pipe flow at supercritical pressure. Int. J. Heat Mass Transf. 2022, 191, 122865. [Google Scholar] [CrossRef]
- Yu, S.; Li, H.; Lei, X.; Feng, Y.; Zhang, Y.; He, H.; Wang, T. Experimental investigation on heat transfer characteristics of supercritical pressure water in a horizontal tube. Exp. Therm. Fluid Sci. 2013, 50, 213–221. [Google Scholar] [CrossRef]
- Aicher, T.; Martin, H. New correlations for mixed turbulent natural and forced convection heat transfer in vertical tubes. Int. J. Heat Mass Transf. 1997, 40, 3617–3626. [Google Scholar] [CrossRef]
- Jackson, J.D. Fluid flow and convective heat transfer to fluids at supercritical pressure. Nucl. Eng. Des. 2013, 264, 24–40. [Google Scholar] [CrossRef]
- Khaled, A.; Siddique, M.; Nazrulislam, N.; Boukhary, A.Y. Recent advances in heat transfer enhancements: A review report. Int. J. Chem. Eng. 2010, 2010, 106461. [Google Scholar]
- Kukulka, D.J.; Smith, R.; Fuller, K.G. Development and evaluation of enhanced heat transfer tubes. Appl. Therm. Eng. 2011, 31, 2141–2145. [Google Scholar] [CrossRef]
- Ackerman, J. Pseudoboiling heat transfer to supercritical pressure water in smooth and ribbed tubes. J. Heat Transf. 1970, 92, 490–497. [Google Scholar] [CrossRef]
- Lee, H.-S.; Kim, H.-J.; Yoon, J.-I.; Choi, K.-H.; Son, C.-H.J.H.; Transfer, M. The cooling heat transfer characteristics of the supercritical CO2 in micro-fin tube. Heat Mass Transf. 2012, 49, 173–184. [Google Scholar] [CrossRef]
- Wang, D.; Tian, R.; Zhang, Y.; Li, L.; Shi, L. Experimental comparison of the heat transfer of supercritical R134a in a micro-fin tube and a smooth tube. Int. J. Heat Mass Transf. 2019, 129, 1194–1205. [Google Scholar] [CrossRef]
- Wang, D.; Tian, R.; Li, L.; Dai, X.; Shi, L. Heat transfer of R134a in a horizontal internally ribbed tube and in a smooth tube under super critical pressure. Appl. Therm. Eng. 2020, 173, 115208. [Google Scholar] [CrossRef]
- Guo, Z.Y.; Li, D.Y.; Wang, B.X. A novel concept for convective heat transfer enhancement. Int. J. Heat Mass Transf. 1998, 41, 2221–2225. [Google Scholar] [CrossRef]
- Meng, J.-A.; Liang, X.-G.; Li, Z.-X. Field synergy optimization and enhanced heat transfer by multi-longitudinal vortexes flow in tube. Int. J. Heat Mass Transf. 2005, 48, 3331–3337. [Google Scholar] [CrossRef]
- Li, X.-W.; Meng, J.-A.; Guo, Z.-Y. Turbulent flow and heat transfer in discrete double inclined ribs tube. Int. J. Heat Mass Transf. 2009, 52, 962–970. [Google Scholar] [CrossRef]
- Wang, Y.; Zhou, B.; Liu, Z.; Tu, Z.; Liu, W. Numerical study and performance analyses of the mini-channel with discrete double-inclined ribs. Int. J. Heat Mass Transf. 2014, 78, 498–505. [Google Scholar] [CrossRef]
- Zheng, N.; Liu, W.; Liu, Z.; Liu, P.; Shan, F. A numerical study on heat transfer enhancement and the flow structure in a heat exchanger tube with discrete double inclined ribs. Appl. Therm. Eng. 2015, 90, 232–241. [Google Scholar] [CrossRef]
- Ariwibowo, T.H.; Miyara, A.J.R. Thermal characteristics of slinky-coil ground heat exchanger with discrete double inclined ribs. Resources 2020, 9, 105. [Google Scholar] [CrossRef]
- Song, W.M.; Meng, J.A.; Li, Z.X. Numerical study of air-side performance of a finned flat tube heat exchanger with crossed discrete double inclined ribs. Appl. Therm. Eng. 2010, 30, 1797–1804. [Google Scholar] [CrossRef]
- Zhang, X.; Cheng, L. Heat Transfer and Fluid Flow Characteristics of Microchannel with Discrete Double Inclined Ribs on Sidewalls. Heat Transf. Eng. 2024, 1–17. [Google Scholar] [CrossRef]
- Yuan, N.; Bi, D.; Zhai, Y.; Jin, Y.; Li, Z.; Wang, H. Flow and heat transfer performance of supercritical pressure carbon dioxide in pipes with discrete double inclined ribs. Int. J. Heat Mass Transf. 2020, 149, 119175. [Google Scholar] [CrossRef]
- Tang, J.; Yuan, N.; Zhai, Y.; Li, Z. Effect of discrete inclined ribs on flow and heat transfer of supercritical R134a in a horizontal tube. J. Supercrit. Fluids 2023, 200, 105980. [Google Scholar] [CrossRef]
- Tian, R.; Wei, M.; Dai, X.; Song, P.; Shi, L. Buoyancy effect on the mixed convection flow and heat transfer of supercritical R134a in heated horizontal tubes. Int. J. Heat Mass Transf. 2019, 144, 118607. [Google Scholar] [CrossRef]
- Abe, K.; Kondoh, T.; Nagano, Y. A new turbulence model for predicting fluid flow and heat transfer in separating and reattaching flows—II. Thermal field calculations. Int. J. Heat Mass Transf. 1995, 38, 1467–1481. [Google Scholar] [CrossRef]
- Lemmon, E.W.; Huber, M.L.; McLinden, M.O. Transport Properties, v. 9. NIST Standard Reference Database 23. 2010. Available online: https://www.nist.gov/system/files/documents/srd/REFPROP8_manua3.htm (accessed on 6 December 2023).
- Tian, R.; Wang, D.; Zhang, Y.; Ma, Y.; Li, H.; Shi, L. Experimental study of the heat transfer characteristics of supercritical pressure R134a in a horizontal tube. Exp. Therm. Fluid Sci. 2019, 100, 49–61. [Google Scholar] [CrossRef]
- Adebiyi, G.A.; Hall, W.B. Experimental investigation of heat transfer to supercritical pressure carbon dioxide in a horizontal pipe. Int. J. Heat Mass Transf. 1976, 19, 715–720. [Google Scholar] [CrossRef]
- Lei, X.; Li, H.; Dinh, N.; Zhang, W. A study of heat transfer scaling of supercritical pressure water in horizontal tubes. Int. J. Heat Mass Transf. 2017, 114, 923–933. [Google Scholar] [CrossRef]

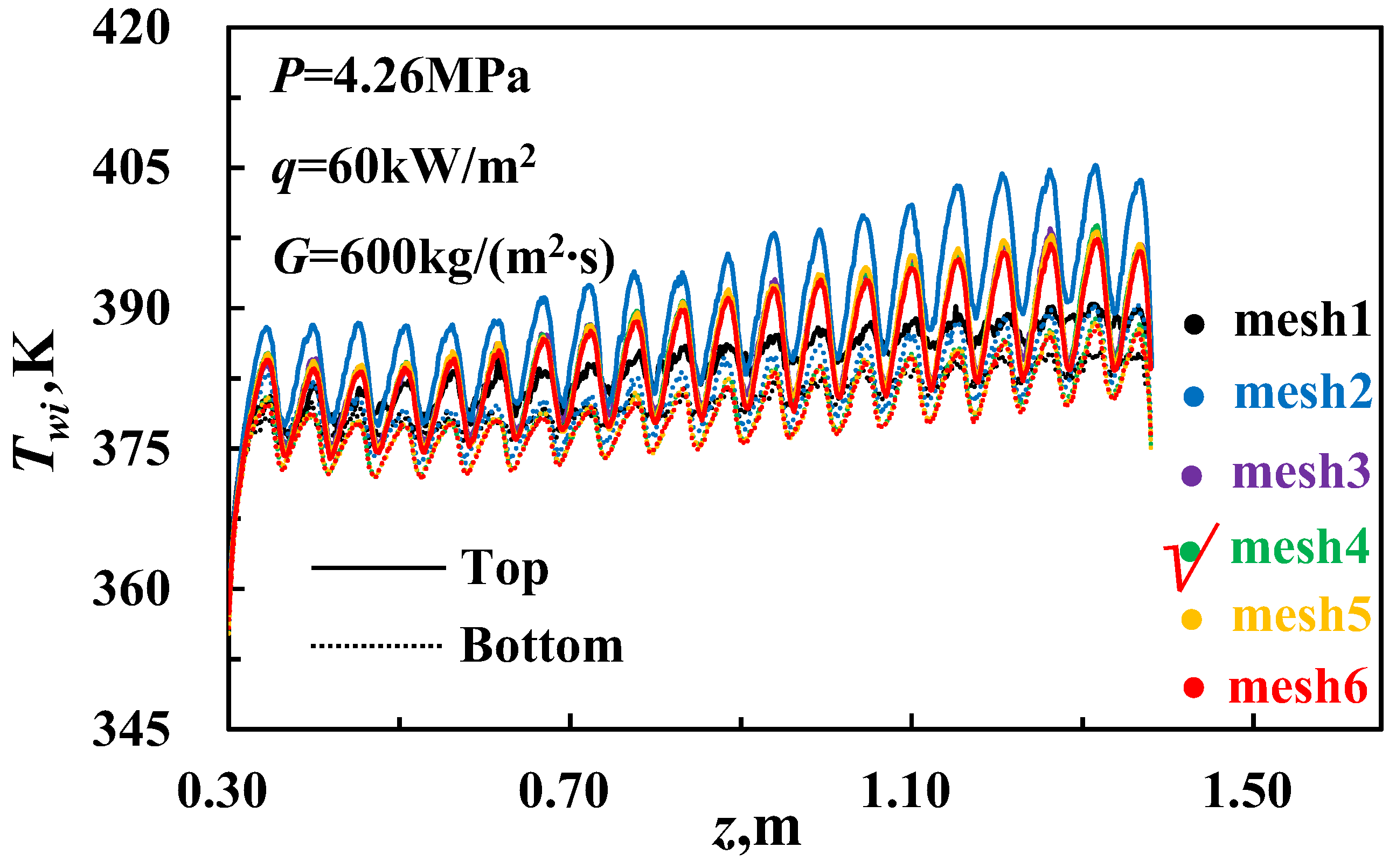


| Mesh No. | Global Mesh Size | Local Grid Size | ) | Maximum Wall Temperature Deviation Compared to Mesh 6 | ||
|---|---|---|---|---|---|---|
| Max (mm) | Factor | Max Ribs (mm) | First Grid Layer Height (mm) | |||
| 1 | 2.0 | 1.5 | 0.5 | 0.05 (y+ > 1) | 1.57 | −14.8‰ |
| 2 | 2.0 | 1.5 | 0.5 | 0.0035 (y+ < 1) | 2.41 | 20.4‰ |
| 3 | 2.0 | 1.5 | 0.2 | 0.0035 | 6.18 | 6.4‰ |
| 4 | 1.3 | 1.3 | 0.5 | 0.0035 | 10.43 | 3.6‰ |
| 5 | 1.2 | 1.2 | 0.1 | 0.0035 | 14.8 | 3.2‰ |
| 6 | 1.0 | 1.0 | 0.1 | 0.0030 | 19.01 | 0 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yang, G.; Tang, J.; Li, Z. Effect of Rotational Angle of Discrete Inclined Ribs on Horizontal Flow and Heat Transfer of Supercritical R134a. Energies 2024, 17, 1631. https://doi.org/10.3390/en17071631
Yang G, Tang J, Li Z. Effect of Rotational Angle of Discrete Inclined Ribs on Horizontal Flow and Heat Transfer of Supercritical R134a. Energies. 2024; 17(7):1631. https://doi.org/10.3390/en17071631
Chicago/Turabian StyleYang, Genxian, Junrui Tang, and Zhouhang Li. 2024. "Effect of Rotational Angle of Discrete Inclined Ribs on Horizontal Flow and Heat Transfer of Supercritical R134a" Energies 17, no. 7: 1631. https://doi.org/10.3390/en17071631
APA StyleYang, G., Tang, J., & Li, Z. (2024). Effect of Rotational Angle of Discrete Inclined Ribs on Horizontal Flow and Heat Transfer of Supercritical R134a. Energies, 17(7), 1631. https://doi.org/10.3390/en17071631





