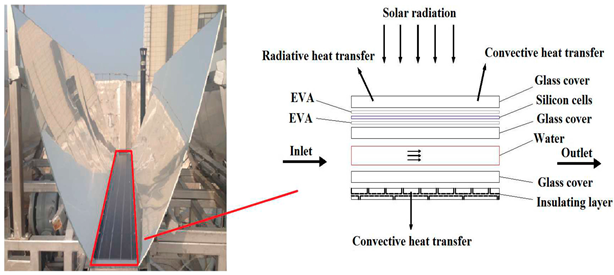
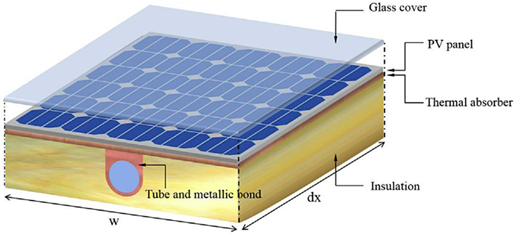
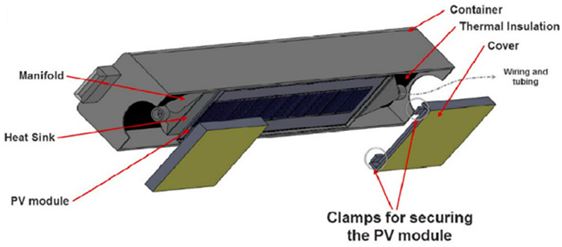
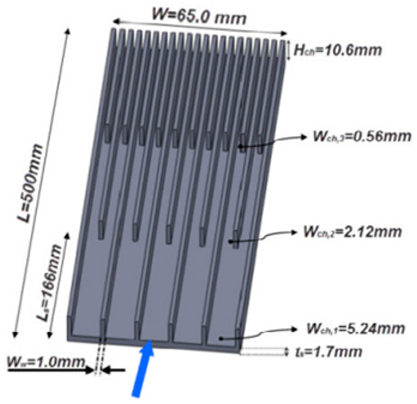
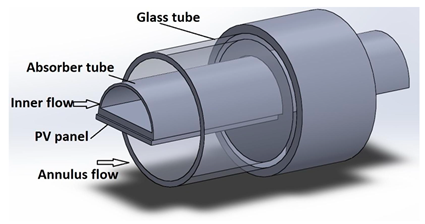
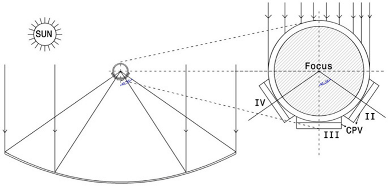
Abstract
This paper is a summary of the last ten years of work on the study of parabolic trough collectors (PTCs) and compound parabolic collectors (CPCs) coupled to photovoltaic and thermal solar receiver collectors (SCR-PVTs). While reviewing the state of the art, numerous review papers were found that focused on conventional solar receiver collector (SRC) technology for solar thermal generation. However, there is a lack of review papers summarizing SRC-PVT hybrid technology for solar electric/thermal generation, which would be beneficial for researchers interested in this area of research. This paper provides a review of SRC-PVT hybrid technologies. The theoretical foundations for analyzing and modeling PTC and CPC concentrators coupled to SRC-PVT are described, with an emphasis on modeling through thermal resistances and energy balances. Additionally, this section provides a concise overview of previous studies that have addressed the modeling of PTC and CPC collectors coupled to SCR-PVT, as well as experimental information useful for the validation of new mathematical models of SRC-PVT.
1. Introduction
Energy consumption is closely related to the development of civilization and the economy. Electrical and thermal energy power the services that improve society’s quality of life. Hence, a diversified and abundant energy supply is considered essential to ensure human progress. Solar photovoltaic thermal concentrator technologies (CPV/T) are potential options to satisfy these needs. These technologies utilize solar radiation as an energy source, making them a form of renewable energy source.
In 2021, worldwide installations of concentrated solar power (CSP) plants were reported to have an energy production capacity of 6 gigawatts. The majority of CSP installations were found in the United States and Spain, whilst countries such as Chile, the United Arab Emirates, China and South Africa are projected to increase their power production through new CSP plant projects. At an industrial level, around 70% of CSP plants currently under construction are based on parabolic trough collectors (PTC), the rest being central tower plants [1]. Despite the efforts made, CSP technology is less advanced than other renewable sources, like conventional solar photovoltaic (PV) or wind energy. Therefore, it is advisable to establish policies that provide financial incentives for CSP plant installation, as well as promoting research and development (R&D) initiatives to decrease installation costs.
In the field of CSP technologies, the parabolic trough collector (PTC) and the compound parabolic collector (CPC) [2,3] are the most investigated solar collectors with linear geometry. Researchers interested in this field can find multiple reviews on the state of the art [4,5,6,7]. These review papers provide information on aspects such as modeling, simulation, trends and compilations of recent studies. However, these recent review papers mainly focus on solar receiver collector (SRC) technology for thermal power generation.
There is an increasing tendency to research solar concentrating technologies with photovoltaic and thermal solar receiver collectors (SRC-PVTs) [8]. The purpose of this review paper is to present a summary of the most recent studies focusing on PTCs and CPCs coupled to SRC-PVTs. This review paper includes trends, modeling strategies and simulation.
The document is structured as follows to meet the objectives of this review paper: Firstly, the introduction provides a justification for the development of the review paper. Second, a summary of previous review papers is presented as a background, as well as a summary of recent studies on PTCs and CPCs coupled to SRC-PVTs. The third section discusses the theoretical fundamentals of PTCs and CPCs, through geometrical, optical and thermal analyses, as well as covering a classification and description of the modeling strategies proposed in the summary of recent studies. The fourth section provides the geometrical characteristics of the different SRC-PVTs and the proposed efficiency equations, as well as parameters and values useful for the validation of the simulated mathematical models. Finally, the fifth section discusses the main points to be considered in the analysis of PTCs and CPCs coupled to SRC-PVTs, together with their areas of opportunity and future perspectives.
2. Methodology of the State-of-the-Art Review
2.1. Previous State-of-the-Art Review Papers
Table 1 includes state-of-the-art review papers that focus on the modeling and classification of PTC and CPC collectors. The papers were identified based on a search for papers that provided background for the objectives of this review. This proved to be a useful exercise for the author, who gained a better knowledge of the topic.

Table 1.
Summary of state-of-the-art review papers focusing on PTC and CPC.
Table 1 presents a summary of the review papers by authors [9,10,11,12,13] that classify and describe the fundamentals of modeling and simulation of CSP systems, especially in PTCs. However, these review papers are focused on conventional SRCs. In contrast, the review paper by Herez [8] provides a clearer overview of the classifications and applications of PVT technologies, but does not include modeling and simulation aspects.
Although many of the fundamentals treated for conventional CSP technologies (such as geometric and optical analysis) are applicable to CPV/Ts, the situation is not the same for the thermal analysis of the SRC-PVT. Previous studies focused on modeling and simulation strategies; however, this topic requires further research. Therefore, this review paper presents an opportunity to expand the scope of the previous reviews.
2.2. Review of Previous Studies
In the review, an initial comprehensive search was carried out for papers reporting on PTCs and CPCs coupled to SRC-PVTs. This search was conducted systematically on various platforms such as Elsevier, MDPI, ASME, Wiley and Google Scholar. The following keywords were utilized:
- PTC—PVT: Parabolic Trough Collector—PhotoVoltaic Thermal;
- CPC—PVT: Compound Parabolic Collector—PhotoVoltaic Thermal;
- CPV/T: Concentrated PhotoVoltaic Thermal;
- LCPV/T: Low Concentrating PhotoVoltaic Thermal;
- HCPV/T: High Concentrating PhotoVoltaic Thermal;
- PTES: Photovoltaic Thermal Electrical System;
- CHAPS: Combined Heat And Power Solar.
Furthermore, a comprehensive search was conducted using the “Research Rabbit 2023” tool in addition to conventional search engines. This particular platform facilitated the identification of articles and researchers linked to a previously provided list of studies by the author (Figure 1) The search was categorized based on factors such as the year, journal, type of collector, and other criteria.
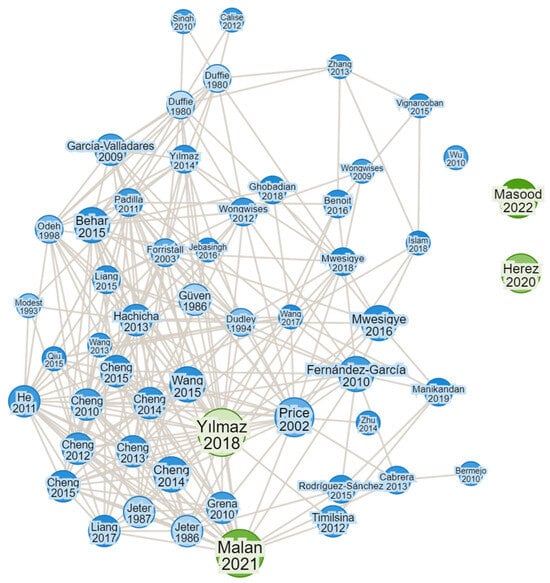
Figure 1.
Search for studies of relevance with the Research Rabbit tool.
The search period covered from 2013 to mid-2023, with a focus on selecting the most recent studies with clear numerical data. The objective was to include a minimum of 100 studies for review. Table 2 provides a summary of all the studies focusing on PTCs, while Table 3 provides a summary of all the studies focusing on CPCs.

Table 2.
Summary of the review studies focusing on PTCs coupled to SRC-PVTs.

Table 3.
Summary of the review studies focusing on CPCs coupled to SRC-PVTs.
Within Table 2 and Table 3, the first three columns correspond to the year of publication, the author of the study and the journal. Column four denotes whether the study is theoretical or experimental. Column five details the main contribution of the study; a classification of seven different types of contributions was established for the summarized studies. This classification excludes contributions related to economic and environmental analyses. Finally, column five provides notes about modeling and simulation considerations.
Figure 2 provides a percentage representation of publishers and journals hosting studies focusing on PTCs and CPCs coupled to SRC-PVTs. Additionally, it presents the publication trend (within the period covered by the review) for the four journals with the highest number of studies and for publishers in general.
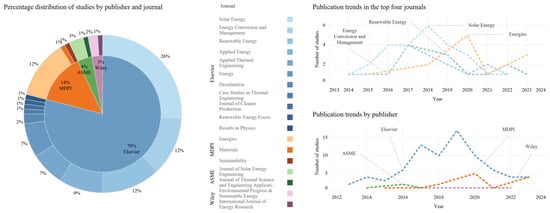
Figure 2.
Percentage distribution of studies by publisher and journal; publication trends in the top four journals and by publisher.
The leading publisher for papers on PTCs and CPCs coupled to SRC-PVTs is Elsevier, with the following journals: Solar Energy with 26%, Renewable Energy with 12% and Energy Conversion and Management with 12%. Following this is MDPI, with the journal Energies (12%). These journals together account for 62% of the summarized studies of review.
The author has a high regard for the Journal of Thermal Science and Engineering Applications, published by ASME. Although it only includes 4% of the summarized studies in the review, it is a journal focused on solar energy issues; Brekke et al. [66] provide valuable information for SRC-PVT modeling. Therefore, it is recommended to consult his future studies [114,115], with the expectation that they will discuss other relevant aspects of PTC and CPC modeling.
As previously discussed, column five of Table 2 and Table 3 established a classification of seven different types of contributions; each of the studies summarized in the review was classified into one of these seven types of contributions. The contribution assigned is a function of the main and most discussed contents in each of the papers. The classification excludes contributions related to economic and environmental analyses. These seven types of contributions are listed below:
- Simulation and/or validation of a mathematical model;
- Evaluation of thermal and/or electrical performance;
- Optical and spectral analysis;
- Energy and exergy analysis;
- Parametric and sensitivity study;
- Development and experimental testing;
- Study of geometries and/or solar tracking.
Figure 3 presents the distribution of studies according to the seven different types of contributions. Furthermore, it presents the distribution of studies within each journal. It also shows the publication trends of the studies for each of the seven types of contribution within the period covered by the review.
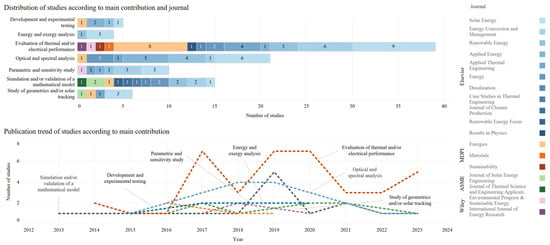
Figure 3.
Distribution of studies according to main contribution and journal; publication trend of studies according to main contribution.
The exclusion of economic and environmental contributions is justified by the need to prioritize the information according to theoretical and experimental contributions, which are more related to the development of mathematical models, test prototypes and validation (which is the objective of this review paper). It is worth mentioning that among the studies summarized, there are contributions focusing on economic and environmental studies, as indicated in the following:
Herez provides a state-of-the-art review of CPV/T systems and presents an overview of power generation using PV and TEG [8]. Additionally, he proposes a model for a PTC collector coupled to SRC-PVT that includes case studies and economic and environmental analysis [25]. Finally, a parametric study of the proposed model is presented [26].
Acosta and Santana analyzed the thermal and electrical performance of a PTC collector coupled with an SRC-PVT for different applications. They conducted an economic feasibility analysis of these applications and provided mathematical formulae details for the calculation of thermal and electrical efficiencies [17,19,31].
Tripathi outlines his methodology for developing a mathematical model of SRC coupled to CPC. The proposed model is evaluated from an energy and exergy perspective, and is experimentally validated [99,104]. Additionally, a parametric study is conducted to determine the optimal configuration of a series of interconnected CPCs and their corresponding mass flow rate for a given operating temperature [105]. In the field of techno-economic feasibility, a lifecycle cost analysis is applied to determine the energy cost of the system [100].
Otanicar and Brekke proposed retrofitting existing conventional PTC collector plants with an SRC-PVT. They conducted a study on the economic impact of this technology [37]. The researchers also conducted experimental tests on heat fluid transfer (HTF) with nanoparticles for the spectral splitting of radiation in the SRC-PVT [55]. Finally, they presented a strategy and mathematical model for SRC-PVT [66].
3. Fundamentals of PTCs and CPCs
PTC and CPC concentrators are derived from cylindrical geometry, as their name indicates. The analysis of these technologies encompasses various areas, including the incidence of the sun’s rays on reflecting mirrors, temperature distribution throughout the concentrator and calculations of stresses on a device’s structure. Therefore, it is suggested to adopt the procedure shown in Figure 4 in order to study and design solar collector systems.
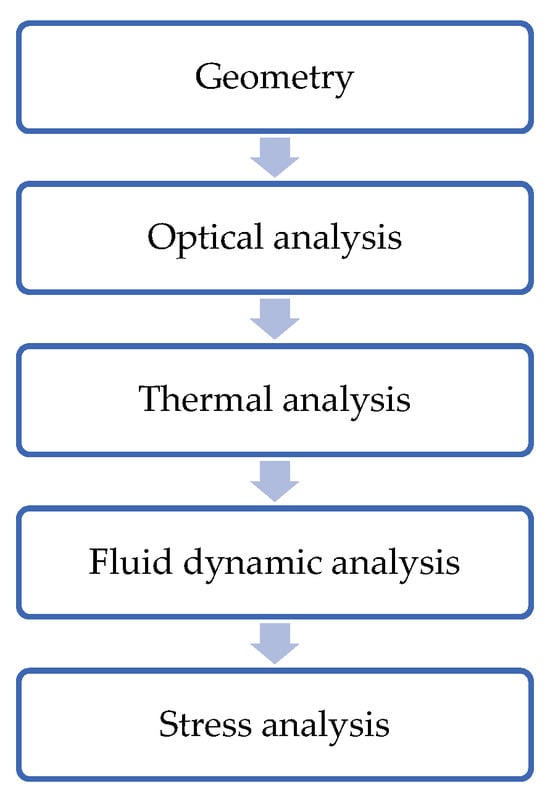
Figure 4.
Analysis and design procedure for solar collector systems.
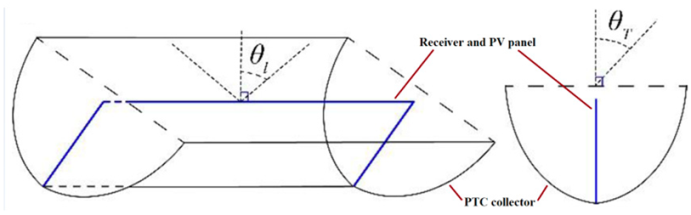
3.1. Geometry for PTCs and CPCs
In this section, the study details the relationship between reflecting parabolic mirrors and the SRC. Duffie et al. [116] and Kalogirou [117] recommend books that provide equations on this topic. The following section presents the proposed geometry equations for PTC.
The focal length, denoted by , is determined using Equation (1):
The aperture radius, denoted by , is determined using Equation (2):
The aperture width, denoted by , is determined using Equation (3):
The edge angle, denoted by , can be obtained from the focal length () and the aperture width (), which is determined using Equation (4):
The width of the image, denoted by , projected on a flat SRC is determined using Equation (5):
The diameter of SRC with cylindrical geometry, denoted by , is determined using Equation (6):
For the CPC collector, the following geometry equations are proposed. The focal length, denoted by , is determined using Equation (7):
The aperture ratio, denoted by , is determined using Equation (8):
The height ratio, denoted by , is determined using Equation (9):
The truncated aperture ratio, denoted by , is determined using Equation (10):
The truncated height ratio, denoted by , is determined using Equation (11):
3.2. Optical Analysis for PTCs and CPCs
Regarding the optical analysis, the following equations are proposed for the PTC. The radiation absorbed by the SRC, denoted by , is determined using Equation (12):
The incident angle modifying factor, denoted by , is determined with Equation (13):
The end loss effect, denoted by , is determined using Equation (14):
For the CPC collector, the following optical equations are proposed. The radiation absorbed by the SRC, denoted by , is determined with Equation (15):
The incident angle modifying factor, denoted by , is determined with Equation (16):
The incident angle modifying factor, denoted by , is determined with Equation (17):
3.3. Thermal Resistance Analysis of the SRC-PVT
The research conducted by Kalogiruo [117,118], Forristall [119] and Behar [120] provides a description of the analysis procedure for conventional SRCs. This information is crucial for comprehending the thermal resistance method and its energy balance equations between the environment and the HTF.
There are studies that analyze the SRC-PVT using their own thermal resistance models. For example, Herez et al. [26] discuss a triangular geometry SRC-PVT model and consider the PV to be in direct contact with the environment. In contrast, Karathanassis et al. [45] present a model of a rectangular-geometry SRC-PVT with seven different layers. The first layer is a glass cover that isolates the PV from the environment. Another example is the study by Brekke et al. [66], which also considers a model of SRC-PVT with rectangular geometry, but on the side exposed to the environment there is a nanofluid that acts as a selective solar radiation filter for the PV.
This review article summarizes several SRC-PVT models focused on different considerations, such as selective filters, TEG and vacuum layers. However, only Forristall [119] considers the conduction heat losses in the SRC supports with the collector, for a conventional SRC model. Therefore, it is appropriate to study this consideration in an SRC-PVT model to evaluate its impact on the overall model response.
Figure 5 shows a cross-section of a simple rectangular SRC-PVT. The diagram indicates the energy flows and considers the conduction heat losses in the supports. This information enables the establishment of the energy balance:
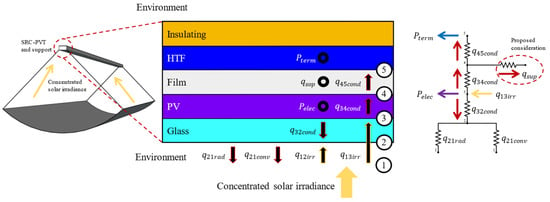
Figure 5.
The thermal resistance model of an SRC-PVT, including the conduction heat losses in the SRC-PVT supports with the collector.
- Effective concentrated solar irradiance () is incident on the side of the glass exposed to the environment, while a heat flux emitted by the PV () is incident on the opposite side;
- A fraction of the incident irradiance on the crystal is converted into heat (), which is added to the heat flux from the PV (). Both of these are then emitted to the environment as radiation () and convection ();
- The irradiation passing through the crystal is incident on the PV () and is converted into electrical energy () due to the photoelectric effect;
- A fraction of the irradiance incident on the PV () is emitted as two heat fluxes, the first in the crystal direction () and the second through the film to the HTF ();
- The heat arriving at the film is again divided into two fluxes, the first in the HTF direction () and the second corresponding to the conduction heat losses in the supports ();
- The heat flow conducted through the PV and the film to the HTF () is extracted as thermal energy ().
In Figure 5, both the effective concentrated solar irradiance and the different heat transfer modes (conductive, “cond”; radiative, “rad”; and convective, “conv”) are represented as energy or heat fluxes, with arrows indicating their direction. The energy balance result is expressed as Equations (18)–(21):
The model presented takes into account the following considerations:
- The energy balance is one-dimensional and steady-state. Uniformity is assumed for all temperatures, heat fluxes and thermodynamic properties. Furthermore, the insulation on the opposite side of the glass is assumed to prevent any heat loss;
- Effective concentrated solar irradiation refers to the amount of solar energy that remains following the consideration of optical and geometrical losses of the concentrator. The energy balance excludes terms that represent concentrator losses;
- The energy flux resulting from effective concentrated solar irradiation corresponds to the amount of light absorbed by the glass and PV (absorbance). This phenomenon is volumetric in nature, but for ease of analysis it is treated as a surface phenomenon under the assumption that the resulting error is relatively minor [119].
It is important to mention that there are defined criteria for modeling each of the three heat transfer modes (Table 4); a more detailed explanation can be found in the book by Incropera et al. [121].

Table 4.
Heat transfer modes and their general modeling equations [121].
3.4. Description of the SRC-PVT Energy Balance Equations
The modeling equations in Table 4 define the terms for the three types of heat transfer modes described in Equations (18) and (20), as well as those concerning heat absorption through solar irradiation. It is important to note that the modeling equations are adapted to the characteristics of the SRC-PVT, such as the geometry.
Equation (18) corresponds to the energy balance of the heat flows in the SRC-PVT crystal and is composed of the following terms of the Equations (25)–(28):
The heat absorbed by the crystal, denoted by , is determined by the following parameters, according to [26,45]:
The conduction heat loss of the crystal, denoted by , is determined by the following parameters, according to [26,45]:
The radiation heat losses of the crystal, denoted by , is determined by the following parameters, according to [26,34,50,66]:
The convective heat losses of the crystal, denoted by , are determined by the following parameters, according to [26]:
Equation (19) corresponds to the energy balance of the heat flows in the PV and is composed of the following terms of the Equations (29) and (30):
The heat absorbed by the PV, denoted by , is determined by the following parameters, according to [26,45]:
The conduction heat loss of the PV, denoted by , is determined by the following parameters, according to [26,45]:
Equation (20) corresponds to the energy balance of the heat flows in the film and is composed of the following terms of the Equation (31):
The conduction heat loss of the film, denoted by , is determined by the following parameters, according to [26,45]:
For the modeling of the terms “” and “”, which correspond to the electrical power produced by the PV and the thermal power extracted by the HTF, as well as the modeling of the conduction heat losses in the supports “”, the following assumptions are made.
3.4.1. Electrical Model of the PV
The electrical power () generated by the PV is part of the energy balance of Equation (19). It has been defined in different ways depending on the complexity and accuracy assumed for the mathematical model. Table 5 presents a summary of the different equations proposed in the studies to model the electrical power produced by the PV.

Table 5.
Summary of equations for modeling PV electrical power proposed in previous studies.
3.4.2. Thermal Model of the HTF
The thermal power () extracted by the HTF is part of the energy balance of Equations (20) and (21); it is defined by Equation (39). This model is generally accepted and has been used in different studies: Ji [122], Haiping [83], Xinxin [85], Karathanassis [45] and Herez [25].
3.4.3. Model of the Conduction Heat Losses in the Supports
The thermal resistance that represents the conduction heat losses in the supports of the SRC with the collector can be modeled by considering an “infinite fin”, as proposed by Forristall [119]. Equation (40) defines the parameters that represent the conduction heat losses in the supports “”, which are present in the energy balance of Equation (20).
3.5. Modeling and Simulation Strategies
In the previous sections, fundamental information has been provided to understand the analysis of CPV/T systems based on PTC and CPC. It is important to note that this information is limited to the thermal analysis step (Figure 4) and is valid for one-dimensional stationary models. Introducing the concept of other modeling strategies would substantially prolong this review paper; moreover, most of the studies summarized are based on the steady-state model. Nevertheless, Figure 6 presents a classification of the strategies found in the state-of-the-art review to be used in the modeling and simulation of PTC and CPC. This classification can be extended to other types of collectors.
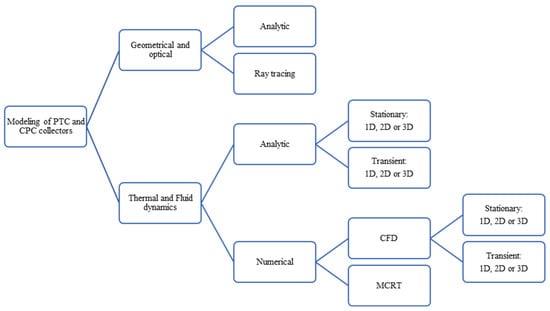
Figure 6.
Modeling strategies for solar collector systems.
3.5.1. Simulation Software
Previous review papers have provided summaries of the main software used to simulate the different steps in the analysis of CSP systems. This is the case for Masood et al. [10], who provide a scheme with the main simulation software focused on the optical analysis of CSP systems. In this review paper, Table 6 presents software focused on optical analysis using numerical and ray tracing techniques, while Table 7 corresponds to the software focused on thermal analysis using numerical and analytical techniques.

Table 6.
Software focused on the optical analysis of CSP systems.

Table 7.
Software focused on the thermal analysis of CSP systems.
3.5.2. Structure for Simulation Development
The development of CPV/T system simulations requires a series of steps based on the analysis procedure detailed in Figure 4, as well as iterative strategies for solving energy balance equations and other numerical methods. A flowchart is an effective tool for defining the structure of simulation development.
Several studies in the review provide examples of a proposed flowchart for simulation development: Malan presents a flowchart detailing the operation of the algorithm used by the Soltrace software for incident irradiance distribution in a PTC using ray tracing techniques [11]. Herez presents a flowchart describing the iteration procedure of the non-linear equations that constitute his mathematical model [25,26]. Haiping presents a flowchart demonstrating the implementation of a procedure for calculating the thermal and electrical performance of his proposed SRC-PVT using MATLAB software [83]. Meanwhile, Ju presents a flowchart detailing the optical analysis, iteration of energy balance equations and thermal and electrical performance calculations for a CPV/T system and a TEG [123].
Programming languages such as Fortran or software such as MATLAB can be used for simulation development. For complex systems, a combination of languages and software is useful to facilitate the development of simulations and mathematical models. Figure 7 shows a flowchart illustrating the procedure for simulating a PTC or CPC coupled to an SRC-PVT using TRNSYS and EES.
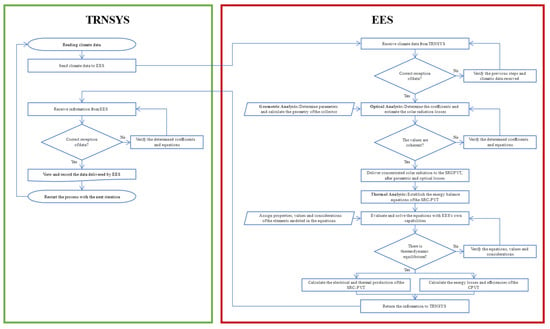
Figure 7.
Diagram proposed by the author to simulate a PTC coupled to SRC-PVT with TRNSYS 18.05 and EES 10.2 software together.
The flowchart broadly describes the following procedure: The climate data of a given region are read from TRNSYS, and subsequently transferred to EES for geometrical, optical and thermal analysis (using energy balance equations). Energy production and losses, as well as thermal and electrical efficiencies, are calculated. The data are then returned to TRNSYS for storage and visualization. The process is then repeated, with a new iteration that updates the climate data.
The reasons for using the two software packages together are as follows:
- TRNSYS is a software with a stage called “kernel” that reads and processes input files (e.g., climate files), solves iteratively, determines convergences and plots variables in conjunction with another stage, which is a library containing a set of mathematical models [124]. It allows the development of renewable energy systems through quasi-dynamic simulations (stationary models iterated several times). However, it does not have a model representing a PTC or CPC coupled to SRC-PVT.
- EES is software focused on solving systems of equations. It includes a database of highly accurate thermodynamic and transport properties for several substances [125]. This attribute facilitates the researcher in considering relevant aspects in their mathematical models. Hence, it is convenient to develop energy balance equations that represent the SRC-PVT in ESS and connect it to TRNSYS.
4. Review Studies Focusing on SRC-PVT Models
4.1. Geometry of SRC-PVTs
There are many options and designs available for an SRC-PTV. These options are determined by electrical or thermal production requirements, manufacturing complexity and heat extraction mechanisms. Table 8 provides a summary of the SRC-PTVs found in the review studies according to their main geometries, a graphical example and a brief description.

Table 8.
Summary of SRC-PVT geometries reported in previous studies.
From the geometries for SRC-PVT listed in Table 8, the following are of interest:
The “Simple Rectangular” geometry type has been reported by several authors, including Xinxin [85], Haiping [83], Xu [70], Hou [15] and Ben Youssef [54]. Xinxin [85] and Haiping [83] focused on desalination at low concentrations and temperatures, presenting energy balance equations of SRC-PVT considering a steady state in one-dimension. Ben Youssef [54] proposed a new mathematical model with differential equations and in two dimensions.
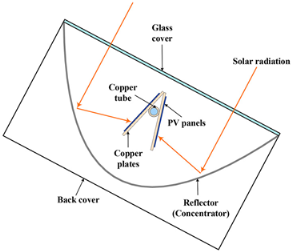
The “Rectangular with cylindrical pipe” geometry has been studied by Ji [122] and Yazdanifard [65] using energy balance equations and steady state in one dimension. Yazdanifard [65] has proposed equations to analyze the SRC-PVT with and without a glass envelope. Meanwhile, Karathanassis [45,60,72] studied the “Rectangular with fins” geometry in detail to enhance heat transfer to the HTF.
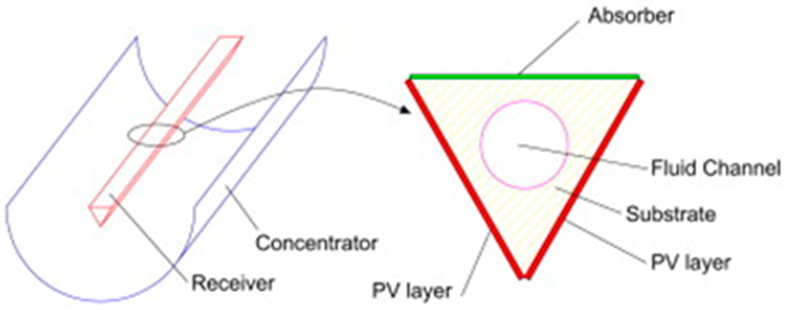
The “Triangular” geometry has been considered by Herez [25], Calise [71], Zheng [18], Santana [17] and Mohsenzadeh [61]. Herez [25] and Calise [71] have proposed steady state in one-dimensional models for this type of SRC-PVT.
Two lesser-known variants of SRC-PVT geometries are the “Wedge” type studied by Gorouh [21] and Cabral [24] and the “Bifacial” type, which has also been studied by Cabral [73]. Both geometries have the objective of enhancing the angle of incidence of solar radiation.
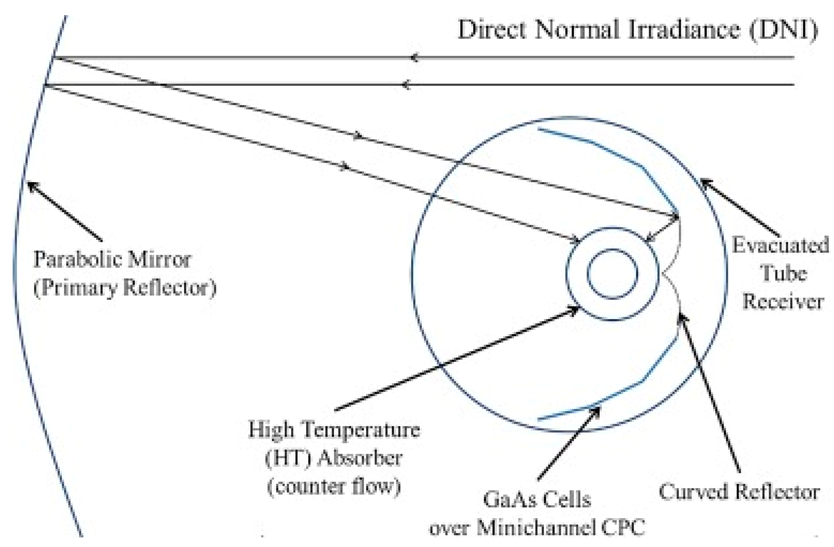
Recently, there has been notable interest in the study of SRC-PVTs with a cylindrical envelope, which can be coupled to industrial PTCs or CPCs. Studies on these geometries have been conducted by the following authors: Widyolar [52,57,58,64], for the “Cylindrical with internal CPC” type, and Gakkhar [34] for the “Cylindrical with intermediate PV” type. Meanwhile, Srivastava [62] and Felsberger [33] have conducted both studies and simulations on the “Cylindrical with PVs on pipe” type.
4.2. Thermal and Electrical Efficiency Equations
Table 9 illustrates a summary of the equations for the calculation of electrical and thermal efficiency proposed by different authors of the review studies.

Table 9.
Summary of equations proposed for electrical and thermal efficiency in previous studies.
4.3. Parameters and Values for the Validation of Mathematical Models
Several experimental studies were excluded from the holistic study due to their publication date. However, some researchers have used their experimental results to validate their mathematical models. Table 10 presents a group of studies with experimental results, divided according to the type of collector and whether it is included in the review or not.

Table 10.
Studies with experimental results for the simulation and validation of SRC-PVT models.
For the author’s consideration, this section presents information from studies conducted by Herez [25,26,128,129], Maatallah [47] and Yazdanifard [65]. These authors demonstrate a method for validating a mathematical model and provide a compilation of relevant parameters and experimental results. Their studies hold significance for future modeling, simulation and validation works.
In Table 11, the parameters used in the simulation by Herez [128] of their SRC-PVT model of a triangular geometry are presented, coupled to PTC. The values correspond to the boundary conditions of the system (determined by the environment) and the intrinsic characteristics of the different components that constitute the SRC-PVT, such as the PV or a TEG.

Table 11.
Parameters used in the simulation of the SRC-PVT model proposed by Herez [128].
The author Herez [128] references the experimental results of Calise [130] and Mohsenzadeh [61] to validate the simulation of their SRC-PVT model. Table 12 details the percentage of variation between the simulated model results and the reference experimental results considered.

Table 12.
Comparison of the results of the SRC-PVT model proposed by Herez [128] and the reference results.
Meanwhile, listed in Table 13 are the parameters required by Yazdanifard [65] to simulate their SRC-PVT model of rectangular geometry and a cylindrical tube coupled to PTC.

Table 13.
Parameters used in the simulation of the SRC-PVT model proposed by Yazdanifard [65].
Maatallah [47] and Yazdanifard [65] validated their mathematical model simulation using experimental results from Ji [122]. Table 14 displays the variations between the simulated model results and the experimental reference results based on HTF outlet temperature and PV temperature.

Table 14.
Comparison of the results of the SRC-PVT model proposed by Yazdanifard [65] and the reference results.
Further studies which provide the necessary parameters for mathematical models of SRC-PVT and collector geometry are Alayi [32], Otanicar [37], Karatanasis [45], Valizadeh [50] and Ben Youssef [53,54] for PTC collectors, while Saberi [75], Haiping [83], Xinxin [85] and Yousef [107] provide values for CPC collectors.
5. Discussion and Conclusions
This review did not examine the correlation between the price of fossil fuels and the studies summarized over the period analyzed. However, studies such as the one presented by the International Renewable Energy Agency [131] demonstrate that concentrating solar power and photovoltaic technologies has reduced their installed cost by 62% and 80%, respectively. This makes them economically viable power generation options compared to their fossil-fuel-based counterparts.
This review paper identifies a group of studies that focus on analyzing the technical–economic feasibility of different proposals for collectors coupled to SRC-PVTs. These studies generally evaluate the levelized cost of energy (LCOE) to determine the payback time. It is generally expected that the costs and payback times will be lower for CSP technology compared to its fossil-fuel-based counterparts. A review of technical economic analyses could be conducted to determine the relationship between technological developments in this field and fossil fuel prices.
5.1. Geometry and Type of Collector
Regarding the geometries of solar collectors, it has been observed that CPCs are commonly used in experimental prototype tests at temperatures of around 100 °C [83,85,97]. These prototypes are typically “handmade”, using a truncated geometry CPC collector and a rectangular SRC (due to the PV structure). Another common CPC configuration involves integrating it into the vacuum layer of a SRC, as seen in the “heat pipe” collector technology or the prototype presented by Widyolar et al. [64].
On the other hand, there is potential in adapting SRC-PVTs for industrial production [34]. The PTC is the dominant collector in this case, with temperature ranges from 100 °C to 400 °C [6]. However, the electrical efficiency of PVs depends on temperature, with significant losses above 120 °C [132]. This limits the operating range of an SRC for industrial applications. To improve the thermal energy transfer and harvesting of the SRC, various solutions have been proposed.
5.2. Solutions
Optically selective filters allow only wavelengths that the PV materials can efficiently convert into electricity to pass. This reduces heating in the PV, maintaining good electrical efficiency. The energy of wavelengths less useful to the PV is rejected by the selective filter, if it is a film, or is absorbed by the selective filter itself if it is a nano-fluid.
Nanofluids are utilized to improve energy quality and heat transfer from SRC to HTF. These fluids contain particles of different materials that can exhibit solar radiation absorption properties, making them useful as selective filters. This allows for the direct absorption of energy by the HTF, preventing its loss to the PV.
Research into nanofluids and their formulation to achieve desired behaviors is of great interest. Nanofluids offer the advantage of being able to handle multiple HTFs for the same collector [55,67]. A first HTF with nanofluid can be used as a selective filter to be irradiated directly by the solar collector. This first HTF can reach higher temperatures than those recommended for PVs. In the background, the PV will be irradiated by the previously filtered wavelengths. A second HTF can be used to cool the PV, which improves its electrical efficiency. However, this may cause the second HTF to reach a lower temperature and energy quality. This configuration is a very attractive solution to the trade-off between the temperature limitations of PVs and the high operating temperatures of industrial PTCs.
Piping with fins can be used to improve power quality and heat transfer from the SRC to the HTF. This can be achieved by developing surfaces and geometries that increase the contact area between the SRC and the HTF [60]. This strategy can even promote phase changes in a fluid, as in the case of MultiEffect Distillation (MED) spray nozzles.
Vacuum layers have been shown to improve thermal efficiency in SRC-PVTs by reducing conduction losses to the atmosphere. However, this can have a negative impact on the electrical efficiency of the PV due to the encapsulation in an isolated environment at a higher temperature.
TEGs are capable of generating an electrical potential difference when exposed to high temperatures. They can replace or complement PVs within an SRC-PVT. However, their electrical energy production is lower compared to that of PVs. Therefore, they have received less research attention.
5.3. Modeling
Mathematical models of SRC-PVT include considerations related to the aforementioned solutions: vacuum layers, glass covers, selective filters, nanofluids or even more accurate mathematical representations of the PV to determine its electrical output. A conventional SRC model presented by Forristall [119] takes into account the conduction heat losses in the SRC supports with the collector. However, previous proposals for SRC-PVT models have not taken this into account. Therefore, Section 3.3 and Section 3.4 of this review paper propose a thermal resistance model that takes into account the conduction heat losses in the SRC-PVT supports with the collector.
5.4. Strategies for Use
On the topic of evaporative desalination, multi-generation “MED” machines are being developed that can produce fresh water, cooling and electricity [133]. The production of electrical energy in these devices is obtained by recycling the residual steam from the process inside a steam turbine. The heating of the seawater before it enters the first effect of the MED can be undertaken with a collector field. It would be interesting to compare the production of electrical energy using the conventional strategy and that produced using a collector field with SRC-PVT, and how this “SRC-PVT + MED” configuration can affect the other dynamics of the process, such as the temperature and pressure of the seawater entering the MED, or the dimensioning of the collector field itself, with an SRC-PVT instead of a conventional collector field.
According to Acosta et al. [31], the main energy production of a collector field with SRC-PVT is as thermal energy. The production of electrical energy is considered “residual” and it is recommended to use it for electricity consumption to receive a discount from the electricity supplier’s tariff. However, thermal energy consumption profiles vary throughout the year, which requires the strategic dimensioning of the collector field. “If the field is dimensioned for the most critical point of the year, it will be oversized for the rest of the year, while if it is dimensioned for the least critical point, it will be undersized”. To ensure optimal performance throughout the year, it is important to find a middle ground when dimensioning a collector field for thermal demand. Typically, a collector field that provides about 80% of the most critical demand of the year will be used. The remaining thermal demand is supported by auxiliary equipment.
In view of the aforementioned considerations, it is reasonable to research the versatility that SRC-PVTs can offer in the dimensioning of the collector field. The same collector field with SRC-PVTs can prioritize thermal or electrical energy production depending on the demand profile. “For example, if thermal demand is low, the mass flow of the HTF can be adjusted to increase PV electrical efficiency. If thermal demand is high, the quality of energy obtained from the HTF can be prioritized over electrical efficiency of the PV”.
In conclusion, future research should consider the following points:
- The impact on the overall response of the SRC-PVT model when considering thermal conduction losses due to the SRC-PVT supports with the collector;
- The impact on collector field dimensioning and MED systems when using SRC-PVTs;
- Strategies and configurations that enable the SRC-PVT to achieve higher temperatures without compromising the electrical efficiency of the PV. These include the use of selective filters, nanofluids and dissipative fins.
Author Contributions
Conceptualization, S.E.D.L.-A. and M.P.-S.; data curation, B.C.-D.; formal analysis, B.C.-D.; funding acquisition, J.A.A.-J., N.V.-L. and F.C.-D.; research, B.C.-D.; methodology, B.C.-D., S.E.D.L.-A. and M.P.-S.; project management, S.E.D.L.-A.; resources, M.P.-S. and S.E.D.L.-A.; supervision, S.E.D.L.-A.; validation, B.C.-D.; visualization, S.E.D.L.-A. and B.C.-D.; writing: original draft, B.C.-D., M.P.-S. and S.E.D.L.-A.; writing: review and editing, B.C.-D.; writing: review and editing S.E.D.L.-A. and B.C.-D.; editing, S.E.D.L.-A. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Conflicts of Interest
The authors declare no conflict of interest.
Abbreviations
| CSP | Concentrated Solar Thermal Power |
| CPVT | Concentrated Photovoltaic Thermal |
| LCOE | Levelized Cost Of Energy |
| MED | Multi-Effect Distillation |
| PV | PhotoVoltaic cell |
| PVT | PhotoVoltaic Thermal |
| SRC | Solar Receiver Collector |
| HCE | Heat Collector Element |
| HTF | Heat Fluid Transfer |
| PTC | Parabolic Trough Collector |
| CPC | Compound Parabolic Collector |
| TEG | ThermoElectric Generation |
References
- Murdock, H.E.; Gibb, D.; Andre, T.; Sawin, J.L.; Brown, A.; Ranalder, L.; Andre, T.; Brown, A.; Collier, U.; Dent, C.; et al. Renewables 2021—Global Status Report; REN21 Secretariat: Paris, France, 2021; ISBN 978-3-948393-03-8. [Google Scholar]
- Ajbar, W.; Parrales, A.; Huicochea, A.; Hernández, J.A. Different ways to improve parabolic trough solar collectors’ performance over the last four decades and their applications: A comprehensive review. Renew. Sustain. Energy Rev. 2022, 156, 111947. [Google Scholar] [CrossRef]
- Islam, M.T.; Huda, N.; Abdullah, A.B.; Saidur, R. A comprehensive review of state-of-the-art concentrating solar power (CSP) technologies: Current status and research trends. Renew. Sustain. Energy Rev. 2018, 91, 987–1018. [Google Scholar] [CrossRef]
- Hachicha, A.A.; Yousef, B.A.A.; Said, Z.; Rodríguez, I. A review study on the modeling of high-temperature solar thermal collector systems. Renew. Sustain. Energy Rev. 2019, 112, 280–298. [Google Scholar] [CrossRef]
- Hasan, A.; Sarwar, J.; Shah, A.H. Concentrated photovoltaic: A review of thermal aspects, challenges and opportunities. Renew. Sustain. Energy Rev. 2018, 94, 835–852. [Google Scholar] [CrossRef]
- Tagle-Salazar, P.D. Parabolic trough Solar Collectors: A General Overview of Technology, Industrial Applications, Energy Market, Modeling, and Standards. Available online: https://www.degruyter.com/document/doi/10.1515/gps-2020-0059/html (accessed on 19 September 2023).
- Jaaz, A.H.; Hasan, H.A.; Sopian, K.; Ruslan, M.H.B.H.; Zaidi, S.H. Design and development of compound parabolic concentrating for photovoltaic solar collector: Review. Renew. Sustain. Energy Rev. 2017, 76, 1108–1121. [Google Scholar] [CrossRef]
- Herez, A.; El Hage, H.; Lemenand, T.; Ramadan, M.; Khaled, M. Review on photovoltaic/thermal hybrid solar collectors: Classifications, applications and new systems. Sol. Energy 2020, 207, 1321–1347. [Google Scholar] [CrossRef]
- Bayareh, M.; Usefian, A. Simulation of parabolic trough solar collectors using various discretization approaches: A review. Eng. Anal. Bound. Elem. 2023, 153, 126–137. [Google Scholar] [CrossRef]
- Singh, R.K.; Chandra, P. Parabolic trough solar collector: A review on geometrical interpretation, mathematical model, and thermal performance augmentation. Eng. Res. Express 2023, 5, 012003. [Google Scholar] [CrossRef]
- Masood, F.; Nor, N.B.M.; Elamvazuthi, I.; Saidur, R.; Alam, M.A.; Akhter, J.; Yusuf, M.; Ali, S.M.; Sattar, M.; Baba, M.; et al. The compound parabolic concentrators for solar photovoltaic applications: Opportunities and challenges. Energy Rep. 2022, 8, 13558–13584. [Google Scholar] [CrossRef]
- Malan, A.; Kumar, K.R. A comprehensive review on optical analysis of parabolic trough solar collector. Sustain. Energy Technol. Assess. 2021, 46, 101305. [Google Scholar] [CrossRef]
- Yılmaz, İ.H.; Mwesigye, A. Modeling, simulation and performance analysis of parabolic trough solar collectors: A comprehensive review. Appl. Energy 2018, 225, 135–174. [Google Scholar] [CrossRef]
- Azizi, M.; Tabatabaeekoloor, R.; Motevali, A.; Seyedi, S.R.M. Evaluation of mono and hybrid nano-fluids on energy and exergy parameters of a photovoltaic-thermal system equipped with an eccentric parabolic trough concentrator. Appl. Therm. Eng. 2023, 223, 119979. [Google Scholar] [CrossRef]
- Hou, Y.; Yu, X.; Yang, B.; Liu, S.; Qi, Y. Optical performance investigation on flat receiver for parabolic trough solar collector based on the MCRT method. Renew. Energy 2023, 202, 525–536. [Google Scholar] [CrossRef]
- Renno, C.; Perone, A.; D’Agostino, D.; Minichiello, F. Performance Evaluation of a Linear CPV/T System in Different Working Conditions. Energies 2023, 16, 2115. [Google Scholar] [CrossRef]
- Santana, J.P.; Rivera-Solorio, C.I.; Chew, J.W.; Tan, Y.Z.; Gijón-Rivera, M.; Acosta-Pazmiño, I. Performance Assessment of Coupled Concentrated Photovoltaic-Thermal and Vacuum Membrane Distillation (CPVT-VMD) System for Water Desalination. Energies 2023, 16, 1541. [Google Scholar] [CrossRef]
- Zheng, N.; Zhang, H.; Duan, L.; Wang, Q.; Bischi, A.; Desideri, U. Techno-economic analysis of a novel solar-driven PEMEC-SOFC-based multi-generation system coupled parabolic trough photovoltaic thermal collector and thermal energy storage. Appl. Energy 2023, 331, 120400. [Google Scholar] [CrossRef]
- Acosta-Pazmiño, I.P.; Rivera-Solorio, C.I.; Gijón-Rivera, M. Hybridization of a parabolic trough-based thermal plant for industrial heat and power generation. Renew. Energy 2022, 191, 961–973. [Google Scholar] [CrossRef]
- Dogahe, S.A.; Javaran, E.J.; Abdolzadeh, M. Energy and economic analysis of photovoltaic, concentrating photovoltaic, and combined concentrating photovoltaic/thermal-organic Rankine cycle power plants in Iran. Environ. Prog. Sustain. Energy 2022, 41, e13763. [Google Scholar] [CrossRef]
- Gorouh, H.A.; Salmanzadeh, M.; Nasseriyan, P.; Hayati, A.; Cabral, D.; Gomes, J.; Karlsson, B. Thermal modelling and experimental evaluation of a novel concentrating photovoltaic thermal collector (CPVT) with parabolic concentrator. Renew. Energy 2022, 181, 535–553. [Google Scholar] [CrossRef]
- Kurşun, B.; Ökten, K. Comprehensive energy, exergy, and economic analysis of the scenario of supplementing pumped thermal energy storage (PTES) with a concentrated photovoltaic thermal system. Energy Convers. Manag. 2022, 260, 115592. [Google Scholar] [CrossRef]
- Zhu, T.; Li, Q.; Yu, A. Analysis of the solar spectrum allocation in a spectral-splitting photovoltaic-thermochemical hybrid system. Sol. Energy 2022, 232, 63–72. [Google Scholar] [CrossRef]
- Cabral, D.; Gomes, J.; Hayati, A.; Karlsson, B. Experimental investigation of a CPVT collector coupled with a wedge PVT receiver. Sol. Energy 2021, 215, 335–345. [Google Scholar] [CrossRef]
- Herez, A.; El Hage, H.; Lemenand, T.; Ramadan, M.; Khaled, M. Parabolic trough Photovoltaic/Thermal hybrid system: Thermal modeling, case studies, and economic and environmental analyzes. Renew. Energy Focus 2021, 38, 9–21. [Google Scholar] [CrossRef]
- Herez, A.; El Hage, H.; Lemenand, T.; Ramadan, M.; Khaled, M. Parabolic trough photovoltaic/thermal hybrid system: Thermal modeling and parametric analysis. Renew. Energy 2021, 165, 224–236. [Google Scholar] [CrossRef]
- Hu, Y.; Zhang, L.; Zhang, H.; Lv, H.; Xu, C. Thermodynamic analysis of a spectral-splitting hybrid PV-thermal system with LiBr/H2O absorption heat transformer. Energy Convers. Manag. 2021, 249, 114868. [Google Scholar] [CrossRef]
- Renno, C.; Perone, A.; D’Agostino, D.; Minichiello, F. Experimental and Economic Analysis of a Concentrating Photovoltaic System Applied to Users of Increasing Size. Energies 2021, 14, 4968. [Google Scholar] [CrossRef]
- Zhang, J.J.; Qu, Z.G.; Wang, Q.; Zhang, J.F.; He, Y.L. Multiscale investigation of the plasmonic solar cell in the spectral splitting concentrating photovoltaic-thermal system. Energy Convers. Manag. 2021, 250, 114846. [Google Scholar] [CrossRef]
- Zima, W.; Cisek, P.; Cebula, A. Mathematical model of an innovative double U-tube sun-tracked PTC and its experimental verification. Energy 2021, 235, 121293. [Google Scholar] [CrossRef]
- Acosta-Pazmiño, I.; Rivera-Solorio, C.; Gijón-Rivera, M. Energetic and Economic Analyses of an LCPV/T Solar Hybrid Plant for a Sports Center Building in Mexico. Energies 2020, 13, 5681. [Google Scholar] [CrossRef]
- Alayi, R.; Kasaeian, A.; Atabi, F. Optical modeling and optimization of parabolic trough concentration photovoltaic/thermal system. Environ. Prog. Sustain. Energy 2020, 39, e13303. [Google Scholar] [CrossRef]
- Felsberger, R.; Buchroithner, A.; Gerl, B.; Wegleiter, H. Conversion and Testing of a Solar Thermal Parabolic trough Collector for CPV-T Application. Energies 2020, 13, 6142. [Google Scholar] [CrossRef]
- Gakkhar, N.; Soni, M.K.; Jakhar, S. Experimental and theoretical analysis of hybrid concentrated photovoltaic/thermal system using parabolic trough collector. Appl. Therm. Eng. 2020, 171, 115069. [Google Scholar] [CrossRef]
- Liang, H.; Wang, F.; Zhang, D.; Cheng, Z.; Zhang, C.; Lin, B.; Xu, H. Experimental investigation of cost-effective ZnO nanofluid based spectral splitting CPV/T system. Energy 2020, 194, 116913. [Google Scholar] [CrossRef]
- Khouya, A. Performance assessment of a heat pump and a concentrated photovoltaic thermal system during the wood drying process. Appl. Therm. Eng. 2020, 180, 115923. [Google Scholar] [CrossRef]
- Otanicar, T.P.; Wingert, R.; Orosz, M.; McPheeters, C. Concentrating photovoltaic retrofit for existing parabolic trough solar collectors: Design, experiments, and levelized cost of electricity. Appl. Energy 2020, 265, 114751. [Google Scholar] [CrossRef]
- Renno, C.; Petito, F.; D’Agostino, D.; Minichiello, F. Modeling of a CPV/T-ORC Combined System Adopted for an Industrial User. Energies 2020, 13, 3476. [Google Scholar] [CrossRef]
- Renno, C. Theoretical and Experimental Evaluation of the Working Fluid Temperature Levels in a CPV/T System. Energies 2020, 13, 3077. [Google Scholar] [CrossRef]
- Riahi, A.; Ali, A.B.H.; Fadhel, A.; Guizani, A.; Balghouthi, M. Performance investigation of a concentrating photovoltaic thermal hybrid solar system combined with thermoelectric generators. Energy Convers. Manag. 2020, 205, 112377. [Google Scholar] [CrossRef]
- Wang, G.; Yao, Y.; Lin, J.; Chen, Z.; Hu, P. Design and thermodynamic analysis of a novel solar CPV and thermal combined system utilizing spectral beam splitter. Renew. Energy 2020, 155, 1091–1102. [Google Scholar] [CrossRef]
- Wingert, R.; O’Hern, H.; Orosz, M.; Harikumar, P.; Roberts, K.; Otanicar, T. Spectral beam splitting retrofit for hybrid PV/T using existing parabolic trough power plants for enhanced power output. Sol. Energy 2020, 202, 1–9. [Google Scholar] [CrossRef]
- Adam, S.A.; Ju, X.; Zhang, Z.; El-Samie, M.M.A.; Xu, C. Theoretical investigation of different CPVT configurations based on liquid absorption spectral beam filter. Energy 2019, 189, 116259. [Google Scholar] [CrossRef]
- Alves, P.; Fernandes, J.F.P.; Torres, J.P.N.; Branco, P.J.C.; Fernandes, C.; Gomes, J. From Sweden to Portugal: The effect of very distinct climate zones on energy efficiency of a concentrating photovoltaic/thermal system (CPV/T). Sol. Energy 2019, 188, 96–110. [Google Scholar] [CrossRef]
- Karathanassis, I.K.; Papanicolaou, E.; Belessiotis, V.; Bergeles, G.C. Dynamic simulation and exergetic optimization of a Concentrating Photovoltaic/ Thermal (CPVT) system. Renew. Energy 2019, 135, 1035–1047. [Google Scholar] [CrossRef]
- Liew, N.J.Y.; Lee, H.-J. Numerical analysis of hybrid photovoltaic-thermal systems utilizing different spectral bandpass filters. Renew. Energy 2019, 144, 15–29. [Google Scholar] [CrossRef]
- Maatallah, T.; Youssef, W.B. Simulation and performance analysis of concentrating photovoltaic/thermal collector (CPV/T) with three-sided thermal insulation based on coupled optothermal model. Sol. Energy 2019, 181, 308–324. [Google Scholar] [CrossRef]
- Renno, C.; D’Agostino, D.; Minichiello, F.; Petito, F.; Balen, I. Performance analysis of a CPV/T-DC integrated system adopted for the energy requirements of a supermarket. Appl. Therm. Eng. 2019, 149, 231–248. [Google Scholar] [CrossRef]
- Renno, C.; Petito, F. Modelling of a linear focus concentrating photovoltaic and thermal system for different load scenarios of a residential user. Energy Convers. Manag. 2019, 188, 214–229. [Google Scholar] [CrossRef]
- Valizadeh, M.; Sarhaddi, F.; Adeli, M.M. Exergy performance assessment of a linear parabolic trough photovoltaic thermal collector. Renew. Energy 2019, 138, 1028–1041. [Google Scholar] [CrossRef]
- Wang, G.; Yao, Y.; Chen, Z.; Hu, P. Thermodynamic and optical analyses of a hybrid solar CPV/T system with high solar concentrating uniformity based on spectral beam splitting technology. Energy 2019, 166, 256–266. [Google Scholar] [CrossRef]
- Widyolar, B.; Jiang, L.; Ferry, J.; Winston, R.; Kirk, A.; Osowski, M.; Cygan, D.; Abbasi, H. Theoretical and experimental performance of a two-stage (50X) hybrid spectrum splitting solar collector tested to 600 °C. Appl. Energy 2019, 239, 514–525. [Google Scholar] [CrossRef]
- Youssef, W.B.; Maatallah, T.; Menezo, C.; Nasrallah, S.B. Modeling and optimization of a solar system based on concentrating photovoltaic/thermal collector. Sol. Energy 2018, 170, 301–313. [Google Scholar] [CrossRef]
- Youssef, W.B.; Maatallah, T.; Menezo, C.; Nasrallah, S.B. Assessment viability of a concentrating photovoltaic/thermal-energy cogeneration system (CPV/T) with storage for a textile industry application. Sol. Energy 2018, 159, 841–851. [Google Scholar] [CrossRef]
- Otanicar, T.; Dale, J.; Orosz, M.; Brekke, N.; DeJarnette, D.; Tunkara, E.; Roberts, K.; Harikumar, P. Experimental evaluation of a prototype hybrid CPV/T system utilizing a nanoparticle fluid absorber at elevated temperatures. Appl. Energy 2018, 228, 1531–1539. [Google Scholar] [CrossRef]
- Renno, C. Experimental and Theoretical Analysis of a Linear Focus CPV/T System for Cogeneration Purposes. Energies 2018, 11, 2960. [Google Scholar] [CrossRef]
- Widyolar, B.; Jiang, L.; Abdelhamid, M.; Winston, R. Design and modeling of a spectrum-splitting hybrid CSP-CPV parabolic trough using two-stage high concentration optics and dual junction InGaP/GaAs solar cells. Sol. Energy 2018, 165, 75–84. [Google Scholar] [CrossRef]
- Widyolar, B.; Jiang, L.; Winston, R. Spectral beam splitting in hybrid PV/T parabolic trough systems for power generation. Appl. Energy 2018, 209, 236–250. [Google Scholar] [CrossRef]
- An, W.; Li, J.; Ni, J.; Taylor, R.A.; Zhu, T. Analysis of a temperature dependent optical window for nanofluid-based spectral splitting in PV/T power generation applications. Energy Convers. Manag. 2017, 151, 23–31. [Google Scholar] [CrossRef]
- Karathanassis, I.K.; Papanicolaou, E.; Belessiotis, V.; Bergeles, G.C. Design and experimental evaluation of a parabolic-trough concentrating photovoltaic/thermal (CPVT) system with high-efficiency cooling. Renew. Energy 2017, 101, 467–483. [Google Scholar] [CrossRef]
- Mohsenzadeh, M.; Shafii, M.B.; Jafari Mosleh, H. A novel concentrating photovoltaic/thermal solar system combined with thermoelectric module in an integrated design. Renew. Energy 2017, 113, 822–834. [Google Scholar] [CrossRef]
- Srivastava, S.; Reddy, K.S. Simulation studies of thermal and electrical performance of solar linear parabolic trough concentrating photovoltaic system. Sol. Energy 2017, 149, 195–213. [Google Scholar] [CrossRef]
- Wang, G.; Chen, Z.; Hu, P. Design and experimental investigation of a Multi-segment plate concentrated photovoltaic solar energy system. Appl. Therm. Eng. 2017, 116, 147–152. [Google Scholar] [CrossRef]
- Widyolar, B.K.; Abdelhamid, M.; Jiang, L.; Winston, R.; Yablonovitch, E.; Scranton, G.; Cygan, D.; Abbasi, H.; Kozlov, A. Design, simulation and experimental characterization of a novel parabolic trough hybrid solar photovoltaic/thermal (PV/T) collector. Renew. Energy 2017, 101, 1379–1389. [Google Scholar] [CrossRef]
- Yazdanifard, F.; Ebrahimnia-Bajestan, E.; Ameri, M. Performance of a parabolic trough concentrating photovoltaic/thermal system: Effects of flow regime, design parameters, and using nanofluids. Energy Convers. Manag. 2017, 148, 1265–1277. [Google Scholar] [CrossRef]
- Brekke, N.; Otanicar, T.; DeJarnette, D.; Hari, P. A Parametric Investigation of a Concentrating Photovoltaic/Thermal System with Spectral Filtering Utilizing a Two-Dimensional Heat Transfer Model. J. Sol. Energy Eng. 2016, 138, 021007. [Google Scholar] [CrossRef]
- Stanley, C.; Mojiri, A.; Rahat, M.; Blakers, A.; Rosengarten, G. Performance testing of a spectral beam splitting hybrid PVT solar receiver for linear concentrators. Appl. Energy 2016, 168, 303–313. [Google Scholar] [CrossRef]
- Al-Nimr, M.A.; Dahdolan, M.-E. Modeling of a novel concentrated PV/T distillation system enhanced with a porous evaporator and an internal condenser. Sol. Energy 2015, 120, 593–602. [Google Scholar] [CrossRef]
- Barrau, J.; Perona, A.; Dollet, A.; Rosell, J. Outdoor test of a hybrid jet impingement/micro-channel cooling device for densely packed concentrated photovoltaic cells. Sol. Energy 2014, 107, 113–121. [Google Scholar] [CrossRef]
- Xu, Z.; Kleinstreuer, C. Computational Analysis of Nanofluid Cooling of High Concentration Photovoltaic Cells. J. Therm. Sci. Eng. Appl. 2014, 6, 031009. [Google Scholar] [CrossRef]
- Calise, F.; Palombo, A.; Vanoli, L. A finite-volume model of a parabolic trough photovoltaic/thermal collector: Energetic and exergetic analyses. Energy 2012, 46, 283–294. [Google Scholar] [CrossRef]
- Karathanassis, I.K.; Papanicolaou, E.; Belessiotis, V.; Bergeles, G.C. Multi-objective design optimization of a micro heat sink for Concentrating Photovoltaic/Thermal (CPVT) systems using a genetic algorithm. Appl. Therm. Eng. 2013, 59, 733–744. [Google Scholar] [CrossRef]
- Cabral, D.; Hayati, A.; Gomes, J.; Gorouh, H.A.; Nasseriyan, P.; Salmanzadeh, M. Experimental Electrical Assessment Evaluation of a Vertical n-PERT Half-Size Bifacial Solar Cell String Receiver on a Parabolic trough Solar Collector. Energies 2023, 16, 2007. [Google Scholar] [CrossRef]
- Korres, D.N.; Papingiotis, T.; Koronaki, I.; Tzivanidis, C. Thermal and Optical Analyses of a Hybrid Solar Photovoltaic/Thermal (PV/T) Collector with Asymmetric Reflector: Numerical Modeling and Validation with Experimental Results. Sustainability 2023, 15, 9932. [Google Scholar] [CrossRef]
- Saberi, Z.; Jarimi, H.; Jumali, M.H.H.; Suhendri, S.; Riffat, S.; Fudholi, A.; Razali, H.H.; Sopian, K. Performance assessment of double pass photovoltaic/thermal solar air collector using bifacial PV with CPC and mirror reflector under Malaysian climate. Case Stud. Therm. Eng. 2023, 44, 102811. [Google Scholar] [CrossRef]
- Li, G.; Lu, Y.; Xuan, Q.; Akhlaghi, Y.G.; Pei, G.; Ji, J.; Zhao, X. Small scale optimization in crystalline silicon solar cell on efficiency enhancement of low-concentrating photovoltaic cell. Sol. Energy 2020, 202, 316–325. [Google Scholar] [CrossRef]
- Li, G.; Lu, Y.; Xuan, Q.; Pei, G.; Ji, J.; Zhao, X. Performance analysis on a crystalline silicon photovoltaic cell under non-uniform illumination distribution with a high electrical efficiency. Sol. Energy 2020, 203, 275–283. [Google Scholar] [CrossRef]
- Li, G.; Lu, Y.; Shittu, S.; Zhao, X. Scale effect on electrical characteristics of CPC-PV. Energy 2020, 192, 116726. [Google Scholar] [CrossRef]
- Nasseriyan, P.; Afzali Gorouh, H.; Gomes, J.; Cabral, D.; Salmanzadeh, M.; Lehmann, T.; Hayati, A. Numerical and Experimental Study of an Asymmetric CPC-PVT Solar Collector. Energies 2020, 13, 1669. [Google Scholar] [CrossRef]
- Cabral, D.; Gomes, J.; Karlsson, B. Performance evaluation of non-uniform illumination on a transverse bifacial PVT receiver in combination with a CPC geometry. Sol. Energy 2019, 194, 696–708. [Google Scholar] [CrossRef]
- Chen, H.; Guo, X.; Zhang, H.; Liu, Y.; Liu, H.; Bu, Y. Experimental study on a flash tank integrated with low concentrating PV/T (FT-LCPVT) hybrid system for desalination. Appl. Therm. Eng. 2019, 159, 113874. [Google Scholar] [CrossRef]
- Chen, H.; Huang, J.; Zhang, H.; Liang, K.; Liu, H.; Liang, S. Experimental investigation of a novel low concentrating photovoltaic/thermal–thermoelectric generator hybrid system. Energy 2019, 166, 83–95. [Google Scholar] [CrossRef]
- Chen, H.; Liu, H.; Zhang, H.; Liang, K.; Guo, X.; Yang, B. Numerical simulation and experimental analysis of an LCPV/T system under real operating conditions. J. Clean. Prod. 2019, 209, 903–915. [Google Scholar] [CrossRef]
- Wang, Z.; Wei, J.; Zhang, G.; Xie, H.; Khalid, M. Design and performance study on a large-scale hybrid CPV/T system based on unsteady-state thermal model. Sol. Energy 2019, 177, 427–439. [Google Scholar] [CrossRef]
- Guo, X.; Zhang, H.; Chen, H.; Liang, K.; Huang, J.; Liu, H. Experimental and theoretical investigation on a hybrid LCPV/T solar still system. Desalination 2019, 468, 114063. [Google Scholar] [CrossRef]
- Yang, L.; Heng, Z.; Haiping, C.; Han, Y.; Fei, Y. Simulating and experimental research on a low-concentrating PV/T triple-generation system. Energy Convers. Manag. 2019, 199, 111942. [Google Scholar] [CrossRef]
- Cabral, D.; Karlsson, B.O. Electrical and thermal performance evaluation of symmetric truncated C-PVT trough solar collectors with vertical bifacial receivers. Sol. Energy 2018, 174, 683–690. [Google Scholar] [CrossRef]
- Gupta, V.S.; Singh, D.B.; Mishra, R.K.; Sharma, S.K.; Tiwari, G.N. Development of characteristic equations for PVT-CPC active solar distillation system. Desalination 2018, 445, 266–279. [Google Scholar] [CrossRef]
- Jaaz, A.H.; Sopian, K.; Gaaz, T.S. Study of the electrical and thermal performances of photovoltaic thermal collector-compound parabolic concentrated. Results Phys. 2018, 9, 500–510. [Google Scholar] [CrossRef]
- Tiwari, G.N.; Meraj, M.; Khan, M.E. Exergy analysis of N-photovoltaic thermal-compound parabolic concentrator (N-PVT-CPC) collector for constant collection temperature for vapor absorption refrigeration (VAR) system. Sol. Energy 2018, 173, 1032–1042. [Google Scholar] [CrossRef]
- Torres, J.P.N.; Fernandes, C.A.; Gomes, J.; Luc, B.; Carine, G.; Olsson, O.; Branco, P.C. Effect of Reflector Geometry in the Annual Received Radiation of Low Concentration Photovoltaic Systems. Energies 2018, 11, 1878. [Google Scholar] [CrossRef]
- Zhang, G.; Wei, J.; Xie, H.; Wang, Z.; Xi, Y.; Khalid, M. Performance investigation on a novel spectral splitting concentrating photovoltaic/thermal system based on direct absorption collection. Sol. Energy 2018, 163, 552–563. [Google Scholar] [CrossRef]
- Chen, H.; Zhang, H.; Bu, Y.; Liu, H.; Zhang, X. The performance analysis and evaluation of C-PV/T aided power generation system. Int. J. Energy Res. 2018, 42, 863–876. [Google Scholar] [CrossRef]
- Zhang, H.; Liu, H.; Chen, H.; Guo, X.; Liang, K.; Yao, P. Research on the Performance of Flat-Box Photovoltaic/Thermal Collector with Cooling Channels. J. Sol. Energy Eng. 2017, 140, 021002. [Google Scholar] [CrossRef]
- Jaaz, A.H.; Hasan, H.A.; Sopian, K.; Kadhum, A.A.H.; Gaaz, T.S.; Al-Amiery, A.A. Outdoor Performance Analysis of a Photovoltaic Thermal (PVT) Collector with Jet Impingement and Compound Parabolic Concentrator (CPC). Materials 2017, 10, 888. [Google Scholar] [CrossRef] [PubMed]
- Liu, L.; Jia, Y.; Lin, Y.; Alva, G.; Fang, G. Numerical study of a novel miniature compound parabolic concentrating photovoltaic/thermal collector with microencapsulated phase change slurry. Energy Convers. Manag. 2017, 153, 106–114. [Google Scholar] [CrossRef]
- Proell, M.; Osgyan, P.; Karrer, H.; Brabec, C.J. Experimental efficiency of a low concentrating CPC PVT flat plate collector. Sol. Energy 2017, 147, 463–469. [Google Scholar] [CrossRef]
- Singh, D.B.; Tiwari, G.N. Performance analysis of basin type solar stills integrated with N identical photovoltaic thermal (PVT) compound parabolic concentrator (CPC) collectors: A comparative study. Sol. Energy 2017, 142, 144–158. [Google Scholar] [CrossRef]
- Tripathi, R.; Tiwari, G.N. Annual performance evaluation (energy and exergy) of fully covered concentrated photovoltaic thermal (PVT) water collector: An experimental validation. Sol. Energy 2017, 146, 180–190. [Google Scholar] [CrossRef]
- Tripathi, R.; Tiwari, G.N.; Dwivedi, V.K. Energy matrices evaluation and exergoeconomic analysis of series connected N partially covered (glass to glass PV module) concentrated-photovoltaic thermal collector: At constant flow rate mode. Energy Convers. Manag. 2017, 145, 353–370. [Google Scholar] [CrossRef]
- Zhang, H.; Chen, H.; Han, Y.; Liu, H.; Li, M. Experimental and simulation studies on a novel compound parabolic concentrator. Renew. Energy 2017, 113, 784–794. [Google Scholar] [CrossRef]
- Atheaya, D.; Tiwari, A.; Tiwari, G.N. Exergy analysis of photovoltaic thermal (PVT) compound parabolic concentrator (CPC) for constant collection temperature mode. Sol. Energy 2016, 135, 222–231. [Google Scholar] [CrossRef]
- Proell, M.; Karrer, H.; Brabec, C.J.; Hauer, A. The influence of CPC reflectors on the electrical incidence angle modifier of c-Si cells in a PVT hybrid collector. Sol. Energy 2016, 126, 220–230. [Google Scholar] [CrossRef]
- Tripathi, R.; Tiwari, G.N.; Al-Helal, I.M. Thermal modelling of N partially covered photovoltaic thermal (PVT)—Compound parabolic concentrator (CPC) collectors connected in series. Sol. Energy 2016, 123, 174–184. [Google Scholar] [CrossRef]
- Tripathi, R.; Tiwari, G.N. Energetic and exergetic analysis of N partially covered photovoltaic thermal-compound parabolic concentrator (PVT-CPC) collectors connected in series. Sol. Energy 2016, 137, 441–451. [Google Scholar] [CrossRef]
- Vance, W.; Gustafson, M.; Huang, H.; Menart, J. Computational Study of a Fixed Orientation Photovoltaic Compound Parabolic Concentrator. J. Sol. Energy Eng. 2016, 139, 021002. [Google Scholar] [CrossRef]
- Yousef, M.S.; Rahman, A.K.A.; Ookawara, S. Performance investigation of low—Concentration photovoltaic systems under hot and arid conditions: Experimental and numerical results. Energy Convers. Manag. 2016, 128, 82–94. [Google Scholar] [CrossRef]
- Li, G.; Pei, G.; Ji, J.; Yang, M.; Su, Y.; Xu, N. Numerical and experimental study on a PV/T system with static miniature solar concentrator. Sol. Energy 2015, 120, 565–574. [Google Scholar] [CrossRef]
- Li, G.; Pei, G.; Ji, J.; Su, Y. Outdoor overall performance of a novel air-gap-lens-walled compound parabolic concentrator (ALCPC) incorporated with photovoltaic/thermal system. Appl. Energy 2015, 144, 214–223. [Google Scholar] [CrossRef]
- Zhou, H.; Su, Y.; Bottarelli, M.; Bortoloni, M.; Wu, S. Numerical Validation of a New Approach to Model Single Junction Low Concentration PV Cells under Non-Uniform Illumination. Energies 2015, 8, 4529–4548. [Google Scholar] [CrossRef]
- Bahaidarah, H.M.; Tanweer, B.; Gandhidasan, P.; Ibrahim, N.; Rehman, S. Experimental and numerical study on non-concentrating and symmetric unglazed compound parabolic photovoltaic concentration systems. Appl. Energy 2014, 136, 527–536. [Google Scholar] [CrossRef]
- Li, G.; Gang, P.; Su, Y.; Wang, Y.; Jie, J. Design and investigation of a novel lens-walled compound parabolic concentrator with air gap. Appl. Energy 2014, 125, 21–27. [Google Scholar] [CrossRef]
- Li, G.; Pei, G.; Yang, M.; Ji, J.; Su, Y. Optical evaluation of a novel static incorporated compound parabolic concentrator with photovoltaic/thermal system and preliminary experiment. Energy Convers. Manag. 2014, 85, 204–211. [Google Scholar] [CrossRef]
- Tiwari, G.N.; Meraj, M.; Khan, M.E.; Dwevedi, V.K. Effect of Series and Parallel Combination of Photovoltaic Thermal Collectors on the Performances of Integrated Active Solar Still. J. Therm. Sci. Eng. Appl. 2022, 14, 081006. [Google Scholar] [CrossRef]
- Tiwari, G.N.; Singh, R.K.; Sinha, A.S.K. Thermal and Electrical Analysis of N-PVT-FPC Hybrid Active Heating of Biogas Plant. J. Therm. Sci. Eng. Appl. 2023, 16, 011005. [Google Scholar] [CrossRef]
- Duffie, J.; Beckman, W. Solar Engineering of Thermal Processes; Wiley: New York, NY, USA, 2006. [Google Scholar]
- Kalogirou, S.A. Solar Energy Engineering: Processes and Systems. In EngineeringPro Collection; Elsevier Science: Burlington, MA, USA; San Diego, CA, USA; London, UK, 2009; Available online: https://books.google.com.mx/books?id=wYRqAAAAQBAJ&printsec=frontcover&hl=es&source=gbs_ge_summary_r&cad=0#v=onepage&q&f=false (accessed on 4 October 2023).
- Kalogirou, S.A. A detailed thermal model of a parabolic trough collector receiver. Energy 2012, 48, 298–306. [Google Scholar] [CrossRef]
- Forristall, R. Heat Transfer Analysis and Modeling of a Parabolic trough Solar Receiver Implemented in Engineering Equation Solver; NREL/TP-550-34169; National Renewable Energy Lab. (NREL): Golden, CO, USA, 2003. [CrossRef]
- Behar, O.; Khellaf, A.; Mohammedi, K. A novel parabolic trough solar collector model—Validation with experimental data and comparison to Engineering Equation Solver (EES). Energy Convers. Manag. 2015, 106, 268–281. [Google Scholar] [CrossRef]
- Incropera, F.P.; DeWitt, D.P.; Bergman, T.L.; Lavine, A.S. Fundamentals of Heat and Mass Transfer; Wiley: New York, NY, USA, 1996; Volume 6. [Google Scholar]
- Ji, X.; Li, M.; Lin, W.; Wang, W.; Wang, L.; Xi, J. Modeling and Characteristic Parameters Analysis of a trough Concentrating Photovoltaic/Thermal System with GaAs and Super Cell Arrays. Int. J. Photoenergy 2012, 2012, 782560. [Google Scholar] [CrossRef]
- Ju, X.; Wang, Z.; Flamant, G.; Li, P.; Zhao, W. Numerical analysis and optimization of a spectrum splitting concentration photovoltaic–thermoelectric hybrid system. Sol. Energy 2012, 86, 1941–1954. [Google Scholar] [CrossRef]
- Welcome|TRNSYS: Transient System Simulation Tool. Available online: http://www.trnsys.com/ (accessed on 4 October 2023).
- EES: Engineering Equation Solver|F-Chart Software: Engineering Software. Available online: https://fchartsoftware.com/ees/ (accessed on 4 October 2023).
- Bernardo, L.R.; Perers, B.; Håkansson, H.; Karlsson, B. Performance evaluation of low concentrating photovoltaic/thermal systems: A case study from Sweden. Sol. Energy 2011, 85, 1499–1510. [Google Scholar] [CrossRef]
- Othman, M.Y.H.; Yatim, B.; Sopian, K.; Bakar, M.N.A. Performance analysis of a double-pass photovoltaic/thermal (PV/T) solar collector with CPC and fins. Renew. Energy 2005, 30, 2005–2017. [Google Scholar] [CrossRef]
- Herez, A.; El Hage, H.; Lemenand, T.; Ramadan, M.; Khaled, M. Parabolic trough photovoltaic thermoelectric hybrid system: Thermal modeling, case studies and economic and environmental analyses. Sustain. Energy Technol. Assess. 2021, 47, 101368. [Google Scholar] [CrossRef]
- Herez, A.; Jaber, H.; El Hage, H.; Lemenand, T.; Chahine, K.; Ramadan, M.; Khaled, M. Parabolic trough photovoltaic thermoelectric hybrid system: Simulation model, parametric analysis, and practical recommendations. Int. J. Thermofluids 2023, 17, 100309. [Google Scholar] [CrossRef]
- Calise, F.; Vanoli, L. Parabolic trough Photovoltaic/Thermal Collectors: Design and Simulation Model. Energies 2012, 5, 4186–4208. [Google Scholar] [CrossRef]
- Renewable Power Generation Costs in 2022. Available online: https://www.irena.org/Publications/2023/Aug/Renewable-Power-Generation-Costs-in-2022 (accessed on 11 March 2024).
- Singh, P.; Ravindra, N.M. Temperature dependence of solar cell performance—An analysis. Sol. Energy Mater. Sol. Cells 2012, 101, 36–45. [Google Scholar] [CrossRef]
- Ghadamyari, M.; Nejad, A.A.; Mehregan, M.; Mohammadkhani, M. Thermodynamic and environmental analysis on a CCHP system based on MCFC-GT integrated with MED-TVC desalination system. Energy Rep. 2024, 11, 1925–1944. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).