Abstract
Motivated by the suboptimal performances observed in existing compressed air energy storage (CAES) systems, this work focuses on the efficiency optimization of CAES through thermal energy storage (TES) integration. The research explores the dependence of CAES performance on power plant layout, charging time, discharging time, available power, and cavern volume. Hence, a range of solutions are examined, encompassing both solid and liquid TES options, alongside the potential utilization of external air heaters. Inefficiencies in solid TES due to significant retention of thermal power within the medium after complete discharge are identified and mitigated through optimization strategies. In addition, solutions to prevent ice formation at the low-pressure expander phase are suggested to avoid icing issues in CAES layouts with liquid TES. Through this comprehensive investigation, the study provides valuable insights into enhancing the efficiency and sustainability of CAES systems. By constructing a volume–power–time conversion table, the research contributes to the advancement of CAES technology, facilitating more efficient energy storage and utilization, thereby addressing critical challenges in the field of energy storage.
1. Introduction
In recent years, the escalating demand for increased energy production has encountered challenges stemming from environmental constraints, particularly in limiting greenhouse gas (GHG) emissions and addressing the rising costs and geo-political market uncertainty associated with fossil fuels. While large-scale renewable power plants present a promising avenue for mitigating GHG emissions, their deployment introduces complexities such as grid congestion and voltage stability issues due to the inherent unpredictability of renewable sources. Furthermore, their intrinsic intermittent nature may lead to unavailability during periods of high demand.
When the production of renewable energy systems (RESs) varies, grid voltage and frequency are maintained within tolerance by balancing power. Regulation can be achieved through existing spinning reservoirs, voltage regulation, and load following, incurring negligible additional system costs up to a market penetration of 20% [1]. Exceeding the 20% causes the incremental costs per kWh to become significant. The costs arise due to the necessity for supplemental generating capacity capable of compensating for power drops [2]. Compressed air energy storage (CAES) systems emerge as a viable solution to attain the target generating capacity.
The fluctuations in generation patterns in wind parks create complexities in electrical grid management, requiring technological solutions to balance supply and demand. CAES systems provide dispatchable power to align with load and market prices, enhancing the capacity factor of a renewable power plant, and contributing to reduce infrastructure transmission costs by mitigating peak energy delivered by wind parks [3].
A techno-economic assessment [4], focused on Net Present Value analyses based on the annual local marginal prices, indicated higher NPV for the integrated CAES system with a Natural Gas Combined Cycle (NGCC) than the NGCC alone for all the regions investigated. The authors reported a levelized cost of energy between USD 136 and 145 /MWh and a round-trip efficiency between 74.6 and 82.5%, demonstrating the potential development of the CAES technology in these markets and regions with a fair enough location marginal price profile.
Kim et al. [5] examined the primary benefits associated with CAES facilities, including insights into site selection and design constraints. The authors delineated key advantages of CAES installations, notably their capacity for grid-scale energy storage and their utilization of compressed air, which offers a minimal environmental footprint. Rabi et al. [6] highlighted the benefits of CAES plants, encompassing clean storage, scalability, low self-discharge, extended discharge times, durability, prolonged response times, limited depth of discharge, and relatively low roundtrip efficiency. Their research provided a thorough examination facilitating the integration of diverse CAES types into energy systems, addressing present constraints and future outlooks. Tong et al. [7] provided insights into CAES development in China, including feasibility, air storage options, and pilot projects, emphasizing its role in grid stability, energy generation, and demand management, even though challenges in their commercialization persist.
Dindorf [8] explored the energy efficiency of compressed air storage tanks in small-scale compressed air energy storage (CAES) and renewable energy systems. Through numerical solutions of a mathematical model, the author evaluated the tanks’ suitability for energy storage and generation, emphasizing their relevance in balancing peak electricity demand and advancing renewable energy sources. Wang et al. [9] proposed a distributed compressed air energy storage combined heat and power model for regional microgrids, addressing geographical and climatic challenges. The model, accounting for thermodynamic characteristics of air storage devices, demonstrated improved system efficiency, offering insights for practical application in complex environments.
Assuming the CAES power plant’s feasibility, He et al. [10] proposed solutions for improving the round-trip efficiency during energy storage and delivery while increasing the utilization of the heat stored during the compression phase. The plant performance increased by controlling the circuit valves between the compressor and expander, thus implying a change in the plant pressure ratio with a step-by-step rise in the inlet pressure at the compressor. This work demonstrated a drop in the compressor power consumption of 12%, an increase in the turbine work of 17.9%, and an increase in the efficiency of 13.1% for a 500-kW adiabatic CAES plant.
Salyga et al. [11] compared three configurations of constant volume CAES, with or without heat recuperation and an adiabatic layout, concluding that the lowest energy density but the highest efficiency is achieved with the A-CAES solution; meanwhile, the D-CAES without recuperation ensures a quick startup, reliability, and high power, due to its simplicity. Soltani et al. [12] assessed energy, exergy, and key thermodynamic parameters, focusing on D-CAES assemblies. Through a techno-economic evaluation, the Huntorf and McIntosh plants were analyzed as mature and commercially viable technologies. Strategies to enhance round-trip efficiency, reduce fuel consumption, and optimize initial costs were identified, with an emphasis on plant hybridization for efficiency improvement. Kotowicz and Jurczyk [13] analyzed the D-CAES technology, focusing on its energy storage principles and utilization during electricity surpluses, and highlighting its advantages and drawbacks, along with the necessity for advancing energy storage solutions, particularly in light of increasing reliance on renewable energy sources.
With the hypothesis of constant inlet pressure at the turbine for the design condition, Zhao et al. [14] modeled the off-design operation of a constant volume A-CAES plant by adjusting the air mass flow rate at a constant inlet temperature. Unlike the variable inlet pressure operation, the authors indicated that a constant inlet pressure to the expander is feasible by throttling the compressed air in the cavern to a fixed pressure.
Through a two-step simulation based on an analytical model of air temperature and pressure and a finite element model for the cavern, Khaledi et al. [15] investigated the thermomechanical behavior of rock salt in caverns. The authors clarified that the cavern’s internal pressure governs its stability, while high-temperature operations affect its long-term serviceability. The conclusion is that setting the minimum pressure in the cavern would reduce the mechanical stresses below the dilatancy threshold while maintaining the air temperature below a threshold would avoid the creep deformation of rock salt and material weakening.
Other works based on A-CAES modeling are briefly outlined. Zhou et al. [16] developed a model to demonstrate variable conditions and the feasibility of an A-CAES system. Tola et al. [17] modeled two A-CAES plant configurations using air and thermal oil. In the oil plant, structural issues arose due to increasing tank pressure, highlighting the importance of tank design and maintenance. Sciacovelli et al. [18] presented a dynamic model for an A-CAES plant with packed bed Thermal Energy Storage (TES), covering full and off-design performance, and highlighting the transient characteristics of thermal storage, cavern dynamics, and compression and expansion phases.
The previous literature underscores different aspects of CAES systems, encompassing the modeling of distinct plant configurations and analyzing thermomechanical characteristics. However, while individual studies have explored specific aspects of CAES systems, a comprehensive assessment of efficiency across different plant configurations is absent.
Therefore, an exhaustive model of CAES power facilities is proposed to determine the performance across different layouts, aiming to investigate key aspects such as efficiency, produced and absorbed energy, charging, and discharging time across a wide range of cavern volumes (from 500 to 200,000 m3), and aiming to consider different heat exchange solutions, including solid or liquid TES, with or without external air heating, and with constant or variable cavern pressure. Moreover, the study focuses on developing algorithms for solid TES to enhance heat exchange during the charging and discharging phases. The simulation outputs allow for the building of a volume–power–time (VPT) conversion table, facilitating the correlation between energy production, efficiencies, and cavern volumes. Overall, the findings provide insights into optimizing CAES power plants for more efficient and sustainable energy storage, thereby facilitating the integration of renewable energy sources into the grid.
A constant-volume CAES is assessed, where a cavern of a specified capacity serves as a reservoir for supplying air to the expander phases, allowing for variable pressure operations. In this sense, the present model diverges from our earlier work [19], which emphasized the theoretically attainable efficiency in constant-pressure underwater CAES (UW-CAES) power plants, achieved through iterative adjustments of the heat exchanger effectiveness while maintaining a constant airflow rate between compression and expansion.
The numerical simulations are performed with the model presented in Section 2 developed in a MATLAB environment, based on several CAES plant layouts, such as the following:
- Solid TES (no external air heating)
- Solid TES with external air heating
- External air heating (no air cooling, no TES)
- External air heating, air cooling (no TES)
- Liquid TES (no air heating)
- High-temperature liquid TES with two aftercoolers
- Low-temperature liquid TES with two aftercoolers
- Liquid TES with external air heating
- Constant-pressure cavern and air cooling (no external air heating, no TES)
Each CAES plant layout is evaluated across various cavern volumes within the range specified in Table 1 to establish the correlation between cavern volume and energy production.

Table 1.
Cavern volume range and mass flow rates.
2. Numerical Model
2.1. System Description
Figure 1 presents the A-CAES plant layout of the model and includes single or multiple compressor phases, an underground cavity, air heaters, and expander phases. The fixed-volume cavern is modeled at a prescribed pressure range compliant with the lower limit imposed by the minimum working pressure of the turbomachinery plus the pressure drops due to the throttling valve and circuit. Intercoolers are added to reduce air temperature between two consecutive compression phases, while aftercoolers allow decreasing air temperature before the injection into the cavern downstream of the compressor. Solid and liquid TES represent optional components modeled to compare the power plant efficiency. The former is modeled with concrete cylinders supplied by tubes of a given diameter [20], ensuring high heat capacity allowed by its high thermal conductivity. The latter operates at higher temperatures (600–900 K) due to the utilization of nitrate salt, implying the installation of hot and cold tanks and a freezing point control to avoid the liquid salt freezing in the pipeline when the plant is not operating. Two external air heaters (heater 1 and heater 2) are modeled as combustion chambers or electric resistances driven by a renewable power source.
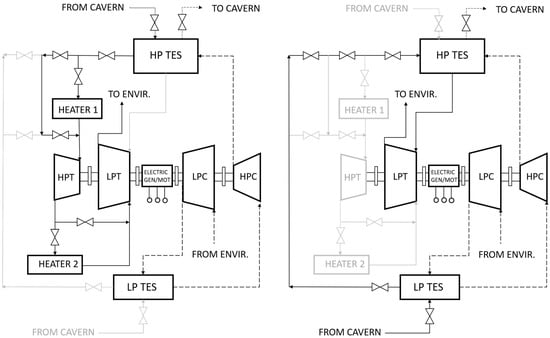
Figure 1.
General CAES plant layout with TES and external air heating in full-load operation (left-hand side) and partial-load (right-hand side). Solid line: active expander phases. Thin solid line: inactive expander phases. Dashed line: compressor phases.
The existing CAES power plants (McIntosh [21], Huntorf [22,23]) are improved with a model implementing TES systems capable of storing the heat extracted from the hot compressed air during each compression phase. The stored heat reheats the cold air from the cavern, eliminating fossil fuel burners or external air heaters. The compressor module is modeled with two phases operating as inter-cooling and after-cooling systems, i.e., low-pressure TES (LP TES) and high-pressure TES (HP TES), respectively. The expander is modeled with two modules (LP exp and HP exp), with both TESs operating as preheaters for each turbine phase. When the cavern pressure reduces from the full-load operation, the plant configuration is modified. The HP expansion phase is bypassed so that HP TES and LP TES are supplied in series. While LP TES preheats the air after the LP compression, the HP TES increases the air temperature to the maximum cycle temperature. An expander high-pressure bypass is inserted to ensure the plant’s operation at the low-pressure ratio.
The power delivered bypassing the HP phase is lower than the full-load operation. Therefore, the power plant can operate in full-load mode (operating HP and LP expansion phases) and partial-load mode (operating LP expansion phase). The throttling valves adapt the sliding cavern pressure to the compressor and expander’s rated working pressures.
The simulations are executed for the cavern volumes indicated in Table 1, with the compressor and expander’s mass flow rates related to each cavern volume. The main parameters of the simulations are specified instead in Table 2. For a given cavern volume, after the initialization of the cavern pressure, the air mass stored in the cavern is determined in time based on the density of the injected air. For an accurate prediction of the cavern-wall temperature, a finite element assessment of the TES is executed to determine the hourly thermal power stored. Hence, the discharging time and extracted power are determined, and so is the round-trip efficiency of the plant. The simulations are performed in full-load operation with the fluid supplied to both HP and LP turbine phases and in partial-load operation with the air bypassing the HP phase at a low cavern pressure.

Table 2.
Main parameters.
In a solid TES layout (without external air heating), the charging mass flow rate is set to 250 kg/s, ensuring 8–9 h of charging time for the maximum cavern volume. The discharging mass flow rates are computed by imposing the cavern discharging mass flow to a charging mass flow ratio equal to 2.2. The mass flow rate is set to 550 kg/s for the maximum cavern volume, allowing an expansion phase duration similar to that of the Huntorf power plant [22,23], i.e., 3–4 h. The other mass flow rates are scaled linearly with cavern volume for the reference volume of 200,000 m3. According to [27], if the mass flow rate ratio increases above 2.2 in solid TES, the air mass from the cavern would be withdrawn too quickly, implying a drop in the efficiency in the expansion phase and non-homogenous heat distribution in the concrete sections.
In a solid TES layout with air heating, the algorithm is the same but includes two external heaters to increase the air temperature from each corresponding TES, one per turbine phase.
The solution with external air heating without cooling (no TES), is used to supply hot compressed air directly into the cavern. With this layout, both air heaters are used. Conversely, the external air heating layout with air cooling (no TES) implies a drop in the air temperature using intercoolers and aftercoolers.
In a liquid TES layout (without external air heating), the heat exchanger heats the air from the cavern, which is expanded in the turbine phases. The variation in the heat exchanger size just slightly influences the round-trip efficiency. The chosen heat exchanger data (Table 2) allow the highest gain efficiency, however moderate. If two aftercoolers are introduced (case a), the algorithm computes the optimum liquid mass flow rate, maximizing its temperature. Alternatively, if the hot liquid temperature is reduced (case b) to 778 K to raise the hot liquid stored mass, the HP exchanger mass flow rate increases from 225 kg/s to 274 kg/s.
In a liquid TES layout with external air heating, an external heater is presented upstream of each expansion phase. Two heat exchangers are modeled upstream of the HP turbine phase because the outlet temperature from the HP turbine phase can be higher than the hot liquid temperature.
In the last layout, with air cooling and external air heating, the cavern pressure is maintained constant at 45 bar during charging and discharging. With intercooling and aftercooling, the air temperature diminished to 330 K to reduce the vapor content. Throttling valves are required to allow the air pressure to match the compressor- and expander-rated pressure.
2.2. Compressor and Turbine Equations
The model incorporates temperature-dependent specific heat, viscosity, conductivity, and air density to ensure precise outputs. The compressor and expander’s performances are estimated by assuming polytropic transformations given the compression and expansion ratios and the main cycle temperatures. The polytropic transformation is modeled according to (1), considering a polytropic index m and specific heat c. The index m serves to model an irreversible process through reversible and quasi-static heat transfer and energy transformation. The Real Gas Law is introduced in Equation (2), with RA being the gas constant.
p × vm = const m = (cp − c)/(cv − c) c = dQ/dT
p × v = RA × T
The final compression temperature for a polytropic process is given in Equation (3), achieved by combining (1) and (2).
Tc,out = Tc,in × (pout/pin)(m−1)/m = Tc,in (βc)ν
For an adiabatic compressive process, the polytropic efficiency ηpol,c is defined as
ηpol,c = v × dp/dhc = cp × [(m − 1)/m]/RA = ν/εc
The exponent ν is achieved by solving Equation (4), and it is substituted in Equation (3), yielding the final compression temperature as a function of initial air temperature Tin, compression ratio βc = pout/pin, polytropic efficiency ηpol,c, and the isentropic exponent εc.
Tc,out = Tc,in × (βc)(εc/ηpol,c)
Hence, the required enthalpy variation for a polytropic compression is given in Equation (6), with specific heat defined as the average value of those computed at the initial and final point, expressed in J/kgK.
Substituting Equation (3) into (6) yields the specific work required to perform a compression from pin to pout with a temperature gain equal to (Tc,out − Tc,in) in Equation (7).
Concerning the turbine, the polytropic efficiency is defined as
ηpol,t = dht/(v × dp) = (m × RA)/[cp × (m − 1)] = εt/ν
Equation (9) describes the air temperature at the end of the expansion phase as a function of the initial expansion temperature Tt,in, the expander polytropic efficiency, and the isentropic exponent εT.
Tt,out = Tt,in × (βc)(εc × ηpol,t)
The polytropic efficiency is calculated with the size parameter method [28] recalled in Equation (10), where Vin denotes the inlet volumetric flow rate in m3/s, and Δhis denotes the isentropic enthalpy drop in J/kg processed by the turbomachine. The size parameter SP correlates statistically ηpol to the characteristic diameter in axial compressors of gas turbines near the optimum characteristic speed NS and represents the denominator of the characteristic diameter, i.e., Ds = D/SP, where D is the mean diameter of the turbomachine. Polytropic efficiencies higher than 90% are achieved in gas turbines from 100 MW (βt = 15 ÷ 18) or aero-derivative gas turbines with βt ≈ 30 [28].
SP = Vin0.5/Δhis0.25
Equations (11) and (12) describe the polytropic efficiency for the compressor phase as a function of the SP, and the polytropic efficiency for the expander, respectively. The chosen parameters for cooled and uncooled phases are ηpol,∞ = 0.89 and ηpol,∞ = 0.925.
SP < 1 ηpol,c(T) = 0.895 × (1 − 0.0718 × log210 SP)
SP ≥ 1 ηpol,c(T) = 0.895
SP < 1 ηpol,t(T) = ηpol,∞ × (1 − 0.002688 × log210 SP)
SP ≥ 1 ηpol,t(T) = ηpol,∞
2.3. Solid TES
The solid thermal energy storage is modeled by solving the unsteady 1-D heat propagation equation through the radial direction of a solid storage media cylinder. The storage is designed to keep the air speed in the pipeline at 8 m/s in the most demanding operating condition, with oversized tubes to allow high performance during compression and discharge (Table 2). The thermal power exchanged between two neighboring elementary volumes is computed based on Equation (13), where the index i denotes the i-th elementary volume of solid media considered; λconcrete denotes the thermal conductivity of the solid elements in W/mK; A and rstep denote the area of the solid storage cylinder in m2 and the elementary step in the radial direction in m, respectively; and (Ti − Ti+1) denotes the discrete temperature variation in K. The heat exchanged between the hot/cold air and the first elementary volume is computed by Equation (14), where 1 denotes the thermal power transferred at the first radial element, (Tair − T1) denotes the temperature variation between the air and the first elementary solid media of area A1, and hpipes denotes the heat transfer coefficient in W/m2K.
The computations are executed with a time step tstep, achieving the discrete heat transfer ΔQ between two elements (15). The updated temperature of the i-th element Ti (16) is derived from the energy conservation, where the mass is denoted by msolid, and the specific heat is denoted by cp,solid. Hence, the whole temperature profile is computed by iterating through the time and radial direction of the solid media storage.
Ti = Ti+1 + ΔQ/(msolid × cp,solid)
The fluid–pipe interaction is modeled according to the heat convection in pipes as shown by equations from (17) to (19), where λpipes denotes the pipe thermal conductivity, Dpipes denotes the pipe diameter, μ denotes the dynamic viscosity, and cp,air represents the air-specific heat. The dimensionless parameters Nu, Re, and Pr represent Nusselt, Reynolds, and Prandtl’s numbers, respectively. If the air is cooled, the exponent n equals 0.3. Diversely, if the air is heated by a solid medium, the exponent n equals 0.4. For solid storage media, the specific heat and density are assumed constant.
hpipes = λpipes × Nu/Dpipes
Nu = Re0.8 × 0.00227 × Prn
Pr = μ × cp, air/λpipes
2.4. Liquid TES
While solid TES systems imply variations in the outlet air temperature Tair,out, liquid TES systems allow it to be kept constant. The liquid thermal energy storage medium is modeled according to the experimental data about molten salt collected from [24,29,30]. The specific heat and density are constant, while the heat exchangers that cool or heat air are modeled according to the experimental results synthesized in [25] and reported in Table 1. For simplicity, the thermal inertia of the heat exchanger is neglected.
According to the schematic of staggered bundles in [27], Xt = Xl = 1. At equilibrium, the heat extracted from the air is equivalent to the heat absorbed by the molten salt. Hence, steady heat exchange is modeled such that air × cp,air × ΔTair = salt × cp,salt × ΔTsalt, with air mass flow rates indicated in Table 1. A drawback of liquid TES is the minimum molten salt temperature Tsalt,min of 550 K due to its freezing point, imposing a higher outlet air temperature Tair,out of 560 K. The molten salt constraints are defined in Table 2. Once the liquid mass flow rate salt that satisfies the constraints is calculated, the heat transfer coefficient based on the Nusselt number correlated with staggered bundles in crossflow is derived according to Equation (20).
The authors in [25] collect several models based on experimental tests to estimate the Nusselt number, as indicated below.
If 2 × 105 ≤ Reb ≤ 2 × 106,
Nub = 0.031 × Cn × Re0.8 × Prb0.4 × (Prb/Prw)0.25 × (Xt/Xl)0.2
If 103 ≤ Reb ≤ 105,
Nub = 0.35 × Cn × Re0.6 × Prb0.36 × (Prb/Prw)0.25 × (Xt/Xl)0.2
If 500 ≤ Reb ≤ 103,
Nub = 0.71 × Cn × Re0.5 × Prb0.36 × (Prb/Prw)0.25 × (Xt/Xl)0.2
Cn denotes a correlation factor for the row number equal to 1 in this model. Prb and Prw represent the Prandtl’s number for heat exchanger bulk and wall. These are estimated by Equations (24) and (25), respectively.
Prb = μair × cp,air/kair
Prw = μsalt × cp,salt/kair
A simplified method to calculate the heat transfer coefficient was presented by Raju et al. [31] in the case of a lack of information about the correlation between the flow and heat transfer coefficient. The cavern wall exchange coefficient was approximated by fitting a two-parameter function that represents the global heat exchange factors until the numerical temperature behavior is close to the experimental temperature of the Huntorf power plant.
The fitted function (26) is used to estimate the cavern temperature in the considered range (Table 2), assuming the thermal exchange coefficient is independent of the cavern volume. Parameters a and b [31] denote natural and forced convection (air injection or withdrawal) factors. These are equal to 0.2356 kJ/m3 and 0.0149 kJ/kgm3, respectively.
2.5. Pipeline Pressure Drop
The pipe head losses are computed according to Equation (27). Velocity Vi and density ρ are determined at each section analyzed. Since the mass flow rate is constant, density variations of the airflow due to the continuous pressure drop generate a gain in the flow speed while the pipeline is assumed adiabatic.
Δp = ρi × (fpipes/Dpipes) × L × (ui2/2)
3. Results
The first output of the simulation is represented by a finite element analysis of the solid TES as a function of the pipe length and radius. Figure 2 shows the temperature profile in the solid medium (concrete) after 8 h of the charging phase; meanwhile, Figure 3 shows the solid medium temperature profile after 3 h of the discharging phase, highlighting the remaining heat flux in the solid medium. This problem is due to the temperature difference between the charging and discharging phases and the solid TES piping configuration during partial-load operation (discharging phase). Since the two TESs are connected in series, the HP module experiences higher inlet air temperature with lower thermal exchange rates.
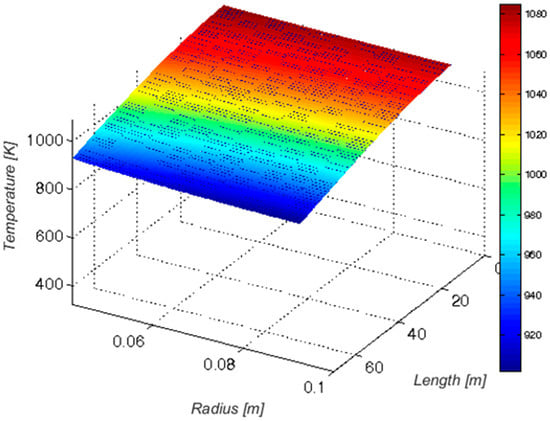
Figure 2.
Solid TES temperature profile after 8 h of charge, according to [27].
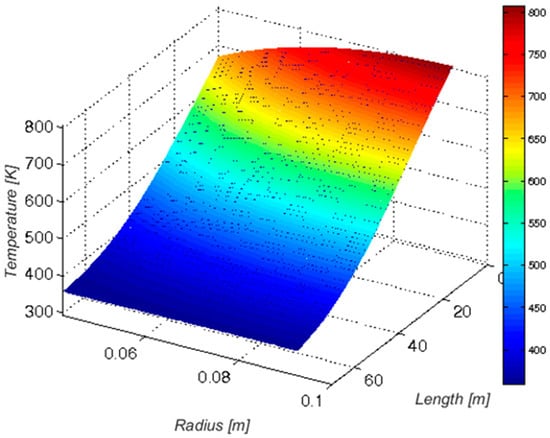
Figure 3.
Solid TES temperature profile after 3 h of discharge, according to [27].
The second output of the simulation is achieved from the CAES configuration with liquid TES and without external air heating systems. The liquid medium (nitrite salt) has a freezing temperature close to 538 K [24], implying an inferior threshold for air temperature at 550 K due to freezing problems in the pipeline and heat exchangers. In a second post-refrigeration system, the storage medium (mineral oil) is added to further reduce the air temperature. This power plant layout experiences an icing problem in the last LP expander phase because the hot liquid stored during the compression phase cannot reheat the air to cover the entire expansion phase.
As depicted in Figure 4, the hot liquid runs out after 4.2 h of expansion. A viable solution consists of decreasing the maximum hot liquid temperature to 738 K to store a higher mass of hot salt during compression, as illustrated in Figure 5.
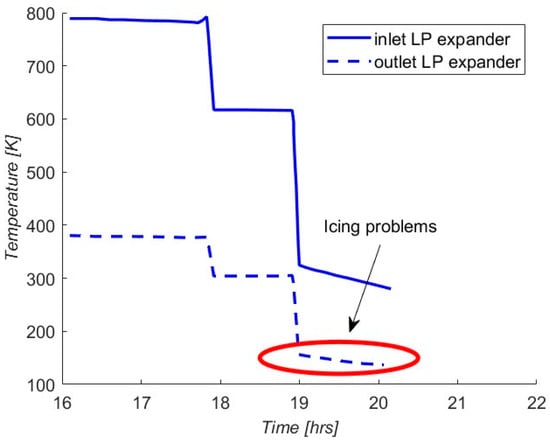
Figure 4.
LP turbine temperature during expansion phase with liquid TES (icing problems). Inlet: solid line, outlet: dashed line.
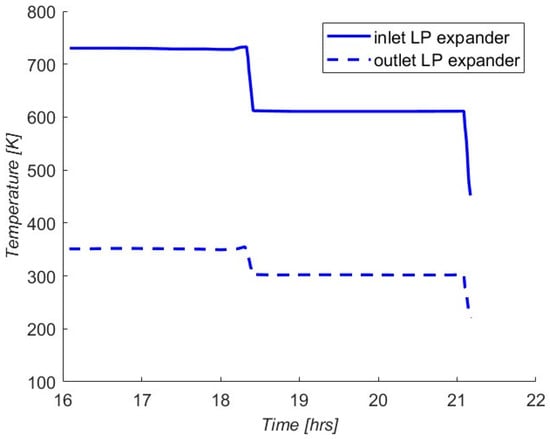
Figure 5.
LP turbine temperature during expansion phase with liquid TES with a lower hot liquid temperature. Inlet: solid line, outlet: dashed line.
A generic air heating system to preheat the air, installed between the air preheater and the expander, represents the second viable solution. With this layout, the air temperature is under control.
The following results synthesize the simulations performed for each cavern volume indicated in Table 1. These are collected in the volume–power–time conversion tables (VPT), which are based on the following assumptions: the produced energy is almost independent of the expansion time; the power is constant during a generic phase (charging, discharging, or air heating); and for each phase duration, a gas turbine can change its mass flow rate according to the new phase duration. The first two assumptions are invalid for power plant layouts with solid TES without an external air heating system. Indeed, concrete does not provide constant cooling/heating air temperature. Hence, the absorbed/delivered power changes during the phases, so no VPT tables exist for this layout, as illustrated in Figure 6.
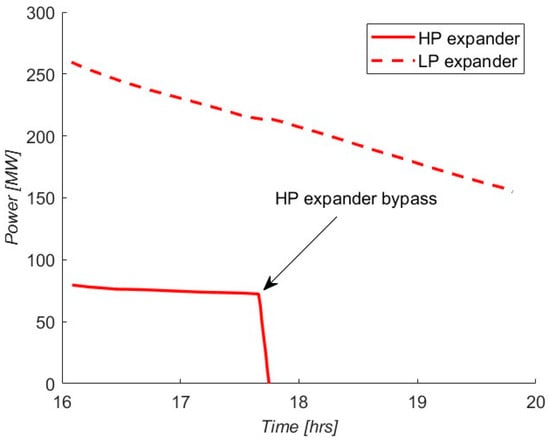
Figure 6.
Power delivered by the CAES system with solid TES and without external air heating. HP expander phase: solid line, LP expander phase: dashed line.
Figure 6 shows the HP and LP expander’s power during the discharging phase and the HP phase bypass occurring 1.75 h after the start of the discharge phase. The chart also indicates the power reduction due to the progressive cooling of the solid TES.
Table 3 represents a VPT conversion table showing the available power during a full-load discharging phase (HP and LP expansion phases operating). A VPT is used by setting a cavern volume (upper row), choosing the duration of the full-load discharge phase [hours] on the first column, and thus finding the corresponding CAES power for that phase.

Table 3.
Example of a volume [m3]-power [kW]-time [hours] conversion table.
The first two rows in Table 3 in bold indicate the simulated duration of the full-load expansion for each cavern volume. The other rows are scaled with the phase duration from the simulated data. These tables are also available for the compression phase, partial-load discharge, and external air heating.
Figure 7 collects the round-trip efficiencies as a function of the cavern volume, defined as the turbine work to compressor work ratio (28). The electrical works of compression and expansion (Wt,el and Wc,el) are calculated taking into account the electromechanical losses of the motor/generator (ηmot-gen in Table 2).
η = Wt,el/Wc,el
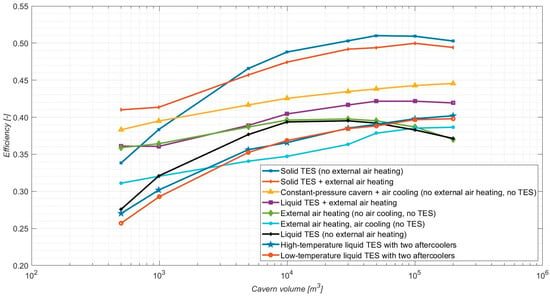
Figure 7.
Efficiency chart of the analyzed CAES plant layouts, according to [27].
The increasing volume within the cavern corresponds to enhanced turbine work and rated power because the higher the volume, the higher the mass stored in the cavern and the higher the mass flow rate processed by the turbine.
Among TES options, solid TES systems demonstrate higher performance than liquid TES and other options. A supplementary external air heating implies a rise in the expander energy produced.
The efficiency outputs of configurations without external heating exhibit a higher dependency on cavern volume, wherein larger volumes allow higher-rated power for expansion. Generally, these plants allow higher efficiency but lower electric work as they rely solely on heat stored during compression. Conversely, configurations incorporating external heating systems show reduced dependency on cavern volumes and lower efficiency, as they necessitate an additional power source.
In layouts with external air heating and air cooling, the power achieved at the expander is higher than the solution without cooling due to the higher stored air mass in the cavern. The increment in the air mass is due to the drop in cavern temperature induced by cooling.
The configuration without TES and air cooling but with external air heating demonstrates higher round-trip efficiency than its counterpart with air cooling. Indeed, the utilization of the hot air stored within the cavern is more efficient. However, it results in a lower mass of air stored, leading to a drop in electric work output, as illustrated in Figure 8.
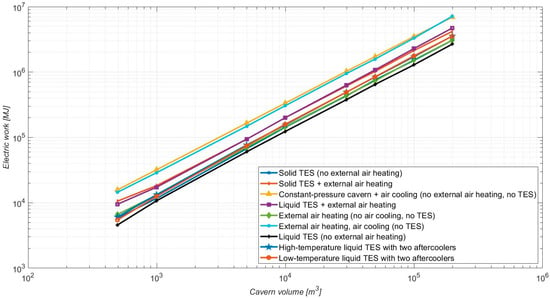
Figure 8.
Produced energy chart of the analyzed CAES plant layouts, according to [27].
High electric work output is achieved in configurations maintaining constant pressure and incorporating external air heating (triangle markers) and in configurations with air cooling and external air heating (circle markers). The two existing CAES plants are an example, wherein air cooled to approximately 50 °C, despite exhibiting low efficiency, yields increased energy production. Conversely, integrating a liquid TES to cool the air to 277 °C substantially enhances efficiency but decreases the stored air mass and the energy output.
In the partial-load operation of the liquid TES layout without external air heating, the temperature of the air stored in the cavern cannot increase above a threshold due to freezing issues in the heat exchanger and pipeline. If the plant includes two aftercoolers (case a), the air mass stored in the cavern increases due to the lower temperature of the supplied air. A higher cavern mass induces more compression work to achieve the design cavern pressure and a longer expansion phase. By reducing the hot liquid temperature in the same plant (case b), a higher mass flow rate of air is available for the expansion phase, even though the stored air mass is lower and the expansion is shorter, implying a lower energy extraction.
Efficiency depends slightly on volume, as shown by the constant pressure layout. Notably, layouts avoiding air cooling in favor of external air heating demonstrate higher efficiency than their counterparts without TES, leveraging the hot air stored within the cavern for efficient operation, albeit with a reduced stored mass and a subsequently lower electric work output.
4. Conclusions
This work presents a comprehensive model of a compressed air energy storage (CAES) system aimed at analyzing key performance parameters across a wide range of cavern volumes (from 500 to 200,000 m3) and various heat exchange solutions, including solid or liquid thermal energy storage (TES), with or without external air heating, and constant or variable cavern pressure.
An optimization algorithm for solid TES parameters is developed to enhance heat exchange efficiency during the charging and discharging operations. However, despite the wide temperature range facilitated by solid TES, the air temperature fluctuations lead to power variability during the charging and discharging phases, exacerbated by the low thermal conductivity of the tested material (reinforced concrete), resulting in suboptimal heat extraction during the discharging phase.
The fragmentation of solid storage into multiple elements is recommended, with excess heat potentially distributed for other purposes, such as industrial or residential heating. Several CAES power plant layouts are evaluated to estimate their performances, including the energy–cavern volume relationship, efficiency, power, and energy.
The liquid TES model highlights issues, such as hot liquid (molten salts) depletion during the discharging phase, potentially leading to icing problems in power plant layouts lacking external air heaters. Solutions include reducing the hot liquid temperature and installing additional aftercoolers with mineral oil to maintain stable air temperature, albeit at the expense of more components and a limited aftercooler outlet air temperature.
The power plant efficiency is influenced by the plant’s layout, with simulations indicating a correlation between cavern volume, compressor-rated power, and cavern temperature. Higher cavern volumes result in higher compressor-rated power and efficiency, while cavern temperature affects efficiency by saving energy required to heat the air stored in the cavern. However, higher cavern temperatures also reduce the air mass storage capacity, ultimately impacting energy production.
Layouts with external air heating generally yield higher electric work but lower efficiency. In contrast, layouts without external air heaters exhibit higher efficiency due to heat stored during the compressive phase.
Volume–power–time conversion tables and energy–volumes and efficiency–volumes maps are developed to establish relationships between energy, efficiencies, and cavern volumes, facilitating parameter setting for CAES power plants. These findings contribute to advancing CAES technology for more efficient energy storage and utilization, aiding the integration of renewable energy sources into the grid.
Author Contributions
Conceptualization, L.B.; methodology, L.B. and E.B.; software, L.C. and E.B.; validation, L.C. and L.B.; formal analysis, L.C. and L.B.; investigation, L.C. and L.B.; resources, L.B.; data curation, E.B.; writing—original draft preparation, L.C. and E.B.; writing—review and editing, L.C. and L.B.; visualization, L.C.; supervision, L.B.; project administration, L.B. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
Data is contained within the article.
Conflicts of Interest
The authors declare no conflicts of interest.
Abbreviations
D-CAES—Diabatic Compressed Air Energy Storage; A-CAES—Adiabatic Compressed Air Energy Storage; TES—Thermal Energy Storage; VPT—Volume–Power–Time.
References
- Greenblatt, J.; Succar, S.; Denkenberg, D.; Williams, R.H.; Socolow, R.H. Baseload Wind Energy: Modeling the Competition Between Gas Turbines and Compressed Air Energy Storage for Supplemental Generation. Energy Policy 2007, 35, 1474–1492. [Google Scholar] [CrossRef]
- Strbac, G. Quantifying the System Costs of Additional Renewables in 2020; A Report to the Department of Trade & Industry (DTI); DTI: London, UK, 2002. [Google Scholar]
- Cavallo, A.J. High-Capacity Factor Wind Energy Systems. J. Solar Energy Eng. Trans. ASME 1995, 117, 137–145. [Google Scholar] [CrossRef]
- Sengalani, P.S.; Haque, M.E.; Zantye, M.S.; Gandhi, A.; Li, M.; Hasan, M.M.F.; Bhattacharyya, D. Techno-Economic Analysis and Optimization of a Compressed-Air Energy Storage System Integrated with a Natural Gas Combined-Cycle Plant. Energies 2023, 16, 4867. [Google Scholar] [CrossRef]
- Kim, S.; Dusseault, M.; Babarinde, O.; Wickens, J. Compressed Air Energy Storage (CAES): Current Status, Geomechanical Aspects, and Future Opportunities. Geol. Soc. Lond. Spec. Publ. 2023, 528, SP528-2022. [Google Scholar] [CrossRef]
- Rabi, A.M.; Radulovic, J.; Buick, J.M. Comprehensive Review of Compressed Air Energy Storage (CAES) Technologies. Thermo 2023, 3, 104–126. [Google Scholar] [CrossRef]
- Tong, Z.; Cheng, Z.; Tong, S. A Review on the Development of Compressed Air Energy Storage in China: Technical and Economic Challenges to Commercialization. Renew. Sustain. Energy Rev. 2021, 135, 110178. [Google Scholar] [CrossRef]
- Dindorf, R. Study of the Energy Efficiency of Compressed Air Storage Tanks. Sustainability 2024, 16, 1664. [Google Scholar] [CrossRef]
- Wang, K.; Zhu, C.; Du, X.; Di, Y.; Laijun, C. Performance Analysis of Distributed Compressed Air Energy Storage under Different Air Storage Chamber Models. J. Phys. 2023, 2495, 012006. [Google Scholar] [CrossRef]
- He, Q.; Li, G.; Lu, C.; Du, D.; Liu, W. A Compressed Air Energy Storage System with Variable Pressure Ratio and its Operation Control. Energy 2019, 169, 881–894. [Google Scholar] [CrossRef]
- Salyga, S.; Szablowski, L.; Badyda, K. Comparison of Constant Volume Energy Storage Systems Based on Compressed Air. Int. J. Energy Res. 2020, 45, 8030–8040. [Google Scholar] [CrossRef]
- Soltani, M.; Kashkooli, F.M.; Jafarizadeh, H.; Hatefi, M.; Fekri, H.; Gharali, K.; Nathwani, J. Diabatic Compressed Air Energy Storage (CAES) Systems: State of the Art. In Reference Module in Earth Systems and Environmental Sciences; Elsevier: Amsterdam, The Netherlands, 2021. [Google Scholar]
- Kotowicz, J.; Jurczyk, M. Efficiency of Diabatic CAES Installation. Rynek Energii 2015, 119, 49–56. [Google Scholar]
- Zhao, P.; Dai, Y.; Wang, J. Design and Thermodynamic Analysis of a Hybrid Energy Storage System Based on A-CAES (Adiabatic Compressed Air Energy Storage) and FESS (Flywheel Energy Storage System) for Wind Power Application. Energy 2014, 70, 674–684. [Google Scholar] [CrossRef]
- Khaledi, K.; Mahmodi, E.; Datcheva, M.; Schanz, T. Analysis of Compressed Air Storage Caverns in Rock Salt Considering Thermo-Mechanical Cyclic Loading. Environ. Earth Sci. 2016, 75, 1149. [Google Scholar] [CrossRef]
- Zhou, Q.; Du, D.; Lu, C.; He, Q.; Liu, W. A Review of Thermal Energy Storage in Compressed Air Energy Storage System. Energy 2019, 188, 115993. [Google Scholar] [CrossRef]
- Tola, V.; Marcello, F.C.; Cocco, D.; Cau, G. Performance Assessment of Low-Temperature A-CAES (Adiabatic Compressed Air Energy Storage) Plants. J. Therm. Sci. 2022, 31, 1279–1292. [Google Scholar] [CrossRef]
- Sciacovelli, A.; Li, Y.; Chen, H.; Wu, Y.; Wang, J.; Garvey, S.; Ding, Y. Dynamic Simulation of Adiabatic Compressed Air Energy Storage (A-CAES) Plant with Integrated Thermal Storage—Link between Components Performance and Plant Performance. Appl. Energy 2017, 185, 16–28. [Google Scholar] [CrossRef]
- Cacciali, L.; Battisti, L.; Occello, D. Efficiency-Driven Iterative Model for Underwater Compressed Air Energy Storage (UW-CAES). Energies 2023, 16, 8013. [Google Scholar] [CrossRef]
- Bai, F.; Xu, C. Performance Analysis of a Two-Stage Thermal Energy Storage System Using Concrete and Steam Accumulator. Appl. Thermal Eng. 2011, 31, 2764–2771. [Google Scholar] [CrossRef]
- De Biasi, V. 110 MW McIntosh CAES Plant Over 90% Availability and 95% Reliability. Gas Turbine World 1998, 28, 26–28. [Google Scholar]
- Crotogino, F.; Mohmeyer, K.U.; Scharf, R. Huntorf CAES: More than 20 Years of Successful Operation. In Proceedings of the Conference: Solution Mining Research Institute (SMRI) Spring Meeting, Orlando, FL, USA, 15–18 April 2001. [Google Scholar]
- Brown Boveri (BBC). Energy Supply—Huntorf Air Storage Gas Turbine Power Plant, D GK 90202E. Available online: https://www.solarplan.org/documents/BBC_Huntorf_engl.pdf (accessed on 29 January 2024).
- Gil, A.; Medrano, M.; Martorell, I.; Làzaro, A.; Dolado, P.; Zalba, B.; Cabeza, L.F. State of the Art on High Temperature Thermal Energy Storage for Power Generation. Part 1—Concepts Material and Modellization. Renew. Sustain. Energy Rev. 2010, 14, 31–55. [Google Scholar] [CrossRef]
- Kakaç, S.; Liu, H.; Pramuanjaroenkij, A. Heat Exchangers: Selection, Rating, and Thermal Design, 2nd ed.; CRC Press: Boca Raton, FL, USA, 2002. [Google Scholar]
- Smits, A.J.; Dussauge, J.-P. Turbulent Sheat Layers in Supersonic Flow, 2nd ed.; Springer: Berlin/Heidelberg, Germany, 2006. [Google Scholar]
- Benini, E. Thermodynamic Analysis of Compressed Air Energy Storage Systems. Master’s Thesis, University of Trento, Trento, Italy, 2011. [Google Scholar]
- Lozza, G. Turbine a Gas e Cicli Combinati, 3rd ed.; Società Editrice Esculapio: Bologna, Italy, 2016. [Google Scholar]
- Nunes, V.M.B.; Lourenco, M.; Santos, F.J.V.; de Castro, C.N. Viscosity of Molten Sodium Nitrate. Int. J. Therm. 2006, 27, 1638–1649. [Google Scholar] [CrossRef]
- Bauer, T.; Dörte, L.; Ulrike, K.; Tamme, R. Sodium Nitrate for High Temperature Latent Heat Storage. In Proceedings of the Effstock 2009—11th International Conference on Thermal Energy Storage, Stockholm, Sweden, 14–17 June 2009. [Google Scholar]
- Raju, M.; Khaitan, S.K. Modeling and Simulation of Compressed Air Storage in Caverns: A Case Study of the Huntorf Plant. Appl. Energy 2012, 89, 474–481. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).