Permeability Prediction of Carbonate Reservoir Based on Nuclear Magnetic Resonance (NMR) Logging and Machine Learning
Abstract
1. Introduction
2. Theory and Methods
2.1. NMR Logging
2.2. Data Preprocessing
2.2.1. Feature Scaling
2.2.2. Principal Component Analysis
2.3. XGBoost Principle
3. Results and Discussion
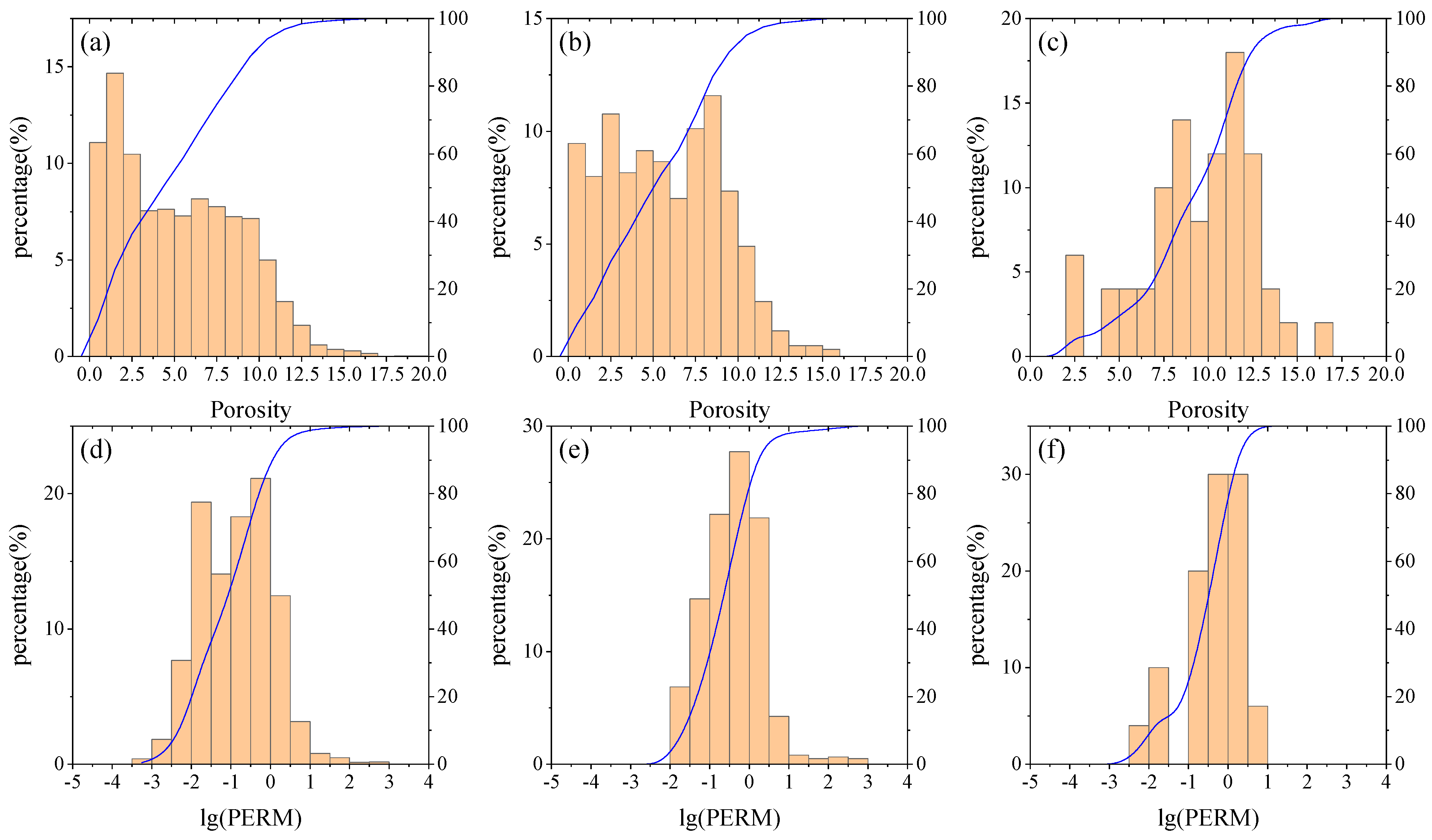
3.1. Data Information
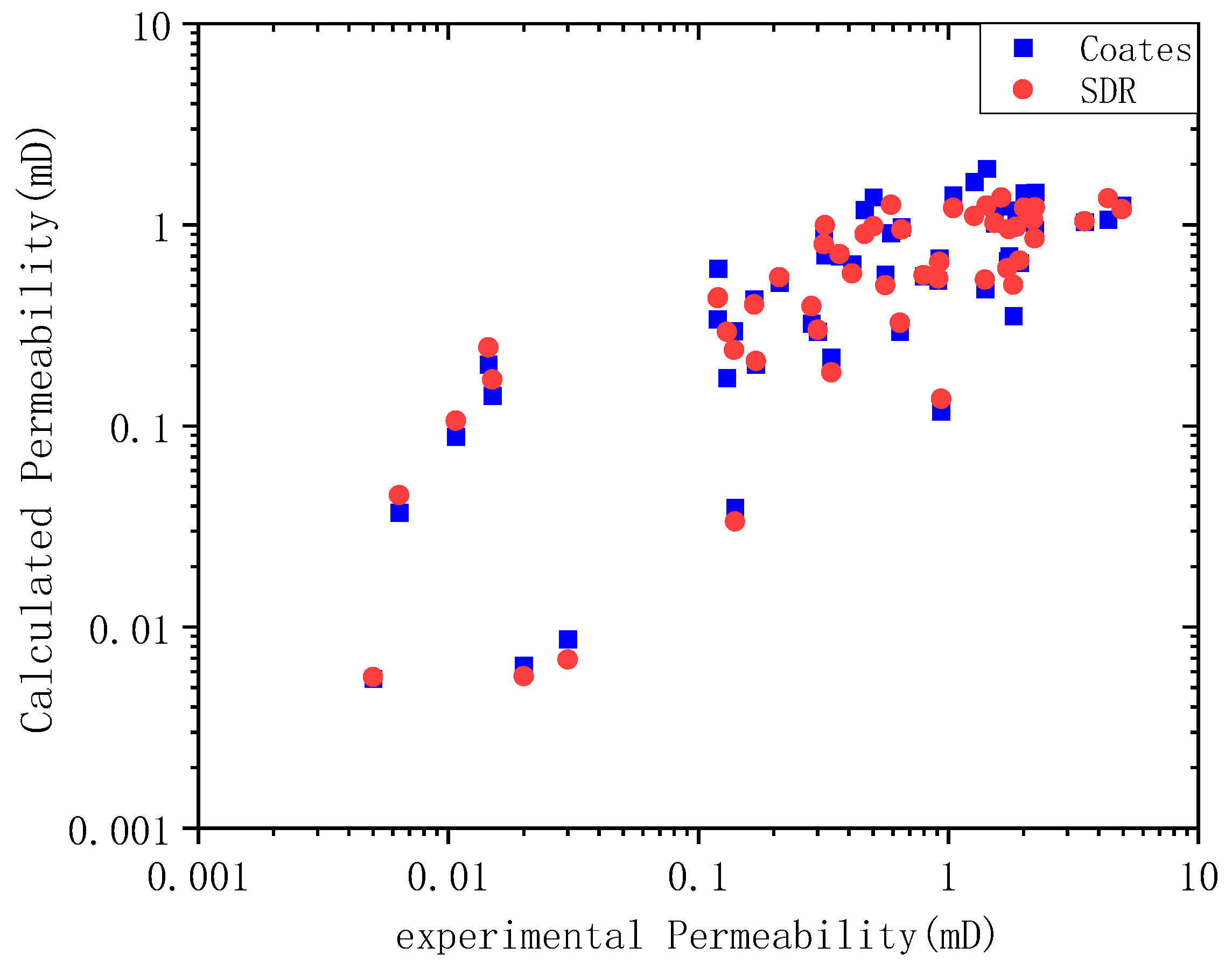
3.2. Permeability Prediction Based on NMR Empirical Equation
3.3. Permeability Prediction Based on XGboost
3.3.1. Feature Selection
3.3.2. Model Parameter Configuration and Analysis of Prediction Results
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Sha, F.; Xiao, L.; Mao, Z.; Jia, C. Petrophysical Characterization and Fractal Analysis of Carbonate Reservoirs of the Eastern Margin of the Pre-Caspian Basin. Energies 2018, 12, 78. [Google Scholar] [CrossRef]
- Chen, X.; Zheng, Y.; Wang, G.; Wang, Y.; Luo, X.; Pan, Q.; Wang, Z.; Ping, W. Pore Structure and Fluid Mobility of Tight Carbonate Reservoirs in the Western Qaidam Basin, China. Energy Sci. Eng. 2023, 11, 3397–3412. [Google Scholar] [CrossRef]
- Li, W.; Mu, L.; Zhao, L.; Li, J.; Wang, S.; Fan, Z.; Shao, D.; Li, C.; Shan, F.; Zhao, W.; et al. Pore-Throat Structure Characteristics and Its Impact on the Porosity and Permeability Relationship of Carboniferous Carbonate Reservoirs in Eastern Edge of Pre-Caspian Basin. Pet. Explor. Dev. 2020, 47, 1027–1041. [Google Scholar] [CrossRef]
- Mo, F.; Du, Z.; Peng, X.; Liang, B.; Tang, Y.; Yue, P. Analysis of Pressure-Dependent Relative Permeability in Permeability Jail of Tight Gas Reservoirs and its Influence on Tight Gas Production. J. Porous Media 2019, 22, 1667–1683. [Google Scholar] [CrossRef]
- Xue, K.; Liu, Y.; Yu, T.; Yang, L.; Zhao, J.; Song, Y. Numerical Simulation of Gas Hydrate Production in Shenhu Area Using Depressurization: The Effect of Reservoir Permeability Heterogeneity. Energy 2023, 271, 126948. [Google Scholar] [CrossRef]
- Sanei, M.; Duran, O.; Devloo, P.R.B.; Santos, E.S.R. Evaluation of the Impact of Strain-Dependent Permeability on Reservoir Productivity Using Iterative Coupled Reservoir Geomechanical Modeling. Geomech. Geophys. Geo-Energy Geo-Resour. 2022, 8, 54. [Google Scholar] [CrossRef]
- Kenyon, W.E.; Day, P.I.; Straley, C.; Willemsen, J.F. A Three-Part Study of NMR Longitudinal Relaxation Properties of Water-Saturated Sandstones. SPE Form. Eval. 1988, 3, 622–636. [Google Scholar] [CrossRef]
- Coates, G.R.; Miller, M.; Gillen, M.; Henderson, C. The MRIL in Conoco 33-1 An Investigation of a New Magnetic Resonance Imaging Log. In Proceedings of the SPWLA 32nd Annual Logging Symposium, Midland, TX, USA, 16 June 1991. [Google Scholar]
- Xiao, L. Some Important Issues for NMR Logging Applications in China. Well Logging Technol. 2007, 31, 401–407. [Google Scholar] [CrossRef]
- Freedman, R. Advances in NMR Logging. J. Pet. Technol. 2006, 58, 60–66. [Google Scholar] [CrossRef]
- Wang, K.; Zhou, H.; Lai, J.; Wang, K.; Liu, Y. Application of NMR technology in characterization of petrophysics and pore structure. Chin. J. Sci. Instrum. 2020, 41, 101–114. [Google Scholar] [CrossRef]
- Wang, M.; Xie, J.; Guo, F.; Zhou, Y.; Yang, X.; Meng, Z. Determination of NMR T2 Cutoff and CT Scanning for Pore Structure Evaluation in Mixed Siliciclastic–Carbonate Rocks before and after Acidification. Energies 2020, 13, 1338. [Google Scholar] [CrossRef]
- Rezaee, R. Synthesizing Nuclear Magnetic Resonance (NMR) Outputs for Clastic Rocks Using Machine Learning Methods, Examples from North West Shelf and Perth Basin, Western Australia. Energies 2022, 15, 518. [Google Scholar] [CrossRef]
- Tamoto, H.; Gioria, R.D.S.; Carneiro, C.D.C. Prediction of Nuclear Magnetic Resonance Porosity Well-Logs in a Carbonate Reservoir Using Supervised Machine Learning Models. J. Pet. Sci. Eng. 2023, 220, 111169. [Google Scholar] [CrossRef]
- Gu, Y.; Zhang, D.; Ruan, J.; Wang, Q.; Bao, Z.; Zhang, H. A new model for permeability prediction in appraisal of petroleum reserves. Prog. Geophys. 2022, 37, 588–599. [Google Scholar]
- Bishop, C.M. Pattern Recognition and Machine Learning; Information Science and Statistics; Springer: New York, NY, USA, 2006; ISBN 978-0-387-31073-2. [Google Scholar]
- Al-Anazi, A.F.; Gates, I.D. Support Vector Regression to Predict Porosity and Permeability: Effect of Sample Size. Comput. Geosci. 2012, 39, 64–76. [Google Scholar] [CrossRef]
- Bagheripour, P. Committee Neural Network Model for Rock Permeability Prediction. J. Appl. Geophys. 2014, 104, 142–148. [Google Scholar] [CrossRef]
- Anifowose, F.; Labadin, J.; Abdulraheem, A. Improving the Prediction of Petroleum Reservoir Characterization with a Stacked Generalization Ensemble Model of Support Vector Machines. Appl. Soft Comput. 2015, 26, 483–496. [Google Scholar] [CrossRef]
- Mahdaviara, M.; Rostami, A.; Keivanimehr, F.; Shahbazi, K. Accurate Determination of Permeability in Carbonate Reservoirs Using Gaussian Process Regression. J. Pet. Sci. Eng. 2021, 196, 107807. [Google Scholar] [CrossRef]
- Ben-Hur, A.; Horn, D.; Siegelmann, H.T.; Vapnik, V. Support Vector Clustering. J. Mach. Learn. Res. 2001, 2, 125–137. [Google Scholar] [CrossRef]
- Al-Bulushi, N.I.; King, P.R.; Blunt, M.J.; Kraaijveld, M. Artificial Neural Networks Workflow and Its Application in the Petroleum Industry. Neural Comput. Appl. 2012, 21, 409–421. [Google Scholar] [CrossRef]
- Mathew Nkurlu, B.; Shen, C.; Asante-Okyere, S.; Mulashani, A.K.; Chungu, J.; Wang, L. Prediction of Permeability Using Group Method of Data Handling (GMDH) Neural Network from Well Log Data. Energies 2020, 13, 551. [Google Scholar] [CrossRef]
- Huang, Z.; Shimeld, J.; Williamson, M.; Katsube, J. Permeability Prediction with Artificial Neural Network Modeling in the Venture Gas Field, Offshore Eastern Canada. Geophysics 1996, 61, 422–436. [Google Scholar] [CrossRef]
- Huang, X.B.; Zhang, Q.; Zhu, H.H.; Zhang, L.Y. An Estimated Method of Intact Rock Strength Using Gaussian Process Regression. In Proceedings of the 51st U.S. Rock Mechanics/Geomechanics Symposium, San Francisco, CA, USA, 25 June 2017; p. ARMA-2017-0125. [Google Scholar]
- Zhu, L.; Zhang, C.; Zhou, X.; Wei, Y.; Huang, Y.; Gao, Q. Nuclear magnetic resonance logging reservoir permeability prediction method based on deep belief network and kernel extreme learning machine algorithm. Comput. Appl. 2017, 37, 3034–3038. [Google Scholar]
- Zhang, G.; Wang, Z.; Mohaghegh, S.; Lin, C.; Sun, Y.; Pei, S. Pattern Visualization and Understanding of Machine Learning Models for Permeability Prediction in Tight Sandstone Reservoirs. J. Pet. Sci. Eng. 2021, 200, 108142. [Google Scholar] [CrossRef]
- Huang, Y.; Feng, J.; Song, W.; Guan, Y.; Zhang, Z. Intelligent prediction of improved permeability in sandstone reservoirs combining NMR transverse relaxation time spectra with piezomercury data. Comput. Tech. Geophys. Geochem. Explor. 2020, 42, 338–344. [Google Scholar]
- Xu, H.; Li, C.; Fan, Y.; Hu, F.; Yu, J.; Zhou, J.; Wang, C.; Yang, C. A New Permeability Predictive Model Based on NMR Data for Sandstone Reservoirs. Arab. J. Geosci. 2020, 13, 1085. [Google Scholar] [CrossRef]
- Wang, Y. Research and Application of Machine Learning for Predicting Porosity. Master’s Thesis, China University of Petroleum, Beijing, China, 2020. [Google Scholar]
- Liu, Y.; Lu, Z.; Lv, J.; Xie, R. Application of Principal Component Analysis Method in Lithology Identification for Shale Formation. Fault Block Oil Gas Field 2017, 24, 360–363. [Google Scholar]
- Li, Y.; Wang, H.; Wang, M.; Lian, P.; Duan, T.; Ji, B. Automatic Identification of Carbonate Sedimentary Facies Based on PCA and KNN Using Logs. Well Logging Technol. 2017, 41, 41–57. [Google Scholar]
- Strang, G. Introduction to Linear Algebra; Wellesley-Cambridge Press: Wellesley, MA, USA, 2022. [Google Scholar]
- Chen, J.; Zhao, F.; Sun, Y.; Yin, Y. Improved XGBoost Model Based on Genetic Algorithm. Int. J. Comput. Appl. Technol. 2020, 62, 240. [Google Scholar] [CrossRef]
- Chen, T.; Guestrin, C. XGBoost: A Scalable Tree Boosting System. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, San Francisco, CA, USA, 13–17 August 2016; ACM Press: San Francisco, CA, USA, 2016; pp. 785–794. [Google Scholar]
- Pan, S.; Zheng, Z.; Guo, Z.; Luo, H. An Optimized XGBoost Method for Predicting Reservoir Porosity Using Petrophysical Logs. J. Pet. Sci. Eng. 2022, 208, 109520. [Google Scholar] [CrossRef]
- Hsu, H.-H.; Hsieh, C.-W. Feature Selection via Correlation Coefficient Clustering. J. Softw. 2010, 5, 1371–1377. [Google Scholar] [CrossRef]
- Ratnasingam, S.; Muñoz-Lopez, J. Distance Correlation-Based Feature Selection in Random Forest. Entropy 2023, 25, 1250. [Google Scholar] [CrossRef] [PubMed]
- Cohen, J. Statistical Power Analysis for the Behavioral Sciences, 2nd ed.; Erlbaum, L., Ed.; Associates: Hillsdale, NJ, USA, 1988; ISBN 978-0-8058-0283-2. [Google Scholar]
- Zhou, C.; Li, C.; Wang, C.; Hu, F. Logging Petrophysics and Evaluation of Complex Clastic Rock; Petroleum Industry Press: Beijing, China, 2013. [Google Scholar]
- Gang, A.; Bajwa, W.U. FAST-PCA: A Fast and Exact Algorithm for Distributed Principal Component Analysis. IEEE Trans. Signal Process 2022, 70, 6080–6095. [Google Scholar] [CrossRef]
- Park, K.-Y.; Woo, D.-O. PMV Dimension Reduction Utilizing Feature Selection Method: Comparison Study on Machine Learning Models. Energies 2023, 16, 2419. [Google Scholar] [CrossRef]
- Bentéjac, C.; Csörgő, A.; Martínez-Muñoz, G. A Comparative Analysis of Gradient Boosting Algorithms. Artif. Intell. Rev. 2021, 54, 1937–1967. [Google Scholar] [CrossRef]
- Caruana, R.; Niculescu-Mizil, A. An Empirical Comparison of Supervised Learning Algorithms. In Proceedings of the 23rd International Conference on Machine Learning—ICML ’06, Pittsburgh, PA, USA, 25–29 June 2006; ACM Press: Pittsburgh, PA, USA, 2006; pp. 161–168. [Google Scholar]





| Experimental Items | Petrophysical Properties of Core Plugs | Petrophysical Properties of Whole Diameter Cores | NMR Experiment of Core Plugs |
|---|---|---|---|
| Number of Samples | 2978 | 613 | 50 |
| Model Name | Equation |
|---|---|
| The Coates model | |
| The SDR model |
| Correlation Strength | Criteria |
|---|---|
| strong correlation | |r| ≥ 0.5 |
| moderate correlation | 0.3 ≤ |r| < 0.5 |
| weak correlation | 0.1 ≤ |r| < 0.3 |
| no correlation | 0 ≤ |r| < 0.1 |
| Correlation Strength | Logging Curve |
|---|---|
| strong correlation | DT, NPHI, RHOB, BFV, FFV, MBP5, MBP6, MRP |
| moderate correlation | RD, RS, T2LM |
| weak correlation | MBP7, MBP8 |
| no correlation | GR, MBP1, MBP2, MBP3, MBP4 |
| Model | Parameters | Value |
|---|---|---|
| XGBRegressor | n_estimators | 60 |
| Learning rate | 0.15 | |
| max_depth | 2 | |
| subsample | 0.9 | |
| colsample_bytr | 0.7 | |
| gamma | 0 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhao, J.; Wang, Q.; Rong, W.; Zeng, J.; Ren, Y.; Chen, H. Permeability Prediction of Carbonate Reservoir Based on Nuclear Magnetic Resonance (NMR) Logging and Machine Learning. Energies 2024, 17, 1458. https://doi.org/10.3390/en17061458
Zhao J, Wang Q, Rong W, Zeng J, Ren Y, Chen H. Permeability Prediction of Carbonate Reservoir Based on Nuclear Magnetic Resonance (NMR) Logging and Machine Learning. Energies. 2024; 17(6):1458. https://doi.org/10.3390/en17061458
Chicago/Turabian StyleZhao, Jianpeng, Qi Wang, Wei Rong, Jingbo Zeng, Yawen Ren, and Hui Chen. 2024. "Permeability Prediction of Carbonate Reservoir Based on Nuclear Magnetic Resonance (NMR) Logging and Machine Learning" Energies 17, no. 6: 1458. https://doi.org/10.3390/en17061458
APA StyleZhao, J., Wang, Q., Rong, W., Zeng, J., Ren, Y., & Chen, H. (2024). Permeability Prediction of Carbonate Reservoir Based on Nuclear Magnetic Resonance (NMR) Logging and Machine Learning. Energies, 17(6), 1458. https://doi.org/10.3390/en17061458





