Abstract
Fuel cell hybrid electric trucks have become a cutting-edge field in understanding urban traffic emissions due to their enormous potential in low-carbon areas. In order to improve the economy of fuel cell hybrid electric trucks and reduce the decline of fuel cell lifespan, this paper proposes a multi-objective energy management strategy that optimizes weight coefficients. On the basis of establishing a fuel cell battery hybrid system model, three modes of uniform speed, acceleration, and deceleration were identified through clustering analysis of vehicle speed. Reinforcement learning algorithms were used to learn the corresponding weights for different modes, which reduced the decline in fuel cell life while improving the economic efficiency. The simulation results indicate that, under the conditions of no load, half load, and full load, the truck only sacrificed 0.9–5.6%, 1.7–2.6%, and 1.2–1.6% SOC, saving 5.7–6.45%, 5.9–6.67%, and 6.1–6.67% in lifespan loss, and reducing hydrogen consumption by 3.0–7.1%, 2.8–4.4%, and 1.0–3.0%, respectively.
1. Introduction
Fuel cell hybrid power systems have tremendous potential for reducing carbon emissions from trucks [1,2]. Especially in the context of the increasing global environmental awareness and the demand for sustainable transportation solutions, this technology is emerging as a forefront area for addressing urban transport emissions and economic efficiency issues [3].
However, to unlock the full potential of such hybrid power systems, we must confront several challenges. A key challenge lies in finding an equilibrium between various conflicting optimization goals, including vehicle efficiency, the State of Charge (SOC) of the battery, and the durability of fuel cells [4,5]. Traditional approaches often rely on experience, rules, or optimization algorithms. Ming et al. developed a strategy for managing energy that employs fuzzy logic control, resulting in significant energy conservation [6]. This approach offers benefits such as a straightforward design, reduced computational demand, and superior operational speed, rendering it more appropriate for real-time energy management applications. Nonetheless, the determination of threshold parameters often depends on empirical knowledge, which may not ensure the optimal improvement in vehicle fuel efficiency. Xie et al. utilized Pontryagin maximum principle (PMP) to solve the energy management problem of plug-in hybrid trucks and verified the effectiveness and flexibility of this strategy in both long-distance and short distance scenarios [7]. This method enhances both the fuel efficiency and the system longevity of fuel cell hybrid vehicles. These energy management strategies are based on optimization theory and constrained by system state or control variables, with hydrogen consumption or other system states as optimization objectives, to optimize energy allocation results [8]. However, these methods do not account for the varying weights of different optimization objectives under different driving modes, making it difficult to achieve precise control over energy allocation, thereby limiting the optimization performance of hybrid power systems [9].
To tackle this challenge, this study presents a learning-based algorithm aimed at exploring an intelligent, adaptive control strategy, facilitating efficient multi-objective optimization [10]. Through the training of weight coefficients across acceleration, steady-speed, and deceleration scenarios, our goal is to attain the optimal balance between vehicle economy, SOC, and fuel cell longevity. This approach not only enhances truck performance but also reduces operational costs, thereby maximizing the lifespan of the hybrid power system [11]. Currently, there is a significant body of research focusing on weight learning, Takayama et al. introduced a new algorithm that uses the framework of inverse reinforcement learning (IRL) to estimate weights based on the reward vectors and expert trajectories of each target [12]. Kang et al. proposed a weight aggregation strategy to calculate weights for problems with two optimization objectives [13]. These rich weight optimization methods provide convenience for our weight training.
While there have been studies on learning multi-objective optimization weight coefficients, research specifically addressing multi-objective weight optimization for fuel cell hybrid electric trucks is lacking. Moreover, the demand power of fuel cell hybrid trucks is significantly influenced by their cargo capacity, presenting challenges for the learning of multi-objective weights.
Building upon the aforementioned analysis, this paper integrates multi-objective optimization weight coefficients with optimization algorithms to learn weights for various driving modes of hybrid electric trucks with different load capacities. The objective is to enhance fuel economy, preserve battery SOC, and mitigate fuel cell degradation. The optimization algorithm is employed to derive power allocation outcomes. The paper offers the following innovations:
- A strategy for managing energy in fuel cell hybrid electric trucks, which employs multi-objective optimization and integrates learned weight parameters, has been put forward. This method has proven to effectively improve fuel economy.
- Cluster the driving speed using the K-means algorithm, dividing it into three driving modes, acceleration, deceleration, and constant speed, and using reinforcement learning to train the weight coefficients under different driving modes.
- To address the significant impact of varying load capacities on truck power demand, reinforcement learning was utilized to calculate weight coefficients customized for different load capacities. The efficiency of the suggested algorithm was confirmed through its application in a variety of driving cycles.
The rest of this document is organized in the following manner: Section 2 outlines a system model for fuel cell hybrid trucks, Section 3 delves into multi-objective optimization strategies designed for these trucks, Section 4 describes methods for driving mode recognition and weight coefficient training, Section 5 discusses the simulation outcomes, and Section 6 wraps up the paper with a conclusion.
2. Fuel Cell Hybrid Electric Trucks System Modeling
This document centers on fuel cell hybrid electric trucks, with fuel cells functioning as the main power source and batteries providing supplementary power. Both systems function as transmission systems through DC/DC converters. The structure is shown in Figure 1.
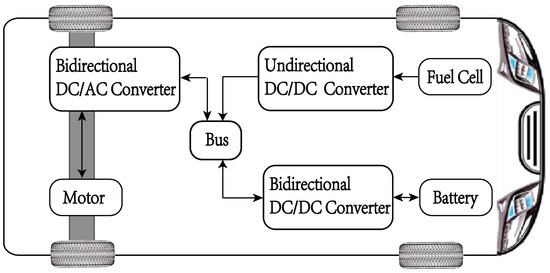
Figure 1.
Structure diagram of fuel cell hybrid electric trucks transmission system.
2.1. Vehicle Demand Power Modeling
Vehicle operational power demand is impacted by factors including acceleration, speed, and incline. These parameters are detailed in Table 1, with the vehicle’s power calculation process described as follows:
in this equation, represents inertial force, represents the component of gravity along the slope direction, represents the resistance that a vehicle needs to overcome while driving, represents the component of the vehicle’s gravity in the vertical direction of the slope, m represents the vehicle mass, represents the rate of change of velocity, c symbolizes the constant rolling resistance coefficient discussed in this paper, g stands for the acceleration due to gravity, z denotes the incline of the road, represents the density of the air, indicates the air resistance coefficient, is the transmission efficiency of the vehicle motors, and signifies the frontal area of the vehicles.

Table 1.
Fuel cell hybrid electric truck parameters.
2.2. Hydrogen Consumption Model and Life Decay Model for Fuel Cell
In this paper, a 150 kW fuel cell system similar to Ballard Power Systems is chosen as the primary focus. The relevant indicators are presented in Table 2. As the working mechanism of the fuel cell is intricate, a balance between model accuracy and computational efficiency is sought. Therefore, hydrogen consumption is modeled based on the efficiency data of the fuel cell. Furthermore, its efficiency curve is depicted in Figure 2. The lower heating value of hydrogen refers to the amount of heat released per unit mass of hydrogen when it is completely combusted and releases heat. Therefore, the actual hydrogen consumption is the ratio of output power to input power. Input power is the product of efficiency and low calorific value. Following this, the hydrogen consumption of the fuel cell is determined by the equation below:

Table 2.
Main parameters of the fuel cell.
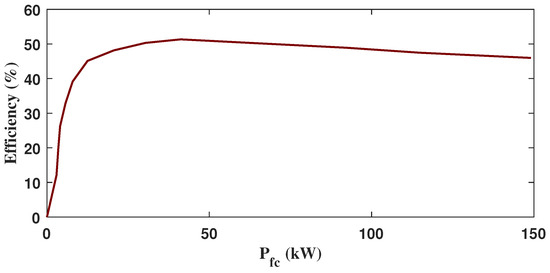
Figure 2.
Power efficiency relationship curve of the fuel cell.
In the equation provided, represents hydrogen consumption, denotes fuel cell efficiency, refers to the power output of the fuel cell, and stands for the low calorific value of hydrogen, set at 120,000 J/g. The curve illustrating the relationship between hydrogen consumption and output power is displayed in Figure 3.
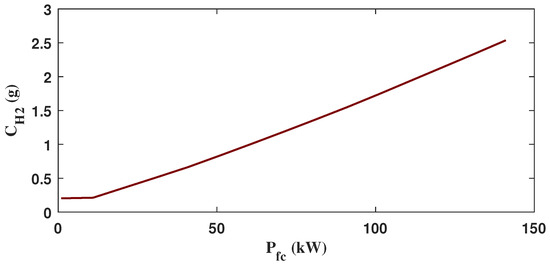
Figure 3.
Relationship curve between hydrogen consumption and output power.
This research utilizes an empirical model for fuel cell degradation to evaluate its effect on the durability of the fuel cell. Degradation in fuel cells mainly occurs due to fluctuations in load, start–stop cycles, periods of idling, and conditions of high-power demand. The model describing fuel cell degradation is presented as Equation (7):
where indicates the percentage degradation of the fuel cell’s lifespan, with , , , and c, respectively, representing the duration of idling, the duration of rapid load changes, the duration of high-power load conditions during the operation of FCHET, and the number of start–stop cycles. The coefficients , , , and correspond to these parameters, while denotes the natural decay rate of the fuel cell. is the correction coefficient for the road system. The values of these parameters can be found in the referenced study.
2.3. Battery State of Charge Model
In fuel cell hybrid electric trucks, batteries serve as secondary sources of energy. The parameters for the batteries discussed are provided in Table 3. Utilizing the equivalent internal resistance model, the current model of the battery, denoted as , is established in the following manner:
where is the battery’s voltage, and is the battery’s resistance. Their relationship with SOC is shown in Figure 4. After knowing the battery resistance and voltage, the SOC can be updated as follows:
where is the battery capacity.

Table 3.
Main parameters of the battery.
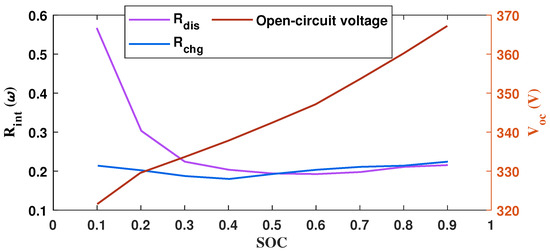
Figure 4.
The relationship curve between the battery’s voltage and resistance varies with the SOC.
3. Multi-Objective Optimization Strategy for FCHETs
The overall process of this study is shown in Figure 5. Firstly, the vehicle speed trajectory is planned for the truck based on road traffic light information. Then, K-means is used to divide the vehicle speed patterns into three categories: constant speed, acceleration, and deceleration. Finally, reinforcement learning is used to learn the weight parameters of the truck under different loading states and driving mode conditions, and Pontryagin maximum principle–model predictive control (PMP-MPC) is used to solve the power allocation.
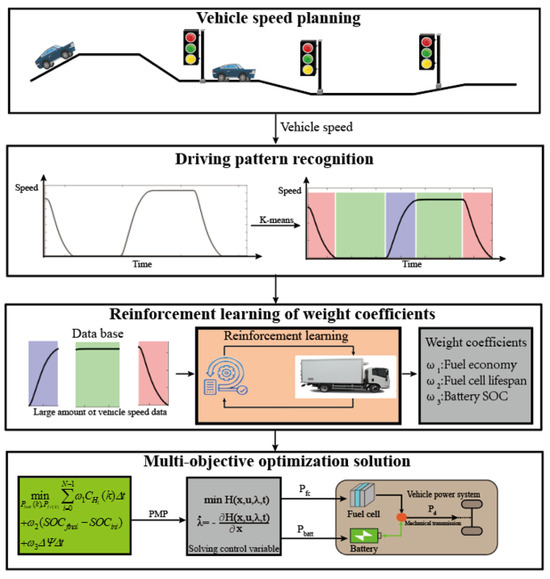
Figure 5.
The overall research flowchart of this paper.
The MPC utilizes fuel cell and battery power as control inputs, with SOC acting as a state variable. It solves the optimization problem while adhering to system constraints. The objective function for optimization is displayed in Equation (11).
In Equation (11), signifies the SOC at the subsequent sampling time, computed through the state transition equation, with indicating its discretized counterpart from Equation (10). The parameters and establish the minimum and maximum thresholds for the battery’s SOC, fixed at 0.2 and 0.8. Additionally, and set the minimum and maximum power outputs for the fuel cell, whereas and define the battery’s power output limits. denotes the power demand of the vehicle, calculated at each speed sample within the forecast horizon N. The weight coefficients , , and are also specified.
This optimization challenge is constrained and first-order, necessitating swift resolution to maintain real-time system efficacy in fulfilling vehicular power needs. The Pontryagin Maximum Principle (PMP) is apt for first-order optimization issues, offering an explicit solution path and accommodating control constraints efficiently, aligning well with the goal. For state variable constraints, penalty functions are integrated into the Hamiltonian function to enforce compliance.
Addressing this optimization requires minimizing the Hamiltonian function, which is structured as follows:
where represents the co-state variable, and denotes the penalty function within the Hamiltonian function, with its specific expression provided as follows:
where z, c, and are adjustment coefficients.
To derive the optimal control input sequence, one must meet the essential conditions set forth by the PMP, using the binary method to solve PMP, determining the range of lambda values, and continuously iterating by calculating the midpoint of the current search range, while continuously narrowing the search range until the final value condition of the optimization objective is met. This optimization challenge is tackled by iteratively navigating through the control input constraint range, choosing intermediary points to gradually refine this interval. Following this, the is integrated into the calculation to find the Hamiltonian function’s minimum value.
4. Driving Pattern Recognition and Weight Learning
The driving route selected for this study traverses a mountainous town area in Japan, encompassing 26 signalized intersections with available traffic light timing, slope details, and speed limit information. Speed planning adheres to the principle of assessing whether driving at the designated speed allows the vehicle to clear the intersection during the green light phase. If passage through the intersection is feasible during the green light phase, the vehicle maintains its speed. However, if passage is not feasible, the vehicle uniformly decelerates before reaching the intersection, eventually coming to a stop and waiting until it can safely proceed through the intersection. The selected speed planning curve of the route and slope information are shown in Figure 6. The dashed line represents the time when the red light is on, indicating that the vehicle cannot move forward at that time.
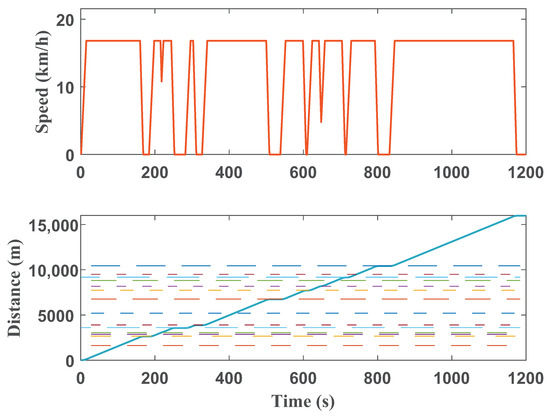
Figure 6.
Speed optimization and driving distance simulation results.
The speed curve from the graph indicates that the planned route mainly consists of three driving modes: constant speed, acceleration, and deceleration. Generally, the optimal weight coefficients within the same driving mode category are also similar. This paper utilizes the K-means algorithm to identify driving cycle patterns and employs reinforcement learning algorithms to learn weight coefficients based on different patterns, aiming to further enhance optimization effectiveness. The non-optimized system can result in being inferior to optimized trained systems in two aspects. This is because non-optimized systems use a uniform weight coefficient for all driving situations, which can result in insufficient use or recovery of the vehicle’s SOC under some high-power or low-power conditions, leading to excessive use or waste of fuel cells and resulting in fuel cell losses.
4.1. Driving Pattern Recognition
This paper employs the K-means to partition driving modes based on acceleration as the feature. Firstly, it calculates the acceleration of the driving cycle, then randomly selects N initial cluster centers. It computes the distance between each acceleration data point and all cluster centers, assigning each object to the closest cluster center. Finally, when all acceleration data are assigned, it recalculates the cluster centers based on the existing objects in each class, until the cluster centers are no longer optimized. The overall flowchart is shown in Figure 7, and the driving pattern recognition result is shown as Figure 8. It can be seen that clustering analysis can effectively identify three driving modes: uniform speed, acceleration, and deceleration, which provides a foundation for weight reinforcement learning.
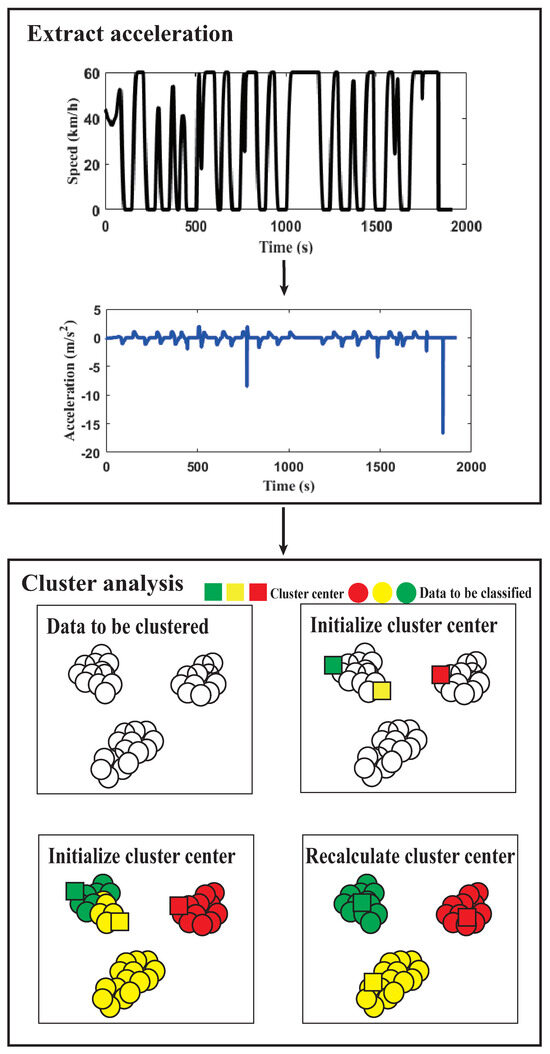
Figure 7.
Cluster analysis flowchart.
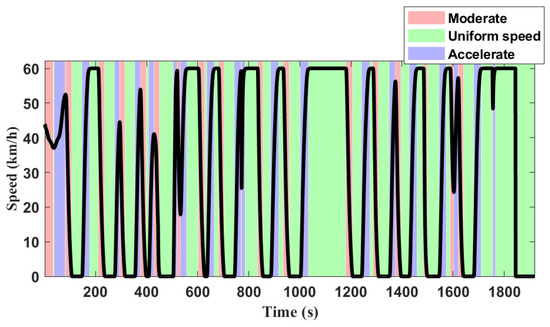
Figure 8.
The figure of driving pattern recognition results.
4.2. Reinforcement Learning Optimization Weights
Reinforcement learning mainly includes elements such as agents, environments, states, actions, and reward functions. The core idea is that agents constantly use trial and error through interaction with the environment, and the environment updates the state based on feedback reward signals, continuously improving strategies. The energy management strategy, incorporating various weight optimization functions, functions as an intelligent agent. It takes in the current state and rewards, initiates actions that influence the environment, and updates the status of hydrogen consumption, SOC, and fuel cell life depreciation according to the predefined model for FCHETs. The objective of the reinforcement learning algorithms is to optimize the expected cumulative returns that agents garner from the environment:
where is the discount rate, E is the expectation, is an instantaneous reward at every moment, and is the expected cumulative return obtained.
On the basis of PMP solving optimization problems, this study uses Q-learning to learn the weight coefficients under a different driving pattern. The Q-learning is a typical temporal differential reinforcement learning algorithm that updates the strategy by iterating the value function and optimizes the strategy by maximizing the Q-value function. The updated rules are as follows:
where represents the value function of the current state action pair, that is, the value of the final optimization objective, , the learning rate. The intelligent agent of reinforcement learning needs to balance exploration and exploitation. On the one hand, it is necessary to leverage existing experience to achieve greater returns and accelerate convergence, but on the other hand, the current strategy may not necessarily be optimal and other possible strategies need to be explored. This study uses the -greedy algorithm to learn weights. The detailed calculation process is shown in Algorithm 1.
| Algorithm 1 Q learning algorithm |
| Initialize , for t = 1:T Select a new weight based on the current Q value, reward signals for receiving feedback , Update Q value Update status → s Obtain the optimal weight coefficient |
In this study, different optimization objective weights were used as actions, the final value of battery SOC was used as the current state, and the optimization objective function value was used as the reward value. Acceleration, deceleration, and uniform speed were used as training conditions, and the obtained rewards were stored in the Q table. The weight coefficients corresponding to different driving modes were iteratively learned. In the real world, it is necessary to adjust the weight coefficients in real-time to achieve the goals of energy saving and reduction in fuel cell life degradation. By reading the state of acceleration, the current driving state of the vehicle can be identified, whether it is in acceleration, constant speed, or deceleration, and then, the weight coefficients can be adjusted accordingly.
5. Simulation Results and Discussion
The load of fuel cell hybrid electric trucks significantly influences the required power. This section compares the optimization effects of trained weights and fixed weights under varying truck loads—no load, half load, and full load—and analyzes the superiority of the proposed strategy. To account for truck speed restrictions, multiple driving cycles with a maximum speed below 90 km/h were selected to evaluate the effectiveness of the proposed approach. The chosen driving cycles include the SC03 comprehensive driving cycle and the HWFET non-stop driving cycle, covering common scenarios encountered by trucks in daily operations. Simulation results are depicted in Figure 9 and Figure 10. In the SC03 driving cycle, for instance, when the truck is unloaded, the fuel cell trained with reinforcement learning weights exhibits smoother and lower power output at 100 s and 300 s, indicating improved fuel economy. Similarly, when the truck operates at half load, the power output of the reinforcement learning-trained PMP is reduced at intervals like 300 s and 450 s to enhance fuel efficiency. At full load, the PMP trained with reinforcement learning weights outputs lower and more stable power at moments such as 100 s and 400 s, thereby reducing both lifespan loss and hydrogen consumption. Additionally, the SOC of the batteries remains consistent across different loading conditions, demonstrating that our proposed algorithm effectively enhances fuel economy while mitigating fuel cell lifespan loss. In the HWFET non-stop high-demand power driving cycle, the weight-trained PMP also yields superior results across varying load conditions. Table 4, Figure 9 and Figure 10 presents quantitative data for a comprehensive understanding of the results depicted in the figures. It is evident across both driving cycles that the PMP algorithm, when fine-tuned with specific weight adjustments, can minimize fuel cell degradation while slightly compromising SOC levels, thus enhancing fuel efficiency under unloaded, partially loaded, and fully loaded conditions.
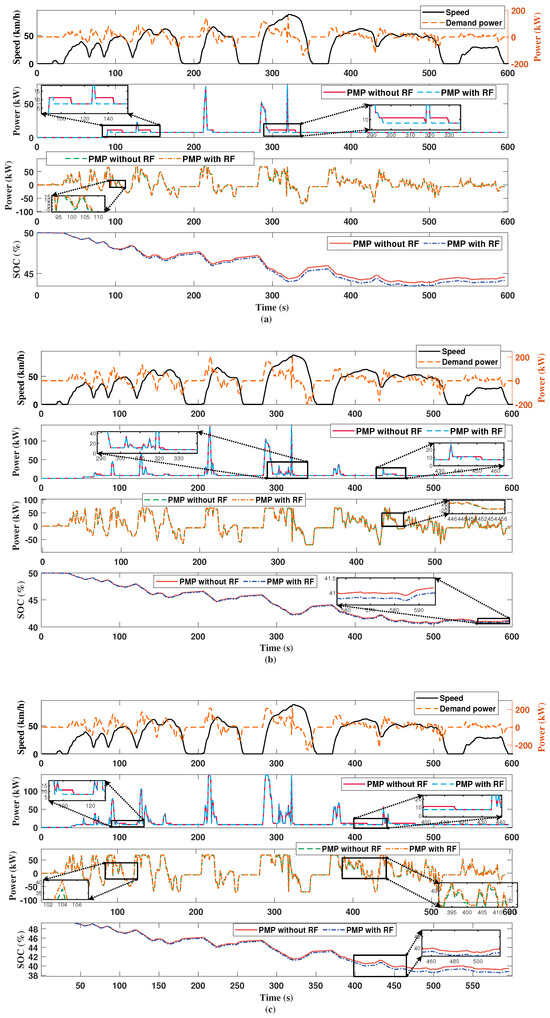
Figure 9.
Comparison of PMP optimization results using reinforcement learning training weights under SC03 driving cycle. (a) Unloaded condition. (b) Half load. (c) Full load.
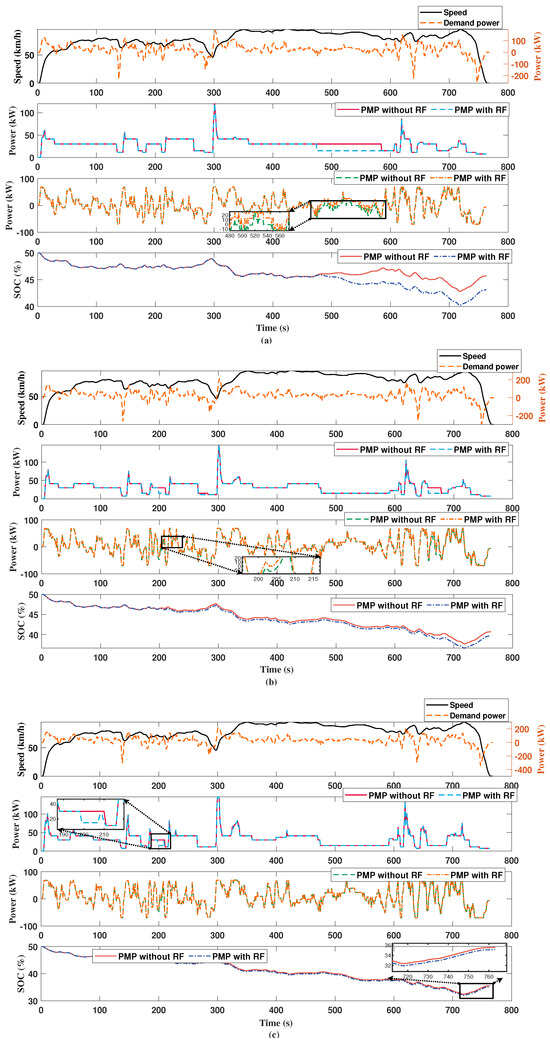
Figure 10.
Comparison of PMP optimization results using reinforcement learning training weights under HWFET driving cycle. (a) Unloaded condition. (b) Half load. (c) Full load.

Table 4.
PMP optimization results of whether reinforcement learning is used to train parameters under SC03 and HWFET driving cycles.
6. Conclusions
To optimize the driving performance of trucks across various loading conditions—specifically during phases of acceleration, maintaining a constant speed, and deceleration—a sophisticated weight learning-based Predictive Model Predictive Control (PMP) optimization strategy is introduced. This innovative approach leverages reinforcement learning to dynamically adjust weight coefficients throughout the optimization process. These adjustments are based on the truck’s current cargo capacity and driving state, enabling a tailored approach to energy management. The primary objective of this strategy is to enhance fuel efficiency and reduce operational costs without compromising the vehicle’s performance. By intelligently managing the trade-off between fuel cell lifespan and hydrogen consumption, the strategy aims to minimize the environmental impact and operational costs of truck operations.
This strategy’s efficacy is demonstrated through its application under varying load conditions, as evidenced by the results obtained from the SC03 driving cycle test. Specifically, the truck exhibited a notable reduction in fuel cell life loss—6.45%, 6.67%, and 6.67% for no-load, half-load, and full-load conditions, respectively. This improvement in fuel cell longevity is achieved at the expense of a slight decrease in the State of Charge (SOC)—0.9%, 1.7%, and 1.6% for each loading condition correspondingly. Despite this, the strategy successfully achieves a significant reduction in hydrogen consumption—3.0%, 4.4%, and 3.0% for no-load, half-load, and full-load conditions, respectively— showcasing the strategy’s ability to balance between operational efficiency and resource conservation.
Further validation of this optimization strategy is seen under the HWFET (Highway Fuel Economy Testing) driving cycle, which simulates uninterrupted driving conditions. In this scenario, the truck demonstrates a reduction in fuel cell lifespan loss by 5.7%, 5.9%, and 6.1% across varying load conditions. Concurrently, hydrogen consumption decreases by 7.1%, 2.8%, and 1.0%, illustrating the strategy’s robustness and adaptability to different driving cycles and load scenarios. This outcome signifies the strategy’s potential to significantly enhance the sustainability and economic viability of truck operations by optimizing fuel cell usage and minimizing hydrogen fuel consumption, all while carefully managing the SOC to ensure operational readiness and performance. In the real world, the reduction in fuel cell losses in the real world will decrease, because in this study, we only considered three optimization objectives: hydrogen consumption, battery lifespan loss, and battery SOC. However, in the real world, more optimization factors need to be considered, so the actual loss may be decreased.
Future research will focus on investigating the impact of more detailed slope and cargo capacity on multi-objective optimization weights.
Author Contributions
R.L.: He played a pivotal role in conceptualizing and framing the research question. He contributed significantly to the literature review, providing insights and analysis that shaped the theoretical foundation of the study. Additionally, He was responsible for collecting and analyzing the primary data, interpreting the results, and writing the majority of the paper’s methodology and results sections. Z.W.: His expertise in the field greatly enhanced the depth and breadth of the paper. He provided valuable feedback and suggestions throughout the writing process, ensuring the paper’s coherence and logic. Specifically, he contributed to the discussion section, offering insights into the implications and significance of the findings. Furthermore, he assisted in the revision process, ensuring the paper adhered to academic standards and guidelines. Z.Z.: His role was crucial in the editing and proofreading of the paper. He meticulously reviewed the manuscript, checking for grammatical errors, typographical mistakes, and inconsistencies in citation and formatting. His attention to detail helped improve the overall clarity and readability of the paper. Additionally, he provided valuable insights into the structure and flow of the paper, ensuring a smooth transition between sections. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
Data are contained within the article.
Conflicts of Interest
The authors declare no conflict of interest.
References
- Lee, D.Y.; Elgowainy, A.; Kotz, A.; Vijayagopal, R.; Marcinkoski, J. Life-cycle implications of hydrogen fuel cell electric vehicle technology for medium- and heavy-duty trucks. Power Sources 2018, 393, 217–229. [Google Scholar] [CrossRef]
- Kast, J.; Vijayagopal, R.; Gangloff, J.J.; Marcinkoski, J. Clean commercial transportation: Medium and heavy duty fuel cell electric trucks. Hydrogen Energy 2017, 42, 4508–4517. [Google Scholar] [CrossRef]
- Liu, F.; Zhao, F.; Liu, Z.; Hao, H. The impact of fuel cell vehicle deployment on road transport greenhouse gas emissions: The China case. Hydrogen Energy 2018, 43, 22604–22621. [Google Scholar] [CrossRef]
- Feng, Y.; Dong, Z. Optimal energy management with balanced fuel economy and battery life for large hybrid electric mining truck. Power Sources 2020, 454, 227948. [Google Scholar] [CrossRef]
- Ilio, G.D.; Giorgio, P.D.; Tribioli, L.; Bella, G.; Jannelli, E. Preliminary design of a fuel cell/battery hybrid powertrain for a heavy-duty yard truck for port logistics. Energy Convers. Manag. 2021, 243, 114423. [Google Scholar] [CrossRef]
- Ming, L.V.; Ying, Y.; Liang, L.; Yao, L.; Zhou, W. Energy Management Strategy of a Plug-in Parallel Hybrid Electric Vehicle Using Fuzzy Control. Energy Procedia 2017, 105, 2660–2665. [Google Scholar] [CrossRef]
- Xie, S.; Hu, X.; Lang, K.; Qi, S.; Liu, T. Powering Mode-integrated Energy Management Strategy for a Plug-in Hybrid Electric Truck with an Automatic Mechanical Transmission Based on Pontryagin’s Minimum Principle. Sustainability 2018, 10, 3758. [Google Scholar] [CrossRef]
- Lü, X.; Wu, Y.; Lian, J.; Zhang, Y.; Chen, C.; Wang, P.; Meng, L. Energy management of hybrid electric vehicles: A review of energy optimization of fuel cell hybrid power system based on genetic algorithm. Energy Convers. Manag. 2020, 205, 112474. [Google Scholar] [CrossRef]
- Guo, Q.; Zhao, Z.; Shen, P.; Zhou, P. Optimization management of hybrid energy source of fuel cell truck based on model predictive control using traffic light information. Theory Technol. 2019, 17, 309–324. [Google Scholar] [CrossRef]
- Deng, K.; Liu, Y.; Hai, D.; Peng, H.; Löwenstein, L.; Pischinger, S.; Hameyer, K. Deep reinforcement learning based energy management strategy of fuel cell hybrid railway vehicles considering fuel cell aging. Energy Convers. Manag. 2022, 251, 115030. [Google Scholar] [CrossRef]
- Barelli, L.; Bidini, G.; Ciupăgeanu, D.; Pianese, C.; Polverino, P.; Sorrentino, M. Stochastic power management approach for a hybrid solid oxide fuel cell/battery auxiliary power unit for heavy duty vehicle applications. Energy Convers. Manag. 2020, 221, 113197. [Google Scholar] [CrossRef]
- Takayama, N.; Arai, S. Multi-objective Deep Inverse Reinforcement Learning for Weight Estimation of Objectives. Artif. Life Robot. 2022, 27, 594–602. [Google Scholar] [CrossRef]
- Kang, Q.; Feng, S.; Zhou, M.; Ammari, A.C.; Sedraoui, K. Optimal Load Scheduling of Plug-in Hybrid Electric Vehicles via Weight-Aggregation Multi-Objective Evolutionary Algorithms. IEEE Trans. Intell. Transp. Syst. 2017, 18, 2557–2568. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).