Advanced Exergy and Exergoeconomic Analysis of Cascade High-Temperature Heat Pump System for Recovery of Low-Temperature Waste Heat
Abstract
1. Introduction
- Both conventional and advanced exergy and exergoeconomic analyses were utilized to explore the enhancement potential provided by the CHTHP system and its components, taking into account both thermodynamic and economic factors. This is expected to provide guidance for the engineering application of CHTHPs in low-temperature waste heat recovery.
- CHTHP systems improved through conventional and advanced exergy analyses can reduce carbon emissions, benefiting the environment.
2. Description of a CHTHP System
3. Modeling
3.1. Basic Hypotheses
- The system works in a steady state.
- The changes in the kinetic and potential energies of the working fluid are negligible.
- The heat dissipation of all components and the pressure drop of the heat exchangers and pipelines are negligible.
- The expansion processes in HTEV and LTEV are considered to be isenthalpic.
3.2. Exergy and Exergoeconomic Analyses’ Modeling
3.2.1. Conventional Exergy and Exergoeconomic Analyses
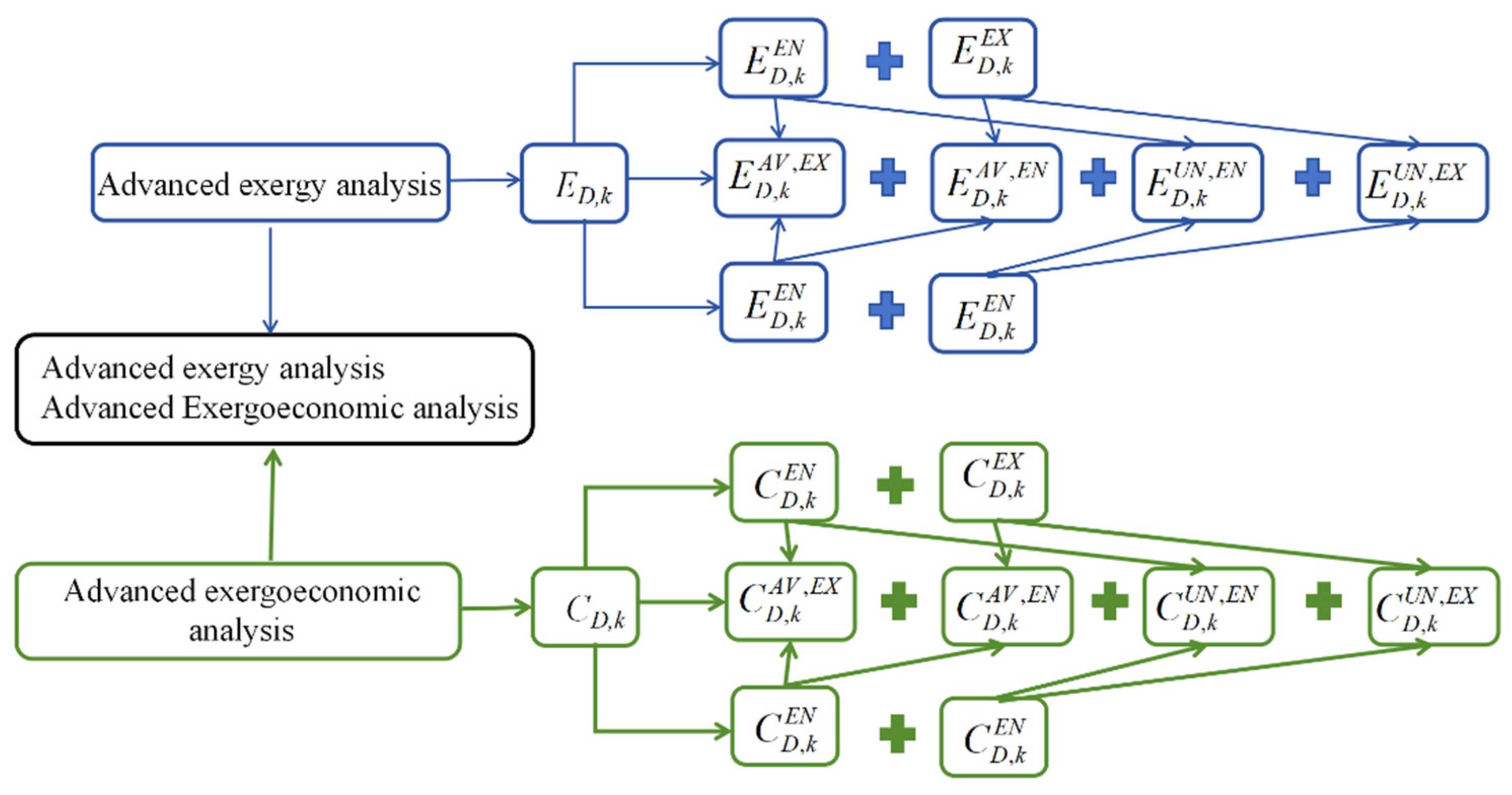
3.2.2. Advanced Exergy and Exergoeconomic Analyses
4. Results and Discussion
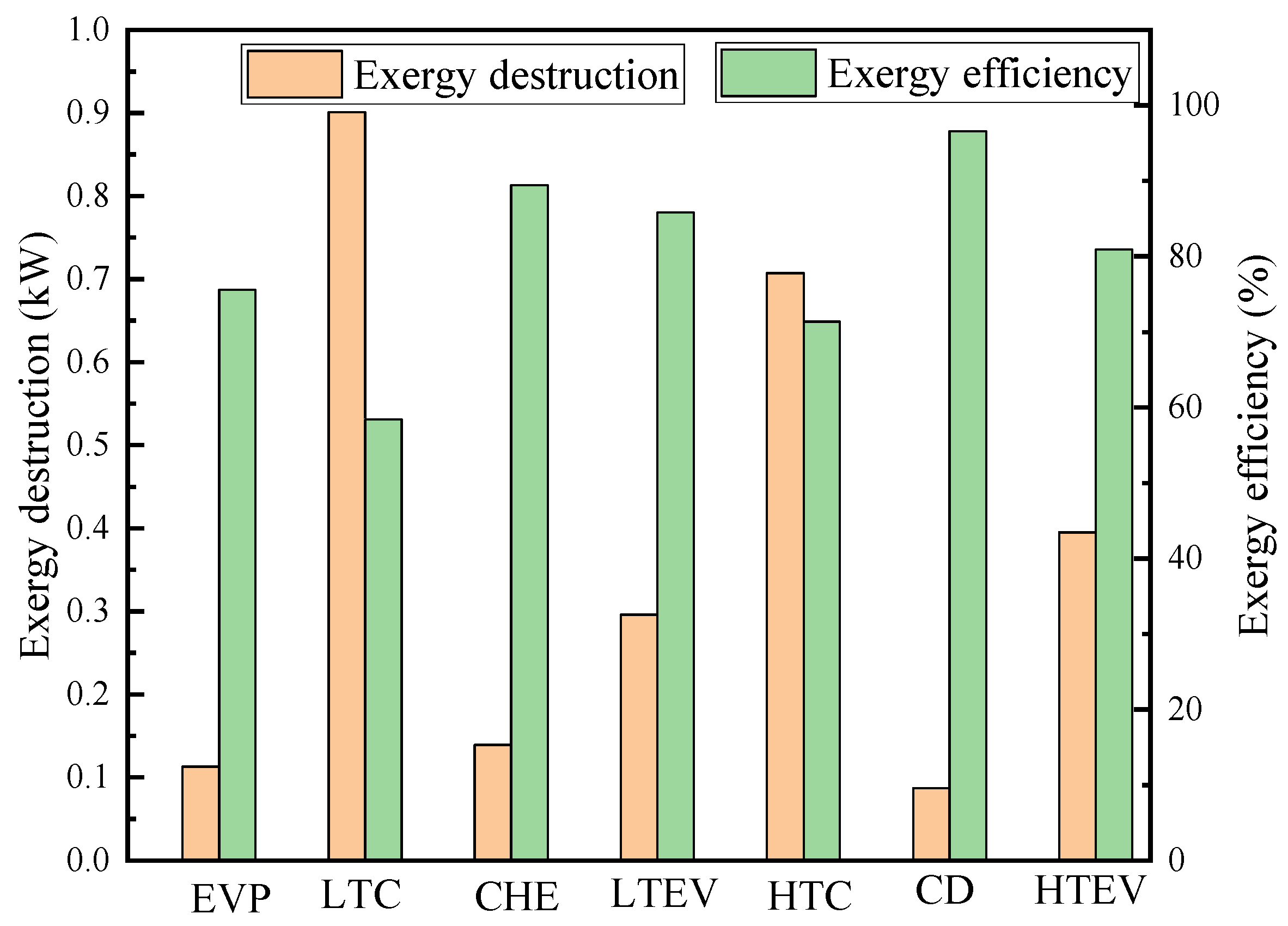
4.1. Conventional Exergy and Exergoeconomic Analyses
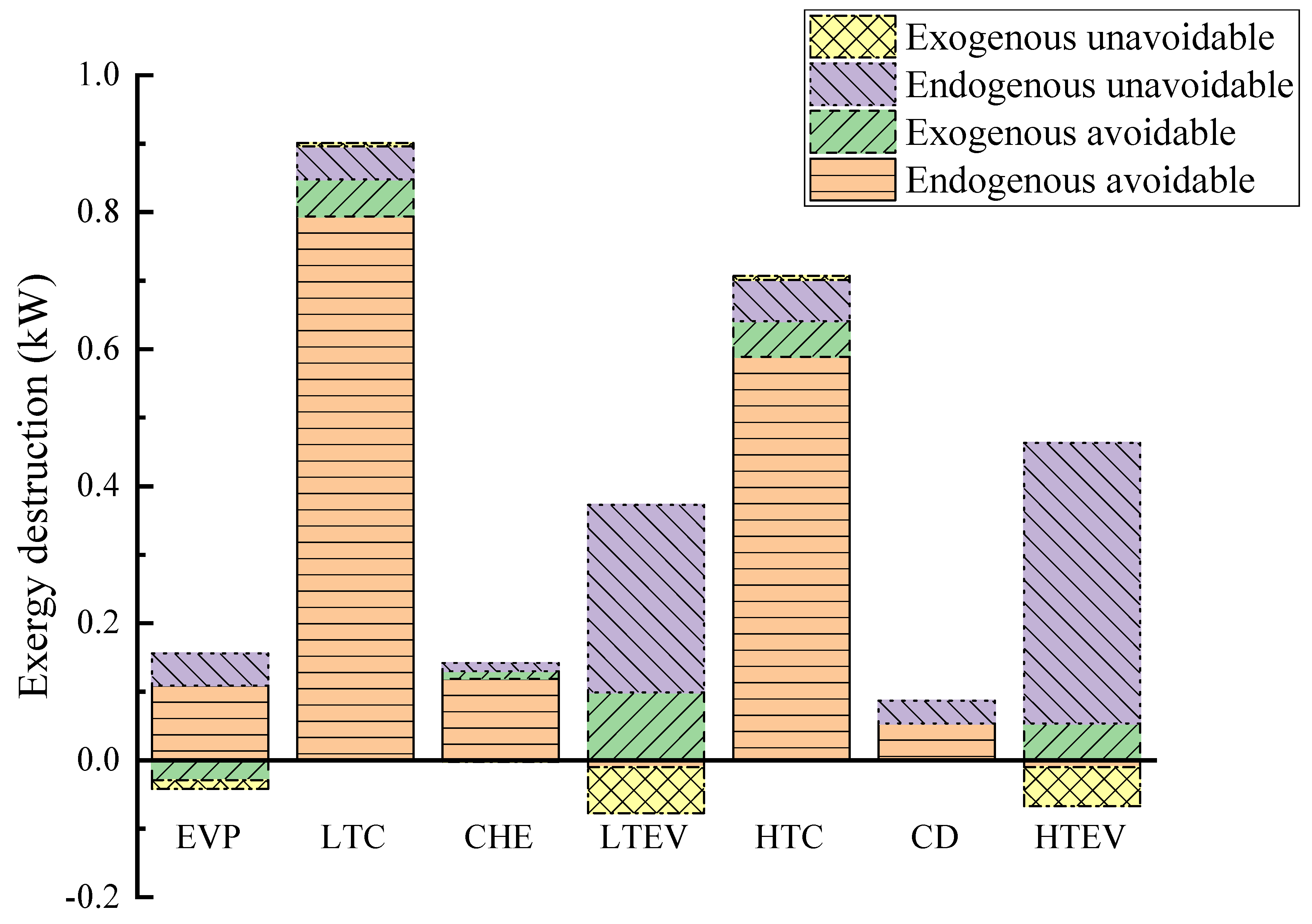
4.2. Advanced Exergy and Exergoeconomic Analyses
5. Conclusions
- (1)
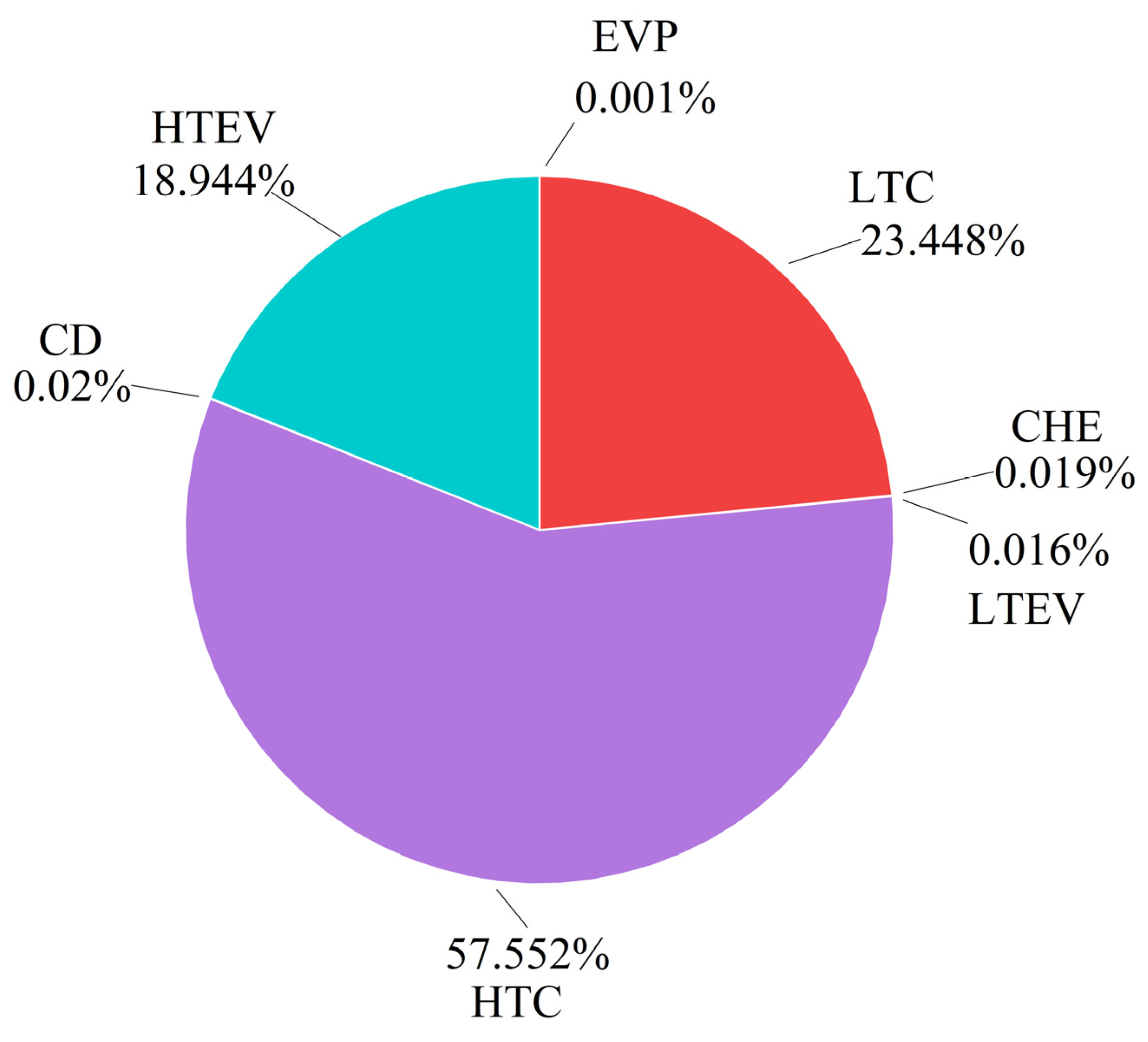
- Conventional exergy analysis showed that the total exergy destruction of the CHTHP system is 2.639 kW, with a lower exergy efficiency of 48.24%, and its exergoeconomic factor is just 0.75%, indicating the high exergy destruction cost. All these values suggest the need for system improvement.
- (2)
- The avoidable endogenous exergy destruction in the system accounts for 62.26% of the total exergy destruction. This indicates that the exergy destruction mainly comes from the components, and the CHTHP system has significant potential for improvement.
- (3)
- The components with the highest endogenous avoidable exergy destruction are the LTC and HTC, accounting for 88.12% and 83.30% of the exergy destruction, respectively. They, along with the highest endogenous avoidable exergy destruction cost, should be prioritized for improvement.
- (4)
- In the comprehensive consideration of thermodynamic and economic performance, the priority for improvement should be given to the HTC, LTC, and CHE in CHTHP systems.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Nomenclature
| Symbols | |
| e | Specific exergy flow rate (J/kg) |
| E | Exergy (kW) |
| f | Exergoeconomic coefficient (%) |
| h | Specific enthalpy (kJ/kg) |
| m | Mass flow rate (kg/s) |
| p | Pressure (kPa) |
| Q | Heat transfer rate (kW) |
| s | Specific entropy (kJ/(kg·K)) |
| t | Hour (h) |
| U | Heat transfer coefficient (W/(m2·K)) |
| y* | Exergy loss ratio (%) |
| Z | Investment cost (USD/h) |
| Z’ | Total cost (USD/h) |
| ε | Exergy efficiency (%) |
| i | Annual interest rate (%) |
| φ | Maintenance cost coefficient |
| Abbreviations | |
| A | Heat exchange area (m2) |
| CD | Condenser |
| C | Exergy cost rate (USD/h) |
| CHTHP | Cascade high-temperature heat pump |
| CRF | Capital recovery coefficient |
| EVP | Evaporator |
| CHE | Cascade heat exchanger |
| HTC | High-temperature compressor |
| HTEV | High-temperature expansion valve |
| HTWT | High-temperature water tank |
| LTC | Low-temperature compressor |
| LTEV | High-temperature expansion valve |
| LTWT | Low-temperature water tank |
| Subscripts | |
| 0 | Environmental state |
| 1~12 | State points |
| D | Destruction |
| F | Fuel |
| i | Inlet |
| k | Cycle component number |
| o | Outlet |
| OP | Annual operating |
| P | Production |
| tot | Total |
| Superscripts | |
| AV | Avoidable |
| UN | Unavoidable |
| EN | Endogenous |
| EX | Exogenous |
| CI | Initial investment |
| OM | Operation and maintenance |
References
- Zhao, J.; Ma, L.; Zayed, M.E.; Elsheikh, A.H.; Li, W.; Yan, Q.; Wang, J. Industrial reheating furnaces: A review of energy efficiency assessments, waste heat recovery potentials, heating process characteristics and perspectives for steel industry. Process Saf. Environ. Prot. 2021, 147, 1209–1228. [Google Scholar] [CrossRef]
- Ononogbo, C.; Nwosu, E.C.; Nwakuba, N.R.; Nwaji, G.N.; Nwufo, O.C.; Chukwuezie, O.C.; Chukwu, M.M.; Anyanwu, E.E. Opportunities of waste heat recovery from various sources: Review of technologies and implementation. Heliyon 2023, 9, e13590. [Google Scholar] [CrossRef]
- Men, Y.; Liu, X.; Zhang, T. A review of boiler waste heat recovery technologies in the medium-low temperature range. Energy 2021, 237, 121560. [Google Scholar] [CrossRef]
- Farhat, O.; Faraj, J.; Hachem, F. A recent review on waste heat recovery methodologies and applications: Comprehensive review, critical analysis and potential recommendations. Clean. Eng. Technol. 2022, 6, 100387. [Google Scholar] [CrossRef]
- Su, Z.; Zhang, M.; Xu, P.; Zhao, Z.; Wang, Z.; Huang, H.; Ouyang, T. Opportunities and strategies for multigrade waste heat utilization in various industries: A recent review. Energy Convers. Manag. 2021, 229, 113769. [Google Scholar] [CrossRef]
- Lee, K.-T.; Lee, D.-S.; Chen, W.-H.; Lin, Y.-L.; Luo, D.; Park, Y.-K.; Bandala, A. An overview of commercialization and marketization of thermoelectric generators for low-temperature waste heat recovery. iScience 2023, 26, 107874. [Google Scholar] [CrossRef]
- Liu, B.; Jia, M.; Liu, Y. Estimation of industrial waste heat recovery potential in China: Based on energy consumption. Appl. Therm. Eng. 2024, 236, 121513. [Google Scholar] [CrossRef]
- Chowdhury, J.I.; Asfand, F.; Ja’fari, M.; Mukherjee, S.; Balta-Ozkan, N. Waste heat recovery integration options for commercial bakeries in a thermo-economic-environmental perspective. Case Stud. Therm. Eng. 2023, 52, 103714. [Google Scholar] [CrossRef]
- Ja, M.; Khan, M.I.; Al-Ghamdi, S.G.; Jaworski, A.J.; Asfand, F. Waste heat recovery in iron and steel industry using organic Rankine cycles. Chem. Eng. J. 2023, 477, 146925. [Google Scholar] [CrossRef]
- Davies, G.; Lagoeiro, H.; Turnell, H.; Wegner, M.; Foster, A.; Evans, J.; Revesz, A.; Leiper, A.; Smyth, K.; Hamilton, J.; et al. Evaluation of low temperature waste heat as a low carbon heat resource in the UK. Appl. Therm. Eng. 2023, 235, 121283. [Google Scholar] [CrossRef]
- Li, C.; Wang, L.; Chen, C.; Zhang, X.; Zhao, W.; Xiang, S. Exergy, economic, and climate performance evaluation of an efficient clean cogeneration system driven by low-temperature waste-heat. J. Clean. Prod. 2023, 403, 136773. [Google Scholar] [CrossRef]
- Qi, X.; Yang, C.; Huang, M.; Ma, Z.; Hnydiuk-Stefan, A.; Feng, K.; Siarry, P.; Królczyk, G.; Li, Z. Comparison study of conventional and advanced exergy analysis on cascade high temperature heat pump system based on experiment. Case Stud. Therm. Eng. 2022, 40, 102552. [Google Scholar] [CrossRef]
- Xu, Y.; Wang, J.; Shen, X.; Sun, Z.; Wang, X.; Han, X. Thermodynamic analyses and performance improvement on a novel cascade-coupling-heating heat pump system for high efficiency hot water production. Energy Convers. Manag. 2023, 293, 117448. [Google Scholar] [CrossRef]
- Li, X.; Zhang, Y.; Ma, X.; Deng, N.; Jin, Z.; Yu, X.; Li, W. Performance analysis of high-temperature water source cascade heat pump using BY3B/BY6 as refrigerants. Appl. Therm. Eng. 2019, 159, 113895. [Google Scholar] [CrossRef]
- Xu, Y.; Zhang, J.; Shen, X.; Han, X.; Chen, H.; Xu, X. Experimental and theoretical investigation on the energetic and economic performance of low-temperature cascade air-source heat pump considering the effects of cascade heat exchanger. Appl. Therm. Eng. 2024, 236, 121672. [Google Scholar] [CrossRef]
- Dong, S.; Meng, X.; Hu, X.; Sun, Z.; Wang, H.; Luo, Y. Investigation of cascade high temperature heat pump optimal design theory based on experiment supporting multi-objective optimization. Energy Convers. Manag. 2022, 267, 115873. [Google Scholar] [CrossRef]
- Dong, Y.; Yan, H.; Wang, R. Significant thermal upgrade via cascade high temperature heat pump with low GWP working fluids. Renew. Sustain. Energy Rev. 2024, 190, 114072. [Google Scholar] [CrossRef]
- Liu, X.; Yu, K.; Wan, X.; Zheng, M.; Li, X. Conventional and advanced exergy analyses of transcritical CO2 ejector refrigeration system equipped with thermoelectric subcooler. Energy Rep. 2021, 7, 1765–1779. [Google Scholar] [CrossRef]
- Yinlong, L.; Qi, C.; Guoqiang, L.; Gang, Y. Energy, modified exergy, exergo-economic and exergo-environmental analyses of a separation-enhanced auto-cascade refrigeration cycle. Energy Convers. Manag. 2024, 299, 117801. [Google Scholar] [CrossRef]
- Kermani, A.A.; Houshfar, E. Design and energy, exergy, and exergoeconomic analyses of a novel biomass-based green hydrogen and power generation system integrated with carbon capture and power-to-gas. Int. J. Hydrogen Energy 2023, 52, 177–189. [Google Scholar] [CrossRef]
- Li, J.; Hu, Y.; Zhan, H. Performance study of thermal-nuclear co-generation system based on exergy and thermal economy analysis. Case Stud. Therm. Eng. 2023, 48, 103119. [Google Scholar] [CrossRef]
- Tian, Y.; Zhang, T.; Xie, N.; Dong, Z.; Yu, Z.; Lyu, M.; Lai, Y.; Xue, X. Conventional and advanced exergy analysis of large-scale adiabatic compressed air energy storage system. J. Energy Storage 2023, 57, 106165. [Google Scholar] [CrossRef]
- Meng, N.; Li, T.; Kong, X.; Gao, X. Advanced exergy and exergoeconomic analyses and a case study of a novel trans-critical CO2 cycle with pressurization process for hot dry rock. Energy Convers. Manag. 2021, 246, 114687. [Google Scholar] [CrossRef]
- Palizdar, A.; Ramezani, T.; Nargessi, Z.; AmirAfshar, S.; Abbasi, M.; Vatani, A. Advanced exergoeconomic evaluation of a mini-scale nitrogen dual expander process for liquefaction of natural gas. Energy 2019, 168, 542–557. [Google Scholar] [CrossRef]
- Wang, Y.; Liu, Y.; Liu, X.; Zhang, W.; Cui, P.; Yu, M.; Liu, Z.; Zhu, Z.; Yang, S. Advanced exergy and exergoeconomic analyses of a cascade absorption heat transformer for the recovery of low grade waste heat. Energy Convers. Manag. 2020, 205, 112392. [Google Scholar] [CrossRef]
- Singh, K.K.; Kumar, R.; Gupta, A. Comparative energy, exergy and economic analysis of a cascade refrigeration system incorporated with flash tank (HTC) and a flash intercooler with indirect subcooler (LTC) using natural refrigerant couples. Sustain. Energy Technol. Assess. 2020, 39, 100716. [Google Scholar] [CrossRef]
- Colorado-Garrido, D.; Mendoza-Bernal, E.; Toledo-Paz, L.M.; Escobedo-Trujillo, B.A. An Ocean Thermal Energy Conversion power plant: Advanced exergy analysis and experimental validation. Renew. Energy 2024, 223, 120018. [Google Scholar] [CrossRef]
- Pirmohamadi, A.; Ghaebi, H.; Ziapour, B.M.; Ebadollahi, M. Exergoeconomic Analysis of a Novel Hybrid System by Integrating the Kalina and Heat Pump Cycles with a Nitrogen Closed Brayton System. Energy Rep. 2021, 7, 546–564. [Google Scholar] [CrossRef]
- Güleryüz, E.H.; Özen, D.N. Advanced exergy and exergo-economic analyses of an advanced adiabatic compressed air energy storage system. J. Energy Storage 2022, 55, 105845. [Google Scholar] [CrossRef]
- Wu, Z.; Wang, X.; Sha, L.; Li, X.; Yang, X.; Ma, X.; Zhang, Y. Performance analysis and multi-objective optimization of the high temperature cascade heat pump system. Energy 2021, 223, 120097. [Google Scholar] [CrossRef]
- Pan, M.; Lu, F.; Zhu, Y.; Huang, G.; Yin, J.; Huang, F.; Chen, G.; Chen, Z. Thermodynamic, exergoeconomic and multi-objective optimization analysis of new ORC and heat pump system for waste heat recovery in waste-to-energy combined heat and power plant. Energy Convers. Manag. 2020, 222, 113200. [Google Scholar] [CrossRef]
- Deymi-Dashtebayaz, M.; Sulin, A.; Ryabova, T.; Sankina, I.; Farahnak, M.; Nazeri, R. Energy, exergoeconomic and environmental optimization of a cascade refrigeration system using different low GWP refrigerants. J. Environ. Chem. Eng. 2021, 9, 106473. [Google Scholar] [CrossRef]
- Hosseinifard, F.; Hosseinpour, M.; Salimi, M.; Amidpour, M. A comprehensive 3E analyses of energy, exergy, and exergoeconomic aspects with solar integration. Sustain. Energy Technol. Assess. 2024, 62, 103626. [Google Scholar] [CrossRef]
- Liu, Z.; Liu, B.; Guo, J.; Xin, X.; Yang, X. Conventional and advanced exergy analysis of a novel transcritical compressed carbon dioxide energy storage system. Energy Convers. Manag. 2019, 198, 111807. [Google Scholar] [CrossRef]
- Prajapati, P.; Raja, B.D.; Savaliya, H.; Patel, V.; Jouhara, H. Thermodynamic evaluation of shell and tube heat exchanger through advanced exergy analysis. Energy 2024, 292, 130421. [Google Scholar] [CrossRef]
- Huang, X.; Chen, W.; Wang, Y.; Wei, W. World Energy Blue Book: World Energy Development Report (2023); Social Science Literature Press: Beijing, China, 2023. [Google Scholar]


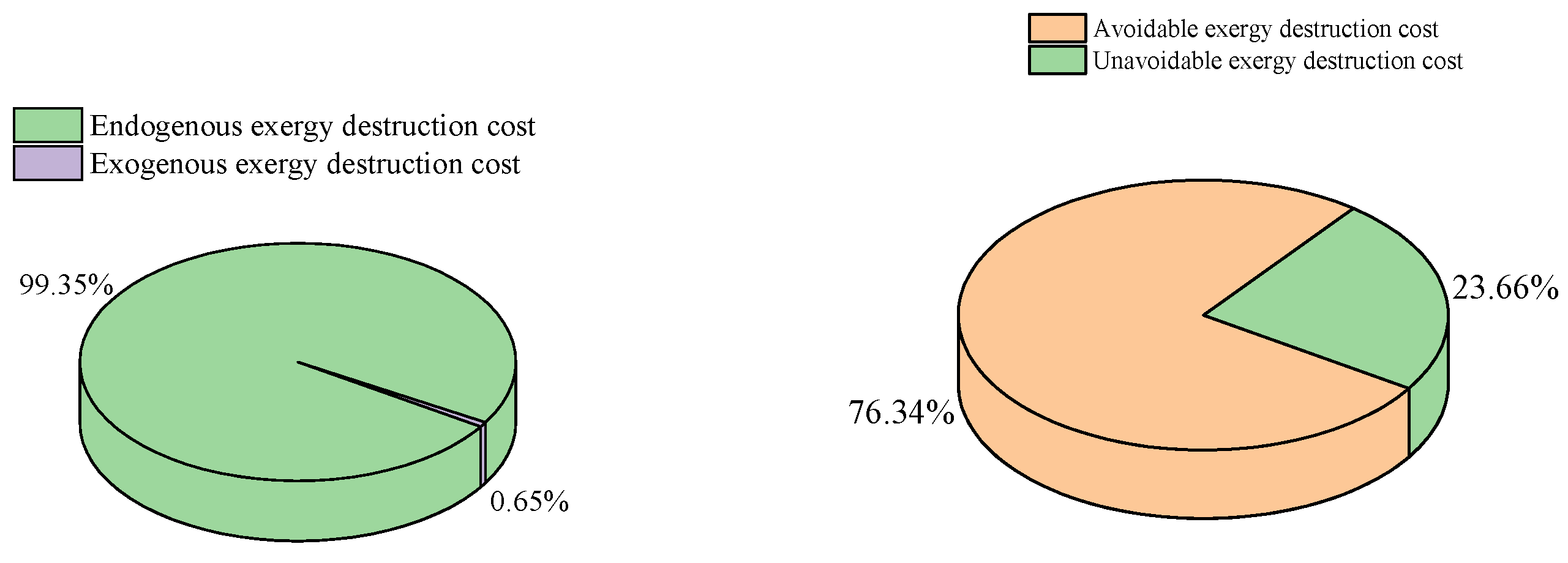
| Component | Energy Balance Equation |
|---|---|
| HTC | WH = (h6 − h5) mf |
| LTC | WL = (h2 − h1) mf |
| EVP | QEVP = (h1 − h4) mf |
| CD | QCD = (h6 − h7) mf |
| CHE | QCHE = (h5 − h8) mf = (h2 − h3) mf |
| HTEV | h7 = h8 |
| LTEV | h3 = h4 |
| Component | Exergy Destruction | Exergy Efficiency |
|---|---|---|
| HTC | E6 − E5 − WH | WH/(E6 − E5) |
| LTC | E2 − E1 − WL | WL/(E2 − E1) |
| EVP | E9 − E1 + E4 − E10 | (E1 − E2)/(E9 − E10) |
| CD | E6 + E11 − E7 − E12 | (E12 − E11)/(E6 − E7) |
| CHE | E2 − E5 − E3 + E8 | (E5 − E8)/(E2 − E3) |
| HTEV | E7 − E8 | E8/E7 |
| LTEV | E3 − E4 | E4/E3 |
| Component | Investment Cost Equation |
|---|---|
| HTC | Z = 1374.9 × W0.46 |
| LTC | Z = 145.5 × W0.46 |
| EVP | Z = 199.6 × A0.89 |
| CD | Z = 199.6 × A0.89 |
| CHE | Z = 54.79 × A0.65 |
| HTEV | Z = 20.64 × m |
| LTEV | Z = 20.64 × m |
| Component | Parameter | Ideal | Unavoidable | Real |
|---|---|---|---|---|
| HTC | Isentropic efficiency (%) | 1 | 0.95 | 0.68 |
| LTC | Isentropic efficiency (%) | 1 | 0.95 | 0.7 |
| EVP | Pinch-point temperature difference (°C) | 0 | 0.5 | 4 |
| CHE | Pinch-point temperature difference (°C) | 0 | 0.5 | 4 |
| CD | Pinch-point temperature difference (°C) | 0 | 0.5 | 4 |
| LTEV/HTEV | -- | Isentropic | Isentropic | Isenthalpic |
| State Point | Working Fluid | Temperature (K) | Pressure (MPa) | Mass Flow Rate (kg/s) | Specific Enthalpy (kJ/kg) | Specific Entropy (kJ/(kg·K)) | Specific Exergy (kJ/kg) |
|---|---|---|---|---|---|---|---|
| 1 | R134a | 308.23 | 0.800 | 0.048 | 419.45 | 1.73 | 44.46 |
| 2 | R134a | 367.68 | 2.540 | 0.048 | 454.52 | 1.76 | 70.67 |
| 3 | R134a | 349.86 | 2.540 | 0.048 | 316.05 | 1.37 | 43.33 |
| 4 | R134a | 305.52 | 0.800 | 0.048 | 316.05 | 1.39 | 37.19 |
| 5 | R245fa | 347.69 | 0.630 | 0.076 | 459.63 | 1.79 | 37.46 |
| 6 | R245fa | 399.07 | 2.090 | 0.076 | 489.07 | 1.81 | 60.59 |
| 7 | R245fa | 393.28 | 2.090 | 0.076 | 372.62 | 1.51 | 27.16 |
| 8 | R245fa | 345.87 | 0.630 | 0.076 | 372.62 | 1.53 | 21.98 |
| 9 | Water | 314.44 | 0.101 | 0.260 | 86.06 | 0.59 | 6.64 |
| 10 | Water | 309.85 | 0.101 | 0.260 | 71.49 | 0.53 | 4.86 |
| 11 | Water | 389.07 | 0.101 | 0.500 | 490.69 | 1.48 | 67.04 |
| 12 | Water | 393.25 | 0.101 | 0.500 | 504.24 | 1.53 | 71.96 |
| State Point | Working Fluid | Temperature (K) | Pressure (MPa) | Mass Flow Rate (kg/s) | Specific Enthalpy (kJ/kg) | Specific Entropy (kJ/(kg·K)) | Specific Exergy (kJ/kg) |
|---|---|---|---|---|---|---|---|
| 1 | R134a | 309.85 | 0.930 | 0.063 | 417.96 | 1.73 | 47.18 |
| 2 | R134a | 351.24 | 2.303 | 0.063 | 435.98 | 1.76 | 65.19 |
| 3 | R134a | 346.95 | 2.303 | 0.063 | 310.97 | 1.37 | 42.17 |
| 4 | R134a | 309.85 | 0.930 | 0.063 | 316.36 | 1.39 | 37.56 |
| 5 | R245fa | 346.95 | 0.674 | 0.087 | 459.63 | 1.79 | 38.08 |
| 6 | R245fa | 393.25 | 1.931 | 0.087 | 489.07 | 1.81 | 55.79 |
| 7 | R245fa | 393.25 | 1.931 | 0.087 | 372.62 | 1.51 | 27.16 |
| 8 | R245fa | 346.95 | 0.674 | 0.087 | 372.62 | 1.53 | 21.45 |
| 9 | Water | 314.44 | 0.101 | 0.364 | 86.06 | 0.59 | 6.73 |
| 10 | Water | 309.85 | 0.101 | 0.364 | 71.49 | 0.53 | 4.95 |
| 11 | Water | 389.07 | 0.101 | 0.500 | 490.69 | 1.48 | 67.04 |
| 12 | Water | 393.25 | 0.101 | 0.500 | 504.24 | 1.53 | 71.96 |
| State Point | Working Fluid | Temperature (K) | Pressure (MPa) | Mass Flow Rate (kg/s) | Specific Enthalpy (kJ/kg) | Specific Entropy (kJ/(kg·K)) | Specific Exergy (kJ/kg) |
|---|---|---|---|---|---|---|---|
| 1 | R134a | 309.35 | 0.917 | 0.058 | 417.73 | 1.73 | 46.95 |
| 2 | R134a | 352.20 | 2.316 | 0.058 | 437.11 | 1.76 | 65.50 |
| 3 | R134a | 347.20 | 2.316 | 0.058 | 311.41 | 1.37 | 42.26 |
| 4 | R134a | 309.35 | 0.917 | 0.058 | 311.41 | 1.39 | 37.90 |
| 5 | R245fa | 346.70 | 0.669 | 0.086 | 457.42 | 1.79 | 37.95 |
| 6 | R245fa | 393.75 | 1.951 | 0.086 | 476.34 | 1.81 | 56.19 |
| 7 | R245fa | 393.75 | 1.951 | 0.086 | 373.56 | 1.51 | 27.35 |
| 8 | R245fa | 346.70 | 0.669 | 0.086 | 373.56 | 1.53 | 22.60 |
| 9 | Water | 314.44 | 0.101 | 0.319 | 86.06 | 0.59 | 6.73 |
| 10 | Water | 309.85 | 0.101 | 0.319 | 71.49 | 0.53 | 4.95 |
| 11 | Water | 389.07 | 0.101 | 0.500 | 490.69 | 1.48 | 67.04 |
| 12 | Water | 393.25 | 0.101 | 0.500 | 504.24 | 1.53 | 71.96 |
| Component | EF (kW) | EP (kW) | ED (kW) | CD (USD/h) | Ε (%) | fk (%) | y* (%) |
|---|---|---|---|---|---|---|---|
| EVP | 0.464 | 0.351 | 0.113 | 1.43 × 10−6 | 75.59 | 98.47 | 4.29 |
| LTC | 2.166 | 1.265 | 0.901 | 0.09359 | 58.40 | 1.4 | 34.14 |
| CHE | 1.319 | 1.180 | 0.139 | 7.71 × 10−5 | 89.44 | 27.59 | 5.28 |
| LTEV | 2.090 | 1.794 | 0.296 | 6.42 × 10−5 | 85.84 | 0.53 | 11.21 |
| HTC | 2.468 | 1.761 | 0.707 | 0.229705 | 71.36 | 0.59 | 26.79 |
| CD | 2.546 | 2.459 | 0.087 | 0.00008 | 96.58 | 69.66 | 3.30 |
| HTEV | 2.069 | 1.674 | 0.395 | 0.07561 | 80.90 | 0.001 | 14.98 |
| System | 5.098 | 2.459 | 2.639 | 0.39914 | 48.24 | 0.75 | 100 |
| Component | (kW) | (kW) | (kW) | (kW) | (kW) | (kW) | (kW) | (kW) |
|---|---|---|---|---|---|---|---|---|
| EVP | 0.155 | −0.042 | 0.079 | 0.034 | 0.109 | −0.029 | 0.047 | −0.013 |
| LTC | 0.842 | 0.059 | 0.848 | 0.053 | 0.794 | 0.054 | 0.048 | 0.005 |
| CHE | 0.130 | 0.009 | 0.129 | 0.010 | 0.119 | 0.011 | 0.012 | −0.002 |
| LTEV | 0.264 | 0.032 | 0.089 | 0.207 | −0.010 | 0.099 | 0.274 | −0.067 |
| HTC | 0.648 | 0.059 | 0.641 | 0.066 | 0.589 | 0.052 | 0.060 | 0.006 |
| CD | 0.086 | 0.000 | 0.054 | 0.033 | 0.054 | 0.000 | 0.033 | 0.000 |
| HTEV | 0.399 | −0.004 | 0.043 | 0.352 | −0.010 | 0.054 | 0.409 | −0.057 |
| System | 2.525 | 0.114 | 1.885 | 0.754 | 1.643 | 0.242 | 0.882 | −0.128 |
| Component | (USD/h) | (USD/h) | (USD/h) | (USD/h) | (USD/h) | (USD/h) | (USD/h) | (USD/h) |
|---|---|---|---|---|---|---|---|---|
| EVP | 2.85 × 10−5 | 0.1 × 10−8 | 1.42 × 10−6 | 1.42 × 10−6 | 1.42 × 10−6 | 1.42 × 10−6 | 0.1 × 10−8 | 0.1 × 10−8 |
| LTC | 0.874585 | 0.00612 | 0.08808 | 0.005505 | 0.082472 | 0.005608 | 0.004985 | 0.00052 |
| CHE | 0.0006 | 4.28 × 10−6 | 0.00006 | 4.28 × 10−6 | 5.57 × 10−5 | 5.71 × 10−6 | 5.71 × 10−6 | −1.42 × 10−6 |
| LTEV | 0.000685 | 8.57 × 10−6 | 2.28 × 10−5 | 5.42 × 10−5 | −2.85 × 10−6 | 2.57 × 10−5 | 7.14 × 10−5 | −1.71 × 10−5 |
| HTC | 2.105342 | 0.019168 | 0.20826 | 0.021442 | 0.191364 | 0.016894 | 0.019494 | 0.00195 |
| CD | 0.0008 | 0 | 0.00005 | 0.00003 | 0.00005 | 0 | 0.00003 | 0 |
| HTEV | 0.763757 | −0.00076 | 0.008231 | 0.067378 | −0.00191 | 0.010337 | 0.07829 | −0.01091 |
| System | 3.745785 | 0.024544 | 0.304707 | 0.094417 | 0.272 | 0.032871 | 0.102877 | −0.00846 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hu, X.; Shi, C.; Liu, Y.; Fu, X.; Ma, T.; Jin, M. Advanced Exergy and Exergoeconomic Analysis of Cascade High-Temperature Heat Pump System for Recovery of Low-Temperature Waste Heat. Energies 2024, 17, 1027. https://doi.org/10.3390/en17051027
Hu X, Shi C, Liu Y, Fu X, Ma T, Jin M. Advanced Exergy and Exergoeconomic Analysis of Cascade High-Temperature Heat Pump System for Recovery of Low-Temperature Waste Heat. Energies. 2024; 17(5):1027. https://doi.org/10.3390/en17051027
Chicago/Turabian StyleHu, Xiaowei, Chenyang Shi, Yong Liu, Xingyu Fu, Tianyao Ma, and Mingsen Jin. 2024. "Advanced Exergy and Exergoeconomic Analysis of Cascade High-Temperature Heat Pump System for Recovery of Low-Temperature Waste Heat" Energies 17, no. 5: 1027. https://doi.org/10.3390/en17051027
APA StyleHu, X., Shi, C., Liu, Y., Fu, X., Ma, T., & Jin, M. (2024). Advanced Exergy and Exergoeconomic Analysis of Cascade High-Temperature Heat Pump System for Recovery of Low-Temperature Waste Heat. Energies, 17(5), 1027. https://doi.org/10.3390/en17051027






