Deep Learning-Based Algorithm for Internal Fault Detection of Power Transformers during Inrush Current at Distribution Substations
Abstract
1. Introduction
1.1. Literature Review and Related Works
1.2. Key Contributions and Organization
- A wide range of applicability, regardless of inrush current magnitude, the residual flux in power transformers, internal fault magnitude, and fault angles;
- An improved discrimination of internal faults, considering winding-ground faults during inrush currents;
- A universal application for other power transformers with different characteristics;
- A data window-based operation without the need for a threshold.
2. Problem Statement
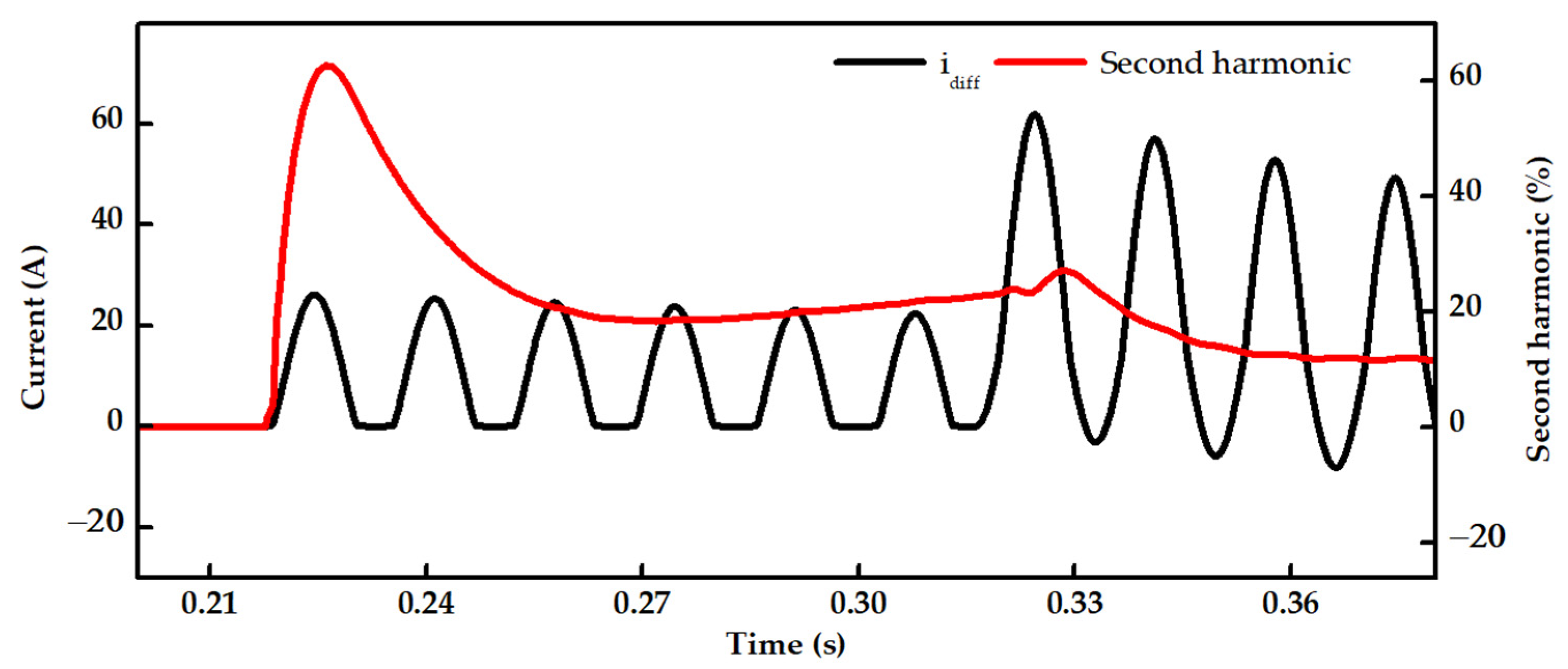
2.1. Overview of Magnetizing Inrush Current and Second Harmonic Ratio
2.2. Data Window of Inrush Current and Internal Faults
2.3. Dataset Acquisition for Training and Testing Procedure
2.4. Dataset Preprocessing for Training
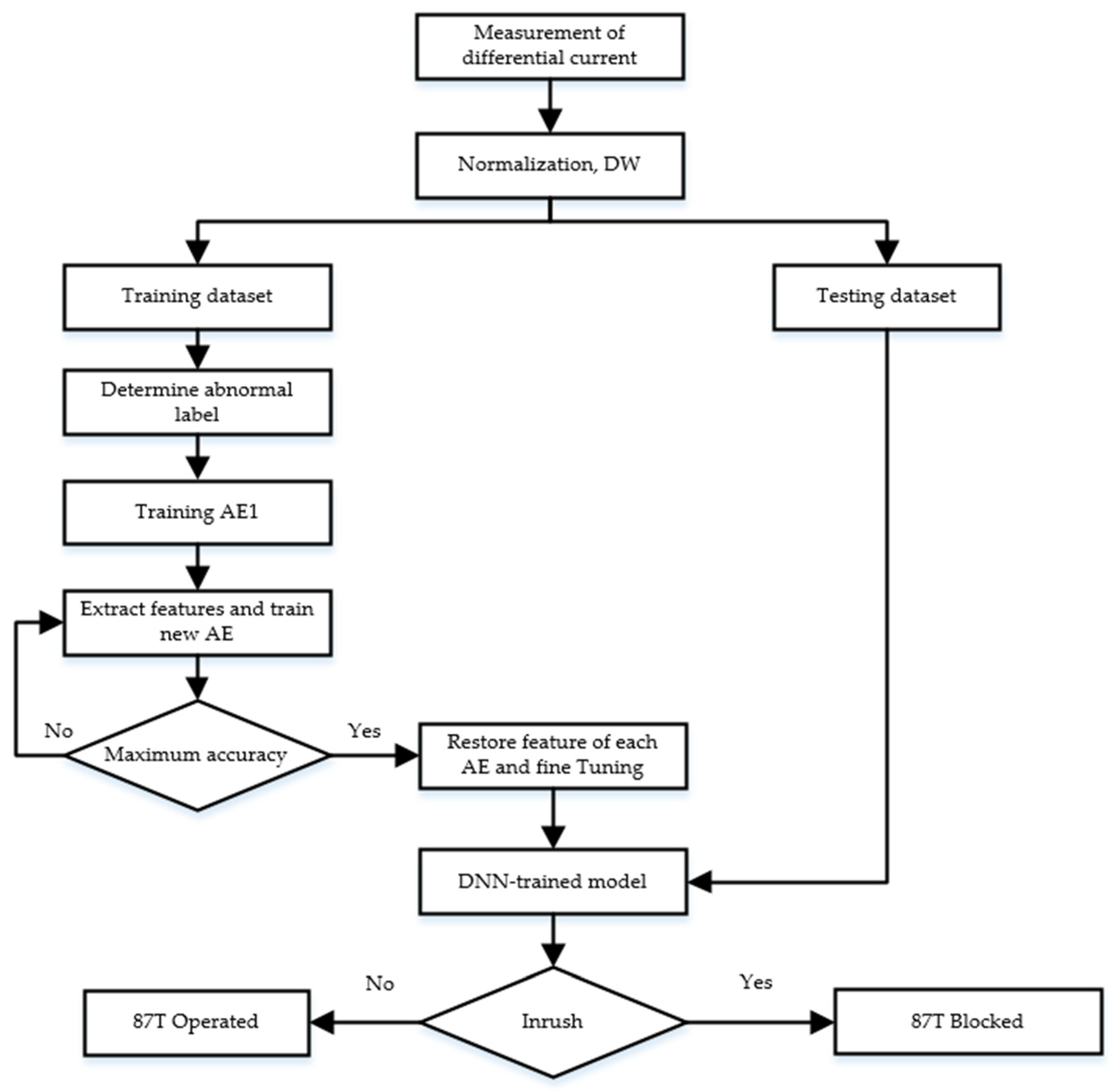
3. Deep Neural Network (DNN)-Based Discrimination
3.1. Principle of Autoencoders
3.2. Framework of Stacked Autoencoder
3.3. Fine-Tuning and SoftMax Classifier
4. Simulation Model
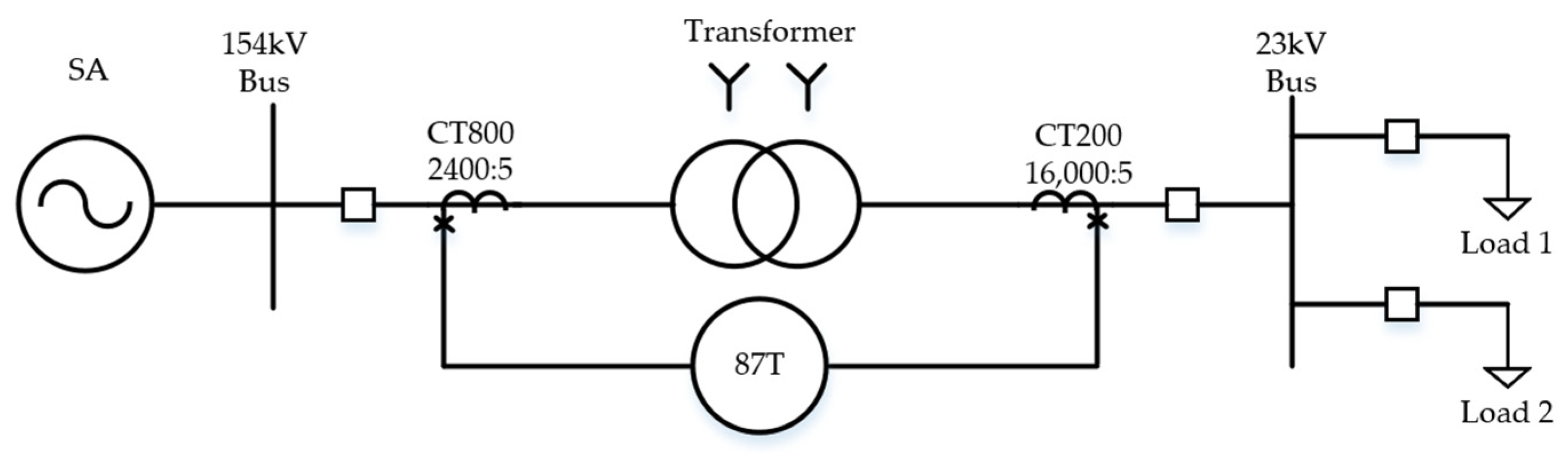
4.1. PSCAD/EMTDC Model
4.2. Deep Neural Network Model
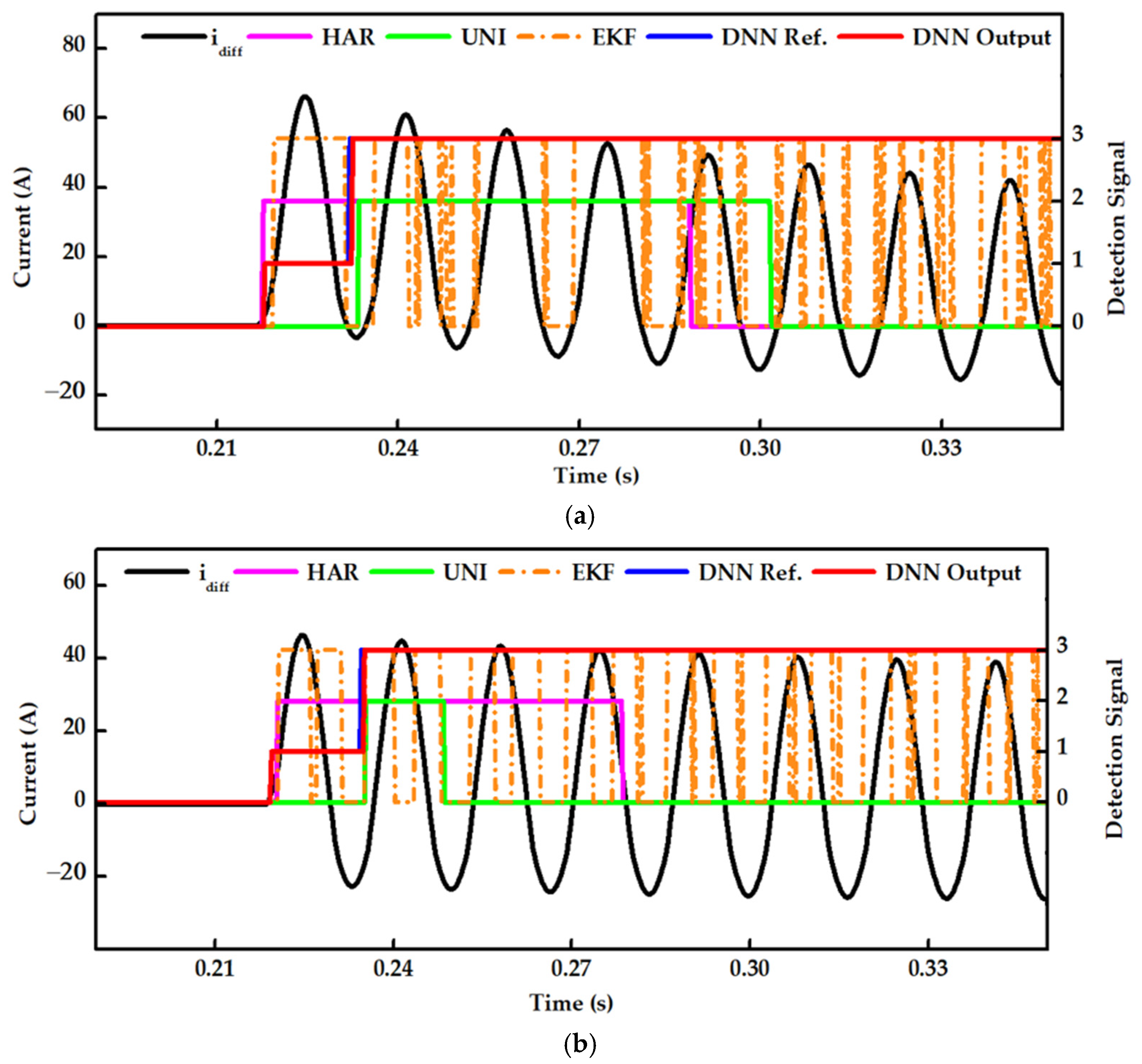
5. Simulation Results
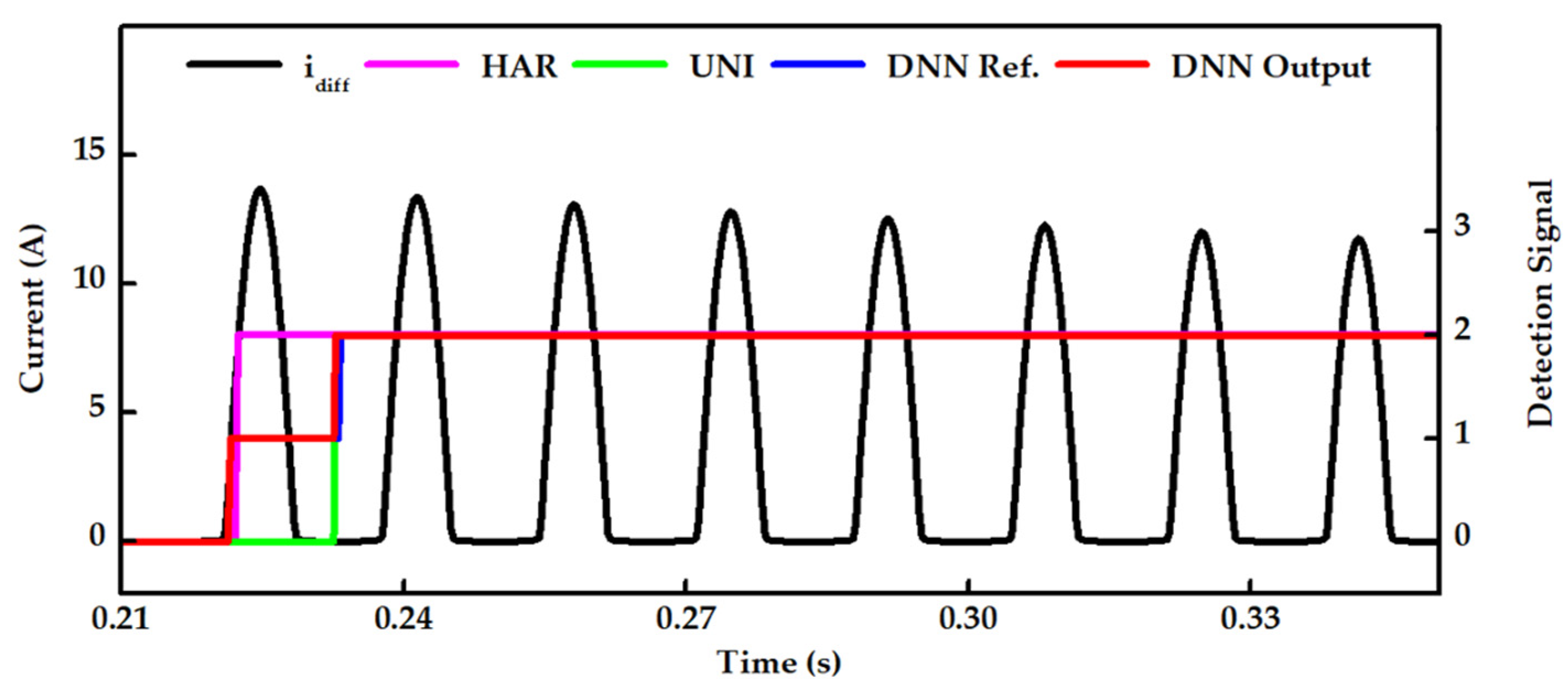
5.1. Case Study 1: Inrush Current at a Switching Angle of 0°
5.2. Case Study 2: Inrush Current at a Switching Angle of 90°
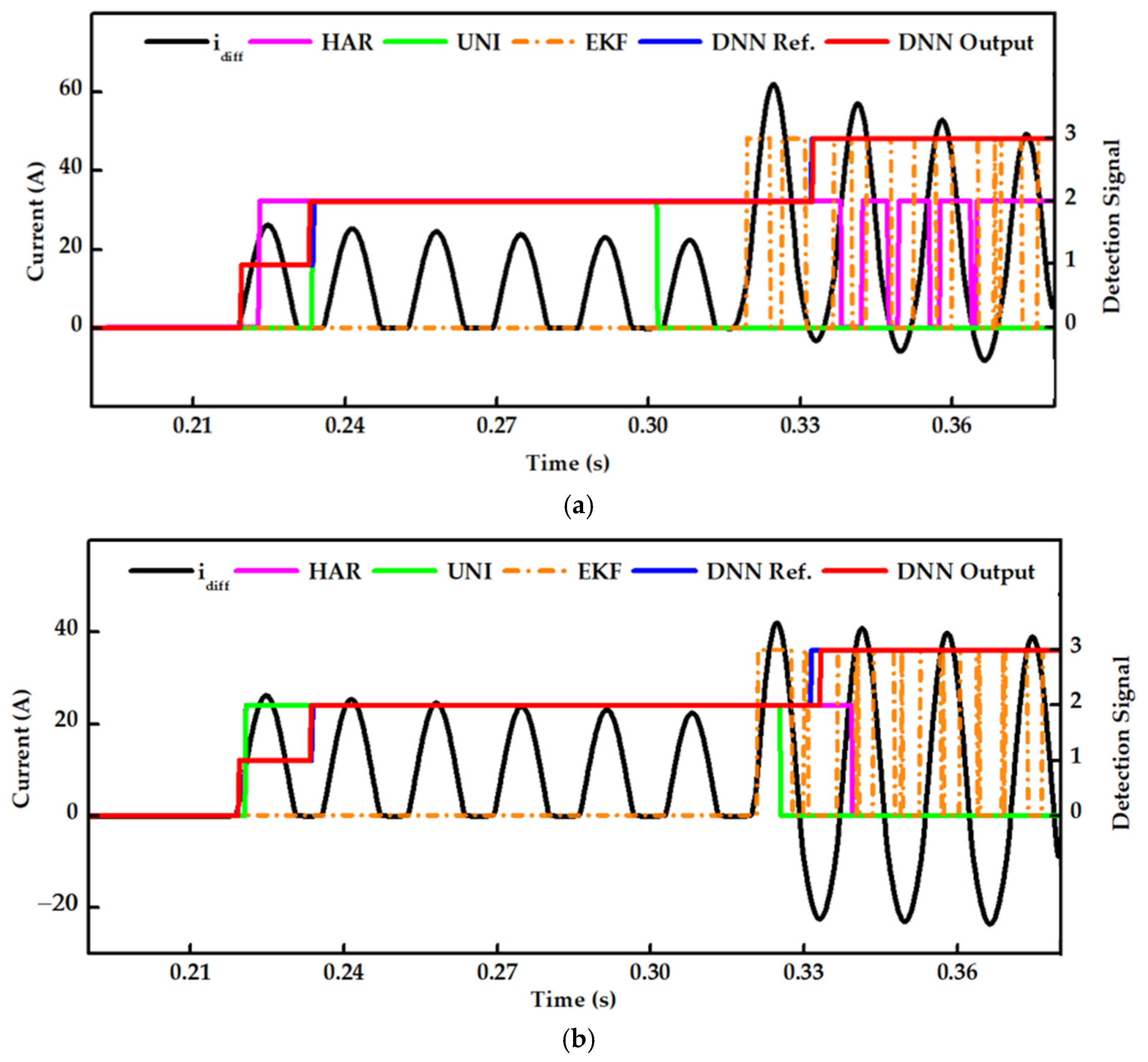
5.3. Case Study 3: Energization of a Power Transformer in the Presence of an Internal Fault
5.4. Case Study 4: Phase-A-to-Ground Internal Faults Occurring during the Energization of a Power Transformer
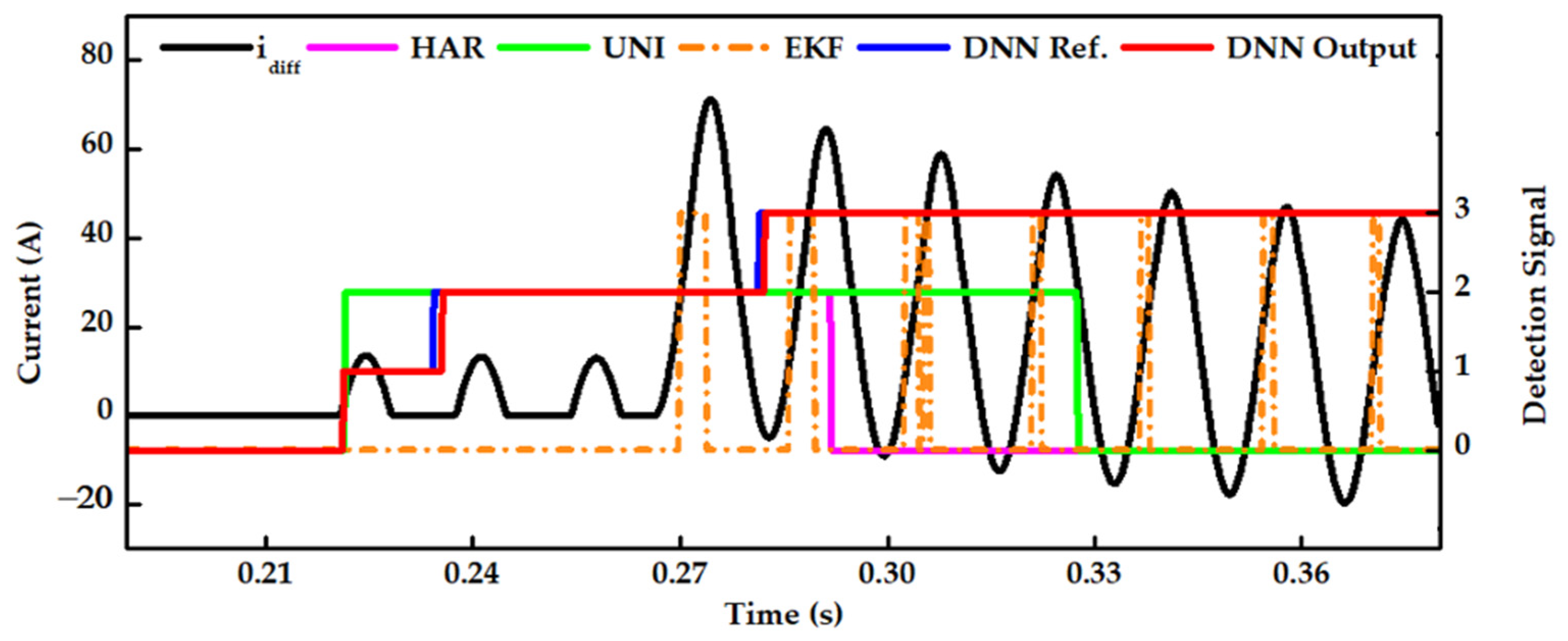
5.5. Case Study 5: Phase-B–C-to-Ground Internal Faults Occurring during the Energization of a Power Transformer
6. Discussion on the Performance Evaluation Metrics
7. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Gopika, R.; Deepa, S. Study on Power Transformer Inrush Current. IOSR J. Electr. Electron. Eng. 2017, 2, 59–63. [Google Scholar]
- Baoming, G.; Dealmeida, A.; Qionglin, Z.; Xiangheng, W. An Equivalent Instantaneous Inductance-Based Technique for Discrimination between Inrush Current and Internal Faults in Power Transformers. IEEE Trans. Power Deliv. 2005, 20, 2473–2482. [Google Scholar] [CrossRef]
- Guzman, A.; Fischer, N.; Labuschagne, C. Improvements in transformer protection and control. In Proceedings of the 2009 62nd Annual Conference for Protective Relay Engineers, College Station, TX, USA, 30 March–2 April 2009; pp. 563–579. [Google Scholar]
- Hamilton, R. Analysis of transformer inrush current and comparison of harmonic restraint methods in transformer protection. IEEE Trans. Ind. Appl. 2013, 49, 1890–1899. [Google Scholar] [CrossRef]
- Zhang, L.; Wu, Q.; Ji, T.; Zhang, A. Identification of inrush currents in power transformers based on higher-order statistics. Electr. Power Syst. Res. 2017, 146, 161–169. [Google Scholar] [CrossRef]
- Mo, C.; Ji, T.; Zhang, L.; Wu, Q. Equivalent statistics based inrush identification method for differential protection of power transformer. Electr. Power Syst. Res. 2022, 203, 107664. [Google Scholar] [CrossRef]
- Hodder, S.; Kasztenny, B.; Fischer, N.; Xia, Y. Low second-harmonic content in transformer inrush currents—Analysis and practical solutions for protection security. In Proceedings of the 2014 67th Annual Conference for Protective Relay Engineers, College Station, TX, USA, 31 March–3 April 2014; pp. 705–722. [Google Scholar]
- Lu, Z.; Tang, W.H.; Ji, T.Y.; Wu, Q.H. A Morphological Scheme for Inrush Identification in Transformer Protection. IEEE Trans. Power Deliv. 2009, 24, 560–568. [Google Scholar] [CrossRef]
- Vazquez, E.; Mijares, I.I.; Chacon, O.L.; Conde, A. Transformer differential protection using principal component analysis. IEEE Trans. Power Deliv. 2008, 23, 67–72. [Google Scholar] [CrossRef]
- Afrasiabi, S.; Afrasiabi, M.; Parang, B.; Mohammadi, M.; Samet, H.; Dragicevic, T. Fast GRNN-Based Method for Distinguishing Inrush Currents in Power Transformers. IEEE Trans. Ind. Electron. 2021, 69, 8501–8512. [Google Scholar] [CrossRef]
- Afrasiabi, S.; Afrasiabi, M.; Parang, B.; Mohammadi, M. Integration of Accelerated Deep Neural Network into Power Transformer Differential Protection. IEEE Trans. Ind. Inform. 2019, 16, 865–876. [Google Scholar] [CrossRef]
- Samet, H.; Ghanbari, T.; Ahmadi, M. An Auto-Correlation Function Based Technique for Discrimination of Internal Fault and Magnetizing Inrush Current in Power Transformers. Electr. Power Compon. Syst. 2015, 43, 399–411. [Google Scholar] [CrossRef]
- Mao, P.; Aggarwal, R. A novel approach to the classification of the transient phenomena in power transformers using combined wavelet transform and neural network. IEEE Trans. Power Deliv. 2001, 16, 654–660. [Google Scholar] [CrossRef]
- Key, S.; Ko, C.-S.; Song, K.-J.; Nam, S.-R. Fast Detection of Current Transformer Saturation Using Stacked Denoising Autoencoders. Energies 2023, 16, 1528. [Google Scholar] [CrossRef]
- Key, S.; Kang, S.-H.; Lee, N.-H.; Nam, S.-R. Bayesian Deep Neural Network to Compensate for Current Transformer Saturation. IEEE Access 2021, 9, 154731–154739. [Google Scholar] [CrossRef]
- Sok, V.; Lee, S.-W.; Kang, S.-H.; Nam, S.-R. Deep Neural Network-Based Removal of a Decaying DC Offset in Less Than One Cycle for Digital Relaying. Energies 2022, 15, 2644. [Google Scholar] [CrossRef]
- Silva, K.; Souza, B.; Brito, N. Fault Detection and Classification in Transmission Lines Based on Wavelet Transform and ANN. IEEE Trans. Power Deliv. 2006, 21, 2058–2063. [Google Scholar] [CrossRef]
- Costa, F.B.; de Souza, B.A.; Brito, N.S.D. Detection and Classification of Transient Disturbances in Power Systems. IEEJ Trans. Power Energy 2010, 130, 910–916. [Google Scholar] [CrossRef]
- Gaouda, A.M.; Salama, M.M.A. DSP Wavelet-Based Tool for Monitoring Transformer Inrush Currents and Internal Faults. IEEE Trans. Power Deliv. 2010, 25, 1258–1267. [Google Scholar] [CrossRef]
- Saleh, S.A.; Scaplen, B.; Rahman, M.A. A new implementation method of wavelet-packet-transform differential protection for power transformers. IEEE Trans. Ind. Appl. 2011, 47, 1003–1012. [Google Scholar] [CrossRef]
- Costa, F.B. Fault-induced transient detection based on real-time analysis of the wavelet coefficient energy. IEEE Trans. Power Deliv. 2014, 29, 140–153. [Google Scholar] [CrossRef]
- Medeiros, R.P.; Costa, F.B.; Silva, K.M. Power Transformer Differential Protection Using the Boundary Discrete Wavelet Transform. IEEE Trans. Power Deliv. 2015, 31, 2083–2095. [Google Scholar] [CrossRef]
- Medeiros, R.P.; Costa, F.B. A Wavelet-Based Transformer Differential Protection with Differential Current Transformer Saturation and Cross-Country Fault Detection. IEEE Trans. Power Deliv. 2017, 33, 789–799. [Google Scholar] [CrossRef]
- Medeiros, R.P.; Costa, F.B. A wavelet-based transformer differential protection: Internal fault detection during inrush conditions. IEEE Trans. Power Deliv. 2018, 33, 2965–2977. [Google Scholar] [CrossRef]
- Ruhan, Z.; Mansor, N.N.B.; Illias, H.A. Identification of Inrush Current Using a GSA-BP Network. Energies 2023, 16, 2340. [Google Scholar] [CrossRef]
- Peng, F.; Gao, H.; Huang, J.; Guo, Y.; Liu, Y.; Zhang, Y. Power Differential Protection for Transformer Based on Fault Component Network. IEEE Trans. Power Deliv. 2023, 38, 2464–2477. [Google Scholar] [CrossRef]
- Ali, E.; Helal, A.; Desouki, H.; Shebl, K.; Abdelkader, S.; Malik, O. Power transformer differential protection using current and voltage ratios. Electr. Power Syst. Res. 2017, 154, 140–150. [Google Scholar] [CrossRef]
- Liu, P.; Jiao, B.; Zhang, P.; Du, S.; Zhu, J.; Song, Y. Countermeasure to Prevent Transformer Differential Protection from False Operations. IEEE Access 2023, 11, 45950–45960. [Google Scholar] [CrossRef]
- He, B.; Zhang, X.; Bo, Z. A New Method to Identify Inrush Current Based on Error Estimation. IEEE Trans. Power Deliv. 2006, 21, 1163–1168. [Google Scholar] [CrossRef]
- Elsadd, M.A.; Yousef, W.; Abdelaziz, A.Y. New adaptive coordination approach between generator-transformer unit overall differential protection and generator capability curves. Int. J. Electr. Power Energy Syst. 2019, 118, 105788. [Google Scholar] [CrossRef]
- Rao, J.G.; Pradhan, A.K. Power-Swing Detection Using Moving Window Averaging of Current Signals. IEEE Trans. Power Deliv. 2014, 30, 368–376. [Google Scholar] [CrossRef]
- Hinton, G.E.; Osindero, S.; Teh, Y.-W. A Fast Learning Algorithm for Deep Belief Nets. Neural Comput. 2006, 18, 1527–1554. [Google Scholar] [CrossRef]
- Bengio, Y.; Lamblin, P.; Popovici, D.; Larochelle, H. Greedy Layer-wise Training of Deep Networks. In Proceedings of the NIPS’06 Proceedings of the 19th International Conference on Neural Information Processing Systems, Vancouver, BC, Canada, 4–7 December 2006; pp. 153–160.
- Ken, B.; Normann, F.; Casper, L. Considerations for Using Harmonic Blocking and Harmonic Restraint Techniques on Transformer Differential Relays. SEL J. Reliab. Power 2011, 2, 1–17. [Google Scholar]
- Gunda, S.K.; Dhanikonda, V.S.S.S.S. Discrimination of Transformer Inrush Currents and Internal Fault Currents Using Ex-tended Kalman Filter Algorithm (EKF). Energies 2021, 14, 6020. [Google Scholar] [CrossRef]




| Acronym | Unit | Definition |
|---|---|---|
| DW | Data window | |
| DNN | Deep neural network | |
| AE | Autoencoder | |
| SAE | Stacked autoencoder | |
| HAR | Second-harmonic restraint | |
| UNI | Unidirectional index | |
| EKF | Extended Kalman filter | |
| idiff | A | Differential current |
| m | Size of data window | |
| k | Last index of differential current | |
| xnorm | A | Normalized differential current |
| Parameter set model | ||
| Stochastic variable of the output class | ||
| S | Activation function | |
| LAE | Reconstruction loss for AE | |
| L | Softmax loss function | |
| Weight decay |
| Case | Parameters | Value |
|---|---|---|
| Inrush | Switching angle (°) | 0, 10, 20, 30, 40, 50, 60, 70, 80, 90 |
| Residual flux (%) | −80, −70, −60, −50, −40, −30, −20, −10, 0, 10, 20, 30, 40, 50, 60, 70, 80 | |
| Internal fault | Fault inception angle (°) | 0, 10, 20, 30, 40, 50, 60, 70, 80, 90 |
| Winding location (%) | 0, 10, 20, 30, 40, 50, 60, 70, 80 |
| Class | Label | Binary Form |
|---|---|---|
| 0 | Normal condition | 0 0 0 1 |
| 1 | Transient | 0 0 1 0 |
| 2 | Inrush current | 0 1 0 0 |
| 3 | Internal fault | 1 0 0 0 |
| Specification | Parameters | Value | |
|---|---|---|---|
| Source | Positive and Negative | R1, R2 | 0.0419 |
| L1, L2 | 0.8921 | ||
| C1, C2 | 0.0128 | ||
| Zero | R0 | 0.0293 | |
| L0 | 2.6657 | ||
| C0 | 0.0042 | ||
| Transformer 154/23 kV | Positive leakage reactance | %Z | 10.99 |
| Air core reactance | %X | 20 | |
| Magnetizing current | %Im | 1 |
| AE1 | AE2 | AE3 | SoftMax Layer | |
|---|---|---|---|---|
| Neuron | 30 | 18 | 9 | 4 |
| Batch size | 128 | 64 | 64 | 64 |
| Learning rate | 0.001 | 0.0024 | 0.0019 | 0.0159 |
| Method | Case | Accuracy (%) | Sensitivity (%) | Precision (%) | |||
|---|---|---|---|---|---|---|---|
| N–6 | N–3 | N–6 | N–3 | N–6 | N–3 | ||
| HAR | Normal | 100 | 100 | 100 | 100 | 100 | 100 |
| UNI | 100 | 100 | 100 | 100 | 100 | 100 | |
| EKF | 100 | 100 | 100 | 100 | 100 | 100 | |
| DNN | 100 | 100 | 100 | 100 | 100 | 100 | |
| HAR | Inrush | 100 | 100 | 100 | 100 | 100 | 100 |
| UNI | 99.852 | 99.932 | 93.814 | 95.613 | 95.724 | 97.741 | |
| EKF | - | - | - | - | - | - | |
| DNN | 99.526 | 100 | 100 | 100 | 99.523 | 100 | |
| HAR | Internal fault | - | - | - | - | - | - |
| UNI | - | - | - | - | - | - | |
| EKF | 90.513 | 92.364 | 69.192 | 72.951 | 71.231 | 72.367 | |
| DNN | 99.931 | 100 | 100 | 100 | 98.842 | 100 | |
| HAR | Inrush and Internal fault | - | - | - | - | - | - |
| UNI | - | - | - | - | - | - | |
| EKF | 91.103 | 92.136 | 69.583 | 71.369 | 70.124 | 70.364 | |
| DNN | 99.651 | 100 | 99.642 | 100 | 100 | 100 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Key, S.; Son, G.-W.; Nam, S.-R. Deep Learning-Based Algorithm for Internal Fault Detection of Power Transformers during Inrush Current at Distribution Substations. Energies 2024, 17, 963. https://doi.org/10.3390/en17040963
Key S, Son G-W, Nam S-R. Deep Learning-Based Algorithm for Internal Fault Detection of Power Transformers during Inrush Current at Distribution Substations. Energies. 2024; 17(4):963. https://doi.org/10.3390/en17040963
Chicago/Turabian StyleKey, Sopheap, Gyu-Won Son, and Soon-Ryul Nam. 2024. "Deep Learning-Based Algorithm for Internal Fault Detection of Power Transformers during Inrush Current at Distribution Substations" Energies 17, no. 4: 963. https://doi.org/10.3390/en17040963
APA StyleKey, S., Son, G.-W., & Nam, S.-R. (2024). Deep Learning-Based Algorithm for Internal Fault Detection of Power Transformers during Inrush Current at Distribution Substations. Energies, 17(4), 963. https://doi.org/10.3390/en17040963







