An Optimization Control Method of IEH Considering User Thermal Comfort

Abstract

In this paper, a user thermal comfort criterion based on predicted mean vote (PMV) values is introduced to realize the optimal operation of an improved energy hub (IEH) while considering thermal inertia and user thermal behavior. A three-layer optimization model based on user thermal comfort is constructed which fully considers user thermal comfort demand, IEH operating costs, and energy network constraints. Moreover, since IEH optimization considering user thermal comfort is a multi-objective bilevel optimization (MNBO) problem, this paper proposes an improved multilayer nested quantum genetic algorithm (IMNQGA) to solve it. Finally, the effectiveness of the proposed optimization model and algorithm is verified through the analysis of the four modes. The examples show that the proposed optimal control method can reduce the system’s operating costs and improve energy efficiency while satisfying user thermal comfort demand.

1. Introduction

The rapid development of renewable energy technology is gradually reducing human dependence on fossil energy [1]. With the development of technology, a new energy field has appeared, including integrated energy systems (IESs), Energy Internet (EI), and other important concepts, the purpose of which is to realize the goal of an environmentally friendly and sustainable energy supply [2].

An energy hub (EH) is the interface between energy infrastructure, producers, and consumers in an IES [3], which is an important model for analyzing the IES [4]. Currently, scholars at home (China) and abroad have conducted considerable research on EH. One study [5] focused on a regional IES containing an electricity/gas/heat system and improved the EH model by considering the influence of coupled units as balancing nodes on the tidal currents of electricity and natural gas networks. Another study [6] proposed a general modeling method for micro-energy networks and further constructed a multi-objective optimal scheduling model for micro-energy networks based on an EH. Study [7] proposed a model containing cooling/heating/electricity tri-generation and sub-EHs, with this being an important model for analyzing the IES. The authors considered electricity cogeneration and sub-EH structure and built its optimal dispatch model. The authors of [8] proposed a day-ahead dispatch framework for EHs in energy and storage markets and analyzed the risk level of EHs using conditional value-at-risk methodology. Study [9] proposed an optimal operation strategy for multi-EHs so that natural gas can provide EHs with peak power during peak power periods. In another study [10], the authors proposed a multi-EH optimization method based on the alternating direction multiplier method to achieve autonomous decision-making for EHs. The authors of [11] proposed a transaction model for multi-EHs based on blockchain technology and designed a series of algorithms to assign priority to the transactions for it. Another study [12] utilized opportunity constraints on the interaction power of power liaison lines and the transmission power of natural gas pipelines and proposed an optimization method for EH systems based on opportunity constraints. Study [13] proposed hybrid policy-based reinforcement learning adaptive energy management to realize optimal operation for the island group energy system with an energy transmission-constrained environment. The authors of [14] proposed an optimal scheduling framework for the real-time operation of smart microgrids in the IIoT environment using an average consensus-based algorithm. Finally, the authors of study [15] proposed proactive scheduling for the resilience enhancement of microgrids.

In the above studies, the power portion of the adopted EH structures was composed of power transformers and energy storage parts in all cases. The power router (PR), as the basic form of an energy router, is one of the key support devices of the EI [16], which can realize the integration of the electrical physical system and the information system, control and manage its access to power sources and energy storage and loads, and is more flexible for the transmission and distribution of electric energy [17]. If the PR is combined with an EH, it can maximize the use of multiple energy sources such as electricity/gas/heat.

Based on this idea, the authors of [18] first proposed an EH containing a PR, i.e., replacing the electrical part of a conventional EH with a PR, which further facilitates the system’s multi-energy convergence and improves the capability of renewable energy consumption and demand-side response. To provide a better understanding, this paper refers to this as an improved energy hub (IEH) and refines the model.

To solve the energy management problem, the authors of [18] modelled energy storage and flexible electric loads as stochastic processes, the virtual queue concept described was adopted, and three queues were constructed to relax the time coupling constraints of energy storage and flexible electric loads into constraints of queue stability. Study [18] mainly focused its efforts on the energy management of the IEH and mobilizing and coordinating the various energy sources of the IEH in order to achieve economic operation. Due to thermal inertia, there will be time differences in heat and electric power scheduling, which leads to a significant impact of heat user behavior on the optimal control of the IEH. Therefore, compared to study [18], this study introduces user thermal comfort to the process of quantifying the behavior of heat users to more accurately mobilize heat loads in the optimization process of IEHs and to improve the efficiency of energy use, taking into account the system operating costs and the quality of energy use by the users.

In addition, it is notable that the optimal control of an IEH after considering user thermal comfort is a multi-objective bilevel optimization (MOBO) problem. Common solution methods for MOBO include fuzzy methods [19], penalty function methods [20], methods based on Karush–Kuhn–Tucker conditions [21], Pareto frontier generators [22], and metaheuristic approaches [23]. As mathematical programming usually requires strong mathematical assumptions of an optimization problem, e.g., the optimization function needs to have linearity, continuous derivatives [24], convexity, etc., nested methods in metaheuristic approaches have become a major methodology for handling complex MOBO. For an IEH, which is a relatively well-defined shape of the fitness function, the genetic algorithm in metaheuristic approaches can have higher performance compared to other algorithms. The quantum genetic algorithm enriches the diversity of the population, and the searchability of the algorithm is improved, which results in a greater improvement in performance compared to the scripture genetic algorithm [25]. In our study, in the process of the algorithm, a quantum rotating gate adjustment strategy was designed to dynamically adjust the size of the rotating angle of the quantum gate, which further improves efficiency and ensures accuracy to a large extent. Therefore, this paper proposes an improved multilayer nested quantum genetic algorithm.

In summary, the contributions of this paper can be expressed as follows:

• For the specificity of the IEH, user thermal comfort is introduced, which can promote the consumption of renewable energy in the IEH, enhance the efficiency of energy use while taking into account user thermal comfort and system operating costs, and significantly improve the user’s environmental quality.
• A three-layer optimization model based on user thermal comfort is developed. User thermal comfort requirements, IEH operating costs, and energy network constraints are considered in the optimization model.
• To solve the MOBO problem of the IEH, an improved multilayer nested quantum genetic algorithm is proposed. The algorithm has better performance and applicability for an IEH with a complex structure.

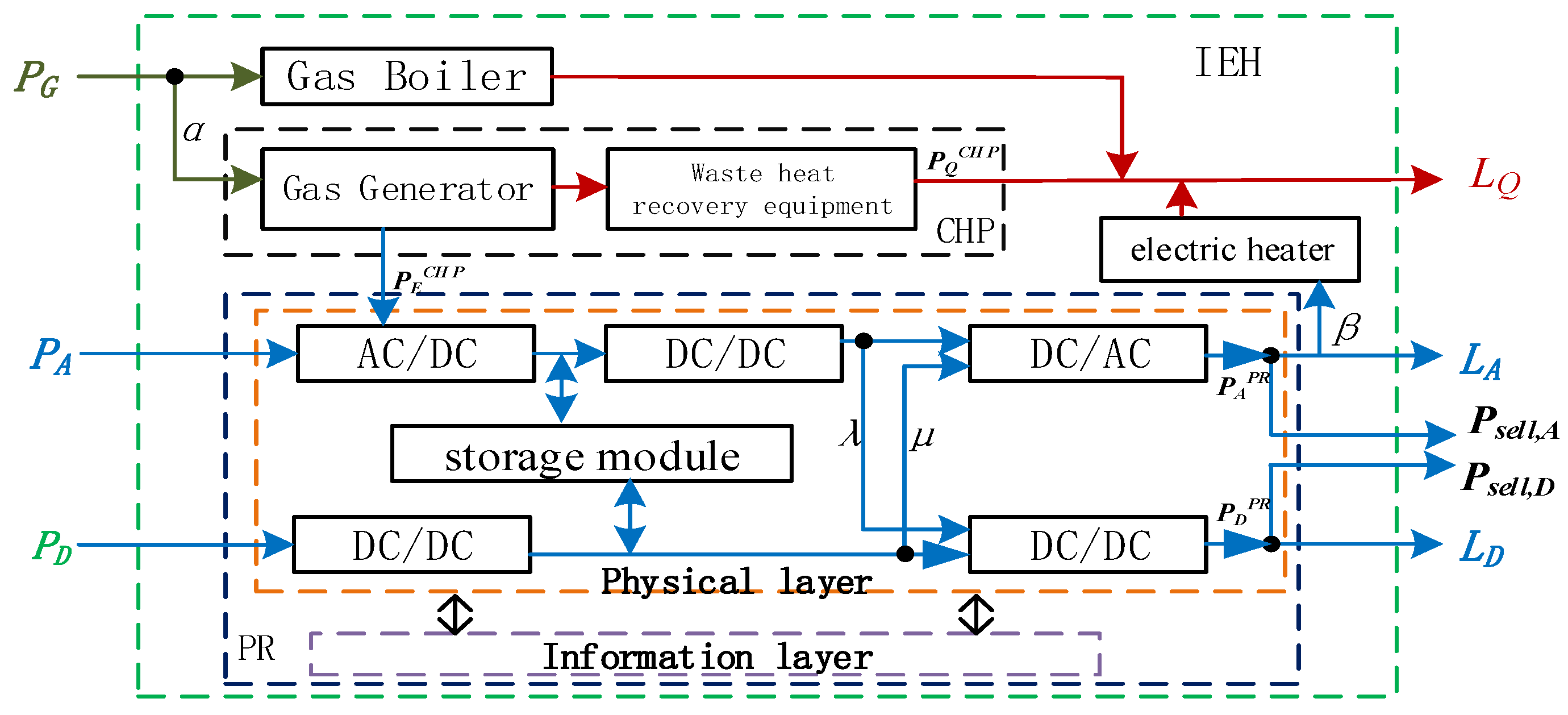
2. Structure of the IEH

Figure 1 shows the structure of the IEH, containing equipment such as a PR, CHP, a converter, and electric heater equipment. The PR contains an information layer and a physical layer. The information layer is mainly responsible for the exchange of information with the outer structure and the control and protection of the PR; the physical layer is mainly responsible for the conversion between AC power and DC power inside the PR.

2.1. Operation Strategy of the PR

Based on the structure of the PR used in this paper, the input–output matrix of this PR can be derived as

$$\left(\begin{array}{l}{P}_A^{PR}\\ P_D^{PR}\end{array}\right)={\eta }_{PR}\left(\begin{array}{cc}{g}_{PR}(1-\lambda )& \mu \\ g_{PR}\lambda & 1-\mu \end{array}\right)\left(\begin{array}{l}{P}_A^{\prime }\\ P_D^{\prime }\end{array}\right)$$

(1)

where $P_A^{\prime }$ and $P_D^{\prime }$ are

$$\{\begin{array}{cc}{P}_A^{\prime }={\eta }_{PR}(P_A+P_E^{CHP})\pm P_{kA}\hfill & (k=c,f)\hfill \\ P_D^{\prime }={\eta }_{PR}{P}_D\pm P_{kD}\hfill & (k=c,f)\hfill \end{array}$$

(2)

Considering the uncertainty of renewable energy source supply, in order to fully utilize renewable energy sources and improve the efficiency of electric energy utilization, this study establishes the operation strategy of the PR under different operating conditions:

(1) Renewable energy sources provide power that can satisfy the demand of electrical load, i.e., ${\eta }_{PR}^2$ P_D ≥ L_D + L_A/(1 − β).

At this time, P_A = 0. If the storage module is in charging mode, the charging power P_cA is

$$\{\begin{array}{cc}{P}_{cA}=P_{c\max }\hfill & ({\eta }_{PR}{P}_E^{CHP}\ge P_{c\max })\hfill \\ P_{cA}={\eta }_{PR}{P}_E^{CHP}\hfill & (P_{c\min }\le {\eta }_{PR}{P}_E^{CHP}<P_{c\max })\hfill \\ P_{cA}=0\hfill & ({\eta }_{PR}{P}_E^{CHP}<P_{c\min })\hfill \end{array}$$

(3)

The charging power P_cD is

$$\{\begin{array}{cc}{P}_{cD}=P_{c\max }\hfill & ({\eta }_{PR}^2{P}_D-(\frac{L_A}{1-\beta }+L_D)\ge P_{c\max })\hfill \\ P_{cD}={\eta }_{PR}^2{P}_D-(\frac{L_A}{1-\beta }+L_D)\hfill & (P_{c\min }\le {\eta }_{PR}^2{P}_D-(\frac{L_A}{1-\beta }+L_D)<P_{c\max })\hfill \\ P_{cD}=0\hfill & ({\eta }_{PR}^2{P}_D-(\frac{L_A}{1-\beta }+L_D)<P_{c\min })\hfill \end{array}$$

(4)

If the storage module is in discharge mode, the discharge power P_fi = P_fmin(i = A, D).

(2) The sum of the power provided by the renewable energy sources and the power provided by the CHP can satisfy the demand of electric load, i.e., ${\eta }_{PR}^2$ (P_D + g_PR $P_E^{CHP}$) ≥ L_D + L_A/(1 − β).

At this time, P_A = 0. If the storage module is in charging mode, the charging power P_ci is

$$\{\begin{array}{cc}{P}_{cA}=P_{c\max },P_{cD}=0\hfill & ({\eta }_{PR}{P}_D<P_{c\min })\hfill \\ P_{cA}=0,P_{cD}=P_{c\max }\hfill & ({\eta }_{PR}{P}_E^{CHP}<P_{c\min })\hfill \\ P_{cA}=P_{c\max },P_{cD}={\eta }_{PR}{P}_D\hfill & (P_{c\min }\le {\eta }_{PR}{P}_D<P_{c\max })\hfill \\ P_{cA}={\eta }_{PR}{P}_E^{CHP},P_{cD}=P_{c\max }\hfill & (P_{c\min }\le {\eta }_{PR}{P}_E^{CHP}<P_{c\max })\hfill \\ P_{cA}=P_{c\max },P_{cD}=P_{c\max }\hfill & ({\eta }_{PR}{P}_D,{\eta }_{PR}{P}_E^{CHP}\ge P_{c\max })\hfill \end{array}$$

(5)

If the storage module is in discharge mode, the discharge power P_fi = P_fmin (i = A, D).

(3) The sum of the power provided by the renewable energy sources and the power provided by the CHP is not sufficient to satisfy the demand of electric load, i.e., ${\eta }_{PR}^2$(P_D + g_PR $P_E^{CHP}$) < L_D + L_A/(1 − β).

At this time, if the storage module is in charging mode, the charging power P_ci and P_A are

$$\{\begin{array}{cc}{P}_{cA}=P_{c\max },P_{cD}=0\hfill & ({\eta }_{PR}{P}_D<P_{c\min })\hfill \\ P_{cA}=0,P_{cD}=P_{c\max }\hfill & ({\eta }_{PR}(P_A+P_E^{CHP})<P_{c\min })\hfill \\ P_{cA}=P_{c\max },P_{cD}={\eta }_{PR}{P}_D\hfill & (P_{c\min }\le {\eta }_{PR}{P}_D<P_{c\max })\hfill \\ P_{cA}={\eta }_{PR}(P_A+P_E^{CHP}),P_{cD}=P_{c\max }\hfill & (P_{c\min }\le {\eta }_{PR}(P_A+P_E^{CHP})<P_{c\max })\hfill \\ P_{cA}=P_{c\max },P_{cD}=P_{c\max }\hfill & ({\eta }_{PR}{P}_D,{\eta }_{PR}(P_A+P_E^{CHP})\ge P_{c\max })\hfill \end{array}$$

(6)

$$P_A\ge [(\frac{L_A}{1-\beta }+L_D)-{\eta }_{PR}^2(P_D+g_{PR}{P}_E^{CHP})+{\eta }_{PR}(g_{PR}{P}_{cA}+P_{cD})]/{\eta }_{PR}^2{g}_{PR}$$

(7)

If the storage module is in discharge mode, the discharge power P_fi = P_fmax (i = A, D) and P_A is

$$P_A\ge [(\frac{L_A}{1-\beta }+L_D)-{\eta }_{PR}^2(P_D+g_{PR}{P}_E^{CHP})-{\eta }_{PR}(g_{PR}{P}_{fA}+P_{fD})]/{\eta }_{PR}^2{g}_{PR}$$

(8)

2.2. Energy Conversion Model

Based on the IEH structure and the PR operation strategy proposed above, the energy conversion matrix of this IEH can be established based on the equivalence of the cooling loads to the superposition of the thermal and electric loads:

$$\left(\begin{array}{c}{L}_Q\\ L_A\\ L_D\end{array}\right)=\left(\begin{array}{ccc}(1-\alpha ){\eta }_{GB}+\alpha {\eta }_Q^{CHP}& \beta {\eta }_{eh}& 0\\ 0& (1-\beta )& 0\\ 0& 0& 1\end{array}\right)\left(\begin{array}{c}{P}_G\\ P_A^{PR}-P_{sell,A}\\ P_D^{PR}-P_{sell,D}\end{array}\right)$$

(9)

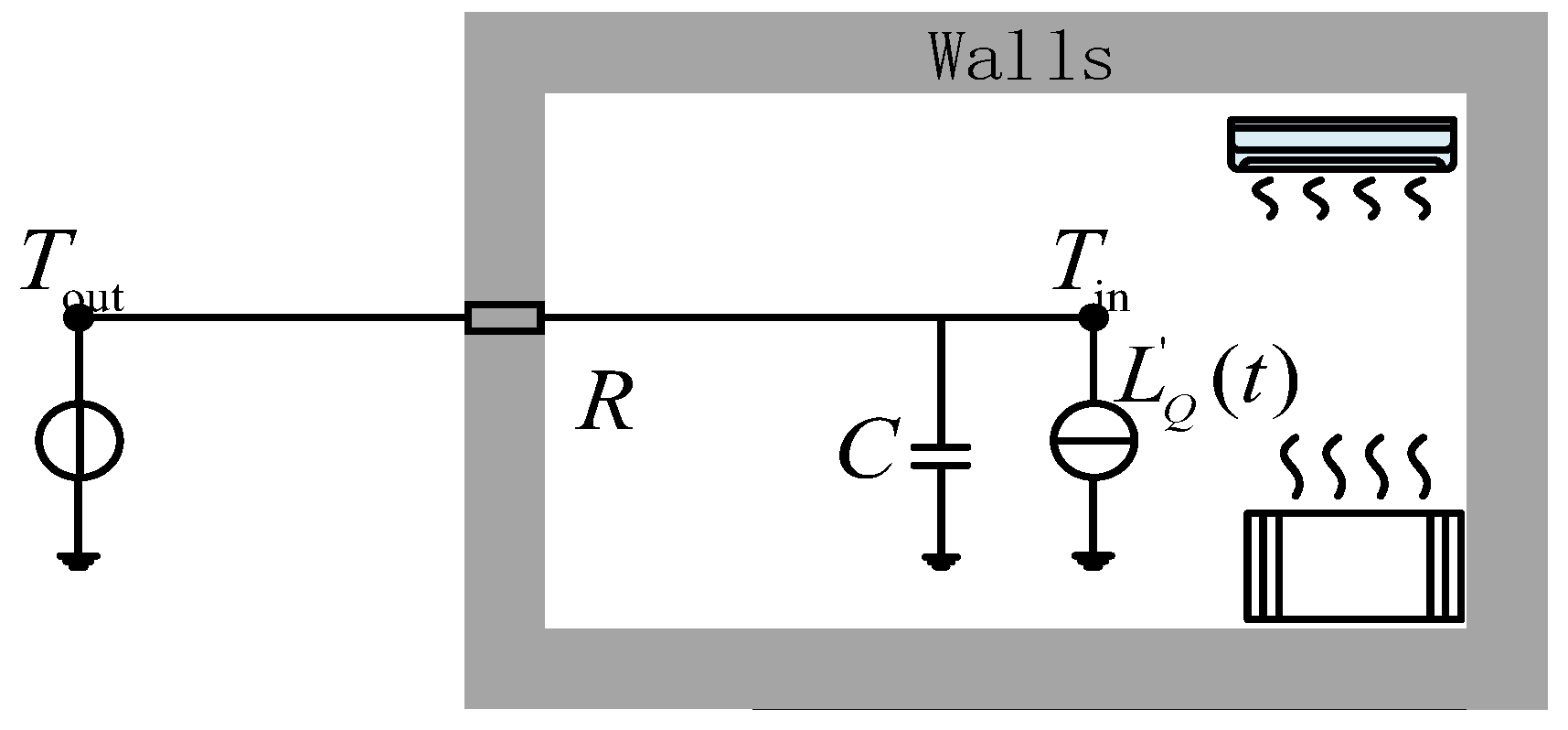
3. The Model of User Thermal Comfort

Currently, there are more studies on modeling related to human thermal comfort, including thermal sensory vote (TSV), standard effective temperature (SET), physiological equivalent temperature (PET), universal thermal climate index (UTCI), PMV value, etc. [26,27,28]. Since the TSV index mainly refers to the user’s subjective voting, the SET index does not consider “cold”, and the PET and the UTCI index are more focused on measuring thermal comfort in the outdoor area. In contrast, the PMV value developed by Fanger [29] and standardized in ASHRAE55 [30] establishes the relationship between the thermal load on the body and the statistical thermal sensation obtained from numerous people, which can better quantify the thermal comfort of the body indoors and has thus been adopted by the majority of studies. This study focuses on users’ indoor thermal comfort sensations. In summary, PMV values were chosen to model user thermal comfort in this study.

The PMV value is a comprehensive index used to evaluate the thermal comfort standard based on the equation of the human body’s heat balance state and considering human physiology, psychology, and other factors. The PMV value represents the average index of the population vote on seven levels of thermal sensation. A PMV value of 0 indicates moderate temperature, a PMV value of −1, −2, or −3 indicates slightly cool, cool, or cold, respectively, and a PMV value of +1, +2, or +3 indicates slightly warm, warm, or hot, respectively. The PMV value can be calculated using the following formula [31]:

$$V_{PMV}=\{\begin{array}{l}0.3895(T_{in,t}-T_0),T_{in,t}\ge T_0\\ 0.4065(T_{in,t}-T_0),T_{in,t}<T_0\end{array}$$

(10)

where a PMV value between −1 and +1 is the comfort zone, and the corresponding indoor temperature is within the range of 23.54 °C and 28.57 °C. The closer the PMV value is to 0, the more comfortable the user is.

From Equation (10), it is clear that PMV values are mainly influenced by indoor temperature. Due to the thermal inertia of the building, the indoor temperature variation is mainly influenced by the heat load, outdoor temperature, and building parameters. The lumped-parameter equivalent model of the indoor temperature change process is shown in Appendix A, Figure A1.

The equation describing the indoor temperature change process can be obtained by listing the transient KCL equation for the equivalent model as

$$C\frac{\mathrm{d}{T}_{\mathrm{in}}(t)}{\mathrm{d}t}=L_Q^{\prime }(t)+\frac{T_{\mathrm{in}}(t)-T_{out}(t)}{R}$$

(11)

The discretization is obtained by discretizing it:

$$\begin{array}{c}{T}_{in,t+1}=T_{in,t}{e}^{-\frac{\Delta t}{\tau }}+(R{L}_Q^{\prime }(t)+T_{out,t})(1-e^{-\frac{\Delta t}{\tau }})\\ \tau =RC\end{array}$$

(12)

From Figure 1, the building heat load $L_Q^{\prime }(t)$ at time t consists of two parts: the output of the CHP and the output of the electric to thermal equipment, i.e.,

$$L_Q^{\prime }(t)=P_Q^{CHP}(t)+(\frac{\beta }{1-\beta }){\eta }_{eh}{L}_A(t)$$

(13)

Therefore, the indoor temperature of the building at time t + 1 is

$$T_{in,t+1}=T_{in,t}{e}^{-\frac{\Delta t}{\tau }}+[R(P_Q^{CHP}(t)+\frac{\beta }{1-\beta }{\eta }_{eh}{L}_A(t))+T_{out,t}](1-e^{-\frac{\Delta t}{\tau }})$$

(14)

4. Optimization Model

The matrix form of the energy conversion model of the EH can be simplified as L = T_(α,β)P; the input–output matrix of the PR can be simplified as P^PR = T_(λ,μ)P. Thus, the fundamental aim of the optimization model is to find the optimal conversion matrices T_(α,β) and T_(λ,μ).

When the EH is optimized, the EH can be optimized as a whole, which means that the coupling relationship of the internal devices does not need to be considered. Thus, the optimal matrix T can be easily found, whereas in the optimization of the IEH proposed in this paper, the outputs $P_A^{PR}$ and $P_D^{PR}$ of the PR need to be solved first. If the outputs $P_A^{PR}$ and $P_D^{PR}$ are wanted, the α and β parameters need to be determined. The β parameter is mainly determined by user thermal comfort. In the optimization, it can be seen that not only should the coupling relationship of each device in the IEH be considered, but also the influence of user behavior on it. Therefore, this study proposes a three-layer optimization model, which comprises a user thermal comfort layer, a PR optimization layer, and an EH optimization layer. The optimization model used is shown in Figure A2 in Appendix A.

In optimization, firstly, we generate n α_i; secondly, the user thermal comfort layer calculates the optimal solution β_i corresponding to α_i based on the thermal load data and α_i; afterward, the PR optimization layer uses n groups (α_i, β_i) to output the optimal solution (λ_i, μ_i) corresponding to each group (α_i, β_i) according to its objective function; lastly, the EH optimization layer calculates the optimal group (α, β, λ, μ) according to the n groups (α_i, β_i, λ_i, μ_i) outputted from the PR optimization layer.

4.1. User Thermal Comfort Layer

The user thermal comfort layer has the objective of satisfying user thermal comfort. Therefore, the objective function of the user thermal comfort layer is

$$\min F({\beta }_2)=\left|V_{PMV}(L_Q(t),L_A(t))\right|$$

(15)

where V_PMV (L_Q(t), L_A(t)) is the user thermal comfort value at time t. After taking the absolute value of the thermal comfort value, its value domain is [0, +∞]; from the above, it can be seen that the thermal comfort value is closer to 0 the more comfortable the user is, so we took its minimum value.

4.2. EH Optimization Layer

The EH optimization layer aims to minimize the overall system operating costs. The system operating costs include the integrated operating cost C(t) and the pollutant emission cost P(t). The decision variables for this objective function are α and β.

$$\min F(\alpha ,\beta )={\displaystyle \sum _{t}C(t)}+{\displaystyle \sum _{t}P(t)}$$

(16)

The integrated operating cost C(t) takes into account the cost of purchased energy C₁ and the cost of energy substitution C_DR, i.e., C = C₁ + C_DR.

$$C_1(t)=\frac{P_G(t)}{Q_{gas}}{\phi }_t^G+P_A(t){\phi }_t^A$$

(17)

where the right side of the equation comprises the cost of purchased gas and the cost of purchased electricity, respectively.

$$C_{DR}(t)=\alpha \frac{P_G(t)}{Q_{gas}}{\phi }_t^G({\eta }_{GB}-{\eta }_Q^{CHP})-P_E^{CHP}(t){\phi }_t^A+\beta (P_A^{PR}(t)-P_{sell,A})(q_t^A-q_t^Q)$$

(18)

where C_DR(t) is the cost of energy substitution, including the cost of CHP heat and electricity substitution and the cost of electricity to heat.

$$P_P(t)=P_Q^{GB}(t)C_{GB}+P_E^{CHP}(t)C_{CHP}+P_A(t)C_A+P_D(t)C_D$$

(19)

4.3. PR Optimization Layer

The PR optimization layer has the objective of maximizing the revenue of the PR. The PR revenue includes the cost of electricity sold C_sell(t), the cost of batteries C_bat(t), and the cost of electricity purchased C_buy(t). The decision variables are λ, μ, and P_A(t). We define the objective function using:

$$\max F(\lambda ,\mu ,P_A(t))=y(t)$$

(20)

where y(t) = C_sell(t) − C_bat(t) − C_buy(t). The objective function varies according to the operating conditions of the PR:

• If the PR is in operating condition 1 or 2 at time t, then y(t) = C_sell(t) − C_bat(t).
• If the PR is in operating condition 3 at time t, then y(t) = C_sell(t) − C_bat(t) − C_buy(t).

The cost of electricity sold in the PR optimization layer C_sell(t) is

$$C_{sell}(t)=P_{sell.A}(t){\nu }_t^A+P_{sell.D}(t){\nu }_t^D$$

(21)

With reference to study [18] in the battery cost calculation method, the operating cost of battery t hours can be obtained as

$$C_{bat}(t)=\frac{\left|\Delta W_{bat}(t)\right|C_B}{2N\times W_B}$$

(22)

where ΔW_B(t) is the loss at the moment of t (ΔW_bat(t) = η_bP_ci(i = A, D) in charging mode and ΔW_bat(t) = P_ci/η_b(i = A, D) in discharging mode). The charging and discharging states of the energy storage device are controllable when the charging and discharging constraints are satisfied.

The cost of power purchase C_buy(t) in the PR optimization layer is

$$C_{buy}(t)=P_A(t){\phi }_t^A$$

(23)

4.4. Constraints

(1) Charge/discharge constraints

The storage module charging and discharging power cannot exceed its minimum and maximum values, i.e.,

$$P_{c\min }\le P_{ci}\le P_{c\max }$$

(24)

$$P_{f\min }\le P_{fi}\le P_{f\max }$$

(25)

At the same time, the storage module can only run in one mode, i.e.,

$$P_{ci}(t)P_{fi}(t)=0$$

(26)

At time t, the storage module charges E_ci(t) = η P_bci(t) and discharges E_fi(t) = P_fi(t)/η_b.

(2) Charge state constraints

$${SOC}_{\min }\le SOC\le {SOC}_{\max }$$

(27)

The energy storage capacity E(t) of the storage module at time t is satisfied:

$$E_{\min }\le E(t)\le E_{\max }$$

(28)

and the energy storage capacity E(t + 1) at time t + 1 is satisfied:

$$E(t+1)=E(t)+(E_{cA}(t)+E_{cD}(t))-(E_{fA}(t)+E_{fD}(t))$$

(29)

(3) Renewable energy constraints

In this study, for renewable energy generation, mainly photovoltaic power generation and wind power generation, there is only active power, and all of them are controlled by maximum power tracking. Their operating power constraints are

$$\{\begin{array}{l}{P}_{pv\min }\le P_{pv}\le P_{pv\max }\\ P_{wt\min }\le P_{wt}\le P_{wt\max }\end{array}$$

(30)

(4) Energy network constraints

The minimum and maximum constraints for the CHP and gas boiler treatments are based on the unit characteristics, respectively:

$$\{\begin{array}{l}0\le P_E^{CHP}\le P_{E.\max }^{CHP}\\ 0\le P_Q^{CHP}\le P_{Q.\max }^{CHP}\end{array}$$

(31)

$$0\le P_Q^{GB}\le P_{Q.\max }^{GB}$$

(32)

In order to minimize the impact of IEHs on the regional grid, the electricity market specifies that power purchases must be within a certain range and also that power purchases need to satisfy the transmission capacity constraints of the equipment involved.

Similarly, the natural gas purchased from the natural gas grid and the electricity sold are also within a determined range and satisfy the transmission capacity constraints of the equipment.

$$\{\begin{array}{l}0\le P_A(t)\le P_{A\max }\\ 0\le P_A(t)\le P_{At\max }\end{array}$$

(33)

$$\{\begin{array}{l}0\le P_G(t)\le P_{G\max }\\ 0\le P_G(t)\le P_{Gt\max }\end{array}$$

(34)

$$\{\begin{array}{l}0\le P_{sell.A}\le P_{sell.A\max }\\ 0\le P_{sell.D}\le P_{sell.D\max }\end{array}$$

(35)

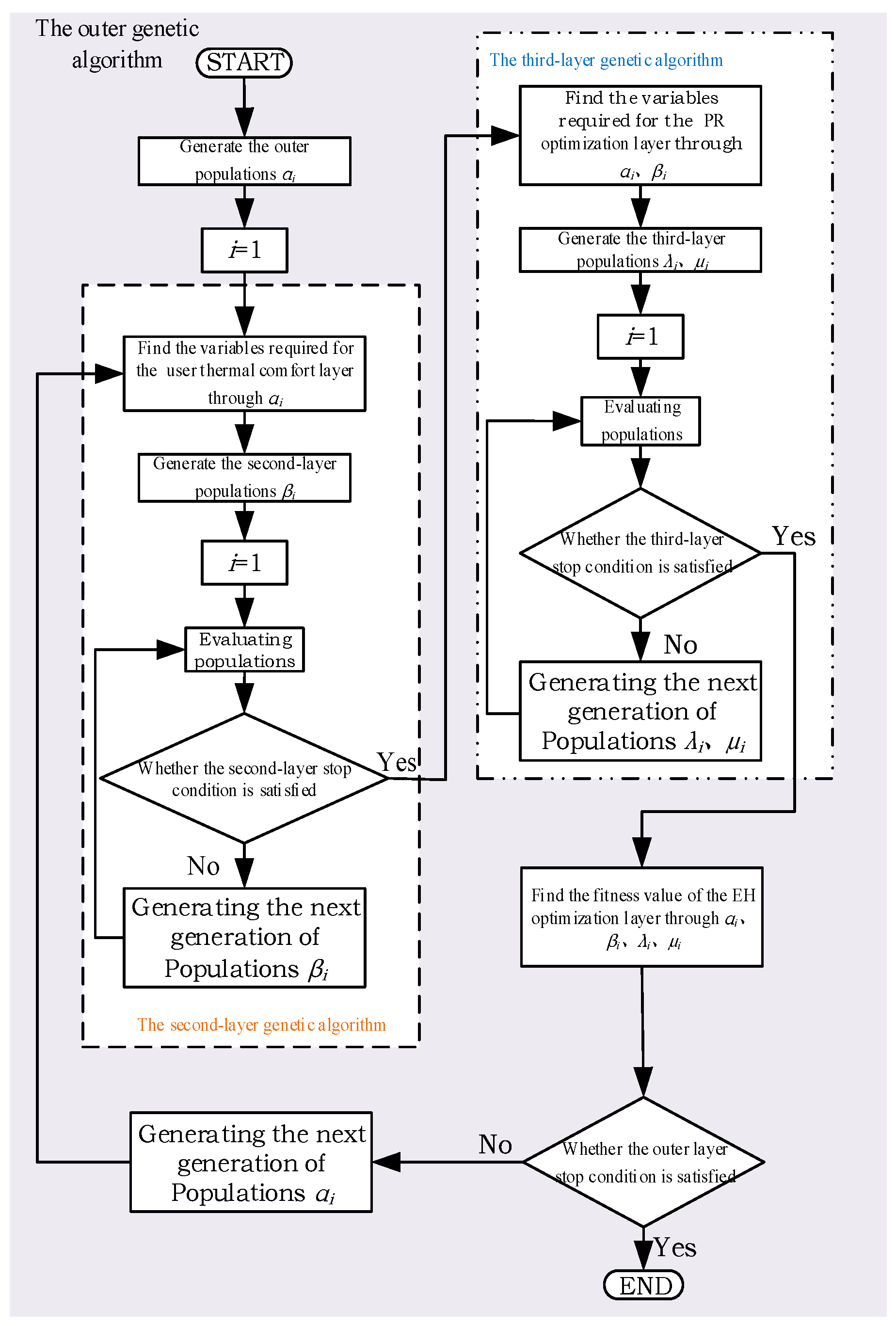
5. Algorithm Flow

This study proposes an improved multi-layer nested quantum genetic algorithm (IMNQGA) to solve this objective function, and the flow chart of the algorithm is shown in Figure 2. In this algorithm, the second-layer genetic algorithm aims to find the optimal β of the user thermal comfort layer; the third-layer genetic algorithm aims to find the optimal λ and μ of the PR optimization layer; and the outer genetic algorithm calculates the optimal solution of the EH optimization layer based on the values of β, λ, and μ obtained by the inner two-layer algorithm. These three layers of the genetic algorithm are articulated and corrected by the constraints and the internal logic of the model, and then the overall optimal solution is obtained.

In addition, the algorithm is a nesting of three layers of genetic algorithms, and the amount of computation and complexity is exponentially more that of an ordinary genetic algorithm. Therefore, in order to reduce the number of calculations and save time, we used the active detection stopping method. When the running cost of the EH optimization layer reaches a certain range or remains unchanged for a long time, it can be considered that the algorithm has found the optimal solution and stops the calculation [32].

6. Example Analysis

In this study, we selected the typical daily data of an apartment complex in Hebei Province during winter as the research object.

The heat loads, AC loads, DC loads, and renewable energy sources that provide power profiles for this apartment complex are shown in Figure 3.

The time-of-use electricity price and other parameter settings in the model were determined with reference to [18,33], and the specific values are shown in

Table 1. Time-of-use electricity price parameters.

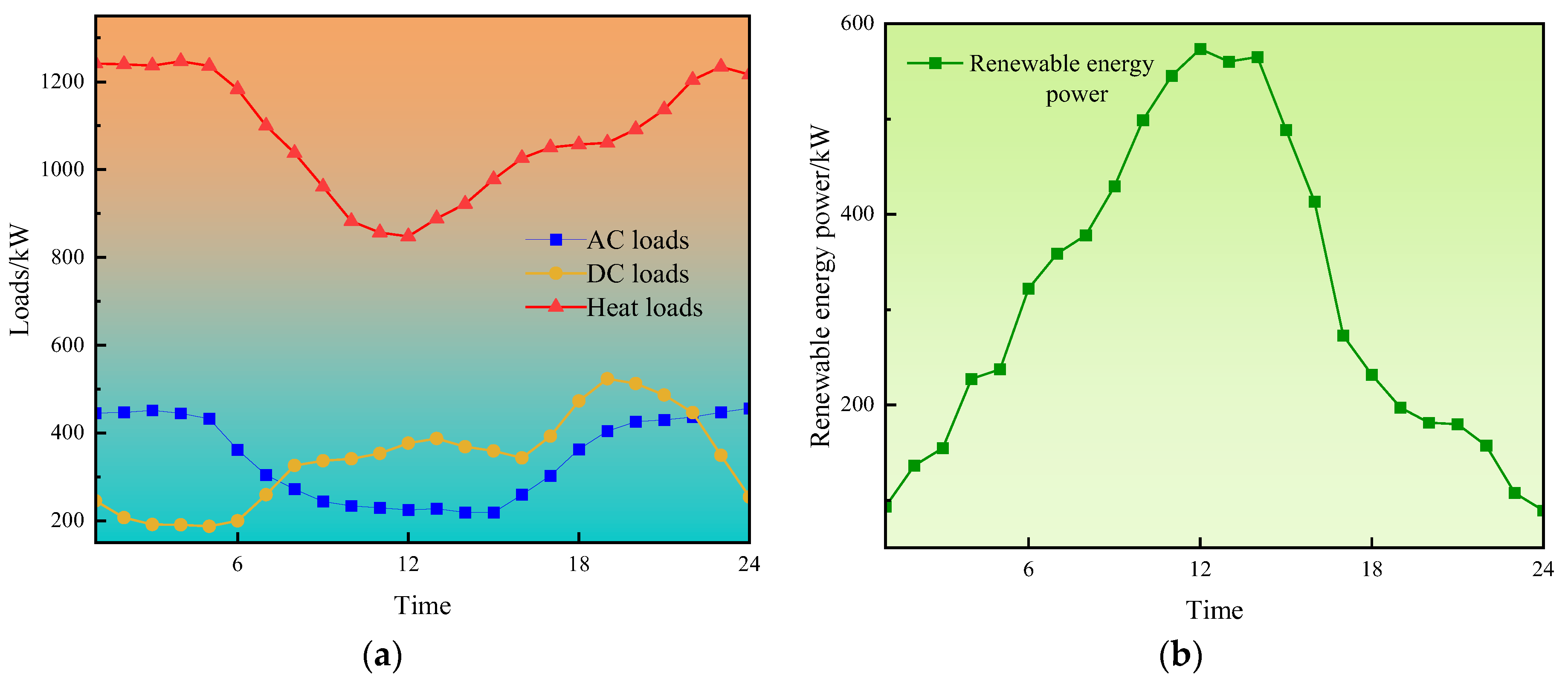
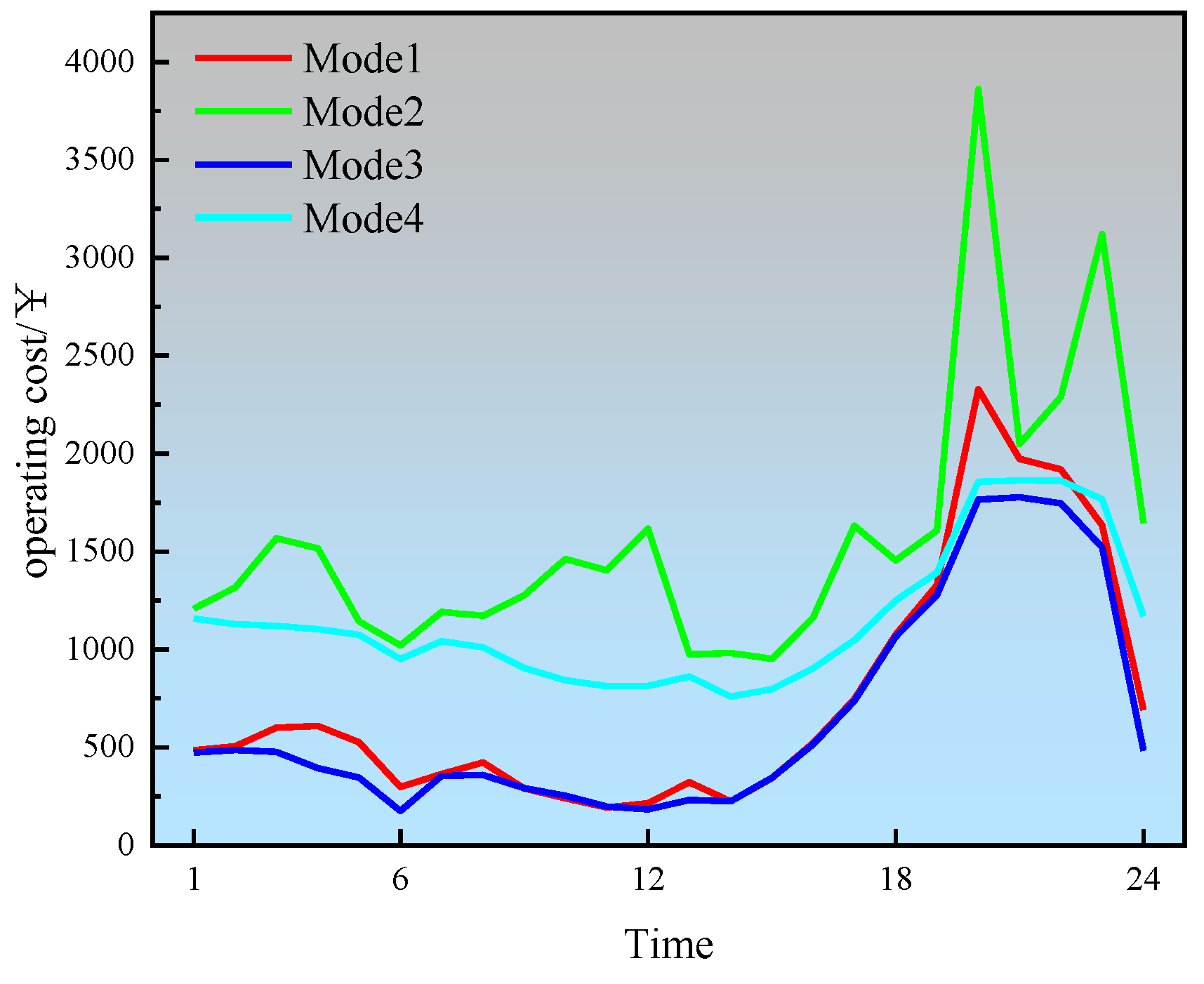
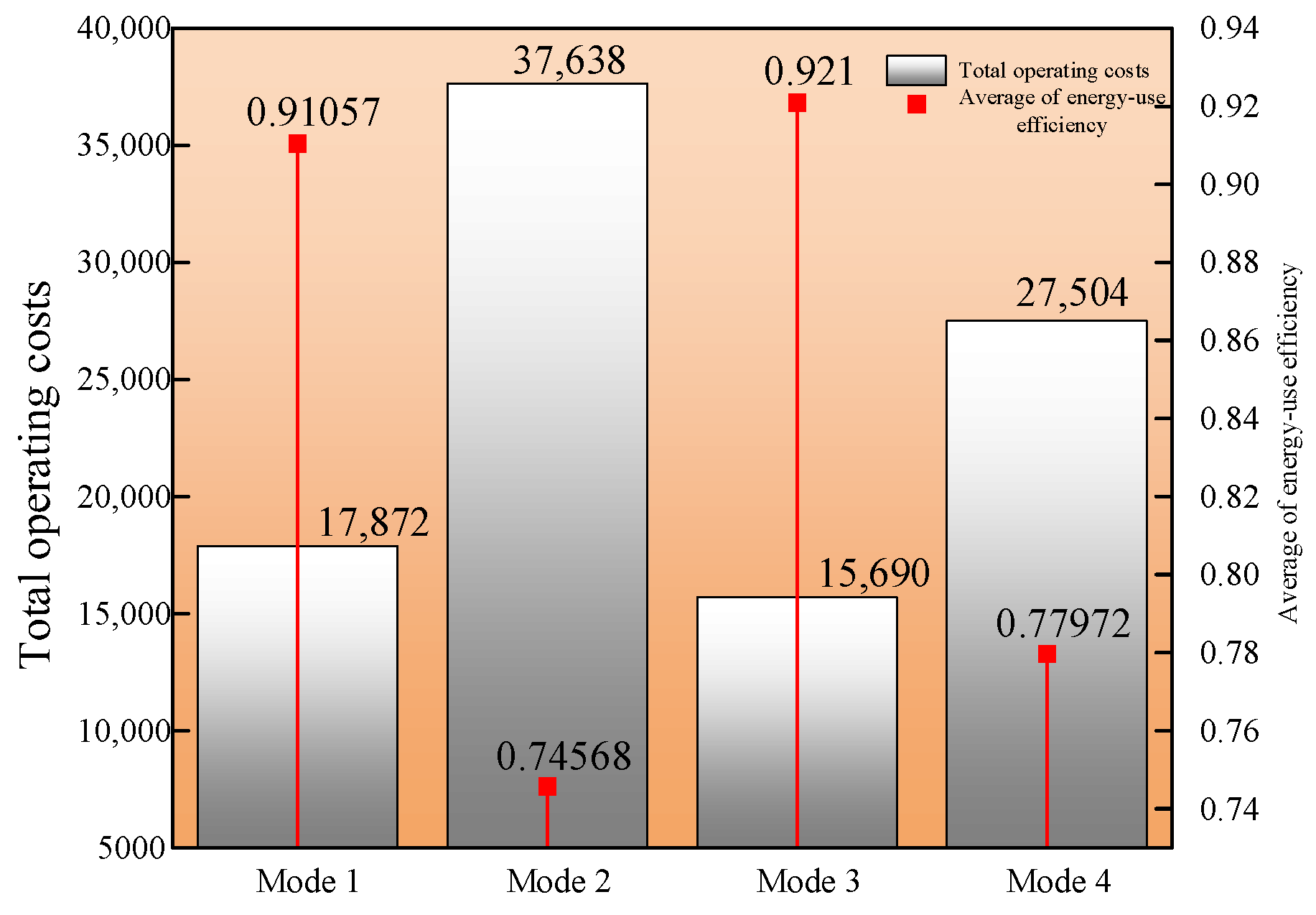
Price of Electricity	Time	CNY/kWh
Time-sharing tariff	1:00–5:00, 23:00–24:00	0.5
	13:00–18:00	0.73
	6:00–12:00, 19:00–22:00	1.21

and

Table 2. Parameter settings.

Parameters	Value	Parameters	Value
ηPR	0.984	CGB	0.107 CNY/kWh
gPR	0.968	CCHP	0.018 CNY/kWh
ηGB	0.916	CA	0.197 CNY/kWh
ηeh	0.45	CD	0.156 CNY/kWh
${\eta }_Q^{CHP}$	0.897	$P_{Emax}^{CHP}$	500 kW
${\eta }_E^{CHP}$	0.36	$P_{Qmax}^{CHP}$	500 kW
ηb	0.9

.

In order to verify the effectiveness of the model, four operational models were constructed for comparison as follows.

Mode 1: Considering user thermal comfort, the parameters α, β, λ, and μ are optimized once per operating period within 24 h using the IEH structure and applying the optimization model proposed in the paper.

Mode 2: Considering user thermal comfort, a conventional EH structure is used, and the structure is shown in Figure A3 in Appendix A. The matrix form of its energy conversion model is:

$$\left[\begin{array}{c}{L}_Q\\ L_E\end{array}\right]=\left[\begin{array}{cc}(1-\alpha ){\eta }_{GB}+\alpha {\eta }_Q^{CHP}+\alpha \beta {\eta }_E^{CHP}& \beta \\ \alpha (1-\beta ){\eta }_E^{CHP}& 1-\beta \end{array}\right]\left[\begin{array}{c}{P}_G\\ P_E\end{array}\right]$$

(36)

where L_E is the electrical load, which is the total load of the AC and DC, i.e., L_E = L_A + η_ADL_D; η_AD is the AC/DC load conversion factor; P_E is the power provided by electricity, which is the total power provided by renewable energy sources when they are integrated into the AC grid, i.e., P_E = P_A + η_DAP_D; and η_DA is the loss coefficient of renewable energy sources when they are integrated into the power grid.

Since the structure of Mode 2 does not contain the PR, the optimization model used in Mode 2 does not contain the PR optimization layer, i.e., the EH optimization layer optimizes the primary parameters α and β through the β output of the user thermal comfort layer for each operation period within the 24 h period.

Mode 3: User thermal comfort is not considered, i.e., β = 0, the optimization model does not include the user thermal comfort layer, and the parameters α, λ, and μ are optimized once for each operation period within 24 h, and the other settings are the same as in Mode 1.

Mode 4: On the basis of Mode 2, user thermal comfort is not considered, i.e., only the operating cost objective of the EH optimization layer needs to be considered in the optimization, and the parameter α is optimized once for each operating period within 24 h, and the other settings are the same as in Mode 2.

The algorithm proposed in this paper is used to solve the above four modes. The changes in the parameters of α, β, λ, and μ of the four modes within 24 h of optimization are shown in Figure 4. The PMV values and operating cost results obtained after optimization are shown in Figure 5 and Figure 6.

As can be seen in Figure 5 and Figure 6, the operating cost of the system with the IEH structure proposed in this paper is significantly reduced. After considering user thermal comfort, the system operating costs show a slight increase, but the PMV values can be overwhelmingly controlled in the range of [−1, 1] and mostly in the range of [−0.5, 0.5], which significantly improves user thermal comfort.

To further verify the validity and feasibility of the model proposed in this paper, the system energy-use efficiency metric E_f = (L_Q + L_A + L_D)/(G + P_A + P_D), i.e., the ratio of total output to input, is defined. The results of the operation in the four modes are organized to obtain the energy-use efficiency curves for each mode, as shown in Figure 7.

In Figure 7, it can be seen that the energy-use efficiency of Mode 1 and Mode 3 is higher than that of Mode 2 and Mode 4, i.e., the adoption of the IEH structure proposed in this paper can enhance the energy-use efficiency of the system and promote the consumption of renewable energy, which is valuable for the study of enhancing the energy efficiency of the system for the utilization of multi-energy complementarity.

The total value of operating costs, the average value of energy-use efficiency, and the mean and standard deviation of user thermal comfort in the four models were further compared, and the results are shown in Figure 8 and Figure 9.

We combine Figure 5, Figure 6, Figure 7, Figure 8 and Figure 9 and compare the differences between the four mode shown. The following conclusions can be drawn. As shown in

Table 3. Comparison summary table of the operation results for the four modes.

√: Better Than; ×: Worse Than; ⚪: About the Same as		Mode 2	Mode 3	Mode 4
Mode 1	Operating cost	√	×	√
	Energy-use efficiency	√	⚪	√
	User thermal comfort	⚪	√	√
Mode 2	Operating cost		×	×
	Energy-use efficiency		×	⚪
	User thermal comfort		√	√
Mode 3	Operating cost			√
	Energy-use efficiency			√
	User thermal comfort			⚪

.

From this table, it can be seen that adopting the IEH structure proposed in this paper can reduce the system’s operating costs and improve the system’s energy-use efficiency; considering user thermal comfort will increase the system’s operating costs, but it can significantly improve user thermal comfort; and by considering user thermal comfort and adopting the IEH structure of the system compared with the conventional EH system that does not consider user thermal comfort, the operating costs can be reduced while keeping user thermal comfort within the comfortable range and improving the energy-use efficiency of the system.

7. Conclusions

This paper introduces user thermal comfort on the basis of the proposed IEH structure; provides an optimization model considering user thermal comfort, system operating costs, and PR revenue; and proposes an improved multi-layer nested quantum genetic algorithm to solve the problem. Finally, a real IES is used as an arithmetic example, which is verified using research results and historical operation data, and the main conclusions are as follows:

(1) The IEH structure replaces the electrical part of the conventional EH with the PR, which further enhances the multi-energy utilization efficiency of the EH, effectively promotes the consumption of renewable energy sources, reduces the system operating costs, and enhances the energy-use efficiency.

(2) The optimization control method proposed in this paper introduces user thermal comfort. From the analysis of other examples, it can be seen that user thermal comfort can be used to describe the thermal inertia problem of heat load and the behavior of heat users. The proposed method can balance user thermal comfort and the system operating costs, which significantly improves the user’s environmental quality.

In addition, although the IMQGA proposed in this study can effectively solve the optimization problem, it still suffers from the problems of long running time and a high number of iterations. Therefore, the direction of our future work is to investigate a more efficient algorithm applicable to IEHs.