A Contactless Coupled Pendulum and Piezoelectric Wave Energy Harvester: Model and Experiment
Abstract
1. Introduction
2. Methodology
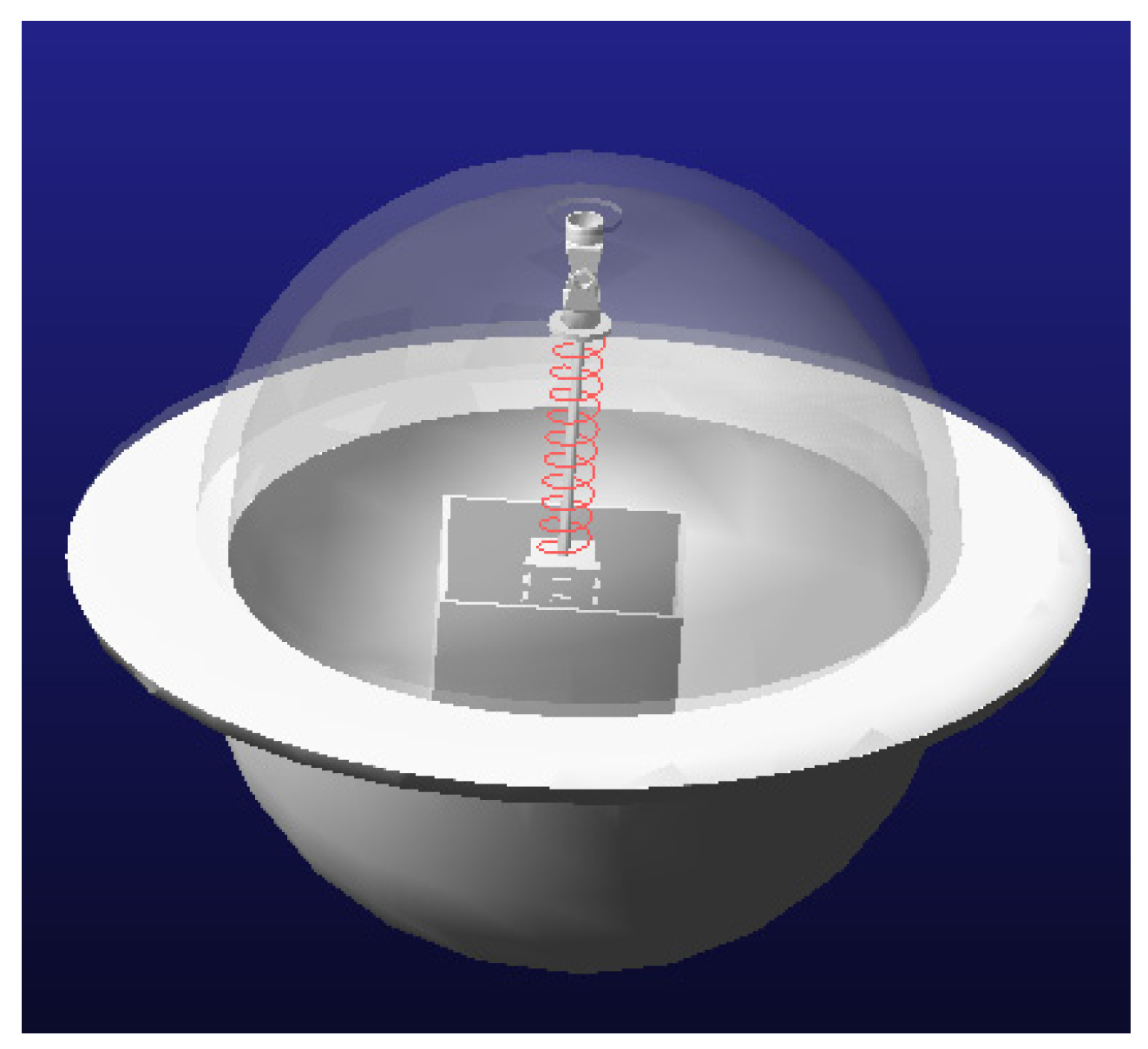
2.1. Structural Design of the Device and Principle of Operation
2.2. WEC Operation
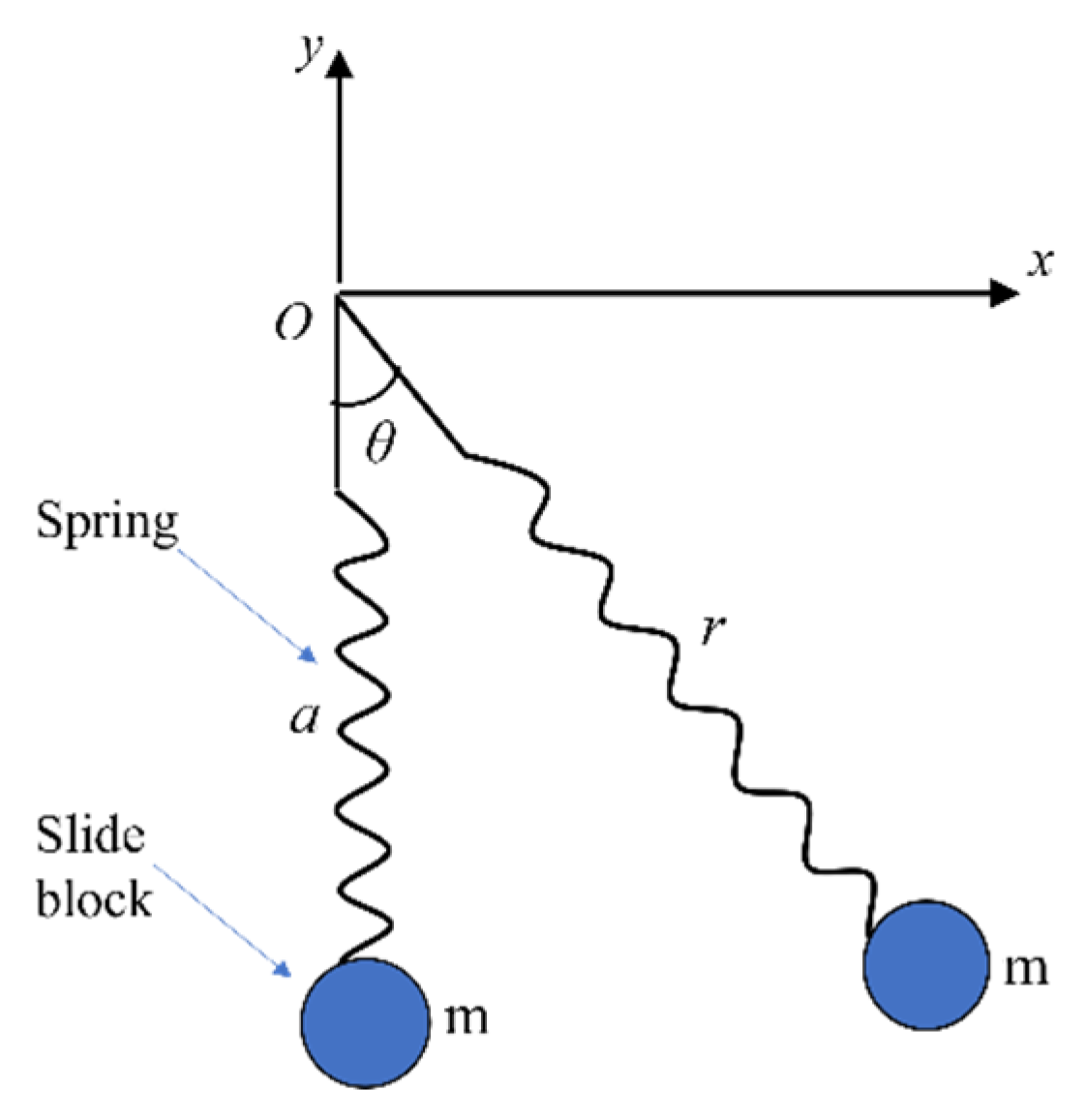
2.3. Governing Equations
2.3.1. Inner pendulum
2.3.2. Spring Pendulum
3. Model Results
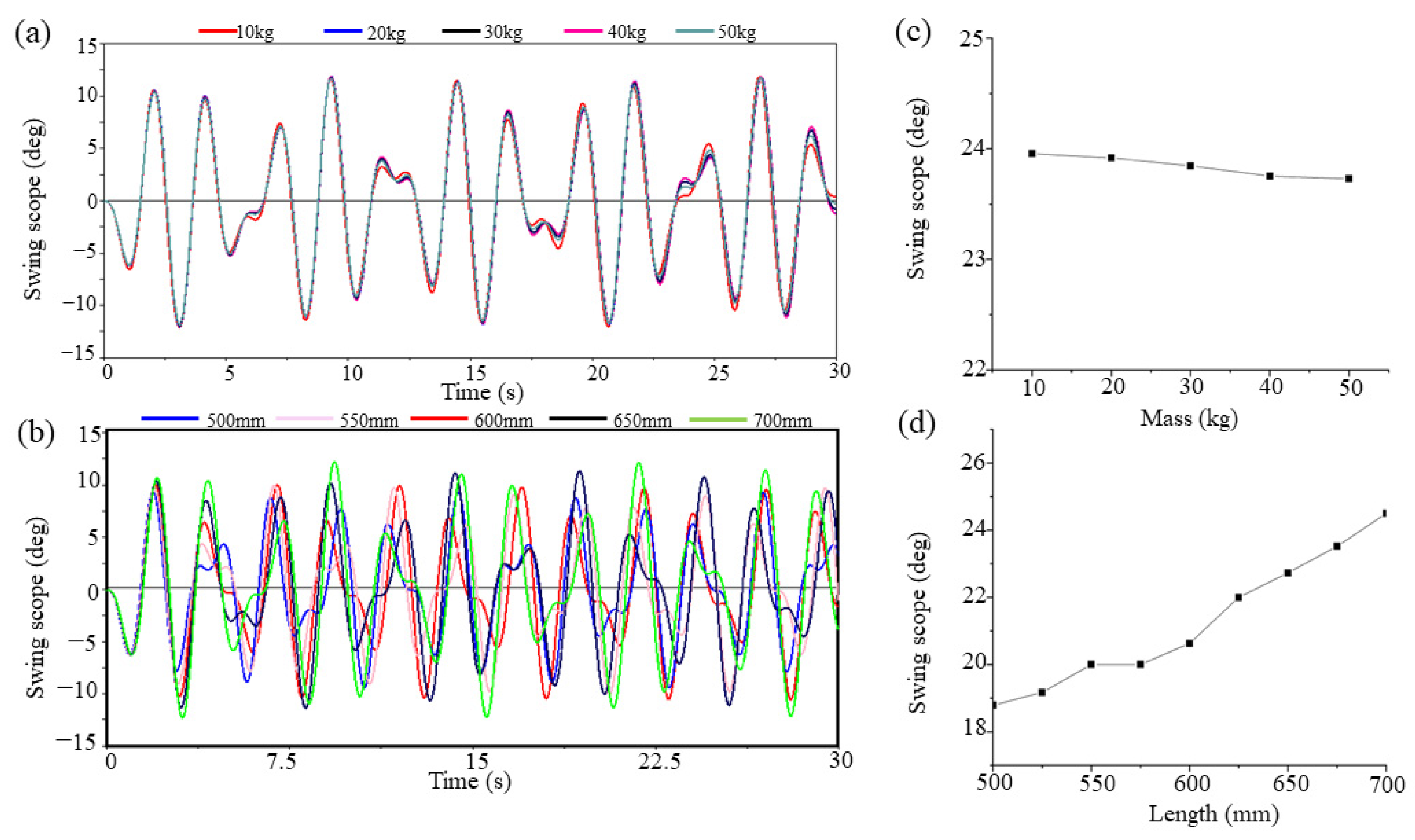
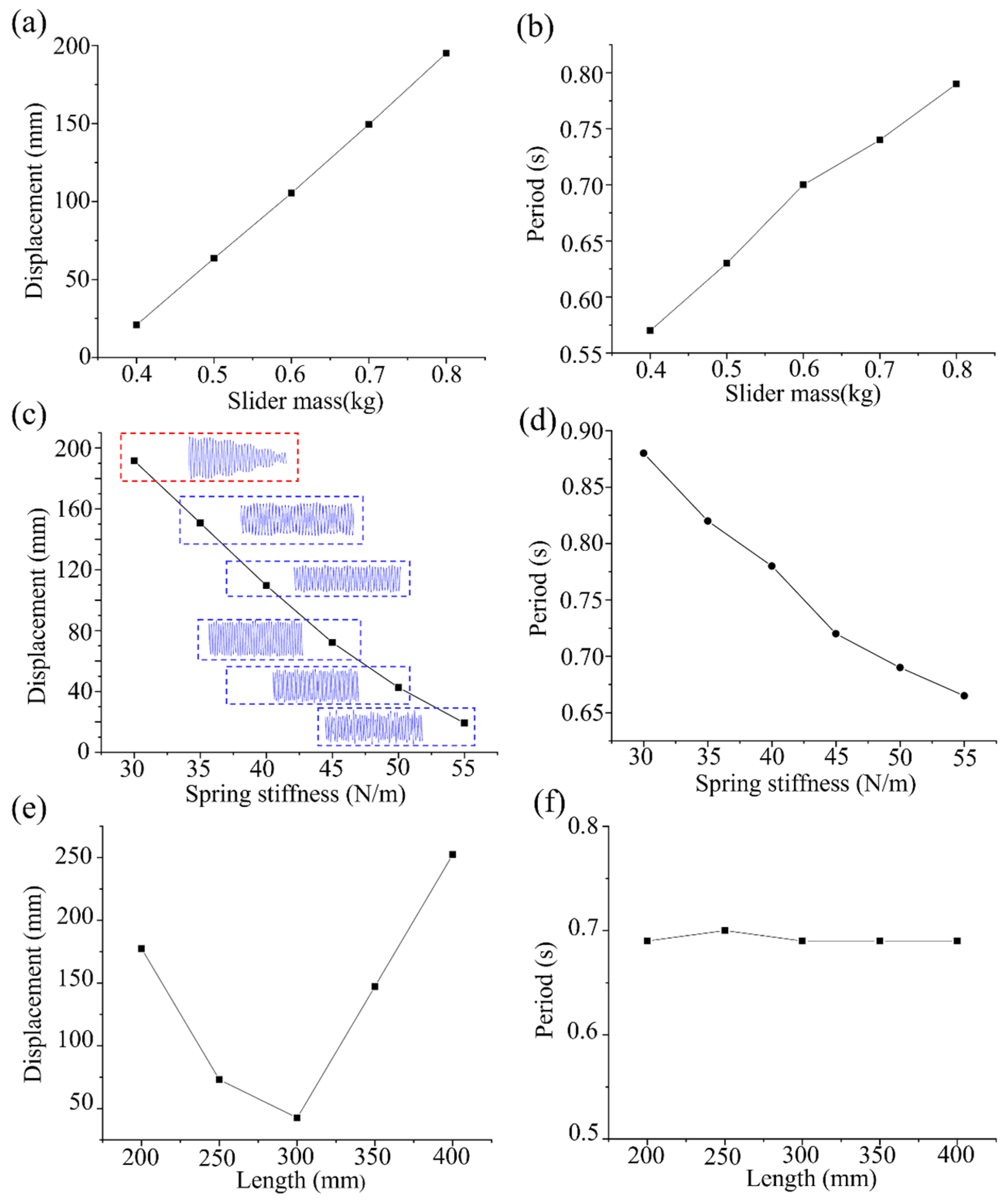
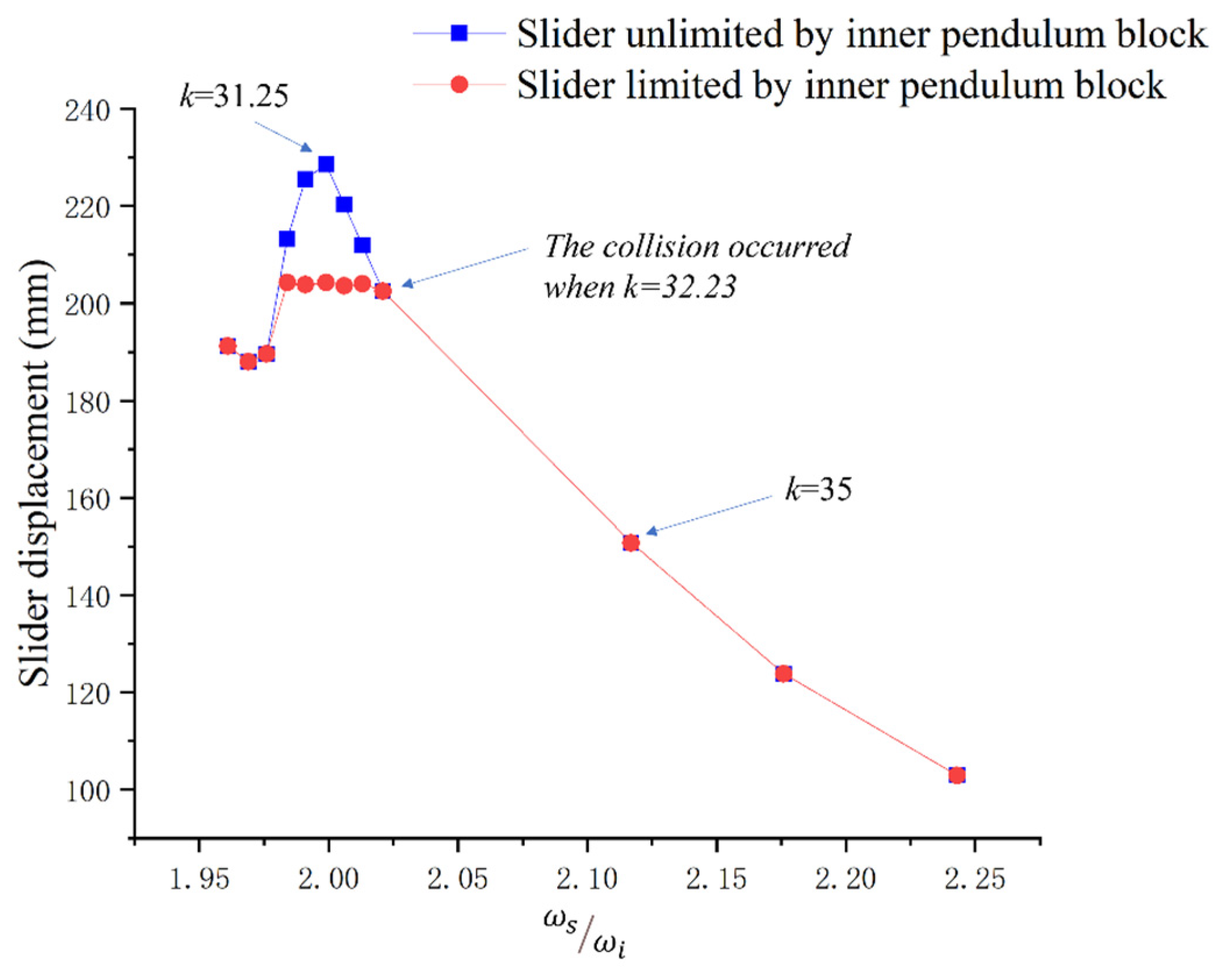
3.1. Effect of Inner Pendulum Parameters on WEC Efficiency
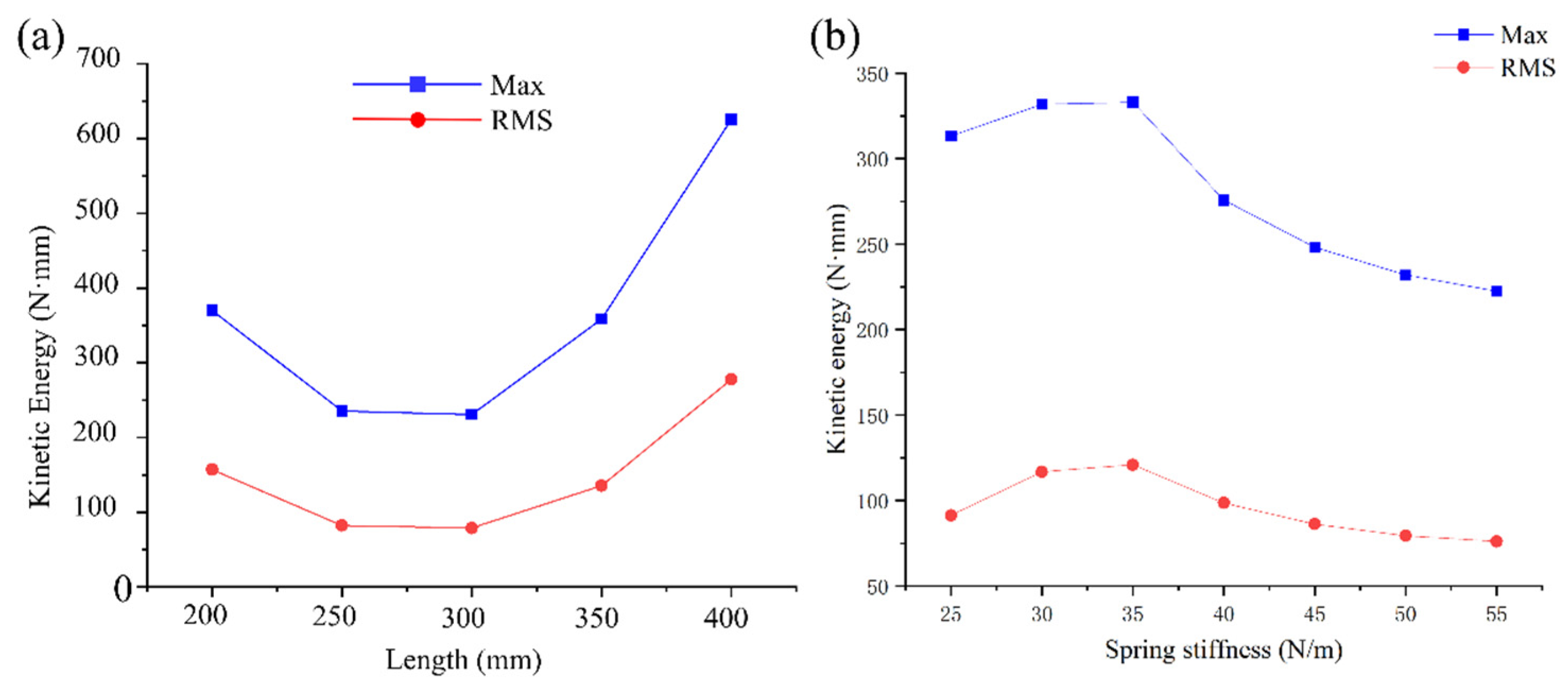
3.2. Effect of the Spring Pendulum on Wave Energy Absorption
3.3. Further Discussion of Model Results
4. Power Conversion Effectiveness
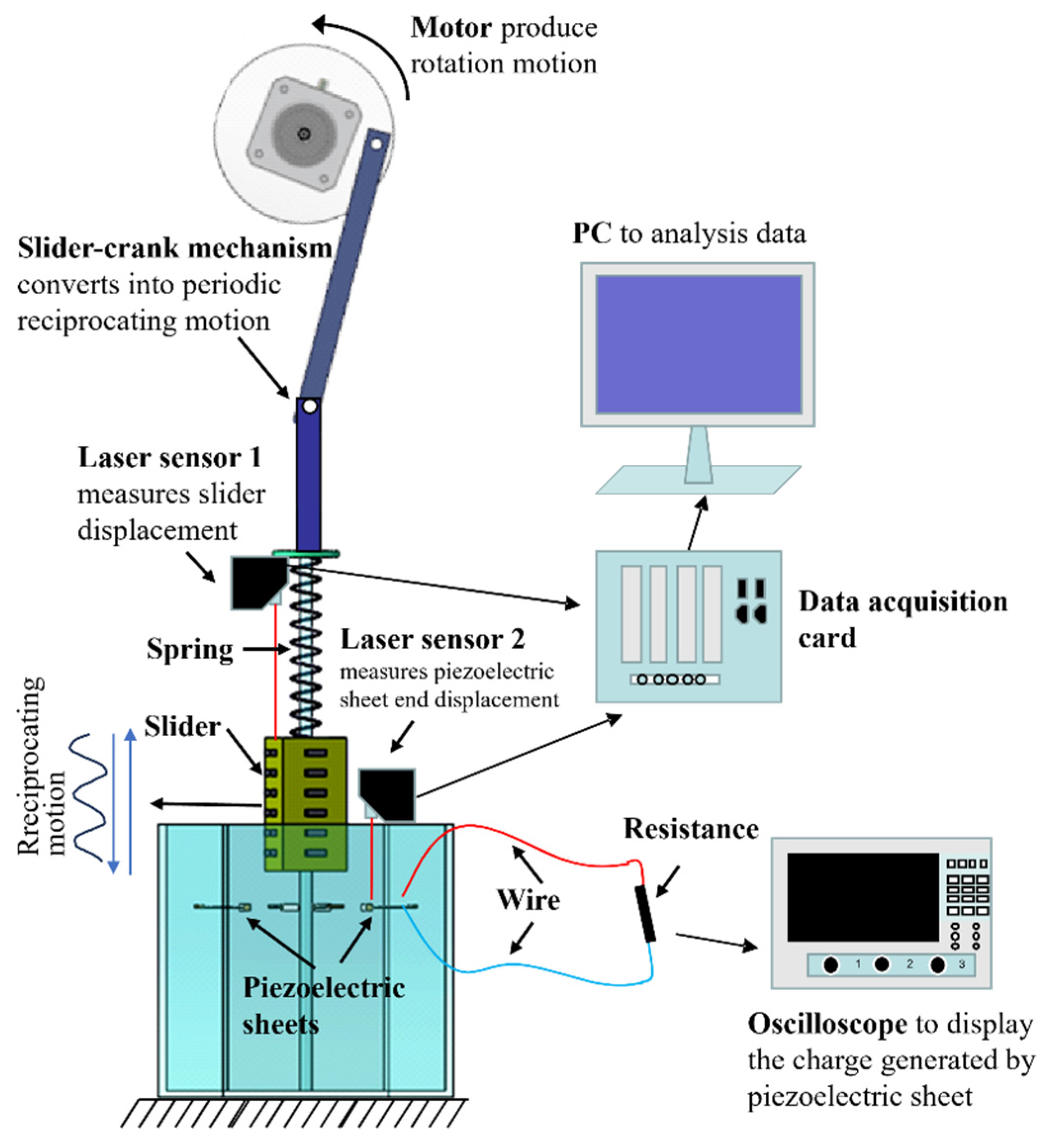
4.1. Experiment Set-Up
4.2. Experimental Results
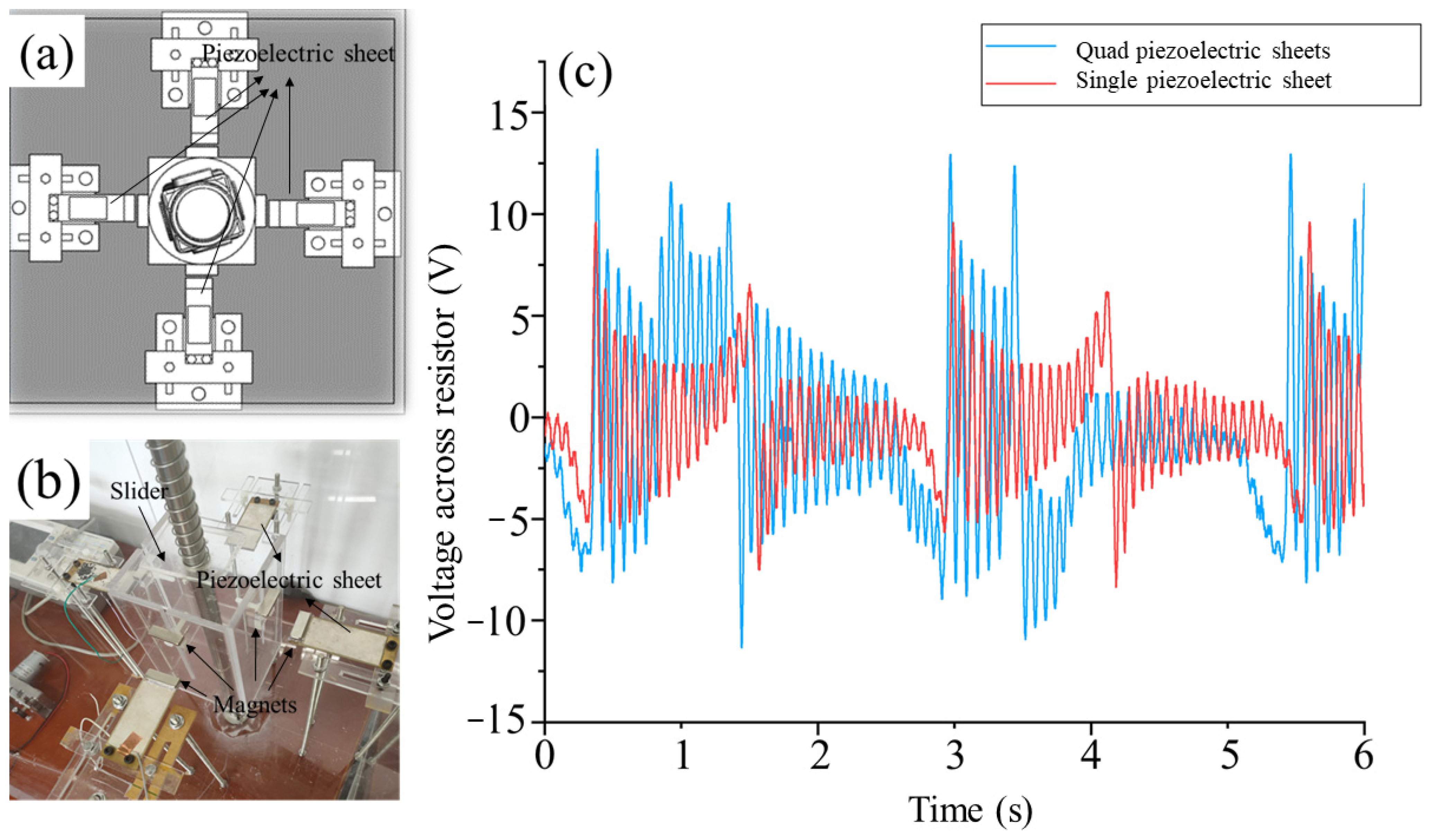
4.2.1. Single Piezoelectric Sheet–Single Magnet Excitation
4.2.2. Single Piezoelectric Sheet–Dual Magnets Excitation
4.2.3. Single Piezoelectric Sheet in Horizontal Array–Single Magnet Excitation
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zhang, Z.G.; Qi, S.B.; Li, S.Z. Marine Observation Beacon Clustering and Recycling Technology Based on Wireless Sensor Networks. Sensors 2019, 19, 3726. [Google Scholar] [CrossRef]
- Ulukus, S.; Yener, A.; Erkip, E.; Simeone, O.; Zorzi, M.; Grover, P.; Huang, K.B. Energy Harvesting Wireless Communications: A Review of Recent Advances. IEEE J. Sel. Areas Commun. 2015, 33, 360–381. [Google Scholar] [CrossRef]
- Kuang, Y.; Sun, J.; Gan, X.J.; Gong, D.W.; Liu, Z.P.; Zha, M.M. Dynamic multi-objective cooperative coevolutionary scheduling for mobile underwater wireless sensor networks. Comput. Ind. Eng. 2021, 156, 107229. [Google Scholar] [CrossRef]
- Li, H.; Wu, X.P.; Zhang, Z.T.; Tan, X.; Pan, Y.J.; Dai, C.T.; Luo, D.B.; Ahmed, A.; Xu, Y.S. An extended-range wave-powered autonomous underwater vehicle applied to underwater wireless sensor networks. iScience 2022, 25, 104738. [Google Scholar] [CrossRef] [PubMed]
- Gavali, A.B.; Kadam, M.V.; Patil, S. Energy optimization using swarm intelligence for IoT-Authorized underwater wireless sensor networks. Microprocess. Microsyst. 2022, 93, 104597. [Google Scholar] [CrossRef]
- Vesecky, J.F.; Laws, K.; Petersen, S.I.; Bazeghi, C.; Wiberg, D. Prototype autonomous mini-buoy for use in a wireless networked, ocean surface sensor array. In Proceedings of the 2007 IEEE International Geoscience and Remote Sensing Symposium, Barcelona, Spain, 23–28 July 2007; pp. 4987–4990. [Google Scholar]
- Feng, W.; Chen, X.; Wang, C.; Shi, Y. Application research on the time–frequency analysis method in the quality detection of ultrasonic wire bonding. Int. J. Distrib. Sens. Netw. 2021, 17, 1–11. [Google Scholar] [CrossRef]
- Albaladejo, C.; Soto, F.; Torres, R.; Sánchez, P.; López, J.A. A low-cost sensor buoy system for monitoring shallow marine environments. Sensors 2012, 12, 9613–9634. [Google Scholar] [CrossRef]
- Rubes, O.; Chalupa, J.; Ksica, F.; Hadas, Z. Development and experimental validation of self-powered wireless vibration sensor node using vibration energy harvester. Mech. Syst. Signal Process. 2021, 160, 107890. [Google Scholar] [CrossRef]
- Luo, A.X.; Zhang, Y.L.; Dai, X.T.; Wang, Y.F.; Xu, W.H.; Lu, Y.; Wang, M.; Fan, K.Q.; Wang, F. An inertial rotary energy harvester for vibrations at ultra-low frequency with high energy conversion efficiency. Appl. Energy 2020, 279, 115762. [Google Scholar] [CrossRef]
- Zhou, G.-D.; Yi, T.-H. Recent Developments on Wireless Sensor Networks Technology for Bridge Health Monitoring. Math. Probl. Eng. 2013, 2013, 947867. [Google Scholar] [CrossRef]
- Zhang, Y.; Zou, Q.P.; Greaves, D. Air-water two-phase flow modelling of hydrodynamic performance of an oscillating water column device. Renew. Energy 2012, 41, 159–170. [Google Scholar] [CrossRef]
- Wang, R.Q.; Ning, D.Z.; Zou, Q. Wave loads on a land-based dual-chamber Oscillating Water Column wave energy device. Coast. Eng. 2020, 160, 103744. [Google Scholar] [CrossRef]
- Monk, K.; Zou, Q.; Conley, D. An approximate solution for the wave energy shadow in the lee of an array of overtopping type wave energy converters. Coast. Eng. 2013, 73, 115–132. [Google Scholar] [CrossRef]
- Wu, N.; Wang, Q.; Xie, X.D. Ocean wave energy harvesting with a piezoelectric coupled buoy structure. Appl. Ocean Res. 2015, 50, 110–118. [Google Scholar] [CrossRef]
- Safaei, M.; Sodano, H.A.; Anton, S.R. A review of energy harvesting using piezoelectric materials: State-of-the-art a decade later (2008–2018). Smart Mater. Struct. 2019, 28, 113001. [Google Scholar] [CrossRef]
- Talaat, M.; Elkholy, M.H.; Farahat, M.A. Operating reserve investigation for the integration of wave, solar and wind energies. Energy 2020, 197, 117207. [Google Scholar] [CrossRef]
- Nabavi, S.F.; Farshidianfar, A.; Afsharfard, A.; Khodaparast, H.H. An ocean wave-based piezoelectric energy harvesting system using breaking wave force. Int. J. Mech. Sci. 2019, 151, 498–507. [Google Scholar] [CrossRef]
- Chen, X.; Gao, L.X.; Chen, J.F.; Lu, S.; Zhou, H.; Wang, T.T.; Wang, A.B.; Zhang, Z.F.; Guo, S.F.; Mu, X.J.; et al. A chaotic pendulum triboelectric-electromagnetic hybridized nanogenerator for wave energy scavenging and self-powered wireless sensing system. Nano Energy 2020, 69, 104440. [Google Scholar] [CrossRef]
- Qi, N.J.; Dai, K.R.; Wang, X.F.; You, Z. Full paper Optimization for piezoelectric energy harvesters with self-coupled structure: A double kill in bandwidth and power. Nano Energy 2022, 102, 107602. [Google Scholar] [CrossRef]
- Kiran, M.R.; Farrok, O.; Abdullah-Al-Mamun, M.; Islam, M.R.; Xu, W. Progress in Piezoelectric Material Based Oceanic Wave Energy Conversion Technology. IEEE Access 2020, 8, 146428–146449. [Google Scholar] [CrossRef]
- Lin, Z.; Zhang, Y.L. Dynamics of a mechanical frequency up-converted device for wave energy harvesting. J. Sound Vib. 2016, 367, 170–184. [Google Scholar] [CrossRef]
- Miles, J.W.; Zou, Q.P. Parametric Excitation of a Detuned Spherical Pendulum. J. Sound Vib. 1993, 164, 237–250. [Google Scholar] [CrossRef]
- Kumar, R.; Gupta, S.; Ali, S.F. Energy harvesting from chaos in base excited double pendulum. Mech. Syst. Signal Process. 2019, 124, 49–64. [Google Scholar] [CrossRef]
- Covaci, C.; Gontean, A. Piezoelectric Energy Harvesting Solutions: A Review. Sensors 2020, 20, 3512. [Google Scholar] [CrossRef] [PubMed]
- Ghazanfarian, J.; Mohammadi, M.M.; Uchino, K. Piezoelectric Energy Harvesting: A Systematic Review of Reviews. Actuators 2021, 10, 312. [Google Scholar] [CrossRef]
- Viet, N.V.; Wang, Q. Ocean wave energy pitching harvester with a frequency tuning capability. Energy 2018, 162, 603–617. [Google Scholar] [CrossRef]
- Wu, Y.P.; Qiu, J.H.; Zhou, S.P.; Ji, H.L.; Chen, Y.; Li, S. A piezoelectric spring pendulum oscillator used for multi-directional and ultra-low frequency vibration energy harvesting. Appl. Energy 2018, 231, 600–614. [Google Scholar] [CrossRef]
- Okada, N.; Yabe, S.; Fujimoto, H.; Murai, M. Experiments on floating wave-power generation using piezoelectric elements and pendulums in the water tank. In Proceedings of the OCEANS 2012-YEOSU, Yeosu, Republic of Korea, 21–24 May 2012; pp. 1–8. [Google Scholar]
- Viñolo, C.; Toma, D.; Mànuel, A.; del Rio, J. An ocean kinetic energy converter for low-power applications using piezoelectric disk elements. Eur. Phys. J. Spec. Top. 2013, 222, 1685–1698. [Google Scholar] [CrossRef]
- Murray, R.; Rastegar, J. Novel two-stage piezoelectric-based ocean wave energy harvesters for moored or unmoored buoys. In Active and Passive Smart Structures and Integrated Systems 2009; SPIE: St Bellingham, WA, USA, 2009. [Google Scholar]
- Wickenheiser, A.M.; Garcia, E. Broadband vibration-based energy harvesting improvement through frequency up-conversion by magnetic excitation. Smart Mater. Struct. 2010, 19, 065020. [Google Scholar] [CrossRef]
- Han, B.; Chu, J.; Xiong, Y.; Fei, Y. Modeling and simulation of the novel wave energy piezoelectric generator. In Proceedings of the 2011 International Conference on Electrical and Control Engineering, Yichang, China, 16–18 September 2011; pp. 1621–1624. [Google Scholar]
- Xie, X.D.; Wang, Q.; Wu, N. Potential of a piezoelectric energy harvester from sea waves. J. Sound Vib. 2014, 333, 1421–1429. [Google Scholar] [CrossRef]
- Chen, S.E.; Yang, R.Y.; Qiu, Z.H.; Wu, C.C. A Piezoelectric Wave Energy Harvester Using Plucking-Driven and Frequency Up-Conversion Mechanism. Energies 2021, 14, 8441. [Google Scholar] [CrossRef]
- Cai, W.Z.; Roussinova, V.; Stoilov, V. Piezoelectric wave energy harvester. Renew. Energy 2022, 196, 973–982. [Google Scholar] [CrossRef]
- Vipin, V.; Trivedi, K.; Koley, S. Performance of a submerged piezoelectric wave energy converter device floating over an undulated seabed. Energy Rep. 2022, 8, 182–188. [Google Scholar]
- Vipin, V.; Koley, S. Mathematical modeling of a submerged piezoelectric wave energy converter device installed over an undulated seabed. Renew. Energy 2022, 200, 1382–1392. [Google Scholar]
- Heidari, M.; Sherbaf, G.R. Theoretical study of a new piezoelectric nonlinear energy harvester from ocean waves. J. Braz. Soc. Mech. Sci. Eng. 2022, 44, 589. [Google Scholar] [CrossRef]
- Shi, G.; Tong, D.K.; Xia, Y.S.; Jia, S.Y.; Chang, J.; Li, Q.; Wang, X.D.; Xia, H.K.; Ye, Y.D. A piezoelectric vibration energy harvester for multi-directional and ultra-low frequency waves with magnetic coupling driven by rotating balls. Appl. Energy 2022, 310, 118511. [Google Scholar] [CrossRef]
- Boccalero, G.; Chesne, S.; Mignot, E.; Riviere, N.; Jean-Mistral, C. Experimental investigations of a new concept of wave energy converter hybridizing piezoelectric and dielectric elastomer generators. Smart Mater. Struct. 2022, 31, 015006. [Google Scholar] [CrossRef]
- Garrison, C.J.; Rao, V.S.; Snider, R.H. Wave Interaction with Large Submerged Objects. In Proceedings of the Offshore Technology Conference, Houston, TX, USA, 22–24 April 1970. [Google Scholar]
- Del Balzo, D.R. Drag body design in support of wave energy harvesting. In Proceedings of the OCEANS 2010 MTS/IEEE SEATTLE, Seattle, WA, USA, 20–23 September 2010. [Google Scholar]
- Li, Y.; Ni, Z. Numerical study of the energy variation of spring pendulum vibration. J. Fuyang Norm. Univ. (Nat. Sci. Ed.) 2009, 26, 45–48. (In Chinese) [Google Scholar]
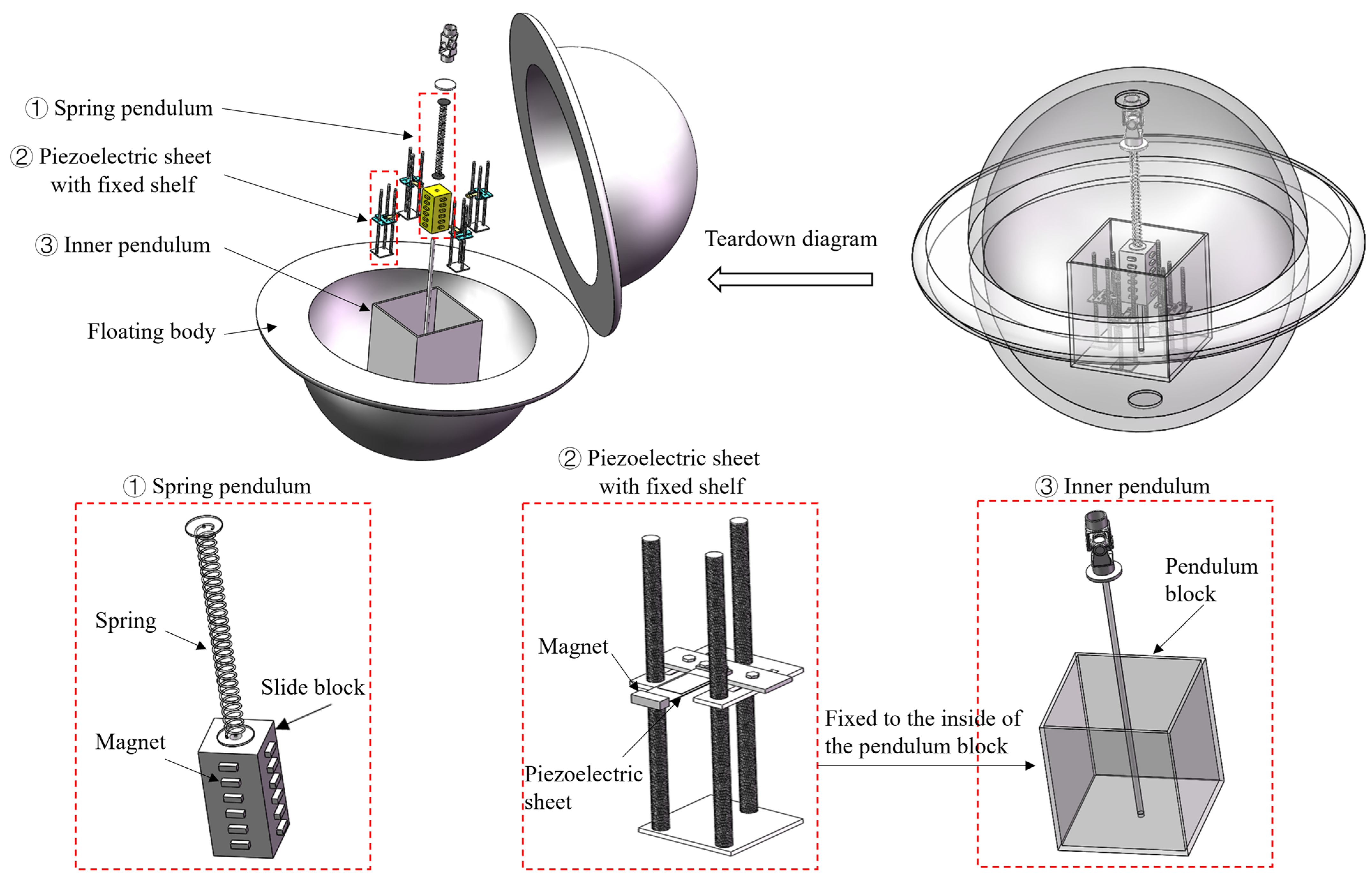








| Components | Dimensions (cm) |
|---|---|
| Inner pendulum block | Length × width × height: 40 × 38 × 38, thickness: 0.5 |
| Smooth linear guide bar | Radius: 0.9, length: 80 |
| Slide block | Length × width × height: 20 × 10 × 10 |
| Spring | Length: 30, pitch: 0.5, diameter: 3 |
| Floating body | Radius: 60, thickness: 5 |
| Parameter | Value | Unit |
|---|---|---|
| Young’s modulus of substrate | 112 | GPa |
| Piezoelectric Young’s modulus | 56 | GPa |
| Substrate density | 8780 | kg/m3 |
| Piezoelectric density | 7500 | kg/m3 |
| Magnet size (L × W × h) | 30 × 10 × 5 | mm |
| Piezoelectric biocrystal beam (L × W × h) | 80 × 33 × 0.6 | mm |
| Piezoelectric coefficient d31 | 186 × 10−12 | C/N |
| Relative dielectric constant | 3130 | |
| Magnet type | N35 |
| Distance | Excitation Method | Pt/mW |
|---|---|---|
| d = 15 mm | Single magnet—single piezoelectric sheet | 4.117 |
| d = 15 mm, D = 30 mm | Dual magnets—single piezoelectric sheet | 6.674 |
| d = 15 mm | Single magnet—quad piezoelectric sheets | 10.015 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Feng, W.; Chen, H.; Zou, Q.; Wang, D.; Luo, X.; Cummins, C.; Zhang, C.; Yang, S.; Su, Y. A Contactless Coupled Pendulum and Piezoelectric Wave Energy Harvester: Model and Experiment. Energies 2024, 17, 876. https://doi.org/10.3390/en17040876
Feng W, Chen H, Zou Q, Wang D, Luo X, Cummins C, Zhang C, Yang S, Su Y. A Contactless Coupled Pendulum and Piezoelectric Wave Energy Harvester: Model and Experiment. Energies. 2024; 17(4):876. https://doi.org/10.3390/en17040876
Chicago/Turabian StyleFeng, Wuwei, Hongya Chen, Qingping Zou, Di Wang, Xiang Luo, Cathal Cummins, Chuanqiang Zhang, Shujie Yang, and Yuxiang Su. 2024. "A Contactless Coupled Pendulum and Piezoelectric Wave Energy Harvester: Model and Experiment" Energies 17, no. 4: 876. https://doi.org/10.3390/en17040876
APA StyleFeng, W., Chen, H., Zou, Q., Wang, D., Luo, X., Cummins, C., Zhang, C., Yang, S., & Su, Y. (2024). A Contactless Coupled Pendulum and Piezoelectric Wave Energy Harvester: Model and Experiment. Energies, 17(4), 876. https://doi.org/10.3390/en17040876







