A Novel Wind Turbine Rolling Element Bearing Fault Diagnosis Method Based on CEEMDAN and Improved TFR Demodulation Analysis
Abstract
1. Introduction
2. Theoretical Background
2.1. CEEMDAN
- (1)
- Sequences are constructed by adding Gaussian white noise with a zero mean into the original signal . can be expressed as:where indicates the Gaussian white noise which is zero mean and unit-variance; represents its amplitude.
- (2)
- Use EMD to decompose into several IMFs and take their mean as the first IMF, which can be written as:where represents the first IMF of CEEMDAN, and denotes the first residue.
- (3)
- After adding Gaussian white noise to the stage residual signal, the data are proceeded by the EMD. The decomposition satisfies the following formulas:where represents the IMF of CEEMDAN; indicates the IMF of EMD; is the Gaussian white noise; is the amplitude of the Gaussian white noise, and denotes the residue.
- (4)
- If the EMD stop condition is met, and the residual signal of the nth decomposition is monotonic, the iteration stops and the decomposition ends.
2.2. TFR Demodulation Method
- (1)
- Execute CWT on the signal to acquire its corresponding time–frequency representation, which can be described as:where is the complex conjugate of the scaled versions of a mother wavelet function; is the scale parameter; denotes the translation parameter.
- (2)
- Add all wavelet coefficients along the frequency axis to obtain the time–frequency envelope signal as:
- (3)
- Employ the fast Fourier transform (FFT) to compute the time–frequency envelope spectrum for fault diagnosis. The corresponding time–frequency envelope spectrum can be defined as:where represents sampling frequency; denotes Nyquist frequency.
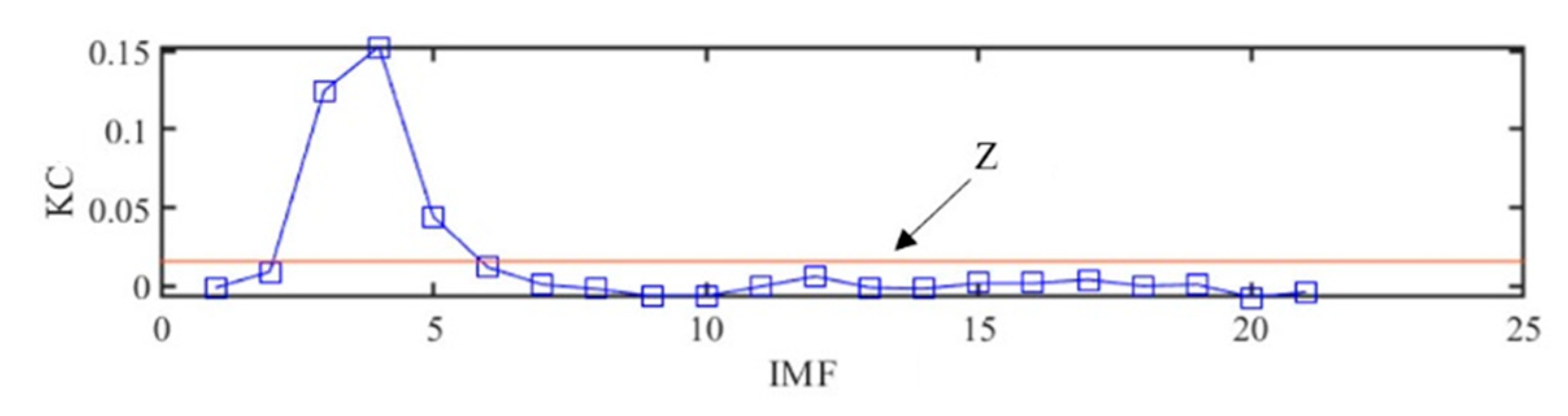
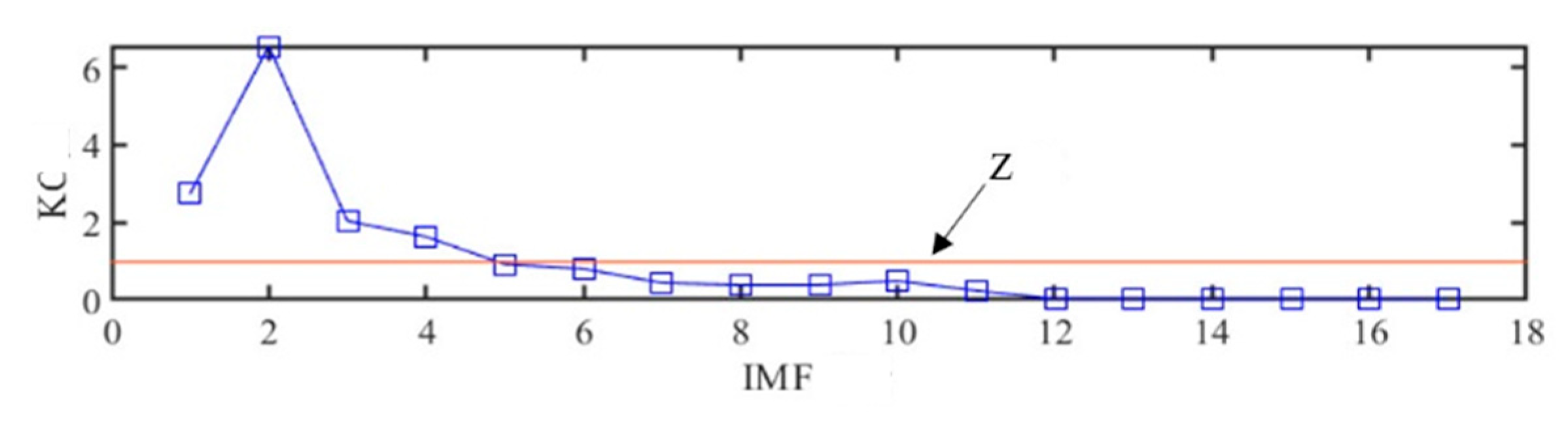
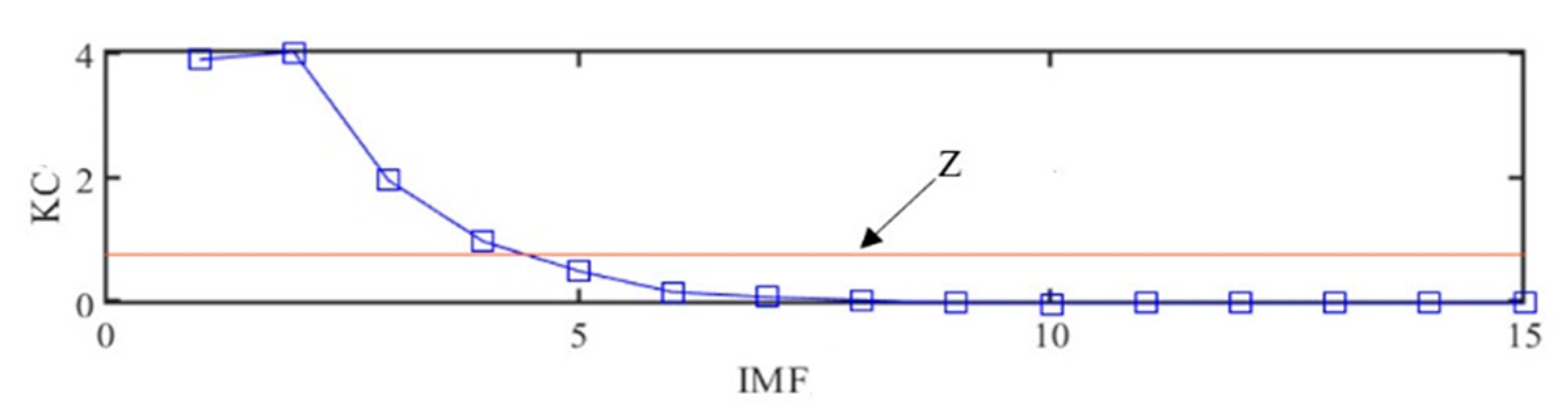
2.3. KC Indicator
2.4. An Improved TFR Demodulation Method
- (1)
- Perform CWT on the denoised signal to obtain the corresponding TFR.
- (2)
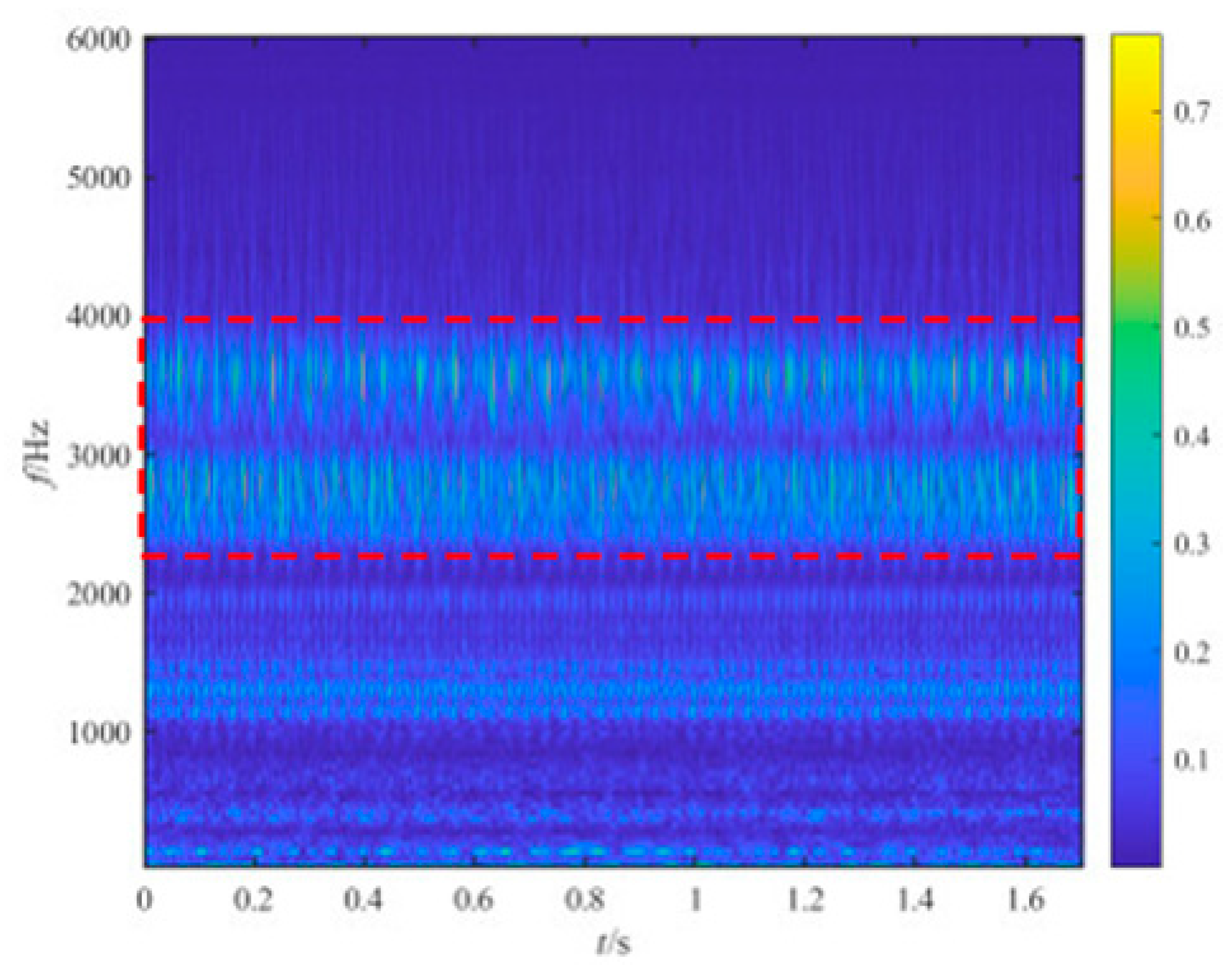
- Find the frequency band with the most energy concentration in the TFR. The intensity of signal energy concentration serves as the criterion for selecting a subset of wavelet coefficients.
- (3)
- Add the complex wavelet coefficients in the frequency band, and then calculate the modulus and convert it into a time–frequency envelope signal.
- (4)
- Perform FFT on the obtained signal to acquire the envelope spectrum used for fault diagnosis.
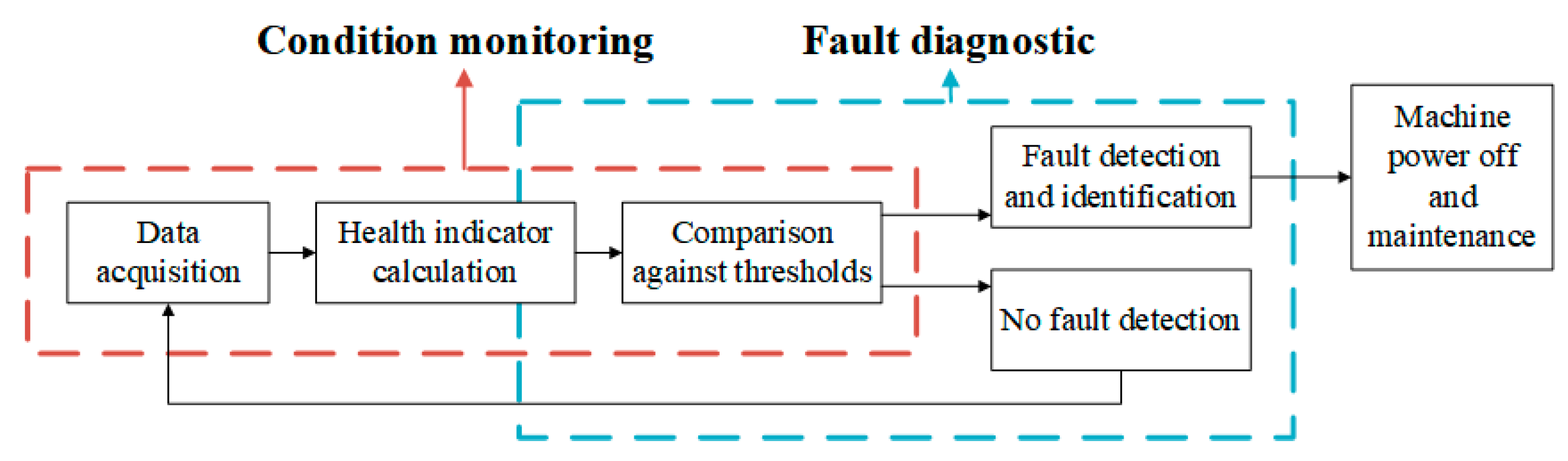
2.5. Fault Diagnosis Based on CEEMDAN and the Improved TFR Demodulation Method
- (1)
- Decompose the vibration signals using CEEMDAN to obtain several IMFs.
- (2)
- Select the effective components based on the KC indicator to reconstruct the signal.
- (3)
- Perform CWT to obtain the TFR of the reconstructed signal.
- (4)
- Extract the envelope spectrum using the improved TFR demodulation method.
3. Numerical Verification
4. Experiment Verification
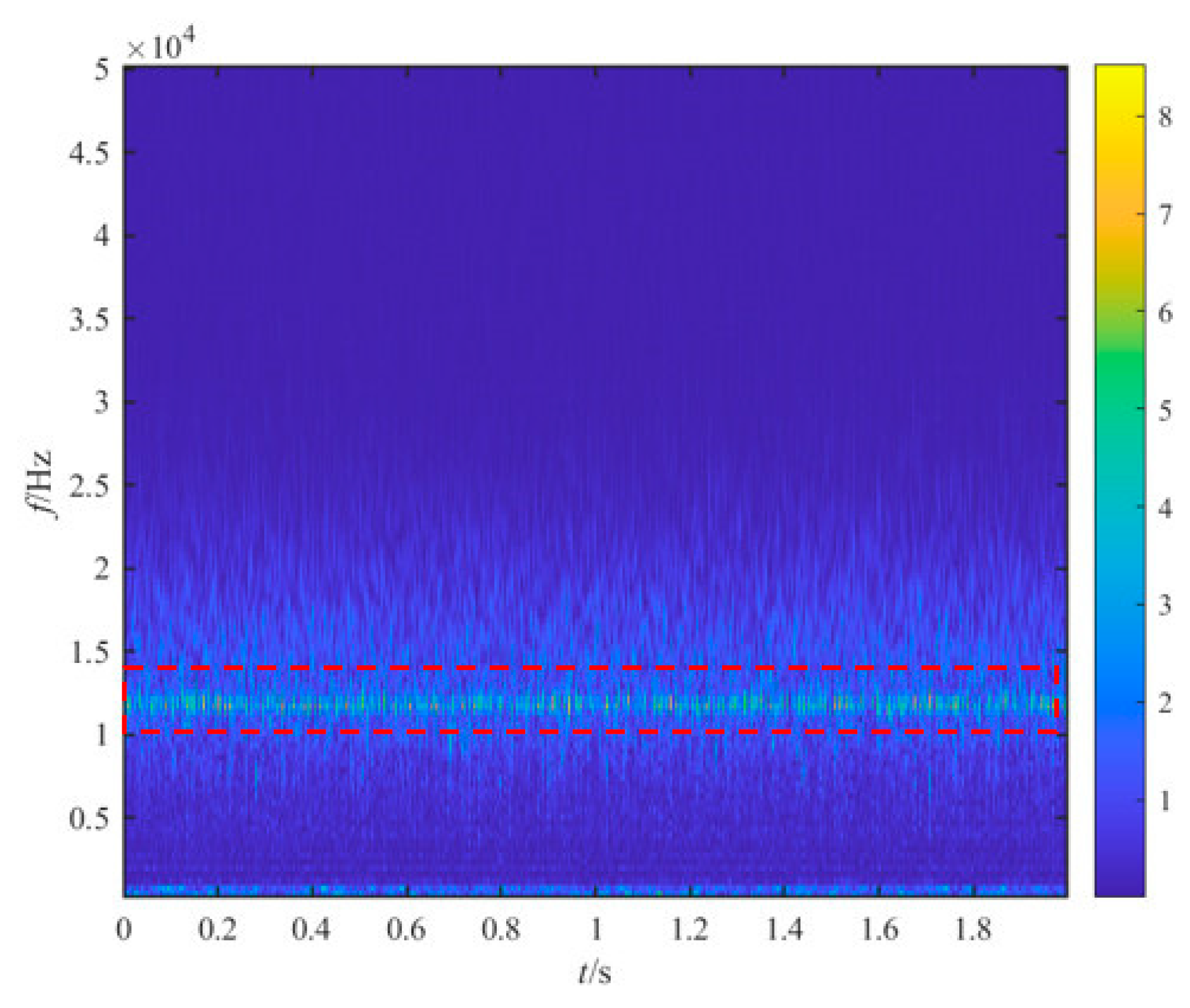
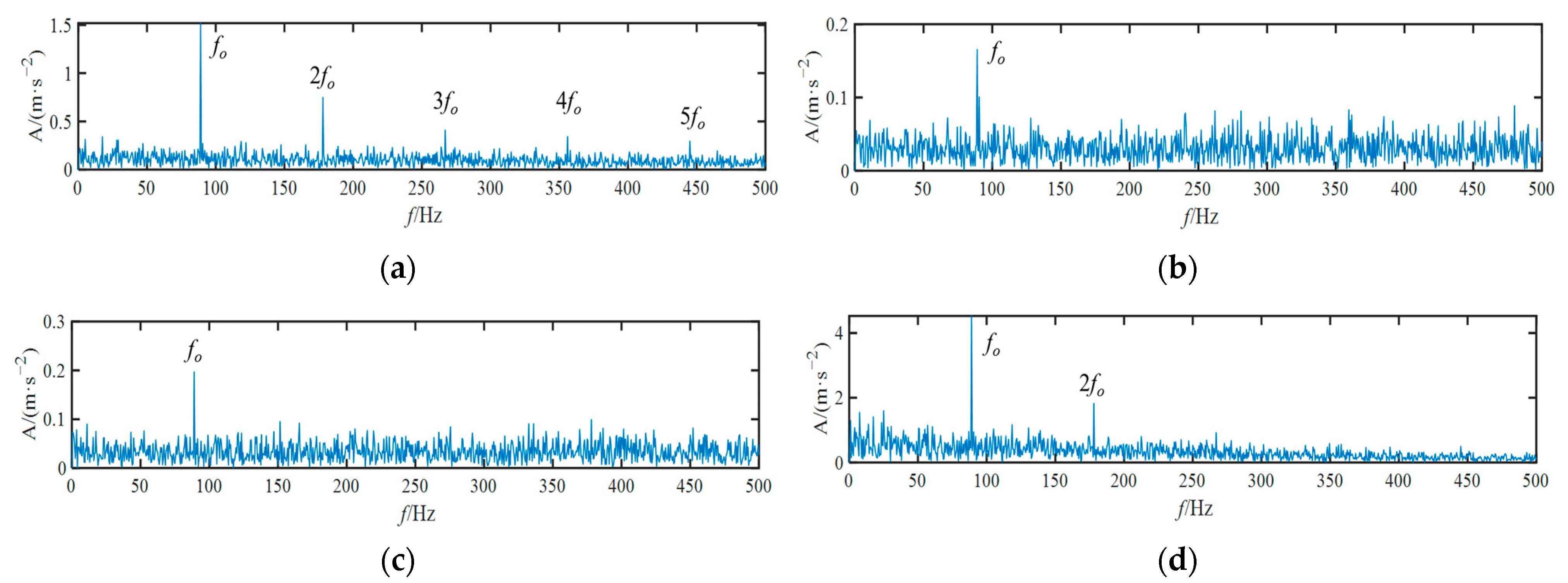
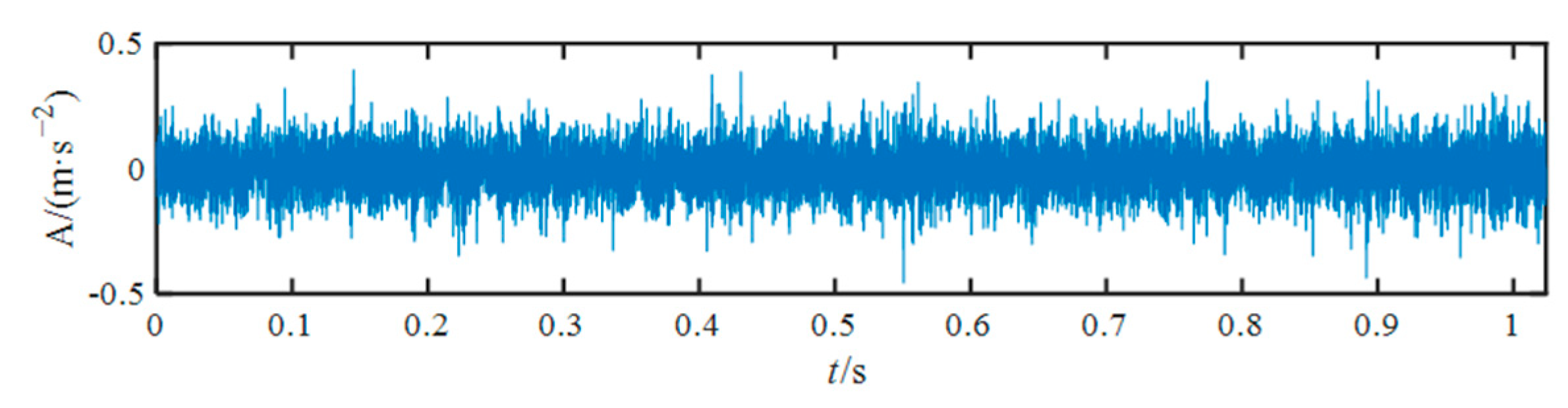
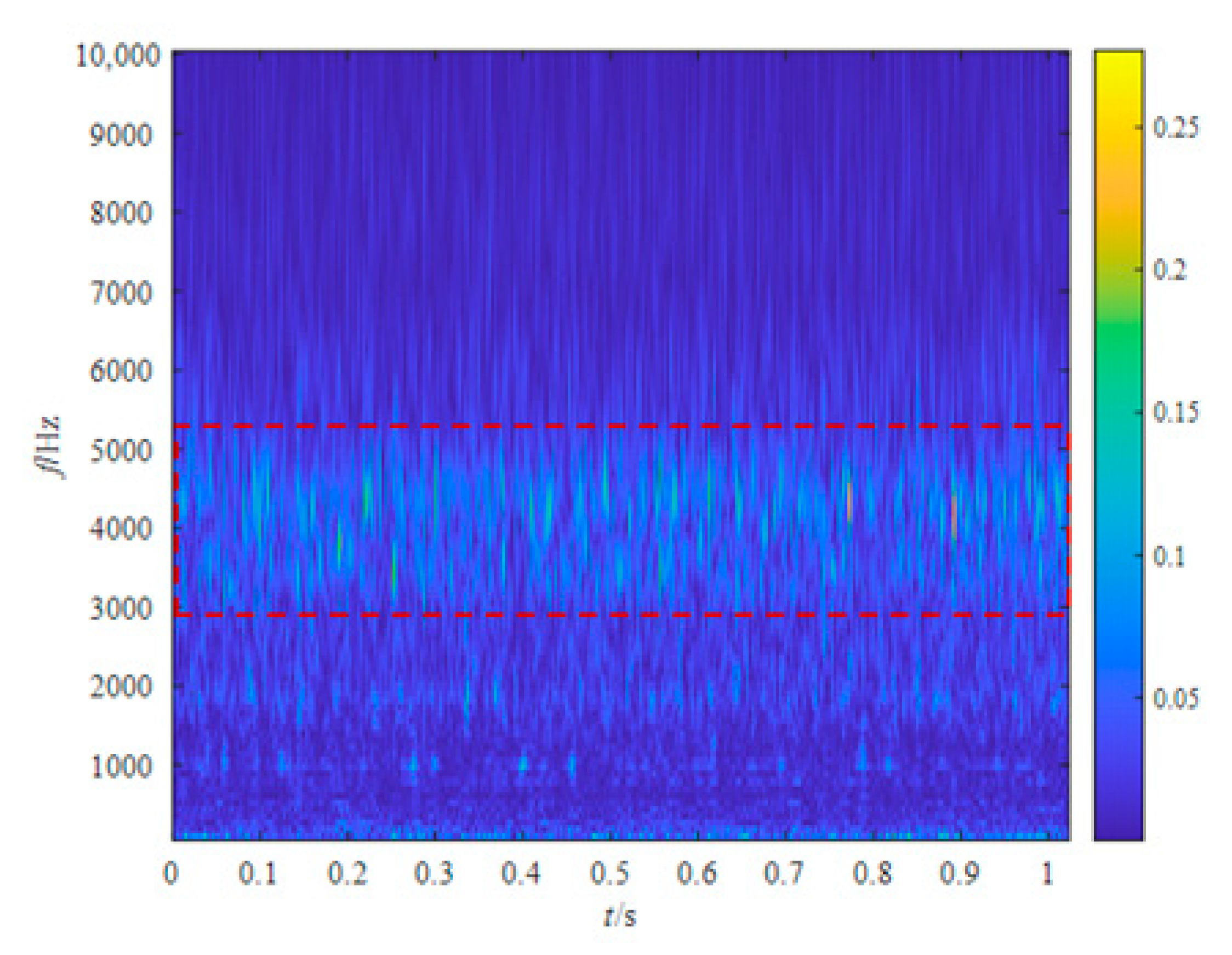
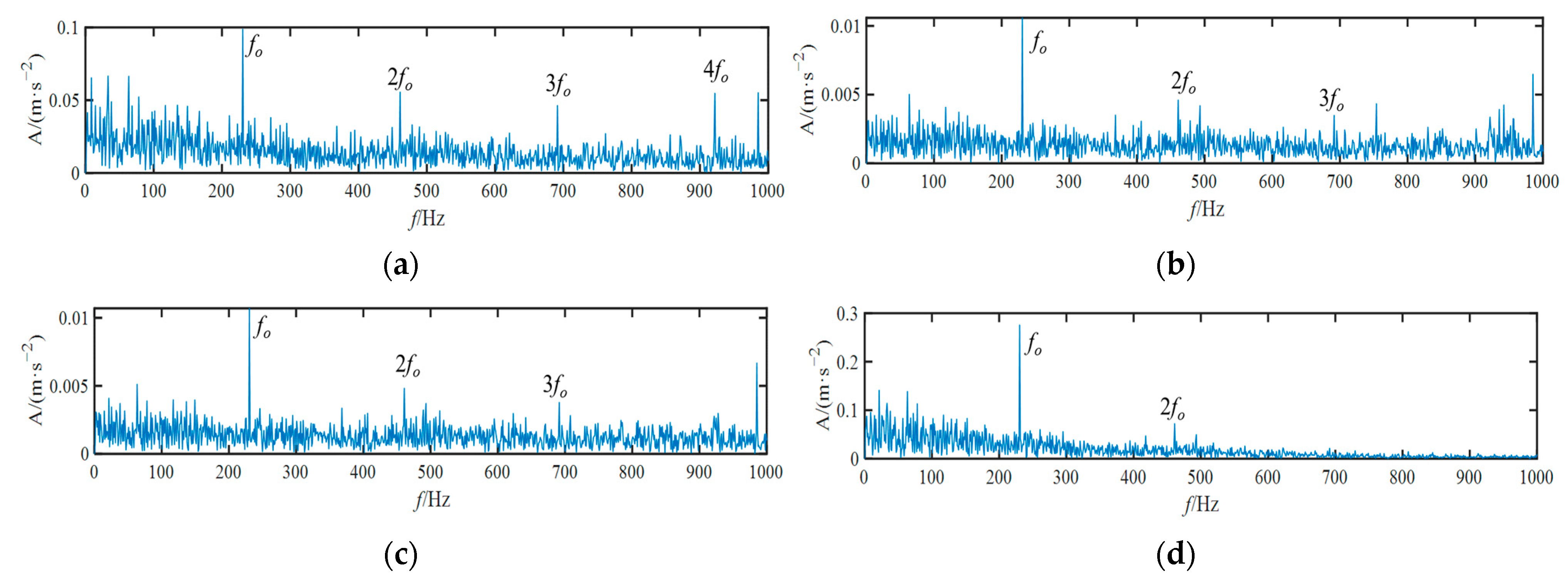
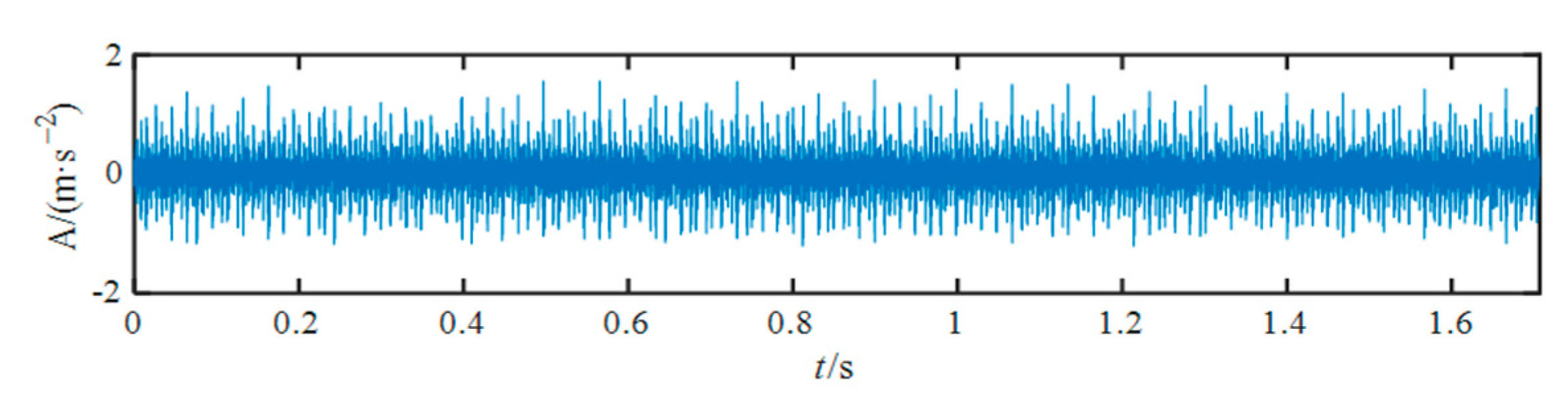
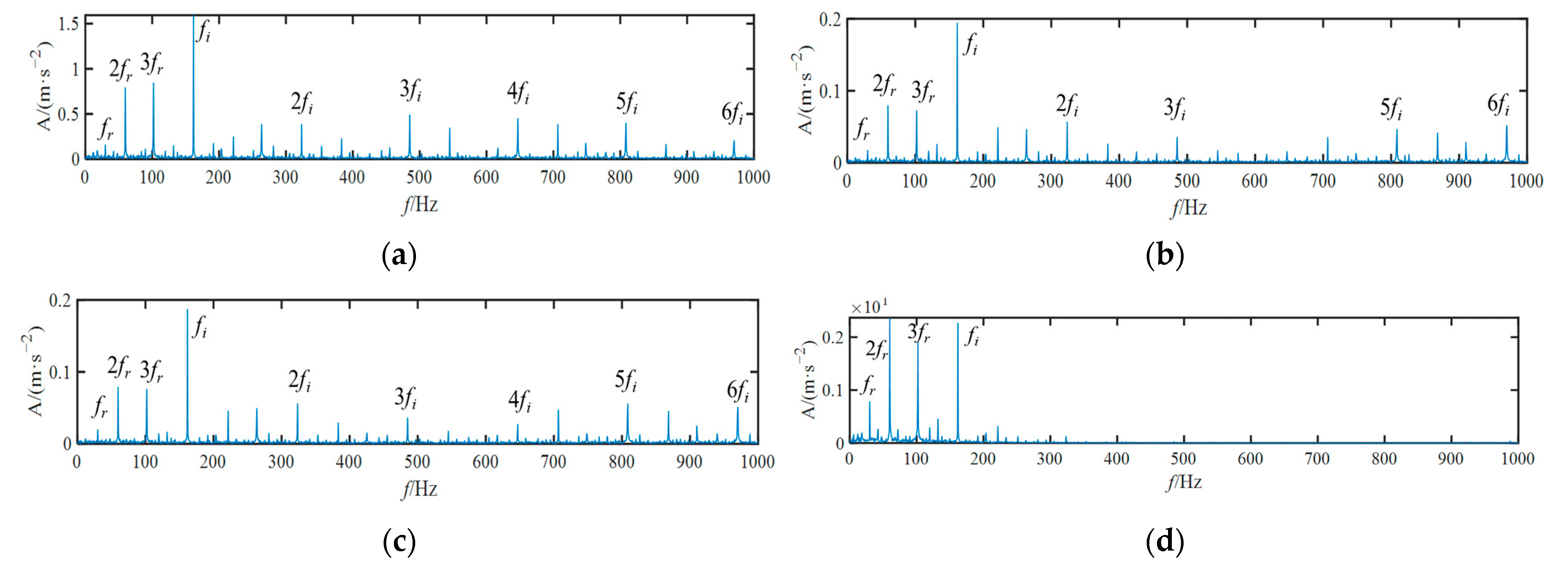
4.1. REB Outer Race Fault Diagnosis
4.2. REB Inner Race Fault Diagnosis
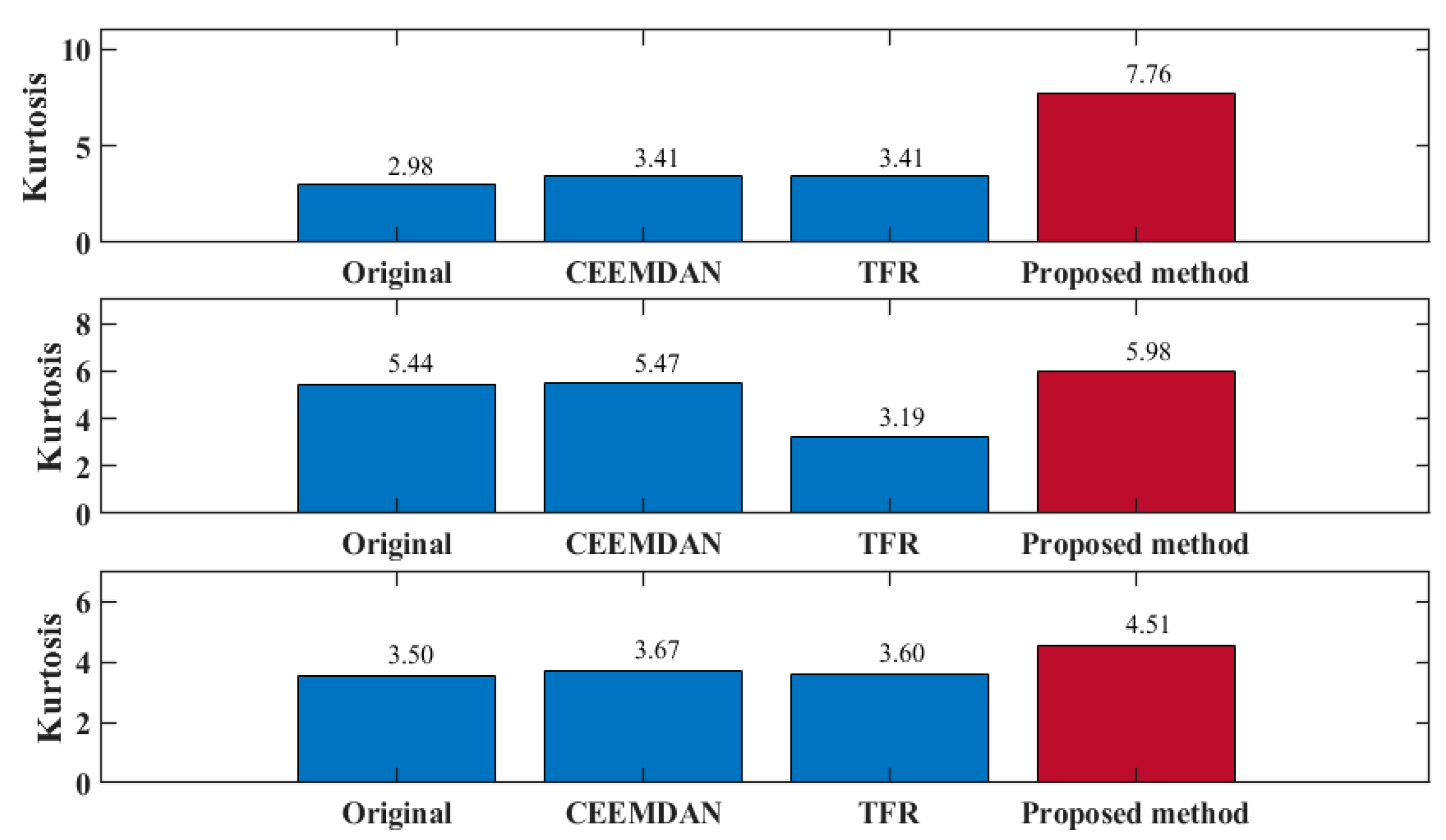
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations/Nomenclature
| CEEMDAN | Complete ensemble empirical mode decomposition with adaptive noise |
| CWT | Continuous wavelet transform |
| CWRU | Case Western Reserve University |
| EDM | Electro-discharge machining |
| EMD | Empirical mode decomposition |
| FCF | Fault characteristic frequency |
| IMF | Intrinsic mode function |
| IMS | Intelligent Maintenance Systems |
| REB | Rolling element bearing |
| TFR | Time–frequency representation |
| Vibration signal of bearings | |
| Vibration signal added with Gaussian white noise | |
| Gaussian white noise | |
| The Gaussian white noise | |
| The amplitude of Gaussian white noise | |
| The amplitude of Gaussian white noise | |
| The IMF of EMD | |
| The intrinsic mode functions | |
| The residue | |
| The CWT of the signal | |
| The complex conjugate of the scaled versions of a mother wavelet function | |
| The scale parameter | |
| The translation parameter | |
| The time–frequency envelope signal | |
| The time–frequency envelope spectrum | |
| Sampling frequency | |
| Nyquist frequency | |
| The length of the signal | |
| Kurtosis | |
| Correlation function | |
| KC indicator | |
| Z value | |
| The Morlet wavelet | |
| The amplitude of the defect | |
| The number of the shock | |
| The Heaviside step function | |
| The FCF of the bearing | |
| The period of the defect | |
| The damping coefficient | |
| The resonance response frequency | |
| The timing of the defect | |
| The outer race fault characteristic frequency |
References
- Chang, L.; Saydaliev, H.B.; Meo, M.S.; Mohsin, M. How Renewable Energy Matter for Environmental Sustainability: Evidence from Top-10 Wind Energy Consumer Countries of European Union. Sustain. Energy Grids Netw. 2022, 31, 100716. [Google Scholar] [CrossRef]
- Sadorsky, P. Wind Energy for Sustainable Development: Driving Factors and Future Outlook. J. Clean. Prod. 2021, 289, 125779. [Google Scholar] [CrossRef]
- Qian, P.; Feng, B.; Zhang, D.; Tian, X.; Si, Y. IoT-Based Approach to Condition Monitoring of the Wave Power Generation System. IET Renew. Power Gener. 2019, 13, 2207–2214. [Google Scholar] [CrossRef]
- McKenna, R.; Pfenninger, S.; Heinrichs, H.; Schmidt, J.; Staffell, I.; Bauer, C.; Gruber, K.; Hahmann, A.N.; Jansen, M.; Klingler, M.; et al. High-Resolution Large-Scale Onshore Wind Energy Assessments: A Review of Potential Definitions, Methodologies and Future Research Needs. Renew. Energy 2022, 182, 659–684. [Google Scholar] [CrossRef]
- Stathopoulos, T.; Alrawashdeh, H.; Al-Quraan, A.; Blocken, B.; Dilimulati, A.; Paraschivoiu, M.; Pilay, P. Urban Wind Energy: Some Views on Potential and Challenges. J. Wind Eng. Ind. Aerodyn. 2018, 179, 146–157. [Google Scholar] [CrossRef]
- Soua, S.; Van Lieshout, P.; Perera, A.; Gan, T.-H.; Bridge, B. Determination of the Combined Vibrational and Acoustic Emission Signature of a Wind Turbine Gearbox and Generator Shaft in Service as a Pre-Requisite for Effective Condition Monitoring. Renew. Energy 2013, 51, 175–181. [Google Scholar] [CrossRef]
- Dhanola, A.; Garg, H.C. Tribological Challenges and Advancements in Wind Turbine Bearings: A Review. Eng. Fail. Anal. 2020, 118, 104885. [Google Scholar] [CrossRef]
- Wang, J.; Liang, Y.; Zheng, Y.; Gao, R.X.; Zhang, F. An Integrated Fault Diagnosis and Prognosis Approach for Predictive Maintenance of Wind Turbine Bearing with Limited Samples. Renew. Energy 2020, 145, 642–650. [Google Scholar] [CrossRef]
- De Azevedo, H.D.M.; Araújo, A.M.; Bouchonneau, N. A Review of Wind Turbine Bearing Condition Monitoring: State of the Art and Challenges. Renew. Sustain. Energy Rev. 2016, 56, 368–379. [Google Scholar] [CrossRef]
- Fischer, K.; Besnard, F.; Bertling, L. Reliability-Centered Maintenance for Wind Turbines Based on Statistical Analysis and Practical Experience. IEEE Trans. Energy Convers. 2012, 27, 184–195. [Google Scholar] [CrossRef]
- Qian, P.; Zhang, D.; Tian, X.; Si, Y.; Li, L. A Novel Wind Turbine Condition Monitoring Method Based on Cloud Computing. Renew. Energy 2019, 135, 390–398. [Google Scholar] [CrossRef]
- Qian, P.; Ma, X.; Zhang, D.; Wang, J. Data-Driven Condition Monitoring Approaches to Improving Power Output of Wind Turbines. IEEE Trans. Ind. Electron. 2019, 66, 6012–6020. [Google Scholar] [CrossRef]
- Liu, Z.; Zhang, L. A Review of Failure Modes, Condition Monitoring and Fault Diagnosis Methods for Large-Scale Wind Turbine Bearings. Measurement 2020, 149, 107002. [Google Scholar] [CrossRef]
- Liu, L.; Wei, Y.; Song, X.; Zhang, L. Fault Diagnosis of Wind Turbine Bearings Based on CEEMDAN-GWO-KELM. Energies 2022, 16, 48. [Google Scholar] [CrossRef]
- Hu, Y.; Zhang, S.; Jiang, A.; Zhang, L.; Jiang, W.; Li, J. A New Method of Wind Turbine Bearing Fault Diagnosis Based on Multi-Masking Empirical Mode Decomposition and Fuzzy C-Means Clustering. Chin. J. Mech. Eng. 2019, 32, 46. [Google Scholar] [CrossRef]
- Randall, R.B.; Antoni, J. Rolling Element Bearing Diagnostics—A Tutorial. Mech. Syst. Signal Process. 2011, 25, 485–520. [Google Scholar] [CrossRef]
- Zhou, J.; Chen, C.; Guo, J.; Wang, L.; Liu, Z.; Feng, C. A Novel Rolling Bearing Fault Diagnosis Method Based on Continuous Hierarchical Fractional Range Entropy. Measurement 2023, 220, 113395. [Google Scholar] [CrossRef]
- Pang, B.; Nazari, M.; Tang, G. Recursive Variational Mode Extraction and Its Application in Rolling Bearing Fault Diagnosis. Mech. Syst. Signal Process. 2022, 165, 108321. [Google Scholar] [CrossRef]
- Xu, Y.; Li, Z.; Wang, S.; Li, W.; Sarkodie-Gyan, T.; Feng, S. A Hybrid Deep-Learning Model for Fault Diagnosis of Rolling Bearings. Measurement 2021, 169, 108502. [Google Scholar] [CrossRef]
- Wang, J.; Mo, Z.; Zhang, H.; Miao, Q. A Deep Learning Method for Bearing Fault Diagnosis Based on Time-Frequency Image. IEEE Access 2019, 7, 42373–42383. [Google Scholar] [CrossRef]
- Saucedo-Dorantes, J.J.; Arellano-Espitia, F.; Delgado-Prieto, M.; Osornio-Rios, R.A. Diagnosis Methodology Based on Deep Feature Learning for Fault Identification in Metallic, Hybrid and Ceramic Bearings. Sensors 2021, 21, 5832. [Google Scholar] [CrossRef]
- Cristescu, N.D.; Craciun, E.-M.; Gaunaurd, G.C. Mechanics of Elastic Composites (CRC Series in Modern Mechanics and Mathematics). Appl. Mech. Rev. 2004, 57, B27. [Google Scholar] [CrossRef]
- Li, Y.; Wang, J.; Feng, D.; Jiang, M.; Peng, C.; Geng, X.; Zhang, F. Bearing Fault Diagnosis Method Based on Maximum Noise Ratio Kurtosis Product Deconvolution with Noise Conditions. Measurement 2023, 221, 113542. [Google Scholar] [CrossRef]
- Wang, Q.; Xu, F. A Novel Rolling Bearing Fault Diagnosis Method Based on Adaptive Denoising Convolutional Neural Network under Noise Background. Measurement 2023, 218, 113209. [Google Scholar] [CrossRef]
- Yin, C.; Wang, Y.; Ma, G.; Wang, Y.; Sun, Y.; He, Y. Weak Fault Feature Extraction of Rolling Bearings Based on Improved Ensemble Noise-Reconstructed EMD and Adaptive Threshold Denoising. Mech. Syst. Signal Process. 2022, 171, 108834. [Google Scholar] [CrossRef]
- Kedadouche, M.; Thomas, M.; Tahan, A. A Comparative Study between Empirical Wavelet Transforms and Empirical Mode Decomposition Methods: Application to Bearing Defect Diagnosis. Mech. Syst. Signal Process. 2016, 81, 88–107. [Google Scholar] [CrossRef]
- Huang, N.E.; Shen, Z.; Long, S.R.; Wu, M.C.; Shih, H.H.; Zheng, Q.; Yen, N.-C.; Tung, C.C.; Liu, H.H. The Empirical Mode Decomposition and the Hilbert Spectrum for Nonlinear and Non-Stationary Time Series Analysis. Proc. R. Soc. London. Ser. A Math. Phys. Eng. Sci. 1998, 454, 903–995. [Google Scholar] [CrossRef]
- Tian, S.; Bian, X.; Tang, Z.; Yang, K.; Li, L. Fault Diagnosis of Gas Pressure Regulators Based on CEEMDAN and Feature Clustering. IEEE Access 2019, 7, 132492–132502. [Google Scholar] [CrossRef]
- Wu, Z.; Huang, N.E. Ensemble Empirical Mode Decomposition: A Noise-Assisted Data Analysis Method. Adv. Adapt. Data Anal. 2009, 1, 1–41. [Google Scholar] [CrossRef]
- Torres, M.E.; Colominas, M.A.; Schlotthauer, G.; Flandrin, P. A Complete Ensemble Empirical Mode Decomposition with Adaptive Noise. In Proceedings of the 2011 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Toronto, ON, Canada, 22–27 May 2011; pp. 4144–4147. [Google Scholar]
- Cheng, Y.; Wang, Z.; Chen, B.; Zhang, W.; Huang, G. An Improved Complementary Ensemble Empirical Mode Decomposition with Adaptive Noise and Its Application to Rolling Element Bearing Fault Diagnosis. ISA Trans. 2019, 91, 218–234. [Google Scholar] [CrossRef]
- Yang, Y.; Li, S.; Li, C.; He, H.; Zhang, Q. Research on Ultrasonic Signal Processing Algorithm Based on CEEMDAN Joint Wavelet Packet Thresholding. Measurement 2022, 201, 111751. [Google Scholar] [CrossRef]
- Zhou, H.; Yan, P.; Yuan, Y.; Wu, D.; Huang, Q. Denoising the Hob Vibration Signal Using Improved Complete Ensemble Empirical Mode Decomposition with Adaptive Noise and Noise Quantization Strategies. ISA Trans. 2022, 131, 715–735. [Google Scholar] [CrossRef] [PubMed]
- Qian, P.; Tian, X.; Kanfoud, J.; Lee, J.; Gan, T.-H. A Novel Condition Monitoring Method of Wind Turbines Based on Long Short-Term Memory Neural Network. Energies 2019, 12, 3411. [Google Scholar] [CrossRef]
- Zhang, X.; Wan, S.; He, Y.; Wang, X.; Dou, L. Teager Energy Spectral Kurtosis of Wavelet Packet Transform and Its Application in Locating the Sound Source of Fault Bearing of Belt Conveyor. Measurement 2021, 173, 108367. [Google Scholar] [CrossRef]
- Han, T.; Liu, Q.; Zhang, L.; Tan, A.C.C. Fault Feature Extraction of Low Speed Roller Bearing Based on Teager Energy Operator and CEEMD. Measurement 2019, 138, 400–408. [Google Scholar] [CrossRef]
- Wang, L.; Shao, Y. Fault Feature Extraction of Rotating Machinery Using a Reweighted Complete Ensemble Empirical Mode Decomposition with Adaptive Noise and Demodulation Analysis. Mech. Syst. Signal Process. 2020, 138, 106545. [Google Scholar] [CrossRef]
- Chen, W.; Li, J.; Wang, Q.; Han, K. Fault Feature Extraction and Diagnosis of Rolling Bearings Based on Wavelet Thresholding Denoising with CEEMDAN Energy Entropy and PSO-LSSVM. Measurement 2021, 172, 108901. [Google Scholar] [CrossRef]
- Sun, H.; He, Z.; Zi, Y.; Yuan, J.; Wang, X.; Chen, J.; He, S. Multiwavelet Transform and Its Applications in Mechanical Fault Diagnosis—A Review. Mech. Syst. Signal Process. 2014, 43, 1–24. [Google Scholar] [CrossRef]
- Zhan, Y.; Halliday, D.; Jiang, P.; Liu, X.; Feng, J. Detecting Time-Dependent Coherence between Non-Stationary Electrophysiological Signals—A Combined Statistical and Time–Frequency Approach. J. Neurosci. Methods 2006, 156, 322–332. [Google Scholar] [CrossRef]
- Zhou, S.; Zhang, Z.-X.; Luo, X.; Niu, S.; Jiang, N.; Yao, Y. Developing a Hybrid CEEMDAN-PE-HE-SWT Method to Remove the Noise of Measured Carbon Dioxide Blast Wave. Measurement 2023, 223, 113797. [Google Scholar] [CrossRef]
- Antoni, J. The Spectral Kurtosis: A Useful Tool for Characterising Non-Stationary Signals. Mech. Syst. Signal Process. 2006, 20, 282–307. [Google Scholar] [CrossRef]
- Antoni, J. Fast Computation of the Kurtogram for the Detection of Transient Faults. Mech. Syst. Signal Process. 2007, 21, 108–124. [Google Scholar] [CrossRef]
- Antoni, J. Cyclostationarity by Examples. Mech. Syst. Signal Process. 2009, 23, 987–1036. [Google Scholar] [CrossRef]
- Gardner, W.A. The Spectral Correlation Theory of Cyclostationary Time-Series. Signal Process. 1986, 11, 13–36. [Google Scholar] [CrossRef]
- Randall, R.B.; Antoni, J.; Chobsaard, S. The Relationship between Spectral Correlation and Envelope Analysis in The Diagnostics of Bearing Faults and Other Cyclostationary Machine Signals. Mech. Syst. Signal Process. 2001, 15, 945–962. [Google Scholar] [CrossRef]
- Moshrefzadeh, A.; Fasana, A. The Autogram: An Effective Approach for Selecting the Optimal Demodulation Band in Rolling Element Bearings Diagnosis. Mech. Syst. Signal Process. 2018, 105, 294–318. [Google Scholar] [CrossRef]
- Sheen, Y.-T.; Hung, C.-K. Constructing a Wavelet-Based Envelope Function for Vibration Signal Analysis. Mech. Syst. Signal Process. 2004, 18, 119–126. [Google Scholar] [CrossRef]
- Tian, X.; Xi Gu, J.; Rehab, I.; Abdalla, G.M.; Gu, F.; Ball, A.D. A Robust Detector for Rolling Element Bearing Condition Monitoring Based on the Modulation Signal Bispectrum and Its Performance Evaluation against the Kurtogram. Mech. Syst. Signal Process. 2018, 100, 167–187. [Google Scholar] [CrossRef]
- Jablonski, A. Hybrid Model of Rolling-Element Bearing Vibration Signal. Energies 2022, 15, 4819. [Google Scholar] [CrossRef]
- Qiu, H.; Lee, J.; Lin, J.; Yu, G. Wavelet Filter-Based Weak Signature Detection Method and Its Application on Rolling Element Bearing Prognostics. J. Sound Vib. 2006, 289, 1066–1090. [Google Scholar] [CrossRef]
- Gousseau, W.; Antoni, J.; Girardin, F.; Lyon, U.; Griffaton, J. Analysis of the Rolling Element Bearing Data Set of the Center for Intelligent Maintenance Systems of the University of Cincinnati. In Proceedings of the CM2016, Charenton, France, 10–12 October 2016. [Google Scholar]
- Smith, W.A.; Randall, R.B. Rolling Element Bearing Diagnostics Using the Case Western Reserve University Data: A Benchmark Study. Mech. Syst. Signal Process. 2015, 64–65, 100–131. [Google Scholar] [CrossRef]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, D.; Wang, Y.; Jiang, Y.; Zhao, T.; Xu, H.; Qian, P.; Li, C. A Novel Wind Turbine Rolling Element Bearing Fault Diagnosis Method Based on CEEMDAN and Improved TFR Demodulation Analysis. Energies 2024, 17, 819. https://doi.org/10.3390/en17040819
Zhang D, Wang Y, Jiang Y, Zhao T, Xu H, Qian P, Li C. A Novel Wind Turbine Rolling Element Bearing Fault Diagnosis Method Based on CEEMDAN and Improved TFR Demodulation Analysis. Energies. 2024; 17(4):819. https://doi.org/10.3390/en17040819
Chicago/Turabian StyleZhang, Dahai, Yiming Wang, Yongjian Jiang, Tao Zhao, Haiyang Xu, Peng Qian, and Chenglong Li. 2024. "A Novel Wind Turbine Rolling Element Bearing Fault Diagnosis Method Based on CEEMDAN and Improved TFR Demodulation Analysis" Energies 17, no. 4: 819. https://doi.org/10.3390/en17040819
APA StyleZhang, D., Wang, Y., Jiang, Y., Zhao, T., Xu, H., Qian, P., & Li, C. (2024). A Novel Wind Turbine Rolling Element Bearing Fault Diagnosis Method Based on CEEMDAN and Improved TFR Demodulation Analysis. Energies, 17(4), 819. https://doi.org/10.3390/en17040819






