Abstract
Accurate instantaneous electricity peak load prediction is crucial for efficient capacity planning and cost-effective electricity network establishment. This paper aims to enhance the accuracy of instantaneous peak load forecasting by employing models incorporating various optimization and machine learning (ML) methods. This study examines the impact of independent inputs on peak load estimation through various combinations and subsets using multilinear regression (MLR) equations. This research utilizes input data from 1980 to 2020, including import and export data, population, and gross domestic product (GDP), to forecast the instantaneous electricity peak load as the output value. The effectiveness of these techniques is evaluated based on error metrics, including mean absolute error (MAE), mean square error (MSE), mean absolute percentage error (MAPE), root mean square error (RMSE), and R2. The comparison extends to popular optimization methods, such as particle swarm optimization (PSO), and the newest method in the field, including dandelion optimizer (DO) and gold rush optimizer (GRO). This comparison is made against conventional machine learning methods, such as support vector regression (SVR) and artificial neural network (ANN), in terms of their prediction accuracy. The findings indicate that the ANN and GRO approaches produce the least statistical errors. Furthermore, the correlation matrix indicates a robust positive linear correlation between GDP and instantaneous peak load. The proposed model demonstrates strong predictive capabilities for estimating peak load, with ANN and GRO performing exceptionally well compared to other methods.
1. Introduction
Estimating energy needs involves addressing various prediction challenges within the utility sector. These challenges include forecasting demand, generation, prices, and power load across different timeframes and capacities [1]. Electricity plays a pivotal role as the primary energy source for powering industries and enabling modern life. Electricity demand is closely intertwined with economic and population growth. Ensuring the stability of electricity supply requires accurate planning of electricity generation capacity, which, in turn, necessitates reliable electricity load forecasting.
Electricity load forecasting aims to achieve a harmonious balance between production and consumption, utilizing the potential of forecasting models [2,3]. Precise electricity load forecasting can mitigate the risk of power outages and reduce the expenses associated with surplus electricity generation capacity. This is particularly relevant for short-term (ST) load forecasting, which involves higher uncertainty levels than long-term (LT) aggregated planning. In essence, ST load forecasting aims to predict electricity demand within hourly to weekly intervals. Its primary objectives are to ensure power security, facilitate the efficient scheduling of power plant operations, and enable effective load dispatching [4,5].
Electricity load forecasting provides valuable insights for maintaining the security and stability of the electricity system, achieving a balance between electricity generation and consumption, and informing decision making in the electricity sector. These efforts aim to minimize economic losses at a national level and safeguard the environment [6]. Power companies primarily aim to deliver their customers an adequate and dependable power supply. As a result, the operation and planning of power systems heavily depend on load forecasting [7]. To facilitate informed decision making and planning, various forecasting models have been developed to predict peak load, energy consumption, and production. These models take into account economic, demographic, geographical, and social factors [8].
Excessive activations of power supply units, resulting in increased energy consumption and surplus reserves, occur when the load estimates exceed electricity demands. Conversely, lower load projections can push the system into a precarious situation, leading to insufficient supply [9]. Nonetheless, load and demand forecasts serve as the foundation for various decisions in the energy market, enabling the efficient, transparent, and dependable planning and administration of electricity markets to meet the sector’s requirements [10].
Machine learning (ML) has gained popularity for automatically identifying valuable patterns in large datasets. ML is a widely used technique for classification and regression tasks and is known for its excellent performance. Supervised machine learning (SML) algorithms are the preferred choice for forecasting studies as they involve generating general hypotheses based on externally provided instances to predict future ones [11]. Various SML techniques have been proposed in the literature, with support vector machines (SVM), artificial neural network (ANN), and naïve Bayes classifier (NBC) being among the most popular [12,13]. Deep learning (DL), also known as ANN, is a subset of ML that enables computers to learn through a hierarchical set of concepts across multiple layers. Each concept is defined in terms of simpler ones, and this hierarchy of concepts facilitates the learning of complex scenarios. ANNs come in various types, categorized based on their network structure and operating algorithms, such as long–short-term memory (LSTM) and multilayer perceptron (MLP) [14]. A study by [15] found that support vector regression (SVR) outperformed binary nonlinear fitting regression in estimating various types of electricity consumption.
Research by [16] employed a hybrid data mining algorithm, the PSO-SVR method, to forecast LT electricity load and demand. Ref. [17] developed a hybrid framework for ST electricity load forecasting. Their model uses linear regression and XGBoost to decompose raw load data into fluctuation sub-series and trend series. The model’s performance was assessed using smart meter data from China and Ireland.
For a significant period, improving the precision of forecasting electrical energy load—both peak load and electricity consumption—has been a significant area of research. Over the years, researchers have developed various prediction techniques [18], categorized into two broad categories: time series models based on econometrics and ML (or deep) models based on AI algorithms [19,20]. Both model types perform well in predicting peak load when electricity market conditions exhibit a consistent trend [21]. However, when the market undergoes rapid nonlinear changes, time series models are unable to provide accurate forecasts because they rely on linear formulations based on previous time steps. In such cases, ML models that can handle nonlinear data outperform time series models [22].
Peak load forecasting has been a topic of substantial interest in both ML and time series models. Moreover, ML models have been applied to forecast factors such as power generation and electricity prices, which are closely linked to peak load and demand [23,24]. Classical methods employ various statistical modelling techniques, including exponential smoothing, Kalman filters, time series analysis, the Box–Jenkins model, and regression. These options offer diverse choices for model creation, such as SVR [25], grey models [26,27,28], autoregressive integrated moving average (ARIMA) methods [29,30], ANNs [31,32,33], and hybrid models [34,35,36].
Both [37] and [38] examined the use of the adaptive neuro-fuzzy inference systems (ANFIS) method for ST load forecasting. Similarly, [39] applied the ANFIS method to predict LT peak loads in Gulf Cooperation Council countries. These studies concluded that the ANFIS method outperformed other models in accuracy. Extensive research has focused on utilizing ML models for forecasting, resulting in hybrid models integrating statistical and traditional models with contemporary ML models [40]. Ref. [41] proposes an ST electric load forecasting model utilizing the back propagation neural network (BPNN) algorithm, employing the particle swarm optimization (PSO) and genetic algorithm (GA) to optimize the BPNN parameters.
Due to their performance, ANNs have gained increasing popularity in the field of energy and peak load estimation. They particularly excel when handling large datasets, as they require substantial data for effective model training [42]. A review by [43] focused on using ANN algorithms to predict hourly energy consumption. The study found that the ANN algorithm consistently delivers excellent results for single- and multistep-ahead forecasting. It concluded that data-driven methods like ANN are well suited for energy load prediction. In another study, the performance of ANN and SVM was compared to forecast the hourly electricity load in office buildings. The dataset included information from 507 buildings, with input features such as meteorological data (wind speed, atmospheric pressure, dew point, outdoor temperature) and building data (floor type and area). The findings indicated that ANN outperformed SVM, as evidenced by a lower root-mean-square error (RMSE) value of 5.71 compared to 7.35, respectively [44].
Recently, researchers have recognized the effectiveness of combining various methods, leading to the development of hybrid models to improve prediction accuracy. These hybrid models integrate techniques such as traditional forecasting models (e.g., linear regression and grey models), seasonal adjustment/quarterly average methods, and intelligent optimization algorithms like PSO [45], sine cosine algorithm (SCA) [46], and whale optimization algorithm (WOA) [9,47], among others. As a result, numerous hybrid forecasting models have emerged and are used in applications in various domains, including electricity load and price prediction [48,49,50,51] and wind energy prediction [32,52,53].
DO and GRO metaheuristic algorithms show significant performance in solving engineering problems. Metaheuristic optimization methods can be used to forecast problems such as energy and electricity peak load forecasting. Often, metaheuristics are used to search for variables in optimization problems, but these methods can also be effective in developing predictive models and obtaining meaningful predictions from complex, dynamic data sets. In energy and electricity peak load prediction, metaheuristics can often be used to optimise model parameters or find the most suitable model structures. For example, to ensure the best performance of a model used for energy consumption prediction, the parameters of these models (e.g., weights and hyperparameters) can be optimized using metaheuristic methods. Investigating different model structures or feature combinations can also be an application area of metaheuristic optimization.
Despite all these positive features, ML and optimization are still faced with challenges when applied to real-world problems. The practical use of ML has faced specific challenges, particularly in engineering or physics-related scenarios [54]. Initially, the training of these methods often necessitates high-quality training data to ensure optimal performance. Nevertheless, obtaining such training data proves to be costly, or data are scarce across various scenarios. Furthermore, ML models can probably generate results that might be physically implausible without attentive design and domain-specific expertise. Lastly, it remains impractical to establish a theoretical assurance regarding the generalizability of ML, meaning that ML cannot ensure consistent performance beyond the data it was trained on [55].
This study compares the performances of traditional methods such as ANN, MLR, PSO, and SVR, which are used in the literature for peak load prediction, and current optimization methods such as GRO and DO. The fact that GRO and DO optimization algorithms have not been used for peak load prediction before and that they are more efficient than other algorithms in the literature has resulted in effective choices for these two new algorithms [56,57].
The contributions of this study can be summarized in the following points:
- Recommends the current and effective optimization algorithm models for estimating instantaneous electricity peak load. Notably, it emphasizes the utilization and advantages of the recently developed DO and GRO in this context, showcasing their efficiency and suitability.
- Through an evaluation process using error metrics applied to inter-monthly data, this study rigorously assesses and analyses the accuracy of forecasting methods for predicting instantaneous peak load, offering comprehensive insights into the precision of the forecasting model.
- Provides predicted instantaneous peak load results as dependable and informative references for optimizing future energy resource planning and allocation strategies, facilitating informed decision making.
- Utilizing the framework of multiple linear regression (MLR), this study systematically investigates and analyses the impact of diverse combinations and subsets of independent inputs on the forecast output, particularly for estimating instantaneous peak load and elucidating critical dependencies and relationships.
- Involves a technical analysis aimed at determining the optimal parameters of the method, utilizing output–input correlation matrices. This reveals the extent to which the input (independent) data influence the output (dependent) data and provides deeper insights into the modelling process.
- The accurate prediction of instantaneous peak load, as accomplished in this study, significantly contributes to operational efficiency by effectively steering the prevention of unnecessary reserves and ensuring the optimized functioning of the energy system, thereby providing effective resource utilization.
The rest of the paper is organised as follows: Section 2 presents the materials and methods, including the MLR, ANN, SVR, PSO, DO, and GRO algorithms, and error metrics. Section 3 details the proposed techniques. In Section 4, we analyse and compare the experimental results of these algorithms. Finally, Section 5 provides the conclusions and outlines future work.
2. Materials and Methods
This research utilized various forecasting techniques, including the MLR, ANN, SVR, PSO, DO, and GRO, to assess the accuracy of estimating instantaneous peak load. The performance of these diverse ML methods underwent evaluation using input variables. Following the analysis, ANN and GRO emerged as the preferred choices due to their enhanced predictive precision.
Furthermore, the comparison extended to both established (PSO) and emerging (DO and GRO) optimization methods within the field, contrasting their prediction accuracy against conventional ML techniques. Based on the results of the statistical analysis, we identified the forecasting method that demonstrated the most favourable performance in predicting the output. Various error metrics (MAE, MAPE, RMSE, MSE, and R2) were utilized to evaluate and compare how effectively the methods estimated outcomes. The correlation matrix illustrates the interrelationships among independent variables (import, export, population, and GDP) and the dependent variable (instantaneous peak load). This matrix highlights the extent to which each variable influences peak load. Furthermore, the input parameters (import, export, GDP, and population) are further split into subsets within different regression equations. These equations unveil the influence of each parameter on R2 and p-value performance, providing insight into how much they affect the output.
2.1. Multiple Linear Regression Modelling
The MLR model is a methodology that establishes the causal relationship between independent and dependent variables through a mathematical framework. The MLR model accurately defines the connections among these variables, precisely characterising their associations [3].
In peak load forecasting, multiple regression analyses find widespread use. In this context, the dependent variable “y” is considered a function of several independent variables (x1, x2, …, xk) [58]. This mathematical relationship can be represented as follows:
Equation (1) represents the peak load demand as variable y, where the regression coefficients a0, a1, and a2 are currently unknown. This equation includes the exogenous variables x1 and x2. Utilizing the multiple regression approach allows for determining a0, a1, and a2 by minimizing the sum of squared projected errors. Moreover, these coefficients elucidate the distinct effects of each independent variable on the dependent variable. Equation (2) can be restated as follows:
Equation (2) employs the parameters a, b, and c in the regression analysis of the mean value of y concerning x1 and x2, with c representing an exogenous factor. These equations can be conveniently expressed using matrix notation [3].
where terms y, x, , and ε are defined through Equations (4)–(7).
where y is the scalar response, to are scalar regression coefficients, and the vector component denoted by x represents each independent parameter. The subscript k is utilized to indicate the number of independent variables, while the subscript n denotes the number of historical observations, and ε1 to εk are the scalar noise terms (biases) of the model. The MLR technique is applied to determine unknown coefficients of to .
In this specific investigation, the technique of least squares fitting has been employed to predict the regression coefficients in the MLR model. The process of creating a fit using a linear model involves minimizing the sum of the squares of the residuals. Graphically representing the residuals offers a deep insight into the appropriateness of the fit. Furthermore, the goodness of fit can be assessed using the coefficient of determination (R²) and the adjusted coefficient of determination (), both of which indicate the degree of correspondence between the obtained values and the model’s dependent variable.
When the least squares method (utilizing metrics like R-squared, F-test, and RMSE) is translated into defined matrix notations to achieve zero error, it can be transformed as shown below:
Certainly, here is the revised paragraph:
By solving Equation (8), the parameters a, b, and c are computed. In this context, y represents the electricity demand, x1i and x2i denote historical independent variables, and Xni (where “n” depends on the number of independent variables) refers to additional variables. Furthermore, “n” stands for the number of years being forecasted.
The peak load forecast results can be obtained by substituting the regression parameters into Equation (2).
2.2. Artificial Neural Networks
Artificial intelligence focuses on researching and developing techniques that enable machines to exhibit cognitive abilities comparable to those of humans. These abilities include reasoning, judgment, emotional experiences, language comprehension, and problem solving. One prominent technique in AI is the use of ANNs, designed to replicate the architecture of the human brain. However, unlike the approximately 15 billion neurons in the human brain, the number used in an ANN is determined by the specific demands of the task at hand [9].
An ANN consists of three fundamental layers: the input, hidden, and output. Every individual neuron establishes a connection with a subsequent neuron in the following layer through weight multiplication. Therefore, weights play a pivotal role in influencing the level of interconnectedness among inputs. In contrast, the summation function constitutes the phase where the product of each input data point (multiplied by its respective weight) is aggregated alongside a threshold data point. The neuron’s output is calculated using Equations (9) and (10), presented in mathematical notation.
In this context, “i“ defines the input parameter data, “Xi” previous layer values, “j” denotes the number of neurons, “a” signifies the weighted inputs sum, “f” represents the transfer function, “w” stands for weight, and “y” corresponds to the output (dependent) data. Equation (11) defines the sigmoid transfer function as shown below:
This paper employs a feedforward multilayer perceptron neural network to forecast instantaneous peak load. The ANN architecture consists of a hidden layer with ten neurons, an input layer with five neurons, and an output layer with one neuron. Input variables, including import, export, population, and GDP, were utilized to predict peak load, which is the ANN model’s output [59].
2.3. Support Vector Regression
A comprehensive study has been conducted to utilize SVM to solve regression problems. In regression problems, when training examples are given in the form of , the response variable is defined as instead of . Let us consider that the conditions stated in Equation (12) are satisfied by the dataset [60].
In Equation (12), represents the input vector in the space of dimension d; w stands for the output vectors, the normal of the hyperplane, which is also the weight vector; and the bias is represented by b.
SVR is divided into linear and nonlinear support vectors. As depicted in Figure 1, in a linear SVR, the assumption is made that the relationship between X and Y is linear. The initial determination of the maximum value of the training error indicates that the error term is represented accurately for data equal to or less than ε [61].
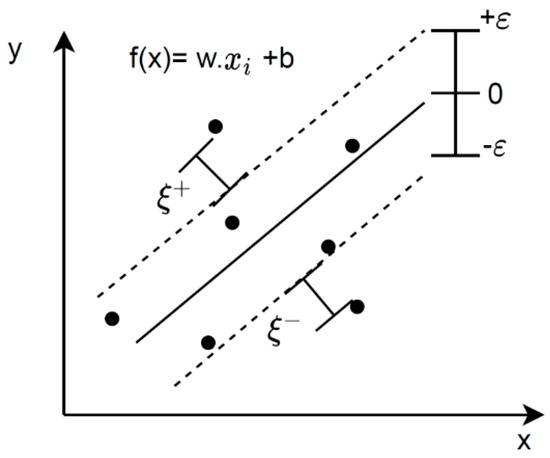
Figure 1.
ε tube for linear regression function.
In nonlinear DVR, by expanding the feature space, nonlinear functions can be created with linear learning machines in the input space given in Figure 2 [61].
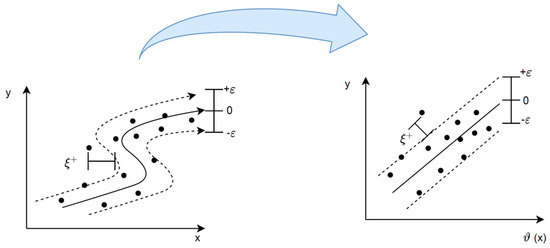
Figure 2.
ε tube for nonlinear regression function.
2.4. Particle Swarm Optimization
PSO, an intelligent stochastic algorithm based on swarm intelligence, effectively addresses optimization challenges across various domains [62,63,64]. In this approach, a swarm, consisting of individual particles representing potential solutions, continuously adjusts its positions within a multidirectional search space until the optimal outcome is achieved, all while considering computational constraints. The speed at which the solution is approached varies randomly, often resulting in individuals within the group finding themselves in improved positions with each new movement. This iterative process concludes upon achieving the defined objective [65,66].
The fundamental factors of utmost significance within the PSO algorithm involve characterizing velocity and position for individual particles. The subsequent renewal regulations, combining stochastic and deterministic components, elucidate the process of updating a particle’s speed and position. The particle’s upcoming position is calculated by employing Equations (13) and (14) to determine the new velocity and position vector. These equations are derived from data pertaining to the particle’s previous positions. The collective velocities of the particles are demonstrated through the velocity vector outlined in Equation (13) [67].
The velocity vector comprises three elements. The first is the inertia coefficient (w), which is necessary to maintain the current velocity and preserve the ongoing direction of motion. The second element corresponds to the cognitive component, often referred to as individual factors in scholarly works. This represents the disparity between each particle’s position and its own best value (PBEST). Lastly, there is the social component. This component delineates each particle separation from the best value (GBEST) achieved by the rest of the swarm collective. The formula incorporates coefficients denoted as r1 and r2, introducing stochastic elements into the algorithm, with values ranging from zero to one. Concurrently, the coefficients c1 and c2 play a role in assigning significance to the stochastic factors’ acceleration. demonstrates the personal best solution. Initial lower limit and upper limit data are randomly assigned in the initial phase. The particle count is set at 50, with both C1 and C2 taking on a value of 2 each. The maximum iteration (MaxIter) is defined as 100, and the inertia values Wmax and Wmin are established as 0.9 and 0.2, respectively [3]. Each individual particle position is:
indicated through the employment of the position vector illustrated in Equation (14).
To define each particle’s next position’ , the velocity value in the next iteration is added to its current position (). In every iteration, there is a continuous update of position, velocity, PBEST, and GBEST values. The index i in the equations signifies the particle number, while the superscript t indicates the iteration count [68]. This study developed a more accurate prediction model by optimizing linear regression parameters with PSO.
2.5. Dandelion Optimizer Algorithm
Heuristics methods are behaviours from natural processes. DO is a next-generation nature-inspired optimization algorithm that uses swarm intelligence to tackle continuous optimization problems. DO was developed with inspiration from the wind-blown behaviour of the dandelion plant. Seeds travel in three stages: ascending, descending, and settling in a random location during the landing stage. As shown in Figure 3a, the pieces that break off from the plant start to fly, spin, and fly away, as shown in Figure 3b. This algorithm has undergone validation and testing using the CEC2017 international standard benchmark functions [56].
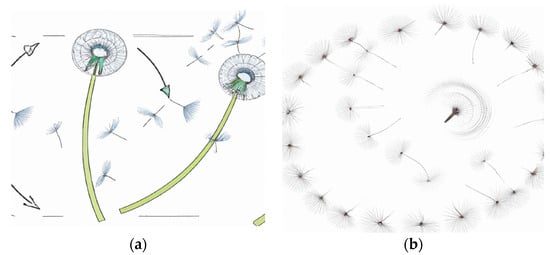
Figure 3.
Dandelion plant spreading behaviour, (a) pieces that break off from the plant/ (b) the state of pieces flying, turning and flying away.
The outlined DO algorithm mathematical procedures can be summarized as shown below:
2.5.1. Initial Population
The random starting points population is defined.
In this context, pop signifies the population magnitude, and Dim represents the dimensionality of the variable. Every potential solution is generated randomly, falling within the range defined by the upper bound (UB) and the lower bound (LB) of the specific problem. The individual i, denoted as Di, is articulated as follows. The term “rand” corresponds to a function that produces values distributed randomly within the interval [0, 1] [69].
2.5.2. Calculation of Fitness Values
Fitness function evaluations are performed for each individual within the problem under optimization. The individual that exhibits the highest fitness value is regarded as the elite candidate. fbest is the most suitable position for the dandelion seed to flourish. The initial elite candidate (Delite) solution can be represented mathematically as follows [69,70]:
2.5.3. Ascension Stage
Individuals’ updated positions are established based on their fitness function values, leading to upward movement. Analogously, chamomile seeds ascend to varying altitudes due to factors like wind speed and air humidity. In this context, weather conditions are categorized into the subsequent two states.
Case 1: Under clear atmospheric conditions, wind velocities can be approximated using a lognormal distribution, lnY∼N (μ, σ2). The computation of the seeds’ updated positions is determined by the expression provided in Equation (18).
In this context, Dt symbolizes the dandelion seed position in the tth iteration. Ds denotes a location within the search region that is randomly selected during the tth iteration. The coefficients vx and vy stand for the lift component factors linked to the distinct aerial motion of the dandelion. δ is a coefficient ranging from 0 to 1, which follows a nonlinear reduction pattern converging towards zero.
The lognormal distribution given in Equation (18) is defined as µ = 0, and σ2 = 1 and can be expressed by the following Equation (19) [56]:
Within the DO algorithm, the selection of the y value is governed by the standard normal distribution within the range of (0, 1). In each iteration of the algorithm, an adaptable factor denoted as ‘γ’ is employed to manage the extent of the search operation across the entirety of T iterations. The formulation of γ is outlined as follows [69,70]:
Case 2: On days characterized by rain, the ascent of dandelion seeds is impeded by elements like air resistance, humidity, and various other variables. Consequently, these seeds exhibit a tendency to remain in proximity to their initial position, and their actions can be accurately elucidated through a specific mathematical equation.
The parameter “p” is employed to control the extent of the local search region for a dandelion, and its calculation is determined by the expression presented in Equation (22). Its value is dynamically adjusted in every iteration, contingent upon both the maximum iteration count and the available number of iterations [71].
In this context, T defines the iterations’ maximum number, and t demonstrates the value of the number of iterations available.
2.5.4. Descent Phase
During the ascension phase, individuals descend to the altitude established and, subsequently, their positions are modified.
In this instance, βt signifies the Brownian motion, which results from selecting a random number from the standard normal distribution, and α is an adaptive parameter used to adjust the search step length [72]. indicates the population mean position in the i th iteration.
2.5.5. Landing Location Determination
As a result of wind and atmospheric conditions, seeds come to rest in a randomly chosen spot in their updated position. As the population advances, the ultimate best solution for the entire group is denoted by Equation (24).
In this context, refers to the best (most optimal) position the dandelion seed attains in the ith iteration. The function levy(λ) is indicative of the Levy flight and its determination is governed by the subsequent equation [73]:
In this equation, B is assigned a random value within the range of [0, 2]. The constant S holds a fixed value of 0.01. It is randomly chosen between the values of ω and t, within the range of [0, 1]. The calculation for σ is as follows [71,72,73]:
2.6. Gold Rush Optimizer Algorithm
GRO, an optimization algorithm rooted in meta-heuristics, draws inspiration from the actions of real gold prospectors. By emulating the movements of these prospectors, the algorithm addresses a range of optimization problems, capitalizing on its exploratory and prospection attributes. The GRO algorithm is structured around five fundamental phases that mimic gold prospectors’ behaviours: exploration, core formation, main core, dispersion, and final decision stage. In each of these stages, new solution contenders are generated by integrating existing solutions with investigative and exploratory potential, all aimed at identifying the most optimal solution from this pool of candidates [57,74].
Gold prospectors’ location is stored in a GGP matrix, as demonstrated in Equation (27). In this equation, Gij defines the position of the i-th seeker in the j-th dimension. d shows dimension, and n represents gold prospector [57,74].
A certain objective function is necessary for appraising the gold prospectors, and the outcomes of assessing the fitness function of these prospectors are logged in the FGP matrix defined by Equation (28). In this matrix, Gij denotes the location of the i-th seeker within the j-th dimension. The variable d signifies the dimension, n stands for the gold prospector, and f indicates the fitness function [57,74].
When a gold mine is found, individuals interested in prospecting for gold move to that region to extract gold. In the process of executing the metaheuristic algorithm, the best point within the exploration area is pinpointed to symbolize the site of the most lucrative gold mine. Because the precise location of this mine is not known, the position of the most successful gold prospector is employed as an estimation for the optimal mine location, as illustrated in Figure 4. The movement of a gold prospector toward the gold mine is simulated through the utilization of Equations (29) and (30) Formun Üstü [57].
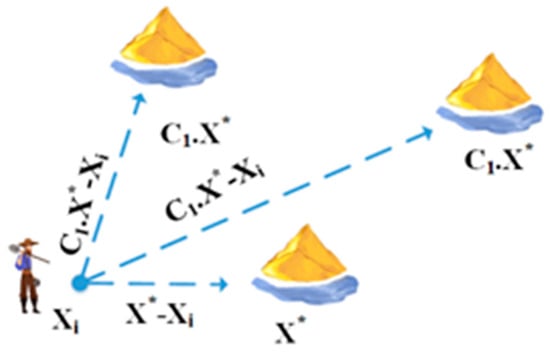
Figure 4.
Equation (22) schematic structure in two dimensions.
, , and t, determine the position of the best gold mine, respectively, the i-th gold prospector position, and t the current iteration. , where i is the new gold prospector position, and and are the vector coefficients calculated as given in Equations (31) and (32) [74].
and , are random vectors whose values are in the range [0, 1]. l1 is the convergence component defined by Equation (33). If e is equal to 1, it decreases linearly from 2 to value and nonlinearly decreases for values greater than 1.
To mathematically represent the scenario of gold prospecting, each gold prospector position approximates a gold mine’s location. The related mathematical correlations pertaining to gold mining are presented in Equations (34) and (35) [57].
, , t, and indicate the randomly chosen gold finder, the position of the i-th gold digger, t the current iteration, and the new position of the i-th gold finder, respectively. A2 is the vector coefficient transformed and defined by Equation (36).
In this equation, the parameter l2 is employed instead of l1 to enhance the mining method’s exploitation potential.
The collaborative nature of gold prospecting has led to the mathematical Equations (37) and (38)’s application to shed light on cooperation among prospectors. In this context, g1 and g2 represent a pair of gold prospectors selected at random. A three-person cooperation is performed between i, gl and g2, and is the cooperation vector [57,74].
Gold prospectors can move their positions as time progresses. While engaged in gold mining, these prospectors can shift from their present locations to explore uncharted regions or discover additional gold deposits. This procedure is mathematically depicted in Equation (39).
The GRO method starts with a gold prospector’s initial population scattered randomly in the exploration region. The most optimal position found during exploration becomes the primary gold mine (global optimum). In each iteration, prospectors move based on three strategies: gold mining, collaboration, or migration. The prospector moves if the gold quantity at the new position (measured by the objective function) is better. This procedure persists until the iteration concludes and the algorithm’s result is determined to be the best solution obtained [57,74].
2.7. Error Metrics
Error metrics, also known as performance metrics or evaluation metrics, are criteria used to assess the performance of a model or an algorithm. These metrics are used to understand how well a model performs and to evaluate the alignment between a model’s predictions and actual values. They encompass several fundamental measures: MAE, which calculates the average absolute differences between actual and predicted values; MSE, determining the average of squared differences between actual and predicted values; and RMSE, the square root of MSE that provides a scaled perspective of errors in relation to actual values. Additionally, MAPE computes the average of absolute percentage errors about actual values, which is particularly useful in evaluating time series data [75,76].
Additionally, the correlation coefficient R defines the correlation between actual and predicted data [77]. The R2 value signifies the extent to which variations in the dependent variable can be changed to differences in the independent variable. Its range lies between 0 and 1, with 0 < R2 < 1, with values closer to 1 indicating a stronger alignment of the regression line. This suggests that alterations in the independent data contribute significantly to changes in the dependent. The mathematical expressions for MSE, R2, MAE, MAPE, and RMSE can be found in Equations (40)–(44) [3,9,78,79,80,81,82,83].
Note: represent the predicted value, actual value, sample size, mean predicted value, and mean actual value, respectively.
3. Proposed Model
This research focuses on analysing potential socio-economic factors impacting the growth of electricity peak load in Turkey’s electrification system. Initially, data from 1980 to 2020 concerning monthly electricity peak load were gathered from the Turkish Electricity Transmission Corporation to comprehend historical patterns [84]. After calculating monthly averages, this process resulted in a dataset of 492 rows and five columns. Subsequently, the investigation aimed to identify the key variables significantly affecting instantaneous electricity peak load prediction. The model was formulated utilizing four input factors encompassing socio-economic indicators and an output factor of electricity peak load measured in megawatt-hours (MWh). Population statistics were sourced from the Turkish Statistical Institute (TSI) [85], while import, export, and GDP data were obtained from the World Bank Open Database [86]. Import, population, export, and GDP figures were used as inputs, with electricity peak load serving as the output variable.
The initial crucial step in developing and training the models involved data pre-processing. Firstly, all variables were consolidated and organised into a single Excel file in an appropriate format. This organized file was then imported into MATLAB R2021b. Following this, the complete dataset was divided into different sets: a test set (20%), a training set (70%), and a validation set (10%), while preserving the chronological order within the data. Specifically, the data from 1980 to 2007 were allocated to the training set, data between 2008 and 2015 were earmarked as the test set, and values from 2016 to 2020 were assigned to the validation set monthly. Whether developing, stagnant, or declining, the direction of GDP growth influences electricity peak load estimation. In a developing nation, industrialization leads to increased income and heightened electricity demands. The new constructions correspond to new consumption points, implying that as a population grows, electricity consumption is likely to increase [87]. Previous research has indicated that exports and imports generally exhibit positive correlations with electricity consumption [88].
The numerical computations were conducted on a laptop with a quad-core processor running at 2.40 GHz and on 16.00 GB of RAM. As mentioned, simulations employed the MLR, ANN, SVR, DO, GRO, and PSO algorithms (Figure 5). MATLAB source codes for MLR, ANN, SVR, PSO, DO, and GRO were adapted and applied to address the prediction of instantaneous electricity peak loads.
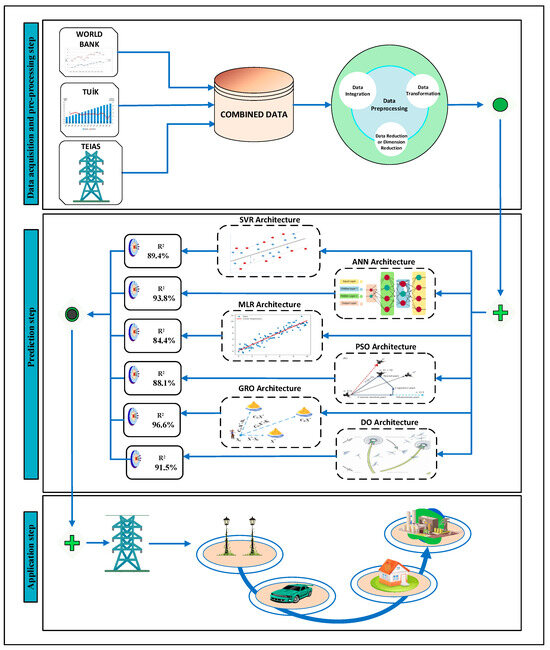
Figure 5.
Methodology diagram.
For all optimization algorithms, a population size of 50 individuals with a maximum of 100 iterations was set. Each optimization was repeated ten times for every modulation index value, and the best outcomes were recorded in tabular form. Input variables such as import, export, population, and GDP were used to predict peak load, serving as the output in the ANN architecture. The MATLAB Neural Network Toolbox was employed for constructing the ANN structure, following the feedforward pattern inherent in multilayer perceptron neural networks regarding layer and neuron arrangement.
4. Results and Discussion
4.1. Instantaneous Peak Load Forecasting
Turkey faces significant electricity demands, with a substantial portion met through imports. As the global landscape has evolved, driven by population growth and the integration of new technologies into daily life, the demand for electricity has increased. Achieving sustainable development requires Turkey’s increasing reliance on domestic sources to power its growing 2023 population. To realize this goal, the primary electricity requirements are calculated for the upcoming years, and strategies are explored to meet these demands. Accurate electricity peak load and demand estimation are essential for strategic investments in power systems and intelligent grid facilities. The choice of the appropriate forecasting approach is of paramount importance, as it can lead to reduced electricity costs and time savings. Economic and demographic factors such as imports, exports, GDP, and population are commonly employed in predicting peak load and electricity demand.
The results produced by the ANN closely match the official findings. Among the various techniques, the GRO method demonstrated superior performance. Figure 6 illustrates a comparison between the output predicted by GRO and the peak load real data. The GRO method generates estimations that closely align with the actual data. Figure 7 compares the real peak load values from 1980 to 2020 with the forecasted data from the six methods (PSO, ANN, SVR, MLR, DO, and GRO). The actual data align with both the GRO and ANN methods.
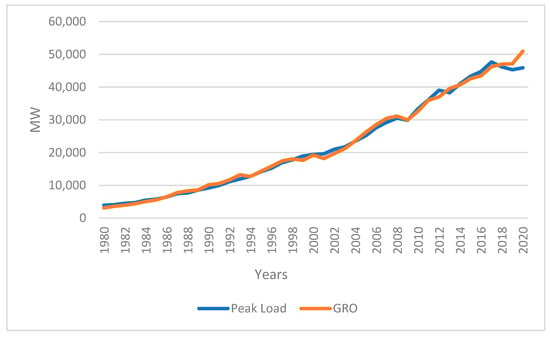
Figure 6.
Real and estimated values for peak load by the GRO method.
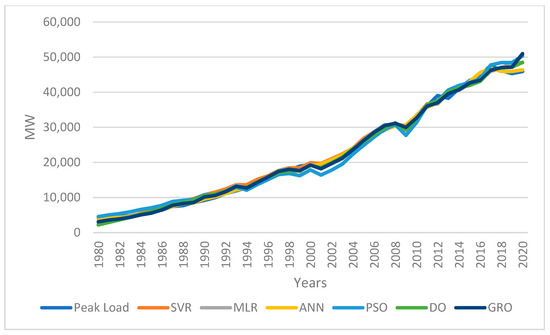
Figure 7.
Comparison between estimated values for peak loads with different uses of models and real data.
4.2. Error Metrics
In the literature and experimental studies, RMSE, MSE, MAE, MAPE, and R2 are commonly chosen and widely used indicators to assess method performance. A higher R2 value shows a more effective prediction by the applied method’s performance. RMSE relies on the sample standard deviation of the differences between estimated and actual values [89]. MAE measures the differences between two data points and is often preferred for its straightforward interpretability, finding application in regression and time series scenarios [90].
Table 1 displays the mean data of MSE, RMSE, MAPE, MAE, and R2 using the ANN, SVR, MLR, PSO, DO and GRO methods. Additionally, it is evident that while the R2 values obtained by GRO and ANN were higher than the others, the MAPE, RMSE, MAE, and MSE data obtained by GRO and ANN were lower than those of the other methods. This suggests that GRO’s forecasting performance outperforms the other methods.

Table 1.
Statistical analysis results.
4.3. Multi Regression Equations
Within Table 2, the initial row displays the multi-regression equation characterized by four parameters (a, b, c, and d, which are import, export, population, GDP), boasting the highest R2 value of 0.995. This underscores the robust representation of the relationship amid the F equations by this four-parameter equation. Notably, the equations that lack the variables c and d in Equation (55) (as shown in Table 2) exhibit low R2 performance, implying limited generalization capabilities for these equations. Nevertheless, the d coefficient incorporation, identified as having the strongest correlation values among Equations (45)–(54), results in improved R2 performance within the equations. Notably, although the R2 performances among Equations (45)–(54) in Table 2 are closely ranked, ‘a’ stands out as the parameter with the least generalization ability, consequently leading to a lower correlation value.

Table 2.
Regression equations, R2 performance, and multiple subset factors.
4.4. Correlation Matrix
The correlation matrix illustrates relationships among multiple variables within a dataset, with these relationships depicted on a scale ranging from −1 to 1. It is commonly understood that as the relationship value approaches 1, the association between the two variables strengthens; conversely, as it moves towards −1, an inverse relationship becomes more pronounced. When the value approaches zero, it indicates the absence of a linear relationship between the variables [3].
This study constructed a correlation matrix to depict the interplay between an output value (dependent) and input values (independent) using various methods such as MLR, ANN, SVR, PSO, DO, and GRO. The correlation matrix in Figure 8 reveals the connections between specific inputs, such as import, export, GDP, population, and the designated output, which is the electricity peak load. A strong positive linear correlation (0.9872) exists between GDP and instantaneous peak load. Similarly, a robust positive linear relationship (0.9692) is observed between GDP and population.
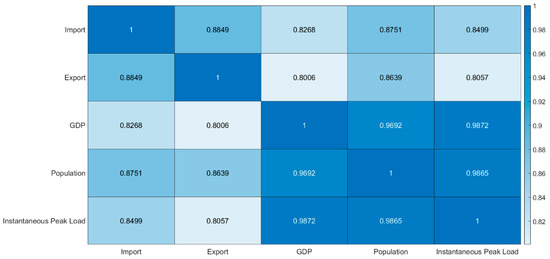
Figure 8.
Correlation matrix for instantaneous peak load between dependent and independent variables.
5. Conclusions
Predicting instantaneous electricity peak load is essential for efficiently planning capacity and establishing cost-effective electricity networks. To ensure precise forecasts, decision makers need to evaluate different approaches and identify the method that offers the most beneficial outcomes. This study aimed to improve the accuracy of instantaneous peak load prediction by employing forecasting models that incorporate various optimization and ML methods. The impact of independent inputs on peak load estimation was assessed using various combinations and subsets within MLR equations.
The research involved technical analysis to determine optimal method parameters using output–input correlation matrices. This analysis provided insight into how independent variables impacted the dependent variable, enhancing our understanding of the forecasting procedure. The accurate prediction of instantaneous peak load as obtained from this study is valuable for avoiding unnecessary reserves and ensuring optimal system operation.
Various forecasting techniques, including MLR, ANN, SVR, PSO, DO, and GRO, were employed in the study. DO and GRO were selected for their accurate predictive capabilities. The comparison of optimization methods (PSO, DO, GRO) with conventional ML techniques highlighted their superior prediction accuracy.
MLR is easier to understand and implement than more complex machine learning algorithms, making it a good starting point for regression analysis. MLR assumes a linear relationship between predictors and the target variable. It may not capture complex nonlinear relationships, reducing accuracy in modelling nonlinear data. ANNs can learn complex patterns and relationships within data, making them robust for tasks like pattern recognition, classification, regression, and function approximation. Also, ANNs require a substantial amount of data for training and are prone to overfitting, especially with small datasets or when the model becomes too complex for the available data. SVR operates within an ε-insensitive tube, establishing a margin of tolerance around predicted values, thereby mitigating the impact of outliers and rendering it less susceptible to overfitting in contrast to traditional regression methods. Nonetheless, when the data exceed a certain number, the prediction performance of SVR decreases.
PSO is relatively simple to implement and understand compared to other optimization techniques. It is based on the principles of swarm intelligence and does not involve complex mathematical computations. The performance of PSO is sensitive to its parameters, such as inertia weight, acceleration coefficients, and population size. Improper tuning of these parameters can affect the convergence speed and final solution quality. Like other swarm-based algorithms, GRO and DO excel in balancing exploration of the search space (searching for new solutions) and exploitation of promising areas (refining existing solutions), aiding in finding optimal or near-optimal solutions. As newer optimization techniques, there might be limited literature, research, and practical applications of GRO and DO compared to more established algorithms. This limitation might restrict their proven efficacy across a wide range of problems.
This research utilized a range of error metrics, such as RMSE, MAPE, R2, MAE, and MSE, to evaluate method performance. The correlation matrix illustrated the relationships between independent variables (population, import, GDP, and export) and the dependent variable (peak load), revealing their respective influences. The results show a strong positive linear correlation between GDP and instantaneous peak load. The proposed model demonstrated strong predictive capabilities for estimating instantaneous peak load, with GRO and ANN performing exceptionally well compared to other methods. This study’s contributions are essential for effective instantaneous electricity peak load estimating, significantly optimizing resource allocation and energy management in power systems.
Both ANN and GRO might entail significant computational requirements. Implementing and training these models on large datasets or complex architectures might demand substantial computational resources, hindering their practicality in certain settings with limited resources. The effectiveness of ANN and GRO might rely heavily on the availability and quality of data. Suppose that these models require extensive and high-quality data for training. In that case, their performance might be limited in sparse or low-quality data scenarios, constraining their utility in certain practical applications. In future studies, machine learning and optimization approaches will be incorporated in hybrid models to assess the accuracy of the forecasting models.
Author Contributions
Conceptualization, M.S. and C.S.; methodology, M.S., X.L., C.S. and O.A.K.; software, M.S.; validation, M.S.; formal analysis, M.S.; data curation, M.S. and O.A.K.; writing—original draft preparation, M.S., X.L., C.S. and O.A.K.; writing—review, and editing, M.S., X.L., C.S. and O.A.K.; visualization, M.S. and O.A.K.; supervision, C.S. All authors have read and agreed to the published version of the manuscript.
Funding
This research received no external funding.
Data Availability Statement
Publicly available data sets were analysed in this study.
Conflicts of Interest
The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.
References
- Pinheiro, M.G.; Madeira, S.C.; Francisco, A.P. Short-term electricity load forecasting—A systematic approach from system level to secondary substations. Appl. Energy 2023, 332, 120493. [Google Scholar] [CrossRef]
- Aswanuwath, L.; Pannakkong, W.; Buddhakulsomsiri, J.; Karnjana, J.; Huynh, V.-N. A Hybrid Model of VMD-EMD-FFT, Similar Days Selection Method, Stepwise Regression, and Artificial Neural Network for Daily Electricity Peak Load Forecasting. Energies 2023, 16, 1860. [Google Scholar] [CrossRef]
- Saglam, M.; Spataru, C.; Karaman, O.A. Electricity Demand Forecasting with Use of Artificial Intelligence: The Case of Gokceada Island. Energies 2022, 15, 5950. [Google Scholar] [CrossRef]
- Li, L.-L.; Sun, J.; Wang, C.-H.; Zhou, Y.-T.; Lin, K.-P. Enhanced Gaussian process mixture model for short-term electric load forecasting. Inf. Sci. 2019, 477, 386–398. [Google Scholar] [CrossRef]
- Singh, P.; Dwivedi, P. A novel hybrid model based on neural network and multi-objective optimization for effective load forecast. Energy 2019, 182, 606–622. [Google Scholar] [CrossRef]
- Wu, H.; Liang, Y.; Heng, J. Pulse-diagnosis-inspired multi-feature extraction deep network for short-term electricity load forecasting. Appl. Energy 2023, 339, 120995. [Google Scholar] [CrossRef]
- Rubasinghe, O.; Zhang, X.; Chau, T.K.; Chow, Y.; Fernando, T.; Iu, H.H.-C. A Novel Sequence to Sequence Data Modelling Based CNN-LSTM Algorithm for Three Years Ahead Monthly Peak Load Forecasting. IEEE Trans. Power Syst. 2023, 39, 1932–1947. [Google Scholar] [CrossRef]
- Nie, R.-X.; Tian, Z.-P.; Long, R.-Y.; Dong, W. Forecasting household electricity demand with hybrid machine learning-based methods: Effects of residents’ psychological preferences and calendar variables. Expert Syst. Appl. 2022, 206, 117854. [Google Scholar] [CrossRef]
- Saglam, M.; Spataru, C.; Karaman, O.A. Forecasting Electricity Demand in Turkey Using Optimization and Machine Learning Algorithms. Energies 2023, 16, 4499. [Google Scholar] [CrossRef]
- Sultana, N.; Hossain, S.M.Z.; Almuhaini, S.H.; Düştegör, D. Bayesian Optimization Algorithm-Based Statistical and Machine Learning Approaches for Forecasting Short-Term Electricity Demand. Energies 2022, 15, 3425. [Google Scholar] [CrossRef]
- Osisanwo, F.Y.; Akinsola, J.E.T.; Awodele, O.; Hinmikaiye, J.O.; Olakanmi, O.; Akinjobi, J. Supervised machine learning algorithms: Classification and comparison. Int. J. Comput. Trends Technol. 2017, 48, 128–138. [Google Scholar]
- Ray, S. A Quick Review of Machine Learning Algorithms; IEEE: Piscataway, NJ, USA, 2019; pp. 35–39. [Google Scholar]
- Mohammed, M.; Khan, M.B.; Bashier, E.B.M. Machine Learning: Algorithms and Applications; CRC Press: Boca Raton, FL, USA, 2016. [Google Scholar]
- Goodfellow, I.; Bengio, Y.; Courville, A. Deep Learning; MIT Press: Cambridge, MA, USA, 2016. [Google Scholar]
- Tang, Z.; Yin, H.; Yang, C.; Yu, J.; Guo, H. Predicting the electricity consumption of urban rail transit based on binary nonlinear fitting regression and support vector regression. Sustain. Cities Soc. 2021, 66, 102690. [Google Scholar] [CrossRef]
- Kazemzadeh, M.-R.; Amjadian, A.; Amraee, T. A hybrid data mining driven algorithm for long term electric peak load and energy demand forecasting. Energy 2020, 204, 117948. [Google Scholar] [CrossRef]
- Wang, Y.; Sun, S.; Chen, X.; Zeng, X.; Kong, Y.; Chen, J.; Guo, Y.; Wang, T. Short-term load forecasting of industrial customers based on SVMD and XGBoost. Int. J. Electr. Power Energy Syst. 2021, 129, 106830. [Google Scholar] [CrossRef]
- Zolfaghari, M.; Golabi, M.R. Modeling and predicting the electricity production in hydropower using conjunction of wavelet transform, long short-term memory and random forest models. Renew. Energy 2021, 170, 1367–1381. [Google Scholar] [CrossRef]
- Liu, X.; Zhang, Z.; Song, Z. A comparative study of the data-driven day-ahead hourly provincial load forecasting methods: From classical data mining to deep learning. Renew. Sustain. Energy Rev. 2020, 119, 109632. [Google Scholar] [CrossRef]
- Prado, F.; Minutolo, M.C.; Kristjanpoller, W. Forecasting based on an ensemble autoregressive moving average-adaptive neuro-fuzzy inference systems neural network-genetic algorithm framework. Energy 2020, 197, 117159. [Google Scholar] [CrossRef]
- Kuster, C.; Rezgui, Y.; Mourshed, M. Electrical load forecasting models: A critical systematic review. Sustain. Cities Soc. 2017, 35, 257–270. [Google Scholar] [CrossRef]
- Zang, H.; Xu, R.; Cheng, L.; Ding, T.; Liu, L.; Wei, Z.; Sun, G. Residential load forecasting based on LSTM fusing self-attention mechanism with pooling. Energy 2021, 229, 120682. [Google Scholar] [CrossRef]
- de Freitas Viscondi, G.; Alves-Souza, S.N. A Systematic Literature Review on big data for solar photovoltaic electricity generation forecasting. Sustain. Energy Technol. Assess. 2019, 31, 54–63. [Google Scholar] [CrossRef]
- Gao, W.; Darvishan, A.; Toghani, M.; Mohammadi, M.; Abedinia, O.; Ghadimi, N. Different states of multi-block based forecast engine for price and load prediction. Int. J. Electr. Power Energy Syst. 2019, 104, 423–435. [Google Scholar] [CrossRef]
- Jiang, P.; Li, R.; Liu, N.; Gao, Y. A novel composite electricity demand forecasting framework by data processing and optimized support vector machine. Appl. Energy 2020, 260, 114243. [Google Scholar] [CrossRef]
- Ma, X.; Xie, M.; Suykens, J.A.K. A novel neural grey system model with Bayesian regularization and its applications. Neurocomputing 2021, 456, 61–75. [Google Scholar] [CrossRef]
- Liu, L.; Wu, L. Forecasting the renewable energy consumption of the European countries by an adjacent non-homogeneous grey model. Appl. Math. Model. 2021, 89, 1932–1948. [Google Scholar] [CrossRef]
- Ding, S.; Hipel, K.W.; Dang, Y.G. Forecasting China’s electricity consumption using a new grey prediction model. Energy 2018, 149, 314–328. [Google Scholar] [CrossRef]
- Salman, A.G.; Kanigoro, B. Visibility forecasting using autoregressive integrated moving average (ARIMA) models. Procedia Comput. Sci. 2021, 179, 252–259. [Google Scholar] [CrossRef]
- Oliveira, E.M.; Cyrino Oliveira, F.L. Forecasting mid-long term electric energy consumption through bagging ARIMA and exponential smoothing methods. Energy 2018, 144, 776–788. [Google Scholar] [CrossRef]
- Jiang, P.; Liu, Z.; Niu, X.; Zhang, L. A combined forecasting system based on statistical method, artificial neural networks, and deep learning methods for short-term wind speed forecasting. Energy 2021, 217, 119361. [Google Scholar] [CrossRef]
- Xiao, L.; Shao, W.; Jin, F.; Wu, Z. A self-adaptive kernel extreme learning machine for short-term wind speed forecasting. Appl. Soft Comput. 2021, 99, 106917. [Google Scholar] [CrossRef]
- Liu, Z.; Jiang, P.; Wang, J.; Zhang, L. Ensemble forecasting system for short-term wind speed forecasting based on optimal sub-model selection and multi objective version of mayfly optimization algorithm. Expert Syst. Appl. 2021, 177, 114974. [Google Scholar] [CrossRef]
- Wang, Y.; Yang, Z.S.; Wang, L.; Ma, X.; Wu, W.Q.; Ye, L.L.; Zhou, Y.; Luo, Y.X. Forecasting China’s energy production and consumption based on a novel structural adaptive Caputo fractional grey prediction model. Energy 2022, 259, 124935. [Google Scholar] [CrossRef]
- Fan, G.F.; Wei, X.; Li, Y.T.; Hong, W.C. Forecasting electricity consumption using a novel hybrid model. Sustain. Cities Soc. 2020, 61, 102320. [Google Scholar] [CrossRef]
- Zhang, W.; Chen, Q.; Yan, J.; Zhang, S.; Xu, J. A novel asynchronous deep reinforcement learning model with adaptive early forecasting method and reward incentive mechanism for short-term load forecasting. Energy 2021, 236, 121492. [Google Scholar] [CrossRef]
- Peng, J.; Gao, S.; Ding, A. Study of the short-term electric load forecast based on ANFIS. In Proceedings of the 2017 32nd Youth Academic Annual Conference of Chinese Association of Automation (YAC), Hefei, China, 19–21 May 2017; pp. 832–836. [Google Scholar]
- Tay, K.G.; Muwafaq, H.; Tiong, W.K.; Choy, Y.Y. Electricity consumption forecasting using adaptive neuro-fuzzy inference system (ANFIS). Univ. J. Electr. Electron. Eng. 2019, 6, 37–48. [Google Scholar] [CrossRef]
- Al-Hamad, M.Y.; Qamber, I.S. GCC electrical long-term peak load forecasting modelling using ANFIS and MLR methods. Arab. J. Basic Appl. Sci. 2019, 26, 269–282. [Google Scholar] [CrossRef]
- Gellert, A.; Fiore, U.; Florea, A.; Chis, R.; Palmieri, F. Forecasting Electricity Consumption and Production in Smart Homes through Statistical Methods. Sustain. Cities Soc. 2022, 76, 103426. [Google Scholar] [CrossRef]
- Hu, Y.; Li, J.; Hong, M.; Ren, J.; Lin, R.; Liu, Y.; Liu, M.; Yi, M. Short term electric load forecasting model and its verification for process industrial enterprises based on hybrid GA-PSO-BPNN algorithmda case study of papermaking process. Energy 2019, 170, 1215–1227. [Google Scholar] [CrossRef]
- Bourhnane, S.; Abid, M.R.; Lghoul, R.; Zine-Dine, K.; Elkamoun, N.; Benhaddou, D. Machine learning for energy consumption prediction and scheduling in smart buildings. SN Appl. Sci. 2020, 2, 297. [Google Scholar] [CrossRef]
- Runge, J.; Zmeureanu, R. Forecasting energy use in buildings using artificial neural networks: A review. Energies 2019, 12, 3254. [Google Scholar] [CrossRef]
- Dong, Z.; Liu, J.; Liu, B.; Li, K.; Li, X. Hourly energy consumption prediction of an office building based on ensemble learning and energy consumption pattern classification. Energy Build. 2021, 241, 110929. [Google Scholar] [CrossRef]
- Shafiei Chafi, Z.; Afrakhte, H. Short-term load forecasting using neural network and particle swarm optimization (PSO) algorithm. Math. Probl. Eng. 2021, 2021, 5598267. [Google Scholar] [CrossRef]
- Mirjalili, S.; Lewis, A. The whale optimization algorithm. Adv. Eng. Softw. 2016, 95, 51–67. [Google Scholar] [CrossRef]
- Mirjalili, S. SCA: A Sine Cosine Algorithm for solving optimization problems. Knowl. Base Syst. 2016, 96, 120–133. [Google Scholar] [CrossRef]
- He, Y.; Zheng, Y. Short-term power load probability density forecasting based on Yeo-Johnson transformation quantile regression and Gaussian kernel function. Energy 2018, 54, 143–156. [Google Scholar] [CrossRef]
- Yang, W.; Wang, J.; Niu, T.; Du, P. A hybrid forecasting system based on a dual decomposition strategy and multi-objective optimization for electricity price forecasting. Appl. Energy 2019, 235, 1205–1225. [Google Scholar] [CrossRef]
- Li, R.; Jiang, P.; Yang, H.; Li, C. A novel hybrid forecasting scheme for electricity demand time series. Sustain. Cities Soc. 2020, 55, 102036. [Google Scholar] [CrossRef]
- Yang, W.; Wang, J.; Niu, T.; Du, P. A novel system for multi-step electricity price forecasting for electricity market management. Appl. Soft Comput. J. 2020, 88, 106029. [Google Scholar] [CrossRef]
- Dong, Y.; Zhang, H.; Wang, C.; Zhou, X. A novel hybrid model based on Bernstein polynomial with mixture of Gaussians for wind power forecasting. Appl. Energy 2021, 286, 116545. [Google Scholar] [CrossRef]
- Karaman, Ö.A. Prediction of Wind Power with Machine Learning Models. Appl. Sci. 2023, 13, 11455. [Google Scholar] [CrossRef]
- Huang, B.; Wang, J. Applications of Physics-Informed Neural Networks in Power Systems—A Review. IEEE Trans. Power Syst. 2023, 38, 572–588. [Google Scholar] [CrossRef]
- Zhang, S.; Wang, M.; Liu, S.; Chen, P.-Y.; Xiong, J. Fast learning of graph neural networks with guaranteed generalizability: One-hiddenlayer case. Int. Conf. Mach. Learn. 2020, 119, 11268–11277. [Google Scholar]
- Zhao, S.; Zhang, T.; Ma, S.; Chen, M. Dandelion Optimizer: A nature-inspired metaheuristic algorithm for engineering applications. Eng. Appl. Artif. Intell. 2022, 114, 105075. [Google Scholar] [CrossRef]
- Zolfi, K. Gold rush optimizer. A new population-based metaheuristic algorithm. Oper. Res. Decis. 2023, 33, 113–150. [Google Scholar] [CrossRef]
- Halepoto, I.A.; Uqaili, M.A.; Chowdhry, B.S. Least Square Regression Based Integrated Multi-Parameteric Demand Modeling for Short Term Load Forecasting. Mehran Univ. Res. J. Eng. Technol. 2014, 33, 215–226. [Google Scholar]
- Karaman, Ö.A. Performance evaluation of seasonal solar irradiation models—Case study: Karapınar town, Turkey. Case Stud. Therm. Eng. 2023, 49, 103228. [Google Scholar] [CrossRef]
- Yalçın, C. Analysis of Instantaneous Fuel Consumption in Aircrafts with Support Vector Regression. Ph.D. Thesis, Mimar Sinan Fine Arts University, Istanbul, Turkey, 2016. [Google Scholar]
- Erdemci, H. Turkey’s Energy Demand Forecast Until 2040 Using Machine Learning Algorithms. Master’s Thesis, Batman University, Batman, Turkey, 2023. [Google Scholar]
- Anand, A.; Suganthi, L. Hybrid GA-PSO Optimization of Artificial Neural Network for Forecasting Electricity Demand. Energies 2018, 11, 728. [Google Scholar] [CrossRef]
- Xu, Y.; Zhang, M.; Ye, L.; Zhu, Q.; Geng, Z.; He, Y.L.; Han, Y. A novel prediction intervals method integrating an error & self-feedback extreme learning machine with particle swarm optimization for energy consumption robust prediction. Energy 2018, 164, 137–146. [Google Scholar]
- Javanmard, M.E.; Ghaderi, S. Energy demand forecasting in seven sectors by an optimization model based on machine learning algorithms. Sustain. Cities Soc. 2023, 95, 104623. [Google Scholar] [CrossRef]
- Chen, W.; Panahi, M.; Pourghasemi, H.R. Performance evaluation of GIS-based new ensemble data mining techniques of adaptive neuro-fuzzy inference system (ANFIS) with genetic algorithm (GA), differential evolution (DE), and particle swarm optimization (PSO) for landslide spatial modelling. Catena 2017, 157, 310–324. [Google Scholar] [CrossRef]
- Saoud, A.; Recioui, A. Load Energy Forecasting based on a Hybrid PSO LSTM-AE Model. Alger. J. Environ. Sci. Technol. 2023, 9, 2938–2946. [Google Scholar]
- Geng, G.; He, Y.; Zhang, J.; Qin, T.; Yang, B. Short-Term Power Load Forecasting Based on PSO-Optimized VMD-TCN-Attention Mechanism. Energies 2023, 16, 4616. [Google Scholar] [CrossRef]
- Hua, H.; Qin, Z.; Dong, N.; Qin, Y.; Ye, M.; Wang, Z.; Chen, X.; Cao, J. Data-Driven Dynamical Control for Bottom-up Energy Internet System. IEEE Trans. Sustain. Energy 2022, 13, 315–327. [Google Scholar] [CrossRef]
- Abbassi, R.; Saidi, S.; Abbassi, A.; Jerbi, H.; Kchaou, M.; Alhasnawi, B.N. Accurate Key Parameters Estimation of PEMFCs’ Models Based on Dandelion Optimization Algorithm. Mathematics 2023, 11, 1298. [Google Scholar] [CrossRef]
- Hu, G.; Zheng, Y.; Abualigah, L.; Hussien, A.G. DETDO: An adaptive hybrid dandelion optimizer for engineering optimization. Adv. Eng. Inform. 2023, 57, 102004. [Google Scholar] [CrossRef]
- Kaveh, A.; Zaerreza, A.; Zaerreza, J. Enhanced dandelion optimizer for optimum design of steel frames. Iran. J. Sci. Technol. Trans. Civ. Eng. 2023, 47, 2591–2604. [Google Scholar] [CrossRef]
- Einstein, A. Investigations on the Theory of the Brownian Movement; Courier Corporation: Chelmsford, MA, USA, 1956. [Google Scholar]
- Shlesinger, M.F.; Klafter, J. Lévy walks versus Lévy flights. In On Growth and Form: Fractal and Non-Fractal Patterns in Physics; Springer: Dordrecht, The Netherlands, 1986; pp. 279–283. [Google Scholar]
- Sarjamei, S.; Massoudi, M.S.; Sarafraz, M.E. Frequency-Constrained Optimization of a Real-Scale Symmetric Structural Using Gold Rush Algorithm. Symmetry 2022, 14, 725. [Google Scholar] [CrossRef]
- Naser, M.Z.; Alavi, A.H. Error Metrics and Performance Fitness Indicators for Artificial Intelligence and Machine Learning in Engineering and Sciences. Archit. Struct. Constr. 2023, 3, 499–517. [Google Scholar] [CrossRef]
- Ran, P.; Dong, K.; Liu, X.; Wang, J. Short-term load forecasting based on CEEMDAN and Transformer. Electr. Power Syst. Res. 2023, 214, 108885. [Google Scholar] [CrossRef]
- Zhang, W.; Zhang, L.; Wang, J.; Niu, X. Hybrid system based on a multi-objective optimization and kernel approximation for multi-scale wind speed forecasting. Appl. Energy 2020, 277, 115561. [Google Scholar] [CrossRef]
- Houimli, R.; Zmami, M.; Ben-Salha, O. Short-term electric load forecasting in Tunisia using artificial neural networks. Energy Syst. 2020, 11, 357–375. [Google Scholar] [CrossRef]
- Cebekhulu, E.; Onumanyi, A.J.; Isaac, S.J. Performance Analysis of Machine Learning Algorithms for Energy Demand–Supply Prediction in Smart Grids. Sustainability 2022, 14, 2546. [Google Scholar] [CrossRef]
- Shah, I.; Jan, F.; Ali, S. Functional Data Approach for Short-Term Electricity Demand Forecasting. Math. Probl. Eng. 2022, 2022, 6709779. [Google Scholar] [CrossRef]
- Soyler, I.; Izgi, E. Electricity Demand Forecasting of Hospital Buildings in Istanbul. Sustainability 2022, 14, 8187. [Google Scholar] [CrossRef]
- Moradzadeh, A.; Moayyed, H.; Zare, K.; Mohammadi-Ivatloo, B. Short-term electricity demand forecasting via variational autoencoders and batch training-based bidirectional long short-term memory. Sustain. Energy Technol. Assess. 2022, 52, 102209. [Google Scholar] [CrossRef]
- Aponte, O.; McConky, K.T. Forecasting an electricity demand threshold to proactively trigger cost saving demand response actions. Energy Build. 2022, 27, 112221. [Google Scholar] [CrossRef]
- Turkish Electricity Transmission Corporation. Available online: https://www.teias.gov.tr/en-US/interconnections (accessed on 13 September 2023).
- Turkish Statistical Institute. Available online: https://data.tuik.gov.tr/Kategori/GetKategori?p=nufus-ve-demografi-109&dil=1 (accessed on 1 September 2023).
- World Bank. Available online: https://data.worldbank.org/?intcid=ecr_hp_BeltD_en_ext (accessed on 23 May 2023).
- Binici, M. Turkey’s Energy Consumption Forecast by Using Mathematical Modeling. Master’s Thesis, Sivas Cumhuriyet University, Sivas, Turkey, 2019. [Google Scholar]
- Kaboli, S.H.A.; Selvaraj, J.; Rahim, N. Long-term electric energy consumption forecasting via artificial cooperative search algorithm. Energy 2016, 115, 857–871. [Google Scholar] [CrossRef]
- Agbulut, Ü. Forecasting of transportation-related energy demand and CO2 emissions in Turkey with different machine learning algorithms. Sustain. Prod. Consum. 2022, 29, 141–157. [Google Scholar] [CrossRef]
- Atik, I. A new CNN-based method for short-term forecasting of electrical energy consumption in the COVID-19 period: The case of Turkey. IEEE Access 2022, 10, 22586–22598. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).