Channel-to-Rib Width Ratio Optimization for the Electrical Performance Enhancement in PEMFC Based on Accurate Strain-Stress Simulation
Abstract
1. Introduction
2. Methods
- The strain of components is ignored except for GDL;
- All gases follow the ideal gas equation;
- All water is in the vapor state;
- The compressive force of PEMFC is perpendicular to the BP;
- All flowing states are laminar;
- All structures of PEMFC are integral.
2.1. Mechanical Model of GDL
2.2. Electrochemistry and Charge Conduction of PEMFC
2.3. Flow, Heat, and Mass Transfer of PEMFC
3. Results
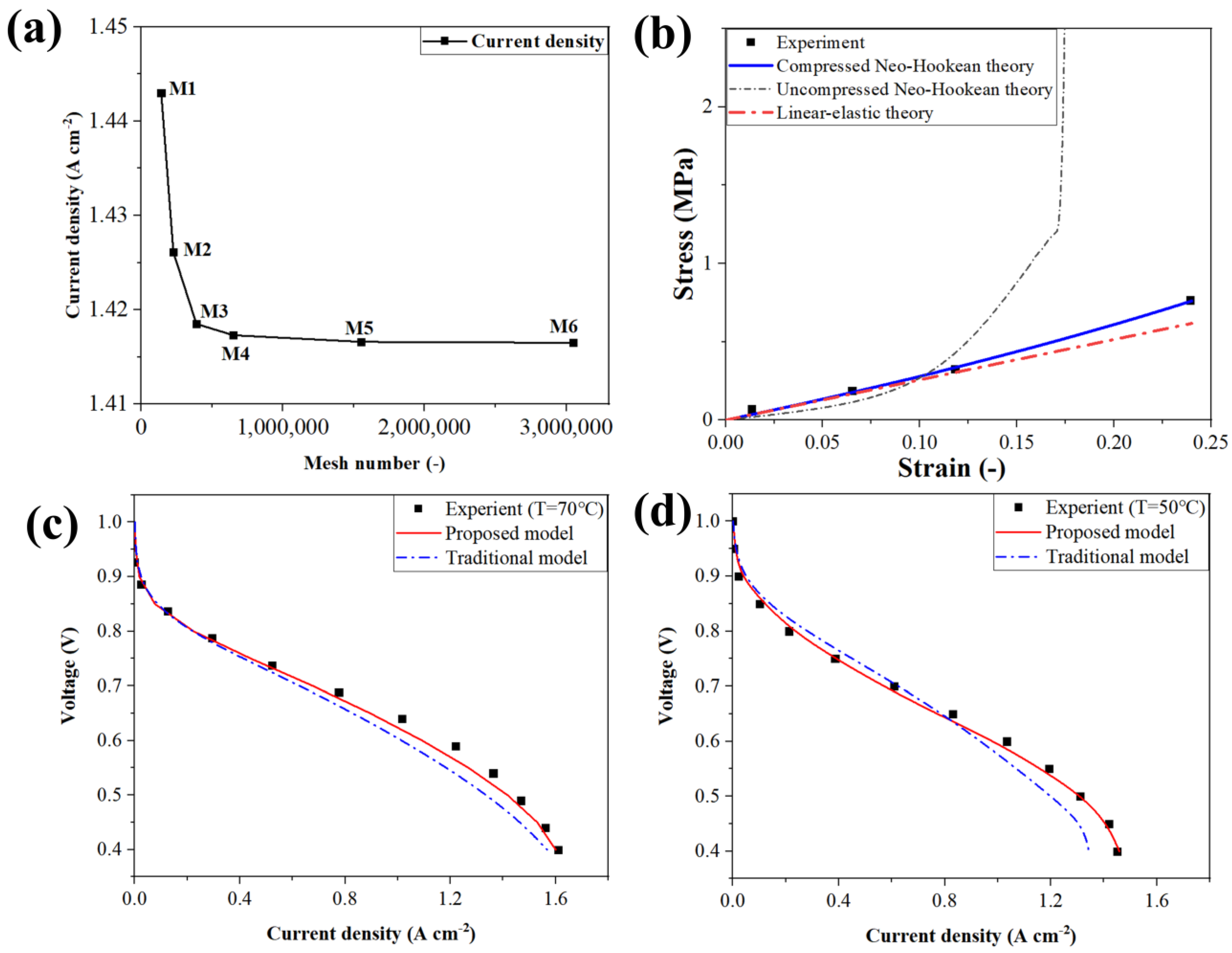
3.1. Mesh Independence and Model Validation
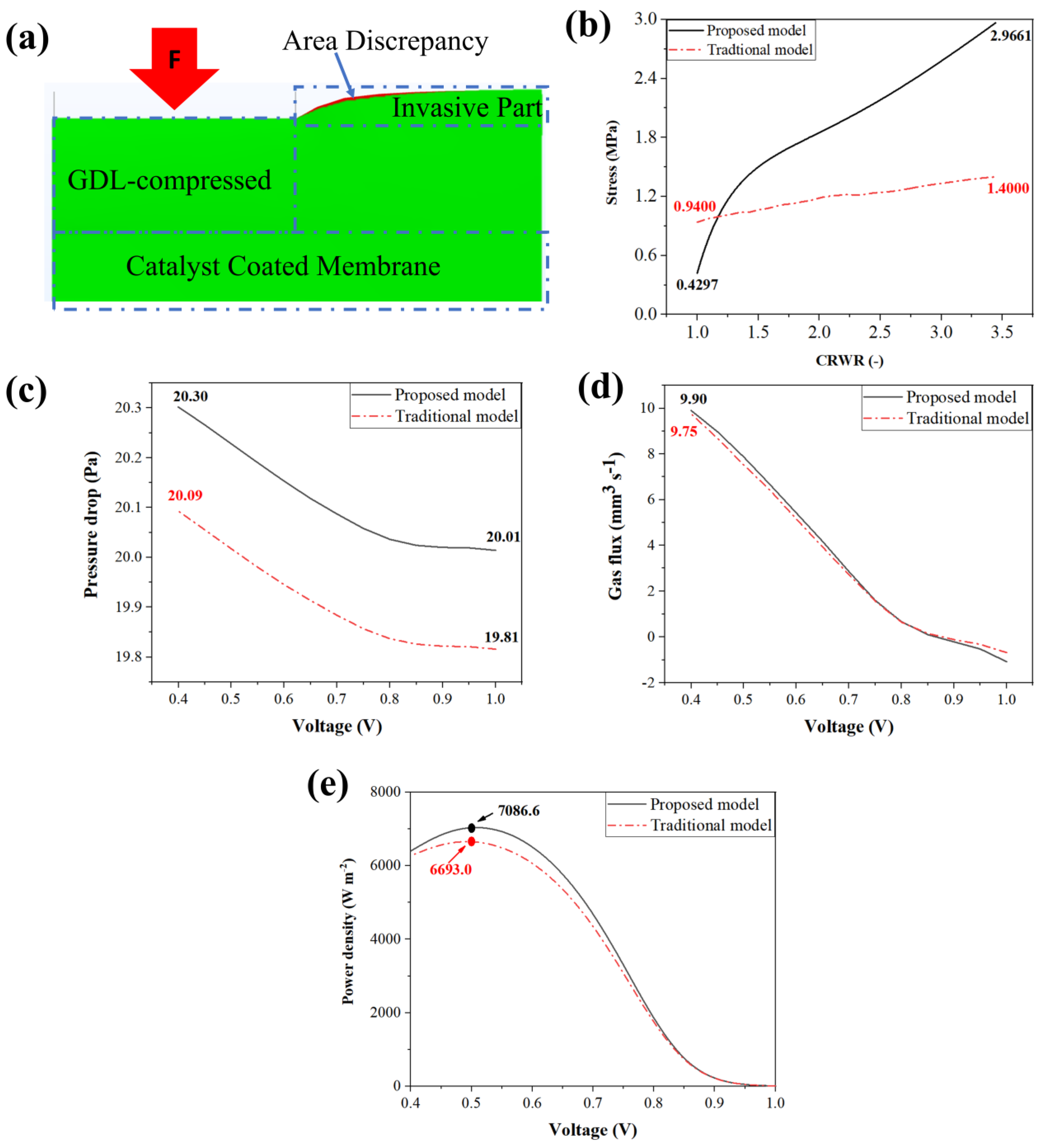
3.2. Comparison of Structural, Heat, and Mass Transfer Parameters with and without GDL Degradation
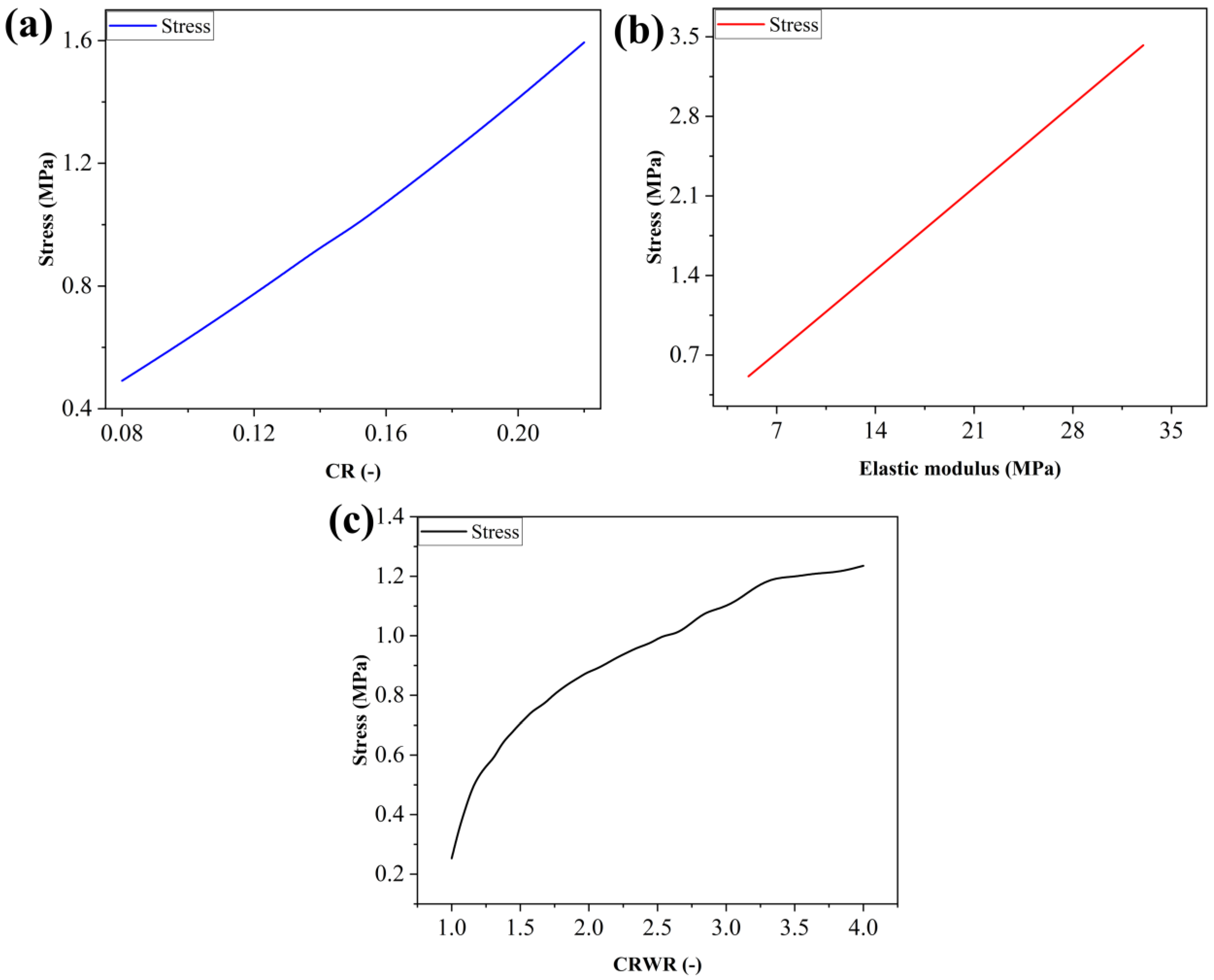
3.3. Relationship among Average Stress, CR, Elastic Modulus, and CRWR
3.4. Comparison of Proposed and Traditional Model with Stress, Gas Flux, Gas Pressure Drop, and Power Density
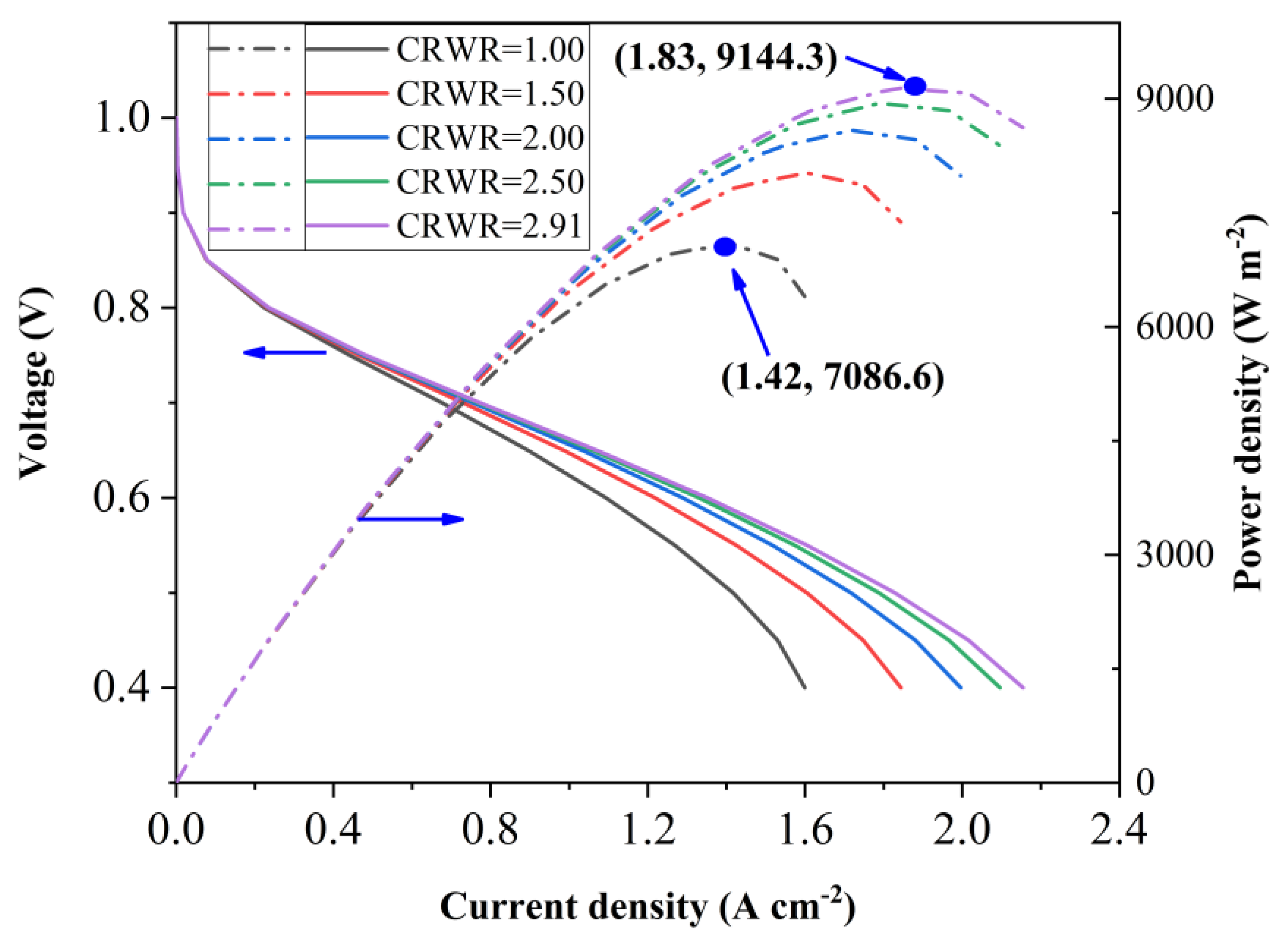
3.5. Polarization Curve and Power Density of PEMFC
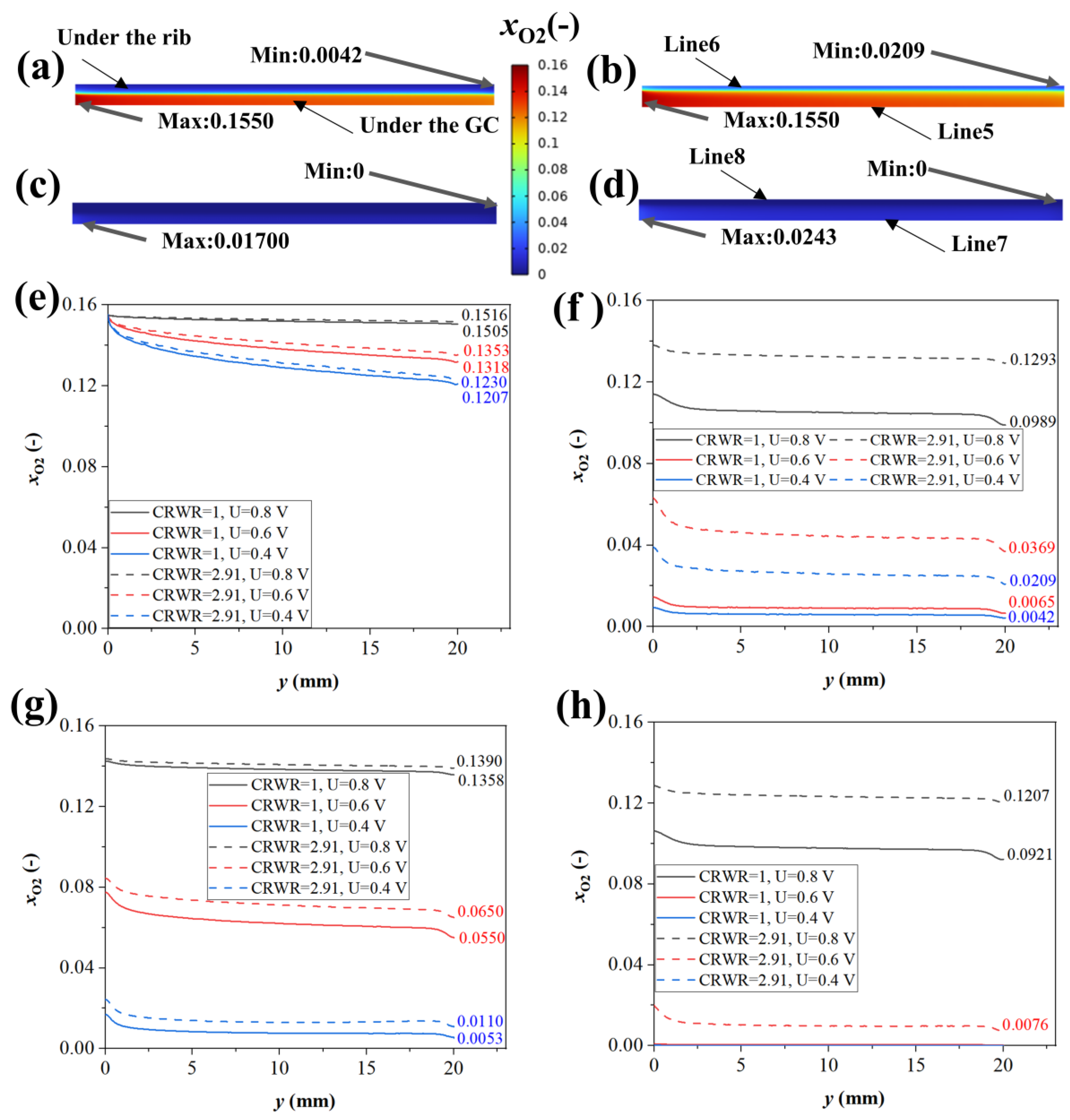
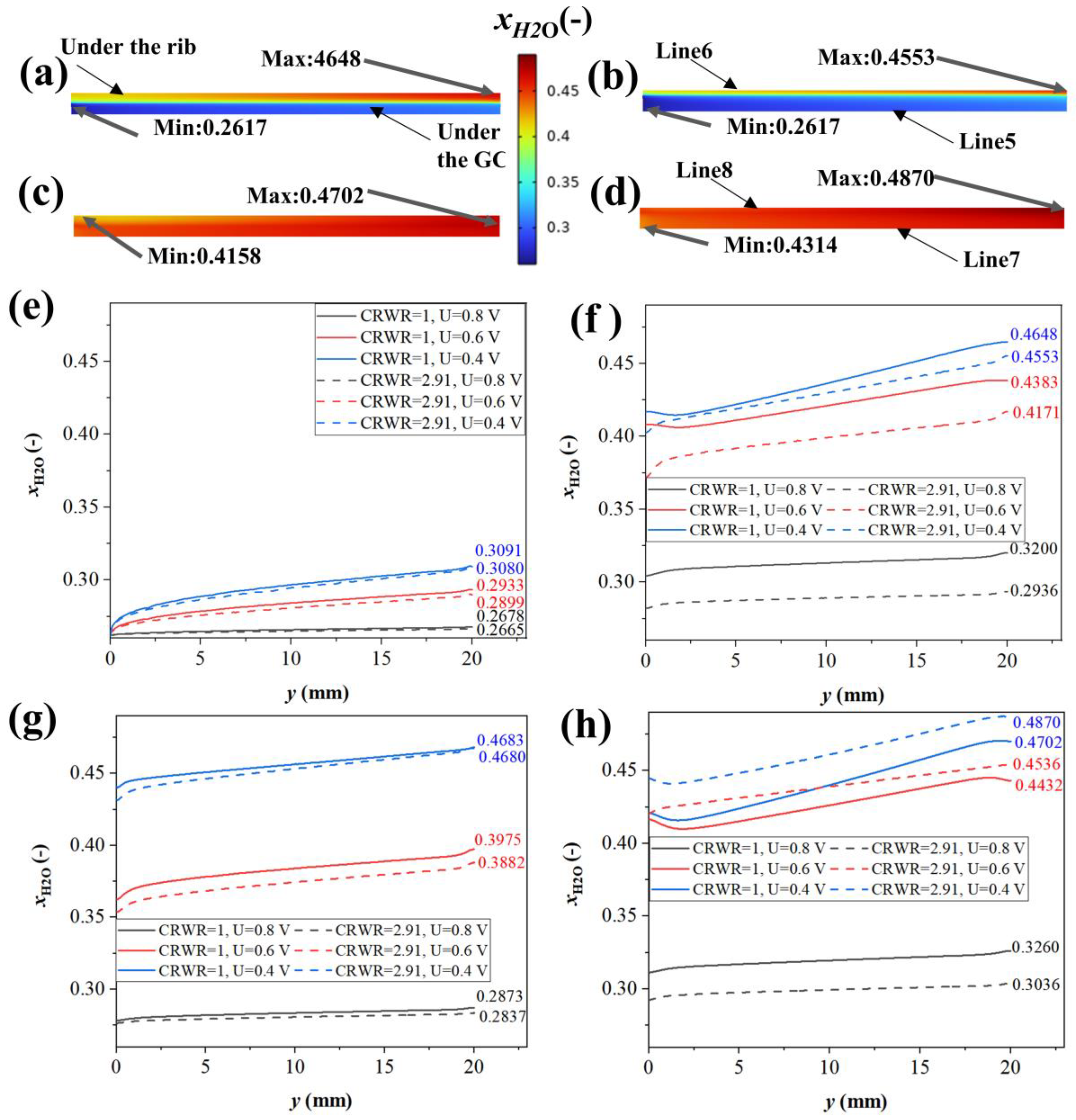
3.6. Distribution of Hydrogen, Oxygen, and Steam in GDM
3.6.1. Hydrogen Distribution in GDL
3.6.2. Oxygen Distribution in GDL
3.6.3. Steam Distribution in GDL
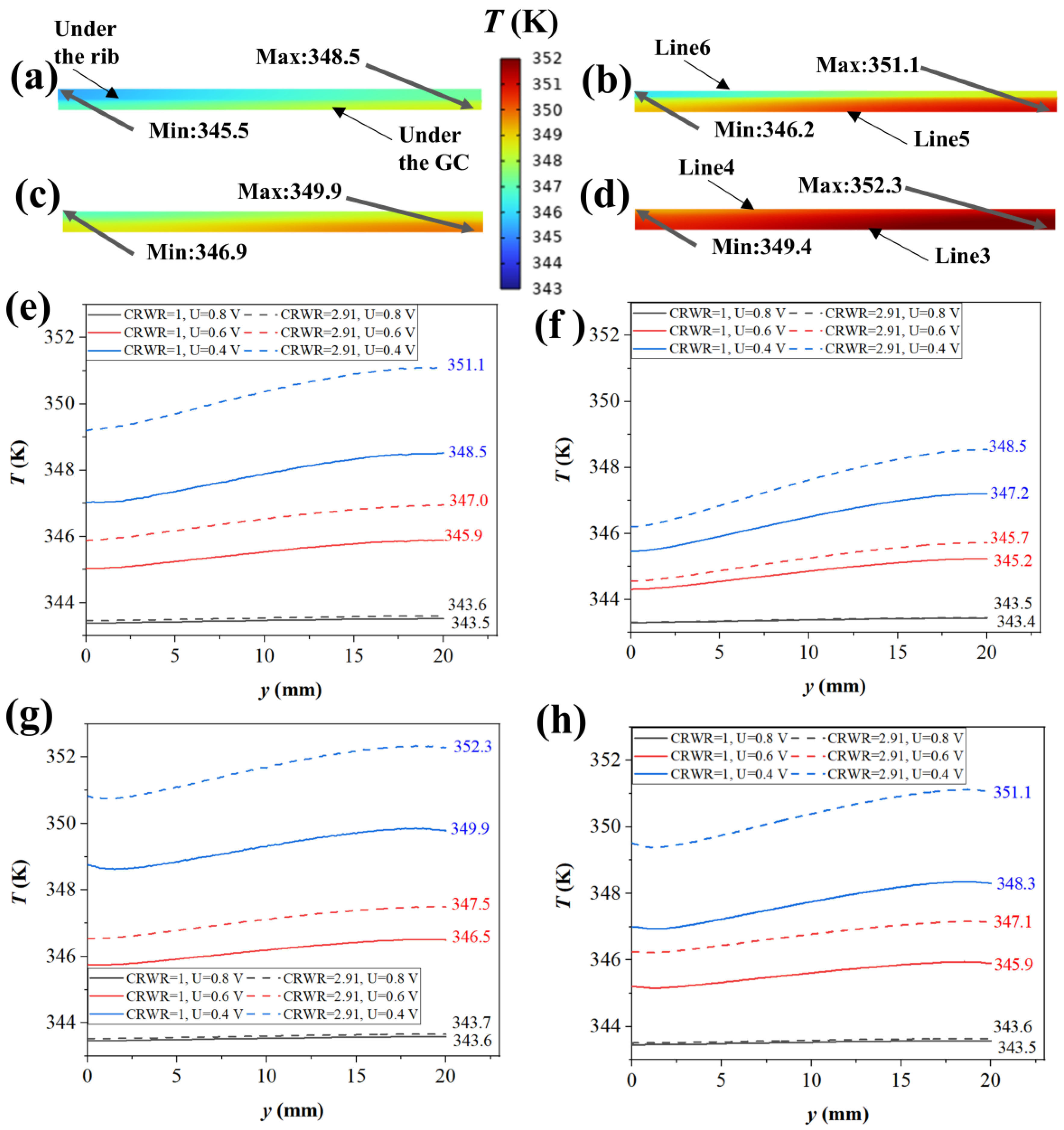
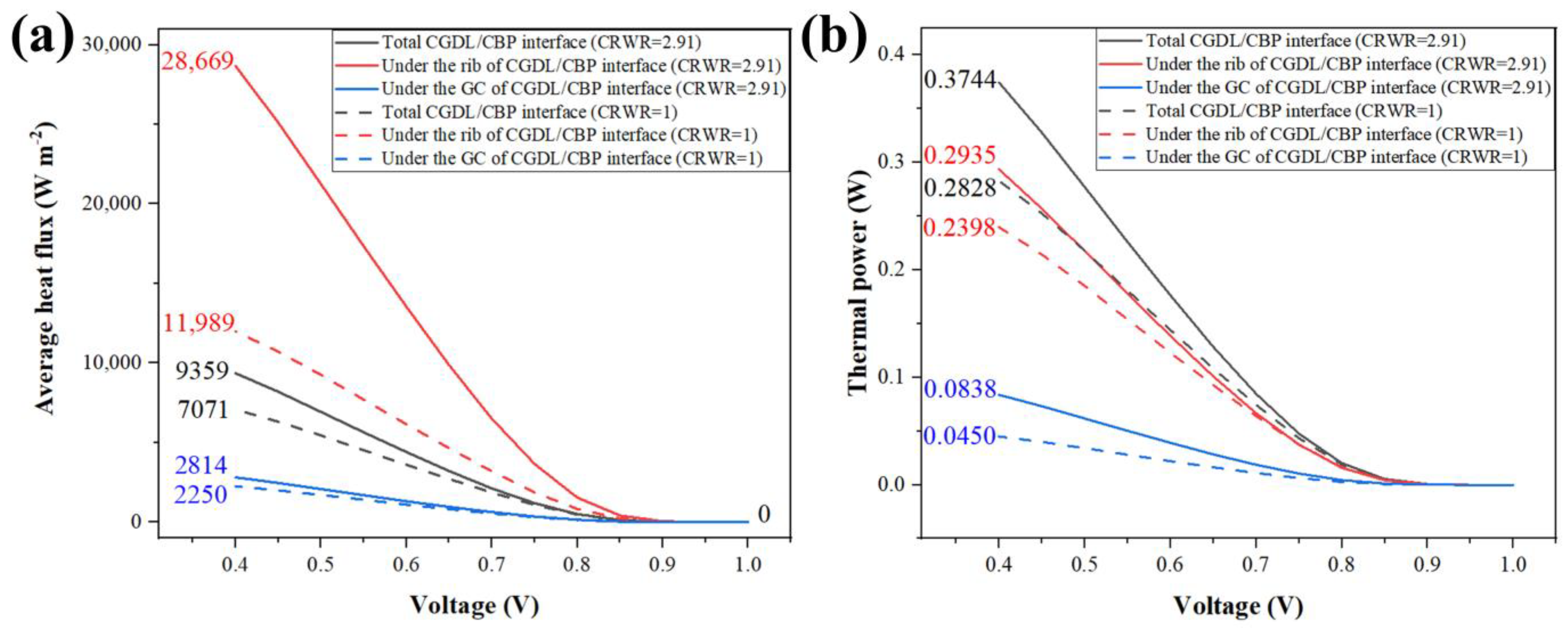
3.7. Distribution of Temperature and Heat Flux in GDM
4. Conclusions
- The average stress deviation from the experiment for the simulation based on the compressed neo-Hookean theory and the simulation based on linear-elastic theory was 1.38% and 14.26%, respectively. The compressed neo-Hookean theory was more accurate than the linear-elastic theory for describing the GDL deformation. The current density deviation from the experiment for the simulation based on the proposed model and the traditional model was 2.55% and 9.81%, respectively. The proposed model (incorporating the compressed neo-Hookean theory) was more accurate than the traditional model (incorporating the linear-elastic theory).
- The correlation among the CRWR of BP, stress, CR, and elastic modulus of GDL was obtained. The average stress deviation of the regression equation from the simulated data was 3.41%. Based on the correlation, the peak CRWR of 2.91 was found at the compressive strength of 2.5 MPa. The peak power density of CRWR = 2.91 was 29.04% higher than that of CRWR = 1.
- The mole fraction of hydrogen and steam between the region under the rib and GC was slightly different (<0.85% for hydrogen, <1.28% for steam). However, the average mole fraction of oxygen in the CGDL/CCL interface for CRWR = 2.91 was 11.39% higher than that for CRWR = 1. The CRWR design had a significant impact on the mass transfer behavior of oxygen. Moreover, the thermal power through the rib was significantly higher than that through the GC (>3.5 times). As the CRWR increases, the importance of heat conduction in the rib becomes more pronounced.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| CRWR | channel-to-rib width ratio |
| GDL | gas diffusion layer |
| BP | bipolar plate |
| PEMFC | proton exchange membrane fuel cell |
| GC | gas channel |
| MEA | membrane electrode assembly |
| CR | compression ratio |
| HOR | hydrogen oxidation reaction |
| ACL | anodic catalyst layer |
| ORR | oxygen reduction reaction |
| CCL | cathodic catalyst layer |
| CCM | catalyst-coated membrane |
| Symbols | Meaning (units) |
| P | First Piola–Kirchhoff stress (Pa) |
| δ | Stress (Pa) |
| F | Deformation gradient tensor (/) |
| Fv | Volume force vector (N m−3) |
| I | Unit matrix (/) |
| u | Displacement field (m) |
| St | Strain (/) |
| fv | Force in the vertical direction (N) |
| S | Second Piola–Kirchhoff stress (Pa) |
| Sinel | Inelastic stress tensor (Pa) |
| Ws | Strain energy density (J m−3) |
| σ | Cauchy stress (Pa) |
| J | Elastic volume ratio (/) |
| ε | Elastic Green-Lagrange strain (/) |
| Jel | Elastic volumetric deformation (/) |
| μ | Lamé parameters (Pa) |
| λ | Lamé parameters (Pa) |
| vp | Poisson ratio (/) |
| Y | Young’s modulus (Pa) |
| I1 | First invariant of the elastic right Cauchy–Green deformation tensor (/) |
| Eeq | Reversible potential (V) |
| R | Ideal gas constant (J kg−1 K−1) |
| T | Operating temperature of PEMFC (K) |
| pH2/pO2/pH2O | Particle pressure of hydrogen/oxygen/steam (Pa) |
| pref | Reference gas pressure (Pa) |
| ian/icath | Anode/cathode electrochemical reaction rate (A m−3) |
| i0,an/i0,cath | Anode/cathode exchange current density (A m−2) |
| aan/acath | Anode/cathode active specific surface region (m−1) |
| η | Activation overpotential (V) |
| Φe/Φp | Electric potential of the electron/proton phase (V) |
| n | Charge number in electrochemical reactions (/) |
| αa/αc | Anode/cathode transfer coefficient (/) |
| vi | Stoichiometric coefficient of the reacting species of index i (/) |
| ΔS | Total reaction entropy (J mol−1 K−1) |
| ΔG | Change in Gibbs free energy (J mol−1) |
| ΔΦ0 | Reversible potential (V) |
| FFC | Faraday constant (C mol−1) |
| ΔSHOR | Reaction entropy of HOR (J mol−1 K−1) |
| ΔSORR | Reaction entropy of ORR (J mol−1 K−1) |
| RH | Relative humidity (%) |
| ΔH | Enthalpy of reaction (J mol−1) |
| psat | Saturated vapor pressure of water (Pa) |
| σe/σp | Electronic/protonic conductivity (S m−1) |
| Se/Sp | Source term of electron/proton transport equation (A m−3) |
| mPt | Specific surface area of Pt (kg m−2) |
| As | Surface area of Pt (m2 g−1) |
| K | Viscous stress tensor (Pa) |
| μ | Dynamic viscosity (kg m−1 s−1) |
| κ | Permeability of gas(m2) |
| ρ | Density (kg m−3) |
| εp | Porosity (/) |
| Qm | Mass source per unit volume of the porous medium (kg m−3 s−1) |
| cF | Forchheimer parameter (/) |
| Cp | Specific heat capacity at constant pressure (J kg−1 K−1) |
| qcond | Heat flux density of heat conduction (W m−2) |
| pc | Pressure of cooling medium (Pa) |
| τ | Viscous stress tensor (Pa) |
| uf | Flow velocity (m s−1) |
| k | Thermal conductivity (W m−1 K−1) |
| kuncomp, GDL | Thermal conductivity of uncompressed GDL (W m−1 K−1) |
| εcomp, GDL | Porosity of compressed GDL (/) |
| εGDL | Porosity of uncompressed GDL (/) |
| CR | compression ratio (/) |
| “/” means dimension is 1. | |
References
- Jiao, K.; Xuan, J.; Du, Q.; Bao, Z.; Xie, B.; Wang, B.; Zhao, Y.; Fan, L.; Wang, H.; Hou, Z.; et al. Designing the next Generation of Proton-Exchange Membrane Fuel Cells. Nature 2021, 595, 361–369. [Google Scholar] [CrossRef]
- Zhang, Q.; Dong, S.; Shao, P.; Zhu, Y.; Mu, Z.; Sheng, D.; Zhang, T.; Jiang, X.; Shao, R.; Ren, Z.; et al. Covalent Organic Framework–Based Porous Ionomers for High-Performance Fuel Cells. Science 2022, 378, 181–186. [Google Scholar] [CrossRef]
- Lim, K.H.; Lee, A.S.; Atanasov, V.; Kerres, J.; Park, E.J.; Adhikari, S.; Maurya, S.; Manriquez, L.D.; Jung, J.; Fujimoto, C.; et al. Protonated Phosphonic Acid Electrodes for High Power Heavy-Duty Vehicle Fuel Cells. Nat. Energy 2022, 7, 248–259. [Google Scholar] [CrossRef]
- Cullen, D.A.; Neyerlin, K.C.; Ahluwalia, R.K.; Mukundan, R.; More, K.L.; Borup, R.L.; Weber, A.Z.; Myers, D.J.; Kusoglu, A. New Roads and Challenges for Fuel Cells in Heavy-Duty Transportation. Nat. Energy 2021, 6, 462–474. [Google Scholar] [CrossRef]
- Zhang, H.; Rahman, M.A.; Mojica, F.; Sui, P.; Chuang, P.A. A Comprehensive Two-Phase Proton Exchange Membrane Fuel Cell Model Coupled with Anisotropic Properties and Mechanical Deformation of the Gas Diffusion Layer. Electrochim. Acta 2021, 382, 138273. [Google Scholar] [CrossRef]
- Pan, Y.; Wang, H.; Brandon, N.P. Gas Diffusion Layer Degradation in Proton Exchange Membrane Fuel Cells: Mechanisms, Characterization Techniques and Modelling Approaches. J. Power Sources 2021, 513, 230560. [Google Scholar] [CrossRef]
- Yan, S.; Yang, M.; Sun, C.; Xu, S. Liquid Water Characteristics in the Compressed Gradient Porosity Gas Diffusion Layer of Proton Exchange Membrane Fuel Cells Using the Lattice Boltzmann Method. Energies 2023, 16, 6010. [Google Scholar] [CrossRef]
- Xia, L.; Xu, Q.; He, Q.; Ni, M.; Seng, M. Numerical Study of High Temperature Proton Exchange Membrane Fuel Cell (HT-PEMFC) with a Focus on Rib Design. Int. J. Hydrogen Energy 2021, 46, 21098–21111. [Google Scholar] [CrossRef]
- Acar, M.C. Channel to Rib Width Ratio Effect on Thermal Performance of Cooling Plate in Polymer Electrolyte Membrane Fuel Cell. Fuel Cells 2022, 22, 154–168. [Google Scholar] [CrossRef]
- Pan, W.; Chen, X.; Wang, F.; Dai, G. Mass Transfer Enhancement of PEM Fuel Cells with Optimized Flow Channel Dimensions. Int. J. Hydrogen Energy 2021, 46, 29541–29555. [Google Scholar] [CrossRef]
- Qiu, D.; Peng, L.; Tang, J.; Lai, X. Numerical Analysis of Air-Cooled Proton Exchange Membrane Fuel Cells with Various Cathode Flow Channels. Energy 2020, 198, 117334. [Google Scholar] [CrossRef]
- Zeng, X.; Ge, Y.; Shen, J.; Zeng, L.; Liu, Z.; Liu, W. The Optimization of Channels for a Proton Exchange Membrane Fuel Cell Applying Genetic Algorithm. Int. J. Heat Mass Transf. 2017, 105, 81–89. [Google Scholar] [CrossRef]
- Zhang, J.; Hu, Y. Sealing Performance and Mechanical Behavior of PEMFCs Sealing System Based on Thermodynamic Coupling. Int. J. Hydrogen Energy 2020, 45, 23480–23489. [Google Scholar] [CrossRef]
- Simon, C.; Hasché, F.; Gasteiger, H.A. Influence of the Gas Diffusion Layer Compression on the Oxygen Transport in PEM Fuel Cells at High Water Saturation Levels. J. Electrochem. Soc. 2017, 164, F591–F599. [Google Scholar] [CrossRef]
- Mason, T.J.; Millichamp, J.; Neville, T.P.; El-kharouf, A.; Pollet, B.G.; Brett, D.J.L. Effect of Clamping Pressure on Ohmic Resistance and Compression of Gas Diffusion Layers for Polymer Electrolyte Fuel Cells. J. Power Sources 2012, 219, 52–59. [Google Scholar] [CrossRef]
- Radhakrishnan, V.; Haridoss, P. Effect of Cyclic Compression on Structure and Properties of a Gas Diffusion Layer Used in PEM Fuel Cells. Int. J. Hydrogen Energy 2010, 35, 11107–11118. [Google Scholar] [CrossRef]
- Niblett, D.; Guo, Z.; Holmes, S.; Niasar, V.; Prosser, R. Utilization of 3D Printed Carbon Gas Diffusion Layers in Polymer Electrolyte Membrane Fuel Cells. Int. J. Hydrog. Energy 2022, 47, 23393–23410. [Google Scholar] [CrossRef]
- Yu, J.; Jiang, Z.; Hou, M.; Liang, D.; Xiao, Y.; Dou, M.; Shao, Z.; Yi, B. Analysis of the Behavior and Degradation in Proton Exchange Membrane Fuel Cells with a Dead-Ended Anode. J. Power Sources 2014, 246, 90–94. [Google Scholar] [CrossRef]
- Kang, M.; Sim, J.; Min, K. Analysis of Surface and Interior Degradation of Gas Diffusion Layer with Accelerated Stress Tests for Polymer Electrolyte Membrane Fuel Cell. Int. J. Hydrogen Energy 2022, 47, 29467–29480. [Google Scholar] [CrossRef]
- Chen, G.; Xu, Q.; Xuan, J.; Liu, J.; Fu, Q.; Shi, W.; Su, H.; Xing, L. Numerical Study of Inhomogeneous Deformation of Gas Diffusion Layers on Proton Exchange Membrane Fuel Cells Performance. J. Energy Storage 2021, 44, 103486. [Google Scholar] [CrossRef]
- Zhou, Y.; Jiao, K.; Du, Q.; Yin, Y.; Li, X. Gas Diffusion Layer Deformation and Its Effect on the Transport Characteristics and Performance of Proton Exchange Membrane Fuel Cell. Int. J. Hydrogen Energy 2013, 38, 12891–12903. [Google Scholar] [CrossRef]
- Bao, Z.; Li, Y.; Zhou, X.; Gao, F.; Du, Q.; Jiao, K. Transport Properties of Gas Diffusion Layer of Proton Exchange Membrane Fuel Cells: Effects of Compression. Int. J. Heat Mass Transf. 2021, 178, 121608. [Google Scholar] [CrossRef]
- Zhou, X.; Niu, Z.; Bao, Z.; Wang, J.; Liu, Z.; Yin, Y.; Du, Q.; Jiao, K. Two-Phase Flow in Compressed Gas Diffusion Layer: Finite Element and Volume of Fluid Modeling. J. Power Sources 2019, 437, 226933. [Google Scholar] [CrossRef]
- Zhang, Z.; He, P.; Dai, Y.-J.; Jin, P.-H.; Tao, W.-Q. Study of the Mechanical Behavior of Paper-Type GDL in PEMFC Based on Microstructure Morphology. Int. J. Hydrogen Energy 2020, 45, 29379–29394. [Google Scholar] [CrossRef]
- Meng, L.; Zhou, P.; Yan, Y.; Guo, D. Compression Properties of Gas Diffusion Layers and Its Constitutive Model under Cyclic Loading. Int. J. Hydrogen Energy 2021, 46, 15965–15975. [Google Scholar] [CrossRef]
- Yan, X.; Lin, C.; Zheng, Z.; Chen, J.; Wei, G.; Zhang, J. Effect of Clamping Pressure on Liquid-Cooled PEMFC Stack Performance Considering Inhomogeneous Gas Diffusion Layer Compression. Appl. Energy 2020, 258, 114073. [Google Scholar] [CrossRef]
- Sadeghi, E.; Djilali, N.; Bahrami, M. Effective Thermal Conductivity and Thermal Contact Resistance of Gas Diffusion Layers in Proton Exchange Membrane Fuel Cells. Part 1: Effect of Compressive Load. J. Power Sources 2011, 196, 246–254. [Google Scholar] [CrossRef]
- Xiao, Y.; Gao, Z.; Gao, F.; Zhang, T.; Zhang, W.; Li, Z.; Ma, X.; Qi, J. Improved Analytical Modeling and Mechanical Characterization of Gas Diffusion Layers under Compression Load. Energy Sci. Eng. 2020, 8, 2799–2807. [Google Scholar] [CrossRef]
- Afrasiab, H.; Emami Gharehhajloo, E.; Barzegari, M.M. Electrical and Mechanical Characterization of the Gas Diffusion Layer during Compression in PEM Fuel Cells. Int. J. Hydrogen Energy 2023, 48, 31996–32010. [Google Scholar] [CrossRef]
- Li, W.Z.; Yang, W.W.; Zhang, W.Y.; Qu, Z.G.; He, Y.L. Three-Dimensional Modeling of a PEMFC with Serpentine Flow Field Incorporating the Impacts of Electrode Inhomogeneous Compression Deformation. Int. J. Hydrogen Energy 2019, 44, 22194–22209. [Google Scholar] [CrossRef]
- Senthil Velan, V.; Velayutham, G.; Rajalakshmi, N.; Dhathathreyan, K.S. Influence of Compressive Stress on the Pore Structure of Carbon Cloth Based Gas Diffusion Layer Investigated by Capillary Flow Porometry. Int. J. Hydrogen Energy 2014, 39, 1752–1759. [Google Scholar] [CrossRef]
- García-Salaberri, P.A.; Vera, M.; Zaera, R. Nonlinear Orthotropic Model of the Inhomogeneous Assembly Compression of PEM Fuel Cell Gas Diffusion Layers. Int. J. Hydrogen Energy 2011, 36, 11856–11870. [Google Scholar] [CrossRef]
- Springer, T.E.; Zawodzinski, T.A.; Gottesfeld, S. Polymer Electrolyte Fuel Cell Model. J. Electrochem. Soc. 1991, 138, 2334–2342. [Google Scholar] [CrossRef]
- Wang, L. A Parametric Study of PEM Fuel Cell Performances. Int. J. Hydrogen Energy 2003, 28, 1263–1272. [Google Scholar] [CrossRef]
- Mohammedi, A.; Sahli, Y.; Moungar, H.; Benhammou, M.; Ben Moussa, H. Investigation, Analysis and Optimization of PEMFC Channel Cross-Section Shape. J. Renew. Energ. 2022, 1, 179. [Google Scholar] [CrossRef]
- Perry’s Chemical Engineers’ Handbook, 9th ed.; Green, D.W., Southard, M.Z., Eds.; 85th anniversary edition; McGraw Hill Education: New York, NY, USA, 2019; ISBN 978-0-07-183409-4. [Google Scholar]
- Xia, L.; Ni, M.; He, Q.; Xu, Q.; Cheng, C. Optimization of Gas Diffusion Layer in High Temperature PEMFC with the Focuses on Thickness and Porosity. Appl. Energy 2021, 300, 117357. [Google Scholar] [CrossRef]
- Mohammedi, A.; Sahli, Y.; Moussa, H.B. Optimization Study of the Produced Electric Power by Planar PEMFC-SCG. Renew. Energy Focus 2020, 35, 72–83. [Google Scholar] [CrossRef]
- Movahedi, M.; Ramiar, A.; Ranjber, A.A. 3D Numerical Investigation of Clamping Pressure Effect on the Performance of Proton Exchange Membrane Fuel Cell with Interdigitated Flow Field. Energy 2018, 142, 617–632. [Google Scholar] [CrossRef]
- Koorata, P.K.; Bhat, S.D. Compressive Cyclic Response of PEM Fuel Cell Gas Diffusion Media. Int. J. Hydrogen Energy 2021, 46, 5570–5579. [Google Scholar] [CrossRef]
- Attard, M.M. Finite Strain––Isotropic Hyperelasticity. Int. J. Solids Struct. 2003, 40, 4353–4378. [Google Scholar] [CrossRef]
- Lampinen, M.; Fomino, M. Analysis of Different Energy Scales in Chemical Thermodynamics and Estimation of Free Energy and Enthalpy Changes for Half Cell Reactions. J. Electrochem. Soc. 1993, 140, 3537. [Google Scholar] [CrossRef]
- NIST Standard Reference Database 13 NIST-JANAF Themochemical Tables. Available online: https://janaf.nist.gov/ (accessed on 14 July 2023).
- Wang, Y.; Liu, T.; Sun, H.; He, W.; Fan, Y.; Wang, S. Investigation of Dry Ionomer Volume Fraction in Cathode Catalyst Layer under Different Relative Humilities and Nonuniform Ionomer-Gradient Distributions for PEM Fuel Cells. Electrochim. Acta 2020, 353, 136491. [Google Scholar] [CrossRef]
- Chen, X.; Luo, X.; Liang, Y.; Chen, J.; He, J.; Yang, Z.; Chen, Y.; Wang, C.; Du, Y. Modeling and Performance Investigation on the Deformed Gas Diffusion Layer of PEM Fuel Cell. Int. J. Hydrogen Energy 2023, 50, 169–180. [Google Scholar] [CrossRef]
- Marr, C.; Li, X. Composition and Performance Modelling of Catalyst Layer in a Proton Exchange Membrane Fuel Cell. J. Power Sources 1999, 77, 0378–7753. [Google Scholar] [CrossRef]
- Bird, R.B.; Stewart, W.E.; Lightfoot, E.N. Transport Phenomena; Revised ed.; Wiley: New York, NY, USA, 2007; ISBN 978-0-470-11539-8. [Google Scholar]
- Torayca® Carbon Paper for Fuel Cells. Available online: https://toray-cfe.com/en/products/carbon-paper/ (accessed on 1 July 2023).
- Zenyuk, I.V.; Parkinson, D.Y.; Connolly, L.G.; Weber, A.Z. Gas-Diffusion-Layer Structural Properties under Compression via X-Ray Tomography. J. Power Sources 2016, 328, 364–376. [Google Scholar] [CrossRef]
- Darling, R.M. Examining Ohmic Losses in Fuel-Cell Catalyst Layers with Different Pt/C Ratios. J. Electrochem. Soc. 2020, 167, 084505. [Google Scholar] [CrossRef]



| Parameters | BPs | GDLs | CLs | PEM |
|---|---|---|---|---|
| Young’s modulus (MPa) | 13,000 | 14 | 249 | 232 |
| Poisson ratio | 0.26 | 0.256 | 0.3 | 0.253 |
| Density (kg m−3) | 1780 | 405 | 2059 | 2000 |
| Porosity (uncompressed) | / | 0.4 | 0.2 | / |
| Parameters | Value |
|---|---|
| Thickness of PEM (μm) | 108 |
| Thickness of CL (μm) | 12.9 |
| Thickness of GDL (μm) | 300 |
| Thickness of BP (μm) | 2000 |
| Width of GC (μm) | 1000 |
| Height of GC (μm) | 1000 |
| Length of PEMFC (mm) | 20 |
| Width of cooling channel (μm) | 1000 |
| Height of cooling channel (μm) | 1000 |
| Parameter (Units) | Value |
|---|---|
| Compression ratio of GDL | 20% |
| Reference temperature (K) | 293.15 |
| Anode transfer coefficient | 0.5 |
| Cathode transfer coefficient | 3 |
| Gas permeability of GDL under the GC (m2) | 1.76 × 10−11 |
| Gas permeability of GDL under the rib (m2) | (1 − CR) × 1.76 × 10−11 |
| Gas permeability of CL (m2) | 1 × 10−13 |
| Hydrogen flow of GC (L min−1) | 17.14 × 10−3 |
| Oxygen flow of GC (L min−1) | 31.43 × 10−3 |
| Thermal conductivity of BP (W m−1 K−1) | 55 |
| In-plane/through-plane thermal conductivity of GDL under GC (uncompressed) (W m−1 K−1) | 8.55/1.71 |
| Thermal conductivity of CL (W m−1 K−1) | 0.27 |
| Thermal conductivity of PEM (W m−1 K−1) | 0.12 |
| Temperature of reaction gases (K) | 343.15 |
| Pressure of reaction gases (atm) | 3 |
| Temperature of cooling fluid (K) | 343.15 |
| Flow rate of cooling fluid (m/s) | 0.05 |
| Tortuosity of GDL | 1.86 |
| Gas Relative Humidity | 85% |
| Is GDL Broken? | Experiment | Simulation | Deviation |
|---|---|---|---|
| Porosity (%) | |||
| Unbroken | 68.89 | 68.96 | 0.10% |
| Broken | 4.20 | 64.94 | 1446.19% |
| Thermal Conductivity (W m−1 K−1) | |||
| Unbroken | 5.32 | 5.31 | −0.19% |
| Broken | 21.58 | 6.09 | −71.78% |
| Gas Permeability (m2) | |||
| Unbroken | 1.72 × 10−12 | 1.74 × 10−12 | 1.16% |
| Broken | 4.12 × 10−17 | 1.14 × 10−12 | 2,770,000% |
| Parameter (Unit) | Location | U = 0.8 V | U = 0.6 V | U = 0.4 V |
|---|---|---|---|---|
| Hydrogen distribution | ||||
| Difference of mole fraction between inlet and outlet | AGDL/ACL of CRWR = 1 | 0.0286 | 0.1386 | 0.2059 |
| AGDL/ACL of CRWR = 2.91 | 0.0234 | 0.1632 | 0.2968 | |
| Average mole fraction of hydrogen | AGDL/ABP interface of CRWR = 1 | 0.7224 | 0.6607 | 0.6237 |
| AGDL/ABP interface of CRWR = 2.91 | 0.7254 | 0.6539 | 0.6016 | |
| AGDL/ACL interface of CRWR = 1 | 0.7209 | 0.6535 | 0.6132 | |
| AGDL/ACL interface of CRWR = 2.91 | 0.7242 | 0.6459 | 0.5754 | |
| Oxygen distribution | ||||
| Difference of mole fraction between inlet and outlet | CGDL/CCL of CRWR = 1 | 0.0562 | 0.1484 | 0.1508 |
| CGDL/CCL of CRWR = 2.91 | 0.0258 | 0.1181 | 0.1341 | |
| Average mole fraction of oxygen | CGDL/CBP interface of CRWR = 1 | 0.1346 | 0.0862 | 0.0781 |
| CGDL/CBP interface of CRWR = 2.91 | 0.1480 | 0.1180 | 0.1052 | |
| CGDL/CCL interface of CRWR = 1 | 0.1220 | 0.0310 | 0.0032 | |
| CGDL/CCL interface of CRWR = 2.91 | 0.1359 | 0.525 | 0.0079 | |
| Steam distribution | ||||
| Average mole fraction of steam | CGDL/CBP interface of CRWR = 1 | 0.2837 | 0.3409 | 0.3562 |
| CGDL/CBP interface of CRWR = 2.91 | 0.2537 | 0.3096 | 0.3285 | |
| CGDL/CCL interface of CRWR = 1 | 0.2985 | 0.4096 | 0.4522 | |
| CGDL/CCL interface of CRWR = 2.91 | 0.2860 | 0.3946 | 0.4580 | |
| Temperature distribution | ||||
| Average temperature (K) | CGDL/CBP interface of CRWR = 1 | 343.41 | 345.09 | 346.98 |
| CGDL/CBP interface of CRWR = 2.91 | 343.47 | 345.94 | 349.10 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, X.; Luo, X.; Wang, C.; Liang, Y.; Chen, J.; Yang, Z.; He, J.; Chen, Y. Channel-to-Rib Width Ratio Optimization for the Electrical Performance Enhancement in PEMFC Based on Accurate Strain-Stress Simulation. Energies 2024, 17, 762. https://doi.org/10.3390/en17030762
Chen X, Luo X, Wang C, Liang Y, Chen J, Yang Z, He J, Chen Y. Channel-to-Rib Width Ratio Optimization for the Electrical Performance Enhancement in PEMFC Based on Accurate Strain-Stress Simulation. Energies. 2024; 17(3):762. https://doi.org/10.3390/en17030762
Chicago/Turabian StyleChen, Xiangyang, Xianglong Luo, Chao Wang, Yingzong Liang, Jianyong Chen, Zhi Yang, Jiacheng He, and Ying Chen. 2024. "Channel-to-Rib Width Ratio Optimization for the Electrical Performance Enhancement in PEMFC Based on Accurate Strain-Stress Simulation" Energies 17, no. 3: 762. https://doi.org/10.3390/en17030762
APA StyleChen, X., Luo, X., Wang, C., Liang, Y., Chen, J., Yang, Z., He, J., & Chen, Y. (2024). Channel-to-Rib Width Ratio Optimization for the Electrical Performance Enhancement in PEMFC Based on Accurate Strain-Stress Simulation. Energies, 17(3), 762. https://doi.org/10.3390/en17030762





