Anti-Freezing Study of High-Level Water-Collecting Natural Draft Wet-Cooling Tower Based on Its Water Temperature Distribution Characteristics
Abstract
1. Introduction
2. Models and Methods
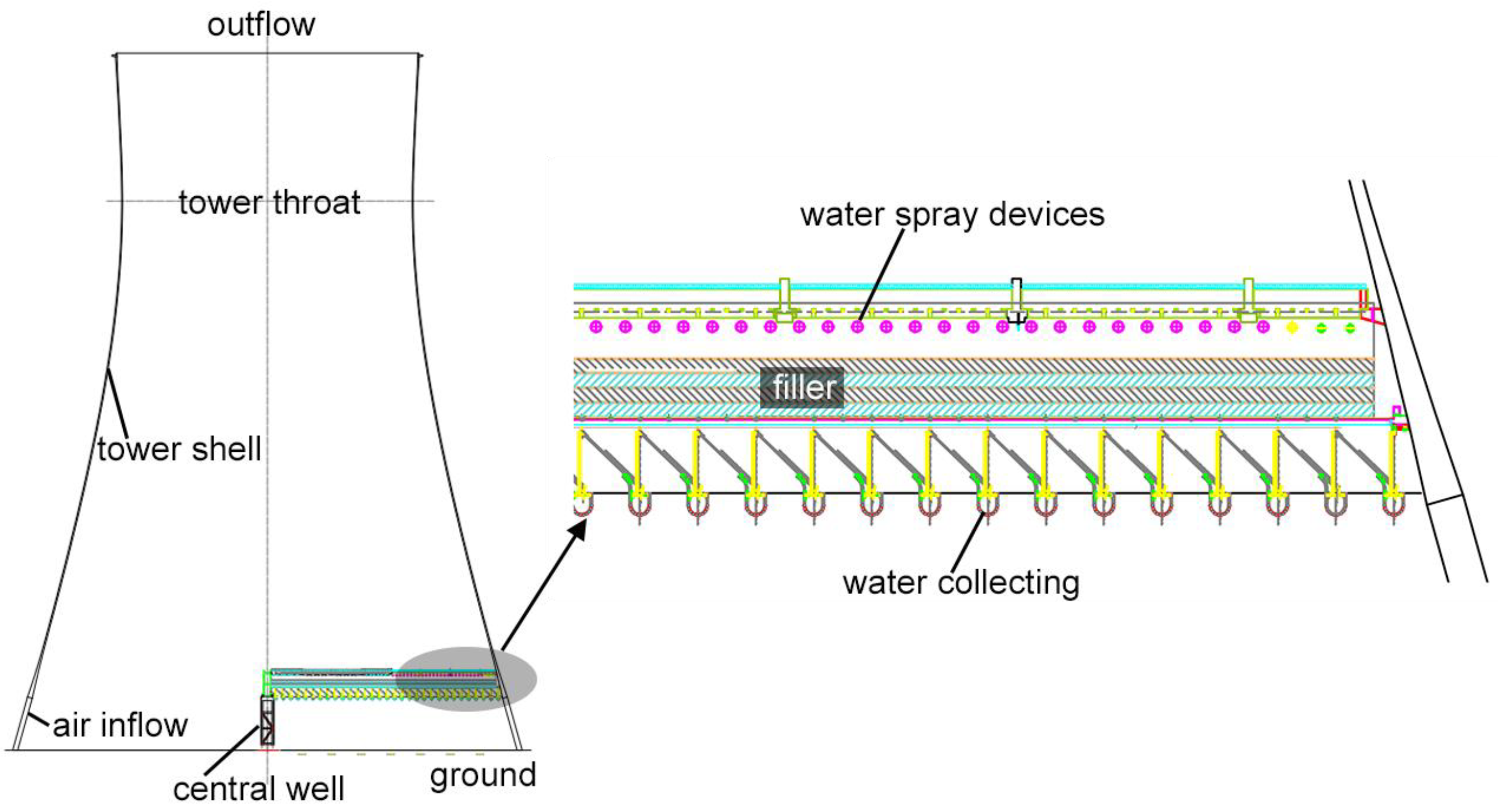
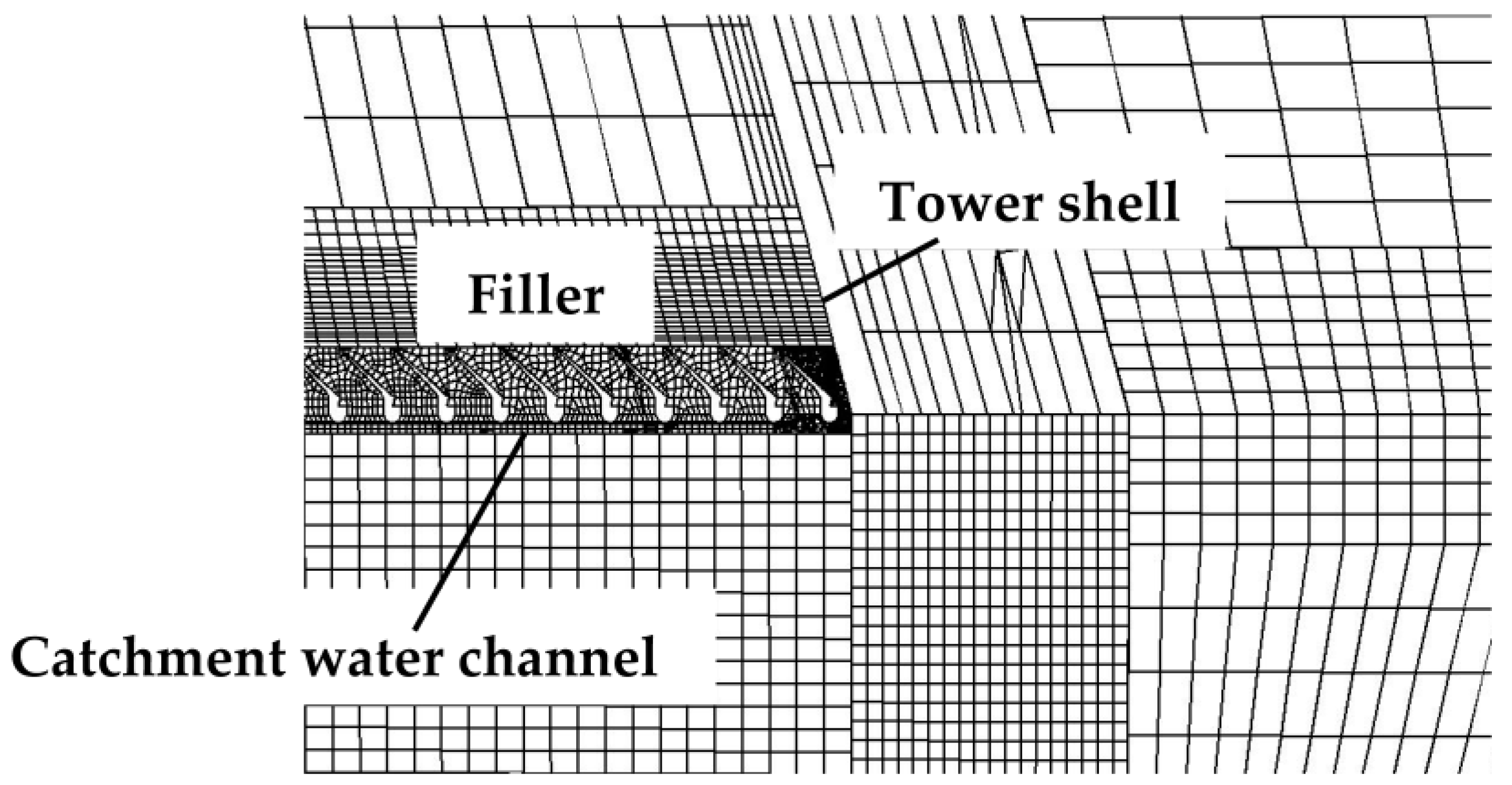
2.1. Geometry Model
2.2. Numerical Model
2.2.1. Governing Equations
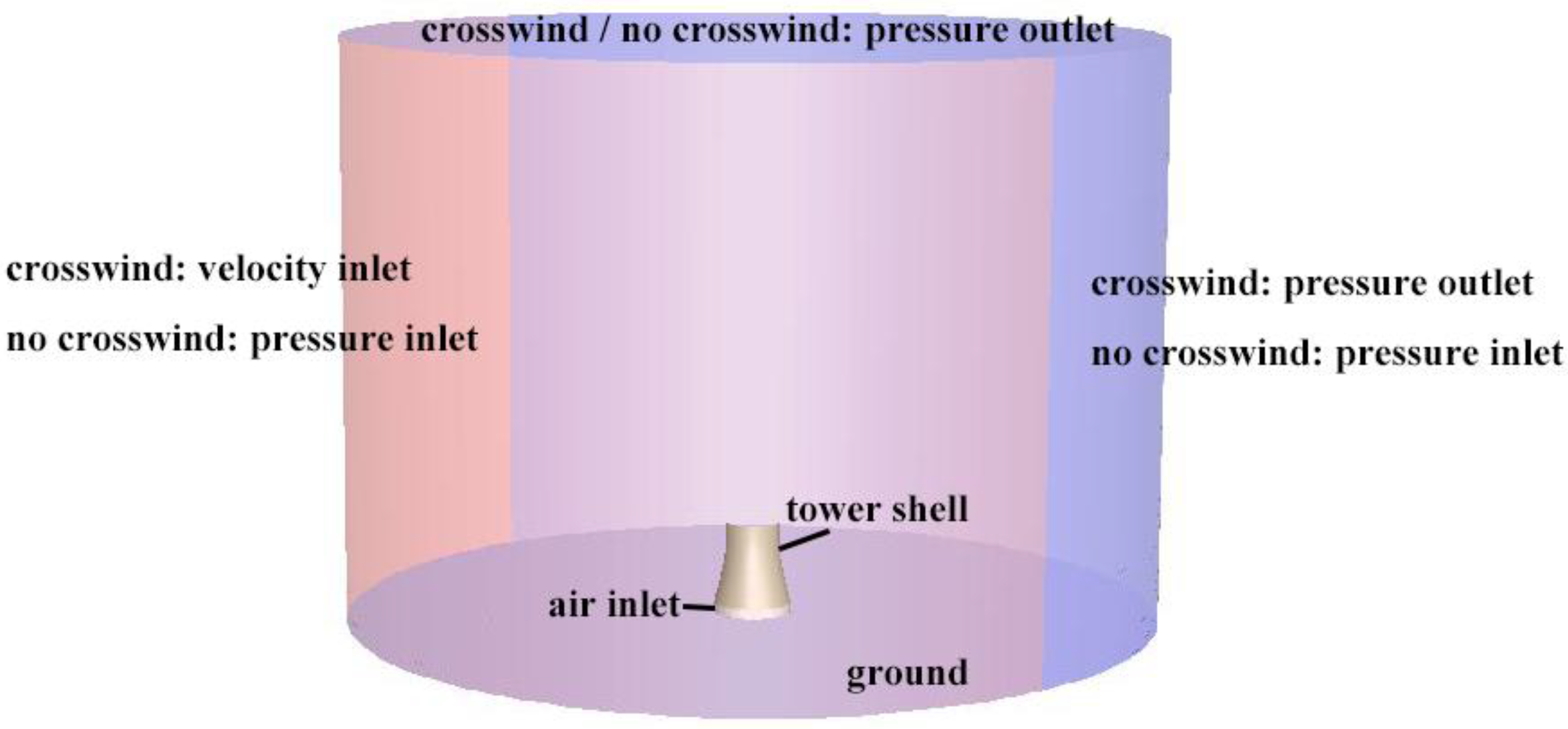
2.2.2. Boundary Conditions
2.2.3. Numerical Model Validation
3. Results and Discussion
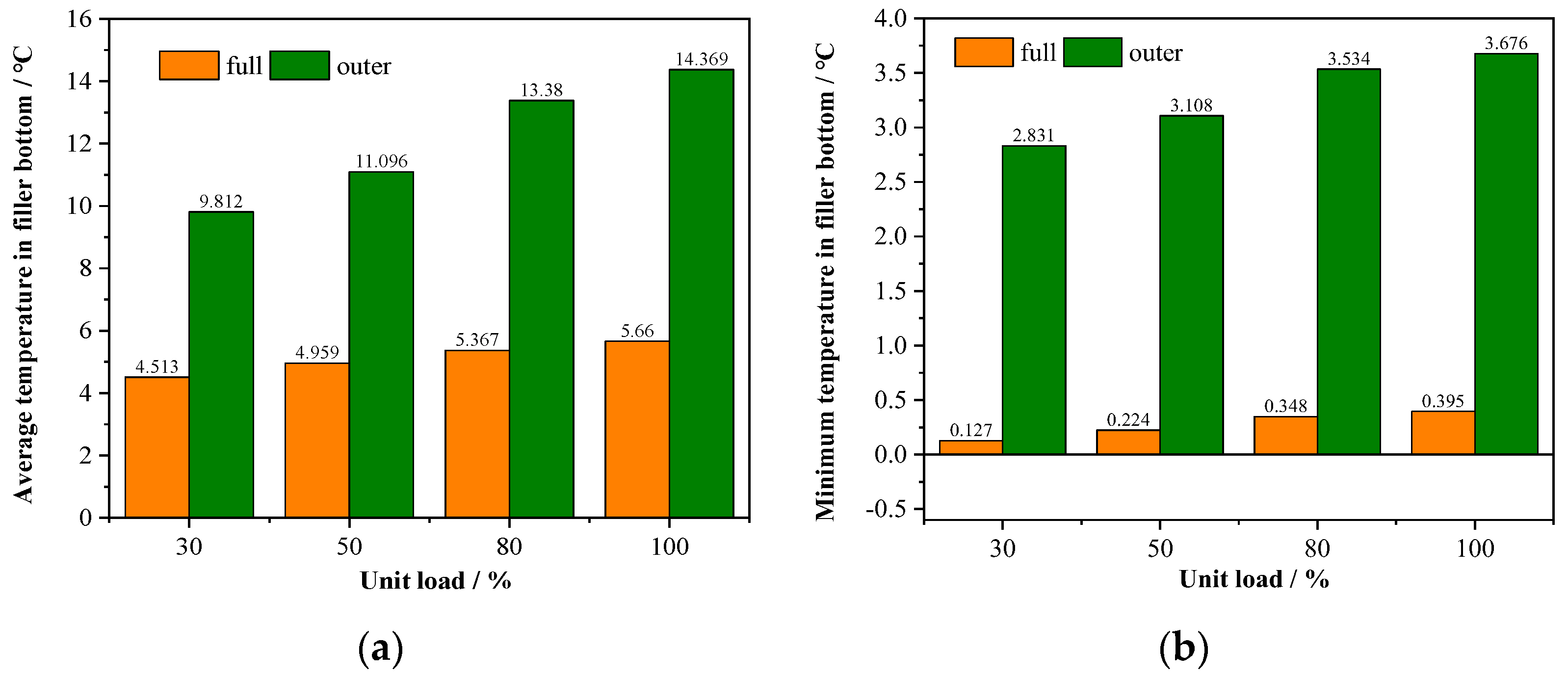
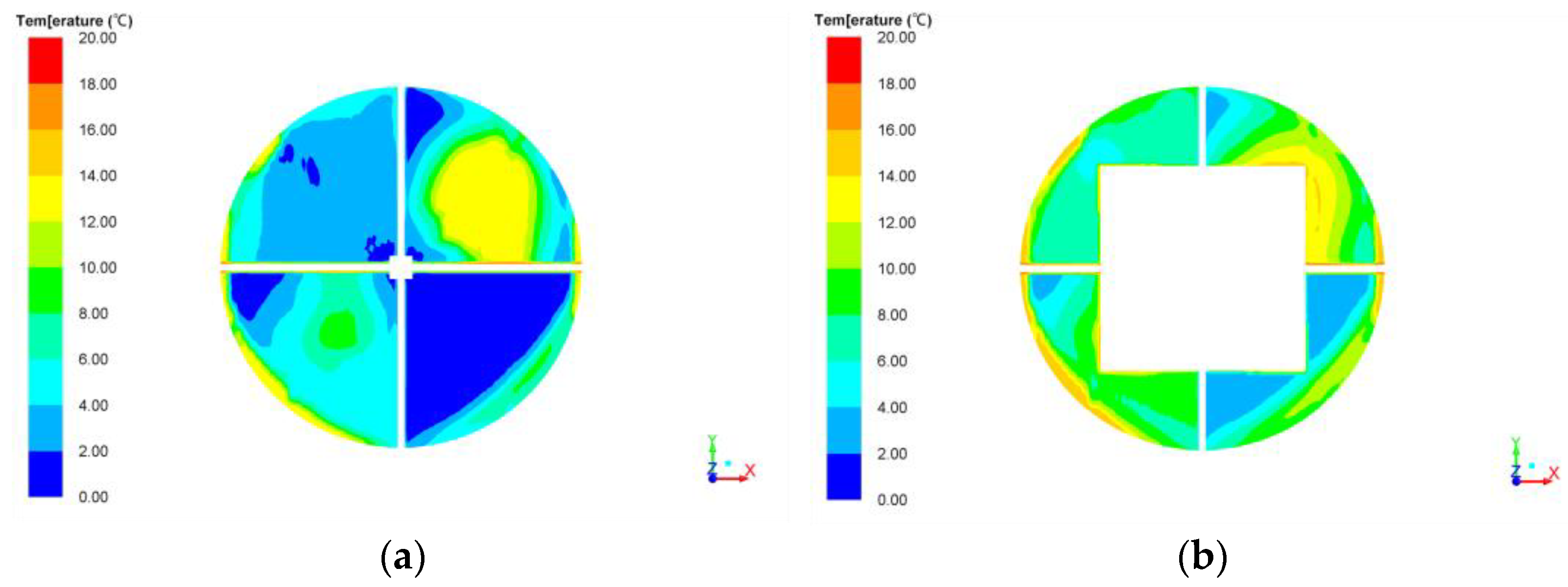
3.1. Comparison under Different Water Distribution Modes
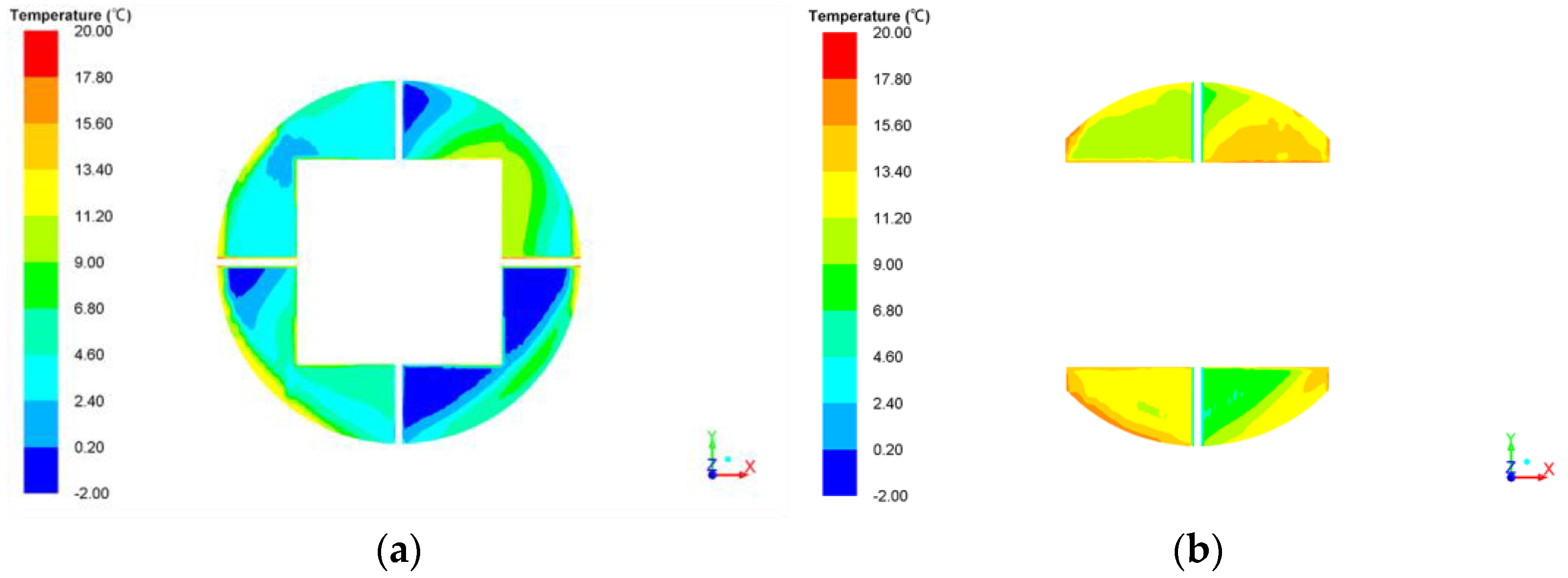
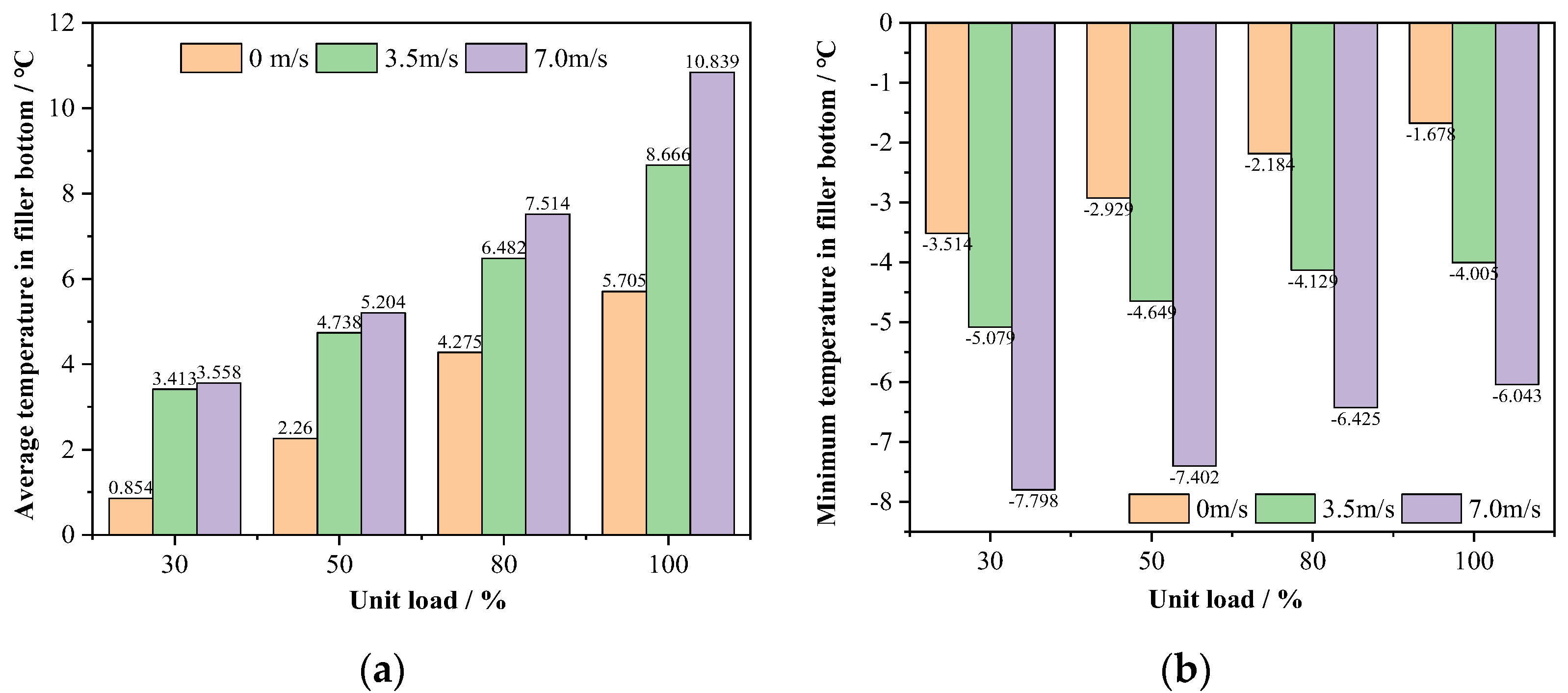
3.2. Comparison under Different Crosswind Velocities
3.3. Comparison under Different Ambient Temperatures
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Lausterer, G.K. Improved Maneuverability of Power Plants for Better Grid Stability. Control Eng. Pract. 1998, 6, 1549–1557. [Google Scholar] [CrossRef]
- Xin, S.; Wang, H.; Li, J.; Wang, G.; Wang, Q.; Cao, P.; Zhang, P.; Lu, X. Discussion on the Feasibility of Deep Peak Regulation for Ultra-Supercritical Circulating Fluidized Bed Boiler. Energies 2022, 15, 7720. [Google Scholar] [CrossRef]
- Lu, H.; Huang, S.; Li, H.; Cheng, Z.; Chang, X.; Dong, L.; Kong, D.; Jing, X. Numerical Simulation of Combustion Characteristics in a 660 MW Tangentially Fired Pulverized Coal Boiler Subjected to Peak-Load Regulation. Case Stud. Therm. Eng. 2023, 49, 103168. [Google Scholar] [CrossRef]
- Ezhov, V.; Zakharov, A.; Ezhova, T.; Kravchenko, S.; Amelin, V. Features of Calculation Technique of the Cooling Tower in the Winter Period Taking into Account the Desigh of the Head Wall. IOP Conf. Ser. Mater. Sci. Eng. 2020, 1001, 012066. [Google Scholar] [CrossRef]
- Zhao, Y.; Sun, F.; Long, G.; Huang, X.; Huang, W.; Lyv, D. Comparative Study on the Cooling Characteristics of High Level Water Collecting Natural Draft Wet Cooling Tower and the Usual Cooling Tower. Energy Convers. Manag. 2016, 116, 150–164. [Google Scholar] [CrossRef]
- Goodarzi, M.; Keimanesh, R. Numerical Analysis on Overall Performance of Savonius Turbines Adjacent to a Natural Draft Cooling Tower. Energy Convers. Manag. 2015, 99, 41–49. [Google Scholar] [CrossRef]
- Goudarzi, M.A. Proposing a New Technique to Enhance Thermal Performance and Reduce Structural Design Wind Loads for Natural Drought Cooling Towers. Energy 2013, 62, 164–172. [Google Scholar] [CrossRef]
- Du Preez, A.F.; Kröger, D.G. The Effect of the Heat Exchanger Arrangement and Wind-Break Walls on the Performance of Natural Draft Dry-Cooling Towers Subjected to Cross-Winds. J. Wind. Eng. Ind. Aerodyn. 1995, 58, 293–303. [Google Scholar] [CrossRef]
- Li, W.; Wang, H.; Wang, J.; Duan, C.; Zhao, Y. Effect Mechanism of Exit-Water Temperature Distribution Characteristics on the Anti-Freezing of Natural Draft Dry Cooling Tower. Appl. Therm. Eng. 2019, 161, 114078. [Google Scholar] [CrossRef]
- Ma, H.; Si, F.; Li, L.; Yan, W.; Zhu, K. Effects of Ambient Temperature and Crosswind on Thermo-Flow Performance of the Tower under Energy Balance of the Indirect Dry Cooling System. Appl. Therm. Eng. 2015, 78, 90–100. [Google Scholar] [CrossRef]
- Derksen, D.D.; Bender, T.J.; Bergstrom, D.J.; Rezkallah, K.S. A Study on the Effects of Wind on the Air Intake Flow Rate of a Cooling Tower: Part 1. Wind Tunnel Study. J. Wind. Eng. Ind. Aerodyn. 1996, 64, 47–59. [Google Scholar] [CrossRef]
- Bender, T.J.; Bergstrom, D.J.; Rezkallah, K.S. A Study on the Effects of Wind on the Air Intake Flow Rate of a Cooling Tower: Part 2. Wind Wall Study. J. Wind. Eng. Ind. Aerodyn. 1996, 64, 61–72. [Google Scholar] [CrossRef]
- Bender, T.J.; Bergstrom, D.J.; Rezkallah, K.S. A Study on the Effects of Wind on the Air Intake Flow Rate of a Cooling Tower: Part 3. Numerical Study. J. Wind. Eng. Ind. Aerodyn. 1996, 64, 73–88. [Google Scholar] [CrossRef]
- Zhao, Y.; Sun, F.; Wang, K.; Gao, M.; Yan, S.; Gao, T. Numerical analysis of crosswind effect on wet cooling tower aerodynamic field. Nucl. Power Eng. 2008, 29, 35–40. [Google Scholar]
- Rossi Di Schio, E.; Ballerini, V.; Dongellini, M.; Valdiserri, P. Defrosting of Air-Source Heat Pumps: Effect of Real Temperature Data on Seasonal Energy Performance for Different Locations in Italy. Appl. Sci. 2021, 11, 8003. [Google Scholar] [CrossRef]
- Dongellini, M.; Naldi, C.; Morini, G.L. Influence of Sizing Strategy and Control Rules on the Energy Saving Potential of Heat Pump Hybrid Systems in a Residential Building. Energy Convers. Manag. 2021, 235, 114022. [Google Scholar] [CrossRef]
- Chen, G.; Zhao, Y.; Ge, W.; Li, W. Critical Guidelines to Cope with the Adverse Impacts of the Inner Peripheral Vortex in the High-Level Water Collecting Natural Draft Wet Cooling Tower. Appl. Therm. Eng. 2020, 168, 114819. [Google Scholar] [CrossRef]
- Wu, Y. Numerical Simulation of Three-Dimensional Thermal Characteristics and Optimization of Water Collecting Device for Natural Ventilation High Level Cooling Tower; Shandong University: Jinan, China, 2016. [Google Scholar]
- Chen, G.; Zhao, Y.; Li, W.; Ge, W. The Efficiency of High-Level Water Collecting Cooling Tower with the Installation of Cross Wall Affect by the Evolution of Aerodynamic Field. Appl. Therm. Eng. 2019, 161, 114181. [Google Scholar] [CrossRef]
- Ma, L.; Ren, J. The Influence and Analysis of Natural Crosswind on Cooling Characteristics of the High Level Water Collecting Natural Draft Wet Cooling Tower. IOP Conf. Ser. Earth Environ. Sci. 2018, 108, 052116. [Google Scholar] [CrossRef]
- Solomon, A.B.; Ramachandran, K.; Asirvatham, L.G.; Pillai, B.C. Numerical Analysis of a Screen Mesh Wick Heat Pipe with Cu/Water Nanofluid. Int. J. Heat Mass Transf. 2014, 75, 523–533. [Google Scholar] [CrossRef]
- Fadhl, B.; Wrobel, L.C.; Jouhara, H. CFD Modelling of a Two-Phase Closed Thermosyphon Charged with R134a and R404a. Appl. Therm. Eng. 2015, 78, 482–490. [Google Scholar] [CrossRef]
- Jaber, H.; Webb, R.L. Design of Cooling Towers by the Effectiveness-NTU Method. J. Heat Transfer 1989, 111, 837–843. [Google Scholar] [CrossRef]
- Gilani, N.; Parpanji, F. Parametric Study on the Outlet Water Temperature in a Shower Cooling Tower and Its Application in Different Iranian Provincial Capitals. Int. J. Therm. Sci. 2018, 124, 174–186. [Google Scholar] [CrossRef]
- Sutherland, J.W. Analysis of Mechanical-Draught Counterflow Air/Water Cooling Towers. J. Heat Transf. 1983, 105, 576–583. [Google Scholar] [CrossRef]
- Nahavandi, A.N.; Kershah, R.M.; Serico, B.J. The Effect of Evaporation Losses in the Analysis of Counterflow Cooling Towers. Nucl. Eng. Des. 1975, 32, 29–36. [Google Scholar] [CrossRef]
- Barbieri, E.S.; Melino, F.; Morini, M. Influence of the Thermal Energy Storage on the Profitability of Micro-CHP Systems for Residential Building Applications. Appl. Energy 2012, 97, 714–722. [Google Scholar] [CrossRef]
- Zhang, H.; Liang, W.; Liu, J.; Wang, J. Modeling and Energy Efficiency Analysis of Thermal Power Plant with High Temperature Thermal Energy Storage (HTTES). J. Therm. Sci. 2020, 29, 1025–1035. [Google Scholar] [CrossRef]
- Williamson, N.; Armfield, S.; Behnia, M. Numerical Simulation of Flow in a Natural Draft Wet Cooling Tower—The Effect of Radial Thermofluid Fields. Appl. Therm. Eng. 2008, 28, 178–189. [Google Scholar] [CrossRef]
- Al-Waked, R.; Behnia, M. CFD Simulation of Wet Cooling Towers. Appl. Therm. Eng. 2006, 26, 382–395. [Google Scholar] [CrossRef]
- Klimanek, A.; Cedzich, M.; Białecki, R. 3D CFD Modeling of Natural Draft Wet-Cooling Tower with Flue Gas Injection. Appl. Therm. Eng. 2015, 91, 824–833. [Google Scholar] [CrossRef]
- Tiwari, A.K.; Jain, S.; Karmakar, S. An Improved Three-Dimensional Numerical Model of a v-Bar Splash Fill in a Wet Cooling Tower. Int. Commun. Heat Mass Transf. 2021, 128, 105617. [Google Scholar] [CrossRef]
- Xi, Y.; Yu, Z.; Zhang, L.; Yu, A.; Liu, L.; Bao, B.; Zhao, Y.; Zhou, C.; Wu, B.; Dong, K. Research on Heat and Mass Transfer Characteristics of a Counterflow Wet Cooling Tower Using a New Type of Straight Wave Packing. Int. J. Therm. Sci. 2023, 193, 108540. [Google Scholar] [CrossRef]
- Al-Waked, R.; Behnia, M. Enhancing Performance of Wet Cooling Towers. Energy Convers. Manag. 2007, 48, 2638–2648. [Google Scholar] [CrossRef]
- Lu, Y.; Yang, Y.; Wu, X.; Wang, L.; Wan, Z.; Zheng, Z.; Xu, J.; Cao, C. Spatiotemporal variations of wet-bulb temperature and its impact factors of Nanjing urban neighborhoo. Chin. J. Appl. Ecol. 2021, 32, 4223–4236. [Google Scholar] [CrossRef]
- Moratiel, R.; Soriano, B.; Centeno, A.; Spano, D.; Snyder, R.L. Wet-Bulb, Dew Point, and Air Temperature Trends in Spain. Theor. Appl. Climatol. 2017, 130, 419–434. [Google Scholar] [CrossRef]



| Grid Number | 2,801,481 | 3,526,840 | 4,337,846 |
|---|---|---|---|
| Outlet water temperature, °C | 14.54 | 14.52 | 14.52 |
| Absolute error, °C | 0.18 | 0.16 | 0.16 |
| Circulating water temperature drop, °C | 7.06 | 7.08 | 7.08 |
| Operation Conditions | C1 | C2 |
|---|---|---|
| Ambient temperature, °C | 14.8 | 4 |
| Relative humidity, % | 61 | 30 |
| Crosswind velocity, m/s | 3.5 | 0.4 |
| Atmosphere pressure, kPa | 101.02 | 102 |
| Circulating water flow rate, m3/h | 82,776 | 34,344 |
| Water distribution modes | Full | Outer ring |
| Test/design inlet water temperature, °C | 28.54 | 21.60 |
| Test/design outlet water temperature, °C | 19.87 | 14.36 |
| Outlet water temperature calculated by numerical model, °C | 20.01 | 14.52 |
| Absolute error, °C | 0.14 | 0.16 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Z.; Yue, Z.; Wang, W.; Ma, C.; Li, X.; Guo, C.; Zhao, Y. Anti-Freezing Study of High-Level Water-Collecting Natural Draft Wet-Cooling Tower Based on Its Water Temperature Distribution Characteristics. Energies 2024, 17, 651. https://doi.org/10.3390/en17030651
Wang Z, Yue Z, Wang W, Ma C, Li X, Guo C, Zhao Y. Anti-Freezing Study of High-Level Water-Collecting Natural Draft Wet-Cooling Tower Based on Its Water Temperature Distribution Characteristics. Energies. 2024; 17(3):651. https://doi.org/10.3390/en17030651
Chicago/Turabian StyleWang, Zhonghua, Zenggang Yue, Wei Wang, Chenghui Ma, Xiaoguang Li, Changmin Guo, and Yuanbin Zhao. 2024. "Anti-Freezing Study of High-Level Water-Collecting Natural Draft Wet-Cooling Tower Based on Its Water Temperature Distribution Characteristics" Energies 17, no. 3: 651. https://doi.org/10.3390/en17030651
APA StyleWang, Z., Yue, Z., Wang, W., Ma, C., Li, X., Guo, C., & Zhao, Y. (2024). Anti-Freezing Study of High-Level Water-Collecting Natural Draft Wet-Cooling Tower Based on Its Water Temperature Distribution Characteristics. Energies, 17(3), 651. https://doi.org/10.3390/en17030651






