A Study on the Effect of Toroidal Propeller Parameters on Efficiency and Thrust
Abstract
1. Introduction
2. Materials and Methods
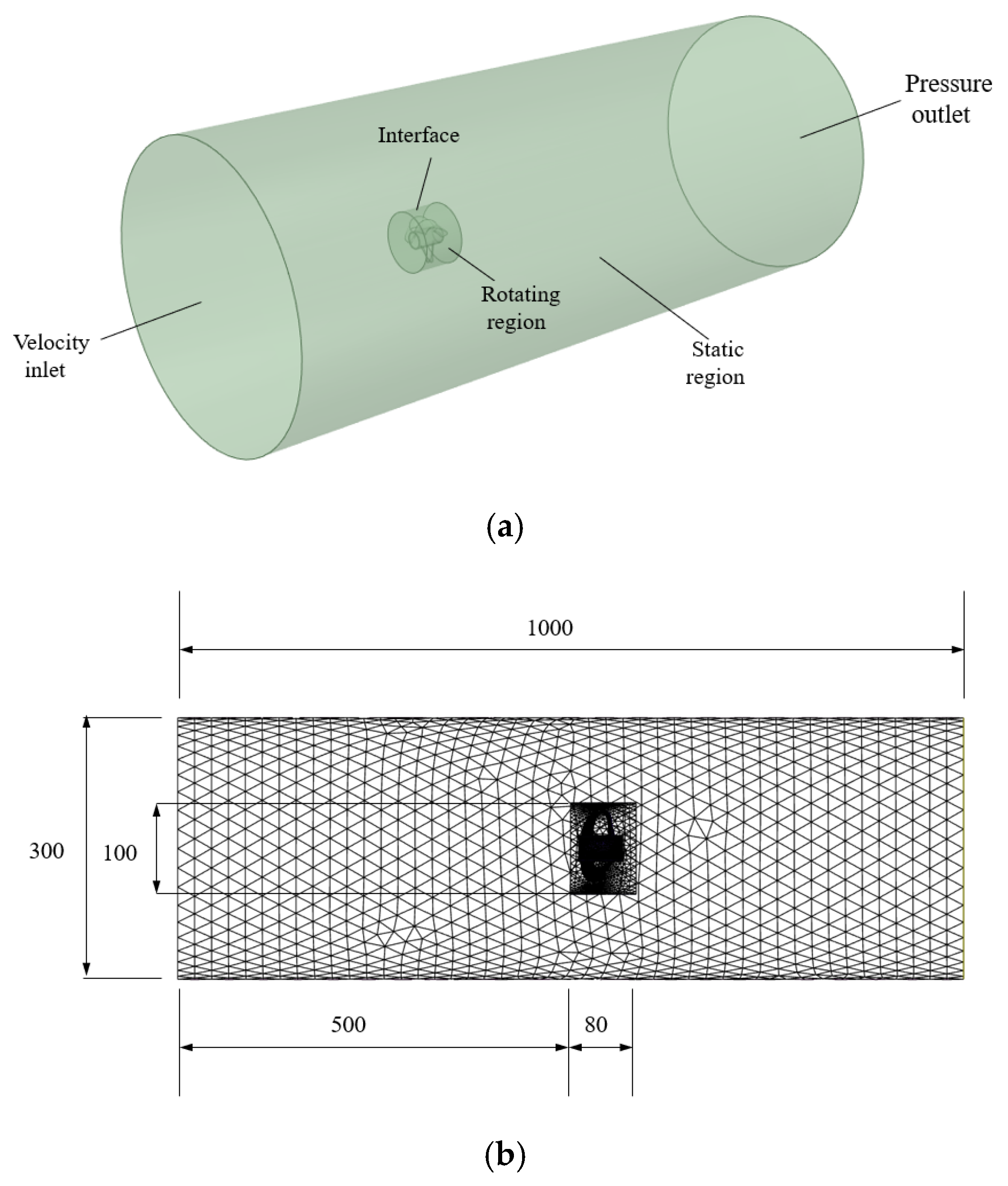
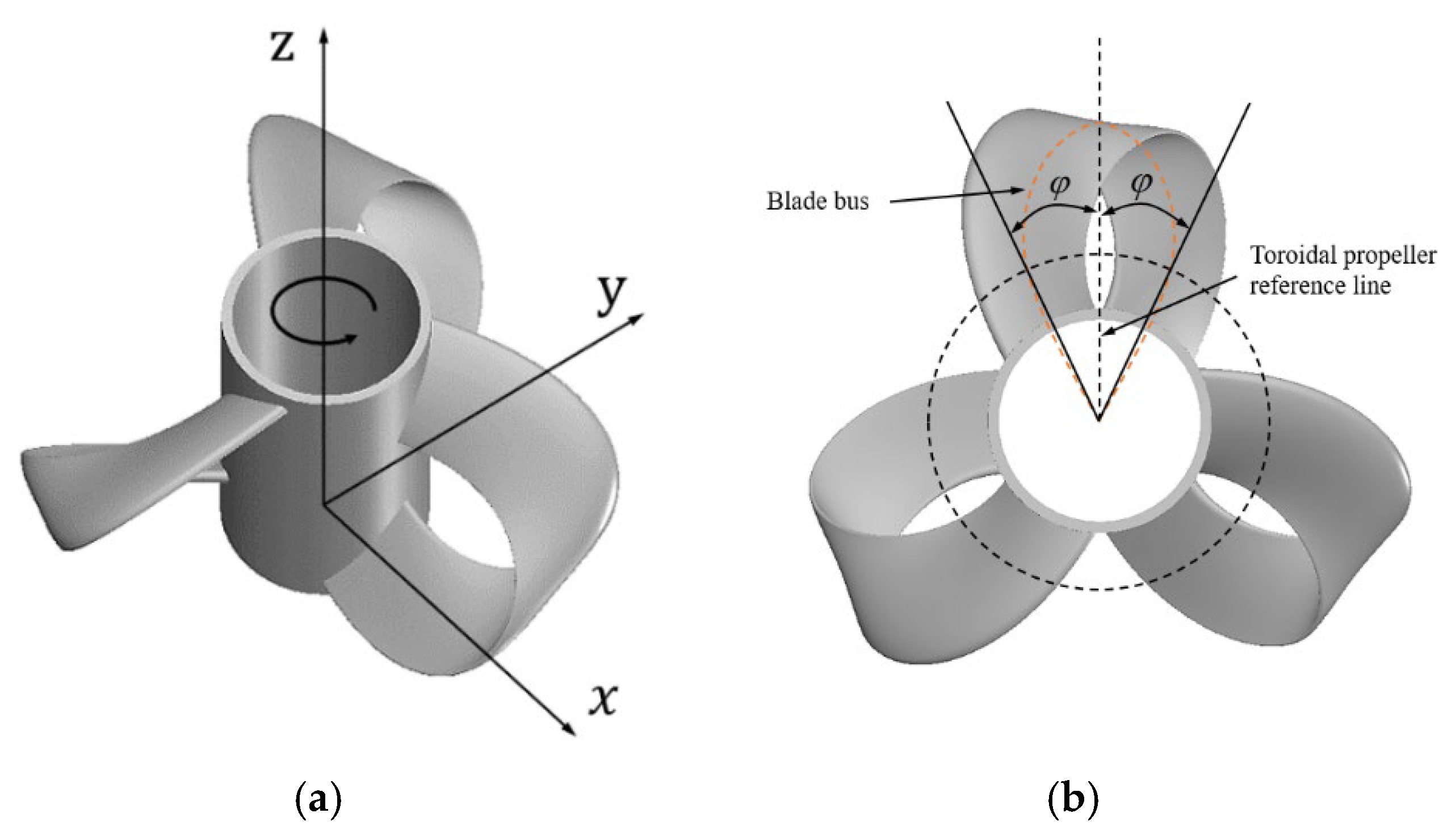
2.1. Geometry and Mesh Generation
2.2. Numerical Modeling
2.3. Propeller Hydrodynamic Theory
2.4. Additional Definitions
2.5. Test Verification
3. Results
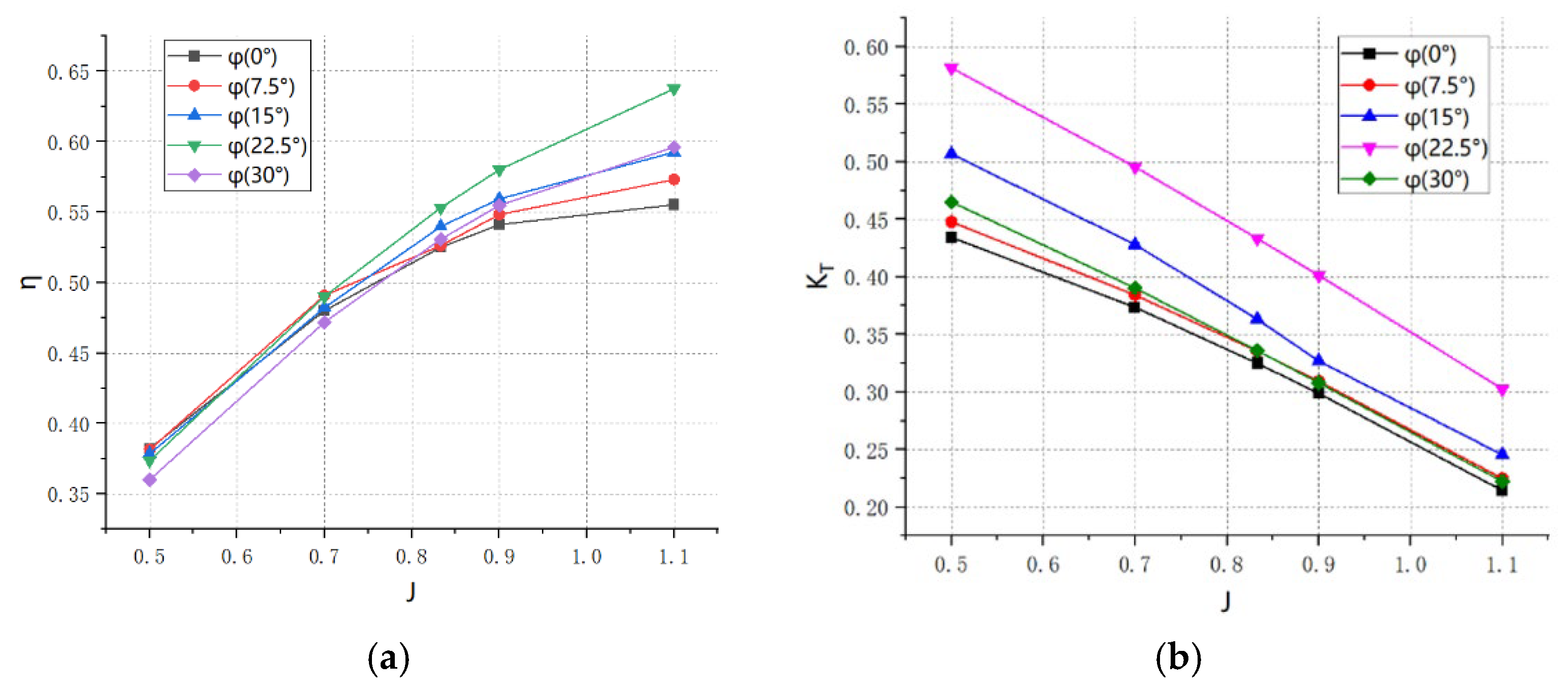
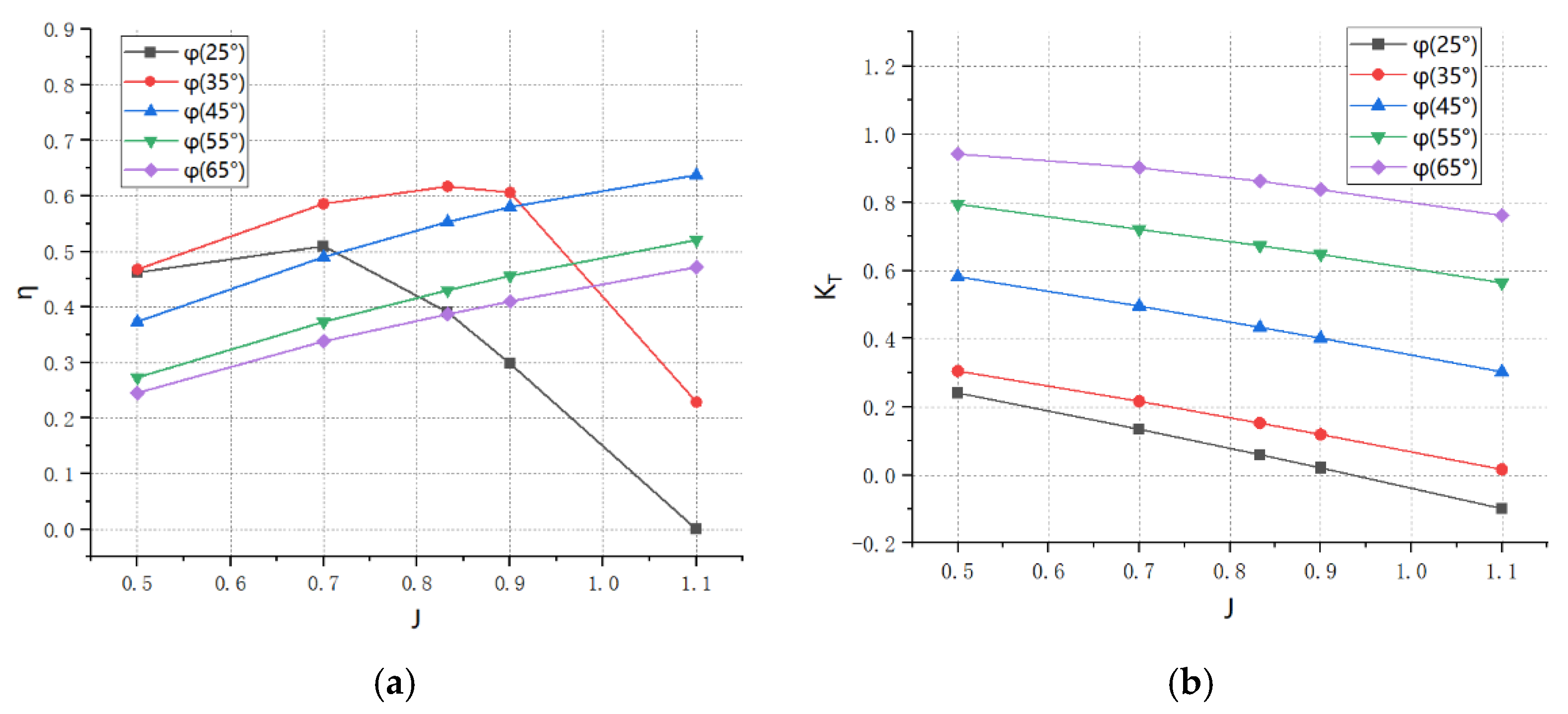
3.1. Effect of Outward Inclination Angle
3.2. Effect of Pitch Angle
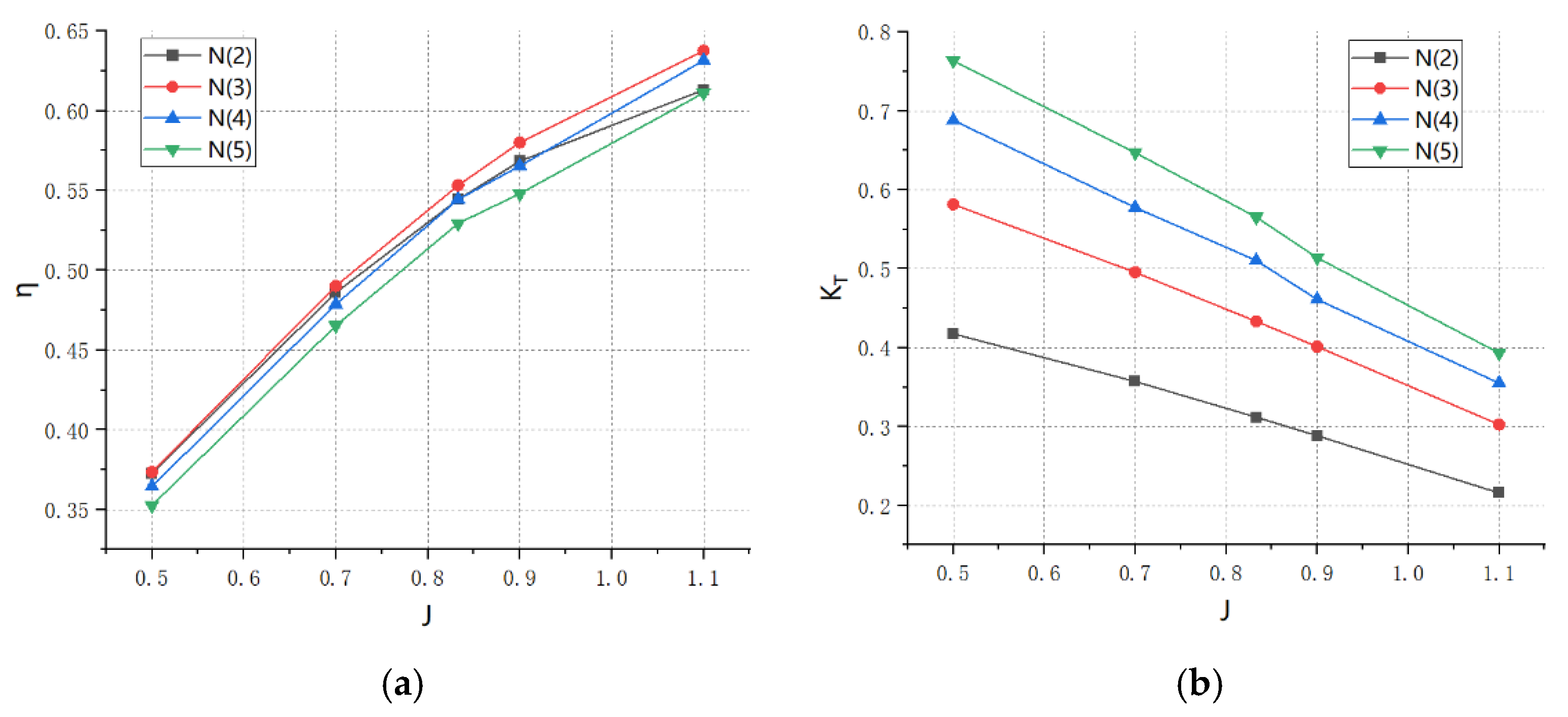
3.3. Effect of the Number of Paddles
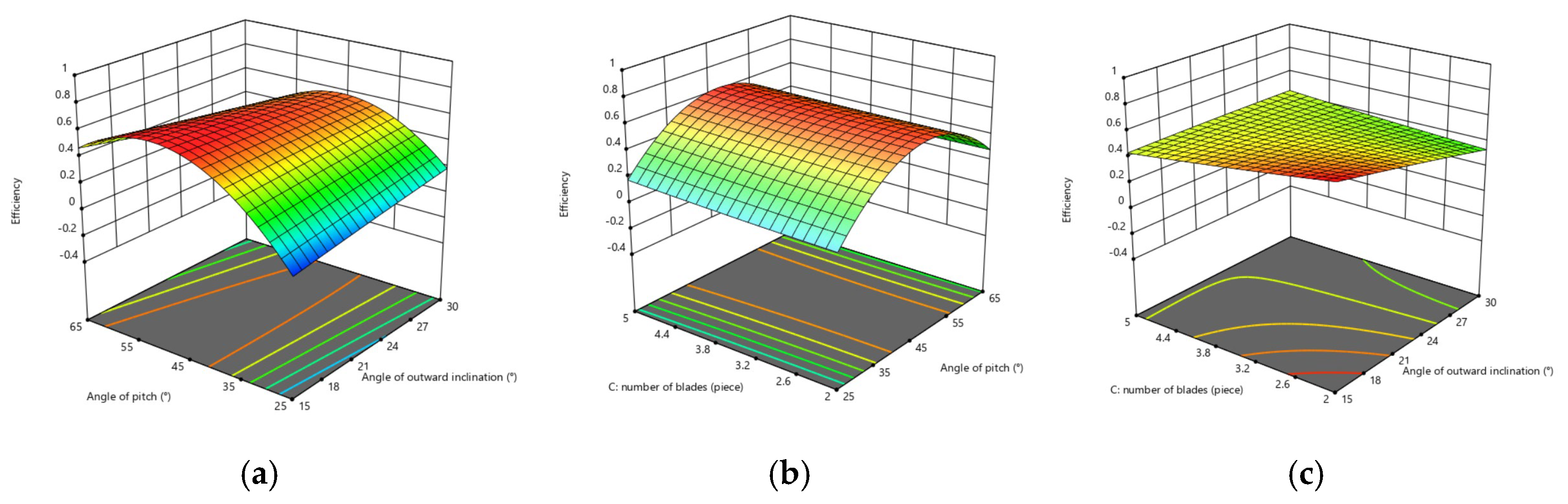
3.4. Multi-Factor Research
4. Discussion
5. Conclusions
- The one-factor study showed that both the efficiency and thrust coefficient of the toroidal propeller increased and then decreased with the increase in the outward inclination angle, and the efficiency and thrust coefficient of the toroidal propeller were optimal at the outward inclination angle of 23.25°.
- Decreasing the pitch angle improves efficiency at advance coefficients less than 0.7, but the 45° pitch angle is the most efficient in conditions where the advance coefficient is greater. In contrast, increasing the pitch angle increases the thrust coefficient.
- The number of blades has a small effect on the efficiency of the propeller, and increasing the number of blades increases the thrust coefficient of the propeller.
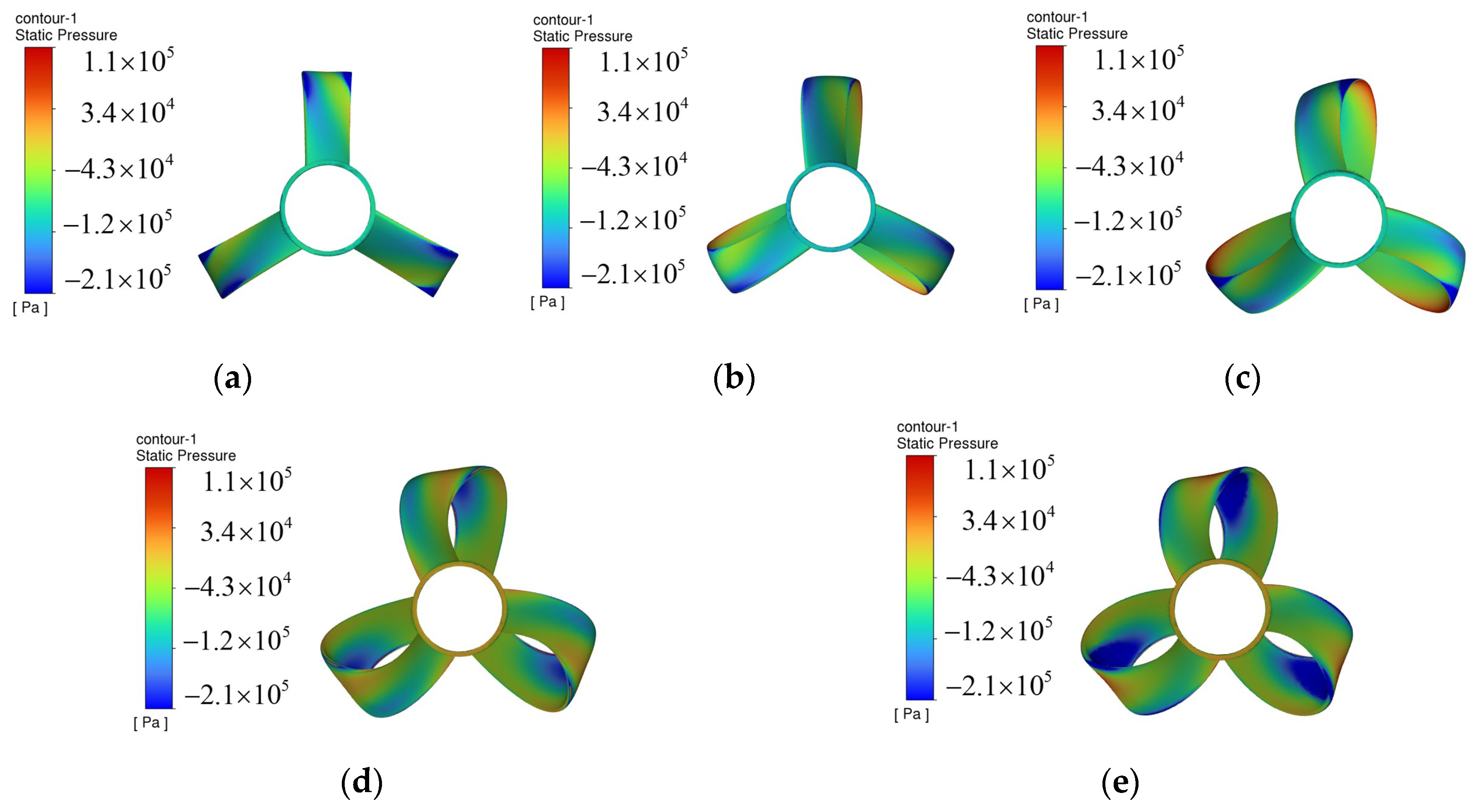
- Cavitation in toroidal propellers occurs in the blade transition section, and adjusting the outward inclination angle will change the location of the cavitation concentration.
- For the efficiency of the propeller, the interaction between outward inclination angle and pitch angle is more obvious, as is the interaction between the pitch angle and the number of blades, and the interaction between outward inclination angle and the number of blades is relatively weak.
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Zhang, Q.; Jaiman, R.K. Numerical analysis on the wake dynamics of a ducted propeller. Ocean Eng. 2019, 171, 202–224. [Google Scholar] [CrossRef]
- Sanchez Santiago, P. Rim-Jet-A Mechanical Design for a Shaft-Less Propulsor. Master’s Thesis, KTH, Stockholm, Sweden, 2019. [Google Scholar]
- Sharrow, G.C. Propeller. U.S. Patent 9,926,058, 27 March 2018. [Google Scholar]
- Sharrow-Propeller. Available online: https://boattest.com/Sharrow-Propeller (accessed on 10 March 2024).
- Sebastian, T.; Strem, C. Toroidal Propeller. U.S. Patent 10836466B2, 17 November 2020. [Google Scholar]
- Zhang, Q.; Jaiman, R.K.; Ma, P.; Liu, J. Investigation on the performance of a ducted propeller in oblique flow. J. Offshore Mech. Arct. Eng. 2020, 142, 011801. [Google Scholar] [CrossRef]
- Rhee, S.H.; Kawamura, T.; Li, H. Propeller cavitation study using an unstructured grid based navier-stoker solver. J. Fluids Eng. 2005, 127, 986–994. [Google Scholar] [CrossRef]
- Sikirica, A.; Čarija, Z.; Kranjčević, L.; Lučin, I. Grid type and turbulence model influence on propeller characteristics prediction. J. Mar. Sci. Eng. 2019, 7, 374. [Google Scholar] [CrossRef]
- Peng, H.H.; Qiu, W.; Ni, S. Effect of turbulence models on RANS computation of propeller vortex flow. Ocean Eng. 2013, 72, 304–317. [Google Scholar] [CrossRef]
- Helal, M.M.; Ahmed, T.M.; Banawan, A.A.; Kotb, M.A. Numerical prediction of sheet cavitation on marine propellers using CFD simulation with transition-sensitive turbulence model. Alex. Eng. J. 2018, 57, 3805–3815. [Google Scholar] [CrossRef]
- Warjito, W.; Nasution, S.B.; Syahputra, M.F.; Budiarso, B.; Adanta, D. Study of turbulence model for performance and flow field prediction of pico hydro types propeller turbine. CFD Lett. 2020, 12, 26–34. [Google Scholar] [CrossRef]
- Subhas, S.; Saji, V.F.; Ramakrishna, S.; Das, H.N. CFD analysis of a propeller flow and cavitation. Int. J. Comput. Appl. 2012, 55, 26–33. [Google Scholar]
- Zhu, Z.; Fang, S. Numerical investigation of cavitation performance of ship propellers. J. Hydrodyn. 2012, 24, 347–353. [Google Scholar] [CrossRef]
- Shi, J.; Zhang, D.; Xu, S.; Chen, Y.; Qin, S.; Liu, X.; Hou, G. Comparative study on related models of propeller cavitation numerical simulation. Chin. J. Ship Res. 2023, 18, 30–38. [Google Scholar]
- Ghasemi, H. The effect of wake flow and skew angle on the ship propeller performance. Sci. Iran. 2009, 16, 149–158. [Google Scholar]
- Belhenniche, S.; Aounallah, M.; Omar, I.; Çelik, F. Effect of geometric configurations on hydrodynamic performance assessment of a marine propeller. Brodogr. Int. J. Nav. Archit. Ocean Eng. Res. Dev. 2016, 67, 31–48. [Google Scholar] [CrossRef][Green Version]
- Gaggero, S.; Dubbioso, G.; Villa, D.; Muscari, R.; Viviani, M. Propeller modeling approaches for off–design operative conditions. Ocean Eng. 2019, 178, 283–305. [Google Scholar] [CrossRef]
- Boucetta, D.; Imine, O. Numerical simulation of the flow around marine propeller series. J. Phys. Sci. Appl. 2016, 6, 55–61. [Google Scholar]
- Tadros, M.; Ventura, M.; Guedes Soares, C. Design of propeller series optimizing fuel consumption and propeller efficiency. J. Mar. Sci. Eng. 2021, 9, 1226. [Google Scholar] [CrossRef]
- Pawar, A.B.; Petkar, T.S.; Pitale, P.S.; Salagare, S.S. Design and simulation of marine propeller with different blade geometry. Int. J. Innov. Sci. Res. Technol. 2019, 4, 109–117. [Google Scholar]
- Jadmiko, E.; Gurning, R.O.S.; Zaman, M.B.; Widjiati, E. Variations Rake Angle Propeller B–Series Towards Performance and Cavitation with CFD Method. J. Adv. Res. Fluid Mech. Therm. Sci. 2023, 106, 78–86. [Google Scholar] [CrossRef]
- Liyu, Y.E.; Chao, W.A.N.G.; Cong, S.U.N.; Chunyu, G.U.O. Mathematical expression method for geometric shape of toroidal propeller. Chin. J. Ship Res. 2023, 18, 224–233. [Google Scholar]
- Yang, J.; Zhou, L.J.; Wang, Z.W. Numerical investigation of the cavitation dynamic parameters in a Francis turbine draft tube with columnar vortex rope. J. Hydrodyn. 2019, 31, 931–939. [Google Scholar] [CrossRef]
- Tan, Y.; Ni, Y.; Xu, W. Key technologies and development trends of the soft abrasive flow finishing method. J. Zhejiang Univ.-Sci. A 2023, 24, 1043–1064. [Google Scholar] [CrossRef]





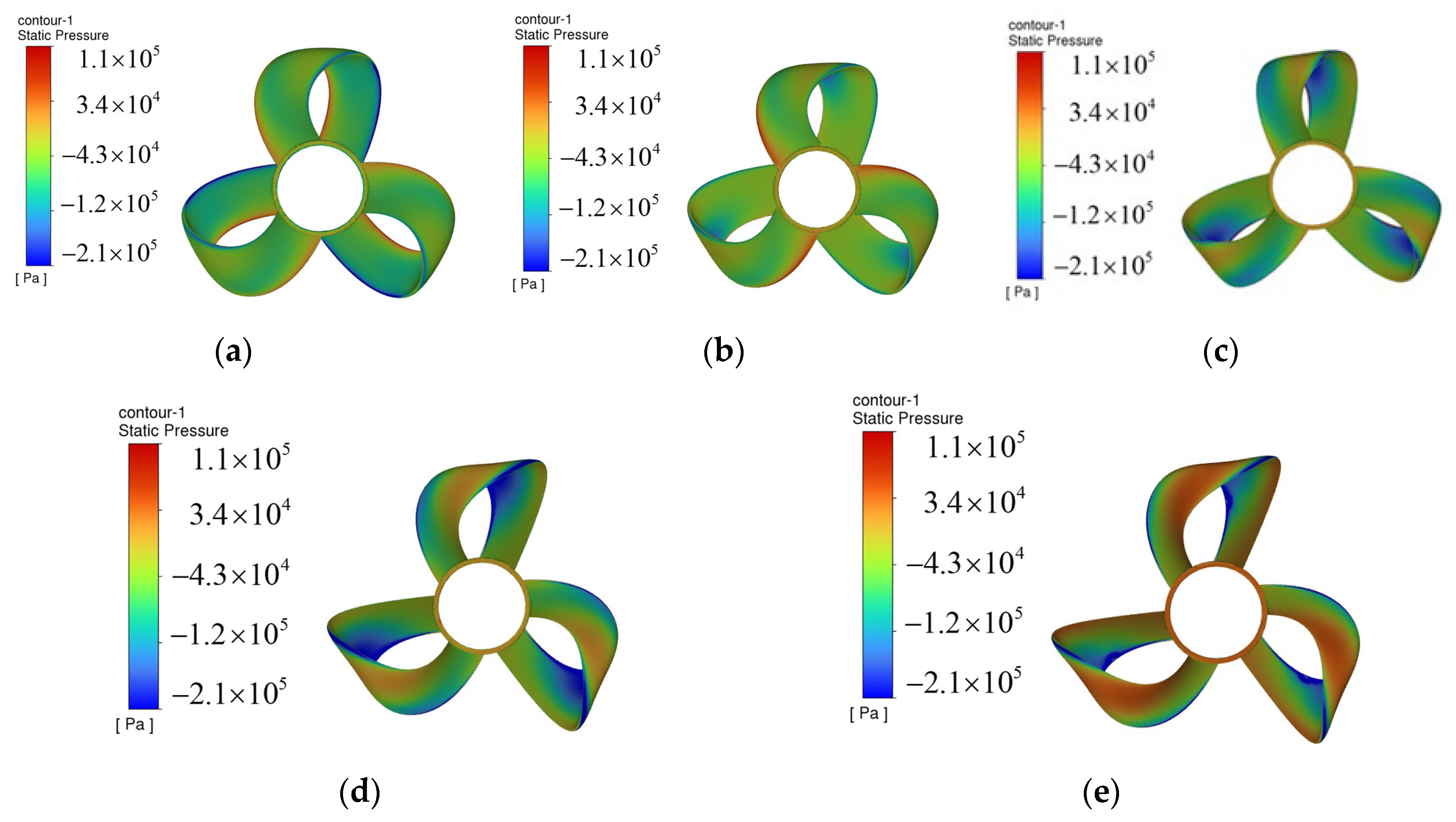

| Mesh Size/m | Thrust Coefficient | Relative Eviation |
|---|---|---|
| 0.008 | 0.2192 | 2.914% |
| 0.004 | 0.2227 | 1.364% |
| 0.002 | 0.2247 | 0.451% |
| 0.001 | 0.2254 | 0.168% |
| 0.0005 | 0.2257 | — |
| J | KT-EXP | 10KQ-EXP | KT-CFD | 10KQ-CFD | ERR-KT | ERR-10KQ |
|---|---|---|---|---|---|---|
| 0.5 | 0.291 | 0.635 | 0.288 | 0.595 | 0.87% | 6.31% |
| 0.7 | 0.253 | 0.586 | 0.247 | 0.546 | 2.44% | 6.78% |
| 0.833 | 0.233 | 0.549 | 0.216 | 0.507 | 7.64% | 7.72% |
| 0.9 | 0.183 | 0.464 | 0.199 | 0.485 | −8.92% | −4.58% |
| 1.1 | 0.143 | 0.403 | 0.149 | 0.411 | −4.63% | −2.12% |
| Serial Number | (°) | (°) | (Piece) | ||
|---|---|---|---|---|---|
| 1 | 15.00 | 45 | 4 | 0.235 | 0.522 |
| 2 | 15.00 | 35 | 3 | 0.114 | 0.486 |
| 3 | 18.75 | 45 | 2 | 0.271 | 0.570 |
| 4 | 22.50 | 25 | 3 | 0.013 | 0.136 |
| 5 | 26.25 | 45 | 3 | 0.414 | 0.554 |
| 6 | 22.50 | 65 | 2 | 0.564 | 0.426 |
| 7 | 22.50 | 45 | 5 | 0.520 | 0.551 |
| 8 | 26.25 | 55 | 4 | 0.754 | 0.470 |
| 9 | 30.00 | 55 | 2 | 0.486 | 0.457 |
| 10 | 18.75 | 55 | 3 | 0.442 | 0.547 |
| 11 | 22.50 | 55 | 2 | 0.447 | 0.511 |
| 12 | 26.25 | 25 | 2 | −0.018 | 0.000 |
| 13 | 30.00 | 35 | 5 | 0.197 | 0.553 |
| 14 | 30.00 | 45 | 2 | 0.217 | 0.576 |
| 15 | 18.75 | 65 | 4 | 0.838 | 0.410 |
| 16 | 30.00 | 65 | 3 | 0.862 | 0.420 |
| 17 | 15.0. | 55 | 5 | 0.560 | 0.498 |
| 18 | 15.00 | 65 | 2 | 0.178 | 0.610 |
| 19 | 15.00 | 25 | 2 | −0.027 | 0.000 |
| 20 | 26.25 | 65 | 5 | 0.941 | 0.440 |
| 21 | 30.00 | 25 | 4 | 0.064 | 0.352 |
| 22 | 18.75 | 35 | 2 | 0.112 | 0.622 |
| 23 | 22.50 | 35 | 4 | 0.125 | 0.567 |
| 24 | 26.25 | 35 | 2 | 0.139 | 0.632 |
| 25 | 18.75 | 25 | 5 | −0.063 | 0.000 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wu, J.; Wang, Q.; Deasy, H.; Hang, J. A Study on the Effect of Toroidal Propeller Parameters on Efficiency and Thrust. Energies 2024, 17, 5938. https://doi.org/10.3390/en17235938
Wu J, Wang Q, Deasy H, Hang J. A Study on the Effect of Toroidal Propeller Parameters on Efficiency and Thrust. Energies. 2024; 17(23):5938. https://doi.org/10.3390/en17235938
Chicago/Turabian StyleWu, Ji, Qingchun Wang, Hugh Deasy, and Junyu Hang. 2024. "A Study on the Effect of Toroidal Propeller Parameters on Efficiency and Thrust" Energies 17, no. 23: 5938. https://doi.org/10.3390/en17235938
APA StyleWu, J., Wang, Q., Deasy, H., & Hang, J. (2024). A Study on the Effect of Toroidal Propeller Parameters on Efficiency and Thrust. Energies, 17(23), 5938. https://doi.org/10.3390/en17235938






